1 Introduction

In recent years, magnetic bearings have become more and more widespread in many industrial applications such as flywheels, satellites and high-speed turbines. According to the principle of producing suspension forces, we can classify magnetic bearings as passive [1], active [2] or hybrid. Among these, hybrid magnetic bearings (HMBs) have attracted attention because the control current of HMBs can be reduced considerably and decreased control current leads to low power loss [3]. However, the dynamics of HMBs has severe nonlinearities such that control of the given system is not easy. In other words, the inherently unstable dynamics of the HMBs, which are associated with the complexity of the rotor dynamics, makes it impossible to operate the concerned system without proper feedback control. This is the reason why various control approaches for HMBs have not been thoroughly researched.

In contrast to HMBs, there have been many studies on control of the passive/active magnetic bearing, such as sliding mode control [4], adaptive control [5], feedback linearization [6], fault-tolerant control [7] and decoupled control [8]. In particular, [9] dealt with robust control for the active magnetic bearing by using the Takagi–Sugeno (T–S) fuzzy model. The main advantage of fuzzy control is the ability to express a nonlinear system using a time-varying convex combination of linear state space models with nonlinear fuzzy membership functions. As a result, it is easy to apply the various control techniques to complex magnetic systems such as output feedback control, decentralized control, \(H_{\infty }\) control, etc. However, as we have already mentioned above, these approaches did not focus on the HMB plant, but on passive/active magnetic bearing systems, and thus it is necessary to re-establish the control algorithm for the HMBs.

During the past three years, some trials have sought to develop design and control methods for HMBs [3, 10–12]. [3] and [11] proposed various structural designs for HMBs and [12] showed dynamic behavior for blower applications. Also, dynamic decoupled control was established in [13] by using a neural network inverse method and the digital control approach was addressed in [10]. However, since their control approaches are based on linearized dynamics, these methods usually require complicated algorithms or are effective only in the limited small neighborhood of the nominal equilibrium point. Moreover, these approaches do not consider robust stabilization problems which are key topics in the study of magnetic bearings. In order to minimize the influence of such problems, it is necessary to develop a novel control algorithm for HMBs.

Motivated by the above observations, this paper presents a novel robust control method for stabilizing the HMBs. To achieve robust stability, we address the parametric uncertainties of the concerned system in the form of the norm-bounded. In other words, we derive robust control methodologies of the HMBs preserving the property and structure of the uncertainties. Also, the principles of the nonparallel distributed compensation (non-PDC) control laws and the parameter-dependent Lyapunov function (PDLF) are extended to the uncertain fuzzy control system. Using these approaches, it is possible to improve the robust stability and stabilization conditions of a given system. Its constructive conditions are provided in linear matrix inequality (LMI) format and therefore are tractable using convex optimization techniques. Finally, the obtained LMIs are applied to the HMBs constructed using the T–S fuzzy model.

This paper is organized as follows: Sect. 2 deals with the T–S fuzzy control scheme via the nonlinear aspect. The robust control methodology based on non-PDC controller is proposed in Sect. 3. The fuzzy modeling of the HMBs and robust simulation results are demonstrated in Sect. 4. This paper is concluded in Sect. 5.

2 Preliminaries

Consider the following nonlinear system

$$\begin{aligned} \dot{x}(t) = f\left( x(t),u(t)\right) \end{aligned}$$
(1)

where \(x(t)\in {\mathbb {R}}^{n}\) constitutes the state vector and \(u(t)\in {\mathbb {R}}^{m}\) is the control input. Define compact sets for x(t) and u(t) as follows:

$$\begin{aligned} {\mathcal {B}}_x= & {} \{x ~|~ \Vert x(t)\Vert \le \Delta _x \} \subset {\mathbb {R}}^n, \\ {\mathcal {B}}_u= & {} \{u ~|~ \Vert u(t)\Vert \le \Delta _u \} \subset {\mathbb {R}}^m \end{aligned}$$

for some \(\Delta _x \in {\mathbb {R}}_{> 0}\) and \(\Delta _u \in \mathbb {R}_{> 0}\).

Then, it is supposed that (1) can be modeled as the T–S fuzzy model

$$\begin{aligned}&R_{i}\text {: }\text {If } z_{1}(t)\text { is }\varGamma _{i1} \text { and }\ldots \text { and } z_{p}(t)\text { is } \varGamma _{ip}\nonumber \\ \text {then }\dot{x}(t)&=(A_{i}+\Delta A_{i})x(t) \nonumber \\&\quad +(B_{i}+\Delta B_{i})u(t) \end{aligned}$$
(2)

where \(R_{i}\), \(i\in \mathcal {I}_{r}=\{1,2,\ldots ,r\}\), denotes the ith fuzzy rule, \(z_{h}(t)\), \(h\in \mathcal {I}_{p}=\{1,2,\ldots ,p\}\), is the hth premise variable, \(\varGamma _{ih}\), \((i,h)\in \mathcal {I}_{r}\times \mathcal {I}_{p}\), is the fuzzy set of \(z_{h}(t)\) in \(R_{i}\), \(A_{i}\) and \(B_{i}\) are known constant matrices with appropriate dimensions, and \(\Delta A_{i}\) and \(\Delta B_{i}\) are unknown matrices.

Using the singleton fuzzifier, product inference engine, and center-average defuzzification [14], (2) is inferred as

$$\begin{aligned} \dot{x}(t)&=\sum _{i=1}^{r}\theta _{i}(z(t))\left( (A_{i}+\Delta A_{i}\right) x(t)\nonumber \\&\quad +\left( B_{i}+\Delta B_{i})u(t)\right) \end{aligned}$$
(3)

where \(\theta _{i}(z(t)) = {w_{i}(z(t))}/ {\sum _{i=1}^{r}w_{i}(z(t))}\), \(w_{i}(z(t)) = \prod _{h=1}^{p} \mu _{\varGamma _{ih}}(z_{h}(t))\) and \(\mu _{\varGamma _{ih}}(z_{h}(t))\): \(U_{z_{h}(t)}\subset \mathbb {R}\rightarrow \mathbb {R}_{[0,1]}\) is the membership function of \(z_{h}(t)\) on the compact set \(U_{z_{h}(t)}\). Suppose that a fuzzy control for (1) is

$$\begin{aligned} R_{i}\text {: }&\text {If } z_{1}(t)\text { is } \varGamma _{i1} \text { and} \ldots \text { and } z_{p}(t) \text { is } \varGamma _{ip}\nonumber \\&\text {then }u(t)=K_ix(t). \end{aligned}$$
(4)

The defuzzified output is given by

$$\begin{aligned} u(t)=\sum _{i=1}^{r}\theta _{i}(z(t))K_i\left( \sum _{j=1}^{r} \theta _{j}(z(t))X_j\right) ^{-1}x(t) \end{aligned}$$
(5)

where \(u(t)\in \mathbb {R}^{m}\) is the control input and \(X_i\in \mathbb {R}^{n \times n}\) is a slack variable and is not necessarily symmetric.

For matrices \(X_i\), \(i\!\in \!\mathcal {I}_{r}\!=\!\{1,2,\ldots ,r\}\), define \(X(x)=\sum ^r_{i=1}\theta _i(z(t))X_i\), \(X^{-1}(x)=\left( \sum ^r_{i=1}\theta _i(z(t))X_i\right) ^{-1}\) where \(x=x(t)\). Then, the closed-loop system is shown as follows:

$$\begin{aligned} \dot{x}&=\left( \left( A(x)+\Delta A(x)\right) +\left( B(x)+\Delta B(x)\right) \right. \nonumber \\&\quad \left. \times K(x)X^{-1}(x)\right) x. \end{aligned}$$
(6)

Remark 1

\(\Delta A(x)\) and \(\Delta B(x)\) are unknown matrices with appropriate dimensions that represent the system uncertainties. In this paper, we assume that \(\Delta A(x)\) and \(\Delta B(x)\) can be described as follows:

$$\begin{aligned} \begin{bmatrix} \Delta A(x)&\Delta B(x) \end{bmatrix} =D(x)F(t) \begin{bmatrix} E_{1}&E_{2} \end{bmatrix} \end{aligned}$$
(7)

where D(x), \(E_{1}\), and \(E_{2}\) are known constant real matrices with appropriate dimensions, and F(t) is an unknown matrix function with Lebesgue measurable elements that satisfies \(F^{T}(t)F(t)\preceq I\).

Remark 2

The controller in 6 is not of the form of the general parallel distributed compensation (PDC), but of a more general form referred to non-PDC. These relaxed conditions and linear matrix inequality-based design methodologies are proposed in [15].

3 Robust fuzzy control approach based on a non-PDC controller

In this section, we present the robust control method for stabilizing the uncertain fuzzy system. To achieve the robust stability, we address the parametric uncertainties of the concerned system in the form of the norm-bounded. The principles of the non-PDC control laws presented in 6 are applied to an uncertain fuzzy control system. Using these approaches, it is possible to improve the robust stability and stabilization conditions of the given system. More precisely, when \(\Delta A(x)=\Delta B(x)=0\), the stabilization condition for the nominal T–S fuzzy system is given as follows:

Theorem 1

Consider that \(|\dot{h}_{\rho }| \le \phi _{\rho }\), where \(\phi _{\rho } \ge 0(\rho = 1, 2,\ldots ,r)\) are given scalars. The nominal T–S fuzzy system 6, which has no parametric uncertainties, is guaranteed to be asymptotically stable if matrices \(\Xi _i = \Xi _i^T\), \(\varGamma _i \succ 0\), \(H_i\), \(L_i\), \(N_i\), \(M_i\), \(X_i\) such that the following inequalities are satisfied:

$$\begin{aligned} \varGamma _{\rho }&- \varLambda _i \succ 0, \end{aligned}$$
(8)
$$\begin{aligned} \varTheta _{ij}&\prec 0, \end{aligned}$$
(9)

where \(\varTheta _{ij}\) is represented as 10 and \((i, j, \rho ) \in (\mathcal {I}_r \times \mathcal {I}_r \times \mathcal {I}_r)\), \(i < j\).

Proof

The proof processes are similar to Theorem 2 in [16] with the non-PDC controller.\(\square \)

$$\begin{aligned} \varTheta _{ij}&= \begin{bmatrix} \Sigma _{\rho =1}^r \phi _{\rho } (\varGamma _{\rho }-\Xi _i) + A_iH_j^T + H_jA_i^T - B_iM_j^T - M_jB_i^T&*&* \\ \varGamma _i - H_j^T + L_jA_i^T - N_jB_i^T&-L_j-L_j^T&* \\ M_j^T - X_jB_i^T&N_j^T&X_j + X_j^T -I \end{bmatrix}, \end{aligned}$$
(10)
$$\begin{aligned} \varOmega _{ij}&= \begin{bmatrix} \left( \begin{matrix} -\sum _{\rho =1}^r \dot{\theta _{\rho }} \left( \dot{\varGamma }_{\rho } + \varLambda _i\right) + A_iH_j^T \\ + H_jA_i^T + B_iK_j + K_j^T B_i^T \end{matrix} \right)&*&*&* \\ \varGamma _i - H_j^T + L_jA_i^T&- L_j - L_j^T&*&* \\ E_{1i}H_j^T + E_{2i} K_j&0&-\epsilon _{ij} I&* \\ D_i^T&0&0&-\epsilon _{ij} I \end{bmatrix}. \end{aligned}$$
(11)

As shown in Theorem 1, there have been numerous research works [16–19] focusing on the design of the robust fuzzy controller using various methods. However, non-PDC-based fuzzy control approaches for an uncertain system have not been sufficiently achieved. Although Ref. [19] tried to address this problem, it did not consider the PDLF problem, but rather the general Lyapunov function. The drawback of [19] is the limited stabilization region such that it is not easy to obtain the proper control gain using 5. In order to solve this problem, we consider the following Lemmas which will be used in the proof of our main results.

Lemma 1

[20] The following two problems are equivalent:

  1. (i)

    Find \(P \succ 0\) such that

    $$\begin{aligned} T+PA^T+AP <0 \end{aligned}$$
  2. (ii)

    Find \(P \succ 0\), L and H such that

    $$\begin{aligned} \begin{bmatrix} T+ & {} HA^T + AH^T&* \\ P- & {} H^T+LA^T&-L-L^T \end{bmatrix}. \end{aligned}$$

Lemma 2

[21] For any real matrices \(\varLambda _{1}=\varLambda _{1}^{T}\), \(\varLambda _{2}\), \(\varLambda _{3}(x)\), and \(\varLambda _{4}\) with appropriate dimensions, the following inequality holds:

$$\begin{aligned} \varLambda _{1}+\varLambda _{2}\varLambda _{3}(x)\varLambda _{4} +\varLambda _{4}^{T}\varLambda _{3}^{T}(x)\varLambda _{2}^{T} \prec 0 \end{aligned}$$

where \(\varLambda _{3}(x)\) satisfies \(\varLambda _{3}(x)^{T}\varLambda _{3}(x) \preceq I\) if and only if

$$\begin{aligned} \varLambda _{1}+ \begin{bmatrix} \epsilon ^{-1}\varLambda _{4}\\ \epsilon \varLambda _{2}^{T} \end{bmatrix}^{T} \begin{bmatrix} \epsilon ^{-1}\varLambda _{4}\\ \epsilon \varLambda _{2}^{T} \end{bmatrix} \prec 0 \end{aligned}$$

for some \( \epsilon >0\).

Lemma 3

[20] The following two problems are equivalent:

  1. (i)

    Find \(P=P^T\) such that

    $$\begin{aligned} \begin{bmatrix} T_1 + A^TPA&* \\ T_2&T_3 \end{bmatrix} \end{aligned}$$
  2. (ii)

    Find \(P=P^T\), \(L_1\), \(L_2\) and H such that

    $$\begin{aligned} \begin{bmatrix} T_1 + A^TL_1^T + L_1A&*&*\\ T_2 +L_2A&T_3&* \\ -L_1^T + H^TA&-L_2^T&P-H-H^T \end{bmatrix} \end{aligned}$$

The main results are summarized as follows:

Theorem 2

Consider that \(|\dot{h}_{\rho }| \le \phi _{\rho }\), where \(\phi _{\rho } \ge 0(\rho = 1, 2,\ldots ,r)\) are given scalars. The nominal T–S fuzzy system 6, which has the parametric uncertain terms \(\Delta A(x)\) and \(\Delta B(x)\), is guaranteed to be asymptotically stable if matrices \(\varLambda _i = \varLambda _i^T\), \(\varGamma _i \succ 0\), \(H_i\), \(L_i\), \(N_i\), \(M_i\), \(X_i\) exist such that the following inequalities are satisfied:

$$\begin{aligned}&\varGamma _{\rho } - \varLambda _i \succ 0, \\&\varOmega _{ii} \prec \varPsi _{ii}, \\&\varOmega _{ij} + \varOmega _{ji} \preceq \varPsi _{ij} + \varPsi _{ji}^T,\\&\varPsi \prec 0 \end{aligned}$$

where \(\varOmega _{ij}\) is shown as 11 for \((i, j, \rho ) \in (\mathcal {I}_r \times \mathcal {I}_r \times \mathcal {I}_r)\), \(i < j\) and

$$\begin{aligned} \varPsi = \begin{bmatrix} \varPsi _{11}&*&\cdots&* \\ \varPsi _{21}&\varPsi _{22}&\cdots&* \\ \vdots&\vdots&\ddots&\vdots \\ \varPsi _{r1}&\varPsi _{r2}&\cdots&\varPsi _{rr} \end{bmatrix}. \end{aligned}$$

Proof

Consider the following PDLFs [20]:

$$\begin{aligned} V(x)=x^{T}\varGamma ^{-1}(x)x. \end{aligned}$$
(12)

From 5 and 6, we have the PDLF candidate as follows:

$$\begin{aligned} \dot{V}(x)&=\dot{x}^T \varGamma ^{-1}(x)x + x^T \varGamma ^{-1}(x) \dot{x}\nonumber \\&\quad - x^T \varGamma ^{-1}(x) \dot{\varGamma }(x) \varGamma ^{-1}(x) x \nonumber \\&= x^T\varGamma ^{-1}(x)\Big \{ (A(x) + \Delta A(x)) \nonumber \\&\quad +(B(x) + \Delta B(x))K(x)\varGamma ^{-1}(x)\Big \}x \nonumber \\&\quad +x^T\Big \{ (A(x) + \Delta A(x)) + (B(x) + \Delta B(x))K(x)\nonumber \\&\quad \times \varGamma ^{-1}(x)\Big \}^T \varGamma ^{-1}(x)x - x^T \varGamma ^{-1}(x)\dot{\varGamma }(x) \varGamma ^{-1}(x)x \nonumber \\&=\bar{x}^T \Big \{\big [(A(x) + \Delta A(x))\varGamma (x) + \varGamma (x)(A(x)\nonumber \\&\quad +\Delta A(x))^T + (B(x) + \Delta B(x))K(x) \nonumber \\&\quad + K(x)^T(B(x) + \Delta B(x))^T\big ] - \dot{\varGamma }(x)\Big \}\bar{x} \end{aligned}$$
(13)

where \(\bar{x} = \varGamma ^{-1}(x)x\). An Eq. 13 is verified if

$$\begin{aligned}&(A(x) + \Delta A(x))\varGamma (x) + \varGamma (x)(A(x) + \Delta A(x))^T\nonumber \\&\quad +(B(x) \!+\! \Delta B(x))K(x) \!+\! K(x)^T(B(x) \!+\! \Delta B(x))^T \nonumber \\&\quad - \dot{\varGamma }(x) + \varLambda (x) < 0 \end{aligned}$$
(14)

where \(\varLambda (x) = \varLambda (x)^T \in \mathbb {R}^{n \times n}, i\in \mathcal {I}_{r}=\{1,2,\ldots ,r\}\) are arbitrary matrices. Let \(T=(B(x) + \Delta B(x))K(x) + K(x)^T(B(x) + \Delta B(x))^T - \dot{\varGamma }(x) + \varLambda (x)\), \(P=\varGamma (x)\) and use Lemma 1 so that we have

$$\begin{aligned}&\varPhi (x) + \left[ \begin{array}{cc} \begin{array}{c} \Delta A(x)H(x)^T + H(x)\Delta A(x)^T \\ + \Delta B(x)K(x) + K(x)^T\Delta B(x)^T \end{array} &{} * \\ 0 &{} 0 \end{array}\right] \prec 0 \end{aligned}$$
(15)

where \(\varPhi (x)\) is shown as (16). By Lemma 2, the above inequality holds for all F(t) satisfying \(F(t)^TF(t) \preceq I\) if and only if there exists a constant \(\epsilon ^{\frac{1}{2}} >0 \) such that

$$\begin{aligned}&\varPhi (x) + \begin{bmatrix} \epsilon ^{-\frac{1}{2}}\left( E_{1}H(x)^T + E_{2}K(x)\right) ^T&\epsilon ^{\frac{1}{2}}D(x)\end{bmatrix} \nonumber \\&\qquad \times \begin{bmatrix} \epsilon ^{-\frac{1}{2}}\left( E_{1}H(x)^T + E_{2}K(x)\right) \\ \epsilon ^{\frac{1}{2}}D(x)^T \end{bmatrix} \nonumber \\&= \varPhi (x) + \begin{bmatrix} \left( E_{1}H(x)^T + E_{2}K(x)\right) ^T&D(x) \end{bmatrix} \nonumber \\&\qquad \times \begin{bmatrix} \epsilon ^{-1}I&0 \\ 0&\epsilon I \end{bmatrix} \begin{bmatrix} E_{1}H(x)^T + E_{2}K(x) \\ D(x)^T \end{bmatrix} \prec 0. \end{aligned}$$
(16)

Applying Lemmas 3 to 17 results in 18 which is equivalent to 19.

To achieve the generality of LMI formats, we reconsider Eq. 19 in the following forms:

$$\begin{aligned} (19)&\Leftrightarrow \sum _{i=1}^r \sum _{j=1}^r \theta _i\theta _j\Xi _{ij} \nonumber \\&\preceq \sum _{i=1}^r \sum _{j=1}^r \theta _i\theta _j \varOmega _{ij}\nonumber \\&= \sum _{i=1}^r \theta _i^2 \varOmega _{ii} + \sum _{i=1}^r \sum _{i<j}^r \theta _i\theta _j (\varOmega _{ij}+\varOmega _{ji}) \nonumber \\&\preceq \sum _{i=1}^r \sum _{j=1}^r \theta _i\theta _j \varPsi _{ij}\nonumber \\&= \sum _{i=1}^r \theta _i^2 \varPsi _{ii} + \sum _{i=1}^r \sum _{i<j}^r \theta _i\theta _j (\varPsi _{ij}+\varPsi _{ji}) \nonumber \\&= \begin{bmatrix} \theta _1 I \\ \theta _2 I \\ \vdots \\ \theta _r I \end{bmatrix}^T \varPsi \begin{bmatrix} \theta _1 I \\ \theta _2 I \\ \vdots \\ \theta _r I \end{bmatrix} \prec 0. \end{aligned}$$
(17)
$$\begin{aligned} \varPhi (x)&= \begin{bmatrix} \left( \begin{matrix} A(x)H(x)^T + H(x)A(x)^T \\ + B(x)K(x) + K(x)^T B(x)^T - \dot{\varGamma }(x) + \varLambda (x) \end{matrix} \right)&* \\ \varGamma (x) - H(x)^T + L(x)A(x)^T&-L(x) - L(x)^T \end{bmatrix}, \end{aligned}$$
(18)
$$\begin{aligned}&\begin{bmatrix} \left( \begin{matrix} A(x) H(x)^T + H(x) A(x)^T + B(x) K(x) \\ &{}\quad + K(x)^T B(x)^T - \dot{\varGamma }(x) + \varLambda (x) \end{matrix} \right)&*&*&* \\ \varGamma (x) - H(x)^T + L(x) A(x)^T&- L(x) - L(x)^T&*&* \\ E_{1} H(x)^T + E_{2} K(x)&0&-\epsilon I&* \\ D(x)^T&0&0&-\epsilon I \end{bmatrix} \prec 0, \end{aligned}$$
(19)
$$\begin{aligned} \Xi (x)&= \begin{bmatrix} \left( \begin{matrix} -\sum _{\rho =1}^r \dot{\theta _{\rho }} (\dot{\varGamma }(x) \!+\! \varLambda (x)) \!+\! A(x) H(x)^T \\ &{}\quad + H(x)A(x)^T + B(x)K(x) + K(x)^T B(x)^T \end{matrix} \right)&*&*&* \\ \varGamma (x) - H(x)^T + L(x) A(x)^T&- L(x) - L(x)^T&*&* \\ E_{1}H(x)^T + E_{2} K(x)&0&-\epsilon I&* \\ D(x)^T&0&0&-\epsilon I \end{bmatrix} \prec 0. \end{aligned}$$
(20)

If \(\varPsi \prec 0\), it is possible to obtain asymptotical stability using the PDLF \(\dot{V}(x) \prec 0\). \(\square \)

Remark 1

This paper makes contributes to the magnetic research field of fuzzy control by considering: (1) the uncertainties in the HMB system ([6, 7, 10, 11, 13] did not consider the uncertainties); (2) the robust stabilization of the HMB system shown in Theorem 2 ([6, 7, 10, 11, 13] considers only stabilization without robustness); (3) Instead of the LMIs in Theorem 2, we can easily extend our discussion to stabilizing various magnetic systems such as passive and active magnetic bearings (the control methodology in [4, 5, 7, 9] is only applied to the concerned systems).

4 Simulation results

4.1 Fuzzy modeling of a HMBs with parametric uncertainty

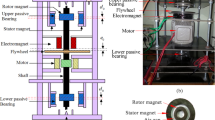
In this section, the HMBs and its fuzzy modeling are discussed. The magnetic flux path of the three-pole radial magnetic bearing is shown in Fig. 1 and an equivalent circuit of the HMBs, which is connected to the power transmission line, is presented in Fig. 2. The control objective of HMBs enables the rotor to rotate without any physical contact using magnetic forces. The dynamics of the concerned system can be presented as follows [13]:

$$\begin{aligned} \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix}&=\begin{bmatrix} -\frac{3}{2m}k_{xy}&-\frac{\sqrt{3}}{2m}k_{xy}&0\\ 0&0&0\\ 0&0&-\frac{2F_m^2 \delta _a \mu _0 S_a}{m \left( 2\delta _a^2 - x_3^2\right) ^2} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix} \nonumber \\&\quad +\begin{bmatrix} \frac{3}{2}k_{ir} \\ \frac{3}{2m}k_{ir} \\ -\frac{2F_m N_z \mu _0 S_a}{m \left( 2\delta _a^2 - x_3^2\right) }\end{bmatrix} u(t) \end{aligned}$$
(21)

where \(F_m\) is the magnetomotive force provided by the permanent magnet, \(N_r\) is the turns of each radial control coil, \(\mu _0\) is the permeability of the vacuum, \(S_a\) is the axial magnetic pole area, \(S_r\) is the radial magnetic pole area, \(\delta _a\) is the axial air gap length, \(\delta _r\) is the radial air gap length, \(k_{ir}\) is the radial force-current coefficient, and \(k_{xy}\) is the radial force-displacement coefficient.

Fig. 1
figure 1

Magnetic flux path of the three-pole radial magnetic bearing

Full size image
Fig. 2
figure 2

Equivalent magnetic circuit for the hybrid-type three-pole bearing

Full size image

Motivated by the above observations, we presume that the HMBs have nonlinear functions \(\frac{2F_m^2 \delta _a \mu _0 S_a}{m \left( 2\delta _a^2 - x_3^2\right) ^2}\) and \(\frac{2F_m N_z \mu _0 S_a}{m \left( 2\delta _a^2 - x_3^2\right) }\), which are related to the state equation. In order to construct the T–S fuzzy model for the HMBs, the nonlinear terms have to be represented as a convex combination of appropriate vertices. To solve this problem, the nonlinear functions should be linearized with respect to the input. The specified processes with operation point \(u^* =0\) are presented as follows:

$$\begin{aligned} f\left( x(t), u(t)\right)&\cong f(x(t), u^*) \!+\! \frac{\delta f(x(t), u(t))}{\delta u(t)}\mid _{u(t)=u^*} \nonumber \\&= \frac{2F_m^2 \delta _a \mu _0 S_a}{m} \Big ( \frac{1}{(2\delta _a^2 - x_3^2)^2} \Big )x_3 \nonumber \\&\quad + \frac{2F_m N_z \mu _0 S_a}{m} \Big (\frac{1}{(2\delta _a^2 - x_3^2)}\Big )u_3. \end{aligned}$$
(22)

We set the above Eq. 22 as

$$\begin{aligned} \sigma _1 := \frac{1}{\left( 2\delta _a^2 - x_3^2\right) ^2}, \quad \sigma _2 := \frac{1}{\left( 2\delta _a^2 - x_3^2\right) }. \end{aligned}$$
(23)

In order to represent the nonlinear terms with convex combinations of appropriate vertices together with the membership functions belonging to the unit simplex [9], we should calculate the minimum and maximum values of \(\sigma _1(t)\) and \(\sigma _2(t)\) under

$$\begin{aligned} x_3(t) \in \mathbb {C} = [-4.992,~~ 4.992] \times 10^{-3}. \end{aligned}$$
(24)

From 24, it is possible to calculate the minimum and maximum as \(\sigma _1(t) = [\underline{\sigma _1}, ~~\overline{\sigma _1}]\) and \(\sigma _2(t) = [\underline{\sigma _2}, ~~\overline{\sigma _2}]\) such that we obtain the following fuzzy relationships of these terms:

$$\begin{aligned} \sigma _1(t)&= \underline{\sigma _1}\varGamma _1^1(\sigma _1(t)) + \overline{\sigma _1}\varGamma _1^2(\sigma _1(t)), \nonumber \\ \sigma _2(t)&= \underline{\sigma _2}\varGamma _2^1(\sigma _2(t)) + \overline{\sigma _2}\varGamma _2^2(\sigma _2(t)) \end{aligned}$$
(25)

where \(\varGamma _1^1(\sigma _1(t)) + \varGamma _1^2(\sigma _1(t))=1\) and \(\varGamma _2^1(\sigma _2(t)) + \varGamma _2^2(\sigma _2(t))=1\). The membership functions are easy to calculate as

$$\begin{aligned}&\varGamma _1^1(\sigma _1(t)) = \frac{\sigma _1(t)-\overline{\sigma _1}}{\overline{\sigma _1}-\underline{\sigma _1}}, \quad \varGamma _1^2(\sigma _1(t)) = \frac{-\sigma _1(t)+\underline{\sigma _1}}{\overline{\sigma _1}-\underline{\sigma _1}}, \\&\varGamma _2^1(\sigma _2(t)) = \frac{\sigma _2(t)-\overline{\sigma _2}}{\overline{\sigma _2}-\underline{\sigma _2}}, \quad \varGamma _2^2(\sigma _2(t)) = \frac{-\sigma _2(t)+\underline{\sigma _2}}{\overline{\sigma _2}-\underline{\sigma _2}}. \end{aligned}$$

Denote \(x^T = [x_1 \quad x_2 \quad x_3]^T\), then the identified T–S fuzzy rules of the HMBs are represented as follows:

$$\begin{aligned} R^{1}\text {: }&\text {IF }x_{1}(t)\text { is }\varGamma _{1}^1\text { and IF } x_{2}(t)\text { is }\varGamma _{2}^1, \\&\text {THEN~}\dot{x}(t) =A_{1}x(t)+B_1 u(t)\\ R^{2}\text {: }&\text {IF }x_{1}(t) \text { is }\varGamma _{1}^2\text { and IF } x_{2}(t)\text { is } \varGamma _{2}^1, \\&\text {THEN~}\dot{x}(t) =A_{2}x(t)+B_2 u(t)\\ R^{3}\text {: }&\text {IF }x_{1}(t)\text { is }\varGamma _{1}^1 \text { and IF } x_{2}(t) \text { is }\varGamma _{2}^2, \\&\text {THEN~}\dot{x}(t) =A_{3}x(t)+B_3 u(t)\\ R^{4}\text {: }&\text {IF } x_{1}(t)\text { is }\varGamma _{1}^2 \text { and IF }x_{2}(t) \text { is }\varGamma _{2}^2, \\&\text {THEN~}\dot{x}(t) =A_{4}x(t)+B_4 u(t) \end{aligned}$$

where

$$\begin{aligned} A_1= & {} A_2 = \begin{bmatrix} -\frac{3}{2m}k_{xy}&-\frac{\sqrt{3}}{2m}k_{xy}&0\\ 0&0&0\\ 0&0&-\frac{2F_m^2 \delta _a \mu _0 S_a}{m} \underline{\sigma _1} \end{bmatrix}, \\ A_3= & {} A_4 = \begin{bmatrix} -\frac{3}{2m}k_{xy}&-\frac{\sqrt{3}}{2m}k_{xy}&0\\ 0&0&0\\ 0&0&-\frac{2F_m^2 \delta _a \mu _0 S_a}{m} \overline{\sigma _1} \end{bmatrix}, \\ B_1= & {} B_3 = \begin{bmatrix} \frac{3}{2}k_{ir} \\ \frac{3}{2m}k_{ir} \\ -\frac{2F_m N_z \mu _0 S_a}{m}\underline{\sigma _2}\end{bmatrix},\\ B_2= & {} B_4 = \begin{bmatrix} \frac{3}{2}k_{ir} \\ \frac{3}{2m}k_{ir} \\ -\frac{2F_m N_z \mu _0 S_a}{m}\overline{\sigma _2}\end{bmatrix}. \end{aligned}$$

4.2 Simulation results for HMBs

To show the effectiveness of the proposed method, the simulation results for HMBs are presented. Table 1 shows the specific system data for the HMBs.

Table 1 Nominal parameters of the HMBs
Full size table

The initial condition of the concerned system is given by \(x(0) = \begin{bmatrix}1&1&1\end{bmatrix}^\top \). During the simulation, all system parameters are randomly varied within the bounds of 5 % of their nominal values so that the uncertain matrices \( \Delta A(x) = D(x)F(t)E_{1}\) and \(\Delta B(x) = D(x)F(t)E_{2}\) are given by

$$\begin{aligned} D(x)= & {} \begin{bmatrix} 0.05&0&0 \\ 0&0.05&0 \\ 0&0&0.05 \end{bmatrix}, E_{1} = \begin{bmatrix} a&b&0 \\ 0&0&0 \\ 0&0&c \end{bmatrix},\\ E_{2}= & {} \begin{bmatrix} ~1~ \\ ~1~ \\ ~0~\end{bmatrix}. \end{aligned}$$

Applying Theorem 2 yields the total fuzzy system control gain matrices

$$\begin{aligned}&K_1= \begin{bmatrix} 1.2353&-2.2514&-3.5521 \end{bmatrix}, \\&K_2= \begin{bmatrix} 3.0460&-42.5685&-2.9811 \end{bmatrix},\\&K_3= \begin{bmatrix} 1.2402&-2.1424&-3.9821 \end{bmatrix}, \\&K_4= \begin{bmatrix} 3.1001&-2.5024&-3.0026 \end{bmatrix}. \end{aligned}$$

As shown in Figs. 3, 4 and 5, all system trajectories converge to zero, indicating that our method guarantees the robust stability of the controlled system despite the system uncertainties.

Fig. 3
figure 3

States of the controlled HMB system of \(x_1\) (5 % uncertain parameter case)

Full size image
Fig. 4
figure 4

States of the controlled HMB system of \(x_2\) (5 % uncertain parameter case)

Full size image
Fig. 5
figure 5

States of the controlled HMB system of \(x_3\) (5 % uncertain parameter case)

Full size image
Fig. 6
figure 6

States of the controlled HMB system of \(x_1\) (15 % uncertain parameter case)

Full size image
Fig. 7
figure 7

States of the controlled HMB system of \(x_2\) (15 % uncertain parameter case)

Full size image
Fig. 8
figure 8

States of the controlled HMB system of \(x_3\) (15 % uncertain parameter case)

Full size image

In order to analyze the influence of the uncertainties, we set the variation of all system parameters to 15 % of their nominal values. That is, the uncertain matrices \( \Delta A(x) = D(x)F(t)E_{1}\) and \(\Delta B(x) = D(x)F(t)E_{2}\) are given by

$$\begin{aligned} D(x)= & {} \begin{bmatrix} 0.15&0&0 \\ 0&0.15&0 \\ 0&0&0.15 \end{bmatrix}, E_{1} = \begin{bmatrix} a&0&0 \\ 0&b&0 \\ 0&0&c \end{bmatrix},\\ E_{2}= & {} \begin{bmatrix} ~0~ \\ ~0~ \\ ~1~\end{bmatrix}. \end{aligned}$$

Utilizing Theorem 2 yields the total fuzzy system control gain matrices as follows:

$$\begin{aligned}&K_1= \begin{bmatrix} 0.0153&-0.0501&-0.2269 \end{bmatrix}, \\&K_2= \begin{bmatrix} 0.0142&-0.0516&-0.3242 \end{bmatrix}, \\&K_3= \begin{bmatrix} 0.0152&-0.0508&-0.2113 \end{bmatrix}, \\&K_4= \begin{bmatrix} 0.0137&-0.0499&-0.3243 \end{bmatrix}. \end{aligned}$$

The simulation results with larger uncertainties are shown in Figs. 6, 7 and 8. As shown in these figures, the proposed method is quite successful even in the presence of larger parametric uncertainties for complex nonlinear systems.

5 Conclusion

This paper has presented a novel robust fuzzy control method for stabilizing the HMBs, which is composed of an uncertain nonlinear system. We have investigated the parametric uncertainties of the concerned system based on the T–S fuzzy model and have achieved robust stability. Utilizing non-PDC control law and PDLF, we have achieved a more relaxed stabilization condition than that obtained using other robust fuzzy controllers. The conditions for robust stabilizing controller designs have been given in terms of solutions to a set of LMI. The simulation results for the HMBs have demonstrated the feasibility of the proposed method.