Hopf bifurcation analysis of coupled two-neuron system with discrete and distributed delays

Abstract

We study the stability and Hopf bifurcation analysis of a coupled two-neuron system involving both discrete and distributed delays. First, we analyze stability of equilibrium point. Choosing delay term as a bifurcation parameter, we also show that Hopf bifurcation occurs under some conditions when the bifurcation parameter passes through a critical value. Moreover, some properties of the bifurcating periodic solutions are determined by using the center manifold theorem and the normal form theory. Finally, numerical examples are provided to support our theoretical results.

1 Introduction

In recent years, researchers in the field of recurrent neural networks (RNNs) have been increasing due to their applications to signal processing, pattern recognition, associative memories, optimization and other fields (see, e.g., [3, 5, 6, 9, 19, 21, 25, 26, 30, 31] and references therein). In 1984, Hopfield [10] described a new neural network model which is capable of performing computational tasks using energy function. Following this pioneer study, due to the transmission of signals in a network, time delays have been incorporated into neural network models by many researchers [1, 2, 15, 16].

In biological neural networks, it is well known that time delay may force a stable system to oscillate (see [31] for a detailed reference list). It is also known that time delay is one of the main sources to lead instability. For example, for biological neurons, it has been observed that autapses (a specific synapse which connects to its dendrite) which include time delays can affect the dynamical behavior of systems [18, 24]. In practical applications, because of finite time of the switching and transmission of signals, time delays are indispensable in the artificial neural networks which underlines that the history influences the present. Since delays may cause oscillation or chaos, effects of time delays have been investigated in neural network models, in particular in RNNs, intensively. RNNs which generate chaotic dynamics can be used to model oscillations in the cortex and to control chaotic dynamical systems [27].

In 1994, Baldi and Atiya [2] studied a network that consists of different delays between the adjacent neurons. Following this work, neural networks including multiple delays have become popular [4, 7, 17, 20, 22, 25, 28]. Also, instead of considering discrete time delays, researchers have incorporated time delays which are continuously distributed over an infinite interval reflecting the fact that the distant past has less influence compared to the most recent neurons’ states on the current states of system. Actually, since a distributed delay becomes a discrete delay when the delay kernel is a Dirac delta function at a certain time, infinite time delay is more general [13, 23, 29]. We refer to [3, 11, 12, 14, 20, 32] and the references therein for related work on networks including distributed delays.

For the motivation of the model, let us first look at the following two-neuron system consisting of discrete time delays that was studied by Guo et al. [17]:

$$\begin{aligned} \begin{aligned} u_{1}^{^{\prime }}(t)&=- u_{1}(t)+ a_{11} f(u_{1}(t-\tau _{1}))\\&\quad + a_{12} f(u_{2}(t-\tau _{2})), \\ u_{2}^{^{\prime }}(t)&=- u_{2}(t)+ a_{21} f(u_{1}(t-\tau _{1})) \\&\quad + a_{22} f(u_{2}(t-\tau _{2})). \end{aligned} \end{aligned}$$

(1)

The authors studied several cases, including $\tau _{1}=\tau _{2}$, $a_{11}=a_{22}$. They found that system (1) undergoes a Hopf bifurcation at certain values of delay.

Recently, Li and Hu [14] studied the following system of differential equations with multiple delays:

$$\begin{aligned} \begin{aligned} x_{1}^{^{\prime }}(t)&=- x_{1}(t)+a_{11} f\left( \int _{-\infty }^{t} F(t-s)x_{1}(s)\hbox {d}s\right) \\&\quad +\,a_{12} f(x_{2}(t-\tau )), \\ x_{2}^{^{\prime }}(t)&=- x_{2}(t)+a_{21} f(x_{1}(t-\tau )) \\&\quad +\,a_{22} f\left( \int _{-\infty }^{t} F(t-s)x_{2}(s)\hbox {d}s\right) . \end{aligned} \end{aligned}$$

(2)

First, they investigated the stability of the zero equilibrium using Routh–Hurwitz criterion when delay term $\tau =0$. And then taking discrete delay term $\tau$ as a bifurcation parameter, they showed the existence of local Hopf bifurcation using Hopf bifurcation theorem.

In this paper, we focus on periodic solutions of a system of two neurons involving multiple discrete and distributed delays. The system we consider has self-feedback terms with distributed time delays as in system (2), but the signals that neurons send to each other is different, that is,

$$\begin{aligned} \begin{aligned} x_{1}^{^{\prime }}(t)&=- x_{1}(t)+a_{11} f_{11}\left( \int _{-\infty }^{t} F(t-s)x_{1}(s)\hbox {d}s\right) \\&\quad +a_{12} f_{12}(x_{2}(t-\tau _{2})), \\ x_{2}^{^{\prime }}(t)&=- x_{2}(t)+a_{21} f_{21}(x_{1}(t-\tau _{1})) \\&\quad +a_{22} f_{22}\left( \int _{-\infty }^{t} F(t-s)x_{2}(s)\hbox {d}s\right) , \end{aligned} \end{aligned}$$

(3)

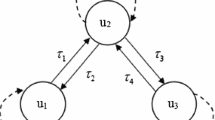
where $x_{i}^{^{\prime }}(t)=\frac{\hbox {d}x_{i}}{\hbox {d}t}$, $x_{i}(t)$ represents the state of the ith neuron at time t and $a_{ij}$ ($i=1,2$ and $j=1,2$) are real constants. Here, $F(\cdot )$ is nonnegative bounded delay kernel defined on $[0,\infty )$ which reflects the influence of the past states on the current dynamics. System (3) is reduced to system (2) if $f_{ij}=f$ ($i=1,2$ and $j=1,2$) and $\tau _{1}=\tau _{2}$. Similarly, it is reduced to system (1) when the delay kernel is taken as Dirac delta function and $f_{ij}=\hbox {tan}h$. Therefore, system (3) that we are interested in is more general than systems (1) and (2). The architecture of system (3) is illustrated in Fig. 1.

Fig. 1

Architecture of the model (3). Two neurons send signals to each other with a discrete delay (solid line), $\tau _{j}$, $j=1,2$. One element receives one delayed input from itself with distributed delay which is denoted by dashed line

This paper is organized as follows. In Sect. 2, we study the stability of the zero solution when $\tau _{1}=0$ and $\tau _{2}=0$. Following it, regarding $\tau =\tau _{1}+\tau _{2}$ as a bifurcation parameter the dynamical behavior near Hopf bifurcation is investigated using Hopf bifurcation theorem. In Sect. 3, the direction of Hopf bifurcation and the stability and period of bifurcating periodic solutions on the center manifold are determined applying the normal form theory in [8]. Finally, in Sect. 4, we consider an example and simulate it by using MATLAB to support our theoretical results.

2 Stability analysis and Hopf bifurcation

In this section, we consider only the weak kernel, that is,

$$\begin{aligned} F(s)=\alpha \hbox {e}^{-\alpha s}, \end{aligned}$$

where $\alpha >0$, and $1/ \alpha$ reflects the mean delay of the weak kernel. In order not to affect the equilibrium values, we normalize the kernel satisfying the normalization condition $\int _{0}^{\infty } F(s)\hbox {d}s=1$. Now, it is necessary to make the following assumptions:

$(H_{1})$ :

$f_{ij}\in C^{3}, \quad f_{ij}(0)=0,\quad (i=1,2 \text{ and } j=1,2),$

$(H_{2})$ :

$\tau =\tau _{1}+\tau _{2}$.

For convenience, we define new variables as follows:

$$\begin{aligned} \begin{aligned} x_{3}(t)=\int _{-\infty }^{t} F(t-s)x_{1}(s)\hbox {d}s,\\ x_{4}(t)=\int _{-\infty }^{t} F(t-s)x_{2}(s)\hbox {d}s. \end{aligned} \end{aligned}$$

Applying the linear chain trick technique, system (3) can be transformed into the following system:

$$\begin{aligned} \begin{aligned} x_{1}^{^{\prime }}(t)&=- x_{1}(t)+a_{11} f_{11}(x_{3}(t))\\&\quad +a_{12} f_{12}(x_{2}(t-\tau _{2})), \\ x_{2}^{^{\prime }}(t)&=- x_{2}(t)+a_{21} f_{21}(x_{1}(t-\tau _{1}))\\&\quad +a_{22} f_{22}(x_{4}(t)), \\ x_{3}^{^{\prime }}(t)&=- \alpha x_{3}(t)+\alpha x_{1}(t), \\ x_{4}^{^{\prime }}(t)&=- \alpha x_{4}(t)+\alpha x_{2}(t). \end{aligned} \end{aligned}$$

(4)

By the hypothesis $H_{1}$, it is easy to see that the origin (0, 0, 0, 0) is an equilibrium point of system (4). Let us define $u_{1}(t)=x_{1}(t-\tau _{1})$, $u_{2}(t)=x_{2}(t)$, $u_{3}(t)=x_{3}(t-\tau _{1})$, $u_{4}(t)=x_{4}(t)$. Now using these new variables together with the hypothesis $H_{2}$, system (4) can be rewritten as the following equivalent system:

$$\begin{aligned} \begin{aligned} u_{1}^{^{\prime }}(t)&=- u_{1}(t)+a_{11} f_{11}(u_{3}(t))+a_{12} f_{12}(u_{2}(t-\tau )), \\ u_{2}^{^{\prime }}(t)&=- u_{2}(t)+a_{21} f_{21}(u_{1}(t)) +a_{22} f_{22}(u_{4}(t)), \\ u_{3}^{^{\prime }}(t)&=- \alpha u_{3}(t)+\alpha u_{1}(t), \\ u_{4}^{^{\prime }}(t)&=- \alpha u_{4}(t)+\alpha u_{2}(t). \end{aligned} \end{aligned}$$

(5)

Under the hypothesis $H_{1}$, the linearization of system (5) at (0, 0, 0, 0) is

$$\begin{aligned} \begin{aligned} u_{1}^{^{\prime }}(t)&=- u_{1}(t)+\alpha _{11}u_{3}(t)+\alpha _{12} u_{2}(t-\tau ), \\ u_{2}^{^{\prime }}(t)&=- u_{2}(t)+\alpha _{21}u_{1}(t)+\alpha _{22} u_{4}(t), \\ u_{3}^{^{\prime }}(t)&=-\alpha u_{3}(t)+\alpha u_{1}(t), \\ u_{4}^{^{\prime }}(t)&=-\alpha u_{4}(t)+\alpha u_{2}(t), \end{aligned} \end{aligned}$$

(6)

where $\alpha _{ij}=a_{ij} \left. \dfrac{\hbox {d}f_{ij}}{\hbox {d}u_{i}} \right| _{u_{i}=0}$, $(i=1,2 \text{ and } j=1,2)$. The corresponding characteristic equation of (6) is

$$\begin{aligned}&\lambda ^{4}+a_{3}\lambda ^{3}+a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}\nonumber \\&\quad +\,(b_{2}\lambda ^{2}+b_{1}\lambda +b_{0})\hbox {e}^{-\lambda \tau }=0, \end{aligned}$$

(7)

where

$$\begin{aligned} \begin{aligned} a_{3}&= 2\alpha +2\\ a_{2}&= \alpha ^{2}+4\alpha +1-\alpha (\alpha _{11}+\alpha _{22})\\ a_{1}&= 2\alpha ^{2}+2\alpha -\alpha (\alpha _{11}+ \alpha _{22})-\alpha ^{2}(\alpha _{11}+\alpha _{22})\\ a_{0}&= \alpha ^{2}-\alpha ^{2}(\alpha _{11}+\alpha _{22})+\alpha ^{2}\alpha _{11}\alpha _{22}\\ b_{2}&= -\alpha _{12} \alpha _{21} \\ b_{1}&= -2\alpha \alpha _{12} \alpha _{21}\\ b_{0}&= - \alpha ^{2} \alpha _{12} \alpha _{21}. \end{aligned} \end{aligned}$$

(8)

If $\tau =0$, that is, when there is no discrete time delay, Eq. (7) will be

$$\begin{aligned}&\lambda ^{4}+a_{3}\lambda ^{3}+(a_{2}+b_{2})\lambda ^{2}\nonumber \\&\quad +\,(a_{1}+b_{1})\lambda +(a_{0}+b_{0})=0. \end{aligned}$$

(9)

Now, it is necessary to investigate the distribution of roots of Eq. (9) in order to determine the stability of the origin. Using Routh–Hurwitz criteria for $n=4$, all roots of the polynomial (9) are negative or have negative real parts if and only if the following conditions hold:

• 1. $a_{3}>0$,

• 2. $a_{0}+b_{0}>0$,

• 3. $a_{1}+b_{1}>0$,

• 4. $a_{3}(a_{1}+b_{1})(a_{2}+b_{2})>(a_{1}+b_{1})^2+a_{3}^2(a_{0}+b_{0})$.

Now, let us take $\tau \ne 0$. We shall investigate the roots of the transcendental equation (7) that lie in the left half of the complex plane. Suppose that $\lambda =i \omega$ be a root of the characteristic equation (7) with $\omega >0$. Substituting this in Eq. (7) and separating real and imaginary parts yield the following equations:

$$\begin{aligned}&\omega ^{4}-a_{2}\omega ^{2}+a_{0}+(b_{0}-b_{2}\omega ^2)\cos \omega \tau \nonumber \\&\quad +\,b_{1}\omega \sin \omega \tau =0, \end{aligned}$$

(10)

$$\begin{aligned}&-\,a_{3}\omega ^{3}+a_{1}\omega +b_{1}\omega \cos \omega \tau \nonumber \\&\quad +\,(b_{2}\omega ^2-b_{0})\sin \omega \tau =0. \end{aligned}$$

(11)

By taking square of (10) and (11) and then adding them up, one obtains

$$\begin{aligned} \omega ^{8}+p \omega ^{6}+q \omega ^{4}+r\omega ^{2}+s=0, \end{aligned}$$

(12)

where $p=-2a_{2}+a_{3}^{2}$, $q=2a_{0}+a_{2}^{2}-2a_{1}a_{3}-b_{2}^{2}$, $r=-2a_{0}a_{2}+a_{1}^{2}+2b_{0}b_{2}-b_{1}^{2}$ and $s=a_{0}^{2}-b_{0}^{2}$. Setting $z=\omega ^{2}$, Eq. (12) can be written as follows:

$$\begin{aligned} z^{4}+p z^{3}+qz^{2}+rz+s=0. \end{aligned}$$

(13)

Let us denote Eq. (13) as

$$\begin{aligned} g(z)=z^{4}+p z^{3}+qz^{2}+rz+s. \end{aligned}$$

(14)

First, suppose that $s<0$. Since $\lim _{z \rightarrow \infty } g(z)=\infty$, Eq. (14) has at least one positive root, as well Eq. (12) . On the other hand, suppose now $s>0$. From Eq. (14), we have

$$\begin{aligned} \frac{\hbox {d}g(z)}{\hbox {d}z}=4z^{3}+3pz^{2}+2qz+r. \end{aligned}$$

(15)

Now, we need to find the roots of Eq. (15). Let us denote the right-hand side of it by $h(z)=4z^{3}+3pz^{2}+2qz+r$. By applying Cardano’s formula and using the transformation: $y=z+\frac{p}{4}$, we obtain the depressed cubic terms, that is,

$$\begin{aligned} y^{3}+3Qy-2R=0, \end{aligned}$$

(16)

where

$$\begin{aligned} Q&= \frac{8q-3p^{2}}{48}, \quad R&= \frac{4pq-8r-p^{3}}{64}. \end{aligned}$$

(17)

Let $y=u+v$, where $uv=-Q$. Then we can obtain the resolvent equation as follows:

$$\begin{aligned} u^{6}-2Ru^{3}-Q^{3}=0. \end{aligned}$$

(18)

Thus, we can write the roots of Eq. (16) as

$$\begin{aligned} y=\left\{ \begin{array}{lll} S+T, \\ -\frac{S+T}{2}+m(S-T),\\ -\frac{S+T}{2}-m(S-T), \end{array} \right. \end{aligned}$$

(19)

where

$$\begin{aligned} S= & {} \root 3 \of {R+\sqrt{\varDelta }},\nonumber \\ \quad T= & {} \root 3 \of {R-\sqrt{\varDelta }}, \end{aligned}$$

(20)

$$\begin{aligned} m= & {} \frac{i\sqrt{3}}{2},\nonumber \\ \quad \varDelta= & {} Q^{3}+R^{2}. \end{aligned}$$

(21)

Since $y=z+\frac{p}{4}$, the roots of Eq. (15) are obtained as

$$\begin{aligned} z_{1}= & {} S+T-\frac{p}{4}, \\ z_{2}= & {} -\frac{S+T}{2}+m(S-T)-\frac{p}{4}, \\ z_{3}= & {} -\frac{S+T}{2}-m(S-T)-\frac{p}{4}. \end{aligned}$$

Assume that $\varDelta >0$, from Cardano’s formula, we know that the equation $h(z)=0$ has only one real root $z_{1}^{*}=z_{1}$. If $\varDelta =0$, then the equation $h(z)=0$ has three real roots, namely $z_{1}$, $z_{2}$ and $z_{3}$ (at least two of them are equal) and we can define $z_{2}^{*}$ as $\max \{z_{1},z_{2},z_{3}\}$. If $\varDelta <0$, then all roots $z_{1}$, $z_{2}$ and $z_{3}$ of the equation $h(z)=0$ are real and distinct. In this case, assume that $z_{3}^{*}=\max \{z_{1},z_{2},z_{3}\}$. Now, we can give the following lemma without proof (see [14] for its proof).

Lemma 1

For Eq. (13), we have the followings:

• 1. If $s<0$, Eq. (13) has at least one positive root.

• 2. If $s\ge 0$, then Eq. (13) has no positive root if one of the following conditions holds: (a) $\varDelta >0$ and $z_{1}^{*}\le 0$; (b) $\varDelta =0$ and $z_{2}^{*}\le 0$; (c) $\varDelta <0$ and $z_{3}^{*}\le 0$.

• 3. If $s\ge 0$, then Eq. (13) has at least one positive root if one of the following conditions holds: (a) $\varDelta >0$, $z_{1}^{*}>0$ and $g(z_{1}^{*})<0$; (b) $\varDelta =0$, $z_{2}^{*}>0$ and $g(z_{2}^{*})<0$; (c) $\varDelta <0$, $z_{3}^{*}>0$ and $g(z_{3}^{*})<0$.

Suppose that Eq. (13) has positive roots. Without loss of generality, we can assume that it has four positive roots denoted by $z_{1}$, $z_{2}$, $z_{3}$ and $z_{4}$, respectively. Then, Eq. (12) has four positive roots $\omega _{1}=\sqrt{z_{1}}$, $\omega _{2}=\sqrt{z_{2}}$, $\omega _{3}=\sqrt{z_{3}}$ and $\omega _{4}=\sqrt{z_{4}}$. For $k=1,2,3,4$, there exists a sequence $\{\tau _{k}^{j}\left| j=1,2,3,\ldots \}\right.$ such that Eq. (7) holds. One can easily obtain

$$\begin{aligned} \tau _{k}^{(j)}= & {} \frac{1}{\omega _{k}} \Big \{\hbox {arccos} \left( \frac{c_{4} \omega ^{6}+c_{3}\omega ^{4}+c_{2}\omega ^{2}+c_{1}}{(b_{2}\omega ^{2}-b_{0})^{2}+b_{1}^{2}\omega ^{2}} \right) +\,2\pi j \Big \},\nonumber \\ \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned} c_{1}&= -a_{0}b_{0}\\ c_{2}&= a_{0}b_{2}+a_{2}b_{0}-a_{1}b_{1}\\ c_{3}&= a_{3}b_{1}-a_{2}b_{2}-b_{0}\\ c_{4}&= b_{2}. \end{aligned} \end{aligned}$$

Thus, $\pm i\omega _{k}$ is a pair of purely imaginary roots of Eq. (7) with $\tau =\tau _{k}^{(j)}$.

Define $\tau _{0}=\tau _{k_{0}}^{(0)}=\min \{\tau _{k}^{(0)}\left| k=1,2,3,4 \right\}$, $\omega _{0}=\omega _{k_{0}}$ and let $\lambda (\tau )=\alpha (\tau )+i\omega (\tau )$ be the root of Eq. (7) near $\tau =\tau _{0}$ satisfying $\alpha (\tau _{0})=0$, $\omega (\tau _{0})=\omega _{0}.$ Then we have the following transversality condition.

Lemma 2

Suppose that $z_{k}=\omega _{k}^{2}$ and $g^{\prime }(z_{k})\ne 0$, where g(z) is defined by (14). Then

$$\begin{aligned} \left[ \frac{\mathrm{d}(Re\lambda (\tau ))}{\mathrm{d}\tau } \right] _{\tau =\tau _{k}^{(j)}} \ne 0 \end{aligned}$$

(23)

and $\left[ (\mathrm{d}(\hbox {Re}\lambda (\tau ))/\mathrm{d}\tau ) \right] _{\tau =\tau _{k}^{(j)}}$ and $g^{\prime }(z_{k})$ have the same sign (see Lemma 4 in [32]).

The following main theorem summarize the results obtained on the stability and Hopf bifurcation of system (5).

Theorem 1

For system (5) the followings hold:

• (i) If $s\ge 0$ and one of the following conditions holds: (a) $\varDelta >0$ and $z_{1}^{*}\le 0$; (b) $\varDelta =0$ and $z_{2}^{*}\le 0$; (c) $\varDelta <0$ and $z_{3}^{*}\le 0$, then the equilibrium point (0, 0, 0, 0) of system (5) is asymptotically stable for all $\tau \ge 0.$

• (ii) If either $s<0$ or $s\ge 0$ and one of the following conditions holds: (a) $\varDelta >0$, $z_{1}^{*}>0$ and $g(z_{1}^{*})<0$; (b) $\varDelta =0$, $z_{2}^{*}>0$ and $g(z_{2}^{*})<0$; (c) $\varDelta <0$, $z_{3}^{*}>0$ and $g(z_{3}^{*})<0$. then the equilibrium point (0, 0, 0, 0) of system (5) is asymptotically stable for $\tau \in [0,\tau _{0})$,

• (iii) If the conditions of (ii) are satisfied, and $g^{\prime }(z_{k})\ne 0$, then system (5) undergoes a Hopf bifurcation at origin when $\tau =\tau _{0}$.

3 Direction and stability of Hopf bifurcation

In Sect. 2, we have shown that system (5) undergoes a Hopf bifurcation when $\tau$ passes through the critical value $\tau _{0}$. In this section, we investigate the direction and stability of periodic solutions by using the normal form theory and center manifold reduction presented in [8].

For fixed $k\in \{1,2,3,4\}$ and $j \in \{0,1,2,\ldots \}$, let us introduce $\mu =\tau -\tau _{k}^{(j)}$ as a new parameter of the system. Normalizing the delay $\tau$ by the time scaling $t\rightarrow t/ \tau$ and denoting $\tau _{k}^{(j)}=\tau ^{(j)}$, Eq. (5) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{l} x_{1}^{\prime }(t) \\ x_{2}^{\prime }(t) \\ x_{3}^{\prime }(t) \\ x_{4}^{\prime }(t) \end{array} \right]&=(\tau ^{(j)}+\mu )A(\tau )\left[ \begin{array}{l} x_{1}(t) \\ x_{2}(t) \\ x_{3}(t) \\ x_{4}(t) \end{array} \right] \nonumber \\&\quad +\,(\tau ^{(j)}+\mu )B(\tau )\left[ \begin{array}{l} x_{1}(t-1) \\ x_{2}(t-1) \\ x_{3}(t-1) \\ x_{4}(t-1) \end{array} \right] \nonumber \\&\nonumber \\&\quad +\,(\tau ^{(j)}+\mu )f(x_{1},x_{2},x_{3},x_{4}), \end{aligned}$$

(24)

where

$$\begin{aligned}&A(\tau )=\left[ \begin{array}{cccc} -1 &{} 0 &{} \alpha _{11} &{} 0 \\ \alpha _{21} &{} -1 &{} 0 &{} \alpha _{22} \\ \alpha &{} 0 &{} -\alpha &{} 0 \\ 0 &{} \alpha &{} 0 &{} -\alpha \end{array} \right] , B(\tau )=\left[ \begin{array}{cccc} 0 &{} \alpha _{12} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\\&f(x_{1},x_{2},x_{3},x_{4}) = (\tau ^{(j)}+\mu ) \left[ \begin{array}{l} f_{1} \\ f_{2} \\ f_{3} \\ f_{4} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} f_{1}&{}=\beta _{11}x_{3}^{2}(t)+\sigma _{11}x_{3}^{3}(t)+\beta _{12}x_{2}^{2}(t-1)\\ &{}\quad +\,\sigma _{12}x_{2}^{3}(t-1)+\hbox {H.O.T.}, \\ f_{2}&{}=\beta _{21}x_{1}^{2}(t)+\sigma _{21}x_{1}^{3}(t)+\beta _{22}x_{4}^{2}(t)+\sigma _{22}x_{4}^{3}(t)\\ &{}\quad +\,\hbox {H.O.T.}, \\ f_{3}&{}=0, \\ f_{4}&{}=0 \end{array} \end{aligned}$$

in which $\beta _{ij}=\frac{1}{2}a_{ij} \left. \dfrac{\hbox {d}^{2}f_{ij}}{\hbox {d}u_{i}^{2}} \right| _{u_{i}=0}$, $\sigma _{ij}=\frac{1}{6}a_{ij} \left. \dfrac{\hbox {d}^{3}f_{ij}}{\hbox {d}u_{i}^{3}} \right| _{u_{i}=0}$ $(i=1,2 \text{ and } j=1,2)$, and H.O.T. denotes the higher-order terms. Notice that all coefficients $\alpha _{ij}$, $\beta _{ij}$ and $\sigma _{ij}$ depend on $a_{ij}$. Let $u(t)=(x_{1}(t),x_{2}(t),x_{3}(t),x_{4}(t))^{T}$. The linearization of Eq. (24) around the origin is given by $u'(t)=(\tau ^{(j)}+\mu )A(\tau )u(t)+(\tau ^{(j)}+\mu )B(\tau )u(t-1).$

For $\phi =(\phi _{1},\phi _{2},\phi _{3},\phi _{4})^{T}\in \varOmega =C([-1,0],{\mathbb {R}}^{4})$ we can define $L_{\mu }:\varOmega \longrightarrow {\mathbb {R}}^{4}$ as follows:

$$\begin{aligned} L_{\mu }(\phi )=(\tau ^{(j)}+\mu )A(\tau )\phi (0)+(\tau ^{(j)}+\mu )B(\tau )\phi (-1). \end{aligned}$$

(25)

Now, system (24) can be written as a functional differential equation in $\varOmega$ as

$$\begin{aligned} u^{\prime }(t)=L_{\mu }(u_{t})+f(\mu ,u_{t}), \end{aligned}$$

(26)

where $u_{t}(\theta )=u(t+\theta )=(x_{1}(t+\theta ),x_{2}(t+\theta ),x_{3}(t+\theta ),x_{4}(t+\theta ))^{T}$ and $f:{\mathbb {R}} \times \varOmega \rightarrow {\mathbb {R}}^4$ where

$$\begin{aligned} \begin{aligned}&f(\mu ,\phi )=(\tau ^{(j)}+\mu )\times \left[ \begin{array}{l} f_{\phi 1} \\ f_{\phi 2} \\ f_{\phi 3} \\ f_{\phi 4} \end{array} \right] \end{aligned} \end{aligned}$$

(27)

in which

$$\begin{aligned} \begin{aligned} f_{\phi 1}&=\beta _{11}\phi _{3}^{2}(0)+\sigma _{11}\phi _{3}^{3}(0)+\beta _{12}\phi _{2}^{2}(-1)\\&\quad +\,\sigma _{12}\phi _{2}^{3}(-1)+\hbox {H.O.T.}, \\ f_{\phi 2}&=\beta _{21}\phi _{1}^{2}(0)+\sigma _{21}\phi _{1}^{3}(0)+\beta _{22}\phi _{4}^{2}(0)\\&\quad +\,\sigma _{22}\phi _{4}^{3}(0)+\hbox {H.O.T.}, \\ f_{\phi 3}&=0, \\ f_{\phi 4}&=0. \end{aligned} \end{aligned}$$

By Riesz Representation theorem, there exists a $4\times 4$ matrix-valued function $\eta (\theta ,\mu )$, $\theta \in [-1,0]$, whose elements are of bounded variation such that

$$\begin{aligned} L_{\mu }\phi = \int _{-1}^{0}\hbox {d}\eta (\theta ,\mu )\phi (\theta ). \end{aligned}$$

(28)

In fact, we can choose

$$\begin{aligned} \eta (\theta ,\mu )= (\tau ^{(j)}+\mu )A \delta (\theta )+(\tau ^{(j)}+\mu )B\delta (\theta +1), \end{aligned}$$

(29)

where $\delta$ is the Dirac delta function. For $\phi \in \varOmega$, define

$$\begin{aligned} A(\mu )\phi =\left\{ \begin{array}{l@{\quad }l} \frac{\hbox {d}\phi (\theta )}{\hbox {d}\theta }, &{} \theta \in [-1,0), \\ \int _{-1}^{0}{\hbox {d}\eta (\xi ,\mu )\phi (\xi )}, &{} \theta =0, \end{array} \right. \end{aligned}$$

(30)

and

$$\begin{aligned} R(\mu )\phi =\left\{ \begin{array}{l@{\quad }l} 0, &{} \theta \in [-1,0), \\ f(\mu ,\phi ), &{} \theta =0. \end{array} \right. \end{aligned}$$

(31)

Then the functional differential equation (26) is equivalent to the following abstract differential equation:

$$\begin{aligned} \overset{.}{u}_{t}=A(\mu )u_{t}+R(\mu )u_{t}, \end{aligned}$$

(32)

where $u_{t}(\theta )=u(t+\theta )$ for $\theta \in [-1,0)$. For $\psi \in C([0,1],({\mathbb {R}}^4)^{*})$, define

$$\begin{aligned} A^{*}\psi (s)=\left\{ \begin{array}{ll} -\frac{\hbox {d}\psi (s)}{\hbox {d}s}, &{} s\in (0,1], \\ \int _{-1}^{0}{\hbox {d}\eta ^\mathrm{T}(\xi ,0)\psi (-\xi )}, &{} s=0, \end{array} \right. \end{aligned}$$

(33)

and a bilinear form

$$\begin{aligned}&\left\langle \psi (s),\phi (\theta )\right\rangle =\overline{\psi }(0)\phi (0)\nonumber \\&\quad -\int \limits _{-1}^{0}\int \limits _{\xi =0}^{\theta }\overline{\psi }(\xi -\theta )\hbox {d}\eta (\theta )\phi (\xi )\hbox {d}\xi , \end{aligned}$$

(34)

where $\eta (\theta )=\eta (\theta ,0)$. Thus, A(0) and $A^{*}(0)$ are adjoint operators. Suppose that $q(\theta )$ and $q^{*}(s)$ are eigenvectors of A(0) and $A^{*}(0)$ corresponding to $\lambda =i\omega _{0}$ and $\overline{\lambda }=-i\omega _{0}$, respectively. Let us take $q(\theta )= \left[ 1,q_{1},q_{2},q_{3} \right] ^\mathrm{T} \hbox {e}^{i\omega _{0}\theta }$ and $q^{*}(s)=\frac{1}{D}\left[ 1,q_{1}^{*},q_{2}^{*} ,q_{3}^{*}\right] ^\mathrm{T} \hbox {e}^{i\omega _{0}s }$. Using $A(0)q(\theta )=i\omega _{0}q(\theta )$ and $A^{*}(0)q^{*}(\theta )=-i\omega _{0}q^{*}(\theta )$, one can easily obtain

$$\begin{aligned} q_{1}= & {} \frac{((\alpha -\alpha \alpha _{11})k^2+(k\alpha +k)i\omega _{0}-\omega _{0}^2)\hbox {e}^{i\omega _{0}}}{\alpha _{12}(k\alpha +i\omega _{0})},\nonumber \\ q_{2}= & {} \frac{k\alpha }{k\alpha +i\omega _{0}}, \nonumber \\ q_{3}= & {} \frac{(k+i\omega _{0})q_{1}-k\alpha _{21}}{\alpha _{22}k},\nonumber \\ q_{1}^{*}= & {} \frac{k+i\omega _{0}-k\alpha q_{2}^{*}}{\alpha _{21}k},\nonumber \\ q_{2}^{*}= & {} \frac{k\alpha _{11}}{k\alpha +i\omega _{0}}, \nonumber \\ q_{3}^{*}= & {} \frac{k\alpha _{22}q_{1}^{*}}{k\alpha +i\omega _{0}}, \end{aligned}$$

(35)

where $k=\tau ^{(j)}$. Furthermore, using the relation $\left\langle q^{*}(s),q(\theta )\right\rangle =1$ one can calculate $\overline{D}$ as follows:

$$\begin{aligned} \overline{D}=1+q_{1}^{*}q_{1}+q_{2}^{*}q_{2}+q_{3}^{*}q_{3}+\tau ^{(j)}\hbox {e}^{-i\omega _{0}}\alpha _{12}q_{1}. \end{aligned}$$

In the remainder of this section, we use the same notations as in [8]. We first compute the coordinates to describe the center manifold $C_{0}$ at $\mu =0$. Let $u_{t}$ be the solution of Eq. (32) with $\mu =0$. Define

$$\begin{aligned} z(t)=\left\langle q^{*},u_{t}\right\rangle ,\quad w(t,\theta )=u_{t}-2\hbox {Re}\{z(t)q(\theta )\}\text {.}\quad \quad \end{aligned}$$

(36)

On the center manifold, we have

$$\begin{aligned} \begin{aligned} w(t,\theta )&=w(z(t),\overline{z}(t),\theta ) \\&=w_{20}(\theta )\frac{z^{2}}{2} +w_{11}(\theta )z\overline{z}+w_{02}(\theta )\frac{\overline{z}^{2}}{2} +\cdots , \end{aligned} \end{aligned}$$

(37)

where z and $\overline{z}$ are local coordinates for the center manifold $C_{0}$ in the direction of q and $q^{*}$. For $u_{t}\in C_{0}$ we have

$$\begin{aligned} \overset{.}{z}(t)= & {} \left\langle q^{*},\overset{.}{u}_{t}\right\rangle =\left\langle q^{*},Au_{t}+Ru_{t}\right\rangle \\= & {} i\omega _{0}\left\langle q^{*},u_{t}\right\rangle +\overline{q^{*} }(0)f_{0}(z,\overline{z})\equiv i\omega _{0}z(t)+g(z,\overline{z}), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} g(z,\overline{z})&=\overline{q^{*}}(0)f_{0}(z,\overline{z})\\&=g_{20}\frac{ z^{2}}{2}+g_{11}z\overline{z}+g_{02}\frac{\overline{z}^{2}}{2}+g_{21}\frac{z^{2}\overline{z}}{2}+\cdots \text {.} \end{aligned} \end{aligned}$$

(38)

Here, $f_{0}(z,\overline{z})$ denotes $f(z,\overline{z})$ at $\mu =0$. Notice that $u_{t}(u_{1t}(\theta ),u_{2t}(\theta ),u_{3t}(\theta ),u_{4t}(\theta ))=w(t,\theta )+zq(\theta )+\overline{zq(\theta )}$ and $q(\theta )=\left[ 1,q_{1},q_{2},q_{3} \right] ^\mathrm{T}\hbox {e}^{i\omega _{0}\theta }$, so we have

$$\begin{aligned} u_{1t}(0)= & {} z+\overline{z}+w_{20}^{(1)}(0)\frac{z^{2}}{2}+w_{11}^{(1)}(0)z \overline{z} \\&+\,w_{02}^{(1)}(0)\frac{\overline{z}^{2}}{2}+O(\left| z, \overline{z}\right| ^{3}), \\ u_{3t}(0)= & {} zq_{2} +\overline{z} \overline{q_{2}}+w_{20}^{(3)}(0)\frac{z^{2}}{2} +w_{11}^{(3)}(0)z\overline{z}\\&+\,w_{02}^{(3)}(0)\frac{\overline{z}^{2}}{2} +O(\left| z,\overline{z}\right| ^{3}), \\ u_{4t}(0)= & {} zq_{3} +\overline{z}\overline{q_{3}}+w_{20}^{(4)}(0)\frac{z^{2}}{2} +w_{11}^{(4)}(0)z\overline{z}\\&+\,w_{02}^{(4)}(0)\frac{\overline{z}^{2}}{2} +O(\left| z,\overline{z}\right| ^{3}), \\ \end{aligned}$$

$$\begin{aligned} u_{2t}(-1)= & {} zq_{1} \hbox {e}^{-i\omega _{0}}+\overline{z}\overline{q_{1}}\hbox {e}^{-i\omega _{0}}+w_{20}^{(2)}(-1)\frac{z^{2}}{2}\\&+\,w_{11}^{(2)}(-1)z\overline{z} +w_{02}^{(2)}(-1)\frac{\overline{z}^{2}}{2}+O(\left| z,\overline{z} \right| ^{3}). \end{aligned}$$

Thus, it follows from the definition of $f(\mu ,\phi )$ and (38) that

$$\begin{aligned} g(z,\overline{z})=\overline{q^{*}}(0)f_{0}(z,\overline{z})=\frac{\tau ^{(j)}}{\overline{D}}[1,\overline{q_{1}^{*}},\overline{q_{2}^{*}},\overline{q_{3}^{*}}]\left[ \begin{array}{c} f_{1}^{0} \\ f_{2}^{0} \\ f_{3}^{0} \\ f_{4}^{0} \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} f_{1}^{0}= & {} \beta _{11}u_{3t}^{2}(0)+\sigma _{11}u_{3t}^{3}(0)+\beta _{12}u_{2t}^{2}(-1)\nonumber \\&+\,\sigma _{12}u_{2t}^{3}(-1), \nonumber \\ f_{2}^{0}= & {} \beta _{21}u_{1t}^{2}(0)+\sigma _{21}u_{1t}^{3}(0)+\beta _{22}u_{4t}^{2}(0)\nonumber \\&+\,\sigma _{22}u_{4t}^{3}(0), \nonumber \\ f_{3}^{0}= & {} 0, \nonumber \\ f_{4}^{0}= & {} 0, \nonumber \end{aligned}$$

so that g has the following form:

$$\begin{aligned} g(z,\overline{z})= & {} \overline{q^{*}}(0)f_{0}(z,\overline{z}) \\= & {} \frac{\tau ^{(j)}}{\overline{D}} \Big \{ \big [ \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i \omega _{0}}\\&\quad +\beta _{21}\overline{q_{1}^{*}}+\beta _{22}\overline{q_{1}^{*}}q_{3}^{2}\big ]z^{2} \\&+\,\big [ 2\beta _{11}q_{2}\overline{q_{2}}+ 2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}}\\&+\,2\beta _{21}\overline{q_{1}^{*}}+2\beta _{22}\overline{q_{1}^{*}}q_{3}\overline{q_{3}}\big ]z\overline{z} \\&+\,\big [ \beta _{11}{\overline{q_{2}}}^{2}+\beta _{12}{\overline{q_{1}}}^{2}\hbox {e}^{-2i\omega _{0}}\\&+\,\beta _{21}\overline{q_{1}^{*}}+\beta _{22}\overline{q_{1}^{*}}{\overline{q_{3}}}^{2} \big ]\overline{z}^{2} +\big [2\beta _{11}q_{2} w_{11}^{3}(0)\\&+\,\beta _{11}\overline{q_{2}} w_{20}^{3}(0)+3\sigma _{11}q_{2}^{2}\overline{q_{2}} \\&+\,2\beta _{12}q_{1}\hbox {e}^{-i\omega _{0}} w_{11}^{2}(-1)\\&+\,\beta _{12}\overline{q_{1}}\hbox {e}^{-i\omega _{0}} w_{20}^{2}(-1) +3\sigma _{12}q_{1}^{2}\overline{q_{1}}\hbox {e}^{-3i\omega _{0}}\\&+\,2\beta _{21}\overline{q_{1}^{*}}w_{11}^{1}(0)+\beta _{21}\overline{q_{1}^{*}}w_{20}^{1}(0)+3\sigma _{21}\overline{q_{1}^{*}} \\&+\,2\beta _{22}q_{3}\overline{q_{1}^{*}}w_{11}^{4}(0)+\beta _{22}\overline{q_{3}}\overline{q_{1}^{*}}w_{20}^{4}(0)\\&+\,3\sigma _{22}\overline{q_{3}}\overline{q_{1}^{*}}q_{3}^{2} \big ]z^{2}\overline{z} \Big \} +\hbox {H.O.T.} \end{aligned}$$

Comparing the coefficients in (38) one obtains the coefficients as follows:

$$\begin{aligned} g_{20}= & {} 2\frac{\tau ^{(j)}}{\overline{D}}\big [ \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i \omega _{0}}+\beta _{21}\overline{q_{1}^{*}}\\&+\,\beta _{22}\overline{q_{1}^{*}}q_{3}^{2}\big ],\\ g_{11}= & {} \frac{\tau ^{(j)}}{\overline{D}} \big [ 2\beta _{11}q_{2}\overline{q_{2}}+ 2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}}+2\beta _{21}\overline{q_{1}^{*}} \\&+\,2\beta _{22}\overline{q_{1}^{*}}q_{3}\overline{q_{3}}\big ],\\ g_{02}= & {} 2\frac{\tau ^{(j)}}{\overline{D}}\big [ \beta _{11}{\overline{q_{2}}}^{2}+\beta _{12}{\overline{q_{1}}}^{2}\hbox {e}^{-2i\omega _{0}}+\beta _{21}\overline{q_{1}^{*}}\\&+\,\beta _{22}\overline{q_{1}^{*}}{\overline{q_{3}}}^{2} \big ],\\ g_{21}= & {} 2\frac{\tau ^{(j)}}{\overline{D}}\big [2\beta _{11}q_{2} w_{11}^{3}(0)+\beta _{11}\overline{q_{2}} w_{20}^{3}(0)\\&+\,3\sigma _{11}q_{2}^{2}\overline{q_{2}}+\,2\beta _{12}q_{1}\hbox {e}^{-i\omega _{0}} w_{11}^{2}(-1)\\&+\,\beta _{12}\overline{q_{1}}\hbox {e}^{-i\omega _{0}} w_{20}^{2}(-1) +\,3\sigma _{12}q_{1}^{2}\overline{q_{1}}\hbox {e}^{-3i\omega _{0}} \\&+\,2\beta _{21}\overline{q_{1}^{*}}w_{11}^{1}(0)+\,\beta _{21}\overline{q_{1}^{*}}w_{20}^{1}(0)+3\sigma _{21}\overline{q_{1}^{*}} \\&+\,2\beta _{22}q_{3}\overline{q_{1}^{*}}w_{11}^{4}(0)+\beta _{22}\overline{q_{3}}\overline{q_{1}^{*}}w_{20}^{4}(0)\\&+\,3\sigma _{22}\overline{q_{3}}\overline{q_{1}^{*}}q_{3}^{2} \big ]. \end{aligned}$$

In order to determine $g_{21}$, we need to compute $w_{11}(\theta )$ and $w_{20}(\theta )$. From (36) we have

$$\begin{aligned} \overset{.}{w}(t,\theta )= & {} \overset{.}{x}_{t}-2\hbox {Re}\{\overset{.}{z(t)} q(\theta )\} \\= & {} \left\{ \begin{array}{ll} Aw-2\hbox {Re}\left\{ {\overline{q^{*}}(0)f_{0}q(\theta )}\right\} , &{} \theta \in [-1,0) \\ Aw-2\hbox {Re}\left\{ {\overline{q^{*}}(0)f_{0}q(\theta )}\right\} +f_{0}, &{} \theta =0 \end{array} \right. \\&:\equiv Aw+H(z,\overline{z},\theta ), \end{aligned}$$

where

$$\begin{aligned} H(z,\overline{z},\theta )=H_{20}\frac{z^{2}}{2}+H_{11}z\overline{z}+H_{02} \frac{\overline{z}^{2}}{2}+\cdots \text {.} \end{aligned}$$

(39)

On the other hand, one has

$$\begin{aligned} \overset{.}{w}=w_{z}\overset{.}{z}+w_{\overline{z}}\overset{.}{\overline{z}} \end{aligned}$$

on the center manifold. Thus, comparing the coefficients one obtains that

$$\begin{aligned}&\left( A-2i\omega _{0}\right) w_{20}(\theta )=-H_{20}(\theta ),\ \nonumber \\&\quad Aw_{11}(\theta )=-H_{11}(\theta ). \end{aligned}$$

(40)

For $\theta \in [-1,0)$, it is easy to see that

$$\begin{aligned} H(z,\overline{z},\theta )=-2\hbox {Re}\{\overset{.}{z}(t)q(\theta )\}\text {.} \end{aligned}$$

Comparing the coefficients of (40) with those of (39) we obtain the following equalities:

$$\begin{aligned} H_{20}(\theta )= & {} -\left( q(\theta )g_{20}+\overline{q}(\theta )\overline{g} _{02}\right) \text {,} \\ H_{11}(\theta )= & {} -\left( q(\theta )g_{11}+\overline{q}(\theta )\overline{g} _{11}\right) \text {,} \\ H_{02}(\theta )= & {} -\left( q(\theta )g_{02}+\overline{q}(\theta )\overline{g} _{20}\right) \text {.} \end{aligned}$$

From (40) and the definition of A (see Eq. 30), we get

$$\begin{aligned} w_{20}^{^{\prime }}(\theta )-2i\omega _{0}w_{20}(\theta )=q(\theta )g_{20}+ \overline{q}(\theta )\overline{g}_{02}\text {.} \end{aligned}$$

Then, since $q(\theta )=q(0)\hbox {e}^{i\omega _{0}\theta }$, we have

$$\begin{aligned} w_{20}(\theta )= & {} \frac{i}{\omega _{0}}g_{20}q(0)\hbox {e}^{i\omega _{0}\theta }+\frac{ i}{3\omega _{0}}\overline{g}_{02}\overline{q}(0)\hbox {e}^{-i\omega _{0}\theta }\\&+\,E_{1}\hbox {e}^{2i\omega _{0}\theta }, \end{aligned}$$

where $E_{1}=\left[ \begin{array}{c} E_{1}^{(1)} \\ E_{1}^{(2)} \\ E_{1}^{(3)} \\ E_{1}^{(4)} \end{array} \right] \in {\mathbb {R}}^{4}$ is a constant vector. Similarly,

$$\begin{aligned} w_{11}(\theta )=\frac{-i}{\omega _{0}}g_{11}q(0)\hbox {e}^{i\omega _{0}\theta }+ \frac{i}{\omega _{0}}\overline{g}_{11}\overline{q}(0)\hbox {e}^{-i\omega _{0}\theta }+E_{2}, \end{aligned}$$

where $E_{2}=\left[ \begin{array}{c} E_{2}^{(1)} \\ E_{2}^{(2)} \\ E_{2}^{(3)} \\ E_{2}^{(4)} \end{array} \right] \in {\mathbb {R}}^{4}$ is a constant vector. Let us find the values of $E_{1}$ and $E_{2}$. If we take $\theta =0$ at (40), then one obtains that

$$\begin{aligned} \int \limits _{-1}^{0}\hbox {d}\eta (\theta )w_{20}(\theta )= & {} 2i\omega _{0}w_{20}(0)-H_{20}(0), \end{aligned}$$

(41)

$$\begin{aligned} \int \limits _{-1}^{0}\hbox {d}\eta (\theta )w_{11}(\theta )= & {} -H_{11}(0). \end{aligned}$$

(42)

Also, for $\theta =0$,

$$\begin{aligned} \begin{aligned} H_{20}(0)&=-g_{20}q(0)-\overline{g}_{02}\overline{q}(0) \\&\quad +\,2\tau ^{(j)}\left[ \begin{array}{c} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} \\ \beta _{21}+\beta _{22}q_{3}^{2}\\ 0 \\ 0 \end{array} \right] \end{aligned} \end{aligned}$$

(43)

and

$$\begin{aligned} \begin{aligned} H_{11}(0)&=-g_{11}q(0)-\overline{g}_{11}\overline{q}(0)\\&\quad +\,\tau ^{(j)}\left[ \begin{array}{c} 2\beta _{11}q_{2}\overline{q_{2}}+2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}}\\ 2\beta _{21}+2\beta _{22}q_{3}\overline{q_{3}}\\ 0 \\ 0 \end{array} \right] . \end{aligned} \end{aligned}$$

(44)

On the other hand, since $A(0)q(0)=i\omega _{0}q(0)$ and $A(0)\overline{q} (0)=i\omega _{0}\overline{q}(0)$ we can write

$$\begin{aligned}&\left[ i\omega _{0}I-\int \limits _{-1}^{0}\hbox {e}^{i\omega _{0}\theta }\hbox {d}\eta (\theta )\right] q(0)=0, \end{aligned}$$

(45)

$$\begin{aligned}&\left[ -i\omega _{0}I-\int \limits _{-1}^{0}\hbox {e}^{-i\omega _{0}\theta }\hbox {d}\eta (\theta )\right] \overline{q}(0)=0. \end{aligned}$$

(46)

Substituting (43) in (41) and then using (45) we obtain

$$\begin{aligned}&\left[ 2i\omega _{0}I-\int \limits _{-1}^{0}\hbox {e}^{2i\omega _{0}\theta }\hbox {d}\eta (\theta )\right] E_{1}\\&\quad =2\tau ^{(j)}\left[ \begin{array}{c} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} \\ \beta _{21}+\beta _{22}q_{3}^{2}\\ 0 \\ 0 \end{array} \right] \end{aligned}$$

which is equal to

$$\begin{aligned}&\left[ \begin{array}{cccc} 2i\omega _{0}+\tau ^{(j)} &{} -\tau ^{(j)}\alpha _{12} &{} -\tau ^{(j)}\alpha _{11} &{} 0 \\ -\tau ^{(j)}\alpha _{21} &{} 2i\omega _{0}-\tau ^{(j)} &{} 0 &{} -\tau ^{(j)}\alpha _{22} \\ -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha &{} 0 \\ 0 &{} -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha \end{array} \right] E_{1}\nonumber \\&\quad =2\tau ^{(j)}\left[ \begin{array}{c} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} \\ \beta _{21}+\beta _{22}q_{3}^{2} \\ 0 \\ 0 \end{array} \right] . \end{aligned}$$

(47)

Now, if one solves this system for $E_{1}$ one can find that

$$\begin{aligned}&E_{1}^{(1)}=\frac{2\tau ^{(j)}}{A_{1}}\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} &{} -\tau ^{(j)}\alpha _{12} &{} -\tau ^{(j)}\alpha _{11} &{} 0 \\ \beta _{21}+\beta _{22}q_{3}^{2} &{} 2i\omega _{0}-\tau ^{(j)} &{} 0 &{} -\tau ^{(j)}\alpha _{22} \\ 0 &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha &{} 0 \\ 0 &{} -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha \end{array} \right| ,\\&E_{1}^{(2)}=\frac{2\tau ^{(j)}}{A_{1}}\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _{0}+\tau ^{(j)} &{} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} &{} -\tau ^{(j)}\alpha _{11} &{} 0 \\ -\tau ^{(j)}\alpha _{21} &{} \beta _{21}+\beta _{22}q_{3}^{2} &{} 0 &{} -\tau ^{(j)}\alpha _{22} \\ -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha &{} 0 \\ 0 &{} 0 &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha \end{array} \right| ,\\&E_{1}^{(3)}=\frac{2\tau ^{(j)}}{A_{1}}\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _{0}+\tau ^{(j)} &{} -\tau ^{(j)}\alpha _{12} &{} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} &{} 0 \\ -\tau ^{(j)}\alpha _{21} &{} 2i\omega _{0}-\tau ^{(j)} &{} \beta _{21}+\beta _{22}q_{3}^{2} &{} -\tau ^{(j)}\alpha _{22} \\ -\tau ^{(j)}\alpha &{} 0 &{} 0 &{} 0 \\ 0 &{} -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha \end{array} \right| ,\\&E_{1}^{(4)}=\frac{2\tau ^{(j)}}{A_{1}}\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 2i\omega _{0}+\tau ^{(j)} &{} -\tau ^{(j)}\alpha _{12} &{} -\tau ^{(j)}\alpha _{11} &{} \beta _{11}q_{2}^{2}+\beta _{12}q_{1}^{2}\hbox {e}^{-2i\omega _{0}} \\ -\tau ^{(j)}\alpha _{21} &{} 2i\omega _{0}-\tau ^{(j)} &{} 0 &{} \beta _{21}+\beta _{22}q_{3}^{2} \\ -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha &{} 0 \\ 0 &{} -\tau ^{(j)}\alpha &{} 0 &{} 0 \end{array} \right| , \end{aligned}$$

where

$$\begin{aligned} A_{1}=\left| \begin{array}{cccc} 2i\omega _{0}+\tau ^{(j)} &{} -\tau ^{(j)}\alpha _{12} &{} -\tau ^{(j)}\alpha _{11} &{} 0 \\ -\tau ^{(j)}\alpha _{21} &{} 2i\omega _{0}-\tau ^{(j)} &{} 0 &{} -\tau ^{(j)}\alpha _{22} \\ -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha &{} 0 \\ 0 &{} -\tau ^{(j)}\alpha &{} 0 &{} 2i\omega _{0}+\tau ^{(j)}\alpha \end{array} \right| . \end{aligned}$$

Similarly, substituting (44) in (42) and then utilizing (46) we can easily get

$$\begin{aligned}&\left[ \begin{array}{cccc} -1 &{} \alpha _{12} &{} \alpha _{11} &{} 0 \\ \alpha _{21} &{} -1 &{} 0 &{} \alpha _{22} \\ \alpha &{} 0 &{} -\alpha &{} 0 \\ 0 &{} \alpha &{} 0 &{} -\alpha \end{array} \right] E_{2}\\&\quad =\left[ \begin{array}{c} -2\beta _{11}q_{2}\overline{q_{2}}-2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}}\\ -2\beta _{21}-2\beta _{22}q_{3}\overline{q_{3}}\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

Solving this system for $E_{2}$, we have

$$\begin{aligned}&E_{2}^{(1)}\\&\quad =\frac{1}{A_{2}}\left| \begin{array}{cccc} -2\beta _{11}q_{2}\overline{q_{2}}-2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}} &{}\quad \alpha _{12} &{}\quad \alpha _{11} &{}\quad 0\\ -2\beta _{21}-2\beta _{22}q_{3}\overline{q_{3}} &{}\quad -1 &{}\quad 0 &{}\quad \alpha _{22}\\ 0 &{}\quad 0 &{}\quad -\alpha &{}\quad 0 \\ 0 &{}\quad \alpha &{}\quad 0 &{}\quad -\alpha \end{array} \right| ,\\&E_{2}^{(2)}\\&\quad =\frac{1}{A_{2}}\left| \begin{array}{cccc} -1 &{}\quad -2\beta _{11}q_{2}\overline{q_{2}}-2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}} &{}\quad \alpha _{11} &{}\quad 0\\ \alpha _{21} &{}\quad -2\beta _{21}-2\beta _{22}q_{3}\overline{q_{3}} &{}\quad 0 &{}\quad \alpha _{22} \\ \alpha &{}\quad 0 &{}\quad -\alpha &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\alpha \end{array} \right| ,\\&E_{2}^{(3)}\\&\quad =\frac{1}{A_{2}}\left| \begin{array}{cccc} -1 &{}\quad \alpha _{12} &{}\quad -2\beta _{11}q_{2}\overline{q_{2}}-2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}} &{}\quad 0\\ \alpha _{21} &{}\quad -1 &{}\quad -2\beta _{21}-2\beta _{22}q_{3}\overline{q_{3}} &{}\quad \alpha _{22} \\ \alpha &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \alpha &{}\quad 0 &{}\quad -\alpha \end{array} \right| ,\\&E_{2}^{(4)}\\&\quad =\frac{1}{A_{2}}\left| \begin{array}{cccc} -1 &{}\quad \alpha _{12} &{}\quad \alpha _{11} &{}\quad -2\beta _{11}q_{2}\overline{q_{2}}-2\beta _{12}q_{1}\overline{q_{1}}\hbox {e}^{-2i\omega _{0}} \\ \alpha _{21} &{}\quad -1 &{}\quad 0 &{}\quad -2\beta _{21}-2\beta _{22}q_{3}\overline{q_{3}} \\ \alpha &{}\quad 0 &{}\quad -\alpha &{}\quad 0 \\ 0 &{}\quad \alpha &{}\quad 0 &{}\quad 0 \end{array} \right| , \end{aligned}$$

where

$$\begin{aligned} A_{2}=\left| \begin{array}{cccc} -1 &{} \alpha _{12} &{} \alpha _{11} &{} 0 \\ \alpha _{21} &{} -1 &{} 0 &{} \alpha _{22} \\ \alpha &{} 0 &{} -\alpha &{} 0 \\ 0 &{} \alpha &{} 0 &{} -\alpha \end{array} \right| . \end{aligned}$$

Finally, we substitute $E_{1}$ and $E_{2}$ in $w_{11}(\theta )$ and $w_{20}(\theta )$ and find the coefficients of $g(z,\overline{z})$ to determine the following formulae to investigate the properties of bifurcating periodic solution on the center manifold at the critical value $\tau _{k}^{(j)}$. The formulae have the following forms:

$$\begin{aligned}&c_{1}(0)=\frac{i}{2\omega _{0}} \big (g_{11}g_{20}-2\left| g_{11} \right| ^{2}-\frac{\left| g_{02}\right| ^{2}}{3} \big )+\frac{g_{21}}{2},\\&\mu _{2}=-\frac{\hbox {Re}\{c_{1}(0)\}}{\hbox {Re}\{\lambda ^{\prime }(\tau _{k}^{(j)})\}},\\&\beta _{2}=2\hbox {Re}\{c_{1}(0)\},\\&T_{2}=-\frac{\hbox {Im}\{c_{1}(0)\}+\mu _{2}\hbox {Im}\{\lambda ^{\prime }(\tau _{k}^{(j)})\}}{\tau _{k}^{(j)}\omega _{0}}. \end{aligned}$$

These are the quantities that determine the properties of bifurcating periodic solutions on the center manifold at $\tau _{k}^{(j)}$. Here, $\mu _{2}$ determines the direction of Hopf bifurcation, $\beta _{2}$ determines the stability of the bifurcating periodic solution and $T_{2}$ determines the period of the bifurcating solution. Hence, we have the following result.

Theorem 2

$\mu _{2}$ determines the direction of Hopf bifurcation;

• If $\mu _{2}>0$, then the Hopf bifurcation is supercritical and the bifurcating periodic solutions exist for $\tau >\tau _{0}$,

• If $\mu _{2}<0$, then the Hopf bifurcation is subcritical and the bifurcating periodic solutions exist for $\tau <\tau _{0}$.

$\beta _{2}$ determines the stability of the bifurcating periodic solution;

• If $\beta _{2}<0$, bifurcating periodic solutions are stable,

• If $\beta _{2}>0$, bifurcating periodic solutions are unstable.

$T_{2}$ determines the period of the bifurcating solution;

• If $T_{2}>0$, the period increases,

• If $T_{2}<0$, the period decreases.

4 Numerical simulations

In this section, we present some numerical simulations to support our results in Lemmas 1, 2 and Theorem 1. As an example, we simulate system (5) with $a_{11}=-0.5$, $a_{12}=-1.8$, $a_{21}=1.3$, $a_{22}=1.7$ and $\alpha =1$. In addition, for simplicity, we take $f_{ij}(.)=tanh(.)$ for $i=1,2$ and $j=1,2$ so that the system we simulate has the following form:

$$\begin{aligned} \begin{aligned} u_{1}^{^{\prime }}(t)&=- u_{1}(t)-0.5 \hbox {tan}h(u_{3}(t))\\&\quad -\,1.8 \hbox {tan}h(u_{2}(t-\tau )), \\ u_{2}^{^{\prime }}(t)&=- u_{2}(t)+1.3 \hbox {tan}h(u_{1}(t))\\&\quad +\,1.7 \hbox {tan}h(u_{4}(t)), \\ u_{3}^{^{\prime }}(t)&=- u_{3}(t)+u_{1}(t), \\ u_{4}^{^{\prime }}(t)&=- u_{4}(t)+u_{2}(t). \end{aligned} \end{aligned}$$

(48)

Then, we have

$$\begin{aligned}&\omega ^{8}+(6.4)\omega ^{6}+(2.6644)\omega ^{4}+(1.6888)\omega ^{2}\nonumber \\&\quad -\,4.3731=0. \end{aligned}$$

(49)

Fig. 2

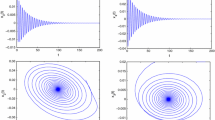
Graphs of solutions of system (5) with $\tau _{1}=0.5$, $\tau _{2}=0.7$, $\tau _{1}+\tau _{2}=1.2<\tau _{0}^{0}$. The origin is asymptotically stable

Fig. 3

Graphs of solutions of system (5) with $\tau _{1}=0.5$, $\tau _{2}=0.7$, $\tau _{1}+\tau _{2}=1.2<\tau _{0}^{0}$. The origin is asymptotically stable

Equation (49) has only one positive root, that is, $\omega _{0}\approx 0.8152$. Also, one can easily obtain $\tau _{0}^{0} \approx 1.4040$ from Eq. (22). For the simulation, we choose $\tau _{1}=0.5$ and $\tau _{2}=0.7$ so that $\tau =\tau _{1}+\tau _{2}=1.2<\tau _{0}^{0}$. Thus, from Theorem 1, the equilibrium (0, 0, 0, 0) is stable when $\tau <\tau _{0}^{0}$ as it can be seen in Figs. 2 and 3. Since $\mu _{2}>0$, when $\tau$ passes through the critical value $\tau _{0}^{0}$, the equilibrium loses its stability and a Hopf bifurcation occurs, i.e., a family of periodic solutions bifurcates from the origin when delay increases. Figures 4 and 5 show the periodic solutions when $\tau =\tau _{1}+\tau _{2}=1.5\approx \tau _{0}^{0}$. Since $T_{2}>0$ and $\beta _{2}<0$, the period of the periodic solutions increases as $\tau$ increases and periodic orbits are stable. If we choose $\tau _{1}=0.9$ and $\tau _{2}=0.9$, then $\tau =\tau _{1}+\tau _{2}=1.8>\tau _{0}^{0}$. When $\tau =1.8>\tau _{0}^{0}$, Figs. 6 and 7 represent that the corresponding periodic solutions have larger period than in Fig. 4. Since our system has four dependent variables (depends on time), one can choose three of them randomly and observe bifurcation diagram partially. One can also see the restricted limit cycles with increasing periods as $\tau$ increases in Fig. 8.

Fig. 4

Bifurcating periodic solutions when $\tau _{1}=0.75$, $\tau _{2}=0.75$, $\tau _{1}+\tau _{2}=1.5>\tau _{0}^{0}$

Fig. 5

Bifurcating periodic solutions when $\tau _{1}=0.75$, $\tau _{2}=0.75$, $\tau _{1}+\tau _{2}=1.5>\tau _{0}^{0}$

Fig. 6

Bifurcating periodic solutions when $\tau _{1}=0.9$, $\tau _{2}=0.9$, $\tau _{1}+\tau _{2}=1.8>\tau _{0}$

Fig. 7

Bifurcating periodic solutions when $\tau _{1}=0.9$, $\tau _{2}=0.9$, $\tau _{1}+\tau _{2}=1.8>\tau _{0}$

Fig. 8

Some limit cycles when $\tau$ increases from $\tau =1.5$ to $\tau =1.58$

5 Conclusion

In this paper, we investigate local stability of the equilibrium (0, 0, 0, 0) and local Hopf bifurcation in a coupled two-neuron system consisting of multiple discrete and distributed delays. We show that the equilibrium is asymptotically stable when $\tau \in [0,\tau _{0})$ and unstable for $\tau >\tau _{0}$. In particular, employing the Routh–Hurwitz criterion and the results on distribution of the zeros of transcendental functions, we get a set of conditions to determine the stability of the fixed point of model (3) and the existence of Hopf bifurcations. Also, we paid attention to the direction and the stability of the bifurcating periodic solutions by applying the normal form theory and the center manifold theorem. Finally, we have performed some numerical simulations to support our analytical results. In particular, if we choose the kernel as delta function instead of weak kernel, that is, $F(s)=\delta (s-\tau _{i})$ $i=1,2$, respectively, and all $f_{ij}(\cdot )=f$ for $i=1,2$ and $j=1,2$, then our system (3) reduces the model (1) that was studied in [17]. In summary, all theoretical results obtained in the present paper are generalization of former studies given in [11, 14, 17].