Principal component analysis for non-stationary time series based on detrended cross-correlation analysis

Abstract

The principal component analysis (PCA) has been extensively studied and proved to be a sophisticated technique for the dimension reduction and the index construction of multidimensional stationary time series. However, the PCA method is often susceptible to external trends of original variables in real-world applications, when data present non-stationarity. In this paper, we propose a non-stationary principal component analysis (NSPCA) for multidimensional time series in the presence of non-stationarity. The new method is based on detrended cross-correlation analysis. We theoretically derive the coefficients relating to the combinations of original variables in the NSPCA method. We also apply the NSPCA method to the autoregressive model, Gaussian distributed variables as well as stock sectors in Chinese stock markets, and compare it with the traditional PCA method. We find that the NSPCA method has the advantage to detect intrinsic cross-correlations among variables and identify the patterns of data in the case of non-stationarity, minimizing the effects of external trends which often make the PCA yields few components assigning similar loadings to all variables.

1 Introduction

Many complex systems in the natural and social sciences consistently produce information along with time, and a large number of variables can therefore be observed from these systems. Typically, these variables are not independent. Conversely, each variable is likely to interact with the other variables. On the one hand, the interactions among multivariate are important for people to make conversion of these variables into complex network structure and to reveal the intrinsic mechanism of these systems [1–3]. On the other hand, people are often confused with a large number of variables with overlapping information, which they expect to reduce to a small number of composites with as little loss of information as possible [4–6]. Principal component analysis (PCA) is considered as an appropriate candidate to perform such data reduction [7]. The PCA method uses orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components [8]. This transformation is defined in such a way that the first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible), and each succeeding component in turn has the highest variance possible under the constraint that it be orthogonal to the preceding components [9]. It is concerned with explaining the variance–covariance structure of the data through a few linear combinations of the original variables. The PCA method has proved to be a sophisticated technique since it was proposed at the beginning of last century, and it has been extensively applied to diverse areas of interest for data reduction and index construction [10–13].

The PCA method is constructed on the linear cross-correlation analysis, and works well when linear correlations exist among stationary variables. However, the linear cross-correlation function used to describe correlations suffers from several limitations [14], including at least (i) it measures linear correlations while fails to measure nonlinear correlations; and (ii) it is restricted to analyze stationary series, when the mean value, variance, and higher statistical moments remain unchanged along with time. Unfortunately, the real-world complex systems are often contaminated by external trends and often have complex structures, giving rise to the data of these systems being non-stationary and nonlinear [15–17]. A nonlinear system does not satisfy the superposition principle of additivity, or homogeneity, or both. Hence, the nonlinear principal component analysis (NLPCA) has been introduced in various ways before [18–21]. Generally, one way is to extract indices which are nonlinear combinations of variables that discriminate maximally in some sense. Another way is to find nonlinear combinations of unobserved components that are approximate to the observed variables. And the third way is to acquire transformations of the variables that optimize the linear PCA fit. A system with non-stationarity has the property of its statistical moments, like the mean and variance if they are present, changing with time. However, the non-stationary principal component analysis (NSPCA) has been few studied [22–24], although it is crucial for the data reduction of non-stationary variables. The core idea of the PCA method is to maximize the variance representing rich information through orthogonal transformation, while in the presence of non-stationarity, e.g., a persistent trend in non-stationary time series would increase the value of variance but bring very poor information, that violates the original intension of PCA. Lansangan and Barrios [23] discussed the effects of non-stationarity in PCA recurring to the autoregressive (AR) model and concluded that the PCA method could yield only one or very few components assigning similar loadings to all variables if the input data has, as columns, non-stationary time series. They also introduced a sparse PCA by imposing constraints on the estimation of the component loadings.

In this paper, we propose a new NSPCA method based on detrended cross-correlation analysis (DCCA) [25] and apply it to the non-stationary variables. The DCCA method was recently introduced by Podobnik and Stanley [25] to quantify cross-correlations between two non-stationary time series. A generalization to detrended cross-correlation coefficient was proposed by Zebende [26], to quantify the level of cross-correlation, that has the merit of ranging between $-1$ and 1. It is a normalization algorithm of the DCCA method, which is a natural derivation from the widely accepted detrended fluctuation analysis (DFA) [27] and DCCA.

The paper is arranged as follows. We first retrospect the DCCA method and the detrended cross-correlation coefficient, then introduce our NSPCA method. In Sect. 3, we apply the NSPCA method to empirical data analysis. Finally, we present a brief conclusion.

2 Methodology

2.1 DCCA and detrended cross-correlation coefficient

To analyze cross-correlations between two non-stationary variables, the DCCA method was proposed [25]. Consider non-stationary variables $\{X^{(1)}, X^{(2)}\}$ of equal length N:

(1) First we determine the profiles $Y^{(1)}_k=\sum _{i=1}^k X^{(1)}_i$ and $Y^{(2)}_k=\sum _{i=1}^k X^{(2)}_i$, respectively, for $k=1,\ldots ,N$.

(2) Then we divide each profile into $N_n\equiv \lfloor N/n \rfloor$ non-overlapping segments of equal length n, where $\lfloor \ldots \rfloor$ is the sign of lower integer and n is the scale length. In each segment v, that starts at $(v-1)n+1$ and ends at vn, we fit the integrated variables by the polynomial functions $\widetilde{Y}^{(1)}_{(v-1)n+i}$ and $\widetilde{Y}^{(2)}_{(v-1)n+i}$($1\le i\le n$) through least square estimation, respectively. Generally, the degree of fitting polynomial can be taken 1, 2, or larger integers in order to eliminate linear, quadratic or higher-order trends of the profiles.

(3) The local detrended covariance in each segment v is calculated by

$$\begin{aligned} f^2(n,v)= & {} \frac{1}{n}\sum _{i=1}^{n} \left[ Y^{(1)}_{(v-1)n+i}- \widetilde{Y}^{(1)}_{(v-1)n+i}\right] \nonumber \\&\times \left[ Y^{(2)}_{(v-1)n+i}- \widetilde{Y}^{(2)}_{(v-1)n+i}\right] , \end{aligned}$$

(1)

for $v=1,\ldots ,N_n$.

(4) Next average over all segments to obtain the detrended covariance,

$$\begin{aligned} \sigma ^2_{X^{(1)},X^{(2)}}(n)= \frac{1}{N_n} \sum _{v=1}^{N_n} f^2(n,v). \end{aligned}$$

(2)

In another way, the detrended covariance function is the covariance of the residuals obtained by the difference between $Y^{(1)}_k$ and $\widetilde{Y}^{(1)}_k$, $Y^{(2)}_k$ and $\widetilde{Y}^{(2)}_k$, respectively [28, 29],

$$\begin{aligned} \sigma ^2_{X^{(1)},X^{(2)}}(n)= \frac{1}{n\cdot N_n} \sum _{k=1}^{n\cdot N_n}\left[ Y^{(1)}_k- \widetilde{Y}^{(1)}_k\right] \left[ Y^{(2)}_k- \widetilde{Y}^{(2)}_k\right] .\nonumber \\ \end{aligned}$$

(3)

$\widetilde{Y}^{(1)}_k$ and $\widetilde{Y}^{(2)}_k$ are related to n, and for a given n, $N \approx n\cdot N_n$ if $N\rightarrow \infty$ or n is a divisor of N.

Here, we define a temporary variable $y^{(i)}$ as $y_k^{(i)} = Y_k^{(i)}-\widetilde{Y}_k^{(i)}$, where $i=1,2$, and $k=1,\ldots ,n\cdot N_n$. Hence, Eq. (3) becomes

$$\begin{aligned} \sigma ^2_{X^{(1)},X^{(2)}}(n)= \frac{1}{n\cdot N_n} \sum _{k=1}^{n\cdot N_n} y_k^{(1)}y_k^{(2)}. \end{aligned}$$

(4)

Based on the fact that $\widetilde{Y}_k^{(i)}$ is determined through the least square estimation of $Y_k^{(i)}$, the mean value of $y^{(i)}$ would be 0. Therefore, on the right side of Eq. (4), we derive the traditional covariance of $y^{(1)}$ and $y^{(2)}$. As a consequence, the detrended covariance of the original variables $X^{(1)}$ and $X^{(2)}$, represented by $\sigma ^2_{X^{(1)},X^{(2)}}(n)$, is equal to the covariance of the temporary variables $y^{(1)}$ and $y^{(2)}$.

If only one variable is considered, i.e., $X^{(1)}\equiv X^{(2)}$, the detrended covariance $\sigma ^2_{X^{(1)},X^{(2)}}(n)$ retrieves back to detrended variance $\sigma ^2_{X^{(1)},X^{(1)}}(n)$ of DFA [25], where

$$\begin{aligned} \sigma ^2_{X^{(1)},X^{(1)}}(n)= \frac{1}{n\cdot N_n} \sum _{k=1}^{n\cdot N_n}\left[ Y^{(1)}_k- \widetilde{Y}^{(1)}_k\right] ^2. \end{aligned}$$

(5)

$\sigma ^2_{X^{(1)},X^{(1)}}(n)$ is always non-negative, whose square root is detrended standard deviation.

The detrended covariance is capable of measuring the cross-correlation between non-stationary variables, while it suffers from the units of measurement that makes people difficult to compare the strength of cross-correlations among different variables. To quantify the level of cross-correlation, a dimensionless measure, detrended cross-correlation coefficient was proposed [26], defined as the ratio between the detrended covariance $\sigma ^2_{X^{(1)},X^{(2)}}(n)$ and the product of detrended standard deviations $\sigma _{X^{(1)},X^{(1)}}(n)\sigma _{X^{(2)},X^{(2)}}(n)$, i.e.

$$\begin{aligned} \rho _{X^{(1)},X^{(2)}}(n)= \frac{\sigma ^2_{X^{(1)},X^{(2)}}(n)}{\sigma _{X^{(1)},X^{(1)}}(n) \sigma _{X^{(2)},X^{(2)}}(n)}. \end{aligned}$$

(6)

$\rho$ ranges between $[-1,1]$. $\rho$ around 0 means there is no cross-correlation, which splits the level of cross-correlation into divergent directions. $\rho = 1$ and $\rho =-1$ both represent deterministic cross-correlations, 1 for the positive cross-correlation while $-1$ for the negative cross-correlation. For variables that are contaminated by external trends, the detrended cross-correlation coefficient is able to measure the intrinsic cross-correlation.

2.2 NSPCA

In this section, we introduce our NSPCA method. When the underlying time series present non-stationarity, typically when the series are contaminated by external trends, the strength of cross-correlations among variables is often overestimated or underestimated, and therefore, the traditional PCA method fails to rely on reliable cross-correlations to guide for the linear transformation of original variables. It is caused by the drawback of the linear cross-correlation analysis that is only applicable to stationary variables, which could give spurious interactions among non-stationary variables. The existence of external trends makes the PCA method often yields few components assigning similar loadings to all variables. The main aim for the proposal of NSPCA is to analyze the multidimensional non-stationary time series for dimension reduction and index reconstruction. As noted before, the DCCA method detects the intrinsic cross-correlations of variables in the presence of non-stationarity. Here in the NSPCA method, we use the detrended covariance or the detrended cross-correlation coefficient as the base to derive principal components, which would have the advantage to analyze non-stationary time series over the PCA method.

The NSPCA method presents linear combinations of p-dimensional variables $\{X^{(1)},X^{(2)},\ldots ,X^{(p)}\}$ (generally $2<p<N$) , i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} Z^{(1)} = a_{11}X^{(1)}+a_{12}X^{(2)}+\cdots +a_{1p}X^{(p)} = A^T_1\mathbf{X}\\ Z^{(2)} = a_{21}X^{(1)}+a_{22}X^{(2)}+\cdots +a_{2p}X^{(p)} = A^T_2\mathbf{X}\\ \qquad \quad \vdots \\ Z^{(p)} = a_{p1}X^{(1)}+a_{p2}X^{(2)}+\cdots +a_{pp}X^{(p)} = A^T_p\mathbf{X},\\ \end{array}\right. } \end{aligned}$$

that is defined on two assumptions:

• (i) The first principal component is the linear combination of original variables with the maximum detrended variance $\sigma ^2_{Z^{(1)},Z^{(1)}}$ in the case of non-stationarity.

• (ii) The kth principal component is to maximize the detrended variance $\sigma ^2_{Z^{(k)},Z^{(k)}}$ under the constraints of $A^T_kA_k=1$ and $A^T_kA_i=0$ $(i<k)$.

In the NSPCA, we maximize $\sigma ^2_{Z^{(1)},Z^{(1)}}=\sigma ^2_{A^T_1\mathbf{X},A^T_1\mathbf{X}}$ under the constraint $A^T_1A_1=1$ in order to obtain unique $A_1$. According to the Lagrange multipliers, to maximize $\sigma ^2_{A^T_1\mathbf{X},A^T_1\mathbf{X}}$, the Lagrange function is defined as:

$$\begin{aligned} \psi _1 =\sigma ^2_{A^T_1\mathbf{X},A^T_1\mathbf{X}} - \lambda \left( A^T_1A_1-1\right) . \end{aligned}$$

(7)

The optimal solution is solved by $\partial \psi _1 /\partial A_1= \partial \sigma ^2_{A^T_1\mathbf{X},A^T_1\mathbf{X}}/\partial A_1 -2\lambda A_1=0$.

To solve Eq. (7), we retrospect the procedures of DCCA. For two non-stationary variables $X^{(i)}$ and $X^{(j)}$ with equal length N, their profiles are $Y^{(i)}_k=\sum _{l=1}^k X^{(i)}_l$ and $Y^{(j)}_k=\sum _{l=1}^k X^{(j)}_l$, respectively. It is straightforward to obtain:

$$\begin{aligned} Y^{(i)}_k+Y^{(j)}_k=\sum _{l=1}^k X^{(i)}_l+\sum _{l=1}^k X^{(j)}_l = \sum _{l=1}^k \left[ X^{(i)}_l+X^{(j)}_l\right] .\nonumber \\ \end{aligned}$$

(8)

Here, we define $Y^{(i)}_k+Y^{(j)}_k \triangleq Y_k^{(i)+(j)}$. For $Y^{(i)}$ and $Y^{(j)}$, we use the polynomial functions of order m (m may be 1, 2, or higher integer) to fit them, and estimate $\widetilde{Y}^{(i)}$ and $\widetilde{Y}^{(j)}$ respectively. We also use the polynomial functions of order m to fit $Y^{(i)+(j)}$. It can be proved that (see the “Appendix”):

$$\begin{aligned} (Y^{(i)}-\widetilde{Y}^{(i)})+(Y^{(j)}-\widetilde{Y}^{(j)})= (Y^{(i)+(j)}-\widetilde{Y}^{(i)+(j)}).\nonumber \\ \end{aligned}$$

(9)

Furthermore, if we multiply any original variable $X^{(i)}$ by a real number a, the profile would be $aY^{(i)}$ and its fitting value would be $a\widetilde{Y}^{(i)}$. Hence, we define a transformation $\mathscr {F}(X^{(i)})$ from $X^{(i)}$ to $Y^{(i)}-\widetilde{Y}^{(i)}$, including (i) calculating the profiles and (ii) eliminating the local trends as specified in the DCCA. It can be derived that:

$$\begin{aligned} \begin{array}{l} X^{(i)} + X^{(j)} \mathop {\longrightarrow }\limits ^{\mathscr {F}} (Y^{(i)}-\widetilde{Y}^{(i)})+(Y^{(j)}-\widetilde{Y}^{(j)}),\\ aX^{(i)} \mathop {\longrightarrow }\limits ^{\mathscr {F}} a(Y^{(i)}-\widetilde{Y}^{(i)}). \end{array} \end{aligned}$$

(10)

Based on Eq. (10), $\mathscr {F}$ is a linear transformation that satisfies the additivity and homogeneity.

Except the polynomial functions, several candidates to eliminate trending effects in non-stationary time series include the moving average method [30, 31], the Fourier filtering technique [32, 33] and the empirical mode decomposition (EMD) [34, 35], etc. The moving average method has almost the same effects with the polynomial functions, since Eq. (9) also holds, and the moving average method has been found to share very similar conclusions with the polynomial functions in most cases [31]. Other methods, like the Fourier filtering technique and the EMD method, although they can be used to eliminate periodic trends and monotonic trends [33, 35], are difficult for people to get an analytical solution, as we cannot make sure that $\mathscr {F}$ in Eq. (10) is a linear transformation in these cases.

For variables with non-stationarity, the cross-correlations are regularly estimated by calculating the detrended covariances between each pair of variables. All these detrended covariances constitute a detrended cross-correlation matrix [29]:

$$\begin{aligned} {\varvec{\varSigma }}_\mathbf{X} =\left[ \begin{array}{c} \sigma _{X^{(1)},X^{(1)}}, \sigma _{X^{(1)},X^{(2)}}, \ldots , \sigma _{X^{(1)},X^{(p)}}\\ \sigma _{X^{(2)},X^{(1)}}, \sigma _{X^{(2)},X^{(2)}}, \ldots , \sigma _{X^{(2)},X^{(p)}}\\ \vdots \\ \sigma _{X^{(p)},X^{(1)}}, \sigma _{X^{(p)},X^{(2)}}, \ldots , \sigma _{X^{(p)},X^{(p)}}\\ \end{array} \right] , \end{aligned}$$

(11)

where $\sigma _{X^{(i)},X^{(j)}}$ denotes the detrended covariance between $X_i$ and $X_j$ for $1\le i,j \le p$. According to the definition of the detrended covariance, ${\varvec{\varSigma }}_\mathbf{X}$ is a real symmetric matrix that could give rise to non-negative eigenvalues $\lambda _1 \ge \lambda _2 \ge \lambda _p \ge 0$.

Moreover, we already defined the temporary variable in Sect. 2.1

$$\begin{aligned} y_k^{(i)} = Y_k^{(i)}-\widetilde{Y}_k^{(i)} = \mathscr {F}(X_k^{(i)}), \end{aligned}$$

(12)

and inferred that the detrended covariance of the original variables is equal to the covariance of temporary variables. Therefore, the detrended covariance matrix ${\varvec{\varSigma }_\mathbf{X}}$ of the original variables is equal to the covariance matrix $\mathbf{S}$ of the temporary variables $\mathbf{y}$, i.e.

$$\begin{aligned} {\varvec{\varSigma }}_\mathbf{X} = \mathbf{S_y = y}^T\mathbf{y}/(n\cdot N_n) \approx \mathbf{y}^T\mathbf{y}/N, \end{aligned}$$

(13)

where $\mathbf{y}$ represents the set of all temporal variables $y^{(i)}$ ($1\le i\le p$), that corresponds to $\mathbf{X}$ which is the set of all original variables $X^{(i)}$ ($1\le i\le p$).

According to Eqs. (10) and (12), we obtain $\mathscr {F}(A^T\mathbf{X}) =A^T\mathbf{y}$. Further considering Eq. (13), we derive:

$$\begin{aligned} {\varvec{\varSigma }}_{A^T\mathbf{X}}= \mathbf{S}_{A^T\mathbf{y}}=(A^T\mathbf{y})^T(A^T\mathbf{y}))/N = A^T{\varvec{\varSigma }}_\mathbf{X}A. \end{aligned}$$

(14)

In the NSPCA method, the detrended variance and the detrended covariance of the linear combinations are $\sigma ^2_{Z^{(i)},Z^{(i)}}= A^T_i{\varvec{\varSigma }}_\mathbf{X}A_i$ and $\sigma ^2_{Z^{(i)},Z^{(j)}}= A^T_i{\varvec{\varSigma }}_\mathbf{X}A_j$ for $1\le i,j\le p$. As we mentioned, the first principal component is the linear combination with the maximum detrended variance, i.e. maximizes $\sigma ^2_{Z^{(1)},Z^{(1)}}= A^T_1{\varvec{\varSigma }}_\mathbf{X}A_1$ under the constraint $A^T_1A_1=1$. According to the Lagrange multipliers, the Lagrange function is defined as:

$$\begin{aligned} \psi _1 = A^T_1{\varvec{\varSigma }}_\mathbf{X}A_1 - \lambda \left( A^T_1A_1-1\right) . \end{aligned}$$

(15)

By $\partial \psi _1 /\partial A_1=2{\varvec{\varSigma }}_\mathbf{X}A_1-2\lambda A_1=0$, we can obtain $({\varvec{\varSigma }}_\mathbf{X}-\lambda \mathbf{I}) A_1 = 0$ and $A^T_1{\varvec{\varSigma }}_\mathbf{X}A_1=\lambda$. Therefore, $\lambda$ is one of the eigenvalues of ${\varvec{\varSigma }}_\mathbf{X}$. To maximum $A^T_1{\varvec{\varSigma }}_\mathbf{X}A_1$, we set $\lambda =\lambda _1$. The eigenvector $\xi _1$ corresponding to $\lambda _1$ through unitization (as $A^{T}_1A=1$) is therefore $A_1$.

The kth principal component is to maximize $A^T_k{\varvec{\varSigma }}_\mathbf{X}A_k$ under the constraints of $A^T_kA_k=1$ and $A^T_kA_i=0$ $(i<k)$. Similarly, the Lagrange function is defined as:

$$\begin{aligned} \psi _k = A^T_k{\varvec{\varSigma }}_\mathbf{X}A_k - \lambda \left( A^T_kA_k-1\right) -2\sum _{i=1}^{k-1}\gamma _i\left( A^T_iA_i\right) .\nonumber \\ \end{aligned}$$

(16)

By $\partial \psi _k /\partial A_k=2{\varvec{\varSigma }}_\mathbf{X}A_k-2\lambda A_k -2\sum _{i=1}^{k-1}\gamma _iA_i=0$, we further obtain $({\varvec{\varSigma }}_\mathbf{X}-\lambda \mathbf{I}) A_k = 0$ and $A^T_k{\varvec{\varSigma }}_\mathbf{X}A_k=\lambda$. So $\lambda$ is still one of the eigenvalues of ${\varvec{\varSigma }}_\mathbf{X}$. As $k-1$ eigenvalues have been used, $\lambda =\lambda _k$. The eigenvector $\xi _k$ corresponding to $\lambda _k$ through unitization would be $A_k$. Therefore, we derive the coefficients of all components $A_k$ ($k=1,2,\ldots ,p$) for the NSPCA method, which correspond to the eigenvalues of detrended cross-correlation matrix. The number of principal components we mainly take into consideration is the minimum integer k that satisfies $\sum _{i=1}^k \lambda _i/\sum _{i=1}^d \lambda _i \geqslant 85\,\%$, where d is the dimension of the variables, and $\lambda$ is the eigenvalue of the detrended cross-correlation matrix.

Here, we note that different variables in the data may have different units of measurement, so it is necessary to normalize data when performing PCA as well as NSPCA. The PCA method calculates a new projection of the data set, and the new axis is based on the standard deviation of the variables. A variable with a high standard deviation will have a higher weight for the calculation of axis than a variable with a low standard deviation. After being normalized, all variables have the same standard deviation; thus, have the same weight and the PCA calculates relevant axis. For non-stationary time series, the mean value and variance of each variable are likely to change over time, and therefore, it makes no sense to normalize the data simply by subtracting the mean value and dividing the standard deviation. Hence, we use the detrended cross-correlation coefficient instead of the detrended covariance in such a case. Of course, if different variables have identical units of measurement, the detrended covariance is still an appropriate candidate for the NSPCA.

3 Empirical analysis

Fig. 1

a We use the AR(1) model to generate 10 variables with $Y(0)\equiv 0$, where $\phi =1$, $\mu =1$, $\varepsilon (t)\sim N(0,8^2)$. Each variable contains 1000 data points. b The eigenvalues $\lambda _i$ of the linear cross-correlation matrix for the data points generated by $Y(t)=\phi Y(t-1)+\mu +\varepsilon (t)$, where $\phi =1$,$\mu =1$, $\varepsilon (t)\sim N(0,8^2)$. There is a dominating eigenvalue that is much larger than other eigenvalues. In the lower panel, we show the eigenvector corresponding to the largest eigenvalue. c The 4 principal components given by the PCA method for the data points generated by $Y(t)=\phi Y(t-1)+\varepsilon (t)$, where $\phi =1$, $\varepsilon (t)\sim N(0,8^2)$. d The 8 principal components given by the NSPCA method for the data points generated by $Y(t)=\phi Y(t-1)+\mu +\varepsilon (t)$, where $\phi =1$, $\mu =1$, $\varepsilon (t)\sim N(0,8^2)$

To test the performance of the NSPCA method, we first consider the autoregressive [AR(1)] model: $Y(t) = \phi Y(t-1)+\mu +\varepsilon (t)$, where Y(t) is the data to be determined at time point t, $\mu$ is a constant describing the drift of series, and $\varepsilon (t)$ represents the random disturbance that obeys $\varepsilon (t)\sim N(0,s^2)$ with variance $s^2$. When $\mu =0$ as well as $|\phi |<1$, the series are stationary. For $\mu \ne 0$, the mean value of Y drifts with time. For $|\phi |\geqslant 1$, the variance of Y drifts with time. Here, we set $\phi =1$, $\mu =1$ and $s=8$ so that Y corresponds to a random walk with drift, where the mean value and the variance both change along with time, and therefore, the data present non-stationary.

We apply the AR(1) model to generate 10 variables containing 1000 data points of each variable, respectively (see Fig. 1a), and also show the random walk without drift, i.e. $\mu =0$. First we use the traditional PCA method to analyze these data. For the random walk with drift ($\phi =1$, $\mu =1$), we obtain only one principal component which explains $92.88\,\%$ of the variance, since the maximum eigenvalue is much larger than other eigenvalues. Although we generate the data separately, the drift term $\mu$ leads to spurious cross-correlations that substantially decreases the number of principal components. The eigenvector of the first principal component assigns similar loadings to all variables (see Fig. 1b). It is the effects of external trends caused by the drift term $\mu$. Unfortunately, the information of intrinsic fluctuations and cross-correlations is covered in such a case. It was also observed in Ref. [23] that the lack of sparsity made the PCA yielded few components assigning similar loadings to all variables and resulted to difficulty in interpretation of results.

We also apply the traditional PCA to the random walk without drift , i.e. $\mu =0$, in which case the obvious trends disappear. The number of principal components increases from 1 (with drift) to 4 (without drift), as indicated in Fig. 1c. Although the mean values of these data stay the same with the original mean value when $\mu =0$, the increase in variance along with time t (being proportional to t for the random walk) also brings spurious cross-correlations among these variables that decreases the number of principal components compared with the number of original variables.

Since the changes of both mean value and variance for each variable give rise to the non-stationarity of the data, we resort to the NSPCA method. In the NSPCA, we consider the random walk with drift ($\phi =1$, $\mu =1$). The drift term can be directly filtered out in the procedure of eliminating the trend of profiles in the DCCA. Furthermore, the variance will also be regulated along with time t in this procedure, to make the variance not be proportional to t. As expected, the number of principal components increases to 8, that is very close to the number of the original variables. The eigenvalues of all components are 1.5948, 1.3116, 1.2558, 1.1395, 0.9810, 0.8984, 0.8455, 0.7769, 0.6345, 0.5619, respectively, so we choose the top 8 principal components into consideration. The eigenvectors corresponding to the eigenvalues of principal components are shown in columns of the matrix below:

$$\begin{aligned} \left[ \begin{array}{cccccccccc} 0.45&{}\quad 0.06&{}\quad 0.22&{}\quad 0.33&{}\quad 0.24&{}\quad -0.13&{}\quad 0.50&{}\quad 0.20\\ 0.15&{}\quad 0.03&{}\quad -0.64&{}\quad 0.12&{}\quad 0.28&{}\quad 0.15&{}\quad -0.05&{}\quad 0.60\\ 0.19&{}\quad -0.02&{}\quad 0.01&{}\quad -0.39&{}\quad 0.81&{}\quad -0.12&{}\quad -0.14&{}\quad -0.34\\ -0.14&{}\quad 0.29&{}\quad -0.53&{}\quad -0.05&{}\quad -0.09&{}\quad -0.15&{}\quad 0.62&{}\quad -0.44\\ -0.25&{}\quad 0.29&{}\quad 0.32&{}\quad 0.31&{}\quad 0.31&{}\quad 0.60&{}\quad 0.24&{}\quad -0.03\\ 0.03&{}\quad -0.63&{}\quad 0.14&{}\quad -0.20&{}\quad -0.01&{}\quad -0.15&{}\quad 0.48&{}\quad 0.21\\ 0.58&{}\quad 0.10&{}\quad -0.20&{}\quad -0.06&{}\quad -0.20&{}\quad 0.27&{}\quad -0.11&{}\quad -0.14\\ -0.08&{}\quad 0.59&{}\quad 0.19&{}\quad -0.12&{}\quad 0.01&{}\quad -0.56&{}\quad -0.03&{}\quad 0.35\\ -0.19&{}\quad 0.15&{}\quad 0.02&{}\quad -0.71&{}\quad -0.05&{}\quad 0.38&{}\quad 0.21&{}\quad 0.31\\ 0.52&{}\quad 0.22&{}\quad 0.26&{}\quad -0.24&{}\quad -0.25&{}\quad 0.11&{}\quad 0.08&{}\quad -0.05 \end{array} \right] \end{aligned}$$

Moreover, we try 100 times and always find number 8 of principal components, which indicates the robustness of the NSPCA method. The intension of this empirical analysis on the AR model is to demonstrate that when there is no intrinsic cross-correlation among variables, there should not be only one or very few principal components that are representative enough for the original variables, since the original variables are not related.

In brief, for the random walk with drift, the mean value as well as the variance of each variable changes with time. These two factors both lead to the non-stationarity of the data, which brings spurious cross-correlations among variables. In such a case, the PCA presents misleading principal components. While in the NSPCA, the drift term corresponding to the mean value of each variable is filtered out, also the variance is regulated, and therefore, we could obtain the reliable results based on intrinsic cross-correlations.

Fig. 2

a Variables $Y^{(1)}$ and $Y^{(2)}$ with quadratic trends. b–f The principal components of the correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend, linear trends, quadratic trends, cubic trends, and periodic trends, respectively, by PCA. g–k The principal components of the same data respectively by the NSPCA method

Next, suppose we have $n+1$ independent and identically distributed (i.i.d) Gaussian variables $X^{(i)}$ ($i=1,2,\ldots ,n+1$), which are not related to each other. Each variable contains $N=10{,}000$ data points. Then we construct another n variables $Y^{(i)}$ using the combinations of these $n+1$ independent realizations, thus making the variables correlated: $Y_j^{(i)} = X_j^{(i)}+X_j^{(n+1)}$ ($i=1,2,\ldots ,n$, and $j=1,2,\ldots ,N$). We consider the cases of $Y^{(i)}$ with diverse types of trends, including no trend, linear trends $T(j) = aj/N$, quadratic trends $T(j)= b(j/N)^2$, cubic trends $T(j) = c(j/N)^3$, and even periodic trends $T(j)=dsin(20\pi j/N)$ (see the discussions in [36, 37], one can remove the non-stationary effects by eliminating local trends with appropriate polynomial order), where $j=1,2,..N$. As a representative image, $Y^{(1)}$ and $Y^{(2)}$ are shown with quadratic trends ($b=6$) in Fig. 2a. Due to adding the quadratic trends, the linear cross-correlation coefficient between $Y^{(1)}$ and $Y^{(2)}$ increases from 0.5069 to 0.8090. The increment of the linear cross-correlation coefficient is determined by the competition between the magnitudes of $Y^{(1)}$, $Y^{(2)}$ and the magnitudes of trends. Compared with the AR model that the trends make the cross-correlations between independent variables change from zero to non-zero values, the trends in this case also make the strength of cross-correlations between correlated variables become much stronger.

We apply the traditional PCA method to the correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend. The eigenvalues corresponding to all components are listed in Table 1. The number of principal components is 7 (see Fig. 2b), which is smaller than 10 but larger than 1. It relies on the fact that there exist cross-correlations among underlying variables so the number of principal components is smaller than 10, and there exist uncertainties in each variable that cannot be determined by other variables so the number of principal components is larger than 1. When we artificially add the linear trends (e.g., $a=6$) to $Y^{(i)}$ and apply the PCA to analyze the composite data, we obtain 3 principal components in Fig. 2c. The decrement on the number of principal components here are determined by the competition between the original variables and the trends. If we increase the value of a that enlarges the magnitude of trends, the number of principal components will continue to reduce until 1. For other cases, we get 3 principal components for quadratic trend ($b=6$, see Fig. 2d), 3 principal components for cubic trends ($c=6$, see Fig. 2e), and 4 principal components for periodic trends ($d=6$, see Fig. 2f). Also if we increase the values of b, c and d, the number of principal components in each case will persistently decrease until 1. The presence of trends spuriously increase the strength of cross-correlations among correlated variables, make the number of principal components decrease, and give rise to unreliable results by the PCA method.

Table 1 The eigenvalues corresponding to each component for the correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend, linear trends, quadratic trends, cubic trends, and periodic trends, respectively by the PCA method

Considering the disadvantage of PCA, we further apply the NSPCA method to analyze the same data. For the correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend, we still get 7 principal components (see Fig. 2g), the same compared with the PCA method. Moreover, when we add diverse types of trends, the number of principal components is always 7 as expected (see Fig. 2h–k), which is apparently different from the number that from PCA. The eigenvalues corresponding to each component for correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend, linear trends, quadratic trends, cubic trends, and periodic trends by the NSPCA method are shown in Table 2. It indicates that the NSPCA method can filter out the effects of trends on the cross-correlations among variables and present reliable principal components even in the presence of diverse types of trends.

Table 2 The eigenvalues corresponding to each component for the correlated variables $Y^{(i)}$ ($i=1,2,\ldots ,10$) with no trend, linear trends, quadratic trends, cubic trends, and periodic trends, respectively by the NSPCA method

Fig. 3

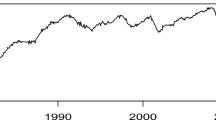
a The closing prices of 18 Chinese sector indexes ranging from January 6, 2009 to May 9, 2012, with a total of 810 daily observations of each sector. b The linear cross-correlation matrix of 18 sectors. c The detrended cross-correlation matrix of 18 sectors. d The eigenvalues of the linear cross-correlation matrix for the PCA and the detrended cross-correlation matrix for the NSPCA, respectively. e The eigenvectors in columns corresponding to all eigenvalues by the NSPCA. f Several principal components given by the NSPCA for the closing prices of 18 Chinese sector indexes. Here we mainly focus on the first two principal components

Although the existence of trends mostly increases the strength of cross-correlations between variables as indicated above, there also exist very few cases that the trends decrease the strength of cross-correlations. Here, we introduce a simple example to demonstrate it. Suppose that two correlated variables $Y^{(1)}$ and $Y^{(2)}$ are added by linear trends, respectively. The trend added to $Y^{(1)}$ persistently increases, while the trend added to $Y^{(2)}$ increases at the first half but decreases at the second half. Briefly, these two trends are not correlated. If the trends dominate the new composite variables, the strength of cross-correlation between them would decrease instead. In such a case, the traditional PCA spuriously raises the number of principal components rather than the opposite, while the NSPCA method could filter the influence of these trends, and resolves appropriate principle components.

As our third example, we further apply the NSPCA to real-world financial markets. The daily closing prices of 18 Chinese sector indexes mixed by Shanghai and Shenzhen markets are investigated. The data expand from January 6, 2009, to May 9, 2012, with a total of 810 daily observations of each sector. They cover almost all fields of industries in Chinese stock markets, including the communication (H11049), construction (H11042), extraction (H11031), finance (H11046), food (H11032), forestry (H11030), information (H11044), machinery (H11039), metals (H11038), paper (H11035), petrochemistry (H11036), real estate (H11047), service (H11048), synthesis (H11050), textile (H11033), utility (H11041), wholesale and retail (H11045), and wood (H11034) industries ( For detailed information, please refer to [38]).

In this period, most sectors present very similar patterns (see Fig. 3a) driven by many common influence factors including the economic, political, technical, and psychosocial factors, etc. Also each sector presents its own behavior. It is clear that (i) the mean values of these closing prices change with time, and (ii) the variances of the closing prices also change with time. The strong non-stationary properties of these data make the PCA fails to give genuine cross-correlations among sectors. For comparison, the linear cross-correlation matrix for the PCA and the detrended cross-correlation matrix for the NSPCA are given, respectively, in Fig. 3b, c. Most sectors still have strong cross-correlations with other sectors even with the removal of external trends since the detrended cross-correlation coefficients in detrended cross-correlation matrix are still large, except the finance sector and the real estate sector. This performance is consistent with our previous analysis in reference [38], while the linear cross-correlation matrix shows an obscure image at this point.

Due to the existence of non-stationarity, we apply the NSPCA method to these closing prices and obtain all the eigenvalues corresponding to each component in Fig. 3d, whose eigenvectors are shown in Fig. 3e. We obtain 2 principal components, the corresponding eigenvalues of which are 14.2783 and 1.4136, and hence the first principal component generally has much larger magnitude than the second one, as shown in Fig. 3f. It indicates that intrinsic cross-correlations still exist among these variables even though we remove the trends and regulate the variances. Moreover, the first principal component shows very similar trace compared to the original variables, demonstrating that the first principal component is representative enough in the NSPCA.

We change the scale n and also change the order of polynomial functions in the procedure of eliminating local trends. The eigenvalues and the eigenvectors of the detrended cross-correlation matrix have no significant difference. It indicates that the NSPCA method is robust enough for non-stationary variables analysis, irrelevant of the scale and the order of polynomial functions.

4 Conclusion

In this paper, we introduce the NSPCA method for non-stationary time series analysis in high-dimensional space based on the DCCA and the detrended cross-correlation coefficient. We theoretically derive that the detrended variances of the principal components correspond to the eigenvalues of the detrended cross-correlation matrix, and the eigenvector corresponding to each eigenvalue becomes the coefficients of linear combinations. We apply the NSPCA method to the AR model, the correlated Gaussian distributed variables, as well as the real-world financial markets. The traditional PCA method fails to detect intrinsic cross-correlations and presents misleading principal components due to the non-stationarity caused by the changes of mean value and variance in the presence of trends. Conversely, the NSPCA method is capable to filter out the change of mean value and regulate the change of variance to detect the intrinsic cross-correlations among variables and therefore provides reliable principal components. The robustness of the NSPCA method for non-stationary time series indicates its wide applications to more real-world data in further studies.

Appendix

To certify Eq. (9), it is necessary to prove $\widetilde{Y}^{(j)} + \widetilde{Y}^{(j)} = \widetilde{Y}^{(i)+(j)}$. Here, we introduce a brief proof. Suppose that we use the polynomial functions $\widetilde{Y} = a_1+a_2x+a_3x^2+\cdots + mx^m$ to eliminate local trends, where $a_1, a_2,\ldots ,a_m$ are the coefficients to be determined through the least square estimation, and x represents the independent variable generally taking $1, 2, \ldots , m$. To solve the equation $Ax=Y$, we resort to the equation $A^TAx=A^TY$, and obtain $\widetilde{Y}=A(A^TA)^{-1}A^TY$, where

$$\begin{aligned} A = \left[ \begin{array}{ccccc} \ 1 &{} \quad x_1 &{} \quad x_1^2&{} \quad \cdots &{} \quad x_1^m \\ \ \ 1 &{} \quad x_2 &{} \quad x_2^2&{} \quad \cdots &{} \quad x_2^m \\ \ \vdots &{} \vdots &{} \vdots &{} \vdots &{}\vdots \\ \ 1 &{} \quad x_{n} &{} \quad x_{n}^2&{} \quad \cdots &{} \quad x_{n}^m \ \end{array} \right] , \end{aligned}$$

and $x=[a_1, a_2, \ldots , a_m]^T$. n represents the length of scale in DCCA. Therefore, we derive $\widetilde{Y}^{(i)}= A(A^TA)^{-1}A^T Y^{(i)}$ as well as $\widetilde{Y}^{(j)}{=} A(A^TA)^{-1}A^T Y^{(j)}$. Also

$$\begin{aligned} \widetilde{Y}^{(i)}+ \widetilde{Y}^{(j)}= & {} A(A^TA)^{-1}A^T Y^{(i)} +A(A^TA)^{-1}A^T Y^{(j)} \\= & {} A(A^TA)^{-1}A^T (Y^{(i)}+Y^{(j)}) \\= & {} A(A^TA)^{-1}A^T Y^{(i)+(j)} = \widetilde{Y}^{(i)+(j)}. \end{aligned}$$