Hopf and zero-Hopf bifurcations in the Hindmarsh–Rose system

Abstract

We prove the existence of the classical Hopf bifurcation and of the zero-Hopf bifurcation in the Hindmarsh–Rose system. For doing this, some adequate change in parameters must be done in order that the computations become easier.

1 Introduction

These last years there was a big interest in studying the three-dimensional Hindmarsh–Rose polynomial ordinary differential system [1]. It appears as a reduction in the conductance based on the Hodgkin–Huxley model for neural spiking (see for more details [2]). This differential system can be written as:

$$\begin{aligned} {\dot{x}}= & {} y-x^3+bx^2+I-z, \nonumber \\ {\dot{y}}= & {} 1-5x^2-y, \nonumber \\ {\dot{z}}= & {} \mu (s(x-x_0)-z), \end{aligned}$$

(1)

where $b,\ I,\ \mu ,\ s,\ x_0$ are parameters and the dot indicates derivative with respect to the time t.

The interest in system (1) basically comes from two main reasons. The first one is due to its simplicity since it is just a differential system in ${\mathbb {R}}^3$ with a polynomial nonlinearity containing only five parameters. And the second one is because it captures the three main dynamical behaviors presented by real neurons: quiescence, tonic spiking and bursting. We can find in the literature many papers that investigate the dynamics presented by system (1) (see, for instance, [3–13]).

The study of the periodic orbits of a differential equation is one of the main objectives of the qualitative theory of differential equations. In general, the periodic orbits are studied numerically because, usually, their analytical study is very difficult. Here, using the averaging theory, we shall study analytically the periodic orbits of the three-dimensional Hindmarsh–Rose polynomial ordinary differential Eq. (1) which bifurcate firstly from a classical Hopf bifurcation and secondly from a zero-Hopf bifurcation.

Among the mentioned papers on the differential system (1), none of them study the occurrence of a Hopf or a zero-Hopf bifurcation in this differentiable system, except the paper [10] where the authors studied numerically the existence of the Hopf bifurcation.

In the present paper, we consider some special choice of parameters that facilitates the study of the classical Hopf bifurcation and also of the zero-Hopf bifurcation. A classical Hopf bifurcation in ${\mathbb {R}}^3$ takes place in an equilibrium point with eigenvalues of the form $\pm \omega i$ and $\delta \ne 0$, while for a zero-Hopf bifurcation the eigenvalues are $\pm \omega i$ and 0. Here an equilibrium point with eigenvalues $\pm \omega i$ and 0 will be called a zero-Hopf equilibrium.

The study of the zero-Hopf bifurcation of system (1) is done in Theorem 2 (see Sect. 4). We note that the local stability or instability of the periodic solution starting in the zero-Hopf bifurcation is described at the end of Sect. 4. Moreover, the proof of Theorem 2 is done using averaging theory, and the method used for proving Theorem 2 can be applied for studying the zero-Hopf bifurcation in other differential systems.

We study the classical Hopf bifurcation of system (1) in Theorem 4 (see Sect. 6). For related proofs of Theorems 2 and 4, see [14] and [15].

2 Preliminaries

The first step of our analysis is to change the parameters s and $x_0$ to new parameters c and d in the following way

$$\begin{aligned} c= & {} \mu s, \nonumber \\ d= & {} \mu s x_0. \end{aligned}$$

(2)

Now we change the parameters b and I to new parameters $\beta$ and $\rho$ in order to obtain a simplified expression of one of the equilibria, and easier computations proving Theorems 2 and 4. We consider the following change in parameters

$$\begin{aligned} b= & {} \displaystyle 5+\frac{c}{\mu \rho }-\frac{\beta }{\rho }+\rho , \nonumber \\ \displaystyle I= & {} -1-\frac{d}{\mu }+\beta \rho . \end{aligned}$$

(3)

Next, lemma shows that under generic hypothesis we can perform the change in parameters (3).

Lemma 1

Let $H:{\mathbb {R}}^7\rightarrow {\mathbb {R}}^2$ be a function given by

$$\begin{aligned} H_1(b,I,c,\mu ,d,\rho ,\beta )= & {} b \mu \rho -5\mu \rho +c-\beta \mu +\rho ^2\mu ,\\ H_2(b,I,c,\mu ,d,\rho ,\beta )= & {} I\mu +\mu -\beta \rho \mu . \end{aligned}$$

For a given $({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}})\in {\mathbb {R}}^5$ that satisfies ${\overline{\mu }}\ne 0$, ${\overline{d}}+{\overline{\mu }}(1+{\overline{I}})\ne 0$ and $R({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}})\ne 0$ where the function $R(b,I,c,\mu ,d)$ is given by

$$\begin{aligned}&\mu ^5 \left( 18 (b-5) c \mu (d+I \mu +\mu )-(b-5)^2 c^2 \mu \right. \nonumber \\&\quad + \mu (d+I \mu +\mu ) (\mu (-4 b ((b-15) b\nonumber \\&\left. \quad + 75)+27 I+527)+27 d)+4 c^3\right) . \end{aligned}$$

(4)

Then, there exists $({\overline{\rho }},{\overline{\beta }})\in {\mathbb {R}}^2$ such that $H({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}},$ ${\overline{\rho }},{\overline{\beta }})=(0,0)$. Moreover, in a small neighborhood of this point, there exist smooth functions $\rho (b,I,c,\mu ,d)$ and $\beta (b,I,c,\mu ,d)$ such that

$$\begin{aligned} H(b,I,c,\mu ,d,\rho (b,I,c,\mu ,d),\beta (b,I,c,\mu ,d))\equiv 0. \end{aligned}$$

Proof

First, we solve the equation $H_1({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}},\rho ,\beta )=0$ in terms of $\beta$ obtaining

$$\begin{aligned} \beta = \frac{{\overline{b}} {\overline{\mu }} \rho +{\overline{c}}+{\overline{\mu }} \rho ^2-5 {\overline{\mu }} \rho }{{\overline{\mu }} }. \end{aligned}$$

(5)

It is possible because ${\overline{\mu }}\ne 0$. Now, we substitute the expression of $\beta$ in the equation $H_2=0$ obtaining an equation $h_1({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}},\rho )=0$, where

$$\begin{aligned} h_1(b,I,c,\mu ,d,\rho )= & {} \mu \rho ^3-\rho ^2 (5 \mu -b \mu )\nonumber \\&+\,c \rho -d-I \mu -\mu , \end{aligned}$$

which is a cubic equation in the variable $\rho$. It is clear that there exists a real solution ${\overline{\rho }}$ of this cubic equation. The hypothesis ${\overline{d}}+{\overline{\mu }}(1+{\overline{I}})\ne 0$ implies that ${\overline{\rho }}\ne 0$. Now, we just substitute the value ${\overline{\rho }}$ in (5), and we get ${\overline{\beta }}$. The second part of lemma follows from the Implicit Function Theorem. The determinant of the jacobian matrix $\displaystyle \frac{\partial (H_1,H_2)}{\partial (\rho ,\beta )}$, with the substitution (5), is

$$\begin{aligned} h_2(b,I,c,\mu ,d,\rho )= & {} \mu \left( b \mu \rho +c+\mu \rho ^2-5 \mu \rho \right) \nonumber \\&+\, b \mu ^2 \rho +2 \mu ^2 \rho ^2-5 \mu ^2 \rho . \end{aligned}$$

In order to finish the proof, it is enough to show that $h_2({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}},{\overline{\rho }})\ne 0$. The resultant of $h_1$ and $h_2$ with respect to the variable $\rho$ is given by (4). The hypothesis $R({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}})\ne 0$ implies that $h_i({\overline{b}},{\overline{I}},{\overline{c}},{\overline{\mu }},{\overline{d}},\rho )=0$, for $i=1,2$, do not share a common root ${\overline{\rho }}$. $\square$

Then, it is easy to verify that

$$\begin{aligned} p_0=\left( \rho ,1-5\rho ^2,s(\rho -x_0)\right) \end{aligned}$$

(6)

is an equilibrium of system (1).

Now, we choose the parameters $\mu$, $\beta$ and s in order that when $\varepsilon =0$ the eigenvalues of the linear part of system (1) at the equilibrium point $p_0$ are $\delta$, $\omega i$ and $-\omega i$. This is an scenario candidate to have a Hopf bifurcation. So, we get

$$\begin{aligned} \mu= & {} \mu _0+\mu _1\varepsilon \nonumber \\ \beta= & {} \beta _0+\beta _1\varepsilon \nonumber \\ c= & {} c_0+c_1\varepsilon \end{aligned}$$

(7)

where

$$\begin{aligned} \mu _0= & {} -\dfrac{{\varDelta } +\delta (1+ \omega ^2)}{10 \rho }, \\ \beta _0= & {} -\dfrac{1}{20 \rho \left( {\varDelta } +\delta (1+ \omega ^2)\right) }\big (\delta ^2 {\varDelta } \left( 1+\omega ^2\right) \\&+\,{\varDelta } \left( {\varDelta } +10 \rho \left( \rho ^2+10 \rho -1\right) \right) \\&+\,2 \delta (1+5 \rho (-4+\rho (20+\rho ))+2 \omega ^2 \\&+\,5 \rho (-4+(-10+\rho ) \rho ) \omega ^2+\omega ^4)\big ), \\ c_0= & {} \dfrac{{\varDelta } \left( (1+\delta -10 \rho )^2+(1+\delta )^2 \omega ^2\right) }{100 \rho ^2}, \end{aligned}$$

with

$$\begin{aligned} {\varDelta }=1-10 \rho +\omega ^2. \end{aligned}$$

(8)

In the next step, we translate the equilibrium point $p_0$ to the origin of coordinates doing the change in variables

$$\begin{aligned} (x,y,z)=({\overline{x}},{\overline{y}},{\overline{z}})+\left( \rho ,1-5\rho ^2, \frac{c\rho -d}{\mu }\right) , \end{aligned}$$

(9)

and we obtain

$$\begin{aligned} \dot{{\overline{x}}}= & {} a_1 {\overline{x}} +{\overline{y}}-{\overline{z}}+a_2{\overline{x}}^2-{\overline{x}}^3\nonumber \\&+\,\varepsilon a_3(2 \rho {\overline{x}} + {\overline{x}}^2 )+{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ \dot{{\overline{y}}}= & {} -10\rho {\overline{x}}-{\overline{y}}-5{\overline{x}}^2, \nonumber \\ \dot{{\overline{z}}}= & {} a_4 {\overline{x}}+a_5 {\overline{z}} +\varepsilon (c_1 {\overline{x}}-\mu _1 {\overline{z}}) , \end{aligned}$$

(10)

where

$$\begin{aligned} a_1= & {} \dfrac{10\rho -(1+\delta ){\varDelta }}{10 \rho },\\ a_2= & {} -\dfrac{1+\delta -20 \rho -10 \delta \rho +30 \rho ^3+(1+\delta ) \omega ^2}{20 \rho ^2},\\ a_3= & {} \dfrac{1}{\rho \left( {\varDelta } +\delta (1+ \omega ^2)\right) ^2}\big ( -10 c_1 \rho \left( {\varDelta } +\delta (1+ \omega ^2)\right) \\&-\mu _1 {\varDelta } \left( (1+\delta -10 \rho )^2+(1+\delta )^2 \omega ^2\right) \big ) -\dfrac{\beta _1}{\rho }, \\ a_4= & {} \dfrac{{\varDelta } \left( (1+\delta -10 \rho )^2+(1+\delta )^2 \omega ^2\right) }{100 \rho ^2},\\ a_5= & {} \dfrac{ {\varDelta } +\delta (1+ \omega ^2)}{10 \rho }. \end{aligned}$$

We remark that the differential system (10) in the variables $({\overline{x}},{\overline{y}},{\overline{z}})$ will be used for proving our main results on the zero-Hopf bifurcation (Theorem 2) and on the classical Hopf bifurcation (Theorem 4).

3 Averaging theory of first order

We consider the initial value problems

$$\begin{aligned} \dot{{\mathbf {x}}}=\varepsilon F_1(t,{\mathbf {x}})+\varepsilon ^2 F_2(t,{\mathbf {x}},\varepsilon ),\quad {\mathbf {x}}(0)={\mathbf {x}}_0, \end{aligned}$$

(11)

and

$$\begin{aligned} \dot{{\mathbf {y}}}=\varepsilon g({\mathbf{y}}),\quad {\mathbf {y}}(0)={\mathbf {x}}_0, \end{aligned}$$

with ${\mathbf {x}}$ , ${\mathbf {y}}$ and ${\mathbf {x}}_0$ in some open ${\varOmega }$ of ${{\mathbb {R}}^n}$, $t\in [0,\infty )$, $\varepsilon \in (0,\varepsilon _0]$. We assume that $\mathbf {F_1}$ and $\mathbf {F_2}$ are periodic of period T in the variable t, and we set

$$\begin{aligned} g({\mathbf {y}})=\dfrac{1}{T}\int \limits _{0}^{T}F_1(t,{\mathbf {y}})dt. \end{aligned}$$

(12)

Theorem 1

Assume that $F_1$, $D_{\mathbf {x}}F_1$ ,$D_\mathbf {xx}F_1$ and $D_{\mathbf {x}}F_2$ are continuous and bounded by a constant independent of $\varepsilon$ in $[0,\infty )\times \ {\varOmega } \times (0,\varepsilon _0]$ and that $y(t)\in {\varOmega }$ for $t\in [0,1/\varepsilon ]$. Then, the following statements hold:

• (a) For $t\in [0,1/\varepsilon ]$, we have ${\mathbf {x}}(t)- {\mathbf {y}}(t)= O(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• (b) If $p \ne 0$ is a singular point of system (12) and $\det D_{\mathbf {y}}g(p) \ne 0$, then there exists a periodic solution $\phi (t,\varepsilon )$ of period T for system (11) which is close to p and such that $\phi (0,\varepsilon )-p=O(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• (c) The stability of the periodic solution $\phi (t, \varepsilon )$ is given by the stability of the singular point.

We have used the notation $D_{\mathbf {x}}g$ for all the first derivatives of g, and $D_\mathbf {xx}g$ for all the second derivatives of g.

For a proof of Theorem 1, see [16].

4 Zero-Hopf bifurcation of system (1)

In this section, we analyze the case $\delta =0$. It means that we are in the scenario of a zero-Hopf bifurcation. Our approach for obtaining the periodic orbits of the system bifurcating from the zero-Hopf equilibrium $p_0$ is through the averaging theory of first order (see Sect. 3).

In the next theorem, we study the zero-Hopf bifurcation in the Hindmarsh–Rose system (1).

Fig. 1

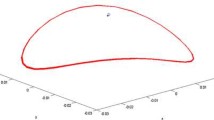
The periodic orbit of Theorem 2 bifurcating from a zero-Hopf bifurcation for the parameters $b=-403/20, I=-2499/2000, \mu =3, s=5, x_0=0,\varepsilon =1/10$. The parallelepiped which appears in the figure containing the periodic orbit has the following dimensions in the variables $(x,y,z)\in [-0.3,0]\times [0.8,0.95]\times [-2,0.5]$

Theorem 2

The equilibrium point $p_0$ of the Hindmarsh–Rose system (1) given in (6) exhibits a zero-Hopf bifurcation for the choice of the parameters given in (2), (3) and (7), when $\varepsilon =\delta =0$, if $(C_2B_1B_0-C_1B_1^2)C_0>0, B_0 D {\varDelta } \ne 0$ (see Sect. 4 for the definitions of $B_0$, $B_1$, $C_0$, $C_1$, $C_2$, ${\varDelta }$ and D). Then, for $\varepsilon \ne 0$ sufficiently small, the bifurcated periodic solution is of the form

$$\begin{aligned} x(t,\varepsilon )= & {} \rho + \dfrac{\varepsilon }{20\rho \omega ^2}\Big (\overline{r_0} (1+\omega ) \cos (\omega t )\nonumber \\&-\,2 \overline{w_0}+\overline{r_0}(1-\omega ) \sin (\omega t ) \Big )+{{\mathcal {O}}(\varepsilon ^2)},\nonumber \\ y(t,\varepsilon )= & {} 1-5\rho ^2 - \dfrac{\varepsilon }{2\omega ^2} \Big (\overline{r_0} \cos (\omega t)+\overline{r_0} \sin (\omega t ) \nonumber \\&-\, 2 \overline{w_0}\Big ) +{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ z(t,\varepsilon )= & {} s(\rho -x_0)+ \dfrac{\varepsilon }{200 \rho ^2 \omega ^2} \nonumber \\ \displaystyle&\,\times \Big (2 \overline{w_0} \big ((1-10 \rho )^2+\omega ^2\big )\Big ) \nonumber \\&+\, \overline{r_0} {\varDelta } (10 \rho +\omega -1) \sin (\omega t )\nonumber \\&+\,\overline{r_0} {\varDelta } (10 \rho -\omega -1) \cos (\omega t ) +{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ \end{aligned}$$

(13)

where $\overline{r_0}$ and $\overline{w_0}$ are given in (20) (See Fig. 1).

In our approach, we want to study the periodic solutions that born at the origin. So we perform the rescaling of variables $({\overline{x}},{\overline{y}},{\overline{z}})=(\varepsilon {\overline{u}},\varepsilon {\overline{v}},\varepsilon {\overline{w}})$. Then, system (10) becomes

$$\begin{aligned} \dot{{\overline{u}}}= & {} \widetilde{a_1} {\overline{u}} +{\overline{v}}-{\overline{w}} +\varepsilon (\widetilde{a_2} {\overline{u}}^2 +2\rho \widetilde{a_3} {\overline{u}} ) + {{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ \dot{{\overline{v}}}= & {} -10\rho {\overline{u}}-{\overline{v}}-5\varepsilon {\overline{u}}^2, \nonumber \\ \dot{{\overline{w}}}= & {} \widetilde{a_4} {\overline{u}}+\widetilde{a_5} {\overline{w}} +\varepsilon (c_1 {\overline{u}}-\mu _1 {\overline{w}}), \end{aligned}$$

(14)

where $\widetilde{a_j}=a_j \left| _{\delta =0}\right.$ for $j=1,2\ldots ,5$.

Now, we put the linear part of system (14) into its real Jordan normal form doing the change in variables

$$\begin{aligned} \left( \begin{array}{c} {\overline{u}} \\ {\overline{v}} \\ {\overline{w}} \end{array}\right) = M^{-1}\left( \begin{array}{c} u \\ v \\ w \end{array}\right) , \end{aligned}$$

(15)

where the matrix M is

$$\begin{aligned} \left( \begin{array}{ccc} {\varDelta } +\omega -{\varDelta } \omega +\omega ^3 &{} {\varDelta } +\omega -\omega ^2 &{} 10\rho \\ {\varDelta } -\omega +{\varDelta } \omega -\omega ^3 &{} {\varDelta } -\omega -\omega ^2 &{} 10 \rho \\ {\varDelta } &{} {\varDelta } &{} 10\rho \end{array}\right) . \end{aligned}$$

So, we obtain

$$\begin{aligned} {\dot{u}}= & {} -\omega v +\varepsilon P_1(u,v,w) +{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ {\dot{v}}= & {} \omega u +\varepsilon P_2(u,v,w) +{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ {\dot{w}}= & {} \varepsilon P_3(u,v,w)+{{\mathcal {O}}}(\varepsilon ^2), \end{aligned}$$

(16)

where the polynomials $P_i(u,v,w)=b_{i1}u+b_{i2}v+b_{i3}w+b_{i4}u^2+b_{i5}uv+ b_{i6}uw+b_{i7}v^2+b_{i8}vw+b_{i9}w^2$ for $i=1,2,3$ are

$$\begin{aligned} P_1= & {} K_1 (400 Q_2 \rho ^3 \omega ^2-100 Q_1^2 \rho ^2 \omega (1-10 \rho +\omega )\\&+\, Q_1 (1+10 \rho (-1+\omega )+\omega ^2) \\&\,\times (K_2-Q_1 \omega (1-20 \rho +30 \rho ^3+\omega ^2))),\\ P_2= & {} K_1 (400 Q_2 \rho ^3 \omega ^2+100 Q_1^2 \rho ^2 \omega (-1+10 \rho +\omega ) \\&+\, Q_1 Q_3 (1+\omega ^2-10 \rho (1+\omega ))), \\ P_3= & {} K_1 (\omega (400 Q_2 \rho ^3 \omega -Q_1^2 {\varDelta } (1-20 \rho +100 \rho ^2\\&+\, 30 \rho ^3+\omega ^2)) +K_2 Q_1 {\varDelta }), \end{aligned}$$

where

$$\begin{aligned} K_1= & {} \dfrac{1}{8000 \rho ^4 \omega ^5}, \\ K_2= & {} -\dfrac{800 \rho ^3 \omega ^3}{{\varDelta }} (\beta _1 {\varDelta } +10 c_1 \rho +\mu _1 (1-20 \rho \\&+\quad 100 \rho ^2+\omega ^2)),\\ Q_1= & {} u+v-2 w+u \omega -v \omega , \\ Q_2= & {} 10 Q_1 c_1 \rho \omega -\mu _1 \omega (-u {\varDelta } (1-10 \rho +\omega )\\&+v {\varDelta } (-1+10 \rho +\omega )+2 w ((1-10 \rho )^2+\omega ^2)), \\ Q_3= & {} K_2-Q_1 \omega (1-20 \rho +30 \rho ^3+\omega ^2). \end{aligned}$$

We pass system (16) to cylindrical coordinates using $u=r\cos \theta$, $v=r\sin \theta$ and $w=w$. We get

$$\begin{aligned} {\dot{r}}= & {} \varepsilon (\cos \theta P_1+\sin \theta P_2)+{{\mathcal {O}}} (\varepsilon ^2),\nonumber \\ {\dot{\theta }}= & {} \omega +\varepsilon (\cos \theta P_2-\sin \theta P_1)/r + {{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ {\dot{w}}= & {} \varepsilon P_3+{{\mathcal {O}}}(\varepsilon ^2), \end{aligned}$$

(17)

where we are denoting $P_i(r\cos \theta ,r\sin \theta ,w)$ just by $P_i$ for $i=1,2,3$.

Now, we take $\theta$ as a new independent variable. So system (17) becomes

$$\begin{aligned} \dfrac{dr}{d\theta }= & {} \varepsilon \displaystyle \frac{\cos \theta P_1+\sin \theta P_2}{\omega }+{{\mathcal {O}}}(\varepsilon ^2),\nonumber \\ \dfrac{dw}{d\theta }= & {} \varepsilon \displaystyle \frac{P_3}{\omega }+{{\mathcal {O}}}(\varepsilon ^2). \end{aligned}$$

(18)

Here we are ready to apply the averaging theory of first order, presented in Sect. 3 to system (18). As in (12), we must compute the integrals

$$\begin{aligned} g_1(r,w)= & {} \displaystyle \frac{1}{2\pi }\int _0^{2\pi }\frac{\cos \theta P_1 +\sin \theta P_2}{\omega }d\theta ,\\ g_2(r,w)= & {} \displaystyle \frac{1}{2\pi }\int _0^{2\pi }\frac{P_3}{\omega }d\theta . \end{aligned}$$

Performing the calculations, we obtain

$$\begin{aligned} g_1(r,w)= & {} \dfrac{r}{2000 \rho ^4 \omega ^5 {\varDelta }} \left( B_0w+B_1\right) ,\nonumber \\ g_2(r,w)= & {} \dfrac{1}{8000 \rho ^4 \omega ^5}\left( C_0r^2+C_1w^2+C_2w\right) , \end{aligned}$$

(19)

where ${\varDelta }$ is given in (8) and

$$\begin{aligned} B_0= & {} {\varDelta } \left( 1-10 \rho (3+\rho (-30+\rho (97+30 \rho )))+2 \omega ^2 \right. \\&\left. +\, 10 \rho (1+2 \rho ) (-2+3 \rho (-2+5 \rho )) \omega ^2\right. \\&\left. +\,(1+10 \rho ) \omega ^4\right) ,\\ B_1= & {} -100 \rho ^3 \omega ^2 (10 c_1 \rho \left( 1-10 \rho +\omega ^2+20 \rho \omega ^2)\right. \\&\left. + \,\mu _1((1-10 \rho )^3+2 (1+200 \rho ^2 (-1+5 \rho )) \omega ^2\right. \\&\left. +\, (1+30 \rho ) \omega ^4\right) \\&+\, 2 \beta _1 {\varDelta } \left( 1+\omega ^2+10 \rho (-1+\omega ^2))\right) \\ C_0= & {} {\varDelta } \left( 1+\omega ^2\right) \left( 20 \rho -30 \rho ^3-100 \rho ^2 -\omega ^2-1\right) ,\\ C_1= & {} 4 {\varDelta } \left( 20 \rho -30 \rho ^3-100 \rho ^2 -\omega ^2-1\right) ,\\ C_2= & {} 800 \rho ^3 \omega ^2 (10 c_1 \rho +\mu _1 ((1-10 \rho )^2+\omega ^2)+2 \beta _1 {\varDelta }). \end{aligned}$$

Consider

$$\begin{aligned} \overline{w_0}=-\frac{B_1}{B_0} \text{ and } \overline{r_0}=\sqrt{\frac{C_2B_1B_0-C_1B_1^2}{C_0B_0^2}}. \end{aligned}$$

(20)

If $\dfrac{C_2B_1B_0-C_1B_1^2}{C_0}>0$ and $C_0 B_0\ne 0$, then $(\overline{r_0},\overline{w_0})$ is a singular point of the system $({\dot{r}},{\dot{w}})=(g_1(r,w),g_2(r,w))$. From (19), we get

$$\begin{aligned} D= & {} \det \left. \left( \begin{array}{cc} \dfrac{\partial g_1}{\partial r} &{}\dfrac{\partial g_1}{\partial w}\\ \dfrac{\partial g_2}{\partial r} &{}\dfrac{\partial g_2}{\partial w} \end{array} \right) \right| _{(r,w)=(\overline{r_0},\overline{w_0})}\\= & {} \dfrac{- B_0 C_0 }{8000000 {\varDelta } \rho ^8 \omega ^{10}}\overline{r_0}^2\ne 0. \end{aligned}$$

So, according to Theorem 1, this solution (when it exists) provides a periodic solution $(r(\theta ,\varepsilon ), w(\theta ,\varepsilon ))$ of the differential system (18) such that $(r(0,\varepsilon ), w(0,\varepsilon ))$ tends to $(\overline{r_0},\overline{w_0})$ when $\varepsilon$ tends to 0.

Going back through the changes in variables and using the statement (a) of Theorem 1, we have

$$\begin{aligned} (r(\theta ,\varepsilon ), w(\theta ,\varepsilon ))=(\overline{r_0},\overline{w_0})+ {{\mathcal {O}}}(\varepsilon ), \end{aligned}$$

Then, in cylindrical coordinates $(r,\theta ,w)$, the periodic solution is

$$\begin{aligned} (r(t,\varepsilon ), \theta (t,\varepsilon ), w(t,\varepsilon ))= (\overline{r_0},\omega t,\overline{w_0})+{{\mathcal {O}}}(\varepsilon ), \end{aligned}$$

and in the variables (u, v, w) the periodic solution becomes

$$\begin{aligned}&(u(t,\varepsilon ), v(t,\varepsilon ), w(t,\varepsilon ))\\&\quad =(\overline{r_0}\cos (\omega t), \overline{r_0}\sin (\omega t),\overline{w_0}) +{{\mathcal {O}}}(\varepsilon ). \end{aligned}$$

Now, undo the linear change in variables (15) that transform system (14) into system (16), and we obtain the periodic solution

$$\begin{aligned} {\overline{u}}(t,\varepsilon )= & {} \dfrac{\overline{r_0} (1-\omega ) \sin (t \omega )+\overline{r_0} (1+\omega ) \cos (\omega t )-2 \overline{w_0}}{20\rho \omega ^2}\\&+\, {{\mathcal {O}}}(\varepsilon ),\\ {\overline{v}}(t,\varepsilon )= & {} -\dfrac{\overline{r_0} \sin (\omega t )+\overline{r_0} \cos (t \omega )-2 \overline{w_0}}{2\omega ^2}+{{\mathcal {O}}}(\varepsilon ), \\ {\overline{w}}(t,\varepsilon )= & {} \dfrac{1}{200 \rho ^2 \omega ^2} ( \overline{r_0} {\varDelta } (10 \rho -\omega -1) \cos (\omega t )\\&+\, 2 \overline{w_0} ((1-10 \rho )^2+\omega ^2). \\&+\, \overline{r_0} {\varDelta } (10 \rho +\omega -1) \sin (\omega t ) )+{{\mathcal {O}}}(\varepsilon ), \end{aligned}$$

of system (14).

Finally, using that $({\overline{x}},{\overline{y}},{\overline{z}})=(\varepsilon {\overline{u}},\varepsilon {\overline{v}},\varepsilon {\overline{w}})$ and (9), we get the periodic solution given in (13).

Note that the periodic solution (13) borns by a zero-Hopf bifurcation from the zero-Hopf equilibrium $p_0$, because when $\varepsilon \rightarrow 0$ this periodic solution tends to the equilibrium $p_0$. Moreover, we know the kind of linear stability of this periodic solution. From Theorem 1, we need to know the eigenvalues of the Jacobian matrix of the map $(g_1,g_2)$ evaluated at $(\overline{r_0},\overline{w_0})$. If both eigenvalues have negative real part, this periodic orbit is an attractor. If both eigenvalues have positive real part, this periodic orbit is a repeller. If both eigenvalues are purely imaginary, then this periodic solution is linear stable. Finally, if one eigenvalue has negative real part and the other has positive real part, the periodic solution has an unstable and a stable invariant manifold formed by two cylinders.

This completes the proof of Theorem 2 and consequently the study of the zero-Hopf bifurcation for the Hindmarsh–Rose differential system at the mentioned equilibrium point. Now, it remains to study the classical Hopf bifurcation.

5 Classical Hopf bifurcation

Assume that a system ${\dot{x}}=F(x)$ has an equilibrium point $p_0$. If its linearization at $p_0$ has a pair of conjugate purely imaginary eigenvalues and the others eigenvalues have nonvanishing real part, then this is the setting for a classical Hopf bifurcation. We can expect to see a small-amplitude limit cycle branching from the equilibrium point $p_0$. It remains to compute the first Lyapunov coefficient $\ell _1(p_0)$ of the system near $p_0$. When $\ell _1(p_0)<0$, the point $p_0$ is a weak focus of system restricted to the central manifold of $p_0$ and the limit cycle that emerges from $p_0$ is stable. In this case, we say that the Hopf bifurcation is supercritical. When $\ell _1(p_0)>0$, the point $p_0$ is also a weak focus of the system restricted to the central manifold of $p_0$, but the limit cycle that borns from $p_0$ is unstable. In this second case, we say that the Hopf bifurcation is subcritical.

Here we use the following result presented on page 180 of the book [17] for computing $\ell _1(p_0)$.

Theorem 3

Let ${\dot{x}}=F(x)$ be a differential system having $p_0$ as an equilibrium point. Consider the third-order Taylor approximation of F around $p_0$ given by $F(x)=Ax +\dfrac{1}{2!}B(x,x)+\dfrac{1}{3!}C(x,x,x)+{\mathcal {O}}(|x|^4)$. Assume that A has a pair of purely imaginary eigenvalues $\pm \omega i$, and these eigenvalues are the only eigenvalues with real part equal to zero. Let q be the eigenvector of A corresponding to the eigenvalue $\omega i$, normalized so that ${\overline{q}}\cdot q=1$, where ${\overline{q}}$ is the conjugate vector of q. Let p be the adjoint eigenvector such that $A^Tp=-\omega i p$ and ${\overline{p}}\cdot q=1$. If $\text{ Id }$ denotes the identity matrix, then

$$\begin{aligned} \ell _1(p_0)= & {} \dfrac{1}{2\omega }Re({\overline{p}}\cdot C(q,q,{\overline{q}})- 2{\overline{p}}\cdot B(q,A^{-1}\nonumber \\&\times B(q,{\overline{q}})) +{\overline{p}}\cdot B({\overline{q}},(2\omega i \text{ Id }-A)^{-1}\\&\times B(q,q)) ). \end{aligned}$$

6 Classical Hopf bifurcation of system (1)

In what follows, we perform the study of a classical Hopf bifurcation using a result that can be found in the book of Kuznetzov (see details in Sect. 5).

Theorem 4

The equilibrium point $p_0$ of the Hindmarsh–Rose system (1) given in (6) exhibits a classical Hopf bifurcation for the choice of the parameters given in (2), (3) and (7), when $\varepsilon =0$, $\delta \ne 0$ and

$$\begin{aligned} \ell _1(p_0)=\displaystyle \frac{(\omega ^2+1)R_1}{400 \delta \rho ^4 \omega ^3 \left( \delta ^2+\omega ^2\right) \left( \delta ^2+4 \omega ^2\right) R_2}\ne 0, \end{aligned}$$

where $R_1$ and $R_2$, given in the end of Sect. 6, are polynomials in the variables $\rho$, $\delta$ and $\omega ^2.$ Moreover, if $\ell _1(p_0)<0$, then the Hopf bifurcation is supercritical; otherwise, it is subcritical.

We recall that these classical Hopf bifurcations have been studied numerically by Storace, Linaro and de Lange in [10].

First of all, we consider system (10), with $\varepsilon =0$, given by

$$\begin{aligned} \dot{{\overline{x}}}= & {} a_1 {\overline{x}} +{\overline{y}}-{\overline{z}}+a_2{\overline{x}}^2-{\overline{x}}^3,\nonumber \\ \dot{{\overline{y}}}= & {} -10\rho {\overline{x}}-{\overline{y}}-5{\overline{x}}^2, \nonumber \\ \dot{{\overline{z}}}= & {} a_4 {\overline{x}}+a_5 {\overline{z}} , \end{aligned}$$

(21)

The matrix of the linear part of (21) is

$$\begin{aligned} A =\left( \begin{array}{ccc} a_1 &{} 1 &{} -1 \\ -10\rho &{} -1 &{} 0 \\ a_4 &{} 0 &{} a_5 \end{array} \right) , \end{aligned}$$

and its eigenvalues are $\delta$, $\omega i$ and $-\omega i$. In order to prove that we have a Hopf bifurcation at the equilibrium point $p_0$, it remains to prove that the first Lyapunov coefficient $\ell _1(p_0)$ is different from zero. According to Theorem 3, to compute $\ell _1(p_0)$, we need not only the matrix A but also the bilinear and trilinear forms, B and C, associate with terms of second and third orders of system (21), the inverse of matrix A and the inverse of the matrix $2\omega i Id-A$, where Id is the identity matrix of ${\mathbb {R}}^3$.

In what follows, the letters u, v and w will denote vectors of ${\mathbb {R}}^3$, and they have no relation with the real variables u, v and w used in the proof of Theorem 2. The bilinear form B evaluated at two vectors $u=(u_1,u_2,u_3)$ and $v=(v_1,v_2,v_3)$ is given by

$$\begin{aligned} B(u,v)=(2a_2u_1v_1,-10u_1v_1,0). \end{aligned}$$

And the trilinear form C evaluated at three vectors $u=(u_1,u_2,u_3)$, $v=(v_1,v_2,v_3)$ and $w=(w_1,w_2,w_3)$ is given by

$$\begin{aligned} C(u,v,w)=(-6u_1v_1w_1,0,0). \end{aligned}$$

Let q be the eigenvector of A corresponding to the eigenvalue $\omega i$, normalized so that ${\overline{q}}\cdot q=1$, where ${\overline{q}}$ is the conjugate vector of q. The expression of q is given by

$$\begin{aligned} q=\displaystyle \frac{1}{\sqrt{q_1\overline{q_1}+q_2\overline{q_2}+ q_3\overline{q_3}}}(q_1,q_2,q_3), \end{aligned}$$

where

$$\begin{aligned} q_1= & {} 10\rho ({\varDelta }+\delta (1+\omega ^2))-100 \rho ^2 \omega i, \\ q_2= & {} -100 (1+\delta -10 \rho ) \rho ^2+100 (1+\delta ) \rho ^2 \omega i, \\ q_3= & {} -{\varDelta } ((1+\delta -10 \rho )^2+(1+\delta )^2 \omega ^2), \\ \end{aligned}$$

Let p be the adjoint eigenvector such that $A^Tp=-\omega i p$ and ${\overline{p}}\cdot q=1$. The expression of p is given by

$$\begin{aligned} p=\displaystyle \frac{\sqrt{q_1\overline{q_1}+q_2\overline{q_2}+ q_3\overline{q_3}}}{q_1\overline{p_1}+q_2\overline{p_2}+ q_3\overline{p_3}}(p_1,p_2,p_3), \end{aligned}$$

where

$$\begin{aligned} p_1= & {} 1+\delta -10 \rho +(1+\delta ) \omega ^2 +10 \rho \omega i,\\ p_2= & {} 1+\delta -10 \rho +i (1+\delta ) \omega ,\\ p_3= & {} 10 \rho . \end{aligned}$$

So, from Theorem 3, the first Lyapunov coefficient is

$$\begin{aligned} \ell _1(p_0)=\dfrac{(1+w^2)R_1}{400 \delta \rho ^4 \omega ^3 (\delta ^2+\omega ^2) (\delta ^2+4 \omega ^2) R_2}, \end{aligned}$$

where $R_1=\sum _{i=0}^{8}r_i\rho ^i,$ $r_i=r_i(\delta ,\omega ^2)$ with

$$\begin{aligned} r_0= & {} W_1^4 \delta _1^5 (\delta ^2+8 \omega ^2+2 \delta \omega ^2),\\ r_1= & {} 10W_1^3 \delta _1^3 (-6 \delta ^2-9 \delta ^3-2 \delta ^4-48 \omega ^2-86 \delta \omega ^2\\&-39 \delta ^2 \omega ^2 -6 \delta ^3 \omega ^2+8 \omega ^4+4 \delta \omega ^4), \\ r_2= & {} -100W_1^2 \delta _1^2 (-15 \delta ^2-29 \delta ^3-12 \delta ^4-\delta ^5 \\&-120 \omega ^2-270 \delta \omega ^2-183 \delta ^2 \omega ^2-55 \delta ^3 \omega ^2\\&-7 \delta ^4 \omega ^2+24 \omega ^4+14 \delta \omega ^4+2 \delta ^2 \omega ^4), \\ \end{aligned}$$

$$\begin{aligned} r_3= & {} 20W_1 \delta _1 (-997 \delta ^2-2291 \delta ^3-1341 \delta ^4-197 \delta ^5\\&-7976 \omega ^2-20922 \delta \omega ^2-18154 \delta ^2 \omega ^2\\&-7590 \delta ^3 \omega ^2-1776 \delta ^4 \omega ^2-144 \delta ^5 \omega ^2+448 \omega ^4\\&-1644 \delta \omega ^4-1667 \delta ^2 \omega ^4157 \delta ^3 \omega ^4+21 \delta ^4 \omega ^4\\&+\, 3 \delta ^5 \omega ^4+424 \omega ^6+478 \delta \omega ^6+90 \delta ^2 \omega ^6\\&+\, 42 \delta ^3 \omega ^6+6 \delta ^4 \omega ^6),\\ \end{aligned}$$

$$\begin{aligned} r_4= & {} 200(\delta ^2 (738+\delta (1908+\delta (1399-3 (-92\\&+\, \delta ) \delta )))+5904 \omega ^2+\delta (17134+\delta (17407\nonumber \\&+\, \delta (8730+\delta (2649 +340 \delta -6 \delta ^2)))) \omega ^2\nonumber \\&+\, (1832+\delta (7028+\delta (6798 +\delta (1898-3 (\delta -1 ) \\&\, \times \delta (17+\delta ))))) \omega ^4-(1+\delta ) (848\\&+\, \delta (398+3 \delta (75+\delta (29+4 \delta )))) \omega ^6\\&+\, 12 (1+\delta )^2 (2+\delta ) \omega ^8), \\ r_5= & {} -1000 (564 \delta ^2+995 \delta ^3+310 \delta ^4-21 \delta ^5+4512 \omega ^2\\&+\, 9258 \delta \omega ^2+5296 \delta ^2 \omega ^2+1164 \delta ^3 \omega ^2+84 \delta ^4 \omega ^2\\ \end{aligned}$$

$$\begin{aligned}&-30 \delta ^5 \omega ^2-192 \omega ^4+244 \delta \omega ^4-336 \delta ^2 \omega ^4\\&-489 \delta ^3 \omega ^4-126 \delta ^4 \omega ^4-9 \delta ^5 \omega ^4+96 \omega ^6\\&+\, 186 \delta \omega ^6+132 \delta ^2 \omega ^6+42 \delta ^3 \omega ^6), \\ r_6= & {} 100 (7609 \delta ^2+4627 \delta ^3-2373 \delta ^4+9 \delta ^5\\&+\, 60872 \omega ^2+49834 \delta \omega ^2 -20212 \delta ^2 \omega ^2\\ \end{aligned}$$

$$\begin{aligned}&-15120 \delta ^3 \omega ^2-2328 \delta ^4 \omega ^2+18 \delta ^5 \omega ^2+2544 \omega ^4 \\&-1932 \delta \omega ^4+849 \delta ^2 \omega ^4-21 \delta ^3 \omega ^4+63 \delta ^4 \omega ^4\\&+\, 9 \delta ^5 \omega ^4 +2472 \omega ^6+234 \delta \omega ^6\\&+\, 270 \delta ^2 \omega ^6+126 \delta ^3 \omega ^6+18 \delta ^4 \omega ^6), \\ r_7= & {} 3000 (-97+3 \delta +3 \omega ^2+3 \delta \omega ^2) (-2 \delta ^2-3 \delta ^3\\&-16 \omega ^2-30 \delta \omega ^2-11 \delta ^2 \omega ^2-2 \delta ^3 \omega ^2+8 \omega ^4\\&+\, 4 \delta \omega ^4), \\ r_8= & {} -90000 (-\delta ^2-2 \delta ^3-8 \omega ^2-20 \delta \omega ^2-11 \delta ^2 \omega ^2\\&-4 \delta ^3 \omega ^2+8 \omega ^4+8 \delta \omega ^4+4 \delta ^2 \omega ^4), \end{aligned}$$

and $R_2=R_2(\rho ,\delta ,\omega ^2)$ is

$$\begin{aligned}&W_1^3 \delta _1^2-20 W_1^2 (2+\delta ) \delta _1 \rho +100 W_1 \delta (6+\delta ) \rho ^2\\&\quad +100 \rho ^2 (7+200 \rho ^2+8 \omega ^2+\omega ^4 \\&\quad -20 \rho (2+\delta +\omega ^2)). \end{aligned}$$

Here, $W_1=1+\omega ^2$ and $\delta _1=1+\delta$.

Now, the proof of Theorem 4 follows directly from Theorem 3.

7 Conclusion section

Choosing special parameters, we have studied the zero-Hopf bifurcation (see Theorem 2) and also the classical Hopf bifurcation (see Theorem 4) of the three-dimensional Hindmarsh–Rose polynomial ordinary differential system (1). The proof of Theorem 2 is done using the averaging theory, while the proof of Theorem 4 uses a result of Kuznetsov.

In general, the technic here described for proving the zero-Hopf bifurcation using the averaging theory can be applied to other differential systems for studying their zero-Hopf bifurcations.