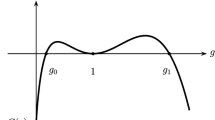
Abstract
Little seems to be known about the solitary waves and their properties of the completely integrable equations with singularity. This paper addresses the solitary waves of an integrable equation based on the bifurcation method of dynamical systems. We highlight two interesting results on the solitary waves. First, for arbitrary wave speed, there do exist infinitely many solitary waves in the integrable equation, which are classified by their expressions and forms of motion. Second, we find a family of solitary waves whose profiles seem like tree stumps.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In 1985, Chowdhury and Roy [1] proposed a modified Harry Dym equation
which is the first member in the positive Camassa–Holm hierarchy [2]. Its generalized form is reciprocally linked with the KdV equation [3].
In 1991, Cao and Geng [4] found a non-confocal generator, from which three soliton hierarchies are given as the isospectral equations of the eigenvalue problems. One of the equations is the form
In 1996, through the tri-Hamiltonian method, Olver and Rosenau [5] derived the integrable equation
Latter in 2010, Li and Qiao [6] considered the bifurcations of traveling wave solutions for the following nonlinear equation
where \(k\in \mathbb {R}\), \(k\ne -1\), 0. They used the bifurcation method of dynamical systems to study all possible traveling wave solutions and their implicit representations for Eq. (1.4) in the cases of \(|k|=1/2\), 2, respectively. Particularly, when \(k=1/2,2\), the existence of the infinitely many solitary wave of Eq. (1.4) is proved. Then Pan and Liu [7] continued to consider the problems on the traveling wave solutions and their bifurcations of Eq. (1.4) for the case of \(|k|=p/q\)(\(p\ne q\) and p, \(q\in \mathbb {Z}^{+}\)). When \(k=2\), Qiao [8, 9] proposed a completely integrable hierarchy from which they drew Eq. (1.4) and gave its bi-Hamiltonian operators. In recent years, Eq. (1.4) has attracted much attention in soliton theory [10–15]. However, the above-mentioned results limit to some properties of Eq. (1.4) with the same degree between \(\left( 1/m^{k}\right) _{xxx}\) and \(\left( 1/m^{k}\right) _{x}\).
In 2014, Pan et al. [16] proposed a completely integrable equation
which is associated with the KdV equation by the reciprocal transformation. By means of the singular transformation \(u(x,t)=-1/m(x,t)\), Eq. (1.5) can be reduced to the following equation
By applying the bifurcation method of dynamical systems, the implicit representations of the cuspons and the periodic cuspons of Eq. (1.6) are presented [16].
Little seems to be known about the infinitely many solitary waves and their properties of the completely integrable equations with singularity. Due to the influence of the singular term 1 / m(x, t), it is therefore of great interest to study dynamic properties of Eq. (1.5) directly. It is worth noting that a family of unbounded solutions of Eq. (1.6) may turn into the solitary wave solutions of Eq. (1.5). Also, the change of the parameters, especially the wave speed, influences the existence of the solitary waves. For this reason, the scope of this paper is to explore the relationship between the existence of the infinitely many solitary waves and the wave speed for Eq. (1.5) by adopting the bifurcation method of dynamical systems [6, 7, 16–23]. We list the other approaches for solving the solitary waves for comparison [5, 8–10, 24, 25]. In this article, for arbitrary wave speed c, we prove that the infinitely many solitary waves exist in Eq. (1.5) via qualitative theory and combining the bifurcation phase portraits. Among these solitary waves, we find a kind of novel solitary wave whose form of motion seems like a tree stump.
The paper is organized as follows. In Sect. 2, the main results are established by choosing the wave speed and Hamiltonian as the bifurcation parameters. In Sect. 3, Hamiltonian and the bifurcation phase portraits of Eq. (1.5) are derived for the proofs of the main results. The conclusions are drawn in Sect. 4.
2 The infinitely many solitary waves
Generally speaking, the existence of the solitary waves depends on the wave speed. Therefore, the wave speed and the other system parameters are chosen as the bifurcation parameters. The infinitely many solitary waves of Eq. (1.5) exist, but it is independent of the parameters completely. We state the main theorem as follows.
Theorem 1
The infinitely many solitary waves do exist in Eq. (1.5) for arbitrary wave speed c.
The proof of Theorem 1 is stated in Sect. 3.
Proposition 1
If let \(\Pi (\cdot ,\cdot ,\cdot )\) be the Legendre’s incomplete elliptic integral of the third kind and \(\Pi (\varphi ,1,k)= \frac{1}{k'^{2}}[k'^2F(\varphi ,k) -E(\varphi ,k)+\text {tan}\varphi \sqrt{1-k^2\text {sin}^2\varphi }]\), \(k'^2=1-k^2\), \(\text {sn}u=\text {sn}^{-1}(u,k)\) be the sine amplitude u (Jacobian elliptic function), \(\text {sn}^{-1}u=\text {sn}^{-1}(u,k)\) be the inverse function of \(\text {sn}u\), Eq. (1.5) possesses the solitary waves \(m=\varphi (\xi )=\varphi (x-ct)\) which are of the following eleven different cases and are classified based on Hamiltonian.
Case 1 When the equation
has three roots as \(\alpha \), \(\beta \), \(\gamma \) (\(\gamma <\beta <\alpha \)), the expression of the solitary wave of Eq. (1.5) can be written as
where \(\gamma <0<\varphi \le \beta \), \(u_{1}=\sqrt{\frac{\alpha (\beta -\varphi )}{\beta (\alpha -\varphi )}}\) and \(k_{1}^{2}=\frac{\beta (\alpha -\gamma )}{\alpha (\beta -\gamma )}\).
Case 2 When \(h=0\) and Eq. (2.1) has two roots as \(\alpha \), \(\beta \), the expression of the solitary wave of Eq. (1.5) can be written as
where \(\beta <0<\varphi \le \alpha \), \(u_{2}=\sqrt{\frac{\alpha -\varphi }{\alpha }}\) and \(k_{2}^{2}=\frac{\alpha }{\alpha -\beta }\).
Case 3 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \), \(\gamma \) (\(\gamma <\beta <\alpha \)), the expression of the solitary wave of Eq. (1.5) can be written as
where \(\beta <0<\varphi \le \alpha \), \(u_{3}=\sqrt{\frac{-\gamma (\alpha -\varphi )}{\alpha (\varphi -\gamma )}}\) and \(k_{3}^{2}=\frac{\alpha (\beta -\gamma )}{(\alpha -\beta )(-\gamma )}\).
Case 4 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \) (\(\beta <\alpha \)) and \(\beta \) is a double root, the expression of the solitary wave of Eq. (1.5) can be written as
where \(\beta <0<\varphi \le \alpha \) and \(u_{4}=\frac{(\alpha -2\beta )\varphi +\alpha \beta }{2\sqrt{\beta ^2-\alpha \beta }\sqrt{\alpha \varphi -\varphi ^2}}\).
Case 5 When \(h=0\) and Eq. (2.1) has two roots as \(\alpha \), \(\beta \) (\(\beta <\alpha \)), the expression of the solitary wave of Eq. (1.5) can be written as
where \(0<\varphi \le \beta \), \(u_{5}=\sqrt{\frac{\alpha (\beta -\varphi )}{\beta (\alpha -\varphi )}}\) and \(k_{4}^{2}=\frac{\beta }{\alpha }\).
Case 6 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \), \(\gamma \) (\(\gamma <\beta <\alpha \)), the expression of the solitary wave of Eq. (1.5) can be written as
where \(0<\varphi \le \gamma \), \(u_{6}=\sqrt{\frac{\beta (\gamma -\varphi )}{\gamma (\beta -\varphi )}}\) and \(k_{5}^{2}=\frac{(\alpha -\beta )\gamma }{(\alpha -\gamma )\beta }\).
Case 7 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \) (\(\beta <\alpha \)) and \(\alpha \) is a double root, the expression of the solitary wave of Eq. (1.5) can be written as
where \(0<\varphi \le \beta \) and \(u_{7}=\frac{(\beta -2\alpha )\varphi +\alpha \beta }{2\sqrt{\alpha ^2-\alpha \beta }\sqrt{\beta \varphi -\varphi ^2}}\).
Case 8 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \) (\(\beta <\alpha \)) and \(\beta \) is a double root, the expression of the solitary wave of Eq. (1.5) can be written as
where \(0<\beta <\varphi \le \alpha \) and \(u_{8}=\frac{\alpha (\varphi -\beta )}{(\alpha -2\beta )\varphi +\alpha \beta +2\sqrt{(\alpha \beta -\beta ^2)(\alpha \varphi -\varphi ^2)}}\).
Case 9 When Eq. (2.1) has three roots as \(\alpha \), \(\beta \) (\(\beta <\alpha \)) and \(\beta \) is a double root, the expression of the solitary wave of Eq. (1.5) can be written as
where \(\beta <\varphi \le \alpha <0\) and \(u_{8}=\frac{-\alpha (\varphi -\beta )}{(2\beta -\alpha )\varphi -\alpha \beta +2\sqrt{(\beta ^2-\alpha \beta )(\varphi ^2-\alpha \varphi )}}\).
Case 10 When \(h=c=0\) and \(\alpha =\frac{2a}{3g}\), the expression of the static solitary wave of Eq. (1.5) can be written as
Case 11 When Eq. (2.1) has three roots, where there exist a pair of conjugate complex roots and a real root \(\alpha \), the solitary wave of Eq. (1.5) exists.
Proposition 2
There exist three different forms (width, height and low) of motion for the infinitely many solitary waves in Eq. (1.5; see Figs. 1, 2, 3).
The profile of the solitary wave (2.2) for \(a=g=c=1\), \(h=\frac{1}{\alpha ^{3}}(2c\alpha ^{2}+g\alpha -\frac{2a}{3})\), \(\alpha =0.618034\)
The profile of the solitary wave (2.9) for \(a=1\), \(g=4\), \(c=-3- 10^{-5}\), \(h=\frac{1}{\beta ^{3}}(2c\beta ^{2}+g\beta -\frac{2a}{3})\), \(\alpha =\frac{2}{h}(c-\beta h)\), \(\beta =\frac{1}{2c}(-g+\sqrt{g^2+4ac})\)
3 The bifurcation phase portraits
Let
where c represents the wave speed. Substituting (3.1) into Eq. (1.5) and integrating once, we have
where g is the integral constant. For convenience, we rewritten Eq. (3.2) as
Letting \(y=\varphi '\), we obtain the planar dynamic system
Note that Sy. (3.4) has a singular line \(\varphi =0\). To avoid the line temporarily, we assume that \(\text {d}\xi =\varphi \text {d}\eta \), so that Sy. (3.4) is equivalent to the system as follows
which has the first integral
where
Sy. (3.4) has the same topological phase portraits as Sy. (3.5) except for the straight line \(\varphi =0\). The phase space orbits of the vector fields defined by Sy. (3.5) determine all traveling wave solutions of Eq. (1.5). Thus, to investigate the bifurcations of traveling wave solutions of Eq. (1.5), we need to analyze the dynamic behavior of Sy. (3.5).
For simplicity, we let
and \((\varphi ,0)\) be one of singular point of Sy. (3.5). Then characteristic values of linearized system of Sy. (3.5) at the singular point \((\varphi ,0)\) are
We therefore know the property of the singular point \((\varphi ,0)\) as follows
-
1.
When \(\varphi f^{'}(\varphi )>0\), \((\varphi ,0)\) is a saddle point of Sy. (3.5).
-
2.
When \(\varphi f^{'}(\varphi )<0\), \((\varphi ,0)\) is a center point of Sy. (3.5).
-
3.
When \(\varphi f^{'}(\varphi )=0\), \((\varphi ,0)\) is a degenerate singular point of Sy. (3.5).
By using the properties of equilibrium points and bifurcation theory, we verify that the original point is the elliptic–hyperbolic point. Further we obtain three bifurcation curves as follows
Then according to the qualitative theory, we obtain the bifurcation phase portraits of Sy. (3.5) as Fig. 4. From the phase portraits, we know that the infinitely many closed orbits connecting with the original point are corresponding to the infinitely many solitary waves.
The phase portrait of Sy. (3.4) for \(a>0\)
By using the above bifurcation phase portraits, we show the representations of the solitary wave solutions of Eq. (1.5), where the dynamics of the level curves \(\Gamma _{i} (i=1,2,\ldots ,10)\) determined by (3.7).
The curves \(\Gamma _{i}(i=1,2,\ldots ,10)\) have the following expressions:
Substituting (3.9–3.18) into \(y=\frac{\text {d}\varphi }{\text {d}\xi }\) and integrating them along the curves \(\Gamma _{i} (i=1,2,\ldots ,10)\), it follows that
In (3.19–3.28), completing the integrals yields Proposition 1. The solitary waves of Eq. (1.5) in Proposition 1 are infinitely many numbers for arbitrary wave speed c because of the infinitely many initial values \(\alpha \), \(\beta \) or \(\gamma \). This indicates that the infinitely many solitary waves of Eq. (1.5) exist for arbitrary wave speed c. Hereto Theorem 1 has been finished.
4 Conclusions
In this paper, we obtained the expressions of the infinitely many solitary waves of Eq. (1.5) and classified these solitary waves based on two different ways, namely, Hamiltonian and forms of motion. Interestingly, there exists a kind of the tree stump solitary wave among the infinitely many solitary waves of Eq. (1.5). From the above discussion, we observed that the nonlinear equation with singularity may exist infinitely many bounded solutions. At the same time, the proposed method in this paper can be used to study the infinitely many bounded solutions of the other singular nonlinear equations. So we do believe that this article may improve the quality of well-studied solitary wave theory from one side, and it may open a possible way to explore the novel solutions of the singular nonlinear equations from the other one. Last but not least, the results on the solitary wave can be help us to understand the mechanism of motion of nonlinear waves.
References
Chowdhury, A.R., Roy, S.: Bi-Hamiltonian structure and Lie-Backlund symmetries for a modified Harry-Dym system. J. Phys. A Math. Gen. 18, L431–L434 (1985)
Qiao, Z.: The Camassa–Holm hierarchy, related N-dimensional integrable systems and algebro-geometric solution on a symplectic submanifold. Commun. Math. Phys. 239, 309–341 (2003)
Hereman, W., Banerjee, P.P., Chatterjee, M.R.: On the nonlocal equations and nonlocal charges associated with the Harry Dym hierarchy Korteweg–de Vries equation. J. Phys. A 22, 241–255 (1989)
Cao, C.W., Geng, X.G.: A noncanfocal generator of involutive systems and three associated soliton hierarchies. J. Math. Phys. 32, 2323–2328 (1991)
Olver, P.J., Rosenau, P.: Tri-Hamiltonian duality between solitons and solitary wave solutions having compact support. Phys. Rev. E 53(2), 1900–1906 (1996)
Li, J.B., Qiao, Z.J.: Bifurcations of travelling wave solutions for an integrable equation. J. Math. Phys. 51, 1–23 (2010)
Pan, C.H., Liu, Z.R.: Further results on the travelling wave solutions for an integrable equation. J. Appl. Math. 2013, 1–7 (2013)
Qiao, Z.J.: New integrable hierarchy, its parametric solutions, cuspons, one-peak solitons, and M/W-shape peak solitons. J. Math. Phys. 48, 082701 (2007)
Qiao, Z.J., Liu, L.P.: A new integrable equation with no smooth solitons. Chaos Solitons Fract. 41(2), 587–593 (2009)
Sakovich, S.: Smooth soliton solutions of a new integrable equation by Qiao. J. Math. Phys. 52(2), 023509 (2011)
Estevez, P.G.: Generalized Qiao hierarchy in \(2+1\) dimensions: reciprocal transformations, spectral problem and non-isospectrality. Phys. Lett. A 375(3), 537–540 (2011)
Yang, Y.Q., Chen, Y.: Prolongation structure of the equation studied by Qiao. Commun. Theor. Phys. 56, 463–466 (2011)
Yao, Y.Q., Huang, Y.H.: The Qiao–Liu equation with self-consistent ssources and its solutions. Commun. Theor. Phys. 57, 909–913 (2012)
Marinakis, V.: Higher-order equations of the KdV type are integrable. Adv. Math. Phys. 2010, 329586 (2010)
Zha, Q.L.: N-soliton solutions of an integrable equation studied by Qiao. Chin. Phys. B 22(4), 040201 (2013)
Pan, C.H., Ling, L.M., Liu, Z.R.: A new integrable equation with cuspons and periodic cuspons. Phys. Scr. 89, 105207 (2014)
Liu, Z.R., Qian, T.F.: Peakons and their bifurcation in a generalized Camassa–Holm equation. Int. J. Bifurc. Chaos 11(3), 781–792 (2001)
Liu, Z.R., Yang, C.X.: The application of bifurcation method to a higher-order KdV equation. J. Math. Anal. Appl. 275(1), 1–12 (2002)
Song, M., Liu, Z.R.: Qualitative analysis and explicit traveling wave solutions for the Davey–Stewartson equation. Math. Methods Appl. Sci. 37(3), 393–401 (2014)
Pan, C.H., Yi, Y.T.: Some extensions on the soliton solutions for the Novikov equation with cubic nonlinearity. J. Nonlinear Math. Phys. 22(2), 308–320 (2015)
Li, J.B.: Bifurcations and exact travelling wave solutions of the generalized two-component Hunter–Saxton system. Discrete Contin. Dyn. Syst. Ser. B 19(6), 1719–1729 (2014)
Liu, H.Z., Li, J.B.: Painlevé analysis, complete Lie group classifications and exact solutions to the time-dependent coefficients Gardner types of equations. Nonlinear Dyn. 80(1–2), 515–527 (2015)
Wen, Z.S.: Several new types of bounded wave solutions for the generalized two-component Camassa–Holm equation. Nonlinear Dyn. 77(3), 849–857 (2014)
Younis, M., Ali, S.: Solitary wave and shock wave solutions of (\(1+1\))-dimensional perturbed Klein–Gordon, (\(1+1\))-dimensional Kaup–Keperschmidt and (\(2+1\))-dimensional Zk–Bbm equations. Open Eng. 5, 124–130 (2015)
Younis, M., Ali, S., Mahmood, S.A.: Solitons for compound KdV-Burgers’ equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2060-y
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos. 11171115, 11401221).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pan, C., Liu, Z. Infinitely many solitary waves of an integrable equation with singularity . Nonlinear Dyn 83, 1469–1475 (2016). https://doi.org/10.1007/s11071-015-2420-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2420-7