1 Introduction

Investigating the integrability of the nonlinear evolution equation (NLEE) has become much more significant because it could be considered as a pretest and the first step of its exact solvability. A lot of important properties could characterize the integrability of the NLEEs, such as bilinear form, infinite conservation laws, Lax pairs, infinite symmetries, bilinear Bäcklund transformation and Painlevé test. As we know, many methods, such as inverse scattering transformation [1], Darboux transformation [2], Bäcklund transformation [3] and Hirota method [4], are proposed to cope with the nonlinear equation. By employing the bilinear form, we can construct a multisoliton solution for a nonlinear equation; furthermore, the bilinear Bäcklund transformation and some other important properties [5–7] could be obtained. In addition to this, an approach that combine the Hirota bilinear form and Riemann theta function is feasible to deal with exact periodic wave solutions for nonlinear equation.

In 1980s, a straight approach is presented by Nakamura to construct a certain kind of quasi-periodic solutions for nonlinear evolution equation in his essay [8]. He obtains the periodic wave solutions of KdV equation and Boussinesq equation, respectively. Recently, this method is extended to study the (2+1)-dimensional Bogoyavlenskii’s breaking soliton equation, KP equation and KdV equation by Fan and Hon [9–11]. Ma [12–14] investigates the resonant solutions and periodic wave solutions of trilinear equations by using Bell polynomials. Chen et al. [15] study the integrability of the modified generalized Vakhnenko equation. Tian et al. [16] extended this method to the Zhiber–Shabat equation, etc. The method is extended to study the integrability and structure the periodic wave solutions for some nonlinear equations, discrete soliton equations and supersymmetric equations by Tian and Zhang [17–21].

Now, many people pay attention to a kind of generalized nonlinear equation since they admit much more widely application in a great number physical fields [22–36]. Through investigating a generalized form for nonlinear evolution equations, many more general properties of the equation(s) can be obtained.

In this paper, we focus on a generalized (3+1)-dimensional nonlinear wave in liquid containing gas bubbles

$$\begin{aligned}&(u_{t}+h_{1}uu_{x}+h_{2}u_{xxx}+h_{3}u_{x})_{x}\nonumber \\&\quad +\,h_{4}u_{yy}+h_{5}u_{zz}=0, \end{aligned}$$
(1)

where \(u=u(x,y,z,t)\), \(h_{i}(i=1,2,3,4,5)\) are free constants. By taking some appropriate parameters for \(h_{i}\), we can construct a variety of nonlinear wave equations. Some important examples are given below.

  • The (3+1)-dimensional KP equation [37]

    $$\begin{aligned} (u_{t}+u_{xxx}-6uu_{x})_{x}+3u_{yy}+3u_{zz}=0, \end{aligned}$$
    (2)

    is investigated by Ablowitz and Segur. Its three-wave soliton-type solutions, Wronskian and Grammian solutions and a wide class of Pfaffianized systems of the equation are investigated by Ma, Xia and Zhu [38, 39].

  • The (3+1)-dimensional nonlinear wave equation [40]

    $$\begin{aligned} (u_{t}+uu_{x}+u_{xxx})_{x}+\frac{1}{2}(u_{yy}+u_{zz})=0, \end{aligned}$$
    (3)

    is given for a description of the pressure waves in admixture liquid and gas bubbles taking into consideration the viscosity of liquid and the heat transfer. Some exact solutions for the nonlinear evolution equation are presented by the application of the Hirota method [40].

  • The Korteweg-de Vries equation [41]

    $$\begin{aligned} u_{t}+6uu_{x}+u_{xxx}=0, \end{aligned}$$
    (4)

    is found to describe many physical and engineering phenomena, such as ion-acoustic waves, geophysical fluid dynamics, lattice dynamics.

The main purpose of this paper is to study the bilinear equation, Bäcklund transformations and infinite conservation laws of the generalized (3+1)-dimensional nonlinear wave Eq. (1) by using Bell polynomial approach. Furthermore, N-soliton solutions and periodic wave solutions with a asymptotic property are also constructed, respectively.

The paper is organized as follows. In Sects. 2–3, the bilinear form, Bäcklund transformation and soliton solutions for Eq. (1) in liquid containing gas bubbles are constructed by employing the binary Bell polynomials. Then, the infinite conservation laws with all conserved densities and fluxes are given by explicit recursion formulas for Eq. (1) in Sect. 4. In Sect. 5, based on the bilinear operator, by combining with Riemann theta function, we get one- and two-periodic wave solutions for Eq. (1). Finally, in Sect. 6, a asymptotic property is investigated in detail, and as a result, the relationship between the periodic wave solutions and soliton solutions is obtained.

2 The bilinear representation and soliton solutions

In this section, we research the bilinear representation for the generalized (3+1)-dimensional nonlinear wave Eq. (1) by using the binary Bell polynomials.

2.1 The bilinear representation

Theorem 1

By employing the following transformation

$$\begin{aligned} u=12h_{2}h_{1}^{-1}(\ln f)_{xx}, \end{aligned}$$
(5)

the generalized (3+1)-dimensional nonlinear wave Eq. (1) admits the following bilinear equation

$$\begin{aligned}&{\mathscr {D}} \left( D_{t},D_{x},D_{y},D_{z}\right) \nonumber \\&\quad \equiv \left( D_{x}D_{t}+h_{2}D_{x}^{4}+h_{3}D_{x}^{2} +h_{4}D_{y}^{2}+h_{5}D_{z}^{2}\right) f\nonumber \\&\quad \quad \cdot f=0. \end{aligned}$$
(6)

Proof

First of all, introducing a transformation

$$\begin{aligned} u=c(t)q_{2x}, \end{aligned}$$
(7)

where c(t) is a free function, one can connect Eq.  (1) with \({\mathcal {P}}\)-polynomials. By the substitution of Eq. (7) into Eq. (1), one has

$$\begin{aligned}&(c_{t}(t)q_{2x}+c(t)q_{2xt}+h_{1}c^{2}(t)q_{2x}q_{3x}+h_{2}c(t)q_{5x}\nonumber \\&\quad +\,h_{3}c(t)q_{3x})_{x}+h_{4}c(t)q_{2x,2y}+h_{5}c(t)q_{2x,2z}=0. \end{aligned}$$
(8)

By integrating Eq. (8) with respect to x, the result is given by

$$\begin{aligned}&c_{t}(t)q_{x}+c(t)q_{xt}+\frac{h_{1}}{2}c^{2}(t)q_{2x}^{2} +h_{2}c(t)q_{4x}\nonumber \\&\quad +\,h_{3}c(t)q_{2x}+h_{4}c(t)q_{2y}+h_{5}c(t)q_{2z}=d, \end{aligned}$$
(9)

i.e.,

$$\begin{aligned} E(q)= & {} \frac{c(t)_{t}}{c(t)}q_{x}+q_{xt}+\frac{h_{1}}{2}c(t)q_{2x}^{2}\nonumber \\&+\,h_{2}q_{4x}+h_{3}q_{2x}+h_{4}q_{2y}+h_{5}q_{2z}=d,\nonumber \\ \end{aligned}$$
(10)

with \(d=d(t,y,z)\) is an integration constant. Letting \(c(t)=6h_{2}h_{1}^{-1}\) and by employing the formula (103), Eq. (10) becomes

$$\begin{aligned} E(q)= & {} P_{xt}(q)+h_{1}P_{6x}(q)+h_{2}P_{3x,y}(q)\nonumber \\&+\,h_{2}P_{2y}(q)+h_{5}P_{xz}(q)=d. \end{aligned}$$
(11)

Finally, based on the property (105) and the following transformation

$$\begin{aligned} q=2\ln f\Longleftrightarrow u=c(t)q_{2x}=12h_{2}h_{1}^{-1}(\ln f)_{xx}, \end{aligned}$$
(12)

the standard identities of the Hirota D-operator

$$\begin{aligned}&D_{x}^{m}D_{y}^{n}D_{z}^{p}D_{t}^{q}f(x,y,z,t)\cdot g(x,y,z,t) \nonumber \\&\quad =(\partial _{x}-\partial _{x'})^{m}(\partial _{y}-\partial _{y'})^{n} \times (\partial _{z}-\partial _{z'})^{p}\nonumber \\&\quad \quad \times (\partial _{t}-\partial _{t'})^{q}f(x,y,z,t)\nonumber \\&\quad \quad \left. \cdot \, g\left( x',y',z',t'\right) \right| _{x=x',y=y',z=z',t=t'}, \end{aligned}$$
(13)

yields the bilinear form of Eq. (1) directly, that is bilinear Eq. (6). \(\square \)

Equation (6) is a new bilinear equation, which can also be reduced to the ones of the equations investigated in [37–41] by taking the appropriate coefficients \(h_{i}\).

Let \(h_{1}=-6, h_{2}=1, h_{3}=0, h_{4}=3, h_{5}=3\), Eq. (1) is reduced to the (3+1)-dimensional KP Eq. (2), the bilinear equation becomes

$$\begin{aligned}&{\mathscr {D}} \left( D_{t},D_{x},D_{y},D_{z}\right) \nonumber \\&\quad \equiv \left( D_{x}D_{t}+D_{x}^{4}+3D_{y}^{2}+3D_{z}^{2}\right) f\cdot f=0. \end{aligned}$$
(14)

Let \(h_{1}=1, h_{2}=1, h_{3}=0, h_{4}=\frac{1}{2}, h_{5}=\frac{1}{2}\), Eq. (1) is degenerated into three-dimensional nonlinear waves Eq. (3), the bilinear equation becomes

$$\begin{aligned}&{\mathscr {D}} \left( D_{t},D_{x},D_{y},D_{z}\right) \nonumber \\&\quad \equiv \left( D_{x}D_{t}+D_{x}^{4}+\frac{1}{2}D_{y}^{2}+\frac{1}{2}D_{z}^{2}\right) f\cdot f=0. \end{aligned}$$
(15)

Let \(h_{1}=6, h_{2}=1, h_{3}=0, h_{4}=0, h_{5}=0\), Eq. (1) is reduced to the Korteweg-de Vries Eq. (4), the bilinear equation becomes

$$\begin{aligned} {\mathscr {D}} \left( D_{t},D_{x}\right) \equiv \left( D_{x}D_{t}+D_{x}^{4}\right) f\cdot f=0. \end{aligned}$$
(16)

2.2 Soliton solutions

Next, based on the bilinear equation, we obtain the N-soliton solution of Eq. (1) as of the form

$$\begin{aligned}&u=12h_{1}^{-1}h_{2}(\ln f)_{xx}, \\&f=\sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{j}\eta _{j}+\sum _{1\le j<i\le N}^{N}\rho _{i}\rho _{j}A_{ij}\right) ,\nonumber \end{aligned}$$
(17)

in which \(\mu _{j}\), \(\nu _{j}\), \(\sigma _{j}\), \(\delta _{j}\) are all free constants, and

$$\begin{aligned} \exp (A_{ij})=-\frac{(\mu _{i}-\mu _{j})(\gamma _{i}-\gamma _{j})+h_{2}(\mu _{i}-\mu _{j})^4+h_{3}(\mu _{i}-\mu _{j})^{2} +h_{4}(\nu _{i}-\nu _{j})^2+h_{5}(\sigma _{i}-\sigma _{j})^2}{(\mu _{i}+\mu _{j})(\gamma _{i}+\gamma _{j})+h_{2}(\mu _{i}+\mu _{j})^4+h_{3}(\mu _{i}+\mu _{j})^{2} +h_{4}(\nu _{i}+\nu _{j})^2+h_{5}(\sigma _{i}+\sigma _{j})^2}. \end{aligned}$$
(18)

with \(\eta _{j}=\mu _{j} x+\nu _{j} y+\sigma _{j} z+\gamma _{j} t+\delta _{j}\), \(\gamma _{j}=-h_{2}\mu _{j}^{3}-h_{3}\mu _{j}-h_{4}\mu _{j}^{-1}\nu _{j}^{2}-h_{5}\mu _{j}^{-1}\sigma _{j}^{2}\) \((1\le j<i\le N)\), \(\sum _{1\le j<i\le N}^{N}\) is the summation over all possible pairs selected from N elements with the condition \((1\le j<i\le N)\), and \(\sum _{\rho =0,1}\) denotes the summation over all possible combinations of \(\rho _{i},\rho _{j}=0,1\) \((i,j=1,2,\ldots ,N)\).

Its one-soliton and two-soliton solution could be easily obtained. For \(N=1\), the one-soliton solution is of the form

$$\begin{aligned} u_{1}= & {} 12h_{1}^{-1}h_{2}\partial ^{2}_{x}\ln \left( 1+e^{\upeta }\right) , \nonumber \\ \eta= & {} \mu x+\nu y+\sigma z\nonumber \\&+\,\left( -h_{2}\mu ^{3}-h_{3}\mu -h_{4}\mu ^{-1}\nu ^{2} -h_{5}\mu ^{-1}\sigma ^{2}\right) t+\delta . \end{aligned}$$
(19)

For \(N=2\), the two-soliton solution is of the form

$$\begin{aligned} u_{2}= & {} 12h_{1}^{-1}h_{2}\partial ^{2}_{x}\ln \left( 1+e^{\upeta _{1}}+e^{\upeta _{2}}+e^{\upeta _{1}+\upeta _{2}+A_{12}}\right) , \nonumber \\ \eta _{j}= & {} \mu _{j} x+\nu _{j} y+\sigma _{j} z\nonumber \\&+\,\left( -h_{2}\mu _{j}^{3}-h_{3}\mu _{j}-h_{4}\mu _{j}^{-1}\nu _{j}^{2}-h_{5}\mu _{j}^{-1}\sigma _{j}^{2}\right) t\nonumber \\&+\,\delta _{j},\quad (j=1,2), \end{aligned}$$
(20)

with

$$\begin{aligned} \exp (A_{12})=-\frac{(\mu _{1}-\mu _{2})(\gamma _{1}-\gamma _{2})+h_{2}(\mu _{1}-\mu _{2})^4+h_{3}(\mu _{1}-\mu _{2})^{2} +h_{4}(\nu _{1}-\nu _{2})^2+h_{5}(\sigma _{1}-\sigma _{2})^2}{(\mu _{1}+\mu _{2})(\gamma _{1}+\gamma _{2})+h_{2}(\mu _{1}+\mu _{2})^4+h_{3}(\mu _{1}+\mu _{2})^{2} +h_{4}(\nu _{1}+\nu _{2})^2+h_{5}(\sigma _{1}+\sigma _{2})^2}. \end{aligned}$$
(21)

As its special cases, the (3+1)-dimensional KP Eq. (2) has a N-soliton wave solution given by

$$\begin{aligned} u= & {} -2(\ln f)_{xx}, \nonumber \\ f= & {} \sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{j}\eta _{j}+\sum _{1\le j<i\le N}^{N}\rho _{i}\rho _{j}A_{ij}\right) , \end{aligned}$$
(22)

where \(\mu _{j}\), \(\nu _{j}\), \(\sigma _{j}\), \(\delta _{j}\) are all free constants, and

$$\begin{aligned} \exp (A_{ij})=-\frac{(\mu _{i}-\mu _{j})(\gamma _{i}-\gamma _{j})+(\mu _{i}-\mu _{j})^4 +3(\nu _{i}-\nu _{j})^2+3(\sigma _{i}-\sigma _{j})^2}{(\mu _{i}+\mu _{j})(\gamma _{i}+\gamma _{j})+(\mu _{i}+\mu _{j})^4 +3(\nu _{i}+\nu _{j})^2+3(\sigma _{i}+\sigma _{j})^2},~~~~(1\le j<i\le N), \end{aligned}$$
(23)

with \(\eta _{j}=\mu _{j} x+\nu _{j} y+\sigma _{j} z+(-\mu _{j}^{3}-3\mu _{j}^{-1}\nu _{j}^{2}-3\mu _{j}^{-1}\sigma _{j}^{2}) t+\delta _{j}\).

For (3+1)-dimensional nonlinear waves Eq. (3), its N-soliton wave solution is given as follows

$$\begin{aligned} u= & {} 12(\ln f)_{xx}, \nonumber \\ f= & {} \sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{j}\eta _{j}+\sum _{1\le j<i\le N}^{N}\rho _{i}\rho _{j}A_{ij}\right) , \end{aligned}$$
(24)

in which \(\mu _{j}\), \(\nu _{j}\), \(\sigma _{j}\), \(\delta _{j}\) are all free constants, and

$$\begin{aligned} \exp (A_{ij})=-\frac{(\mu _{i}-\mu _{j})(\gamma _{i}-\gamma _{j})+(\mu _{i}-\mu _{j})^4 +\frac{1}{2}(\nu _{i}-\nu _{j})^2+\frac{1}{2}(\sigma _{i}-\sigma _{j})^2}{(\mu _{i}+\mu _{j})(\gamma _{i}+\gamma _{j})+(\mu _{i}+\mu _{j})^4 +\frac{1}{2}(\nu _{i}+\nu _{j})^2+\frac{1}{2}(\sigma _{i}+\sigma _{j})^2},~~~~(1\le j<i\le N) \end{aligned}$$
(25)

with \(\eta _{j}=\mu _{j} x+\nu _{j} y+\sigma _{j} z+(-\mu _{j}^{3}-\frac{1}{2}\mu _{j}^{-1}\nu _{j}^{2}-\frac{1}{2}\mu _{j}^{-1}\sigma _{j}^{2}) t+\delta _{j}\).

For the Korteweg-de Vries Eq. (4), we also obtain its N-soliton wave solution, which has the following form,

$$\begin{aligned}&u=2(\ln f)_{xx}, \nonumber \\&f=\sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{j}\eta _{j}+\sum _{1\le j<i\le N}^{N}\rho _{i}\rho _{j}A_{ij}\right) , \end{aligned}$$
(26)

with

$$\begin{aligned} \exp (A_{ij})=-\frac{(\mu _{i}-\mu _{j})(\gamma _{i}-\gamma _{j})+(\mu _{i}-\mu _{j})^4}{(\mu _{i}+\mu _{j})(\gamma _{i}+\gamma _{j})+(\mu _{i}+\mu _{j})^4}, \end{aligned}$$
(27)

and \(\eta _{j}=\mu _{j} x+\nu _{j} y+\sigma _{j} z-\mu _{j}^{3} t+\delta _{j}\).

The graph of Fig. 1 shows the one-soliton wave solution (19) plotted through selecting the appropriate parameters (see Fig. 1).

Fig. 1
figure 1

(Color online) Spatial structures of the one-soliton solution (19) with the parameters \( h_{1}=-1, h_{2} =-1, h_{3} =3, h_{4}=1, h_{5} =1, \mu =-1, \nu =1.5, \sigma =2\) and \(\delta =1\). a The perspective view of the wave as \(y=0,z=0\). b The perspective view of the wave as \(t=0,z=0\). c The perspective view of the wave as \(y=0,t=0\). d The corresponding contour plot as \(y=0,z=0\). e The corresponding contour plot as \(t=0,z=0\). f The corresponding contour plot as \(y=0,t=0\)

Full size image

The graph of Fig. 2 shows the two-soliton wave solution (20) plotted by choosing the appropriate parameters (see Fig. 2).

Fig. 2
figure 2

(Color online) Spatial structures of the two-soliton solution (20) with the parameters \( h_{1} =2, h_{2} =-1, h_{3} =-3, h_{4}=1, h_{5} =1, \mu _{1}=1, \mu _{2}=-1,\nu _{1}=1, \nu _{2}=1, \sigma _{1}=2, \sigma _{2}=2.5\) and \(\delta _{1}=1, \delta _{2}=1\). a The perspective view of the wave as \(y=0,z=0\). b The perspective view of the wave as \(t=0,z=0\). c The perspective view of the wave as \(y=0,t=0\). d The corresponding contour plot as \(y=0,z=0\). e The corresponding contour plot as \(t=0,z=0\). f The corresponding contour plot as \(y=0,t=0\)

Full size image

3 Bäcklund transformation

Theorem 2

Let f be a solution of Eq. (6), if g satisfies the following system

$$\begin{aligned}&(D_{x}^{2}+M D_{z}-\lambda )f\cdot g=0, \nonumber \\&\left[ \partial _{x}\left( D_{t}+h_{2}D_{x}^{3} +(3h_{2}\lambda +h_{3})D_{x}-3Mh_{2}D_{x}D_{z}\right) \right. \nonumber \\&\quad \left. +\,\partial _{y}(h_{4}D_{y})\right] f\cdot g=0, \end{aligned}$$
(28)

where \(M^{2}=h_{5}/3h_{2}\), then g is another solution of the Eq. (6). The system (28) is called a Bäcklund transformation of the generalized \((3+1)\)-dimensional nonlinear wave Eq. (1).

Proof

In order to obtain the Bäcklund transformation of the generalized (3+1)-dimensional nonlinear wave Eq. (1), let

$$\begin{aligned} q=2\ln g, \quad q'=2\ln f, \end{aligned}$$
(29)

be two different solutions for Eq. (10). Considering Eq. (29) and Eq. (10), one then has

$$\begin{aligned} E(q')-E(q)= & {} \left( q'-q\right) _{xt}+h_{2}\left( q'-q\right) _{4x}\nonumber \\&+\,3h_{2}\left( q'+q\right) _{2x}\left( q'-q\right) _{2x}\nonumber \\&+\,h_{3}\left( q'-q\right) _{2x} +h_{4}\left( q'-q\right) _{2y}\nonumber \\&+\,h_{5}\left( q'-q\right) _{2z}=0. \end{aligned}$$
(30)

When under suitable additional constraints, it can produce the transformation.

Introducing the following two new auxiliary variables

$$\begin{aligned}&\upsilon =\left( q'-q\right) /2=\ln (f/g),\nonumber \\&\quad \omega =\left( q'+q\right) /2=\ln (fg), \end{aligned}$$
(31)

and the condition (30) could be rewritten as another form

$$\begin{aligned} E(q')-E(q)= & {} E(\omega +\upsilon )-E(\omega -\upsilon )=\upsilon _{xt}\nonumber \\&+\,h_{2}\left( \upsilon _{4x}+6\omega _{2x}\upsilon _{2x}\right) +h_{3}\upsilon _{2x}\nonumber \\&+\,h_{4}\upsilon _{2y}+h_{5}\upsilon _{2z} \nonumber \\= & {} \partial _{x}\left[ {\mathscr {Y}}_{t}(\upsilon ) +h_{2}{\mathscr {Y}}_{3x}(\upsilon ,\omega )\right] \nonumber \\&+\,{\mathscr {R}}(\upsilon ,\omega )=0, \end{aligned}$$
(32)

where

$$\begin{aligned} {\mathscr {R}}(\upsilon ,\omega )= & {} 3h_{2}\omega _{2x}\upsilon _{2x}-3h_{2} \upsilon _{x}\omega _{3x}-3h_{2}\upsilon _{x}^{2}\upsilon _{2x}\nonumber \\&+\,h_{3}\upsilon _{2x}+h_{4}\upsilon _{2y} +h_{5}\upsilon _{2z} \nonumber \\= & {} 3h_{2}\mathrm{Wronskian}\left[ {\mathscr {Y}}_{2x}(\upsilon ,\omega ), {\mathscr {Y}}_{x}(\upsilon )\right] \nonumber \\&+\,h_{3}\upsilon _{2x}+h_{4}\upsilon _{2y}+h_{5}\upsilon _{2z}. \end{aligned}$$
(33)

For writing \({\mathscr {R}}(\upsilon ,\omega )\) as the form of \({\mathscr {Y}}\)-polynomials with x-derivative, we introduce the following constraint

$$\begin{aligned} {\mathscr {Y}}_{2x}(\upsilon ,\omega )+M {\mathscr {Y}}_{z}(\upsilon ,\omega )=\lambda , \end{aligned}$$
(34)

in which M is an undetermined constant, and \(\lambda \) is an arbitrary parameter. By employing Eq. (34), \({\mathscr {R}}(\upsilon ,\omega )\) can be rewritten as follows

$$\begin{aligned} {\mathscr {R}}(\upsilon ,\omega )= & {} 3h_{2}\lambda \upsilon _{2x}-M^{-1}\nonumber \\&\times \left( h_{5}\omega _{2x,z}+(2h_{5}-3M^{2}h_{2}) \upsilon _{x}\upsilon _{x,z}\right. \nonumber \\&\left. +\,3M^{2}h_{2}\upsilon _{2x}\upsilon _{z}\right) \nonumber \\&+\,h_{3}\upsilon _{2x}+h_{4}\upsilon _{2y}, \end{aligned}$$
(35)

and under the constraint \(3M^2h_{2}=h_{5}\), it is equivalent to the following expression

$$\begin{aligned} {\mathscr {R}}(\upsilon ,\omega )= & {} \partial _{x} \left[ (3h_{2}\lambda +h_{3}){\mathscr {Y}}_{x}(\upsilon ) -3Mh_{2}{\mathscr {Y}}_{x,z}(\upsilon ,\omega )\right] \nonumber \\&+\,\partial _{y}\left( h_{4}{\mathscr {Y}}_{y}(\upsilon )\right) , \end{aligned}$$
(36)

Finally, linking Eqs. (34)–(36), the \({\mathscr {Y}}\)-polynomials could be derived as follows

$$\begin{aligned}&{\mathscr {Y}}_{2x}(\upsilon ,\omega )+M {\mathscr {Y}}_{z}(\upsilon ,\omega )-\lambda =0, \nonumber \\&\quad \partial _{x}\left[ {\mathscr {Y}}_{t}(\upsilon )+h_{2}{\mathscr {Y}}_{3x}(\upsilon ,\omega )+(3h_{2}\lambda +h_{3}){\mathscr {Y}}_{x}(\upsilon )\right. \nonumber \\&\quad \quad \left. -3Mh_{2}{\mathscr {Y}}_{x,z}(\upsilon ,\omega )\right] +\partial _{y}\left( h_{4}{\mathscr {Y}}_{y}(\upsilon )\right) =0. \end{aligned}$$
(37)

Through employing the identity (102), the system (37) leads to the Bäcklund transformation (28) at once. \(\square \)

In order to benefit more interested audience in the research community, one can also construct the bilinear Bäcklund transformation involving a few free parameters by using the same way presented by Ma and Abdeljabbar [42].

4 Infinite conservation laws

Theorem 3

The generalized \((3+1)\)-dimensional nonlinear wave Eq. (1) admits the following infinite conservation laws

$$\begin{aligned} {\mathscr {I}}_{n,t}+{\mathscr {H}}_{n,x}+{\mathscr {G}}_{n,y}+{\mathscr {K}}_{n,z}=0,~~n=1,2,\ldots . \end{aligned}$$
(38)

The conversed densities \({\mathscr {I}}_{n}'s\) are presented by the following recursion formulas

$$\begin{aligned}&{\mathscr {I}}_{1}=-\frac{1}{2}q_{2x}=-\frac{1}{12}h_{1}h_{2}^{-1}u, \nonumber \\&{\mathscr {I}}_{2}=\frac{1}{4}q_{3x}+\frac{1}{4}Mq_{xz}=\frac{1}{24}h_{1}h_{2}^{-1}\left( u_{x}+M\partial _{x}^{-1}u_{z}\right) , \nonumber \\&{\mathscr {I}}_{n+1}=-\frac{1}{2}\left( {\mathscr {I}}_{n,x}+M\partial _{x}^{-1}{\mathscr {I}}_{n,z}+\sum _{i=1}^{n-1}{\mathscr {I}}_{i}{\mathscr {I}}_{n-i}\right) , \nonumber \\&\quad n=2,3,\ldots , \end{aligned}$$
(39)

the first fluxes \({\mathscr {H}}_{n}'s\) are presented by

$$\begin{aligned} {\mathscr {H}}_{1}= & {} h_{2}{\mathscr {I}}_{1,2x}+h_{3}{\mathscr {I}}_{1}-6h_{2}{\mathscr {I}}_{1}^{2}-6h_{2}M\partial _{x}^{-1}{\mathscr {I}}_{2,z}, \nonumber \\ {\mathscr {H}}_{2}= & {} h_{2}{\mathscr {I}}_{2,2x}+h_{3}{\mathscr {I}}_{2}-12h_{2}{\mathscr {I}}_{1}{\mathscr {I}}_{2}\nonumber \\&-\,6h_{2}M\partial _{x}^{-1}{\mathscr {I}}_{3,z}-6h_{2}M{\mathscr {I}}_{1}\partial _{x}^{-1}{\mathscr {I}}_{1,z}, \nonumber \\ {\mathscr {H}}_{n}= & {} h_{2}\left( {\mathscr {I}}_{n,2x}-6\sum _{i=1}^{n}{\mathscr {I}}_{i}{\mathscr {I}}_{n+1-i}\right. \nonumber \\&\left. -\,2\sum _{k_{1}+k_{2}+k_{3}=n}{\mathscr {I}}_{k_{1}}{\mathscr {I}}_{k_{2}}{\mathscr {I}}_{k_{3}}\right) \nonumber \\&-\,6h_{2}M\left( \partial _{x}^{-1}{\mathscr {I}}_{n+1,z}+\sum _{k=1}^{n}{\mathscr {I}}_{k}\partial _{x}^{-1}{\mathscr {I}}_{n-k,y}\right) \nonumber \\&+\,h_{3}{\mathscr {I}}_{n} \quad n=3,4,\ldots , \end{aligned}$$
(40)

the second fluxes \({\mathscr {G}}_{n}'s\) are given by

$$\begin{aligned}&{\mathscr {G}}_{1} =h_{4}\partial _{x}^{-1}{\mathscr {I}}_{1,y} =-\frac{1}{2}h_{4}q_{xy}=-\frac{1}{12}h_{1}h_{4}h_{2}^{-1}\partial _{x}^{-1}u_{y}, \nonumber \\&\begin{aligned} {\mathscr {G}}_{2}&=h_{4}\partial _{x}^{-1}{\mathscr {I}}_{2,y}=\frac{1}{4}h_{4}\left( q_{2xy}+Mq_{yz}\right) \\&=\frac{1}{24}h_{1}h_{4}h_{2}^{-1}\left( u_{y}+M\partial _{xx}^{-1}u_{yz}\right) , \end{aligned}\nonumber \\&{\mathscr {G}}_{n+1}=h_{4}\partial _{x}^{-1}{\mathscr {I}}_{n,y},~~n=2,3,\ldots , \end{aligned}$$
(41)

where \(\partial _{xx}^{-1}\) means integrating with respect to x twice, and the third fluxes \({\mathscr {K}}_{n}'s\) are presented by

$$\begin{aligned}&{\mathscr {K}}_{1}=6h_{2}M{\mathscr {I}}_{2}+h_{5}\partial _{x}^{-1}{\mathscr {I}}_{1,z}, \nonumber \\&{\mathscr {K}}_{2}=3h_{2}M{\mathscr {I}}_{1}^{2}+6h_{2}M{\mathscr {I}}_{3}+h_{5}\partial _{x}^{-1}{\mathscr {I}}_{2,z}, \nonumber \\&{\mathscr {K}}_{n+1}=3h_{2}M\sum _{i=1}^{n-1}{\mathscr {I}}_{i}{\mathscr {I}}_{n-i}+6h_{2}M{\mathscr {I}}_{n+1}\nonumber \\&\quad +\,h_{5}\partial _{x}^{-1}{\mathscr {I}}_{n,z},~~n=2,3,\ldots . \end{aligned}$$
(42)

Proof

The \({\mathscr {R}}(\upsilon ,\omega )\) that in the two-field condition (30) can be rewritten as another form

$$\begin{aligned} {\mathscr {R}}(\upsilon ,\omega )= & {} \partial _{x}\left[ (3h_{2}\lambda +h_{3})\upsilon _{x}-3Mh_{2}\upsilon _{x}\upsilon _{z}\right] \nonumber \\&+\,\partial _{z}(-3Mh_{2}w_{2x})+\partial _{y}(h_{4}\upsilon _{y})=0, \end{aligned}$$
(43)

by employing the relationship \(\partial _{x}(\upsilon _{t})=\partial _{t}(\upsilon _{x})=\upsilon _{xt}\). The system (37) admits a conserved form

$$\begin{aligned}&\omega _{2x}+\upsilon _{x}^{2}+M\upsilon _{z}-\lambda =0, \nonumber \\&\partial _{t}(\upsilon _{x})+\partial _{x}\left[ h_{2}\upsilon _{3x}+3h_{2}\upsilon _{x}\omega _{2x}+h_{2}\upsilon _{x}^{3}\right. \nonumber \\&\quad \left. +\,(3h_{2}\lambda +h_{3})\upsilon _{x}-3Mh_{2}\upsilon _{x}\upsilon _{z}\right] \nonumber \\&\quad +\,\partial _{z}\left[ -3Mh_{2}\lambda +h_{5}\upsilon _{z}+3Mh_{2}\upsilon _{x}^{2}\right] +\partial _{y}(h_{4}\upsilon _{y})=0. \end{aligned}$$
(44)

We introduce a new potential function

$$\begin{aligned} \eta =\left( q'_{x}-q_{x}\right) /2, \end{aligned}$$
(45)

and based on the relationship (31), we have

$$\begin{aligned} \upsilon _{x}=\eta ,~~\omega _{x}=q_{x}+\eta . \end{aligned}$$
(46)

By substituting (46) into (44), system (32) can be reduced to a Riccati-type equation

$$\begin{aligned} q_{2x}+\eta _{x}+\eta ^{2}+M\partial _{x}^{-1}\eta _{z}-\varepsilon ^{2}=0, \end{aligned}$$
(47)

which is a new potential function with regard to q. Similarly, from Eq. (47), one can obtain the following divergence-type equation

$$\begin{aligned}&\eta _{t}+\partial _{x}\Big [h_{2}\eta _{2x}+6\varepsilon ^{2}h_{2}\eta -2h_{2}\eta ^{3}\nonumber \\&\quad -\,6h_{2}M\eta \partial _{x}^{-1}\eta _{z}+h_{3}\eta \Big ]+\partial _{y}(h_{4}\partial _{x}^{-1}\eta _{y})\nonumber \\&\quad +\,\partial _{z}\left( -3Mh_{2}\varepsilon ^{2} +h_{5}\partial _{x}^{-1}\eta _{z}+3Mh_{2}\eta ^{2}\right) =0, \end{aligned}$$
(48)

by taking \(\lambda =\varepsilon ^{2}\). Inserting the following formula

$$\begin{aligned} \eta =\varepsilon +\sum _{n=1}^{\infty }{\mathscr {I}}_{n}(q,q_{x},q_{2x},\cdots )\varepsilon ^{-n}, \end{aligned}$$
(49)

into Eq. (47) and considering the coefficients with regard to the power of \(\varepsilon \), then one can directly derive the recursion relationship (39) of the conserved densities \({\mathscr {I}}_{n}\) as follows

$$\begin{aligned}&q_{2x}+\sum _{n=1}^{\infty }{\mathscr {I}}_{n,x}\varepsilon ^{-n}+M\partial _{x}^{-1}\sum _{n=1}^{\infty }{\mathscr {I}}_{n,z}\varepsilon ^{-n}+2{\mathscr {I}}_{1}\nonumber \\&\quad +\,2\sum _{n=1}^{\infty }{\mathscr {I}}_{n+1} \varepsilon ^{-n}+\sum _{n=1}^{\infty }\left( \sum _{n=1}^{n-1}{\mathscr {I}}_{i}{\mathscr {I}}_{n-i}\varepsilon ^{-n}\right) =0. \end{aligned}$$
(50)

Additionally, combining the expansion (49) with divergence-type Eq. (48), we have

$$\begin{aligned}&\sum _{n=1}^{\infty }{\mathscr {I}}_{n,t}\varepsilon ^{-n}+\partial _{x}\left\{ h_{2}\sum _{n=1}^{\infty }{\mathscr {I}}_{n,2x}\varepsilon ^{-n}+4\varepsilon ^{3}h_{2}\right. \nonumber \\&\quad -\,2h_{2}\sum _{n=1}^{\infty }\left( \sum _{k_{1}+k_{2}+k_{3}=n}{\mathscr {I}}_{k_{1}}{\mathscr {I}}_{k_{2}}{\mathscr {I}}_{k_{3}}\varepsilon ^{-n}\right) \nonumber \\&\quad -\,6h_{2}\varepsilon \sum _{n=1}^{\infty }\left( \sum _{i=1}^{n-1}{\mathscr {I}}_{i}{\mathscr {I}}_{n-i}\varepsilon ^{-n}\right) \nonumber \\&\quad -\,6h_{2}M\varepsilon \partial _{x}^{-1}\left( \sum _{n=1}^{\infty }{\mathscr {I}}_{n,z}\varepsilon ^{-n}\right) \nonumber \\&\quad -\,6h_{2}M\left( \sum _{n=1}^{\infty }{\mathscr {I}}_{n}\varepsilon ^{-n}\right) \partial _{x}^{-1}\left( \sum _{n=1}^{\infty }{\mathscr {I}}_{n,z}\varepsilon ^{-n}\right) \nonumber \\&\quad \left. +\,h_{3}\left( \varepsilon +\sum _{n=1}^{\infty }{\mathscr {I}}_{n}\varepsilon ^{-n}\right) \right\} \nonumber \\&\quad +\,\partial _{y}\left( h_{4}\partial _{x}^{-1}\sum _{n=1}^{\infty }{\mathscr {I}}_{n,y}\varepsilon ^{-n}\right) \nonumber \\&\quad +\,\partial _{z}\left\{ 3h_{2}M\left[ \sum _{n=1}^{\infty } \left( \sum _{i=1}^{n-1}{\mathscr {I}}_{i}{\mathscr {I}}_{n-i} \varepsilon ^{-n}\right) \right. \right. \nonumber \\&\quad \left. +\,2\left( {\mathscr {I}}_{1}+\sum _{n=1}^{\infty }{\mathscr {I}}_{n+1}\varepsilon ^{-n}\right) \right] \nonumber \\&\quad \left. +\,h_{5}\left( \partial _{x}^{-1}\sum _{n=1}^{\infty }{\mathscr {I}}_{n,z}\varepsilon ^{-n}\right) \right\} =0, \end{aligned}$$
(51)

which shows the infinite conservation laws (38)

$$\begin{aligned} {\mathscr {I}}_{n,t}+{\mathscr {H}}_{n,x}+{\mathscr {G}}_{n,y}+{\mathscr {K}}_{n,z}=0,~~n=1,2,\ldots , \end{aligned}$$
(52)

where \({\mathscr {H}}_{n}'s\) are determined by system (40), and \({\mathscr {G}}_{n}'s\), \({\mathscr {K}}_{n}'s\) are determined by system (41), (42), respectively. \(\square \)

5 Riemann theta function periodic wave solutions

5.1 Riemann theta function preliminary

To begin with, we provide some fundamental definitions about Riemann theta function. The Riemann theta function with genus n is defined as

$$\begin{aligned} \vartheta (\xi )=\vartheta (\xi ,\tau )=\sum _{n\in {\mathbb {Z}}^{N}}e^{\pi i\langle n \tau , n\rangle +2\pi i\langle \xi , n\rangle }, \end{aligned}$$
(53)

where \(\xi =(\xi _{1},\cdots ,\xi _{N})^{T}\in {\mathbb {C}}^{N}\) and \(n=(n_{1},\cdots ,n_{N})^{T}\in {\mathbb {Z}}^{N}\). Let \(f=(f_{1},\cdots ,f_{N})^{T}\) and \(g=(g_{1},\cdots ,g_{N})^{T}\) be two vectors, the inner product is defined as

$$\begin{aligned} \langle f,g\rangle =f_{1}g_{1}+f_{2}g_{2}+\cdots +f_{N}g_{N}. \end{aligned}$$
(54)

In particular, let \(N=1\), the Riemann theta function (53) becomes

$$\begin{aligned} \vartheta (\xi ,\tau )=\sum _{n=-\infty }^{+\infty }e^{\pi i n^{2}\tau +2\pi i n\xi }, \end{aligned}$$
(55)

with the phase variable \(\xi =\alpha x+\beta y+\rho z+\omega t+\varepsilon \) and \(\text{ Im }(\tau )>0\). Let \(N=2\), the Riemann theta function (53) becomes

$$\begin{aligned} \vartheta (\xi ,\tau )=\vartheta (\xi _{1},\xi _{2},\tau )=\sum _{n\in {\mathbb {Z}}^{2}}e^{\pi i\langle \tau n ,n\rangle +2\pi i\langle \xi ,n\rangle }, \end{aligned}$$
(56)

with the phase variable \(\xi _{i}=\alpha _{i}x+\beta _{i}y+\rho _{i} z+\omega _{i} t+\varepsilon _{i}\), \(i=1,2,\) \(n=(n_{1},n_{2})^{T}\in {\mathbb {Z}}^{2}\), \(\xi =(\xi _{1},\xi _{2})\in {\mathbb {C}}^{2}\), and \(-i\tau \) is a positive definite and real-valued symmetric \(2\times 2\) matrix which is given by

$$\begin{aligned}&\tau =\left( \begin{array}{c@{\quad }c} \tau _{11}&{}\tau _{12}\\ \tau _{12}&{}\tau _{22}\end{array} \right) ,~~\mathrm{Im}(\tau _{11})>0,~~\mathrm{Im}(\tau _{22})>0,\nonumber \\&\quad \tau _{11}\tau _{22}-\tau _{12}^{2}<0. \end{aligned}$$
(57)

For obtaining the periodic wave solutions, a more generalized bilinear equation should be considered. Suppose that Eq. (1) admits \(u\rightarrow u_{0}\) when \(|\xi |\rightarrow 0\), the periodic wave solution of Eq. (1) satisfies

$$\begin{aligned} u=u_{0}+12h_{2}h_{1}^{-1}\partial _{x}^{2}\ln \vartheta (\xi ), \end{aligned}$$
(58)

where \(\xi =(\xi _{1},\ldots ,\xi _{N})^{T}\), \(\xi _{i}=\alpha _{i}x+\beta _{i}y+\rho _{i} z+\omega _{i} t+\varepsilon _{i}\), \(i=1,2\ldots ,N\), \(u_{0}\) is a special solution with constant of Eq. (1). Linking Eq. (1) with Eq. (58), a more generalized bilinear equation is derived as

$$\begin{aligned}&{\mathscr {W}}(D_{x},D_{y},D_{z},D_{t})\vartheta (\xi )\cdot \vartheta (\xi ) \nonumber \\&\quad =\left( D_{x}D_{t}+h_{2}D_{x}^{4}+u_{0}h_{2}D_{x}^{4}+h_{3}D_{x}^{2}\right. \nonumber \\&\quad \quad \left. +\,h_{4}D_{y}^{2} +h_{5}D_{z}^{2}+c\right) \vartheta (\xi )\cdot \vartheta (\xi )=0, \end{aligned}$$
(59)

with \(c=c(y,z,t)\) being an integration constant.

5.2 One-periodic wave solutions

Theorem 4

If \(\vartheta (\xi ,\tau )\) is one Riemann theta function (55) as \(N=1\), a one-periodic wave solution of the generalized (3+1)-dimensional nonlinear wave Eq. (1) is given by

$$\begin{aligned} u=u_{0}+12h_{1}^{-1}h_{2}\partial _{x}^{2}\ln \vartheta (\xi ), \end{aligned}$$
(60)

with

$$\begin{aligned} \omega =\frac{b_{1}a_{22}-b_{2}a_{12}}{a_{11}a_{22}-a_{12}a_{21}},~~~~~~~~~ c=\frac{b_{1}a_{21}-b_{2}a_{11}}{a_{12}a_{21}-a_{11}a_{22}}, \end{aligned}$$
(61)

and

$$\begin{aligned} \begin{aligned}&a_{11}=-\sum _{n=-\infty }^{\infty }16\pi ^{2}n^{2}\alpha \wp ^{2n^{2}},~~a_{12}=\sum _{n=-\infty }^{\infty }\wp ^{2n^{2}}, \\&a_{21}=-\sum _{n=-\infty }^{\infty }4\pi ^{2}(2n-1)^{2}\alpha \wp ^{2n^{2}-2n+1},\\&a_{22}=\sum _{n=-\infty }^{\infty }\wp ^{2n^{2}-2n+1}, \\&\begin{aligned} b_{1}&=\sum _{n=-\infty }^{\infty } \left( -256h_{2}\pi ^{4}n^{4}\alpha ^4-256h_{2}u_{0}\pi ^{4}n^{4}\alpha ^4\right. \\&\quad \left. +16h_{3}n^{2}\pi ^{2}\alpha ^{2}+16h_{4}n^{2}\pi ^{2}\beta ^{2} +16h_{5}n^{2}\pi ^{2}\rho ^{2}\right) \wp ^{2n^{2}}, \end{aligned}\\&\begin{aligned} b_{2}&=\sum _{n=-\infty }^{\infty } (-16h_{2}\pi ^{4}(2n-1)^{4}\alpha ^4 -16h_{2}u_{0}\pi ^{4}(2n-1)^{4}\alpha ^4\\&\quad +4h_{3}\pi ^{2}(2n-1)^{2}\alpha ^{2}+4h_{4}\pi ^{2}(2n-1)^{2}\beta ^2 \\&\quad +4h_{5}\pi ^{2}(2n-1)^{2}\rho ^2)\wp ^{2n^{2}-2n+1}, \wp =e^{\pi i\tau }, \end{aligned} \end{aligned} \end{aligned}$$
(62)

where \(\alpha ,\beta ,\rho ,\tau ,\varepsilon \) are arbitrary parameters.

Proof

The parameters \(\alpha ,\beta ,\rho ,\omega ,\varepsilon \) should satisfy the following system based on Theorem 1 in Ref. [17]

$$\begin{aligned}&\sum _{n=-\infty }^{+\infty }{\mathscr {W}}(4n\pi i\alpha ,4n\pi i\beta ,4n\pi i\rho ,4n\pi i\omega )e^{2n^{2}\pi i\tau }=0, \end{aligned}$$
(63a)
$$\begin{aligned}&\sum _{n=-\infty }^{+\infty }{\mathscr {W}}(2\pi i(2n-1)\alpha ,2\pi i(2n-1)\beta ,2\pi i\nonumber \\&\quad \times (2n-1)\rho ,2\pi i(2n-1)\omega )e^{(2n^{2}-2n+1)\pi i\tau }=0. \end{aligned}$$
(63b)

Substituting the bilinear Eq. (59) into the system (63a) and (63b), one can obtain the following results

$$\begin{aligned} \widetilde{{\mathscr {W}}}(0)= & {} \sum _{n=-\infty }^{\infty }\left( -16\pi ^{2}n^{2}\alpha \omega +256h_{2}\pi ^{4}n^{4}\alpha ^4\right. \\&+\,256h_{2}u_{0}\pi ^{4}n^{4}\alpha ^4-16h_{3}n^{2}\pi ^{2}\alpha ^{2}\\&\left. -16h_{4}n^{2}\pi ^{2}\beta ^{2}-16h_{5}n^{2}\pi ^{2}\rho ^{2}+c\right) \\&\times \, e^{2\pi i n^{2}\tau }=0,\\ \widetilde{{\mathscr {W}}}(1)= & {} \sum _{n=-\infty }^{\infty }\left( -4\pi ^{2}(2n-1)^{2}\alpha \omega +16h_{2}\pi ^{4}\right. \\&\times \,(2n-1)^{4}\alpha ^{4}+16h_{2}u_{0}\pi ^{4}(2n-1)^{4}\alpha ^{4}\\&-\,4h_{3}\pi ^{2}(2n-1)^{2}\alpha ^{2}-4h_{4}\pi ^{2}(2n-1)^{2}\beta ^{2}\\&\left. -\,4h_{5}\pi ^{2}(2n-1)^{2}\rho ^{2} +c\right) e^{\pi i (2n^{2}-2n+1)\tau }\nonumber \\= & {} 0, \end{aligned}$$

which can be equivalently rewritten as the following system with the notations (62)

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} a_{11} &{} a_{12}\\ a_{21} &{}a_{22} \end{array} \right) \left( \begin{array}{c} \omega \\ c \end{array} \right) =\left( \begin{array}{c} b_{1}\\ b_{2} \end{array} \right) . \end{aligned}$$
(64)

From system (64), one can obtain the following a one-periodic wave solution

$$\begin{aligned} u=u_{0}+12h_{1}^{-1}h_{2}\partial _{x}^{2}\ln \vartheta (\xi ), \end{aligned}$$
(65)

which is also determined by the free parameters \(\alpha ,\beta ,\rho ,\varepsilon \) and \(\tau \). \(\square \)

The graph of Fig. 3 shows the one-periodic wave solution (60) plotted through selecting the appropriate parameters (see Fig. 3) .

Fig. 3
figure 3

(Color online) Spatial structures of the one-periodic wave solution (60) with the parameters \( h_{1}=1, h_{2}=-1, h_{3}=1, h_{4}=1, h_{5}=1, \tau =i, \alpha =1, \beta =1, \rho =2, u_{0}=0\) and \(\varepsilon =0\). a The perspective view of the wave as \(y=0,z=0\). b The perspective view of the wave as \(t=0,z=0\). c The perspective view of the wave as \(y=0,t=0\). d The wave propagation pattern of the wave along the x axis. e The wave propagation pattern of the wave along the y axis. f The wave propagation pattern of the wave along the z axis

Full size image

5.3 Two-periodic wave solutions

Theorem 5

If \(\vartheta (\xi _{1},\xi _{2},\tau )\) is Riemann theta function (56) as \(N=2\), a two-periodic wave solution of the generalized \((3+1)\)-dimensional nonlinear wave Eq. (1) is given by

$$\begin{aligned} u=u_{0}+12h_{1}^{-1}h_{2}\partial _{x}^{2}\ln \vartheta (\xi _{1},\xi _{2},\tau ), \end{aligned}$$
(66)

with the parameters \(\omega _{1},\omega _{2},u_{0},c\) have the following system

$$\begin{aligned} H(\omega _{1},\omega _{2},u_{0},c)^{T}=b, \end{aligned}$$
(67)

in which

$$\begin{aligned}&H=(h_{ij})_{4\times 4},~~b=(b_{1},b_{2},b_{3},b_{4})^{T}, \nonumber \\&h_{i1}=-4\pi ^{2}\sum _{(n_{1},n_{2})\in {\mathbb {Z}}^{2}}\langle 2n-\theta _{i},\alpha \rangle (2n_{1}-\theta _{i}^{1})\mathfrak {I}_{i}(n), \nonumber \\&h_{i2}=-4\pi ^{2}\sum _{(n_{1},n_{2})\in {\mathbb {Z}}^{2}}\langle 2n-\theta _{i},\alpha \rangle (2n_{2}-\theta _{i}^{2})\mathfrak {I}_{i}(n), \nonumber \\&h_{i3}=\sum _{(n_{1},n_{2})\in {\mathbb {Z}}^{2}}16h_{2}\pi ^{4}\langle 2n-\theta _{i},\alpha \rangle ^{4}\mathfrak {I}_{i}(n), \nonumber \\&h_{i4}=\sum _{(n_{1},n_{2})\in {\mathbb {Z}}^{2}}\mathfrak {I}_{i}(n), \nonumber \\&\begin{aligned} b_{i}&=\sum _{(n_{1},n_{2})\in {\mathbb {Z}}^{2}}\left( -16h_{2}\pi ^{4}\langle 2n-\theta _{i},\alpha \rangle ^{4}\right. \\&\quad +4h_{3}\pi ^2\langle 2n-\theta _{i},\alpha \rangle ^{2}+4h_{4}\pi ^2\langle 2n-\theta _{i},\beta \rangle ^{2}\\&\quad \left. +\,4h_{5}\pi ^2\langle 2n-\theta _{i},\rho \rangle ^{2}\right) \mathfrak {I}_{i}(n) \end{aligned}\nonumber \\&\mathfrak {I}_{i}(n)=\wp _{1}^{n_{1}^{2}+(n_{1}-\theta _{i}^{1})^{2}}\wp _{2}^{n_{2}^{2}+(n_{2}-\theta _{i}^{2})^{2}}\wp _{3}^{n_{1}n_{2}+(n_{1}-\theta _{i}^{1})(n_{2}-\theta _{i}^{2})}, \nonumber \\&\wp _{1}=e^{\pi i\tau _{11}},~~ \wp _{2}=e^{\pi i\tau _{22}}, ~~\wp _{3}=e^{2\pi i\tau _{12}},~~ i=1,2,3,4, \end{aligned}$$
(68)

and \( \theta _{i}=(\theta _{i}^{1},\theta _{i}^{2})^{T}\) , \(\theta _{1}=(0,0)^{T}\), \(\theta _{2}=(1,0)^{T}\), \(\theta _{3}=(0,1)^{T}\), \(\theta _{4}=(1,1)^{T}\), \( i=1,2,3,4\); \(\alpha _{i},\beta _{i},\rho _{i},\tau _{ij},\varepsilon _{i}\) \((i,j=1,2)\) are all free parameters.

Proof

Based on Theorem 2 in Ref. [17], the parameters \(\alpha _{i},\beta _{i},\rho _{i},\omega _{i},\varepsilon _{i}\) \((i=1,2)\) should satisfy

$$\begin{aligned}&\widetilde{{\mathscr {W}}}(0,0)\nonumber \\&\quad =\sum _{n\in {\mathbb {Z}}^{2}}{\mathscr {W}}(2\pi i\langle 2n-\theta _{1},\alpha \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{1},\beta \rangle , 2\pi i\langle 2n-\theta _{1},\rho \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{1},\omega \rangle e^{\pi i[ \langle \tau (n-\theta _{1}),n-\theta _{1}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(69a)
$$\begin{aligned}&\widetilde{{\mathscr {W}}}(1,0)\nonumber \\&\quad =\sum _{n\in {\mathbb {Z}}^{2}} {\mathscr {W}}(2\pi i\langle 2n-\theta _{2},\alpha \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{2},\beta \rangle , 2\pi i\langle 2n-\theta _{2},\rho \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{2},\omega \rangle e^{\pi i[ \langle \tau (n-\theta _{2}),n-\theta _{2}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(69b)
$$\begin{aligned}&\widetilde{{\mathscr {W}}}(0,1)\nonumber \\&\quad =\sum _{n\in {\mathbb {Z}}^{2}}{\mathscr {W}}(2\pi i\langle 2n-\theta _{3},\alpha \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{3},\beta \rangle , 2\pi i\langle 2n-\theta _{3},\rho \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{3},\omega \rangle e^{\pi i[ \langle \tau (n-\theta _{3}),n-\theta _{3}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(69c)
$$\begin{aligned}&\widetilde{{\mathscr {W}}}(1,1)\nonumber \\&\quad =\sum _{n\in {\mathbb {Z}}^{2}}{\mathscr {W}}(2\pi i\langle 2n-\theta _{4},\alpha \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{4},\beta \rangle , 2\pi i\langle 2n-\theta _{4},\rho \rangle ,\nonumber \\&\qquad 2\pi i\langle 2n-\theta _{4},\omega \rangle e^{\pi i[ \langle \tau (n-\theta _{4}),n-\theta _{4}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(69d)

where \( \theta _{i}=(\theta _{i}^{1},\theta _{i}^{2})^{T}\) , \(\theta _{1}=(0,0)^{T}\), \(\theta _{2}=(1,0)^{T}\), \(\theta _{3}=(0,1)^{T}\), \(\theta _{4}=(1,1)^{T}\), \( i=1,2,3,4\).

Considering (69a)–(69d) with (59), we have the following system

$$\begin{aligned}&\sum _{n\in {\mathbb {Z}}^{2}}\left[ -4\pi ^{2}\langle 2n-\theta _{1}, \alpha \rangle \langle 2n-\theta _{1},\omega \rangle \right. \nonumber \\&\quad +\,16h_{2}\pi ^{4}\langle 2n-\theta _{1},\alpha \rangle ^{4}\nonumber \\&\quad +\, 16u_{0}h_{2}\pi ^{4}\langle 2n-\theta _{1}, \alpha \rangle ^{4}-4h_{3}\pi ^{2}\langle 2n-\theta _{1}, \alpha \rangle ^{2} \nonumber \\&\quad -\,4h_{4}\pi ^{2}\langle 2n-\theta _{1},\beta \rangle ^2-4h_{5} \pi ^2\langle 2n-\theta _{1},\rho \rangle ^2 +c\Big ]\nonumber \\&\quad \times \, e^{\pi i[\langle \tau (n-\theta _{1}),n-\theta _{1}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(70a)
$$\begin{aligned}&\sum _{n\in {\mathbb {Z}}^{2}}\left[ -4\pi ^{2}\langle 2n-\theta _{2},\alpha \rangle \langle 2n-\theta _{2},\omega \rangle \right. \nonumber \\&\quad +16h_{2}\pi ^{4}\langle 2n-\theta _{2},\alpha \rangle ^{4}\nonumber \\&\quad +16u_{0}h_{2}\pi ^{4}\langle 2n-\theta _{2},\alpha \rangle ^{4} -4h_{3}\pi ^{2}\langle 2n-\theta _{2},\alpha \rangle ^{2} \nonumber \\&\quad -\,4h_{4}\pi ^{2}\langle 2n-\theta _{2},\beta \rangle ^2-4h_{5}\pi ^2\langle 2n-\theta _{2},\rho \rangle ^2 +c\Big ]\nonumber \\&\quad \times \, e^{\pi i[\langle \tau (n-\theta _{2}),n-\theta _{2}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(70b)
$$\begin{aligned}&\sum _{n\in {\mathbb {Z}}^{2}}\left[ -4\pi ^{2}\langle 2n-\theta _{3},\alpha \rangle \langle 2n-\theta _{3},\omega \rangle \right. \nonumber \\&\quad +\,16h_{2}\pi ^{4}\langle 2n-\theta _{3},\alpha \rangle ^{4}\nonumber \\&\quad +\,16u_{0}h_{2}\pi ^{4}\langle 2n-\theta _{3},\alpha \rangle ^{4}-4h_{3}\pi ^{2}\langle 2n-\theta _{3},\alpha \rangle ^{2} \nonumber \\&\quad -\,4h_{4}\pi ^{2}\langle 2n-\theta _{3},\beta \rangle ^2-4h_{5}\pi ^2\langle 2n-\theta _{3},\rho \rangle ^2 +c\Big ]\nonumber \\&\quad \times \, e^{\pi i[\langle \tau (n-\theta _{3}),n-\theta _{3}\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$
(70c)
$$\begin{aligned}&\sum _{n\in {\mathbb {Z}}^{2}}\left[ -4\pi ^{2}\langle 2n-\theta _{4},\alpha \rangle \langle 2n-\theta _{4},\omega \rangle \right. \nonumber \\&\quad +\,16h_{2}\pi ^{4}\langle 2n-\theta _{4},\alpha \rangle ^{4}\nonumber \\&\quad +\,16u_{0}h_{2}\pi ^{4}\langle 2n-\theta _{4},\alpha \rangle ^{4}-4h_{3}\pi ^{2}\langle 2n-\theta _{4},\alpha \rangle ^{2} \nonumber \\&\quad -\,4h_{4}\pi ^{2}\langle 2n-\theta _{4},\beta \rangle ^2-4h_{5} \pi ^2\langle 2n-\theta _{4},\rho \rangle ^2 +c\Big ]\nonumber \\&\quad \times \, e^{\pi i[\langle \tau (n-\theta _{4}),n-\theta _{4}\rangle +\langle \tau n,n\rangle ]}=0. \end{aligned}$$
(70d)

From (68), the above system can be equivalent to

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} h_{11} &{} h_{12} &{} h_{13} &{} h_{14}\\ h_{21} &{} h_{22} &{}h_{23} &{}h_{24}\\ h_{31} &{} h_{32} &{}h_{33} &{}h_{34}\\ h_{41} &{} h_{42} &{}h_{43} &{}h_{44} \end{array} \right) \left( \begin{array}{c} \omega _{1} \\ \omega _{2}\\ u_{0}\\ c \end{array} \right) =\left( \begin{array}{c} b_{1} \\ b_{2}\\ b_{3}\\ b_{4} \end{array} \right) . \end{aligned}$$
(71)

From system (71), one can get the following two-periodic wave solution

$$\begin{aligned} u=u_{0}+12h_{1}^{-1}h_{2}\partial _{x}^{2}\ln \vartheta (\xi _{1},\xi _{2},\tau ). \end{aligned}$$
(72)

The two-periodic wave solution is also determined by the free parameters \(\alpha _{i},\beta _{i},\rho _{i},\varepsilon _{i}\) and \(\tau _{ij}\). \(\square \)

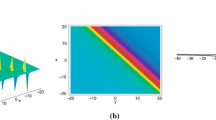
The graph of Fig. 4 shows a degenerate two-periodic wave solution plotted through selecting the suitable parameters (see Fig. 4).

Fig. 4
figure 4

(Color online) Spatial structures of a degenerate two-periodic wave solution with the parameters \( h_{1} =1, h_{2} =-1, h_{3}=-3, h_{4}=1, h_{5}=1, \alpha _{1}=0.1, \alpha _{2}=0.3, \beta _{1}=1, \beta _{2}=0.3, \rho _{1}=0.1, \rho _{2}=1\), \(\tau _{11}=i\), \(\tau _{12}=0.5i\), \(\tau _{22}=2i\) and \(\varepsilon _{1}=0, \varepsilon _{2}=0\). a The perspective view of the wave as \(y=0,z=0\). b The perspective view of the wave as \(t=0,z=0\). c The perspective view of the wave as \(y=0,t=0\). d The wave propagation pattern of the wave along the x axis. e The wave propagation pattern of the wave along the y axis. f The wave propagation pattern of the wave along the z axis

Full size image

6 Asymptotic analysis

In this section, the asymptotic behavior of the periodic wave solutions is researched. Here we deduce the relationship between the periodic wave solutions and soliton solutions.

Theorem 6

Let \((\omega , c)^{T}\) be a solution for system (64), we take

$$\begin{aligned}&u_{0}=0, ~~ \alpha =\frac{\mu }{2\pi i},~~\beta =\frac{\nu }{2\pi i},~~\rho =\frac{\sigma }{2\pi i},\nonumber \\&\quad \varepsilon =\frac{\delta +\pi \tau }{2\pi i} \end{aligned}$$
(73)

for the one-periodic wave solution (60), in which \(\mu ,\nu ,\sigma \) and \(\delta \) are determined by Eq. (19). The limiting properties are as follows

$$\begin{aligned}&c\rightarrow 0, ~~\xi \rightarrow \frac{\eta +\pi \tau }{2\pi i},~~ \vartheta (\xi ,\tau )\rightarrow 1+e^{\eta },\nonumber \\&\quad \text{ when } ~~\wp \rightarrow 0. \end{aligned}$$
(74)

The above equations imply that the periodic wave solution (60) can be reduced to the soliton solution (19) where \((u,\wp )\longrightarrow (u_{1},0)\).

Proof

By employing Eqs. (62), expanding the matrix elements \(a_{ij}(i,j=1,2)\) and \(b_{i}(i=1,2)\) as \(\wp \), we have

$$\begin{aligned} a_{11}= & {} -32\pi ^{2}\alpha \left( \wp ^{2}+4\wp ^{8}+\cdots +n^{2}\wp ^{2n^{2}}+\cdots \right) , \nonumber \\ a_{12}= & {} 1+2\left( \wp ^{2}+\wp ^{8}+\cdots +\wp ^{2n^{2}}+\cdots \right) , \nonumber \\ a_{21}= & {} -8\pi ^{2}\alpha \Big (\wp +9\wp ^{5}+\cdots +(2n-1)^{2}\wp ^{2n^{2}-2n+1}\nonumber \\&+\,\cdots \Big ),\nonumber \\ a_{22}= & {} 2\left( \wp +\wp ^{5}+\cdots +\wp ^{2n^{2}-2n+1}+\cdots \right) , \end{aligned}$$
$$\begin{aligned} b_{1}= & {} 32\pi ^{2}\left( -16h_{2}\pi ^{2}\alpha ^{4}-16h_{2}u_{0}\pi ^{2}\alpha ^{4}+h_{3}\alpha ^2\right. \nonumber \\&\left. +\,h_{4}\beta ^2+h_{5}\rho ^2\right) \wp ^{2}\nonumber \\&+\,128\pi ^{2}(-64h_{2}\pi ^{2}\alpha ^{4}-64u_{0}h_{2}\pi ^{2}\alpha ^{4}+h_{3}\alpha ^2 \nonumber \\&+\,h_{4}\beta ^2+h_{5}\rho ^2)\wp ^{8}+\cdots +32\pi ^{2}\nonumber \\&\times \left( -16h_{2}\pi ^{2}n^4\alpha ^4-16h_{2}u_{0}\pi ^{2}n^4\alpha ^{4}\right. \nonumber \\&\left. +\,h_{3}n^2\alpha ^2+h_{4}n^2\beta ^2+h_{5}n^2\rho ^2\right) \wp ^{2n^{2}}+\cdots , \nonumber \\ b_{2}= & {} 8\pi ^{2}\left( -4h_{2}\pi ^2\alpha ^4-4h_{2}u_{0}\pi ^2\alpha ^{4}+h_{3}\alpha ^2\right. \nonumber \\&\left. +\,h_{4}\beta ^2+h_{5}\rho ^2\right) \wp + 72\pi ^2\Big (-36h_{2}\pi ^2\alpha ^4\nonumber \\&-\,36h_{2}u_{0}\pi ^2\alpha ^4+h_{3}\alpha ^2 +h_{4}\beta ^2+h_{5}\rho ^2\Big )\wp ^{5}\nonumber \\&+\,\cdots +8\pi ^{2}\Big (-4h_{2}\pi ^2\alpha ^4(2n-1)^4\nonumber \\&-\,4h_{2}u_{0}\pi ^2\alpha ^4(2n-1)^4+h_{3}\alpha ^2(2n-1)^2 \nonumber \\&+\,h_{4}\beta ^2(2n-1)^2+h_{5}\rho ^2(2n-1)^2\Big )\wp ^{2n^{2}-2n+1}\nonumber \\&+\,\cdots . \end{aligned}$$
(75)

The following formulas can be obtained by using Eqs. (4.10) and (4.12) in Ref. [17]

$$\begin{aligned} A_{0}= & {} \left( \begin{array}{c@{\quad }c} 0&{}1\\ 0&{}0\end{array} \right) , \quad A_{1}=\left( \begin{array}{c@{\quad }c} 0&{}0\\ -8\pi ^{2}\alpha &{}2\end{array} \right) , \nonumber \\ A_{2}= & {} \left( \begin{array}{c@{\quad }c} -32\pi ^{2}\alpha &{}2\\ 0&{}0\end{array} \right) ,\quad A_{5}=\left( \begin{array}{c@{\quad }c} 0&{}0\\ -72\pi ^{2}\alpha &{}2\end{array} \right) ,\quad \nonumber \\ A_{3}= & {} A_{4}=0,\ldots , \nonumber \\ B_{0}= & {} 0,~~ B_{1}=\left( 0,8\pi ^{2}(-4h_{2}\pi ^2\alpha ^4-4u_{0}h_{2}\pi ^2\alpha ^4\right. \nonumber \\&\left. +\,h_{3}\alpha ^2+h_{4}\beta ^{2}+h_{5}\rho ^2)\right) ^{T}, \nonumber \\ B_{2}= & {} \left( 32\pi ^{2}(-16h_{2}\pi ^2\alpha ^4-16u_{0}h_{2}\pi ^2\alpha ^4\right. \nonumber \\&\left. +\,h_{3}\alpha ^2+h_{4}\beta ^{2}+h_{5}\rho ^2),0\right) ^{T},~~B_{3}=0, \nonumber \\ B_{5}= & {} \left( 0,72\pi ^{2}(-36h_{2}\pi ^2\alpha ^4-36u_{0}h_{2}\pi ^2\alpha ^4\right. \nonumber \\&\left. +\,h_{3}\alpha ^2+h_{4}\beta ^{2}+h_{5}\rho ^2)\right) ^{T},~~B_{4}=0,\ldots . \end{aligned}$$
(76)

Considering Proposition 3 in Ref. [17], system (76) yields

$$\begin{aligned}&X_{0}=\left( \begin{array}{c}4h_{2}\pi ^2\alpha ^3+4h_{2}u_{0}\pi ^2\alpha ^3-h_{3}\alpha -h_{4}\beta ^2\alpha ^{-1}-h_{5}\rho ^2\alpha ^{-1}\\ 0 \end{array}\right) , \nonumber \\&X_{2}=\left( \begin{array}{c} 8\left( 4h_{2}\pi ^2\alpha ^3+4h_{2}u_{0}\pi ^2\alpha ^3-h_{3}\alpha -h_{4}\beta ^2\alpha ^{-1}-h_{5}\rho ^2\alpha ^{-1}\right) \\ 128h_{2}\pi ^4\alpha ^4+128h_{2}u_{0}\pi ^4\alpha ^4-32h_{3}\pi ^2\alpha ^2-32h_{4}\pi ^2\beta ^2-32h_{5}\pi ^2\rho ^2 \end{array}\right) , \nonumber \\&X_{4}=\left( \begin{array}{c} 480h_{2}\pi ^2\alpha ^3+480h_{2}u_{0}\pi ^2\alpha ^3-48h_{3}\alpha -48h_{4}\beta ^2\alpha ^{-1}-48h_{5}\rho ^2\alpha ^{-1}\\ 768h_{2}\pi ^4\alpha ^4+768h_{2}u_{0}\pi ^4\alpha ^4-192h_{3}\pi ^2\alpha ^2-192h_{4}\pi ^2\beta ^2-192h_{5}\pi ^2\rho ^2 \end{array}\right) , \nonumber \\&X_{1}=X_{3}=0,\ldots , \end{aligned}$$
(77)

and from system (4.11) in Ref. [17], we have the following formulas

$$\begin{aligned} \omega= & {} \Big (4h_{2}\pi ^2\alpha ^3+4h_{2}u_{0}\pi ^2\alpha ^3-h_{3}\alpha -h_{4}\beta ^2\alpha ^{-1}\nonumber \\&-\,h_{5}\rho ^2\alpha ^{-1}\Big )+8\Big (4h_{2}\pi ^2\alpha ^3+4h_{2}u_{0}\pi ^2\alpha ^3\nonumber \\&-\,h_{3}\alpha -h_{4}\beta ^2\alpha ^{-1}-h_{5}\rho ^2\alpha ^{-1}\Big )\wp ^{2}\nonumber \\&+\,\left( 480h_{2}\pi ^2\alpha ^3+480h_{2}u_{0}\pi ^2\alpha ^3\right. \nonumber \\&\left. -\,48h_{3}\alpha -48h_{4}\beta ^2\alpha ^{-1}-48h_{5}\rho ^2\alpha ^{-1}\right) \wp ^{4}\nonumber \\&+\,o(\wp ^{4}), \nonumber \\ c= & {} \left( 128h_{2}\pi ^4\alpha ^4+128h_{2}u_{0}\pi ^4\alpha ^4-32h_{3}\pi ^2\alpha ^2\right. \nonumber \\&\left. -\,32h_{4}\pi ^2\beta ^2-32h_{5}\pi ^2\rho ^2\right) \wp ^{2}\nonumber \\&+\,\left( 768h_{2}\pi ^4\alpha ^4+768h_{2}u_{0}\pi ^4\alpha ^4\right. \nonumber \\&\left. -\,192h_{3}\pi ^2\alpha ^2-192h_{4}\pi ^2\beta ^2-192h_{5}\pi ^2\rho ^2\right) \wp ^{4}\nonumber \\&+\,o(\wp ^{4}). \end{aligned}$$
(78)

Considering the formulas (73) and the condition \(\wp \rightarrow 0\), one has

$$\begin{aligned}&c\rightarrow 0,~~~~ \omega \rightarrow 4h_{2}\pi ^2\alpha ^3+4h_{2}u_{0}\pi ^2\alpha ^3\nonumber \\&\quad -\,h_{3}\alpha -h_{4}\beta ^2\alpha ^{-1} -h_{5}\rho ^2\alpha ^{-1}, \end{aligned}$$
(79)

i.e.,

$$\begin{aligned} 2\pi i\omega \rightarrow -h_{2}\mu ^{3}-h_{3}\mu -h_{4}\nu ^2\mu ^{-1}-h_{5}\sigma ^2\mu ^{-1}. \end{aligned}$$
(80)

In addition, the periodic function \(\vartheta (\xi )\) could be rewritten as follows

$$\begin{aligned} \vartheta (\xi ,\tau )= & {} 1+\left( e^{2\pi i \xi }+e^{-2\pi i \xi }\right) \wp \nonumber \\&+\,\left( e^{4\pi i \xi }+e^{-4\pi i \xi }\right) \wp ^{4}+\cdots . \end{aligned}$$
(81)

On account of the transformation (73), one has

$$\begin{aligned}&\begin{aligned} \vartheta (\xi ,\tau )&=1+e^{\tilde{\xi }}+\left( e^{-\tilde{\xi }}+e^{2\tilde{\xi }}\right) \wp ^{2} +\left( e^{-2\tilde{\xi }}+e^{3\tilde{\xi }}\right) \wp ^{6}\\&\quad +\cdots \rightarrow 1+e^{\tilde{\xi }}, ~~\mathrm{when}~~\wp \rightarrow 0, \end{aligned}\nonumber \\&\tilde{\xi }=2\pi i\xi -\pi \tau =\mu x+\nu y+\sigma z+2\pi i \omega t+\delta , \end{aligned}$$
(82)

from system (80) to (82), the following formulas can be obtained by

$$\begin{aligned} \tilde{\xi }\rightarrow & {} \mu x+\nu y+\sigma z\nonumber \\&+\,\left( -h_{2}\mu ^{3}-h_{3}\mu -h_{4}\nu ^2\mu ^{-1}-h_{5}\sigma ^2\mu ^{-1}\right) t \nonumber \\&+\,\delta =\eta ,~~\mathrm{when}~~\wp \rightarrow 0, \nonumber \\ \xi\rightarrow & {} \frac{\eta +\pi \tau }{2\pi i},~~\mathrm{when}~~\wp \rightarrow 0. \end{aligned}$$
(83)

From system (82) and system (83), one finally derives

$$\begin{aligned} \vartheta (\xi )\rightarrow 1+e^{\eta },~~\mathrm{when}~~\wp \rightarrow 0. \end{aligned}$$
(84)

From all above analyses, it implies that the conclusion of Theorem 6 is hold when \(\wp \rightarrow 0.\) \(\square \)

Theorem 7

Let \((\omega _{1},\omega _{2},u_{0},c)^{T}\) be a solution for the system (71), we take

$$\begin{aligned} \alpha _{i}= & {} \frac{\mu _{i}}{2\pi i}, ~~~~\beta _{i}=\frac{\nu _{i}}{2\pi i}, ~~~~\rho _{i}=\frac{\sigma _{i}}{2\pi i}, \nonumber \\ \varepsilon _{i}= & {} \frac{\delta _{i}+\pi \tau _{ij}}{2\pi i}, ~~~~ \tau _{12}=\frac{A_{12}}{2\pi i}, ~~~~i=1,2, \end{aligned}$$
(85)

for the two-periodic wave solution (66), in which \(\mu _{i},\nu _{i},\sigma _{i},\delta _{i},A_{12}\) \(i=1,2\) depend on Eq. (20) and (21). The limiting properties as follows

$$\begin{aligned}&u_{0}\rightarrow 0,\quad c\rightarrow 0,\quad \xi _{i}\rightarrow \frac{\eta _{i}+\pi \tau _{ij}}{2\pi i}, \quad i=1,2, \nonumber \\&\vartheta (\xi _{1},\xi _{2},\tau )\rightarrow 1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{1}+\eta _{2}+A_{12}},\nonumber \\&\quad \text{ as } \quad \wp _{1},\wp _{2}\rightarrow 0. \end{aligned}$$
(86)

which shows that the periodic wave solution (66) can be degraded to the soliton solution (20) when \((u,\wp _{1},\wp _{2})\rightarrow (u_{1},0,0)\).

Proof

At beginning, expanding the functions \(H,b,(\omega _{1},\omega _{2},u_{0},c)^{T}\) in terms of the series about \(\wp \)

$$\begin{aligned} \begin{aligned}&\begin{aligned} H&=H_{0}+H_{1}\wp _{1}+H_{2}\wp _{2}+H_{3}\wp _{1}^2+H_{4}\wp _{2}^{2}\\&\quad +H_{5}\wp _{1}\wp _{2}+H_{6}\wp _{1}\wp _{2}\wp _{3} +\cdots \end{aligned}\\&\begin{aligned} b&=B_{1}\wp _{1}+B_{2}\wp _{2}+B_{3}\wp _{1}^2+B_{4}\wp _{2}^{2}\\&\quad +B_{5}\wp _{1}\wp _{2}+B_{6}\wp _{1}\wp _{2}\wp _{3}\\&\quad +\cdots \left( \omega _{1},\omega _{2},u_{0},c\right) ^{T}=\varLambda _{0}+\varLambda _{1}\wp _{1}+\varLambda _{2}\wp _{2}\\&\quad +\varLambda _{3}\wp _{1}^2+\varLambda _{4}\wp _{2}^{2}+\varLambda _{5}\wp _{1}\wp _{2}+\varLambda _{6}\wp _{1}\wp _{2}\wp _{3}\\&\quad +\cdots . \end{aligned} \end{aligned} \end{aligned}$$
(87)

According to Eqs. (68) and (87), we obtain

$$\begin{aligned} H= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\end{array} \right) +\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{}0\\ -8\pi ^{2}\alpha _{1}&{}0&{}32h_{2}\pi ^4\alpha _{1}^4&{}2\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\end{array} \right) \wp _{1}\nonumber \\&+\,\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}-8\pi ^{2}\alpha _{2}&{}32h_{2}\pi ^4\alpha _{2}^4&{}2\\ 0&{}0&{}0&{}0\end{array} \right) \wp _{2} \nonumber \\&+\,\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -32\pi ^{2}\alpha _{1}&{}0&{}512h_{2}\pi ^4\alpha _{1}^4&{}2\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\end{array} \right) \wp _{1}^{2}\nonumber \\&+\,\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}-32\pi ^{2}\alpha _{2}&{}512h_{2}\pi ^4\alpha _{2}^4&{}2\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\end{array} \right) \wp _{2}^{2}\nonumber \\&+\,\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ \varDelta _{1}&{}-\varDelta _{1} &{}\varDelta _{2}&{}-2\end{array} \right) \wp _{1}\wp _{2} \nonumber \\&+\,\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ \varDelta _{3}&{}\varDelta _{3} &{}\varDelta _{4}&{}-2\end{array} \right) \wp _{1}\wp _{2}\wp _{3}\nonumber \\&+\,o\left( \wp _{1}^{i}\wp _{2}^{j}\wp _{3}^{k}\right) ,\quad ~~i+j+k\ge 3 , \end{aligned}$$
(88)
$$\begin{aligned} b= & {} \left( \begin{array}{c} 0\\ \varUpsilon _{1}\\ 0\\ 0\end{array} \right) \wp _{1}+\left( \begin{array}{c} 0\\ 0\\ \varUpsilon _{2}\\ 0\end{array} \right) \wp _{2}+\left( \begin{array}{c} \varUpsilon _{3}\\ 0\\ 0\\ 0\end{array} \right) \wp _{1}^{2}\nonumber \\&+\,\left( \begin{array}{c} \varUpsilon _{4}\\ 0\\ 0\\ 0\end{array} \right) \wp _{2}^{2}+\left( \begin{array}{c} 0\\ 0\\ 0\\ \varUpsilon _{5}\end{array} \right) \wp _{1}\wp _{2}+\left( \begin{array}{c} 0\\ 0\\ 0\\ \varUpsilon _{6}\end{array} \right) \wp _{1}\wp _{2}\wp _{3}\nonumber \\&+\,o\left( \wp _{1}^{i}\wp _{2}^{j}\wp _{3}^{k}\right) ,\quad ~~i+j+k\ge 3, \end{aligned}$$
(89)
$$\begin{aligned} \left( \begin{array}{c} \omega _{1}\\ \omega _{2}\\ u_{0}\\ c\end{array} \right)= & {} \left( \begin{array}{c} \omega _{1}^{(00)}\\ \omega _{2}^{(00)}\\ u_{0}^{(00)}\\ c^{(00)}\end{array} \right) +\left( \begin{array}{c} \omega _{1}^{(11)}\\ \omega _{2}^{(11)}\\ u_{0}^{(11)}\\ c^{(11)}\end{array} \right) \wp _{1}+\left( \begin{array}{c} \omega _{1}^{(21)}\\ \omega _{2}^{(21)}\\ u_{0}^{(21)}\\ c^{(21)}\end{array} \right) \wp _{2}\nonumber \\&+\,\left( \begin{array}{c} \omega _{1}^{(12)}\\ \omega _{2}^{(12)}\\ u_{0}^{(12)}\\ c^{(12)}\end{array} \right) \wp _{1}^{2}+\left( \begin{array}{c} \omega _{1}^{(22)}\\ \omega _{2}^{(22)}\\ u_{0}^{(22)}\\ c^{(22)}\end{array} \right) \wp _{2}^{2}\nonumber \\&+\,\left( \begin{array}{c} \omega _{1}^{(2)}\\ \omega _{2}^{(2)}\\ u_{0}^{(2)}\\ c^{(2)}\end{array} \right) \wp _{1}\wp _{2} +\left( \begin{array}{c} \upomega _{1}^{(3)}\\ \upomega _{2}^{(3)}\\ u_{0}^{(3)}\\ c^{(3)}\end{array} \right) \wp _{1}\wp _{2}\wp _{3}\nonumber \\&+\,o\left( \wp _{1}^{i}\wp _{2}^{j}\wp _{3}^{k}\right) ,\quad ~~i+j+k\ge 3 , \end{aligned}$$
(90)

with

$$\begin{aligned} \varDelta _{1}= & {} -8\pi ^{2}(\alpha _{1}-\alpha _{2}),~~~~ \varDelta _{2}=32h_{2}\pi ^{4}(\alpha _{1}-\alpha _{2})^4, \nonumber \\ \varDelta _{3}= & {} -8\pi ^{2}(\alpha _{1}+\alpha _{2}),~~~~ \varDelta _{4}=32h_{2}\pi ^{4}(\alpha _{1}+\alpha _{2})^4, \nonumber \\ \varUpsilon _{1}= & {} -32h_{2}\pi ^{4}\alpha _{1}^4+8h_{3}\pi ^{2}\alpha _{1}^{2}+8h_{4}\pi ^{2}\beta _{1}^{2}\nonumber \\&+\,8h_{5}\pi ^{2}\rho _{1}^{2}, \nonumber \\ \varUpsilon _{2}= & {} -32h_{2}\pi ^{4}\alpha _{2}^4+8h_{3}\pi ^{2}\alpha _{2}^{2}+8h_{4}\pi ^{2}\beta _{2}^{2}\nonumber \\&+\,8h_{5}\pi ^{2}\rho _{2}^{2}, \nonumber \\ \varUpsilon _{3}= & {} -512h_{2}\pi ^{4}\alpha _{1}^{4}+32h_{3}\pi ^{2}\alpha _{1}^{2}+32h_{4}\pi ^{2}\beta _{1}^{2}\nonumber \\&+\,32h_{5}\pi ^{2}\rho _{1}^{2}, \nonumber \\ \varUpsilon _{4}= & {} -512h_{2}\pi ^{4}\alpha _{2}^{4}+32h_{3}\pi ^{2}\alpha _{2}^{2}+32h_{4}\pi ^{2}\beta _{2}^{2}\nonumber \\&+\,32h_{5}\pi ^{2}\rho _{2}^{2}, \nonumber \\ \varUpsilon _{5}= & {} -32h_{2}\pi ^{4}(\alpha _{1}-\alpha _{2})^{4}+8h_{3}\pi ^{2}\left( \alpha _{1}-\alpha _{2}\right) ^{2}\nonumber \\&+\,8h_{4}\pi ^{2}(\beta _{1}-\beta _{2})^2+8h_{5}\pi ^{2}(\rho _{1}-\rho _{2})^2, \nonumber \\ \varUpsilon _{6}= & {} -32h_{2}\pi ^{4}(\alpha _{1}+\alpha _{2})^{4}+8h_{3}\pi ^{2}(\alpha _{1}+\alpha _{2})^{2}\nonumber \\&+\,8h_{4}\pi ^{2}(\beta _{1}+\beta _{2})^2+8h_{5}\pi ^{2}(\rho _{1}+\rho _{2})^2. \end{aligned}$$
(91)

Substituting Eqs.(88)–(91) into the system (71) yields the following system

$$\begin{aligned}&c^{(00)}=c^{(11)}=c^{(21)}=c^{(2)}=c^{(3)}=0, \nonumber \\&\quad -\,8\pi ^2\alpha _{1}\omega _{1}^{(00)}+32h_{2}\pi ^4\alpha _{1}^4u_{0}^{(00)}=\varUpsilon _{1}, \nonumber \\&\quad -\,8\pi ^2\alpha _{2}\omega _{2}^{(00)}+32h_{2}\pi ^4\alpha _{2}^4u_{0}^{(00)}=\varUpsilon _{2}, \nonumber \\&c^{(12)}-32\pi ^2\alpha _{1}\omega _{1}^{(00)}+512h_{2}\pi ^4\alpha _{1}^4u_{0}^{(00)}=\varUpsilon _{3} \nonumber \\&\quad -\,8\pi ^2\alpha _{1}\omega _{1}^{(11)}+32h_{2}\pi ^4\alpha _{1}^4u_{0}^{(11)}=0, \nonumber \\&c^{(22)}-32\pi ^2\alpha _{2}\omega _{2}^{(00)}+512h_{2}\pi ^4\alpha _{2}^4u_{0}^{(00)}=\varUpsilon _{4} \nonumber \\&\quad -\,8\pi ^2\alpha _{2}\omega _{2}^{(21)}+32h_{2}\pi ^4\alpha _{2}^4u_{0}^{(21)}=0, \nonumber \\&\quad -\,8\pi ^2\alpha _{1}\omega _{1}^{(21)}+32h_{2}\pi ^4\alpha _{1}^4u_{0}^{(21)}=0, \nonumber \\&\quad -\,8\pi ^2\alpha _{2}\omega _{2}^{(11)}+32h_{2}\pi ^4\alpha _{2}^4u_{0}^{(11)}=0, \nonumber \\&\varDelta _{1}\omega _{1}^{(00)}-\varDelta _{1}\omega _{2}^{(00)}+\varDelta _{2}u_{0}^{(00)}=\varUpsilon _{5}. \end{aligned}$$
(92)

By the consideration of \(u_{0}^{(00)}=0\), one has

$$\begin{aligned} \begin{aligned}&u_{0}=o(\wp _{1},\wp _{2})\rightarrow 0, \\&\begin{aligned} c&=-384h_{2}\pi ^{4}\alpha _{1}^{4}\wp _{1}^{2}-384h_{2}\pi ^4\alpha _{2}^4\wp _{2}^{2}\\&\quad +o(\wp _{1}\wp _{2})\rightarrow 0, \end{aligned}\\&\begin{aligned} \omega _{1}&=4h_{2}\pi ^2\alpha _{1}^{3}-h_{3}\alpha _{1}-h_{4}\beta _{1}^2\alpha _{1}^{-1}-h_{5}\rho _{1}^2\alpha _{1}^{-1}\\&\quad +o\left( \wp _{1}\wp _{2}\right) \rightarrow 4h_{2}\pi ^2\alpha _{1}^{3}-h_{3}\alpha _{1}\\&\quad -h_{4}\beta _{1}^2\alpha _{1}^{-1}-h_{5}\rho _{1}^2\alpha _{1}^{-1}, \end{aligned}\\&\begin{aligned} \omega _{2}&=4h_{2}\pi ^2\alpha _{2}^{3}-h_{3}\alpha _{2}-h_{4}\beta _{2}^2\alpha _{2}^{-1}-h_{5}\rho _{2}^2\alpha _{2}^{-1}\\&\quad +o\left( \wp _{1}\wp _{2}\right) \rightarrow 4h_{2}\pi ^2\alpha _{2}^{3}-h_{3}\alpha _{2}\\&\quad -h_{4}\beta _{2}^2\alpha _{2}^{-1}-h_{5}\rho _{2}^2\alpha _{2}^{-1}, \\&\quad \mathrm{when}~~(\wp _{1}\wp _{2})\rightarrow (0,0) . \end{aligned} \end{aligned} \end{aligned}$$
(93)

Considering (85) yields

$$\begin{aligned}&2\pi i\omega _{1}\rightarrow -h_{2}\mu _{1}^{3}-h_{3}\mu _{1}-h_{4}\nu _{1}^{2}\mu _{1}^{-1}-h_{5}\sigma _{1}^2\mu _{1}^{-1}, \nonumber \\&2\pi i\omega _{2}\rightarrow -h_{2}\mu _{2}^{3}-h_{3}\mu _{2}\nonumber \\&\quad -\,h_{4}\nu _{2}^{2}\mu _{2}^{-1}-h_{5}\sigma _{2}^2\mu _{2}^{-1},\mathrm{when}~~(\wp _{1}\wp _{2})\rightarrow (0,0). \end{aligned}$$
(94)

Next, the periodic wave function \(\vartheta (\xi _{1},\xi _{2},\tau )\) can be rewritten as the following form

$$\begin{aligned} \vartheta (\xi _{1},\xi _{2},\tau )= & {} 1+\left( e^{2\pi i\xi _{1}}+e^{-2\pi i\xi _{1}}\right) e^{\pi \tau _{11}}\nonumber \\&+\,\left( e^{2\pi i\xi _{2}}+e^{-2\pi i\xi _{2}}\right) e^{\pi \tau _{22}}\nonumber \\&+\,\left( e^{2\pi i(\xi _{1}+\xi _{2})}+e^{-2\pi i(\xi _{1}+\xi _{2})}\right) \nonumber \\&\times \, e^{\pi \left( \tau _{11}+2\tau _{12}+\tau _{22}\right) }+\cdots . \end{aligned}$$
(95)

Considering the transformation (85), we have

$$\begin{aligned} \vartheta (\xi _{1},\xi _{2},\tau )= & {} 1+e^{\tilde{\xi }_{1}}+e^{ \tilde{\xi }_{2}}+e^{\tilde{\xi }_{1}+\tilde{\xi }_{2}-2\pi \tau _{12}}\nonumber \\&+\, \wp _{1}^{2}e^{-\tilde{\xi }_{1}}+\wp _{2}^{2}e^{-\tilde{\xi }_{2}}\nonumber \\&+\,\wp _{1}^{2}\wp _{2}^{2}e^{-\tilde{\xi }_{1}^{2}-\tilde{\xi }_{2}-2\pi \tau _{12}}+\cdots \nonumber \\&\rightarrow \, 1+e^{\tilde{\xi }_{1}}+e^{ \tilde{\xi }_{2}}\nonumber \\&+\,e^{\tilde{\xi }_{1}+\tilde{\xi }_{2}+A_{12}},\quad \mathrm{as}~~\wp _{1},\wp _{2}\rightarrow 0, \end{aligned}$$
(96)

where \(\tilde{\xi }_{i}=\mu _{i}x+\nu _{i}y+\sigma _{i}z+2\pi i\omega _{i}t+\delta _{i}\), \(i=1,2.\) From Eqs. (93) and (96), we get

$$\begin{aligned}&\tilde{\xi }_{i}\rightarrow \mu _{i}x+\nu _{i}y+\sigma _{i}z\nonumber \\&\quad +\,(-h_{2}\mu _{i}^{3}-h_{3}\mu _{i}-h_{4}\mu _{i}^{-1}\nu _{i}^{2}-h_{5}\mu _{i}^{-1}\sigma _{i}^{2})t\nonumber \\&\quad +\,\delta _{i}=\eta _{i}, \xi _{i}\rightarrow \frac{\eta _{i}+\pi \tau _{ij}}{2\pi i}~~~~\mathrm{as}~~\wp _{1},\wp _{2}\rightarrow 0. \end{aligned}$$
(97)

Combining Eq. (96) with Eq. (97), we obtain

$$\begin{aligned}&\vartheta (\xi _{1},\xi _{2},\tau )\rightarrow 1+e^{\eta _{1}}\nonumber \\&\quad +\,e^{\eta _{2}}+e^{\eta _{1}+\eta _{2}+A_{12}}, \quad \text{ as } \quad \wp _{1},\wp _{2}\rightarrow 0. \end{aligned}$$
(98)

It implies that the conclusion of Theorem 7 is hold when \((u,\wp _{1},\wp _{2})\rightarrow (u_{1},0,0)\). \(\square \)

7 Conclusions

In this paper, the integrability properties of the generalized (3+1)-dimensional nonlinear waves (1) in liquid containing gas bubbles are researched. The bilinear equation, Bäcklund transformation, infinite conservation laws, N-soliton solution for Eq. (1) are systematically structured based on the binary Bell polynomials. These results can be reduced to the analogues of (3+1)-dimensional KP equation, (3+1)-dimensional nonlinear wave equation and Korteweg-de Vries equation, respectively. Furthermore, by the virtue of Riemann theta functions, we construct one- and two-periodic wave solutions for Eq.  (1). Finally, we present a asymptotic property in detail, which implies that the periodic wave solutions can be degraded to the soliton solutions. All the results verify that the approach which combines the Hirota bilinear method and Riemann theta function is feasible and efficient to deal with the integrability properties of NLEE.