1 Introduction

The ultra-precision press with multi-link transmission mechanism, as “less/non-chip finish” high-effective machine tool as well as one of the key industrial equipments, can manufacture metal parts closer to their final shapes and comply better with the requirements of highly advocated clean and green production. With the increase in rotational speed, the impact frequency between revolute joints increases dramatically as a result of clearance, which reduces the stability of the transmission mechanism and causes its lower working accuracy. Therefore, in order to improve the performance of multi-link mechanism, it is essential to investigate the effect of the clearance and lubrication on its performance.

The main feature of the multi-link mechanism is the existence of clearance and lubrication for multiple revolute and spherical joints and complex structure of mechanism, which transforms the dynamics of the entire multi-link mechanism into strongly nonlinear one. Furthermore, the effect of the inertia force and balance mechanism should be also considered. Therefore, it is difficult to establish the dynamic model of the multi-link mechanism with clearance and lubrication to study its dynamic performance.

There have been a number of publications on the dynamics of multi-body system with clearance. The previous models can be divided into three categories: rigid model with dry clearance joints, flexible model with dry clearance joints, and model with lubricated clearance joints. As far as rigid model with dry clearance joints be concerned, Flores [1] presented a parametric study which shows the large effect of the clearance size on the dynamic load and overall system behavior of a slider–crank mechanism. Using both the spring-damping model and the collision model, Mukras [2, 3] developed a dynamic model of the slider–crank mechanism based on the Archard model to study the effect of the wear on the mechanism. Farahanchi and Shaw [4] studied the influence of the clearance size, friction, and speed of crank shaft on dynamic response. Jia and Wang [5] considered the clearance of joints as a rigid linkage and investigated the dynamic errors of the slider–crank mechanism for closed high-speed presses based on the continuous contact model. In order to stabilize the slider–crank mechanism with a revolute joint between the slider and the connecting rod and prevent its chaotic behavior, Olyaei and Ghazavi [6] proposed a control mechanism using Pyragas method. Muvengei et al. [7] studied the parametric effects of differently located frictionless revolute joints on the dynamic characteristics of a planar slider–crank mechanism. The simulation results demonstrate that different joints in a multi-body system have different sensitivities to clearance size. Gummer and Sauer [8] have developed a methodology to calculate a slider–crank mechanism with a revolute clearance joint based on the commercial MBS tool RecurDyn, and the validity of the methodology was verified and compared with results in other papers. Megahed and Haroun [9] established a model of slider–crank mechanism with multiple clearance joints in Solidworks/CosmosMotion, which has an embedded ADAMS engine for conducting the simulation. Muvengei et al. [10] studied the behavior of planar rigid-body mechanical systems due to the dynamic interaction of multiple revolute clearance joints by using a slider–crank mechanism and found that clearance joints in a multi-body mechanical system had a strong dynamic interaction. Erkaya et al. [11–13] studied dynamic response of mechanism having revolute joints with clearance, which demonstrates that the joint clearance leads to chaotic behavior on kinematic and dynamic outputs of mechanism and the optimal adjusting of suitable design variables gives a certain decrease in shaking forces and their moments on the mechanism frame. Machado et al. [14] analyzed the main issues associated with the most common compliant contact force models and presented results in terms of the dynamic simulations of multi-body systems. Varedi et al. [15] optimized the mass distribution of the links of a mechanism to reduce the impact forces in the clearance joint and solved the highly nonlinear optimization problem for slider–crank mechanism with a revolute clearance joint between the slider and connecting rod based on PSO algorithm. Askari et al. [16] considered a quasi-static analysis and a multi-body dynamic approach to study the effect of friction-induced vibration and contact mechanics on the maximum contact pressure and moment of artificial hip implants and observed that the friction-induced vibration influences the contact pressure. Varedi et al. [17] also solved the highly nonlinear optimization problem for a slider–crank mechanism with revolute clearance joints by PSO algorithm and found that the linear and angular accelerations of the links and the contact forces in the optimal design are very smooth and bounded. Brutti et al. [18] presented a general computer-aided model of a 3D revolute joint with clearance suitable for implementation in multi-body dynamic solvers. Koshy et al. [19] presented a computational and experimental study on the contact forces developed in revolute clearance joints and concluded that the selection of the appropriate contact force model with proper dissipative damping plays a significant role in the dynamic response of mechanical systems involving contact events at low or moderate impact velocities. Yan et al. [20] proposed a comprehensive model for 3D revolute joints with radial and axial clearances which is firstly conducted to reveal the characteristics of the relative motion between the journal and bearing and characterized the axial movement of the journal relative to the bearing and misalignment between the two elements.

For flexible model with dry clearance joints case, Bauchau and Rodriguez [21] developed the dynamic equations of flexible multi-body system with clearance based on the nonlinear dynamic theory and studied the effect of clearance and flexibility on the dynamic response of slider–crank mechanism. Khemili and Romdhane [22] established a rigid-flexible coupling model of slider–crank mechanism with clearance and studied its dynamic response with the connecting rod considered to be a flexible body. Dupac and Beale [23] discretized the connecting rod into several rods and studied the dynamic response of the flexible slider–crank mechanism with clearance and analyzed its stability using Lyapunov equations. Schwab et al. [24] analyzed the dynamic behavior characteristics of a slider–crank mechanism when the coupler is rigid or flexible. The simulation results show that the flexibility of the connecting rod has a smoothing effect on its dynamic responses and acts as a suspension for the mechanism compared to the rigid one. Gu et al. [25] studied the dynamic response of the flexible slider–crank mechanism with clearance and confirmed the chaotic and periodic motion of the mechanism using numerical and experimental methods. Erkaya and Uzmay [26, 27] also investigated the effects of joint clearance on the dynamics of flexible mechanism by computational methodology. The authors [28] have also studied the effect of the joint clearance on the dynamics of flexible slider–crank mechanism for press system. Alves et al. [29] compared the identified contact force models for simple solid impact problems and found that the prediction of the dynamic behavior of contacting solids strongly depends on the selection of the contact force model. Pereira et al. [30] used a tooth fixed coordinate system in the methodology of describing the tooth profile and allowing for the contact detection to evaluate all quantities required by the contact force model.

For model with lubricated clearance joints case, Flores et al. [31–35] proposed dynamic models of revolute clearance joints with lubrication and spherical clearance joints, respectively. Based on the lubrication model, Alshaer et al. [36] established a dynamic model of the slider–crank mechanism with clearance and investigated its dynamic response by numerical method. Compared to the dry friction model, the simulation results show that the lubrication model increases damping and stiffness. Machado et al. [37] investigated a comprehensive methodology for dynamic modeling and analysis of planar multi-body systems with lubricated revolute joints and established three different hydrodynamic force models. Tian et al. [38, 39] presented a new computational methodology for modeling and analysis of flexible planar and spatial multi-body systems with clearance and lubricated revolute joints and incorporated several efficient methods in the proposed model. Tian et al. [40] also proposed a new methodology for the dynamic analysis of rigid-flexible multi-body systems with ElastoHydroDynamic (EHD) lubricated cylindrical joints and found that the bearing flexibility played a significant role in the system responses, extended the lubricant distribution space, and reduced the lubricant pressure. Tian et al. [41] studied the coupling dynamics of a geared multi-body system supported by ElastoHydroDynamic (EHD) lubricated cylindrical joints by proposing a comprehensive computational methodology. Liu et al. [42] gave a survey of the basic friction models, tested and compared five friction models, and provided contributions to motion control systems with friction, especially for micro-stick-slip or step motion systems as well as general micro-motion systems.

As far as we know, the previous dynamic models of multi-link mechanism rarely considers the effect of flexibility, revolute and spherical clearance joints, and lubrication together, which leads to a low-precision dynamic analysis. The primary objective of this work is to analyze the dynamic behavior of multi-link mechanism for presses in a more reasonable and accurate way. In this work, the effect of revolute and spherical clearance joints, lubrication, and flexibility of crank shaft and linkage is considered and a complete dynamic model of flexible multi-link mechanism with clearance and lubrication for ultra-precision presses is established.

This paper is organized as follows: The working principle and configuration of the multi-link mechanism with clearance for presses is described briefly in Sect. 2. The dry and lubricated revolute joint clearances and dry spherical joint clearance are modeled in Sect. 3. The flexible dynamic model of multi-link mechanism with clearance and lubrication is established in Sect. 4. Numerical simulations of the dynamic model are described and discussed in Sect. 5. The presented flexible model of multi-link mechanism with clearance and lubrication for presses is summarized in Sect. 5, and the conclusions are also presented in this section.

2 Physical description of multi-link mechanism with clearance

The working principle and configuration of the multi-link mechanism for presses is shown in Fig. 1. Motion and energy from the motor are transmitted to the main slider (10) through a transmission system, which can manufacture the metal parts closer to their final shapes. The belt transmits the motion of the motor from the small pulley to the big pulley, and then, the motion is transmitted to the main crank shaft (2) from the big pulley. The upper end of the linkage (3) is connected to the crank shaft, and the lower end is connected to the slider (4), which converts the rotary motion of the crank shaft into a straight reciprocating motion. In order to balance the inertia force, additional weight (12, 12\('\)) is added. To meet the needs of the production process, the slider is alternately in motion and motionless so the press must have a brake and clutch. Such presses often have a fly wheel to keep the load-bearing requirements on the motor uniform and to make the press more energy efficient.

Fig. 1
figure 1

Working principle and configuration of multi-link mechanism

Full size image

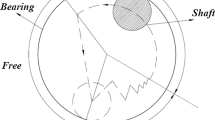
It is assumed that there exist revolute joints with clearance between the crank shaft and the main linkage, and between the main linkage and the main slider. The load acted on the revolute joint along the axial direction of the multi-link mechanism for high-speed press system is smaller than that along the radial direction, especially under high-speed blanking condition, and its axial effect of clearance revolute joint can be neglected in this work. The difference in radius between the bearing and the journal defines the size of radial clearance. A generic configuration of revolute joint with clearance in the multi-link mechanism is shown in Fig. 2a. When the mechanism operates, the dynamic behavior of the revolute joint with clearance can be expressed as an oblique eccentric impact between the journal and the bearing. When contact between the journal and bearing exists, the impact force will develop at the revolute joint. When the contact is lost, no constrains or impact forces are caused by the revolute joint. The mechanics of the impact involves the normal and tangential forces [43, 44]. Therefore, once the impact occurs, a certain contact law must be applied and the resulting impact forces are introduced as a generalized force to affect the motion of the system [45].

Fig. 2
figure 2

Generic configuration of revolute and spherical joint with clearance: a revolute joint, b spherical joint

Full size image

When some amount of clearance is included in a spherical joint, the ball and socket can move relative to each other. When the multi-link mechanism operates under high-speed blanking condition, the effect of spherical joints with clearance should be considered. Figure 2b illustrates the different possible types of ball motion inside the socket, namely: contact or following mode, free flight mode, and impact mode. In the contact or following mode, the ball and the socket are in permanent contact and a rolling or sliding motion relative to each other exists. This mode ends when the ball and socket separate from each other, and the ball centers in free flight mode. In the free flight motion, the ball moves freely inside the socket boundaries. In the impact mode, impact forces are applied to the system. The stiction between ball and socket is not considered in the present work.

3 Modeling of joints with clearance

3.1 Model of dry revolute joints with clearance

The centers of journal and bearing coincide in the classical analysis of a revolute joint, which is considered as ideal or perfect revolute joint. The clearance separates the two centers. From practical point of view, the clearance always exists in revolute joints in order to allow relative motion between the journal and the bearing. Therefore, compared with an ideal joint, two extra degrees of freedom are added to the system for a model with a clearance joint.

It is clear that a revolute joint with clearance does not impose any kinematic constraints on the system, but limits the journal orbit inside the bearing’s boundaries. Three different types of motion between the journal and bearing can be observed during the dynamics of the revolute joint clearance: (1) free flight mode, in which the journal moves freely within the bearing’s boundaries, that is, the journal and the bearing joint are not in contact; (2) impact mode, which occurs at the termination of the free flight mode, being impact forces applied to and removed from the system; and (3) permanent contact or following mode, in which contact is always maintained although the relative penetration depth between the bearing and journal varies along the circumference of the journal [46].

If there is no lubricant, the journal can move freely within the bearing until contact between the two bodies takes place. When the journal impacts the bearing wall, normal and tangential contact forces are developed and guide the dynamics of the journal–bearing, as shown in Fig. 3a. These forces are of a complex nature, and their corresponding impulse is transmitted throughout the system. The impact which has both normal and tangential relative velocities is treated as an eccentric oblique collision between two bodies. The normal velocity determines whether the contact bodies are approaching or separating, whereas the tangential velocity defines whether the bodies are sliding or sticking.

Fig. 3
figure 3

Representation of a revolute joint with clearance: a normal and tangential forces, b relation of two bodies

Full size image

For the actual dynamic configuration of the system, the relative penetration depth between the journal and the bearing is given by:

$$\begin{aligned} \delta =e-c>0 \end{aligned}$$
(1)

This geometric condition relates the location of the centers of the bearing and journal relative to the radial clearance in the point. The magnitude of the eccentricity vector is expressed as:

$$\begin{aligned} e=\sqrt{e_x^2 +e_y^2 } \end{aligned}$$
(2)

The journal is considered in free flight motion relative to the bearing until the geometric inequality criterion of Eq. (1) is verified and the contact mode is initialized. When \(\delta =e-c=0 \), the bearing and the journal get into contact with each other. However, a tolerance is introduced to accommodate for inaccuracies in the numerical results as a result of the accumulation of computation round-off errors. The bearing and journal are considered to be in contact when the penetration depth is larger than \(1.0\times 10^{-10} \) throughout this paper.

The relation of two bodies for a revolute clearance joint is shown in Fig. 3b, and the global position of points \(Q_i \) and \(Q_j \) is given by [47]:

$$\begin{aligned} \mathbf{u}_k^Q =\mathbf{u}_k +\mathbf{g}_k^Q +R_k \mathbf{n}, \quad (k=i,j) \end{aligned}$$
(3)

The vector \(\mathbf{n} \) is the unit vector normal to the plane of collision, which is defined by:

$$\begin{aligned} \mathbf{n}=\frac{\mathbf{e}}{\sqrt{e_x^2 +e_y^2 }} \end{aligned}$$
(4)

The vector \(\mathbf{n} \) is along the direction between the journal and bearing center, which can be determined by calculating the position of journal and bearing center. The velocity of contact points \(Q_i \) and \(Q_j \) is obtained by differentiating Eq. (3) with respect to time.

$$\begin{aligned} {\dot{\mathbf{u}}}_k^Q ={ \dot{\mathbf{u}}}_k +{ \dot{\mathbf{g}}}_k^Q +R_k { \dot{\mathbf{n}}}, \quad (k=i,j) \end{aligned}$$
(5)

The relative contact velocity, necessary to evaluate the contact force, can be defined as:

$$\begin{aligned} {\dot{\varvec{\updelta }}}=\left( {{\dot{\mathbf{u}}}_j -{ \dot{\mathbf{u}}}_i}\right) +\left( {{ \dot{\mathbf{g}}}_j^Q -{ \dot{\mathbf{g}}}_i^Q } \right) +\left( {R_j -R_{i}}\right) {\dot{\mathbf{n}}} \end{aligned}$$
(6)

The relative contact velocity has to be projected onto the normal and tangential direction to determine the components of the normal and tangential velocities.

The dynamics of a dry journal–bearing is characterized by two different situations. Firstly, when the journal and bearing are not in contact with each other, there is no contact force associated to the journal–bearing. Secondly, when the contact between the two bodies occurs, the contact–impact forces are modeled according to a nonlinear Hertz’s force law (normal force) together with LuGre friction law (tangential force). These two conditions can be expressed as:

$$\begin{aligned} F=\left\{ {{\begin{array}{ll} 0&{}\quad {\delta <0} \\ {F_\mathrm{N} +F_\mathrm{T} }&{} \quad {\delta \ge 0} \\ \end{array} }} \right. \end{aligned}$$
(7)

3.2 Model of lubricated revolute joints with clearance

When the space between the journal and the bearing is filled with an oil lubricant, a hydrodynamic resistance force develops in opposition to the journal’s motion. The hydrodynamic force results from both squeeze-film and wedge-film actions. In the squeeze-film effect, the pressure generation is caused by relative radial velocity of the journal–bearing surfaces. However, the wedge-film effect corresponds to the relative rotational velocity.

Dividing the eccentricity e by radial clearance c yields the eccentricity ratio \(\varepsilon \) written as:

$$\begin{aligned} \varepsilon =\frac{e}{c} \end{aligned}$$
(8)

The time rate change in eccentricity ratio \(\dot{\varepsilon } \) can be obtained by differentiating Eq. (8) with respect to time, that is

$$\begin{aligned} \dot{\varepsilon }=\frac{\dot{e}}{c} \end{aligned}$$
(9)

The angle \(\gamma \) between the X and Y components of eccentricity vector \(\mathbf{e} \) is given by [31]:

$$\begin{aligned} \gamma =\arctan \left( \frac{e_y }{e_x }\right) \end{aligned}$$
(10)

The time rate of parameter \(\dot{\gamma } \) can be obtained by differentiating Eq. (10) with respect to the time, that is

$$\begin{aligned} \dot{\gamma }=\frac{e_x \dot{e}_y -\dot{e}_x e_y }{e^{2}} \end{aligned}$$
(11)

In dynamically loaded journal–bearings, evaluation of the force components obtained from the integration of the Reynolds equation only over the positive pressure regions, by assuming null the pressure in the remaining portions, involves finding the zero points. The variable \(\gamma \) is used to determine the angle for which positive pressure begins and the angle for which the pressure is null.

3.3 Model of spherical joints with clearance

The connecting points of two bodies that are connected by an ideal spherical joint are coincident. The spherical clearance joint separates the two points, and the bodies can move freely relative to each other. The spherical clearance joint cannot constrain degree of freedom like the traditional ideal spherical joint any longer. In a spherical joint with clearance, the dynamics of the joint is controlled by contact–impact forces as a result of the collision between the bodies connected, which can be considered as force joints.

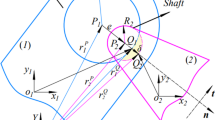
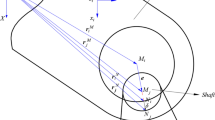
Two bodies i and j are connected by a spherical clearance joint shown in Fig. 4. The ball part of body j is located inside of a spherical part of body i , the socket. The radius of socket and ball are represented by \(R_i \) and \(R_j \) , respectively. The difference in radius between the socket and the ball defines the radial clearance. The mass center of bodies i and j are located at \(O_i \) and \(O_j \). Body-fixed coordinate systems \(\xi \eta \zeta \) are attached at their mass center, while XYZ represents the global coordinate system. Point \(P_i \) indicates the center of the socket, being the center of the ball denoted by \(P_j \). The vector that connects the point \(P_i \) to point \(P_j \) is used to define the eccentricity vector \(\mathbf{e} \). In practice, the magnitude of the eccentricity is much smaller than the radius of the socket and ball.

Fig. 4
figure 4

Spherical joint with clearance

Full size image

The eccentricity vector \(\mathbf{e} \) shown in Fig. 4, which connects the centers of the socket and the ball, can be given by [32]:

$$\begin{aligned} \mathbf{e}=\mathbf{u}_j^P -\mathbf{u}_i^P \end{aligned}$$
(12)

The global position vector of point P is expressed by:

$$\begin{aligned} {\begin{array}{ll} {\mathbf{u}_k^P =\mathbf{u}_k +\mathbf{g}_k^P =\mathbf{u}_k +\mathbf{A}_k \mathbf{{g}}_k^{\prime P} }&{} \quad {(k=i,j)} \\ \end{array} } \end{aligned}$$
(13)

The magnitude of the eccentricity vector can be calculated as:

$$\begin{aligned} e=\sqrt{\mathbf{e}^{T}\mathbf{e}} \end{aligned}$$
(14)

The magnitude of the eccentricity vector shown in the global coordinates is written as:

$$\begin{aligned} e=\left[ {\left( {x_j^P -x_i^P } \right) ^{2}+\left( {y_j^P -y_i^P } \right) ^{2}+\left( {z_j^P -z_i^P } \right) ^{2}} \right] ^{1/2} \end{aligned}$$
(15)

and the rate of change in the eccentricity in the radial direction, that is, in the direction of the line of centers of the socket and the ball is

$$\begin{aligned} {\dot{e}}= & {} \left[ \left( {x_j^P -x_i^P } \right) \left( {\dot{x}_j^P -\dot{x}_i^P } \right) +\left( {y_j^P -y_i^P } \right) \left( {\dot{y}_j^P -\dot{y}_i^P } \right) \right. \nonumber \\&\left. +\left( {z_j^P -z_i^P } \right) \left( {\dot{z}_j^P -\dot{z}_i^P } \right) \right] \Big /e \end{aligned}$$
(16)

in which the dot denotes the derivative with respect to time.

A unit vector \(\mathbf{n} \) along the eccentricity direction is given by:

$$\begin{aligned} \mathbf{n}=\frac{\mathbf{e}}{e} \end{aligned}$$
(17)

As shown in Fig. 5, the socket and the ball bodies are in contact, which is identified by the existence of a relative penetration. The contact or control points on bodies i and j are denoted as \(Q_i \) and \(Q_j \) , respectively. The global position of the contact points in the socket and ball are given by [35]:

$$\begin{aligned} {\begin{array}{ll} {\mathbf{u}_k^Q =\mathbf{u}_k +\mathbf{A}_k \mathbf{{g}}_k^{\prime Q} +\mathbf{R}_k \mathbf{n}}&{} \quad {(k=i,j)} \\ \end{array}} \end{aligned}$$
(18)
Fig. 5
figure 5

Penetration between the socket and the ball

Full size image

The velocity of the contact points \(Q_i \) and \(Q_j \) in the global coordinate system can be obtained by differentiating Eq. (18) with respect to time, which yields

$$\begin{aligned} {\begin{array}{ll} {{\dot{\mathbf{u}}}_k^Q ={ \dot{\mathbf{u}}}_k +{\dot{\mathbf{A}}}_k \mathbf{{g}}_k^{\prime Q} +\mathbf{R}_k { \dot{\mathbf{n}}}}&{} \quad {(k=i,j)} \\ \end{array} } \end{aligned}$$
(19)

It is assumed that there is no contact between the ball and the opening area in the socket. The relative normal velocity determines whether the contact bodies are approaching or separating, and the relative tangential velocity determines whether the contact bodies are sliding or sticking. The relative scalar velocities, normal and tangential to the surface of collision, can be obtained by projecting the relative impact velocity onto the tangential and normal directions.

$$\begin{aligned} \left\{ {\begin{array}{l} \nu _\mathrm{N} =\left[ \left( {{ \dot{\mathbf{u}}}_j^Q -{ \dot{\mathbf{u}}}_i^Q } \right) ^{T}\mathbf{n}\right] \mathbf{n} \\ \nu _\mathrm{T} =\left( {{ \dot{\mathbf{u}}}_j^Q -{ \dot{\mathbf{u}}}_i^Q } \right) ^{T}-\nu _\mathrm{N} \equiv \nu _\mathrm{T} \mathbf{t} \\ \end{array}} \right. \end{aligned}$$
(20)

Similarly, when the magnitude of the eccentricity vector is smaller than the radial clearance, there is no contact between the socket and the ball and, consequently, they can freely move relative to each other. When the magnitude of eccentricity is larger than radial clearance, there is contact between the socket and ball, being the relative penetration. Then, a constitutive contact law, such as the continuous contact force model proposed by Lankarani and Nikravesh [43], is applied to evaluate the contact force developed in the direction perpendicular to the plane of collision.

As these forces do not act through the mass center of the bodies i and j , the moment components for each body need to be evaluated. Furthermore, the contribution of the contact forces to generalized vector of forces are found by projecting the normal and tangential forces onto the X, Y , and Z directions. The equivalent forces and moments acting on the mass center of body i shown in Fig. 6 are given by:

$$\begin{aligned}&{\mathbf{f}_i }={\mathbf{f}_\mathrm{N}}+ {\mathbf{f}_\mathrm{T} } \nonumber \\&{\mathbf{M}_i } ={{\tilde{\mathbf{g}}}_i^Q } {\mathbf{f}_i } \end{aligned}$$
(21)

where a tilde \((\sim )\) placed over a vector indicates that the components of the vector are used to generate a skew-symmetric matrix. The forces and moments acting on body j are written as:

$$\begin{aligned}&{\mathbf{f}_j }= {\mathbf{f}_\mathrm{N} } + {\mathbf{f}_\mathrm{T} }\nonumber \\&{\mathbf{M}_j } = {{\tilde{\mathbf{g}}}_j^Q } {\mathbf{f}_j } \end{aligned}$$
(22)
Fig. 6
figure 6

Contact forces defined at the contact points between socket and ball

Full size image

3.4 Model of normal contact force

The contact method based on the IMPACT function was used to model the normal contact force under ADAMS. In this method, the contact force from the IMPACT function is calculated by the ADAMS function library. The contact force is typically modeled as a spring damper element. If this element is linear, the approach is known as the Kelvin Voigt model [48]. In this work, the relation is nonlinear and the contact force between the journal and bearing under ADAMS is essentially modeled as elastic-damping contact model.

The normal contact force for a joint is composed of rigidity and viscous damping. The rigidity is a function with respect to penetration \(\delta \), and the viscous damping is a function with respect to the speed of penetration \(\dot{\delta } \). The normal contact force can be given by:

$$\begin{aligned} F_\mathrm{N} = \left\{ {{\begin{array}{ll} {K\delta ^{n}} + {\hbox {STEP}\left( {\delta ,0,0,d_{\max } ,c_{\max } } \right) } {\dot{\delta }}&{}\quad {\delta >0} \\ 0&{}\quad {\delta \le 0} \\ \end{array} }} \right. \end{aligned}$$
(23)

where \(\hbox {STEP}(\cdot )\) represents a function with respect to \(\delta \), \(d_{\max } \) and \(c_{\max } \). A reasonable value for the parameter \(d_{\max } \) is 0.01 mm.

The normal contact force can be rewritten as:

$$\begin{aligned} F_\mathrm{N} =K\delta ^{n}+C(\delta )\dot{\delta }\quad (\delta >0) \end{aligned}$$
(24)

where \(C(\delta )\) is a cubic step function of the penetration in ADAMS software package shown in Fig. 7.

The instantaneous damping coefficient can be given by:

$$\begin{aligned} C(\delta )= & {} \hbox {STEP}(\delta ,0,0,d_{\max } ,c_{\max } )\nonumber \\= & {} \left\{ {{\begin{array}{ll} 0 &{}\quad \delta \le 0 \\ {c_{\max } (\delta /{d_{\max } })^{2}(3-{2\delta }/{d_{\max } })},&{} \quad 0<\delta <d_{\max }\\ {c_{\max } }&{}\quad \delta \ge d_{\max } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(25)

The damping coefficient is considered to be about 1 % of the stiffness coefficient \(K_n \), and then, the normal maximum damping coefficient \(c_{\max } \) is 0.01.

Based on Hertz model [49], the exponent n of the force deformation characteristics was set to be 1.5 for the metallic surfaces of the joint and normal stiffness coefficient can be expressed as:

$$\begin{aligned} K=4ER^{1/2}/3 \end{aligned}$$
(26)

where \(1/R=1/{R_1 }+1/{R_2 } \), \(1/E={(1-\mu _1 ^{2})}/{E_1 +}{(1-\mu _2 ^{2})}/{E_2 } \).

Fig. 7
figure 7

Schematic diagram of the step function

Full size image

3.5 Model of friction force

The purpose of the modified Coulomb’s law is to avoid discontinuity of friction force at zero relative tangential velocity and does not represent accurately the physical processes associated with the friction phenomenon at the revolute clearance joints. Therefore, it is essential to model the actual physical friction phenomenon, that is, the sliding friction, stiction friction, and the stick-slip transition motion both at microscopic and macroscopic levels. In this work, the LuGre friction model is selected to simulate the stick-slip friction in revolute joints of multi-link mechanism for high-speed press system. Since the normal contact force at a revolute clearance joint can be obtained from the contact force models as illustrated in Eq. (23), then from the classical definition of friction based on the LuGre friction law [50], we have:

$$\begin{aligned} F_\mathrm{T} =\mu F_\mathrm{N} \end{aligned}$$
(27)

The instantaneous coefficient of friction \((\mu )\) to be used in Eq. (27) can be represented as:

$$\begin{aligned} \mu = \sigma _0 z + \sigma _1 \dot{z} + \sigma _2 \upsilon _\mathrm{T} \end{aligned}$$
(28)

The differential equation for the average bristle deflection can be given by:

$$\begin{aligned} \dot{z}=\frac{\mathrm{d}z}{\mathrm{d}t}=\upsilon _\mathrm{T} -\frac{\sigma _0 \left| {\upsilon _\mathrm{T} } \right| }{\mu _\mathrm{k} +(\mu _\mathrm{s} -\mu _\mathrm{k} )e^{-\left| {\frac{\upsilon _\mathrm{T} }{\upsilon _\mathrm{S} }} \right| \gamma }}z \end{aligned}$$
(29)

Substituting Eq. (29) into Eq. (28) yields:

$$\begin{aligned} \mu = \sigma _0 z\left[ {1-\frac{\sigma _0 \left| {\upsilon _\mathrm{T} } \right| }{\mu _\mathrm{k} +\left( {\mu _\mathrm{s} -\mu _\mathrm{k} } \right) e^{-\left| {\upsilon _\mathrm{T} /\upsilon _\mathrm{S} } \right| \gamma }}} \right] + \left( {\sigma _1 +\sigma _2 } \right) \upsilon _\mathrm{T} \end{aligned}$$
(30)

Writing Eq. (28) and Eq. (29) in non-dimensional forms as illustrated [51], we have

$$\begin{aligned} \bar{{\mu }}= \left( {1-\bar{{\beta }}\bar{{\sigma }}_1 } \right) \bar{{z}} + \left( {\bar{{\sigma }}_1 +\bar{{\sigma }}_2 } \right) \bar{{\upsilon }}_\mathrm{T} \end{aligned}$$
(31)

where

$$\begin{aligned}&{\bar{\mu }}=\frac{\mu }{\mu _\mathrm{k} },\quad \bar{{\upsilon }}_\mathrm{T} =\frac{\upsilon _\mathrm{T} }{\upsilon _\mathrm{S} },\quad \bar{{\dot{z}}}=\frac{\dot{z}}{\upsilon _\mathrm{S} },\quad \bar{{z}}=\frac{\sigma _0 z}{\mu _\mathrm{k} }, \\&\quad \hbox {g}\left( \bar{{\upsilon }}_\mathrm{T} \right) =1+\left( \frac{\mu _\mathrm{S} }{\mu _\mathrm{k} }-1\right) e^{\left| {\bar{{\upsilon }}_\mathrm{T} } \right| \gamma }, \quad \bar{{\beta }}=\frac{\bar{{\upsilon }}_\mathrm{T} }{\hbox {g}\left( \bar{{\upsilon }}_\mathrm{T} \right) },\quad \nonumber \\&\quad \bar{{\sigma }}_1 =\frac{\sigma _1 \upsilon _\mathrm{S} }{\mu _\mathrm{k} },\quad \bar{{\sigma }}_2 =\frac{\sigma _2 \upsilon _\mathrm{S} }{\mu _\mathrm{k} } \end{aligned}$$

Therefore, the friction force in Eq. (27) becomes:

$$\begin{aligned} F_\mathrm{T} = {\bar{\mu }}\mu _\mathrm{k} F_\mathrm{N} \end{aligned}$$
(32)

The LuGre friction model is characterized by three dynamic parameters; z , \(\sigma _0 \), and \(\sigma _1 \); and five static parameters; \(\mu _\mathrm{k} \), \(\mu _\mathrm{s} \), \(\upsilon _\mathrm{S} \), \(\gamma \), and \(\sigma _2 \).The selection of these parameters is of great importance, which has influences on the results. The static parameters are first estimated by performing open-loop experiments. These parameters are then used to estimate the dynamic parameters using nonlinear numerical methods in dynamic experiments [52]. Swevers et al. [51] and Kermani et al. [53] presented experimental methodologies that can be used to identify the parameters of LuGre friction model for the joint of an industrial robot. The first step when identifying the friction parameters of a manipulator’s joint is to obtain an experimental plot between the friction force and the velocity at the joint [53]. Then, based on the derived analytical LuGre model, the plot is used to estimate the friction parameters dynamically; however, it is not feasible to obtain such a friction–velocity plot by running the joint at different constant velocities and measuring the friction force [54].

In this work, the choice of z and \(\sigma _2 \) was based on the following assumptions:

  1. (a)

    since simulations at steady-state condition are required, then the average bristle deflection (z) was assumed to be constant for a particular value of relative tangential velocity of the journal and bearing. Hence, at steady state [54], we have

    $$\begin{aligned}&\dot{z}=\frac{\mathrm{d}z}{\mathrm{d}t}=\upsilon _\mathrm{T} -\frac{\sigma _0 \left| {\upsilon _\mathrm{T} } \right| }{\mu _\mathrm{k} +(\mu _\mathrm{s} -\mu _\mathrm{k} )e^{-\left| {\upsilon _\mathrm{T} /\upsilon _\mathrm{S} } \right| \gamma }}z=0 \nonumber \\&z=\frac{\upsilon _\mathrm{T} }{\left| {\upsilon _\mathrm{T} } \right| }\times \frac{\mu _\mathrm{k} +(\mu _\mathrm{s} -\mu _\mathrm{k} )e^{-\left| {\upsilon _\mathrm{T} /\upsilon _\mathrm{S} } \right| \gamma }}{\sigma _0 } \end{aligned}$$
    (33)
  2. (b)

    since the work here was concerned with dry friction at the joints, then the viscous friction coefficient (\(\sigma _2 \)) which models the lubricant’s viscous properties was assumed to be zero.

The values of \(\sigma _0 \), \(\sigma _1 \), \(\upsilon _\mathrm{S} \), and \(\gamma \) were chosen based on observations by other researchers as follows:

  1. (1)

    A lot of friction models are sufficiently described using \(\gamma =2 \) [54].

  2. (2)

    \(\sigma _0 =100{,}000 \) N/m [55].

  3. (3)

    \(\sigma _1 =400 \) N s/m [53].

  4. (4)

    The characteristic Stribeck velocity \(\upsilon _\mathrm{S}\) is usually chosen to be small compared to the maximum relative velocity encountered during the simulation. In every simulation, \(\upsilon _\mathrm{S}\) was chosen to be 1 % of the maximum tangential velocity achieved.

4 Flexible model of multi-link mechanism with clearance and lubrication

Although the crank shaft is relatively more solid than others, the flexibility of crank shaft must be considered as a result of the inertia force and load under high-speed blanking condition. When the press system operates under blanking condition, the impact load from the upper and lower mold will cause the current links under large deformation. Therefore, the crank shaft and the linkage should be considered as flexible bodies. The crank shaft and linkage were established under the finite element software ANSYS, which enabled us to obtain the eigenfrequencies and eigenmodes of the crank shaft and linkage. The material properties of the crank shaft and linkage are listed in Table 1, and the first twenty modes with corresponding natural frequencies were chosen for the simulation of dynamic behavior of the multi-link mechanism with clearance. The five typical natural frequencies of the crank shaft were 538.192, 2221.68, 2334.63, 5080.91, and 7633.93 Hz, and the corresponding five natural frequencies of linkage were 5657.49, 8024.39, 8258.71, 10,250.3, and 12,973.3 Hz, as shown in Figs. 8 and  9. The flexible crank shaft and linkage were then exported to the ADAMS to connect with other rigid components of the mechanism, which were used to obtain more accurate response in the simulation tests. The flexible model of the multi-link mechanism with lubricated revolute clearance joint and dry spherical joints for ultra-precision press system under ADAMS is shown in Fig. 10. In this model, the revolute joint between the crank shaft (2) and the linkage (3), and spherical joints between the linkage (9) and the slider (10) were modeled as clearance joints.

Fig. 8
figure 8

Five typical eigenmodes of flexible crank shaft: a undeformed flexible element of crank shaft, b second mode, c fifth mode, d sixth mode, e tenth mode, f sixteenth mode

Full size image
Fig. 9
figure 9

Five typical eigenmodes of flexible linkage: a undeformed flexible element of crank shaft, b second mode, c fifth mode, d sixth mode, e tenth mode, f sixteenth mode

Full size image
Fig. 10
figure 10

Flexible model of multi-link mechanism with clearance and lubrication

Full size image
Table 1 Material property of flexible components
Full size table

It is assumed that the pressure gradient around the circumference is small compared to those along the length and the pressure distribution is integrated only over the positive region by setting the pressure in the remaining portion equal to zero. These are known as the Gumbel’s boundary conditions. The component forces along eccentricity direction and its perpendicular direction are, for \(\dot{\varepsilon }>0 \), given by [37],

$$\begin{aligned} F_r= & {} -\frac{\mu L_\mathrm{B} R_\mathrm{J}^3 }{c^{2}}\frac{6\dot{\varepsilon }}{(2+\varepsilon ^{2})(1-\varepsilon ^{2})^{3/2}}\nonumber \\&\times \left[ 4k\varepsilon ^{2}+(2+\varepsilon ^{2})\pi \frac{k+3}{k+3/2}\right] \end{aligned}$$
(34a)
$$\begin{aligned} F_t= & {} \frac{\mu L_\mathrm{B} R_\mathrm{J}^3 }{c^{2}} \frac{6\pi \varepsilon \left( {\omega -2\dot{\gamma }} \right) }{\left( {2+\varepsilon ^{2}} \right) \left( {1-\varepsilon ^{2}} \right) ^{1/2}} \frac{k+3}{k+3/2} \end{aligned}$$
(34b)

And for \(\dot{\varepsilon }<0 \)

$$\begin{aligned} F_r= & {} -\frac{\mu L_\mathrm{B} R_\mathrm{J}^3 }{c^{2}}\frac{6\dot{\varepsilon }}{(2+\varepsilon ^{2})(1-\varepsilon ^{2})^{3/2}}\nonumber \\&\times \left[ 4k\varepsilon ^{2}-(2+\varepsilon ^{2})\pi \frac{k}{k+3/2}\right] \end{aligned}$$
(35a)
$$\begin{aligned} F_t= & {} \frac{\mu L_\mathrm{B} R_\mathrm{J}^3 }{c^{2}} \frac{6\pi \varepsilon \left( {\omega -2\dot{\gamma }} \right) }{\left( {2+\varepsilon ^{2}} \right) \left( {1-\varepsilon ^{2}} \right) ^{1/2}} \frac{k}{k+3/2} \end{aligned}$$
(35b)

where

$$\begin{aligned} k^{2}=(1-\varepsilon ^{2})\left[ \left( \frac{\omega -2\dot{\gamma }}{2\dot{\varepsilon }}\right) ^{2}+\frac{1}{\varepsilon ^{2}}\right] \end{aligned}$$

The contact module by default in the ADAMS is used to simulate the dry revolute and spherical joints with clearance. The radial clearance size of the revolute and spherical joints was considered to be 0.1 mm for the present work, which was supplied by the manufacturer. A damping ratio of 2 % was used in this model, and it was also possible to modify these parameters. In order to simulate the effect of lubrication, the radial and tangential force between the lubricated journal and bearing under ADAMS can be user-defined as function.

5 Results and discussion

It is shown in Fig. 8 that the multi-link mechanism used in the simulation conformed to the characteristics presented in Table 2. To solve the differential equations of motion, we used the software ADAMS, which allows computation using several integrators. ADAMS/Solver uses multi-step integration methods that contain a predictor and a corrector. Four stiff integrators and one non-stiff integrator are currently available. The four stiff integrators are composed of CONSTANT_BDF, RKF45, GSTIFF, and WSTIFF.

Table 2 Simulation characteristics
Full size table

We choose the gear stiff integrator (GSTIFF) used by default, which gave the best results. The method used a backward differentiation formula (BDF) to integrate differential and algebraic standard index-three equations. It provides good solutions for simulations of stiff models (models with a mix of high and low frequencies). During the simulation, the integration tolerance was set to be 0.001 and the step size was set to be 0.001 s. The maximum number of iterations for the Newton–Raphson iterations to get converged solution of the nonlinear equations was 10. We choose the integrator formulation (SI1) for the selected integration method (GSTIFF), which takes into account the constraint derivatives when solving the equations of motion and monitors the integration error on the impulse of the Lagrange multipliers in the system. The Jacobian matrix remains stable at small step sizes, which in turn increases the stability and robustness of the corrector at small step sizes.

Kinematic analysis on each revolute clearance joint is performed simultaneously to determine the indentation depth, eccentricity ratio, as well as the normal and tangential components of relative velocity. In the dry clearance joint case, if the indentation depth on a joint is greater or equal to zero, the normal contact force in Eq. (23) and the LuGre friction law given in Eq. (27) are computed, respectively. Otherwise, the normal contact and frictional forces are zero. In the lubricated clearance joint case, if the eccentricity ratio is greater than zero, the hydrodynamic force components along the direction of the eccentricity and of its normal in Eqs. (34a) and (34b) are computed. For negative eccentricity ratio, the normal hydrodynamic and frictional forces given in Eqs. (35a) and (35b) are calculated. The present methodology can deal with contact scenarios of arbitrary shape surfaces and does not need to know the accurate contact position before contacting. The contact may be a surface in virtue of the contacting surfaces as a result of link flexibility in the ADAMS software.

The object of the simulation tests was to study the effect of joint clearance, lubrication, and flexibility on the performance of multi-link mechanism under no-load and blanking conditions. The blanking working condition is generally used in the process of factory inspection and test after the products of press are manufactured. The impact load under blanking condition can be described as triangular shape of pulse load [56] shown in Fig. 11. The impact load can be given by:

$$\begin{aligned} F(t)=\left\{ {{\begin{array}{ll} 0&{} \quad {0\le t<T_0 } \\ {\frac{F_{\max } }{2\tau }t}&{} \quad {T_0 \le t<T_0 +2\tau } \\ {\frac{F_{\max } }{\tau }(3\tau -t)}&{}\quad {T_0 +2\tau \le t<T_0 +3\tau } \\ 0&{} \quad {T_0 +3\tau \le t<T_0 +T} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(36)
Fig. 11
figure 11

Impact load under blanking condition

Full size image

It is assumed that the revolute joint clearance between the crank shaft (2) and the linkage (3), and spherical joints clearances between the linkage (9) and the slider (10) are considered in this work. The essential parameters for the simulation are presented in Table 2. In order to verify the validity of the proposed model, the test platform of multi-link mechanism for high-speed press system is set up. The physical figure of test platform and the principle diagram of the test are shown in Figs. 12 and  13. The test platform includes the L-type conductor, holder, eddy current sensor, and Selber GX accuracy tester. The L-type conductor is fixed on the slider, and the eddy current sensor is installed on the press table. When the press operates, the displacement signals of slider is obtained by eddy current sensor and collected by the Selber GX accuracy tester through data lines. The corresponding velocity and acceleration of slider can be also obtained by differentiating the displacement. In this simulation, the rotation speed of the crank shaft was 240 rpm and the clearance size was 0.01 mm. When the maximum blanking force \(F_{\max } \) is 10 KN and the simulation characteristics were applied to flexible model of multi-link mechanism with/without lubricated clearance joint under no-load and blanking conditions, the displacement, velocity, acceleration, and journal center path of multi-link mechanism for ultra-precision press are shown in Figs. 14, 15, 16, 17, and 18.

Fig. 12
figure 12

Physical figure of test platform

Full size image
Fig. 13
figure 13

Principle diagram of the test

Full size image
Fig. 14
figure 14

Displacement of slider: a no-load, b blanking

Full size image
Fig. 15
figure 15

Velocity of slider: a no-load, b blanking

Full size image
Fig. 16
figure 16

Acceleration of slider: a no-load, b blanking

Full size image
Fig. 17
figure 17

Journal center path of revolute joint: a no-load, b blanking

Full size image
Fig. 18
figure 18

Ball center path of spherical joint: a no-load, b blanking

Full size image

Figure 14 shows that the low dead point position of slider for flexible multi-link mechanism with/without lubricated clearance joint under no-load condition is at the location of 0.466 and 0.4688 m, respectively, and that for flexible multi-link mechanism with lubricated clearance joint under 10 KN, blanking condition is at the location of 0.467 m, while the traditional ideal low dead point position of multi-link mechanism is 0.47 m and the measured low dead point position of slider for flexible model of multi-link mechanism is 0.466 m. Compared to the ideal rigid case, the low dead point position of slider for flexible model of multi-link mechanism with/without lubricated clearance joint clearances under no-load or blanking conditions drops dramatically. Figure 15 shows that oscillation exists during the velocity response occasionally and the frequency of oscillation for flexible model without lubrication is larger than that with lubrication. It is also shown that the frequency of oscillation for flexible model of multi-link mechanism with lubricated clearance joint under blanking condition is larger than that under no-load condition. Figure 16 shows that fierce oscillation exists during the acceleration response and the maximum peak value of slider’s acceleration for flexible model of multi-link mechanism with/without lubricated clearance joint under no-load condition is 29.4 and 57.44 m/s\(^{2} \), respectively, and that for flexible model ofmulti-link mechanism with lubricated clearance joint under 10 KN blanking condition is 40.4 m/s\(^{2} \), which demonstrates that the flexibility of crank shaft and linkages, and lubrication as well as blanking force act as a suspension for multi-link mechanism and absorbs part of the kinetic energy and the metal-to-metal contact to produce smoother responses. The maximum peak value of slider’s measured acceleration for multi-link mechanism under no-load condition is 17.8 m/s\(^{2} \). Therefore, the computational results of flexible multi-link mechanism with lubricated clearance joint model agree better with experimental data than those with dry clearance model, and the validity of the proposed model is verified. Figures 17 and  18 show that only two modes: free motion and impact with penetration, can be identified from the journal center path of revolute joint and ball center path of spherical joint and permanent contact mode can be neglected, which may result from the effect of spherical joint clearances and flexibility of crank shaft and linkages as well as lubrication and cause strong nonlinearity of the mechanism.

5.1 Influence of the clearance size

The influence of the clearance size on the dynamic behavior of flexible multi-link mechanism with clearance and lubrication under no-load condition is investigated. In the simulation, the revolute joint between the crank shaft (2) and the linkage (3), and spherical joints between the linkage (9) and the slider (10) were modeled as clearance joints, and the effect of lubrication between the revolute joint is also considered. The slider displacement, velocity, and acceleration of the mechanism with different clearance sizes are shown in Figs. 19, 20, and 21.

Fig. 19
figure 19

Displacement of slider under different clearance sizes

Full size image
Fig. 20
figure 20

Velocity of slider under different clearance sizes

Full size image
Fig. 21
figure 21

Acceleration of slider under different clearance sizes: a 0.05 mm, b 0.1 mm, c 0.15 mm, d 0.2 mm

Full size image

It can be seen in Fig. 19 that the existence of the clearance for revolute and spherical joint and flexible parts as well as lubrication affects the slider’s displacement in a significant manner, and the slider displacement of the flexible multi-link mechanism with clearance 0.05 mm was generally consistent with that of clearance 0.15 mm. With the increase in clearance size, the maximum deviation value of the displacement at the low dead point firstly rose and then dropped gradually relative to the rigid ideal case. Figure 20 shows that the oscillation frequency of the velocity becomes larger and when the clearance size increased from 0.05 to 0.2 mm, and in sharp contrast, the corresponding maximum peak value of the velocity decreases and then increases. The slider acceleration was affected by the clearance size dramatically, and the maximum peak value of slider’s acceleration increased from 70.2 to 105 m/s\(^{2} \), as shown in Fig. 21. Unlike reports in other studies [57, 58], the increase in the clearance size did not increase the level of accelerations strongly. The reason for this phenomenon may be that the elastic crank shaft and linkage, and lubrication acted as a suspension for the multi-link mechanism. Therefore, too small or large clearance size will damage the performance of multi-link mechanism, and the approximate clearance size for multi-link mechanism of ultra-precision presses is considered to be 0.1 mm.

5.2 Influence of the rotation speed of crank shaft

The influence of the input speed of crank shaft on the dynamic behavior of the flexible multi-link mechanism with lubricated clearance joint under no-load condition is reported in this section. Again, in the simulation of the multi-link mechanism, the revolute joint between the crank shaft (2) and the linkage (3), and spherical joints between the linkage (9) and the slider (10) were modeled as a clearance joint and the radial clearance size of the revolute and spherical joints was considered to be 0.1 mm, and the effect of lubrication between the revolute joint is also considered. The slider’s displacement, velocity, and acceleration of the flexible multi-link mechanism with lubricated clearance joint under different crank shaft speeds are shown in Figs. 22, 23, and 24.

Figure 22 shows that the influence of the crank shaft speed on the slider displacement is significant, and the low dead point position of slider for flexible multi-link mechanism with revolute and spherical joint clearances drops dramatically, compared to the ideal rigid case. With the increase in the crank shaft speed, the slider position and the maximum deviation value of the displacement rose at the low dead point generally. Figure 23 shows that the oscillation frequency of the velocity becomes larger and when the crank shaft speed increased from 200 to 500 rpm and slider’s velocity at the low dead point position increased from 0.438 to 0.904 m/s. The effect of the crank shaft speed is evident on the system’s acceleration response, namely in high peaks on slider acceleration, as shown in Fig. 24. The slider’s acceleration is affected by the crank shaft speed strongly, and the maximum peak value of slider acceleration increased from 34 to 445 m/s\(^{2} \). Therefore, with the increase in input speed of crank shaft, the dynamic responses of multi-link mechanism increase tremendously.

Fig. 22
figure 22

Displacement of slider under different crank shaft speeds

Full size image
Fig. 23
figure 23

Velocity of slider under different crank shaft speeds

Full size image
Fig. 24
figure 24

Acceleration of slider under different crank shaft speeds: a 200 rpm, b 300 rpm, c 400 rpm, d 500 rpm

Full size image

5.3 Influence of blanking force

The influence of blanking force on the dynamic behavior of flexible multi-link mechanism with clearance and lubrication is investigated. In the simulation, the revolute joint between the crank shaft (2) and the linkage (3), and spherical joints between the linkage (9) and the slider (10) were modeled as clearance joints, and the effect of lubrication between the revolute joint is also considered. The slider displacement, velocity, and acceleration of the multi-link mechanism for different blanking forces are shown in Figs. 25, 26, and 27, where the radial clearance size of the revolute and spherical joints was considered to be 0.1 mm and input crank shaft speed was 240 rpm.

Fig. 25
figure 25

Displacement of slider under different blanking forces

Full size image
Fig. 26
figure 26

Velocity of slider under different blanking forces

Full size image
Fig. 27
figure 27

Acceleration of slider under different blanking forces: a 10 KN, b 20 KN, c 30 KN, d 40 KN

Full size image

It can be seen in Fig. 25 that the existence of the blanking force applied to the flexible multi-link mechanism with lubricated clearance joint does not affect the slider’s displacement in a significant manner, and the slider displacement of the flexible multi-link mechanism under blanking force 10 KN was generally consistent with that under 20, 30, and 40 KN. With the increase in blanking force, the maximum deviation value of the displacement at the low dead point firstly rose and then dropped gradually. Figure 26 shows that the oscillation frequency of the velocity becomes larger and when the blanking force increased from 10 to 40 KN, the corresponding maximum peak value of the velocity also increased and then decreased in a similar way. The slider acceleration was affected by the clearance size dramatically, and the maximum peak value of slider’s acceleration increased from 23.5 to 69.1 m/s\(^{2} \), as shown in Fig. 27.

6 Conclusion

In this work, an improved dynamic model of flexible multi-link mechanism with clearance and lubrication was established using ADAMS software, where the crank shaft and linkage were considered as flexible bodies, and where the effect of the revolute clearance joint between the crank shaft and the linkage, and the spherical clearance joints between the linkage and the slider as well as the lubrication were considered. The dynamic responses of flexible multi-link mechanism were explored both under the case with lubricated clearance joint and dry clearance joint. It is demonstrated that the dynamic responses of flexible multi-link mechanism with lubricated clearance joint model agree more with experimental data than those with dry clearance model, and the validity of the proposed model is verified. The simulation results also showed that the dynamic responses of flexible multi-link mechanism and its oscillation frequency were reduced greatly by the lubrication when compared to the case with dry clearance joint and the existence of lubrication act as a suspension of multi-link mechanism. The dynamic responses of flexible multi-link mechanism with lubricated clearance joint under blanking condition fail to become larger than those under no-load condition. The motion of the crank shaft center and ball center of spherical joints was mainly characterized by only two phases: a free flight motion and an impact motion. The permanent contact mode can be neglected, which may result from the effect of spherical joint clearances and flexibility of crank shaft and linkages as well as lubrication and strong nonlinearity of the mechanism. Furthermore, the influence of clearance size and input speed of crank shaft as well as blanking force on the dynamic responses of the multi-link mechanism was also investigated. With the increase in clearance size, the dynamic responses of flexible multi-link mechanism with lubricated clearance joint decrease firstly and then increase dramatically. The selection of approximate clearance size plays an important role in improving the performance of multi-link mechanism. With the increase in input crank shaft speed and blanking force, the dynamic responses of multi-link mechanism increase tremendously.