Nonlinear dynamic characterization of a new hysteretic device: experiments and computations

Abstract

The nonlinear dynamical behavior of the hysteretic rheological device proposed in Carboni et al. (J Eng Mech 2014) is investigated. The device can provide nonlinear hysteretic forces to a one-degree-of-freedom (one-dof) mass through suitable assemblies of NiTiNOL and steel wire ropes subject to tension–flexure cycles. The simultaneous occurrence of interwire friction, phase transformations and geometric nonlinearities is the key feature of the obtained material behavior. Frequency-response curves (FRCs) of the system subject to base excitation are obtained numerically via a continuation procedure together with stability analysis and experimentally by carrying out shaking table tests, respectively. The phenomenological identification of the material behaviors through force–displacement cycles, reported in Carboni et al. (J Eng Mech 2014), is employed for the computation of the FRCs and the equivalent damping ratios as function of the displacement amplitude. The different restoring forces give rise to whole new families of nonlinear hysteretic oscillators governed by softening, hardening and softening–hardening behaviors depending on the oscillation amplitude.

1 Introduction

The hysteretic restoring force of short wire ropes subject to coupled tension–flexure states is characterized by a strong nonlinear and (stiffness-wise) discontinuous mechanical behavior due to the frictional contacts between the wires. Moreover, if the wires are made of shape memory alloy (SMA), the phase transformations concur to the energy dissipation. The modeling difficulties are often overcome employing phenomenological models and extensive experimental campaigns for the parameters identification. A comprehensive discussion on the mathematical modeling and identification of a large class of hysteretic mechanical behaviors can be found in [4, 26, 36]. One of the most popular model is the so-called Bouc–Wen (BW) model, introduced by Bouc [6] and later extended by Wen [37]. Baber and Wen enriched [3] the model to take into account stiffness and/or strength degradation as a function of the hysteretic energy dissipation. Baber and Noori [1, 2] further modified the original model by adding the so-called pinching function. Foliente [15] generalized the pinching function of the Bouc–Wen–Baber–Noori model. Other modified versions of the original model were proposed to take into account asymmetric tension–compression hysteresis loops [20, 31, 32]. Sireteanu et al. [35] proposed an extended BW model able to describe an inflexion point on the loading branches. Sauter and Hagedorn [34] used distributed Jenkin elements to model the cable of a Stockbridge damper. Rafik and Gerges [17] developed a semi-analytical model of wire rope springs deforming in tension–compression cycles.

Carboni et al. [12] proposed a modified version of the Bouc–Wen model to consider symmetric pinching around the origin of the force–displacement curves. This model has the virtue of simplicity since the introduced pinching function is designed to depend on two parameters correlated with the pinching severity and its extension around the origin. The modified BW model was developed to describe the hysteresis cycles provided by several assemblies of NiTiNOL, steel and mixed NiTiNOL–steel wire ropes arranged in a rheological device. The latter provides different nonlinear hysteretic restoring forces exploiting the wire ropes bending and tensile stiffnesses, the damping due to interwire friction and phase transformation together with geometric nonlinear effects. The concurrence of energy dissipation due to frictional forces and to martensitic transitions determines a pinching around the origin of the force–displacement cycles. In fact, phase transformations take place for large displacements and induce variations of the area enclosed in the loop along the loading and unloading branches.

Hysteresis is a highly nonlinear phenomenon. Mechanical systems exhibiting hysteresis can undergo dynamic instabilities due to bifurcations suffered by the dynamical response. Analytical techniques such as the method of slowly varying parameters [14] and the method of harmonic balance were employed to obtain the approximate steady-state dynamics. The method of harmonic balance was used in [10, 11] to investigate stiffness degrading and stiffness–strength degrading hysteretic systems. The results reported in the literature are based on approximate combined analytical/numerical techniques. However, in cases such as higher dimensional systems, the use of numerical techniques becomes unavoidable. A multi-harmonic balance method was used in [7] to investigate either degrading or nondegrading systems.

As an alternative to time-domain techniques, the Poincaré map method seems to be a powerful numerical strategy, based on well-established theoretical foundations and easily used in conjunction with Floquet theory for stability analyses [21, 30]. Capecchi [8] investigated the response of elastoplastic oscillators together with their stability. Later, the responses of the BW and Masing one-dof systems were investigated in [9] including the subharmonically resonant solutions. Lacarbonara et al. [25] addressed the study of systems with material nonlinearities possessing a nondifferentiable vector field employing the Poincaré map method. The Jacobian of the map was evaluated via a finite-difference approach, and the method was combined with a pseudo-arclength algorithm to perform path-following analyses and to investigate the bifurcation behavior. The same method was used to study nonlinear thermomechanical responses of shape memory oscillators in [22] in order to detect bifurcations leading to nonperiodic responses such as the Neimark–Sacker and period-doubling bifurcations. A reference work for a comprehensive understanding of the dynamics of the Masing and BW hysteresis models is [24]. Lacarbonara et al. [23] used this method to investigate the rich dynamics of SMA oscillators in both isothermal and nonisothermal conditions. The authors adopted the Ivshin model [5, 19] for the constitutive representation of the SMA oscillator.

In this paper, the dynamical behavior of the rheological device presented in [12] is investigated. This mechanism yields nonlinear hysteretic restoring forces characterized by four distinct material behaviors: quasilinear-softening (QS) hysteresis, quasilinear-softening pinched (QSP) hysteresis, strongly hardening and pinched hysteresis (STHP), and slightly hardening and pinched (SLHP) hysteresis. The hysteretic restoring forces are applied, in turn, to a one-dof oscillating mass. The FRCs of the device in each of the four configurations are evaluated numerically and experimentally for several excitation amplitudes in the frequency bandwidth around the primary resonance. In the first case, a continuation procedure [21] together with the phenomenological identifications reported in [12] is employed for computing the stable and unstable periodic solutions of the one-dof dynamical system. In the second case, shaking table tests are performed measuring the oscillating mass displacements relative to the shaking table. The response of some of the devised configurations exhibits fold bifurcation points that can be captured through forward and backward frequency sweeps. The damping capacity of every device configuration is evaluated through the equivalent damping ratio expressed as function of the displacement amplitude. The nonlinear features of the four constitutive behaviors are reflected on the FRCs giving rise to new classes of nonlinear hysteretic oscillators which exhibit hardening, softening and softening–hardening behaviors depending on the displacement amplitude.

2 The device and force–displacement behaviors

The device proposed in [12] is based on several assemblies of NiTiNOL spiroidal wire ropes, strands and single NiTiNOL wires, steel strands and mixed NiTiNOL–steel strands arranged in a mechanism according to a specific architecture. This provides several types of nonlinear hysteretic restoring forces exploiting the bending and tensile stiffnesses of the strands working in parallel and in series, the damping due to interwire friction and phase transformations of SMA and the induced geometric nonlinearities. The device is shown in Fig. 1 in one of the configurations adopted in [12] for measuring the force–displacement curves by means of the Material Testing System (MTS) machine in the DISG Laboratory (Sapienza University of Rome). The device is constituted by the main rectangular steel frame (F1) whose two opposite vertical bars host a number of wire ropes clamps. A secondary frame (F2) is placed at the center of F1 and is formed by two thick steel bars (b2) which host the other wire rope clamps and another steel bar (b1). Two smooth rods (denoted by s1 and s2) and one threaded cylindrical rod (denoted by s3) pass through the bars b2 and b1 to which they are fixed at the midspan. The threaded rod s3 goes through bars b2 without being in contact with them, while clinched joints are placed between the smooth rods s1, s2 and the bars b2 to allow a relative frictionless sliding. The principal stiffness group (PSG) of the device is constituted by spiroidal wire ropes or strands with one end clamped to the frame F1 and the other end clamped to the bars b2. The secondary stiffness group (SSG) is represented by a number of strands or individual wires connecting the bars b2. The working principle consists in the relative translation between the frames F2 and F1 in the direction orthogonal to the ropes. This can occur according to three different modes: the first, denoted by S1, in which the sliding of bars b2 on the smooth rods s1 and s2 is prevented by four bolts on the threaded bar s3; the second, referred to as S2, in which the sliding of b2 on s1 and s2 is free; the third, indicated by S3, in which the sliding of b2 is restrained by the axial stiffness of the SSG. According to the operating mode, the restoring force that is opposed to the relative translation of the frames F1 and F2 presents different constitutive features, some of which depend on the fact that the PSG can be subject to bending or coupled bending–tensile loads. A detailed description of the mechanisms is reported in [12]. Several assemblies were tested by connecting with a steel fork the frame F2 (see Fig. 1a) to a load cell and prescribing displacements to the frame F1 by means of the MTS hydraulic actuator.

Fig. 1

Proposed device: Part (a) shows the actual device mounted on the MTS, while part (b) gives a schematic representation

The configurations investigated in [12] are listed in Table 1, and the cross sections of the wire ropes are shown in Fig. 2. The experimental rheological behaviors were described via a phenomenological approach. To this end, a modified version of the BW model of hysteresis was proposed to describe the pinching of the force–displacement curves due to the concurrence of interwire friction and phase transformations. The accurate identification of the model parameters was performed using the differential evolutionary (DE) algorithm. The expression of the restoring force that was assumed for the identification of configurations S1a, S3a, S3b and S3c (see Table 1) is

$$\begin{aligned} f=b(k_e x+z)+(1-b)k_3 x^3, \end{aligned}$$

(1)

where x denotes the displacement, $k_e$ and $k_3$ are the linear and cubic elastic stiffness coefficients, $b \in [0,1]$ is a weighting parameter, and z represents the hysteretic force whose evolution is regulated by

$$\begin{aligned} \dot{z}=[k_d h(x)-(\gamma +\beta \text{ sgn }(z \dot{x}))\left| z\right| ^n]\dot{x}. \end{aligned}$$

(2)

The overdot denotes differentiation with respect to time, $(k_d,\gamma ,\beta ,n)$ are the constitutive parameters, and h(x) is the pinching function which modifies the classical BW model according to

$$\begin{aligned} h(x)=1-\xi \text{ e }^{-\frac{x^2}{x_c}}. \end{aligned}$$

(3)

The two parameters $\xi \in [0,1)$ and $x_c>0$ regulate the pinching severity and its extension about the origin, respectively. Configuration S2b was identified using the restoring force expression (1) with $b=1$, while configuration S2a was identified setting also the pinching function h(x) to 1.

Fig. 2

The cross sections of the wire ropes employed in the device where the cross sections represent NiTiNOL, while the unfilled cross sections represent steel

Table 1 Device configurations with the rope types (see Fig. 2), the ropes number, the ropes length and the hysteresis types

The identification of the experimentally obtained restoring forces for several displacement amplitudes is reported in [12]. In the present work, the identified set of parameters for each device configuration is employed for the FRCs computations. Table 2 shows the parameters set associated with each device configuration.

Table 2 The sets of constitutive parameters which reproduce the force–displacement cycles provided by the different device configurations

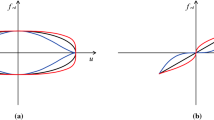
Figure 3 shows the hysteresis cycles exhibited by the device configurations listed in Table 1. They are obtained using the constitutive parameters of Table 2 which represent the DE identifications of the experimental tests discussed in [12].

Fig. 3

Hysteresis loops of the different device configurations (the identified constitutive parameters are given in Table 2)

3 Numerical and experimental frequency responses and equivalent damping ratio

The dynamical behavior of the device is investigated through a path following construction of the FRCs of a one-dof oscillating mass constrained by means of the hysteretic forces provided by the device. The base is subject to a harmonic acceleration with the frequency varying in a range centered about the system resonance frequency.

A common approach to characterize the dissipation inherent in nonlinear hysteretic oscillators is the computation of the equivalent damping ratio as a function of the displacement amplitude by prescribing the equivalence between the actual dissipated energy to that dissipated by a linear viscoelastic oscillator.

The equation of motion is

$$\begin{aligned} m \ddot{x} + f\big (x,\dot{x},x^t\big )= m\varOmega _g^2 x_g \sin \varOmega t, \end{aligned}$$

(4)

where x is the displacement of the mass m, the function $x^t$ represents the past history of x, $\varOmega _g^2 x_g$ represents the base acceleration amplitude obtained by multiplying the squared circular frequency and the amplitude of the base displacement $x_g$, $\varOmega$ and t are the excitation frequency and time, respectively. The restoring force $f(x,\dot{x},x^t)$ is defined by Eqs. (1), (2) and (3). The nondimensional form of Eqs. (4) and (2) is:

$$\begin{aligned}&\ddot{\tilde{x}}+ \delta \tilde{x} + (1-\delta ) \tilde{z}+ \tilde{k}_3 \tilde{x}^3 = \tilde{a}\sin \tilde{\varOmega } \tilde{t} \end{aligned}$$

(5)

$$\begin{aligned}&\dot{\tilde{z}}=\left[ \tilde{h}-(\tilde{\gamma }+\tilde{\beta } \text{ sgn }(\tilde{z} \dot{\tilde{x}}))\left| \tilde{z}\right| ^n\right] \dot{\tilde{x}} \end{aligned}$$

(6)

where, here and henceforth, the overdot denotes differentiation with respect to the nondimensional time, and the following nondimensional variables and parameters are introduced:

$$\begin{aligned} \begin{aligned}&\tilde{x}=\frac{x}{x_0}, \qquad \tilde{t}=\omega t, \qquad \tilde{z}=\frac{z}{z_0}, \qquad \delta =\frac{k_e}{k_e+k_d}, \\&\tilde{k}_3=\frac{k_3 x_0^2}{k_e+k_d}. \end{aligned} \end{aligned}$$

(7)

The parameter $x_0$ is a characteristic displacement, $z_0=k_d x_0$, $\omega =\sqrt{N_0/(x_0 m)}$, $N_0=(k_e+k_d)x_0$. The nondimensional pinching function is

$$\begin{aligned} \tilde{h}=1-\xi \text{ e }^{-\frac{\tilde{x}^2}{\tilde{x}_c}} \end{aligned}$$

(8)

where $\tilde{x}_c=\frac{x_c}{x_0^2}$. The other nondimensional parameters are

$$\begin{aligned}&(\tilde{\gamma }, \tilde{\beta })=(\gamma ,\beta ) x_0 z_0^{n-1}, \quad \tilde{a}=m\varOmega _g^2 x_g/N_0,\nonumber \\&\quad \tilde{\varOmega }=\varOmega /\omega . \end{aligned}$$

(9)

From a design point of view, it is important to investigate how the periodic response changes upon variation of some of the forcing parameters or to investigate the sensitivity to variations of the constitutive parameters (i.e., detunings). The analytical investigation of nonlinear hysteretic systems can be performed employing several methods such as the complexification–averaging procedure [16, 27, 29], the multiple scale approach [13, 33] or mixed analytical–numerical formulations [28]. In particular, we are interested in the computation of frequency-response curves for various excitation magnitudes. To this end, a continuation procedure based on the Jacobian of the Poincaré map (i.e., the monodromy matrix), computed via finite differences in the state space ([21, 30]), is applied to the nonlinear oscillator whose constitutive behavior is regulated by the parameters in Table 2.

The set of Eqs. (5) and (6) is recast in state space form as

(10)

where $\tilde{{{\mathbf {x}}}}^\mathrm {T}=(\tilde{x},\dot{\tilde{x}},\tilde{z})$ is the space state vector, the dependence on time $\tilde{t}$ (nonautonomous system) and the control parameter $\tilde{\varOmega }$ is explicit. The eigenvalues of the monodromy matrix (i.e., Floquet multipliers) allow to ascertain the stability and bifurcations of the response. In our computations, the Poincaré map is evaluated employing a fourth-order Runge–Kutta integration scheme in MATLAB [18].

Families of FRCs are obtained experimentally for some device configurations by carrying out dynamic tests on the shaking table (see Fig. 4). The frame F1 (see Sect. 2) is fixed to the table, while the frame F2, connected to F1 through the wire ropes arrangements, can oscillate relative to the table. The bar b1 is placed on a steel plate to which 4 ball bearings are connected. These pass through two cylindrical shafts whose ends are fixed to the frame F1. Thus the frame F2 (i.e, the oscillator mass) can move in the direction parallel to the shafts guide. Input displacement signals are prescribed to the shaking table, while both accelerations and displacements of the oscillating mass are acquired using an accelerometer and an inductive displacement transducer, respectively. The FRCs are obtained for harmonic base motions of the shaking table and considering the steady-state amplitude of the mass displacement time history (frame F2). The frequency sweeps are performed taking increments of 0.1 Hz while keeping the base acceleration amplitude constant. A control loop that modifies the base displacement for each frequency is implemented so as to obtain the acceleration amplitude constant.

Fig. 4

The device mounted on the shaking table

3.1 Frequency responses and damping ratios

In this section, the FRCs of the different device configurations for increasing values of the base accelerations are discussed. The curves are obtained computing the periodic solutions of Eqs. (5) and (6) where the restoring force is defined, in turn, taking the values of the parameters in Table 2. The oscillating mass is equal to 6.46 kg and coincides with the mass of the secondary frame. The continuation method described above allows to evaluate the bifurcation points and to path-follow the unstable branches. Moreover, the experimentally obtained FRCs for some device configurations are shown. The numerical and experimental curves present the same qualitative features, but for a good match new identification of the material parameters based on the experimentally obtained FRCs is required. For each device configuration, the trend of the damping ratio is also computed as function of the displacement amplitude.

The FRCs of the S1a configuration are reported in Fig. 5. The strong hardening behavior is reflected into a high bending of the backbone of the curves expressing the steep increase in the resonance frequency with the increase in the base excitation. Figure 5a shows the dimensional results, while in Fig. 5b the displacement amplitudes and the frequencies are scaled by the peak displacement and associated frequency of the lowest curve, respectively. Note that the chosen rescaling is due to the fact that the oscillator of the S1a configuration does not possess a linear frequency since it has negligible tangent stiffness at the origin. In other words, this oscillator is essentially nonlinear. Note that for an increment of the resonance displacement about 3.5 times the resonance frequency is more than doubled. All curves present an unstable branch bracketed by fold points where jumps of the stable periodic motion occur, as for example from A to B and from C to D (see Fig. 5a), obtained by increasing and decreasing the external excitation frequency, respectively. Figure 6 shows the jump from the unstable solution at A to the stable solution on the nonresonant branch at B (see Fig. 5a). This jump occurs near the fold bifurcation. Part (a) shows the time history of the unstable periodic solution, indicated by A in Fig. 5, which jumps to the stable periodic solution indicated by B. Part (b) shows the phase portrait of such transition.

Fig. 5

Numerical FRCs for configuration S1a in (a) dimensional and (b) nondimensional forms, where the solid and the dashed-dotted lines represent the stable and unstable branches, respectively. The mass is equal to 6.46 kg, and the constitutive parameters are reported in Table 2; the lowest two curves are obtained for a base acceleration of 0.016 and 0.032 g; the subsequent curves are obtained for a constant increment of 0.0322 g up to 0.3863 g; the dimensionless curves are obtained normalizing with respect to the peak displacement and associated frequency of the curve corresponding to the lowest excitation level, respectively

Fig. 6

Part a shows the time history of the response starting from the unstable solution part and b the phase portrait of the jump suffered by the response

In Fig. 7, the trend of the equivalent damping ratio is shown as function of the displacement amplitude. The equivalent damping ratio $\xi _0$ is computed according to $\xi _0=W_D/(4 \pi W_E)$ assuming the equivalent viscous damper at the resonance frequency. The stored energy $W_E$ is computed as the area subtended by the elastic part of the identified phenomenological constitutive response. The parameter $\xi _0$ reaches a maximum value past which it decreases. This behavior can be explained analyzing the hysteretic force z of the modified BW model. Past a threshold displacement, the hysteretic force is saturated to a constant value and the dissipated energy grows linearly with the displacement. Conversely, the stored energy continues to grow up to the second order with the displacement causing a strong reduction in the damping ratio.

Fig. 7

The equivalent damping ratio versus the displacement amplitude for configuration S1a

The FRCs of the S2a and S2b configurations are shown in Fig. 8a, c, respectively. The FRCs reveal a softening behavior, whereby the resonance frequency decreases upon increasing the oscillation amplitude and the base excitation level. Figure 8b, d shows the nondimensionalized FRCs with respect to the peak displacements and associated frequencies of the lowest curves. The resonance frequency is reduced by about 30 % for an increment of the peak displacement by about 60 times for configuration S2a, while the reduction in the resonance frequency is about 40 % for an increment of the resonance displacement equal to 30 times for configuration S2b. Figure 9a, b shows the trend of the equivalent damping ratio versus the displacement amplitude for configurations S2a and S2b, respectively.

The resonance frequency of both configurations tends to become constant past a certain oscillation amplitude. This behavior can be explained observing the force–displacement cycles in Fig. 3. Above a threshold displacement amplitude, the hysteretic force z reaches its maximum value at a plateau, thereby the total stiffness of the restoring force attains the constant value $k_e$. However, the pinching in the force–displacement behavior of configuration S2b has the twofold effect of reducing the variation range of the resonance frequency and increasing the threshold displacement for which the resonance frequency becomes constant (see Fig. 8c, d).

The configuration S2a suffers a strong damping reduction (see Fig. 9a) that determines a steeper trend of the frequency response. On the contrary, the mixed NITiNOL–steel wire ropes play a crucial role for configuration S2b. The equivalent damping has a strong variation at low displacement amplitudes, but past a certain amplitude it becomes almost constant (see Fig. 9b). This is due to the phase transformations of the NiTiNOL wires which occur at large displacement amplitudes increasing the dissipated energy and keeping almost constant the ratio with the elastic energy. This behavior is reflected on the FRCs. When the resonance frequency becomes constant at high levels of base excitation, the shape of the curves is smooth without cusp points as was the case with the response of configuration S2a.

Fig. 8

Numerical FRCs for the S2a and S2b configurations: dimensional FRCs in (a) and (c) and nondimensional FRCs in (b) and (d), respectively, where the solid lines represent the stable branches; the mass is equal to 6.46 kg, and the constitutive parameters are those reported in Table 2; in (a) the lowest two curves are obtained for base accelerations equal to 0.016 and 0.032 g, and the subsequent curves are obtained for a constant increment of 0.032 g up to 0.3702 g; in c the curves from the lowest to the highest are obtained for base accelerations equal to 0.145, 0.171, 0.209, 0.225, 0.257, 0.290, 0.322, 0.354 and 0.386 g, respectively; the displacement amplitudes and the frequencies are rendered nondimensional dividing them by peak displacements and associated frequencies of the FRCs obtained for the lowest excitation magnitudes, respectively

Fig. 9

Equivalent damping ratio versus displacement amplitude a for S2a configuration and b for S2b configuration

The experimental FRCs for configuration S2a are shown in Fig. 10. Figure 11 portrays the periodic response at the resonance frequency (part a) and the amplitude of the associated FFT in logarithmic scale (part b). The curves reveal a softening behavior as predicted by the path-following analysis. By comparing the experimental curves with the numerical curves, the experimental responses turn out to be more damped. This behavior was expected for several reasons. The theoretical FRCs were obtained using the phenomenological constitutive parameters identified on quasistatic cyclic tests. Therefore, the viscous dissipation intrinsic in the material does not occur in the static tests during which the strain rate is almost zero. Another aspect is the different operating modes of the device between static and dynamic tests. In the dynamic tests, the oscillating mass (frame F2) slides on two cylindrical shafts by means of four ball bearings. This mechanism, notwithstanding the presence of lubrication, introduces an additional frictional damping. Another consideration is that the set of constitutive parameters used in the computations was very accurately identified only at one individual displacement amplitude.

Fig. 10

Experimental FRCs for configuration S2a; the mass is equal to 6.46 kg, and the response curves are obtained for base accelerations equal to 0.212, 0.258, 0.403, 0.524, 0.657 g, respectively

Fig. 11

Dynamic test for configuration S2a: a displacement time history at the resonance frequency for a base acceleration equal to 0.657 g; b the associated FFT in logarithmic scale

To reproduce the periodic solutions for configuration S2a, a further identification of the phenomenological parameters is performed. The DE algorithm implemented in [12] is here employed to identify several sets of phenomenological parameters suitable to fit the experimental FRCs obtained for several base accelerations. The mean square error is computed as

$$\begin{aligned} {\text {MSE}}=\frac{100}{N \sigma _A^2} \sum _{k=1}^N \left( A(f)-\widehat{A}(f)\right) ^2, \end{aligned}$$

(11)

where $\sigma _A^2$ and N are the variance and the number of points of the experimental measurements, respectively, while A(f) and $\widehat{A}(f)$ are the displacement amplitudes of the experimentally and numerically obtained frequency responses, respectively. In Fig. 12, three experimental FRCs are compared with those obtained numerically. The lowest two curves are well identified, while the highest curve shows some discrepancies. Table 3 gives the phenomenological parameters obtained from the identification of the experimental FRCs, subsequently used to compute the numerical FRCs in Fig. 12. The assumed restoring force is that provided by the classic BW model according to the fact that the S2b configuration is constituted by steel wire ropes and the nonpinched hysteresis is only due to interwire friction.

Fig. 12

The black circles denote the experimental FRCs for configuration S2a, while the red solid lines represent the numerical identifications; the curves are obtained for base accelerations equal to 0.212, 0.403 and 0.657 g, respectively. (Color figure online)

Table 3 Results of the constitutive identification for configuration S2a that best fits the experimental FRCs

The experimental FRCs for configuration S2b are reported in Fig. 13. The softening behavior is also confirmed for this case, and the theoretical prediction about the plateau in the resonance frequency is correct. However, the same drawbacks, referred to the levels of base acceleration for which the numerical displacement amplitudes are achieved, are encountered. The additional material damping, the friction in the shafts guide and the limitation about the single parameters set used in the computation altogether play an important role. New parameter sets that can better describe the experimental FRCs are evaluated employing the DE algorithm. Figure 14 shows the periodic response at the resonance frequency (part a) and its FFT in logarithmic scale (part b). The comparison between the experimental and the numerical FRCs for configuration S2b is shown in Fig. 15. As in the previous case, the curves obtained for low levels of excitation are better identified. Table 4 gives the phenomenological parameters arising from the identification of the experimental FRCs and used to compute the numerical FRCs in Fig. 15. The assumed restoring force is that provided by the modified BW model that well reproduces the pinching about the origin of the hysteresis cycles.

Fig. 13

Experimental FRCs for configuration S2b; the mass is equal to 6.46 kg, and the response curves are obtained for base accelerations equal to 0.348, 0.533, 0.594, 0.648, 0.660, 0.751, 0.784 g, respectively

Fig. 14

Dynamic tests for configuration S2b: a displacement time history at the resonance frequency for a base acceleration equal to 0.784 g; b FFT in logarithmic scale

Fig. 15

The black circles denote the experimental FRCs for configuration S2b, while the red solid lines represent the numerical identifications; the curves are obtained for base accelerations equal to 0.648, 0.751, 0.784 g, respectively. (Color figure online)

Table 4 Results of the constitutive identification for configuration S2b that best fits the experimental FRCs

The FRCs of the S3a configuration are reported in Fig. 16a. The FRCs exhibit a softening behavior for weak base excitations and a hardening behavior for strong base excitations. The dotted line in Fig. 16a is the backbone curve of the system. The resonance frequency first decreases and thereafter increases significantly. The frequency reduction is equal to 15 % for a displacement increment equal to 3 times, while the associated increment is about 40 % for a displacement increment equal to 28 times (see Fig. 16b).

Fig. 16

FRCs obtained via path following for the S3a, S3b and S3c configurations: dimensional FRCs in (a), (c) and (e) and nondimensional FRCs in (b), (d) and (f), respectively, where the solid, dashed-dotted, and dotted lines represent the stable and unstable branches and the backbone curves, respectively; the mass is equal to 6.46 kg, and the constitutive parameters are those reported in Table 2; in (a), the lowest two curves are obtained for base accelerations equal to 0.016 g, and 0.032 g, and the subsequent curves are obtained for a constant increment of 0.032 g up to 0.386 g for the highest curve; in (c), the response curves are obtained for base accelerations equal to 0.193, 0.258, 0.322, 0.386, 0.451, 0.579, 0.644, 0.708, 0.773, 0.837 and 0.901 g, respectively; in (e), the response curves are obtained for base accelerations equal to 0.193, 0.258, 0.322, 0.386, 0.451, 0.579, 0.644, 0.708, 0.773, 0.837 and 0.901 g, respectively; the dimensionless curves are obtained rescaling with respect to the peak displacements and associated frequencies of the curves corresponding to the lowest excitation levels, respectively

In Fig. 17a, variation of the equivalent damping with the displacement amplitude is shown. For large displacements, the phase transitions of the NiTiNOL wires are such that the damping ratio becomes nearly constant. The softening–hardening behavior is a unique feature of this device. It depends on the stiffness ratio between the SSG and PSG (see Sect. 2). By adjusting this ratio, the softening–hardening behavior can be regulated depending on the displacement range of interest. Here, the hardening behavior is predominant. When the system reaches the fold bifurcation at A, the stable and unstable periodic solutions coalesce, and the periodic solution at A (see Fig. 16a) jumps to the stable solution at B (see Fig. 18a, b). At the same time when the lower fold bifurcation is reached at C, the system departs from the degenerate solution at C to settle onto the stable solution at D (see Fig. 18c, d).

Fig. 17

Equivalent damping ratio versus displacement amplitude in a, b and c for configurations S3a, S3b and S3c, respectively

Fig. 18

Some responses for configuration S3a; part a shows the time history of the system with initial conditions and base acceleration corresponding to the unstable periodic solution indicated by A in Fig. 16 (a); the system jumps to stable orbit denoted by B; part b shows the phase portrait for the transition from the unstable to the stable response; parts c, d portray the time history and the phase portrait of the backward jump from the unstable periodic solution indicated by C to the stable periodic solution denoted by D, respectively

The dimensional and nondimensional FRCs associated with the S3b configuration shown in Fig. 16c, d, respectively, exhibit a softening behavior for weak excitations and a hardening behavior for harder excitations. The switching from softening to hardening is better appreciated in the backbone curve represented by the dotted line in Fig. 16c. For the considered configuration, the ratio between the PSG and SSG is such that the amounts of softening and hardening behaviors are comparable. Figure 17b shows variation of the equivalent damping ratio with the displacement amplitude.

Also the FRCs of the S3c configuration shown in Fig. 16e exhibit a softening behavior for soft excitations and a hardening behavior for hard excitations. The softening behavior is here predominant considering the low axial stiffness of the SSG with respect to the PSG. The reduction in the resonance frequency is about 40 % if the displacement is increased five times (see Fig. 16f). On the other hand, as shown in Fig. 17c the equivalent damping ratio becomes very low at high amplitudes, thus explaining the very steep trend of the hardening FRCs. For configuration S3c, the SSG is constituted by NiTiNOL wires which do not provide a great amount of energy dissipation to the overall system. This is why when phase tranformations occur, at large displacements, the response of the system is lightly damped and presents unstable branches (see Fig. 16e, f). Conversely, when the SSG is constituted by NiTiNOL strands as with configuration S3b, a different behavior is obtained. The amount of energy dissipation due to phase transformations is quite higher, and this is reflected into a more damped character of the FRCs (see Fig. 16c, d).

The experimental FRCs for configuration S3a are portrayed in Fig. 19. The hardening behavior is clearly detected in the results. The curves are obtained performing forward and backward frequency sweeps, and when the fold points are approached, the system jumps to the next stable periodic solution. Figure 20a, c shows the experimental time history of the jump from point A to point B indicated in Fig. 19 and its phase portrait, respectively. The velocity is obtained differentiating the displacement time history with respect to time. In Fig. 20b, the FFT of the displacement in the time interval around the jump is represented in logarithmic scale. Figure 21a, c shows the time history and phase portrait of the jump obtained with the backward frequency sweep (see points C and D in Fig. 19). Figure 21b shows the FFT of the displacement in the time interval around the jump.

Fig. 19

The experimental FRCs for the configuration S3a where the black circles and the red times denote the responses obtained through forward and backward frequency sweeps, respectively; the mass is equal to 6.46 kg, and the response curves are obtained for base accelerations equal to 0.228, 0.298 g, respectively. (Color figure online)

Fig. 20

Dynamic tests for configuration S3a; part a shows the time history of the system with initial conditions and base acceleration corresponding to the periodic solution at A in Fig. 19; the system jumps to the stable solution at B; part b is the FFT in logarithmic scale; part c shows the phase portrait of the transition from the resonant to the nonresonant stable response

Fig. 21

Dynamic tests for configuration S3a; part a time history of the system with initial conditions and base acceleration corresponding to the periodic solution at C in Fig. 19; the system jumps to the stable periodic solution at D; part b FFT in logarithmic scale; part c the phase portrait of the transition from the nonresonant to the resonant stable response

4 Conclusions

A theoretical and experimental study of a nonlinear one-dof device exhibiting different hysteretic behaviors [12] was addressed. The investigated one-dof nonlinear oscillator reflects the features of a multi-configuration device in which the moving frame representing the oscillating mass is connected to the main frame through different wire rope assemblies. The main frame is fixed to the moving platform of the shaking table providing the base excitation.

The theoretical part of the study was mainly based on the unfolding of families of frequency-response curves obtained for various base excitation levels. The FRCs of the different device configurations were computed via a path-following procedure based on the Poincaré map whose Jacobian (i.e., the monondromy matrix) was calculated via finite differences in state space. The stability analysis was concurrently carried out by path following the Floquet multipliers. Initially the constitutive identifications of the device based on the static tests were used in the computations of the FRCs. The results highlighted a prominent nonlinear feature, namely, the switching from softening to hardening behaviors occurring at threshold amplitudes which depend on the type of device architecture/configuration. Moreover, the equivalent viscoelastic damping ratio was computed as function of the displacement amplitude. A few selected device configurations were investigated experimentally acquiring the FRCs via shaking table tests. The experimental FRCs turned out to be more damped than the theoretical predictions based on the static tests identification. This is due to the additional damping sources arising in the dynamical tests. To overcome these shortcomings associated with a quasistatic identification, other sets of constitutive parameters were identified so as to best fit the experimental FRCs. This goal was proven to be achievable. However, there is an upper bound on the excitation magnitude since the material behavior of the hysteretic device depends on the oscillation amplitude; hence, there is not a unique set of constitutive parameters that describes the material behaviors across a large range of amplitudes. In the dynamical simulations, one parameters set was used to compute a FRC with the consequence that, for high excitation amplitudes, near the resonance frequency, the identified set of parameters for the lower amplitudes was no longer effective.

The nonlinear dynamical investigations conducted both numerically and experimentally confirmed the richness of nonlinear material behaviors that can be provided by the proposed device. The device can exhibit softening, hardening and softening–hardening responses under harmonic excitations by just changing the wire ropes arrangements and the operating modes. The dynamic response can be designed to exhibit the desired nonlinear properties depending on the targeted application. The discussed device represents an innovative rheological element that can be employed in several applications from the macro- to the microscale.