Delayed impulsive synchronization of discrete-time complex networks with distributed delays

Abstract

In this paper, a novel delayed impulsive control strategy is proposed for synchronization of discrete-time complex networks with distributed delays. Different from the existing results, the involving time delays include distributed delays and impulsive input delays. Employing the Razumikhin theorem and the mathematical induction method, several sufficient criteria are derived in terms of algebraic conditions, which depend on impulsive input delays and impulsive control gains. Meanwhile, the derived criteria also reveal the relationship between the bounds of impulsive intervals and impulsive input delays. Finally, two examples are given to illustrate the effectiveness of the proposed approach.

1 Introduction

The study of discrete-time complex networks is originated from analysis of continuous-time dynamical systems. One of its primitive aims is to help us to implement computer-based simulation and computation with the offer of better reliability, e.g., quadratic optimization problems, system identification, distributed computation, time series analysis and image processing [21, 22]. Therefore, discrete-time complex networks have been an active research field during the past two decades [13–15, 43]. On the other hand, the most striking dynamical behavior of discrete-time complex networks is their ability to show cooperative collective phenomena. Among them, synchronization as a ubiquitous phenomenon has extensively attracted attention in almost all branches of natural sciences, engineering and social sciences [1, 17, 27–30, 39, 41].

In network environments, time delays cannot be neglected due to the finite speed of transmitting signals and traffic congestions. They have close relation with the overall performance of many real networks, e.g., instability, divergence and even chaotic phenomena. In the past decade, various analysis techniques have been introduced to solve the synchronization problems of delayed complex networks, e.g., the Halanay inequality, the Razumkhin theorem, the Linear matrix inequality (LMI) approach and the comparison principle [15–18, 23, 24, 26]. For example, Razumikhin-type synchronization criteria with less restrictive assumptions for delayed coupled discrete networks have been established in [15]. By utilizing the LMI approach, additive time-varying delays have been proposed in complex networks with control packet loss in [23]. In practical, the transmitting signals are not instantaneous and the network usually has a presence of an amount of parallel pathways of a variety of sizes and lengths. There may be a distribution of conduction velocities along these pathways that wiil lead to a distribution of propagation delays [6, 17]. In these circumstances, distributed delays are more appropriate ways than discrete delays to describe the above phenomena [6, 17, 44]. A paradigmatic example can be seen in [44], where distributed delays have been introduced in Hopfield neural networks.

On the other hand, when the states of each node are asynchronization, many control strategies have been proposed to control coupled systems into the reference node [12, 19, 20, 29, 32, 35, 37, 43, 45], e.g., feedback control [32], adaptive control [36, 45] and impulsive control [8, 12, 19, 37, 43]. Compared with continuous control strategies, impulsive control possesses simple structure and potential advantage at the discrete-time domain. The main idea of synchronizing impulsive control is that the states of coupled system can be forced into a synchronization manifold by using the measured information at discrete-time domain. In views of control theory, these measured information, i.e., impulses, can be regarded as samples of the output variables of the systems. Actually, impulsive control has been extensively studied because it provides an efficient way to apply systems that can not allows continuous control inputs [2, 8, 19, 37]. For example, an impulsive controller has been introduced for stochastic complex networks with switching topology and some synchronization criteria have been obtained by using the Razumikhin theorem in [12]. In [37], an impulsive control strategy has been proposed to achieve synchronization for complex dynamical networks with unknown coupling. Based on synchronizing impulses, the asymptotic synchronization problems of two nonlinear systems have been examined in [35].

Note that most of the existing results did not consider the effects of time delays on impulsive control strategies. However, in the digital control devices, impulsive input delays may be unavoidable when impulsive control signals are transmitted and received in networked environments. In general, networked control systems can induce two kinds of time delays, sensor-to-controller delays $\tau _{m}^{sc}$ and controller-to-actuator delays $\tau _{m}^{ca}$. As was shown in [2, 40], the impulsive input delay can be lumped together as $\tau _{m}=\tau _{m}^{sc}+\tau _{m}^{ca}$. Therefore, it is of great importance to take into account impulsive input delays when using impulsive control strategy. Recently, impulsive input delays have been considered in continuous-time impulsive systems [3, 4, 34]. Based on these results, delayed impulsive control strategies, which are more general than the general impulsive control, have been proposed in [2, 40]. For example, in [40], the synchronization problem has been tackled for continuous-time complex networks under delayed impulsive control. To the best of our knowledge, although synchronization of continuous-time complex networks under delayed impulsive control has been investigated in [2, 40], input impulsive delays are still overlooked in discrete-time impulsive control networked systems due to their complexity in mathematics, not to mention that distributed delays are also taken into account.

Actually, impulsive control has provided an effective approach for a class of dynamical systems including biomedical engineering and neural networks [2, 8, 10, 11, 19, 25, 35, 36, 40]. Despite its engineering importance, there still exist some fundamental difficulties in theory that delayed impulsive control is used to synchronize discrete-time complex networks with distributed delays. The reason is mainly threefold: (1) As we known, distributed delays can be regarded as a better way to describe some phenomena in complex networks. How can we find an effective method to handle the coexistence of impulsive input delays and distributed delays? (2) As was shown in [14], the dynamic behaviors of delayed impulses in discrete-time systems have been supposed to quite different from continuous-time ones. How can we get the relationship between impulsive input delays and the impulsive control gains in discrete-time systems? (3) Recently, discrete-time systems with delayed impulses have received some limited attention [14, 42], in which impulsive input delays were required some strict conditions, e.g., $\tau _{m}\le \sigma$ is necessary, where $\sigma$ is the lower bound of impulsive intervals. Thus, how can we analyze the synchronization problem of discrete-time complex networks without this restrict condition? Hence, from the viewpoint of the theory and practical applications, it is of great importance to investigate synchronization of discrete-time complex networks with delayed impulsive effects. These motivate us to investigate delayed impulsive control problem for discrete-time complex networks with distributed delays.

Based on the above considerations, the purpose of this paper is to explore the synchronization of discrete-time complex networks with distributed delays by using delayed impulsive control. Based on the Razumikhin theorem, several criteria for synchronization of discrete-time complex networks are obtained under delayed impulsive control. Two numerical examples are provided to illustrate the effectiveness of our results. The contributions of this paper can be listed as follows: (1) A new strategy of delayed impulsive control is presented to synchronize discrete-time complex networks, which is more general than the usual impulsive control strategies. (2) Distributed and impulsive input delays are considered simultaneously in the proposed model, which renders more practical applications of our current research.

Notations: Throughout this paper, $\mathbb {R}^{n\times n}$ and $\mathbb {R}^{n}$ denote the set of $n\times n$ real matrix and the n-dimensional Euclidean space, respectively. $\mathbb {N}=\{0, 1, 2,\ldots \}$, $\mathbb {N}^{+}=\{1, 2,\ldots \}$ and $\mathbb {N}_{-\tau }=\{-\tau , -\tau -1,\ldots , -1, 0\}$. $I_{n}$ denotes n-dimensional identity matrix. $\Vert A\Vert$ is the norm of the matrix $A\in \mathbb {R}^{n\times n}$ by the Euclidean vector norm. $\lambda _{\min }(\cdot )$ denotes the minimum eigenvalue. Moreover, for vector $x\in \mathbb {R}^{n}$, $\Vert x\Vert ^{2}=x^{T}x$. For a given integer $\tau$, let $D=\{\varphi :\mathbb {N}_{-\tau }\rightarrow \mathbb {R}^{n}\}$, we define $\parallel \varphi \parallel _{\tau }=\sup _{\theta \in \mathbb {N}_{-\tau }}\parallel \varphi (\theta )\parallel$.

2 Model description and some preliminaries

In this paper, we consider the following coupled discrete-time complex network consisting of N-identical nodes, in which each node is an n-dimensional dynamical system

$$\begin{aligned} x_{i}(k+1)&=Cx_{i}(k)+\sum _{d=1}^{d_{M}}\rho _{d}f(x_{i}(k-d))\nonumber \\&\quad +c\sum ^{N}_{j=1}w_{ij}{\varGamma } x_{j}(k), i={1,2,\ldots ,N}, \end{aligned}$$

(1)

where $x_{i}(k)=[x_{i1}(k),\ldots ,x_{in}(k)]^{T}$ denotes the state vector of the i-th node at time k, $k\in \mathbb {N}$. $C\in \mathbb {R}^{n\times n}$. $f(\cdot )$ is nonlinear vector-valued function satisfying certain condition given later. The constants $\rho _{d}\ge 0$ ($d=1,2,\ldots ,d_{M}$) satisfy the following convergent conditions:

$$\begin{aligned} \sum _{d=1}^{d_{M}}\rho _{d}=\overline{\rho },\quad \sum _{d=1}^{d_{M}}\rho _{d}d=\widetilde{\rho }. \end{aligned}$$

c is the coupling strength. ${\varGamma }=\text {diag}\{\nu _{1},\nu _{2},\ldots ,\nu _{n}\}$ is the inner-coupling matrix. $W^{T}=W=(w_{ij})_{N\times N}$ is the coupling configuration matrix representing the topological structure of the network, $w_{ij}$ is defined as follows: If there is a connection from node j to i $(j\ne {i})$, then $w_{ij}=w_{ji}>0$, otherwise $w_{ij}=w_{ji}=0$, and the diagonal entries of matrix W are defined by

$$\begin{aligned} w_{ii}=-\sum ^{N}_{j=1,j\ne {i}}w_{ij}=-\sum ^{N}_{j=1,j\ne {i}}w_{ji}. \end{aligned}$$

The initial conditions of the discrete-time complex network in (1) are given by $x_{i}(k_{0}+\theta )=\phi _{i}(k_{0}+\theta )$, $\theta \in \mathbb {N}_{-\tau }$, $i=1,2,\ldots ,N.$

Let s(k) be a solution of an isolated node described by

$$\begin{aligned} s(k+1)=Cs(k)+\sum _{d=1}^{d_{M}}\rho _{d}f(s(k-d)). \end{aligned}$$

(2)

where $s(k)=[s_{1}(k),\ldots ,s_{n}(k)]^{T}$ may be an equilibrium point or a periodic orbit in the phase space. The initial condition of s(k) is given by $s(k_{0}+\theta )=\varphi (k_{0}+\theta )$, $\theta \in \mathbb {N}_{-\tau }$, $i=1,2,\ldots ,N$.

The aim of this paper is to synchronize all the states of the discrete-time complex network in (1) into the following manifold

$$\begin{aligned} x_{1}(k)=x_{2}(k)=\cdots =x_{N}(k)=s(k),\quad \text {as}\quad k\rightarrow \infty . \end{aligned}$$

Remark 1

In the control theory, forcing a asynchronous coupled system to a desired trajectory is one of the basic problems. In networked environments, it can be presented by a lot of methods, e.g., master–slave systems in [13], synchronization error systems in [37]. Inspired by [23, 40], our control goal is to drive the discrete-time complex network in (1) into the desired trajectory s(k). As was shown in [16], it has been revealed that the trajectory of s(k) can be the synchronization state if s(k) is stable itself for the uncoupled system in (2).

Let $e_{i}(k)=x_{i}(k)-s(k)$ be the error state of the node i. Then, the impulsive controller $U_{i}(k)\in \mathbb {R}^{n}$ can be designed as

$$\begin{aligned} U_{i}(k)=\sum ^{\infty }_{m=1}\mu _{m}e_{i}(k_{m}-\tau _{m})\delta (k-k_{m}-1),\quad m\in {\mathbb {N}^{+}}, \end{aligned}$$

(3)

where $\delta (\cdot )$ denotes the Dirac discrete-time function. The impulsive time instants $k_{m}$ satisfy $0<k_{1}<\ldots <k_{m}<\ldots$ and $\lim _{m\rightarrow \infty }k_{m}=+\infty$, $m\in \mathbb {N}^{+}$. $\mu _{m}$ are the impulsive control gains to be determined and $\tau _{m}$ are the impulsive input delays at instants $k_{m}$. Moreover, we assume that $\tau _{m}$ satisfy $1\le \tau _{m}\le \overline{\tau }$.

Remark 2

Impulsive control is a kind of discontinuous control strategies, which means that it can change the state variables at discrete-time instants. Recently, impulsive control has provided an effective approach for a class of dynamical systems including biomedical engineering, robotic manipulators, formation control and neural networks [2, 8, 10, 11, 19, 25, 35, 36, 40]. For example, in [25], nonlinear impulsive control could be applied to dynamical systems from biomedical engineering processes. In [10], impulsive control have been considered to synchronize neural networks with reaction-diffusion terms. Compared with continuous-time counterparts, impulsive control imposes controllers only at a quite sparse sequence of time when applying in discrete-time complex networks [12, 14, 38]. It can drastically reduce the amount of information transmitted, and therefore, it is more efficient and easy to be implemented.

Note that $c\sum ^{N}_{j=1}w_{ij}{\varGamma } s(k)=0$, subtracting impulsive controller (3) to the discrete-time complex network (1), one can obtain the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} e_{i}(k+1)=Ce_{i}(k)+\sum _{d=1}^{d_{M}}\rho _{d}\widetilde{f}(e_{i}(k-d))\\ \qquad \qquad +\,c\sum ^{N}_{j=1}w_{ij}{\varGamma } e_{j}(k),\quad k\ne k_{m}-1,\\ e_{i}(k_{m})-e_{i}(k_{m}-1)=\mu _{m}e_{i}(k_{m}-\tau _{m}),\quad m\in {\mathbb {N}^{+}}, \end{array}\right. } \end{aligned}$$

(4)

where $\widetilde{f}(e_{i}(k-d))=f(x_{i}(k-d))-f(s(k-d))$. The initial conditions of discrete-time complex network in (4) are given by $e_{i}(k_{0}+\theta )=\phi _{i}(k_{0}+\theta )-\varphi (k_{0}+\theta )$, $\theta \in \mathbb {N}_{-\tau }$, $i=1,2,\ldots ,N$.

Remark 3

Recently, the impulsive control problems of discrete-time systems have widely studied [12, 33, 43]. However, in [12, 33, 43], the impulsive controllers have the form $e(k_{m})=(1+\mu _{m})e(k_{m}-1)$, where the impulsive input delays have been overlooked. Actually, when designing impulsive control strategies, impulsive input delays are important sources affecting overall performance of complex networks. Neglecting them may lead to design flaws or incorrect analytical conclusions. In addition to this main differences, in this paper, the distributed delays are also considered. Therefore, the delayed impulsive control strategy is more general and our model can render more practical applications [12, 33, 43].

Remark 4

From (4), we can see that the synchronization of discrete-time complex networks under delayed impulsive control is transformed into the stabilization problem of discrete-time systems with delayed impulses. Recently, delayed impulsive effects have considered in stability and synchronization problems of various impulsive continuous-time systems [2–4, 34, 40]. It should be mentioned that a delayed impulsive control strategy has been proposed to guarantee the synchronization of continuous-time complex networks in [40], which can generalize several impulsive control strategies, e.g., [2, 8, 35, 36]. In this paper, the delayed synchronizing impulse is applied to enhance synchronization of discrete-time complex networks, which is inspired by analogous control strategy in [2, 40]. However, compared with continuous-time systems, synchronization of discrete-time complex networks is more challenging since the stabilization problem of discrete-time systems is more difficult than the continuous-time counterpart.

In order to investigate the synchronization problem for discrete-time complex network in (4), we need the following definition, assumptions and lemmas.

Definition 1

The discrete-time complex network in (1) is said to be globally exponentially synchronized to the objective state s(k) if there exist positive constants $\varsigma$ and M, such that for any initial values $\gamma \triangleq \Vert \phi -\psi \Vert _{\tau }^{2}$

$$\begin{aligned} \Vert x_{i}(k)-s(k)\Vert \le M\gamma e^{-\varsigma (k-k_{0})},\quad i=1,2,\ldots ,N. \end{aligned}$$

Assumption 1

There exists positive constant $L_{f}$ such that $f(\cdot )$ in discrete-time complex network in (1) satisfies the following Lipschitz condition

$$\begin{aligned} \Vert f(x)-f(y)\Vert \le L_{f}\Vert {x-y}\Vert , \end{aligned}$$

where $x,y\in \mathbb {R}^{n}$.

Assumption 2

There exist positive integers $\sigma _{1}$ and $\sigma _{2}$, such that $\sigma _{1}\le k_{m}-k_{m-1}-1\le \sigma _{2}$.

Lemma 1

[17] Let $P\in \mathbb {R}^{n\times n}$ be a positive semidefinite matrix, $x_{i}\in \mathbb {R}^{n}$, and scalar constant $a_{i}\le 0$ $(i=1,2,\ldots )$. If the series concerned is convergent, then the following inequality holds:

$$\begin{aligned} \Big (\sum _{i=1}^{\infty }a_{i}x_{i}\Big )^{T}P\Big (\sum _{i=1}^{\infty }a_{i}x_{i}\Big ) \le \Big (\sum _{i=1}^{\infty }a_{i}\Big )\sum _{i=1}^{\infty }a_{i}x_{i}^{T}Px_{i}. \end{aligned}$$

Lemma 2

(Discrete Gronwall Inequality) [5] Let $\{x_{n}\}^{\infty }_{n=0}$, $\{a_{n}\}^{\infty }_{n=0}$ and $\{b_{n}\}^{\infty }_{n=0}$ be sequences of real numbers, with the $b_{n}\ge 0$, which satisfy

$$\begin{aligned} x_{n}\le a_{n}+\sum _{j=n_{0}}^{n-1}b_{j}x_{j}, \quad n=n_{0},n_{0}+1,\ldots . \end{aligned}$$

For any integer $N>n_{0}$, let $S(n_{0},N)=\{k$ where $x_{k}(\prod ^{k-1}_{j=n_{0}}(1+b_{j}))^{-1}$ is maximized in $\{n_{0},\cdots ,N\}\}$. Then, for any $\theta \in S(n_{0},N)$,

$$\begin{aligned} x_{n}\le a_{\theta }\prod _{j=n_{0}}^{n-1}(1+b_{j}), \quad n=n_{0},n_{0}+1,\ldots ,N. \end{aligned}$$

Lemma 3

[17] For any real matrices X, Y with appropriate dimensions, the following inequality holds,

$$\begin{aligned} 2X^{T}Y\le X^{T}X+Y^{T}Y. \end{aligned}$$

Lemma 4

[9] Let $\otimes$ denote the Kronecker-product, A,  B,  C and D are matrices with appropriate dimensions. The following properties are satisfied:

• (1) $(aA)\otimes B=A\otimes (aB),$ where a is a constant;

• (2) $(A + B)\otimes C=A\otimes C + B\otimes C;$

• (3) $(A\otimes B)(C\otimes D)=(AC)\otimes (BD).$

3 Main results

In this section, the exponential synchronization of the discrete-time complex network in (1) under delayed impulsive controller (3) is investigated by utilizing the Razumikhin theorem. Before starting the main results, we denote the following notations. Let $e(k)=[e_{1}(k)^{T},\ldots ,$ $e_{N}(k)^{T}]^{T}$, $\mathbf f (e(k-d))=[\widetilde{f}(e_{1}(k-d))^{T},\ldots ,\widetilde{f}(e_{N}(k-d))^{T}]^{T}$, $I_{N}\otimes A=\mathbf C$, $c(W\otimes {\varGamma })=\mathbf W$. Thus, the discrete-time complex network in (4) can be rewritten in the following Kronecker-product from

$$\begin{aligned} {\left\{ \begin{array}{ll} e(k+1)=\mathbf C e(k)+\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))+\mathbf W e(k),\\ \qquad \qquad \quad k\ne k_{m}-1,\\ e(k_{m})-e(k_{m}-1)=\mu _{m}e(k_{m}-\tau _{m}),\quad m\in {\mathbb {N}^{+}}. \end{array}\right. } \end{aligned}$$

(5)

Theorem 1

Suppose that Assumptions  1–2 hold. If there exist positive scalars $\varsigma$ and $p>1$, such that the following conditions hold

$$\begin{aligned}&\ln (1+\eta )-\varsigma \le 0 \text { and } \eta \ge 0;\end{aligned}$$

(6)

$$\begin{aligned}&2[(1+\mu )^{2}e^{\varsigma }+\mu ^{2}\varrho _{1}]-p^{-1}\le 0;\end{aligned}$$

(7)

$$\begin{aligned}&\ln p-\varsigma \sigma _{2}\ge 0; \end{aligned}$$

(8)

where $\eta =\alpha /(1-\beta p)-1$, $\alpha =3e^{\varsigma }\Vert \mathbf C \Vert ^{2}+3e^{\varsigma }\lambda \Vert \varvec{{\varGamma }}\Vert ^{2}-1$, $\beta =3\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e^{\varsigma (d+1)}$, $\varvec{{\varGamma }}=c(I_{N}\otimes {\varGamma })$, $\lambda \ge \lambda _{\min }^{2}(W)$, $\varrho _{1}=\frac{3(\overline{\tau }-l)^{2}}{\overline{\tau }}\varrho e^{\varsigma (\overline{\tau }+d_{M})}+2l\mu ^{2}e^{2\varsigma \overline{\tau }}$, $\varrho =4\overline{\tau }(\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}+\overline{\rho } \sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2})$, $\mu =\max _{1\le \ell \le l_{m}}\{\mu _{m_{\ell }}\}$, $l_{m}\le l$ denotes the number of impulsive instants on interval $[k_{m}-\overline{\tau },k_{m}-1]$ and $\mu _{m_{\ell }}$ is the corresponding impulsive strengths. Then the discrete-time complex network in (5) is exponentially synchronized.

Proof

Let $V(k)=e^{T}(k)e(k)$. Then we claim that

$$\begin{aligned} V(k)\le M\gamma e^{-\varsigma (k-k_{0}-\overline{\tau })},\quad k\in [k_{0}-\tau ,+\infty ), \end{aligned}$$

(9)

where M is a positive constant satisfying a certain condition given later, $\gamma \triangleq \Vert \phi -\psi \Vert _{\tau }^{2}$.

When $k\in [k_{m},k_{m}-1], m\in \mathbb {N}^{+}$, let $W(k)=e^{\varsigma (k-k_{0}-\overline{\tau })}V(k)$. Thus, claim (9) is equivalent to the following inequality

$$\begin{aligned} W(k)\le M\gamma ,\quad k\in [k_{0}-\tau ,+\infty ). \end{aligned}$$

(10)

In order to prove (10), the mathematical induction method will be used here. In the following, we divide the proof into the following three steps.

Step I: When $k\in [k_{0}-\tau ,k_{0}+\overline{\tau }]$, we will prove that

$$\begin{aligned} W(k)\le M\gamma . \end{aligned}$$

(11)

Since $\overline{\tau }\ge 0$, $\sigma _{1}>0$, one can always find a natural $l_{0}$ such that $(l_{0}-1)\sigma _{1}\le \overline{\tau }\le l_{0}\sigma _{1}$, which means that the maximum number of impulsive instants on $[k_{0},k_{0}+\overline{\tau }]$ is less than $l_{0}$. Then, we assume that impulsive instants on the interval $[k_{0},k_{0}+\overline{\tau }]$ are $\overline{k}_{r}$, $r=1,2,\ldots ,l_{0}$. Note that $\Vert e(k_{0})\Vert ^{2}\le \Vert \phi -\psi \Vert _{\tau }^{2}=\gamma$. When $k\in [k_{0},\overline{k}_{1}-1]$ and $s\in \mathbb {N}_{-\tau }$, we will divide the proof into following two cases.

Case (1): When $k+s\le k_{0}$, it is easy to see that $\Vert e(k+s)\Vert ^{2}\le \gamma$.

Case (2): When $k+s\ge k_{0}$, from Chebyshev Sum Inequality [7] and the first Eq. of (5),

$$\begin{aligned} \Vert e(k+s)\Vert ^{2}&=\left\| e(k_{0})+\sum _{h=k_{0}}^{k+s-1}{\varDelta } e(h)\right\| ^{2}\nonumber \\&\le 2\Vert e(k_{0})\Vert ^{2}+2\left\| \sum _{h=k_{0}}^{k+s-1}{\varDelta } e(h)\right\| ^{2}\nonumber \\&\le 2\gamma +2\left\| \sum _{h=k_{0}}^{k+s-1}\Big (e(h+1)-e(h)\Big )\right\| ^{2}\nonumber \\&=2\gamma +2\Biggl \Vert \sum _{h=k_{0}}^{k+s-1}\Big [(\mathbf C +\mathbf W -I_{Nn})e(h)\nonumber \\&\quad +\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(h-d))\Big ]\Biggr \Vert ^{2}, \end{aligned}$$

(12)

where ${\varDelta } e(h)=e(h+1)-e(h)$.

From Chebyshev Sum Inequality [7], Assumption 1 and Lemma 1, we can deduce

$$\begin{aligned}&\Biggl \Vert \sum _{h=k_{0}}^{k+s-1}\Big [(\mathbf C +\mathbf W -I_{Nn})e(h)+\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(h-d))\Big ]\Biggr \Vert ^{2}\nonumber \\&\quad \le (k+s-k_{0})\sum _{h=k_{0}}^{k+s-1}\Biggl (2\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\Vert e(h)\Vert ^{2}\nonumber \\&\qquad +2\Biggl \Vert \sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(h-d))\Biggr ]\Biggr \Vert ^{2} \Biggr )\nonumber \\&\quad \le 2\overline{\tau }\sum _{h=k_{0}}^{k+s-1}\Bigg [\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\Vert e(h)\Vert ^{2}\nonumber \\&\qquad +\left( \sum _{d=1}^{d_{M}}\rho _{d}\right) \sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}\Vert e(h-d)]\Vert ^{2}\Bigg ]. \end{aligned}$$

(13)

Hence, in view of (12) and (13), we know that

$$\begin{aligned} \Vert e(k)\Vert ^{2}_{\tau }&\le 2\gamma +4\overline{\tau } \sum _{h=k_{0}}^{k+s-1}\Biggl (\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\Vert e(h)\Vert ^{2}\nonumber \\&\quad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}\Vert e(h-d)\Vert ^{2}\Biggr )\nonumber \\&\le 2\gamma +4\overline{\tau }\sum _{h=k_{0}}^{k+s-1}\Biggl (\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\nonumber \\&\quad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2})\Vert e(h)\Biggr )\Vert ^{2}_{\tau }. \end{aligned}$$

(14)

From Lemma 2 and (14), we get

$$\begin{aligned} \Vert e(k)\Vert ^{2}_{\tau }\le 2(\varrho +1)^{k-k_{0}}\gamma ,\quad k\in [k_{0},\overline{k}_{1}-1], \end{aligned}$$

(15)

where $\varrho =4\overline{\tau }(\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}+\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2})$.

When $k=\overline{k}_{1}$, from the second Eq. of (5), we have

$$\begin{aligned} \Vert e(\overline{k}_{1})\Vert ^{2}&=\Vert e(\overline{k}_{1}-1)+\mu _{1}e(\overline{k}_{1}-\overline{\tau }_{1})\Vert ^{2}\nonumber \\&\le 2\Vert e(\overline{k}_{1}-1)\Vert ^{2}+2\mu _{1}^{2}\Vert e(\overline{k}_{1}-\overline{\tau }_{1})\Vert ^{2}. \end{aligned}$$

(16)

By means of (15) and (16), we have $\Vert e(\overline{k}_{1})\Vert ^{2}\le 4(\varrho +1)^{\overline{k}_{1}-k_{0}-1}(1+\mu _{1}^{2})\gamma$. By a simple induction, when $k\in [k_{0},\overline{k}_{l_{0}}-1]$, we can deduce $\Vert e(k)\Vert ^{2}\le 2[\prod _{r=1}^{{l_{0}-1}}2(1+\mu _{r}^{2})](1+\varrho )^{k-k_{0}-l_{0}+1}\gamma$ and $\Vert e(\overline{k}_{l_{0}})\Vert ^{2}\le 2[\prod _{r=1}^{{l_{0}}}2(1+\mu _{r}^{2})](1+\varrho )^{\overline{k}_{l_{0}}-k_{0}-l_{0}}\gamma$. Hence, one observes

$$\begin{aligned} \Vert e(\overline{k}_{l_{0}})\Vert ^{2}_{\tau }\le 2\Big [\prod _{r=1}^{{l_{0}}}2(1+\mu _{r}^{2})\Big ](1+\varrho )^{\overline{k}_{l_{0}}-k_{0}-l_{0}}\gamma . \end{aligned}$$

(17)

Since there are no impulses on $[\overline{k}_{l_{0}},k_{0}+\overline{\tau }]$, we can obtain

$$\begin{aligned} \Vert e(k)\Vert ^{2}&\le 2(\varrho +1)^{k-\overline{k}_{l_{0}}}\Vert e(\overline{k}_{l_{0}})\Vert ^{2}_{\tau }\nonumber \\&\le 2(\varrho +1)^{\overline{\tau }}[2\overline{\mu }/(\varrho +1)]^{l_{0}}\gamma \triangleq M_{1}\gamma . \end{aligned}$$

(18)

where $\overline{\mu }=\max _{1\le r\le l_{0}}\{1+\mu _{r}^{2}\}$.

From (18), one can always find positive constants $p>1$ and $M\ge M_{1}p$, such that

$$\begin{aligned} W(k)&=e^{\varsigma (k-k_{0}-\overline{\tau })}V(k)\nonumber \\&\le \Vert e(k)\Vert ^{2}\le M_{1}\gamma \nonumber \\&\le M\gamma p^{-1}\le M\gamma ,\quad k\in [k_{0}-\tau ,k_{0}+\overline{\tau }]. \end{aligned}$$

(19)

Step II: When $k\in [k_{0}+\overline{\tau },k_{1}-1]$, we claim that

$$\begin{aligned} W(k)\le M\gamma . \end{aligned}$$

(20)

If (20) is not true, there exists at least one $k\in [k_{0}+\overline{\tau }, k_{1}-1]$ such that

$$\begin{aligned} W(k)> M\gamma . \end{aligned}$$

Let $k^{*}_{1}=\inf \{k\in [k_{0}+\overline{\tau }, k_{1}-1]|W(k)>M\gamma \}$. Since $W(k_{0}+\overline{\tau })\le M\gamma$, we know that $k_{0}+\overline{\tau }+1\le k^{*}_{1}\le k_{1}-1$. By the definition of $k^{*}_{1}$, we have $W(k^{*}_{1})>M\gamma$ and $W(k)\le M\gamma$ for $k\in [k_{0}+\overline{\tau }, k^{*}_{1}-1]$. Let $k_{*1}=\sup \{k\in [k_{0}+\overline{\tau }, k^{*}_{1}-1]|W(k)\le M\gamma p^{-1}\}$, from which we have $k_{*1}<k^{*}_{1}$ and $W(k)> M\gamma p^{-1}$ for $k\in [k_{*1}+1,k^{*}_{1}-1]$.

Hence, $W(k_{*1})\le W(k)< W(k^{*}_{1})$, $k\in [k_{*1},k^{*}_{1}-1]$. Moreover, for any $s\in \mathbb {N}_{-\tau }$ and $k\in [k_{*1},k^{*}_{1}-1]$, we get

$$\begin{aligned} W(k+s)\le M\gamma \le pW(k+1). \end{aligned}$$

(21)

Since $V(k)=e^{T}(k)e(k)$ and $W(k)=e^{\varsigma (k-k_{0}-\overline{\tau })}V(k)$, one can obtain that, for $[k_{*1}+1, k^{*}_{1}-1]$,

$$\begin{aligned} W(k+1)&=e^{\varsigma (k+1-k_{0}-\overline{\tau })} \Big [\mathbf C e(k)+\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\nonumber \\&\quad +\mathbf W e(k)\Big ]^{T}\nonumber \\&\quad \,\Big [\mathbf C e(k)+\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))+\mathbf W e(k)\Big ]\nonumber \\&=e^{\varsigma (k+1-k_{0}-\overline{\tau })}\Big [e^{T}(k)\mathbf C ^{T}\mathbf C e(k)\nonumber \\&\quad +e^{T}(k)\mathbf W ^{T}\mathbf W e(k)+\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big )^{T}\nonumber \\&\quad \times \Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big ) +2e^{T}(k)\mathbf C ^{T}\mathbf W e(k)\nonumber \\&\quad +2e^{T}(k)\mathbf C ^{T}\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big )\nonumber \\&\quad +2e^{T}(k)\mathbf W ^{T}\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big )\Big ]. \end{aligned}$$

(22)

In view of Lemma 1 and Assumption 1, we obtain

$$\begin{aligned} \Big (\sum _{d=1}^{d_{M}}&\rho _{d}\mathbf f (e(k-d))\Big )^{T}\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big )\nonumber \\&\le \Big (\sum _{d=1}^{d_{M}}\rho _{d}\Big )\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))^{T}\mathbf f (e(k-d))\Big )\nonumber \\&\le \Big (\sum _{d=1}^{d_{M}}\rho _{d}\Big )\Big (\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}e(k-d)\Big )\nonumber \\&=\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}e(k-d)). \end{aligned}$$

(23)

From (23) and Lemma 3, we have

$$\begin{aligned}&2e^{T}(k)\mathbf C ^{T}\mathbf W e(k)\nonumber \\&\quad \le e^{T}(k)\mathbf C ^{T}\mathbf C e(k)+e^{T}(k)\mathbf W ^{T}\mathbf W e(k), \end{aligned}$$

(24)

$$\begin{aligned}&2e^{T}(k)\mathbf C ^{T}\Big (\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))\Big )\nonumber \\&\quad \le e^{T}(k)\mathbf C ^{T}\mathbf C e(k)+\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}e(k-d),\end{aligned}$$

(25)

$$\begin{aligned}&2e^{T}(k)\mathbf W ^{T}\Big (\sum _{d=1}^{d_{M}}\rho _{d}(\mathbf f e(k-d))\Big )\nonumber \\&\quad \le e^{T}(k)\mathbf W ^{T}\mathbf W e(k)+\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}e(k-d). \end{aligned}$$

(26)

From (22) to (26), we get

$$\begin{aligned} W(k+1)&\le 3e^{\varsigma (k+1-k_{0}-\overline{\tau })} \Big [e^{T}(k)\mathbf C ^{T}\mathbf C e(k)\nonumber \\&\quad +e^{T}(k)\mathbf W ^{T}\mathbf W e(k)+\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}\nonumber \\&\quad \times e(k-d)\Big ]. \end{aligned}$$

(27)

Since $W^{T}=W$ is a real symmetric matrix, there exists a unitary matrix $U=[u_{1},u_{2},\ldots ,u_{N}]\in \mathbb {R}^{N\times N}$ with $u_{i}=[u_{1i},u_{2i},\ldots ,u_{Ni}]^{T}\in \mathbb {R}^{N}$ such that $U^{T}WU={\varLambda }$, where $U^{T}U=I_{N}$, ${\varLambda }=\text {diag}\{\lambda _{1},\lambda _{2},\ldots ,\lambda _{N}\}$, $\lambda _{i}$ $(i\in \mathbb {N}^{+})$ are the eigenvalues of W. From Perron Frobenius theorem ([9]), the eigenvalues of matrix W can be arranged as follows: $0=\lambda _{1}\ge \lambda _{2}\ge \cdots \ge \lambda _{N}=\lambda _{\min }(W)$. When $\lambda _{1}=0$, we construct $u_{1}=1/\sqrt{N}(1,1,\ldots ,1)^{T}\in \mathbb {R}^{N}$.

Using the unitary transform $y(k)=(U^{T}\otimes I)e(k)=[y_{1}^{T},y_{2}^{T},\ldots ,y_{N}^{T}]^{T}\in \mathbb {R}^{n\times N}$, we obtain that

$$\begin{aligned} e^{T}(k)\mathbf W ^{T}\mathbf W e(k)&=c^{2}e^{T}(k)(W\otimes {\varGamma })^{T}(W\otimes {\varGamma })e(k)\nonumber \\&=c^{2}y^{T}(k)(U^{T}\otimes I_{N})(W\otimes {\varGamma })^{T}\nonumber \\&\quad \times (W\otimes {\varGamma })(U\otimes I_{N})y(k)\nonumber \\&=c^{2}y^{T}(k)(U^{T}W^{T}WU\otimes {\varGamma }^{2})y(k)\nonumber \\&\le \lambda _{N}^{2}c^{2}y^{T}(k)(I_{N}\otimes {\varGamma }^{2})y(k)\nonumber \\&\le \lambda c^{2}y^{T}(k)(I_{N}\otimes {\varGamma }^{2})y(k)\nonumber \\&=\lambda c^{2}e^{T}(k)(I_{N}\otimes {\varGamma }^{2})e(k)\nonumber \\&=\lambda e^{T}(k)\varvec{{\varGamma }}^{T}\varvec{{\varGamma }}e(k). \end{aligned}$$

(28)

where $\lambda \ge \lambda _{N}^{2}(W)$.

From (27) and (28) we can get

$$\begin{aligned} W(k+1)&\le 3e^{\varsigma (k+1-k_{0}-\overline{\tau })}\nonumber \\&\quad \,\Big [e^{T}(k)\mathbf C ^{T}\mathbf C e(k)+\lambda e^{T}(k)\varvec{{\varGamma }}^{T}\varvec{{\varGamma }}e(k)\nonumber \\&\quad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e(k-d)^{T}e(k-d)\Big ]. \end{aligned}$$

(29)

Therefore, it follows from (21) and (29) that

$$\begin{aligned} W(k+1)&\le 3e^{\varsigma }\Vert \mathbf C \Vert ^{2}W(k)+3e^{\varsigma }\lambda \Vert \varvec{{\varGamma }}\Vert ^{2}W(k)\nonumber \\&\quad +3\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e^{\varsigma (d+1)}W(k-d)-W(k)\nonumber \\&=(3e^{\varsigma }\Vert \mathbf C \Vert ^{2}+3e^{\varsigma }\lambda \Vert \varvec{{\varGamma }}\Vert ^{2}-1)W(k)\nonumber \\&\quad +3\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e^{\varsigma (d+1)}W(k-d)\nonumber \\&\le (3e^{\varsigma }\Vert \mathbf C \Vert ^{2}+3e^{\varsigma }\lambda \Vert \varvec{{\varGamma }}\Vert ^{2}-1)W(k) \nonumber \\&\quad +3\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}e^{\varsigma (d+1)}pW(k+1)\nonumber \\&\triangleq \alpha W(k)+\beta pW(k+1). \end{aligned}$$

(30)

From (30), one can observe that $W(k+1)\le \alpha /(1-\beta p)W(k)\triangleq (1+\eta )W(k)$, $k\in [k_{*1}+1, k^{*}_{1}-1]$. From this and (6), one observes that

$$\begin{aligned} W(k^{*}_{1})&\le (1+\eta )W(k^{*}_{1}-1)\nonumber \\&\le \cdots \le (1+\eta )^{k^{*}_{1}-k_{*1}}W(k_{*1})\nonumber \\&\le (1+\eta )^{\sigma _{2}}M\gamma p^{-1}\nonumber \\&\le (1+\eta )^{\sigma _{2}}M\gamma e^{-\varsigma \sigma _{2}}\nonumber \\&\le M\gamma <W(k^{*}_{1}). \end{aligned}$$

(31)

This is contradiction. Hence, (20) holds.

Form Step I and Step II, we can conclude that $V(k)\le M\gamma e^{-\varsigma (k-k_{0}-\overline{\tau })}$, $k\in [k_{0}-\tau , k_{1}-1]$. When $k\in [k_{0}-\tau ,k_{m}-1]$, $m=1,2,\cdots ,\overline{m}$ $(\overline{m}>1)$, we assume that the following inequality holds

$$\begin{aligned} W(k)\le M\gamma . \end{aligned}$$

(32)

In the following step, we will prove that

$$\begin{aligned} V(k)\le M\gamma e^{-\varsigma (k-k_{0}-\overline{\tau })}, \quad k\in [k_{\overline{m}},k_{\overline{m}+1}-1]. \end{aligned}$$

Step III: When $k\in [k_{\overline{m}},k_{\overline{m}+1}-1]$, we will prove that

$$\begin{aligned} W(k)\le M\gamma , \end{aligned}$$

(33)

which implies $V(k)\le M\gamma e^{-\varsigma (k-k_{0}-\overline{\tau })}$, for $k\in [k_{\overline{m}},k_{\overline{m}+1}-1]$. Form (32), it is obvious that $\Vert e(k_{\overline{m}}-1)\Vert ^{2}\le e^{\varsigma }$ $M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}$. In the following, we will proof that $\Vert e(k_{\overline{m}}-1)-e(k_{\overline{m}}-\tau _{\overline{m}})\Vert ^{2}\le \varrho _{1}M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}$. Similar to Step I, since $\sigma _{1}\le k_{m+1}-k_{m}-1\le \sigma _{2}$, there are at most l impulsive instants on the interval $[k_{\overline{m}}-\overline{\tau },k_{\overline{m}}-1]$. We assume that the impulsive instants are $k_{\overline{m}_{\ell }}$, $\ell =1,2,\cdots ,l_{\overline{m}}$, $l_{\overline{m}}\le l$. From Chebyshev Sum Inequality [7],

$$\begin{aligned}&\Vert e(k_{\overline{m}}-1)-e(k_{\overline{m}}-\tau _{\overline{m}})\Vert ^{2}\nonumber \\&\quad =\Biggl \Vert \sum _{h=k_{\overline{m}}-\tau _{\overline{m}}}^{k_{\overline{m}_{1}}-2}{\varDelta } e(h) +\sum _{h=k_{\overline{m}_{l_{\overline{m}}}}}^{k_{\overline{m}}-2}{\varDelta } e(h)\nonumber \\&\qquad +\sum _{\theta =1}^{l_{\overline{m}-1}}\sum _{h={k_{\overline{m}_{\theta }}}}^{k_{\overline{m}_{\theta +1}}-2}{\varDelta } e(h) +\sum _{\ell =1}^{l_{\overline{m}}}\mu _{\overline{m}_{\ell }}e(k_{\overline{m}_{\ell }}-\tau _{\overline{m}_{\ell }})\Biggr \Vert ^{2}\nonumber \\&\quad \le 2\Bigg [\Biggl \Vert \sum _{h=k_{\overline{m}}-\tau _{\overline{m}}}^{k_{\overline{m}_{1}}-2}{\varDelta } e(h) +\sum _{h=k_{\overline{m}_{l_{\overline{m}}}}}^{k_{\overline{m}}-2}{\varDelta } e(h)\nonumber \\&\qquad +\sum _{\theta =1}^{l_{\overline{m}-1}}\sum _{h={k_{\overline{m}_{\theta }}}}^{k_{\overline{m}_{\theta +1}}-2}{\varDelta } e(h)\Biggr \Vert ^{2}\nonumber \\&\quad \quad + \Biggl \Vert \sum _{\ell =1}^{l_{\overline{m}}}\mu _{\overline{m}_{\ell }}e(k_{\overline{m}_{\ell }}-\tau _{\overline{m}_{\ell }})\Biggr \Vert ^{2}\Bigg ]\nonumber \\&\quad \le 6\Biggl \Vert \sum _{h=k_{\overline{m}}-\tau _{\overline{m}}}^{k_{\overline{m}_{1}}-2}{\varDelta } e(h)\Biggr \Vert ^{2} +6\Biggl \Vert \sum _{h=k_{\overline{m}_{l_{\overline{m}}}}}^{k_{\overline{m}}-2}{\varDelta } e(h)\Biggr \Vert ^{2}\nonumber \\&\qquad +6\Biggl \Vert \sum _{\theta =1}^{l_{\overline{m}-1}} \sum _{h={k_{\overline{m}_{\theta }}}}^{k_{\overline{m}_{\theta +1}}-2} {\varDelta } e(h)\Biggr \Vert ^{2}\nonumber \\&\qquad +2\Biggl \Vert \sum _{\ell =1}^{l_{\overline{m}}} \mu _{\overline{m}_{\ell }}e(k_{\overline{m}_{\ell }}-\tau _{\overline{m}_{\ell }})\Biggr \Vert ^{2}. \end{aligned}$$

(34)

Similar to (12) and (13) in Step I,

$$\begin{aligned}&\Biggl \Vert \sum _{h=k_{\overline{m}}-\tau _{\overline{m}}} ^{k_{\overline{m}_{1}}-2}{\varDelta } e(h)\Biggr \Vert ^{2}\le 2 (k_{\overline{m}_{1}}-1-k_{\overline{m}}+ \tau _{\overline{m}})\nonumber \\&\qquad \times \sum _{h=k_{\overline{m}}-\tau _{\overline{m}}} ^{k_{\overline{m}}-2}\Biggl (\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\nonumber \\&\qquad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}\Biggr )\Vert e(h)\Vert _{\tau }^{2},\end{aligned}$$

(35)

$$\begin{aligned}&\Biggl \Vert \sum _{h=k_{\overline{m}_{l_{\overline{m}}}}}^{k_{\overline{m}}-2}{\varDelta } e(h)\Biggr \Vert ^{2}\le 2(k_{\overline{m}}-1-k_{\overline{m}_{l_{\overline{m}}}})\nonumber \\&\qquad \times \sum _{h=k_{\overline{m}_{l_{\overline{m}}}}}^{k_{\overline{m}}-2} \Biggl (\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}\nonumber \\&\qquad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}\Biggr ) \Vert e(h)\Vert _{\tau }^{2},\end{aligned}$$

(36)

$$\begin{aligned}&\Biggl \Vert \sum _{\theta =1}^{l_{\overline{m}-1}} \sum _{h={k_{\overline{m}_{\theta }}}}^{k_{\overline{m}_{\theta +1}}-2} {\varDelta } e(h)\Biggr \Vert ^{2}\le \sum _{\theta =1}^{l_{\overline{m}-1}} \Big [(k_{\overline{m}_{\theta +1}}-1-k_{\overline{m}_{\theta }})\nonumber \\&\qquad \times 2\sum _{h=k_{\overline{m}_{l_{\overline{m}}}}} ^{k_{\overline{m}}-2}\Biggl (\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2} \nonumber \\&\qquad +\overline{\rho }\sum _{d=1}^{d_{M}}\rho _{d}L_{f}^{2}\Biggr ) \Vert e(h)\Vert _{\tau }^{2}\Big ],\end{aligned}$$

(37)

$$\begin{aligned}&\Biggl \Vert \sum _{\ell =1}^{l_{\overline{m}}}\mu _{\overline{m}_{\ell }} e(k_{\overline{m}_{\ell }}-\tau _{\overline{m}_{\ell }}) \Biggr \Vert ^{2}\nonumber \\&\quad \le l\mu ^{2}M\gamma e^{-\varsigma (k_{\overline{m}_{l}-} -\overline{\tau }-k_{0}-\overline{\tau })}. \end{aligned}$$

(38)

From (34) to (38), we obtain

$$\begin{aligned}&\Vert e(k_{\overline{m}}-1)-e(k_{\overline{m}}-\tau _{\overline{m}})\Vert ^{2}\nonumber \\&\quad \le 2\Biggl \{3 \Biggl [(k_{\overline{m}_{1}}-1-k_{\overline{m}}-\tau _{\overline{m}}) +(k_{\overline{m}}-1-k_{\overline{m}_{l_{\overline{m}}}})\nonumber \\&\qquad +\sum _{\theta =1}^{l_{\overline{m}-1}}(k_{\overline{m}_{\theta +1}}-1-k_{\overline{m}_{\theta }} ) \Biggr ]M\gamma e^{-\varsigma (k_{\overline{m}}-\overline{\tau }-d_{M}-k_{0}-\overline{\tau }) }\nonumber \\&\qquad \times \frac{\varrho (\overline{\tau }-l)}{2\overline{\tau }} +l\mu ^{2}M\gamma e^{-\varsigma (k_{\overline{m}_{l}}-\overline{\tau }-k_{0}-\overline{\tau })} \Biggr \}\nonumber \\&\quad \le \Big [\frac{3(\overline{\tau }-l)^{2}}{\overline{\tau }}\varrho e^{\varsigma (\overline{\tau }+d_{M})}+2l\mu ^{2} e^{\varsigma (k_{\overline{m}}-k_{\overline{m}_{l}}+\overline{\tau })}\Big ]\nonumber \\&\qquad \times M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}\nonumber \\&\quad \le \Big [\frac{3(\overline{\tau }-l)^{2}}{\overline{\tau }}\varrho e^{\varsigma (\overline{\tau }+d_{M})}+2l\mu ^{2} e^{2\varsigma \overline{\tau }}\Big ]\nonumber \\&\quad \quad \times M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}\nonumber \\&\quad \triangleq \varrho _{1}M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}. \end{aligned}$$

(39)

Form (39) and the second equation of network (5), we can obtain

$$\begin{aligned} e(k_{\overline{m}})^{T}e(k_{\overline{m}})&=\Big (e(k_{\overline{m}}-1)+\mu _{\overline{m}}e(k_{\overline{m}}-\tau _{\overline{m}})\Big )^{T}\nonumber \\&\quad \times \Big (e(k_{\overline{m}}-1)+\mu _{\overline{m}}e(k_{\overline{m}}-\tau _{\overline{m}})\Big )\nonumber \\&=\Big [(1+\mu _{\overline{m}})e(k_{\overline{m}}-1)+\mu _{\overline{m}}\Big (e(k_{\overline{m}}-\tau _{\overline{m}})\nonumber \\&\quad -e(k_{\overline{m}}-1)\Big )\Big ]^{T}\Big [(1+\mu _{\overline{m}})e(k_{\overline{m}}-1)\nonumber \\&\quad +\mu _{\overline{m}}\Big (e(k_{\overline{m}}-\tau _{\overline{m}})-e(k_{\overline{m}}-1)\Big )\Big ]\nonumber \\&\le 2(1+\mu _{\overline{m}})^{2}\Vert e(k_{\overline{m}}-1)\Vert ^{2}\nonumber \\&\quad +2\mu _{\overline{m}}^{2}\Vert e(k_{\overline{m}}-\tau _{\overline{m}})-e(k_{\overline{m}}-1)\Vert ^{2}\nonumber \\&\le 2[(1+\mu _{\overline{m}})^{2}e^{\varsigma }+\mu _{\overline{m}}^{2}\varrho _{1}]\nonumber \\&\quad M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}\nonumber \\&\le p^{-1}M\gamma e^{-\varsigma (k_{\overline{m}}-k_{0}-\overline{\tau })}. \end{aligned}$$

(40)

In the following, we will prove (33) by the contradiction method. If (33) is not true, there exists at least one $k\in [k_{\overline{m}}, k_{\overline{m}+1}-1]$ such that $W(k)> M\gamma$. Let $k^{*}_{\overline{m}+1}=\inf \{k\in [k_{\overline{m}}, k_{\overline{m}+1}-1]|W(k)>M\gamma \}$. Obviously, $k_{\overline{m}}<k^{*}_{\overline{m}+1}$ and $W(k_{\overline{m}})<W(k_{\overline{m}+1}^{*})$. Let $k_{*\overline{m}+1}=\sup \{k\in [k_{\overline{m}}, k^{*}_{\overline{m}+1}-1]|W(k)\le M\gamma p^{-1}\}$.

One observes that $k_{*\overline{m}+1}<k^{*}_{\overline{m}+1}$ and

$$\begin{aligned}&W(k)\le M\gamma p^{-1}, \quad k\in [k_{*\overline{m}+1}+1,k^{*}_{\overline{m}+1}),\\&W(k_{*\overline{m}+1})\le W(k)< W(k^{*}_{\overline{m}+1}),\\&\quad k\in [k_{*\overline{m}+1}+1,k^{*}_{\overline{m}+1}). \end{aligned}$$

For any $s\in \mathbb {N}_{-\tau }$, when $k\in [k_{*\overline{m}+1},k^{*}_{\overline{m}+1}-1]$, we have

$$\begin{aligned} W(k+s)\le M\gamma \le pW(k+1). \end{aligned}$$

(41)

Therefore, similar to (22–30), we have $W(k+1)\le (1+\eta )W(k)$ for $k\in [k_{*\overline{m}+1}+1,k^{*}_{\overline{m}+1}-1]$. Let $k=k^{*}_{\overline{m}+1}-1$, we obtain

$$\begin{aligned} W(k^{*}_{\overline{m}+1})&\le (1+\eta )W(k^{*}_{\overline{m}+1}-1)\nonumber \\&\le (1+\eta )^{k^{*}_{\overline{m}+1}-k_{*\overline{m}+1}}W(k_{*\overline{m}+1})\nonumber \\&\le (1+\eta )^{\sigma _{2}}M\gamma p^{-1}\nonumber \\&\le (1+\eta )^{\sigma _{2}}M\gamma e^{-\varsigma \sigma _{2}}\nonumber \\&\le M\gamma <W(k^{*}_{\overline{m}+1}). \end{aligned}$$

(42)

This is contradiction. Hence, (33) holds. By the mathematical induction method, for all $m\in \mathbb {N}$, the claim in (9) holds. The proof is completed. $\square$

Remark 5

In Theorem 1, by using the delayed impulsive control strategy, synchronization problem is investigated for a class of discrete-time complex networks with distributed delays in (5). From (6) and (8), the convergent rate $\varsigma$ relies on the upper bound of impulsive intervals. Moreover, it can be seen that the criterion (7) reveals the relationship among distributed delays, impulsive input delays and impulsive control gains. Therefore, the obtained criteria in Theorem 1 depend on not only impulsive intervals but also impulsive strengths, which mean that the frequency of impulsive occurrence and impulsive strengths can heavily affect the synchronization of discrete-time complex networks.

Remark 6

Recently, stability and synchronization of delayed systems with impulsive effects have been widely investigated in discrete-time complex networks [11, 12, 14, 15, 33, 42, 43]. Compared with above works, the novelty of the main results is threefold: (1) In [11, 12, 15, 33, 43], distributed delays were neglected due to the mathematical difficult. (2) Different from the results in [12, 43], impulsive input delays are considered in this paper, which makes our research more challenging. (3) Some strict conditions were imposed on impulsive input delays and the impulsive effects in [14, 42], e.g., on the one hand, $\tau _{m}\le \sigma$ is necessary, where $\sigma$ is the lower bound of impulsive intervals, on the other hand, delayed impulses have the form $e(k_{m})=\mu _{1}e(k_{m}-1)+\mu _{2}e(k_{m}-\tau _{m})$, where $\mu _{1}, \mu _{2}\ge 0$ and the restriction $\mu _{1}+\mu _{2}\le 1$ is required. Obviously, these restrictions on the size of impulsive input delays and impulsive strengths encumber the wide applications of these results in [12, 14, 42, 43] to specified real-world network.

If there are no impulsive input delays in (3), i.e., $\tau _{m}=1$, the model (5) reduces to the following discrete-time complex network with impulsive control:

$$\begin{aligned} {\left\{ \begin{array}{ll} e(k+1)=\mathbf C e(k)+\sum _{d=1}^{d_{M}}\rho _{d}\mathbf f (e(k-d))+\mathbf W e(k),\\ \qquad \qquad k\ne k_{m}-1\\ e(k_{m})-e(k_{m}-1)=\mu _{m}e(k_{m}-1),\quad m\in {\mathbb {N}^{+}}. \end{array}\right. } \end{aligned}$$

(43)

Then, the following corollary can be obtained:

Corollary 1

Suppose that Assumptions 1–2 hold. If there exist positive scalars $\varsigma$ and p, such that the following conditions hold

$$\begin{aligned}&\ln (1+\eta )-\varsigma \le 0 \text { and } \alpha \ge 0;\end{aligned}$$

(44)

$$\begin{aligned}&(1+\mu )^{2}-p^{-1}\le 0;\end{aligned}$$

(45)

$$\begin{aligned}&\ln p-\varsigma \sigma _{2}\ge 0; \end{aligned}$$

(46)

where the parameters are defined in Theorem 1. Then the discrete-time complex network in (43) is exponentially synchronized.

If the distributed delays in (5) are replaced by the discrete delays, the model (5) becomes to the following discrete-time complex network with delayed impulsive control:

$$\begin{aligned} {\left\{ \begin{array}{ll} e(k+1)=\mathbf C e(k)+\mathbf f (e(k-d))+\mathbf W e(k),\\ \qquad \qquad k\ne k_{m}-1,\\ e(k_{m})-e(k_{m}-1)=\mu _{m}e(k_{m}-\tau _{m}),\quad m\in \mathbb {N}^{+}. \end{array}\right. } \end{aligned}$$

(47)

Then, the following corollary can be obtained:

Corollary 2

Suppose that Assumptions 1–2 hold. If there exist positive scalars $\varsigma$ and p, such that the following conditions hold

$$\begin{aligned}&\ln (1+\tilde{\eta })-\varsigma \le 0\text { and } \tilde{\eta }\ge 0;\end{aligned}$$

(48)

$$\begin{aligned}&\ln 2[(1+\mu )^{2}e^{\varsigma }+\mu ^{2}\varrho _{2}]-p^{-1}\le 0;\end{aligned}$$

(49)

$$\begin{aligned}&\ln p-\varsigma \sigma _{2}\ge 0; \end{aligned}$$

(50)

where $\tilde{\eta }=\alpha /(1-\tilde{\beta }p)-1$, $\tilde{\beta }=3L_{f}^{2}e^{\varsigma (d+1)}$, $\varrho _{2}=\frac{3(\overline{\tau }-l)^{2}}{\overline{\tau }}\tilde{\varrho } e^{\varsigma (\overline{\tau }+d)}+2l\mu ^{2}e^{2\varsigma \overline{\tau }}$, $\tilde{\varrho }=4\overline{\tau }(\Vert \mathbf C +\mathbf W -I_{Nn}\Vert ^{2}+L_{f}^{2})$, the other parameters are defined in Theorem 1. Then the discrete-time complex network in (47) is exponentially synchronized.

If there are no impulsive input delays in (47), i.e., $\tau _{m}=1$, the model (47) reduces to the following discrete-time complex network with impulsive control:

$$\begin{aligned} {\left\{ \begin{array}{ll} e(k+1)=\mathbf C e(k)+\mathbf f (e(k-d))+\mathbf W e(k),\\ \qquad \qquad k\ne k_{m}-1,\\ e(k_{m})-e(k_{m}-1)=\mu _{m}e(k_{m}-1),\quad m\in \mathbb {N}^{+}. \end{array}\right. } \end{aligned}$$

(51)

Then, the following corollary can be obtained:

Corollary 3

Suppose that Assumptions1–2 hold. If there exist positive scalars $\varsigma$ and p, such that the following conditions hold

$$\begin{aligned}&\ln (1+\tilde{\eta })-\varsigma \le 0\text { and } \tilde{\eta }\ge 0;\end{aligned}$$

(52)

$$\begin{aligned}&(1+\mu )^{2}-p^{-1}\le 0;\end{aligned}$$

(53)

$$\begin{aligned}&\ln p-\varsigma \sigma _{2}\ge 0; \end{aligned}$$

(54)

where the parameters are defined in Theorem 1 and Corollary 2. Then the discrete-time complex network in (51) is exponentially synchronized.

Remark 7

It is worth pointing out that we consider three special cases in the above corollaries. In Corollarys 1 and 3, we show that our main results can be applied to the impulsive control strategy without delays. In Corollary 2, we consider the synchronization of discrete-time complex networks with discrete delays under delayed impulsive control, in which the delayed impulsive control strategy is more general than the existing results in [12, 38, 43].

4 Numerical examples

In this section, two numerical examples are given to show the effectiveness of the main results.

Example 1

In this example, we will consider the following small world network with 50 dynamical nodes:

$$\begin{aligned} x_{i}(k+1)&=Cx_{i}(k)+\sum _{d=1}^{d_{M}}\rho _{d}f(x_{i}(k-d))\nonumber \\&\quad +c\sum ^{N}_{j=1}w_{ij}{\varGamma } x_{j}(k),\nonumber \\&\quad i={1,2,\ldots ,50},\quad k\in \mathbb {N}, \end{aligned}$$

(55)

where $f(x)=B\tanh (0.8x(k-d))$. The other parameters are given as:

$$\begin{aligned} C&=\left[ \begin{array}{c@{\quad }c}-0.02&{}0.02\\ 0.02&{}-0.06\end{array}\right] , B=\left[ \begin{array}{c@{\quad }c}0.03&{}0.15\\ 0&{}0.03\end{array}\right] ,\\ {\varGamma }&=\left[ \begin{array}{c@{\quad }c}0.2&{}0\\ 0&{}0.2\end{array}\right] , \end{aligned}$$

$c=0.01$, $d_{M}=4$, $\rho _{d}=0.2$ and $\tau _{m}=2$.

Fig. 1

a State trajectory of $x_{i1}$ without impulsive control in (55). b State trajectory of $x_{i2}$ without impulsive control in (55)

Fig. 2

a State trajectory of $e_{i1}$ under delayed impulsive control in (55). b State trajectory of $e_{i2}$ under delayed impulsive control in (55)

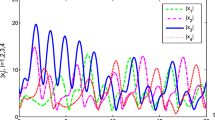
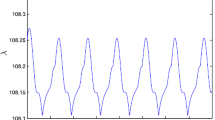
We select the isolated node as $s(t)=0$. From condition (6), we can obtain that $p=1.05$ and $\varsigma =0.01$ are feasible solutions of (6) by choosing the parameter $\lambda =127$. Solving (8), we choose $\sigma _{2}=1$. Based on condition (7), it is easy to obtain that $\mu \in [-0.377,-0.449]$ is feasible interval. According to Theorem 1, it can be concluded that the discrete-time complex network in (55) is globally exponentially synchronized under delayed impulsive controller (3). Figure 1 shows that the synchronization errors $x_{i}(k)-s(k)$ of the discrete-time complex networks in (55). Figure 2 shows the synchronized errors of the discrete-time complex network in (55) by choosing the impulsive control gains $\mu _{m}=-0.4$ and impulsive interval $\sigma _{2}=1$. From Fig. 2, we can see that the delayed impulsive effects can enforce the states of the discrete-time complex network in (55) to the state of the isolated node $s(t)=0$. The simulations confirm our results well. Table 1 shows the relationship between $\mu$ and $\varsigma _{\max }$ when $\sigma _{1}=\sigma _{2}=1$. Table 2 shows the relationship between $\sigma$ and $\varsigma _{\max }$ when $\tau _{m}=1$ and $\mu =-0.4$. Form Tables 1 and 2, it can be seen that the impulsive intervals and impulsive control gains can heavily affect the synchronization of discrete-time complex networks.

Table 1 The relationship between $\mu$ and $\varsigma _{\max }$

Table 2 The relationship between $\sigma$ and $\varsigma _{\max }$

Example 2

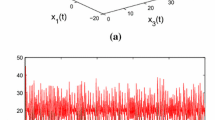
In this example, we will consider the following discrete-time brain cortical network of the cat with 53 cortical regions connected by about 830 fibers of different densities in [31], in which topological structure can be seen in Fig. 3:

$$\begin{aligned} x_{i}(k+1)&=-Cx_{i}(k)+f(x_{i}(k-d))\nonumber \\&\quad +\,c\sum ^{N}_{j=1}w_{ij}{\varGamma } x_{j}(k),\nonumber \\&\quad i={1,2,\ldots ,53},\quad k\in \mathbb {N}, \end{aligned}$$

(56)

where $f(x)=B\widetilde{f}(x)$, and $\widetilde{f}(x)=1/(1+e^{-x})$ is activation function. The other parameters are given as:

$$\begin{aligned} C&=\left[ \begin{array}{cc}-0.01 &{}0\\ 0&{}-0.03\end{array}\right] , B=\left[ \begin{array}{cc}0.01&{}-0.05\\ 0&{}-0.01\end{array}\right] ,\\ {\varGamma }&=\left[ \begin{array}{cc}0.2&{}0\\ 0&{}0.2\end{array}\right] , \end{aligned}$$

$c=0.001$, $d=2$ and $\tau _{m}$ is unknown impulsive input delay.

Fig. 3

The topological structure of the brain cortical network of the cat with 53 cortical regions in [31]

Fig. 4

a State trajectory of $x_{i1}$ without impulsive control in (56). b State trajectory of $x_{i2}$ without impulsive control in (56)

We select the isolated node as $s(t)=0$. From Corollary 2, we can obtain that $p=1.01$ and $\varsigma =0.0001$ are feasible solutions of (48)–(50) by choosing $\sigma _{1}=\sigma _{2}=1$ and $\mu =-0.38$. Based on the condition (49), it is easy to obtain that $\tau _{m}\in [1,3]$ is the feasible interval. According to Corollary 2, it can be concluded that the discrete-time brain cortical network in (56) is globally exponentially synchronized under delayed impulsive controller (3). Figure 4 shows the synchronization errors $x_{i}(k)-s(k)$ of the discrete-time brain cortical network without impulsive control in (56). Figure 5 shows the synchronized errors of the discrete-time brain cortical network in (56) by choosing the impulsive control gains $\mu _{m}=-0.38$ and impulsive interval $\sigma =1$. From Fig. 4, we can see that the delayed impulsive effects can enforce the states of the discrete-time brain cortical network in (56) to the state of the isolated node $s(t)=0$. Compared with existing results [12, 14, 42], Table 3 shows the maximal allowable bounds of impulsive input delay. Apparently, our results provide more feasible interval of impulsive input delays.

Fig. 5

a State trajectory of $e_{i1}$ under delayed impulsive control in (56). b State trajectory of $e_{i2}$ under delayed impulsive control in (56)

Table 3 The maximal allowable bounds of impulsive input delay $\tau _{m}$

Remark 8

In this paper, a new strategy of delayed impulsive control has been introduced into the discrete-time complex networks with distributed delays. Apparently, delayed impulsive controller in (3) is more general than the usual impulsive control strategies in [12, 14, 38]. On the other hand, synchronization criteria in this paper are derived in terms of algebraic conditions by utilizing Razumikhin-type theorem. It can be seen that the criteria with less restrictive assumptions are easy to check and reveal the relationship among the time delays, control parameter and state equation. However, a little bit of conservatism may be unavoidable, e.g., there exists less feasible interval of impulsive control gains in above simulation examples. Therefore, we will try to avoid conservativeness in the following work.

5 Conclusion

In this paper, the synchronization of discrete-time complex network with distributed delays using delayed impulsive control is investigated. A new delayed impulsive control strategy has been presented to synchronize the discrete-time complex network with distributed delays. By using the Razumikhin theorem and the discrete Gronwall inequality, several synchronization criteria have been obtained. The criteria are heavily dependent on the frequency of impulsive occurrence, impulsive control gains and impulsive input delays. Finally, two example are given to show the effectiveness of our results. Our further research topics include delayed impulsive control of time-varying systems and quantization problem.