Response of a three-degree-of-freedom wing with stiffness and aerodynamic nonlinearities at hypersonic speeds

Abstract

In the design of high-speed aircraft particular attention must be given to the effect of stiffness and aerodynamic nonlinearities. Additionally the thermal effects cannot be ignored since the harsh thermal environment influences the dynamic behaviour of a structure. In the current paper the aeroelastic response of a three-degree-of-freedom wing with a control surface, and stiffness and aerodynamic nonlinearities has been analysed. The nonlinear unsteady aerodynamic forces applied to the model are calculated using third-order piston theory and piecewise linear, and cubic stiffening nonlinearities are implemented in the control surface. The effect of temperature on the model is determined by a steady-state analysis with a predefined temperature distribution. The onset of limit cycle oscillations and the bifurcation behaviours is compared for the different nonlinearities. The effect of initial conditions is determined to quantify their impact on the limit cycle behaviour. This article extends the nonlinear analysis of the aeroelastic response of a wing at hypersonic speeds with an added control surface degree of freedom, with the effect of nonlinear aerodynamics and stiffness included in the model. The results show that different nonlinearities influence the response of the system uniquely and heat plays an important role in the order of excited harmonics.

1 Introduction

For many years linear models have served the aeroelastician well. Most of our understanding of aeroelastic phenomena, such as divergence and flutter, has been obtained by the study of linear models. The success of linear models can be ascertained to the small effects of nonlinearities. However sometimes nonlinear effects are crucial to the survival of the model [12], and many experiments have shown phenomena that cannot be predicted using linear theory [1]. Examples of this are limit cycle oscillations (LCOs) and chaotic responses of the aero-surfaces [21], which have been observed during flight [11]. Limit cycle oscillations of wing models in low subsonic flow have been extensively studied by Tang et al. [39–41]; however application of aerodynamic and stiffness nonlinearities to high-speed flow on three-dimensional models with a control degree of freedom has not been analysed.

Several examples of aerodynamic and stiffness nonlinearities exist in aircraft. Control surfaces with loose or worn hinges is a case of a concentrated stiffness nonlinearity, which can lead to limit cycle oscillations. Lee and Tron [21] showed that loose control surfaces can be adequately represented via either a bilinear spring stiffness or a cubic nonlinearity, by modelling the LCOs seen in the CF-18 aircraft. A considerable amount of research has gone into investigating the aeroelastic response of an aerofoil with bilinear nonlinearities in either the plunge or pitch degrees of freedom [2, 22, 29, 32, 33, 36], with limited research on three-dimensional aeroelastic models for high-speed application [3, 4, 23, 30]. Free-play nonlinearities usually occur in the control surface [16], whereas the cubic stiffness comes mainly from the large amplitude oscillation of the flexible wing [19]. Aerodynamic nonlinearities arise from: high wing angles of attack, shock waves in transonic [45], supersonic and hypersonic regimes and high-speed phenomena such as ionisation and plasma in the free-stream [25, 26]. Librescu et al. [24] performed a flutter analysis on infinitely long flat panels in a high-temperature field and concluded that the effect of temperature tended to reduce the flutter speed.

A sensitivity analysis on the aeroelastic response to the initial conditions has been performed for two-dimensional cases [8, 33]. The presence of LCOs is strongly dependent on the initial conditions of the aerofoil. Price et al. [33] concluded that LCOs can occur for velocities well below the linear flutter boundary, and this is in agreement with the numerical predictions of McIntosh et al. [27] and Yang and Zhao [50]. Woolston et al. [48] and Shen [35] performed experiments using a rigid two-dimensional wing section with a free-play in the pitching degree of freedom. They showed that a response of the nonlinear system to an initial displacement in pitching could produce flutter well below the critical flutter speed obtained through linear analysis.

Jiffri and Mottershead [17] addressed the control of systems with non-smooth stiffness nonlinearities, namely free-play, for a system with pitch, plunge and flap degrees of freedom. Wang et al. [47] looked at the response of flexible control surfaces at hypersonic speeds. Li et al. [22] analysed the dynamic response of a typical two-dimensional aerofoil section with three degrees of freedom, with a free-play nonlinearity in the control surface. Daochun and Jinwu [9] investigated the chaotic response of an aerofoil with cubic nonlinearity, for the case when the moment caused by circulatory flow is not zero. Tang and Dowell [37] developed a component modal analysis to derive the structural equations of motion for a delta wing with a store. A free-play nonlinearity is added to the store connection, and the results are compared with wind tunnel test results.

Recently Abdelkefi et al. [4] performed an analytical and experimental investigation into the dynamics of a two-dimensional plunging and pitching aerofoil, with a nonlinearity in the pitch degree of freedom. When the unsteady aerodynamics were incorporated into the analytical model, the results agreed with the experimental analysis. Padmanabhan et al. [30] analysed the spanwise varying displacement of a wing carrying a store, modelled by a beam-rod representation with two degrees of freedom.

The present study focuses on extending this work to a three-degree-of-freedom wing, with an added control surface degree of freedom, and coupling the nonlinear structural dynamics with the nonlinear aerodynamics and a steady-state heat model. The analysis of stiffness nonlinearities and the effects of initial conditions on two-dimensional aerofoils has been studied [20]. Previous investigations have also focused on the effects of unsteady aerodynamics on the flutter response of aerofoil geometries [1]. The aeroelastic response of three-dimensional wings has been analysed with structural nonlinearities in the store connection [30] and for flexible wings with high aspect ratios [5] and dynamic stall considerations [6, 31]. Finally research has been done on the reduction in the flutter boundary due to a harsh thermal environment [43].

2 Theoretical analysis

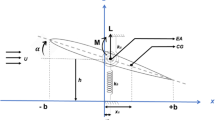
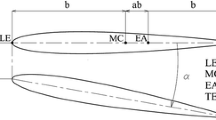
The aeroelastic model used for this analysis is the Hancock model [14]. It is composed of a uniform rigid rectangular wing with pitch $(\theta )$, flap $(\gamma )$ and control surface $(\beta )$ degrees of freedom. These degrees of freedom are introduced via three springs at the root of the wing, two at the flexural axis and one on the control surface hinge line, as shown in Fig. 1.

Fig. 1

Aeroelastic model with control surface

2.1 Structural model

The general equations of motion for the aeroelastic system used in this article can be written as:

$$\begin{aligned} \mathbf{A } \underline{\ddot{q}} + \left( \mathbf{B } + \rho U\mathbf{C }\right) \underline{\dot{q}} + \left( \mathbf{D } + \rho U^2\mathbf{E }\right) \underline{q} = \underline{Q} \end{aligned}$$

(1)

where ${{{\underline{q}}}}=\left[ \begin{array}{ccc}\gamma&\theta&\beta \end{array}\right] ^T$ represents the displacement vector of the system, A is the inertia matrix, B, D, C and E are the structural damping, structural stiffness, aerodynamic damping and aerodynamic stiffness matrices, respectively, $\rho$ is the air density, U is the aircraft velocity and Q is the external force excitation vector. Using the axis system defined in Fig. 1, the vertical displacement of the wing, $z_w$, can be written as a function of the x and y positions as well as the angles, $\gamma$, $\theta$ and $\beta$. Assuming all displacement angles are small leads to the following expression:

$$\begin{aligned} z_w(x,y) = y\gamma + (x - x_f)\theta \end{aligned}$$

(2)

Further, the vertical displacement for the control surface can be defined as:

$$\begin{aligned} z_c(x,y) = y\gamma + (x - x_f)\theta + (x - x_h)\beta \end{aligned}$$

(3)

where $x_f$ is the chord position of the flexural axis and $x_h$ is the chord location of the hinge axis (Fig. 1).

With the geometric equations defined, the equations of motion (Eq. 1) can be defined using Lagrange’s equation. Lagrange’s equation for a multiple-degree-of-freedom system is defined by:

$$\begin{aligned} \frac{d}{\mathrm{d}t}\frac{\partial T_e}{\partial \dot{\underline{q}}} + \frac{\partial V_e}{\partial \underline{q}} = Q_x = \frac{\partial (\delta W)}{\partial (\delta \underline{q})} \end{aligned}$$

(4)

where $T_e$ is the kinetic energy of the system and can be expressed in terms of the three degrees of freedom of the system:

$$\begin{aligned} T_e= & {} I_\gamma \frac{\dot{\gamma }^2}{2} + I_\theta \frac{\dot{\theta }^2}{2} + I_\beta \frac{\dot{\beta }^2}{2} + I_{\gamma \theta }\left( \dot{\gamma }\dot{\theta }\right) \nonumber \\&+\, I_{\gamma \beta }\left( \dot{\gamma }\dot{\beta }\right) + I_{\theta \beta }\left( \dot{\theta }\dot{\beta }\right) \end{aligned}$$

(5)

and $V_e$ is the potential energy of the system and is defined as:

$$\begin{aligned} V_e = \frac{1}{2}\left( K_\gamma \right) \gamma ^2 + \frac{1}{2}\left( K_\theta \right) \theta ^2 + \frac{1}{2}\left( K_\beta \right) \beta ^2 \end{aligned}$$

(6)

where $K_\gamma , K_\theta$ and $K_\beta$ represent the spring stiffness of the restraining spring in each degree of freedom and $I_{\gamma }, I_{\theta }$ and $I_{\beta }$ are the mass moments of inertia about the three degrees of freedom. The equations of motion for the system prior to the implementation of the aerodynamic and temperature models are given by:

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c} I_\gamma &{} I_{\gamma \theta } &{} I_{\gamma \beta } \\ I_{\gamma \theta } &{} I_\theta &{} I_{\theta \beta } \\ I_{\gamma \beta } &{} I_{\theta \beta } &{} I_\beta \\ \end{array} \right] \left\{ \begin{array}{c} \ddot{\gamma } \\ \ddot{\theta } \\ \ddot{\beta } \\ \end{array} \right\} \nonumber \\&\quad + \left[ \begin{array}{c@{\quad }c@{\quad }c} K_\gamma &{} 0 &{} 0 \\ 0 &{} K_\theta &{} 0 \\ 0 &{} 0 &{} K_\beta \\ \end{array} \right] \left\{ \begin{array}{c} \gamma \\ \theta \\ \beta \end{array} \right\} = \left\{ \begin{array}{c} Q_\gamma \\ Q_\theta \\ Q_\beta \end{array} \right\} \end{aligned}$$

(7)

2.2 Aerodynamic model

In the high Mach number (up to 7 [25]) flight regime, the pressure distribution across the wing is significantly influenced by the presence of the shock wave [25]. As a result, the pressure distribution across the wing becomes a function of the location of a single point, the shock wave [7, 13]. This behaviour is modelled using piston theory. Piston theory depends on the premise that the pressure on a wing surface can be assumed to be equivalent to the movement of a piston in a column of air. For a 2D wing section this gives:

$$\begin{aligned} p(x) = p_\infty \left( 1 + \frac{\gamma _c - 1}{2}\frac{w(x)}{a_\infty }\right) ^\frac{2\gamma _c}{\gamma _c - 1} \end{aligned}$$

(8)

where $p_{\infty }$ and $a_{\infty }$ are the pressure and speed of sound of the free-stream, respectively, $\gamma _c$ is the ratio of specific heats and $w(x)$ is the downwash velocity of the wing. Equation 8 provides an exact solution for an expansion and an approximate solution for a compression due to the presence of the shock wave [25]. However the power term $\frac{2\gamma _c}{\gamma _c-1}$, does not provide an explicit solution to the integration of Eq. 8. Therefore as outlined by Lighthill [25], an approximate solution can be determined accurate to within 0.06 % of the given value using the third-order binomial expansion:

$$\begin{aligned} p(x)= & {} 1 + \gamma _c\left( \frac{w(x)}{a_\infty }\right) \lambda + \frac{\gamma _c(\gamma _c+1)}{4}\left( \frac{w(x)}{a_\infty }\right) ^2\lambda ^2\nonumber \\&+ \frac{\gamma _c(\gamma _c+1)}{12}\left( \frac{w(x)}{a_\infty }\right) ^3\lambda ^3 \end{aligned}$$

(9)

where:

$$\begin{aligned} \lambda = \frac{M_\infty }{\sqrt{M_\infty ^2 - 1}} \end{aligned}$$

(10)

$M_{\infty }$ is the Mach number of the free-stream. The pressure $p(x)$ can then be integrated across the chord, $c$, and strip theory can be used to generalise the solution for the three-degree-of-freedom wing [18].

2.2.1 Aerodynamic coefficients

The lift across a 2D aerofoil section, $l$, is defined as the summation of the difference in pressure, $\varDelta p$, of the upper and lower surface.

$$\begin{aligned} l = \int \limits _0^{x_c} \varDelta p \mathrm{d}x + \int \limits _{x_c}^c \varDelta p \mathrm{d}x \end{aligned}$$

(11)

Equation 11 includes the lift contribution from the control surface. Strip theory is then applied to determine the lift of the three-degree-of-freedom wing, $L$, by integrating across the span, $s$:

$$\begin{aligned} L = \int \limits _0^s l \mathrm{d}y \end{aligned}$$

(12)

similarly, the expression for the moment about the flexural axis, $M_{fa}$, and the hinge moment, $M_{ha}$, due to the control surface can be defined by:

$$\begin{aligned} M_{fa}= & {} \int \limits _0^{x_c} \varDelta p(x - x_f)\mathrm{d}x + \int \limits _{x_c}^c \varDelta p(x - x_f)\mathrm{d}x \end{aligned}$$

(13a)

$$\begin{aligned} M_{ha}= & {} \int \limits _{x_c}^{c} \varDelta p(x-x_h)\mathrm{d}x \end{aligned}$$

(13b)

Substituting the binomial expansion for pressure (Eq. 9) into the above equations gives the expressions for the lift and moments across the aerofoil chord. Strip theory was verified by Jones and Gallagher [18] in which they confirmed the “surface pressure distribution to be predicted using strip theory with reasonable accuracy up to angles of attack of $27^{\circ }$”.

2.3 Temperature model

This section describes the method for applying a temperature load to the aeroelastic model and how the model parameters are updated.

2.3.1 Updating the stiffness

Heating the structure results in a reduction in stiffness [42]. This is a consequence of the reduction in elastic modulus of the material with increase in temperature. Vosteen [46] showed that it is appropriate to use the dynamic reduction in Young’s modulus with varying temperature for aeroelastic structures. The following method can be developed for determining the equivalent stiffness reduction in $K_\gamma$, $K_\theta$ and $K_\beta$ that represents the structural stiffness reduction due to the applied temperature loads. The dynamic modulus is defined as a function of the oscillating frequency, $\omega _n$ by:

$$\begin{aligned} E = \frac{4\pi ^2s^4\varGamma A\omega _n^2}{\lambda ^2I_i \left( 1+\alpha _m\varDelta T\right) } \end{aligned}$$

(14)

where $s$ is the length of the wing model, $\alpha _m$ is the coefficient of thermal expansion, $\varGamma = \frac{\rho _m}{s}$ with $\rho _m$ being the material density, $A$ is the area of the structure, $\lambda$ is the eigenvalue of the mode, the subscript $i$ represents the degree of freedom, $I_i$ is the heated moment of inertia of each mode and $\varDelta T$ is the change in temperature acting on the structure. The above equation can be rearranged to get the heated natural frequency for a particular mode:

$$\begin{aligned} \omega _n = \sqrt{\frac{E\lambda ^2I_i(1+\alpha _m\varDelta T)}{4\pi ^2s^4\varGamma A}} \end{aligned}$$

(15)

where E is extracted from Fig. 2. The heated natural frequency $\omega _n$ for each mode can be used to obtain the heated values for $K_\gamma$, $K_\theta$ and $K_\beta$ using the following equation:

$$\begin{aligned} K_i = (2\pi \omega _{ni})^2I_i \end{aligned}$$

(16)

Fig. 2

Variation of aluminium 2024-T3 Young’s modulus with temperature

Fig. 3

Applied temperature distribution adapted from [28]

2.3.2 Applying the temperature distribution

The temperature distribution was applied by approximating experimental data gained from the X-15 aircraft [28]. These temperature distributions can be found in Fig. 3. Two primary distribution types are shown in Fig. 3, the hot curves and the spike curves. The hot curves represent a fairly uniform temperature distribution, and the spike curves represent a leading edge concentrated temperature distribution [28]. The spike 1 and hot 1 represent 100 % temperature loading, spike 2 and hot 2 represent 50 % temperature loading, scaled down for use with aluminium. The flutter velocity for each temperature distribution is calculated, and the temperature distribution with the lowest flutter velocity is applied to the nonlinear cases. The temperature distributions shown in Fig. 3 are applied to the aeroelastic model (Sect. 2.1) of the wing through a panel method. This method splits the wing into a series of panels, in the span and chordwise directions, that can be heated individually. This allows any temperature distribution to be implemented over the span and chord. Since the aeroelastic model has a small thickness, the temperature gradient across the thickness of the plate is considered to be orders of magnitude less than that across the chord and span. Therefore the gradient across the thickness of the plate is assumed to be uniform for each panel.

2.3.3 Updating the inertia

Aerodynamic heating of a vehicle at a given flight condition changes a number of parameters that affect the aeroelastic system of equations, mainly elastic modulus degradation, due to stiffness reduction, and changes in inertia, due to the expansion of a material under heat. The inertia equations can be solved using the panel method, where the moments of inertia are equal to the sum of the inertia evaluated for each panel across the entire wing. Hence the moment of inertia equations, see Eq. 5, can be defined as:

$$\begin{aligned} I_\gamma = \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _mt(i,j)\left[ x_{i+1} - x_i\right] \left[ \frac{y_{i+1}^3}{3} - \frac{y_i^3}{3}\right] \end{aligned}$$

(17)

$$\begin{aligned} I_\theta= & {} \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _{mt}(i,j)\left[ \begin{array}{l} \left( \frac{x_{i+1}^3}{3} - x_{i+1}^2x_f + x_{i+1}x_f^2\right) \\ -\left( \frac{x_i^3}{3}-x_i^2x_f+x_ix_f^2 \right) \end{array}\right] \nonumber \\&\times \left[ y_{i+1} - y_i\right] \end{aligned}$$

(18)

$$\begin{aligned} I_\beta= & {} \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _mt(i,j)\left[ \begin{array}{l} \left( \frac{x_{i+1}^3}{3} - x_{i+1}^2x_h + x_{i+1}x_h^2\right) \\ -\left( \frac{x_i^3}{3}-x_i^2x_h+x_ix_h^2 \right) \end{array}\right] \nonumber \\&\times \left[ y_{i+1} - y_i\right] \end{aligned}$$

(19)

$$\begin{aligned} I_{\gamma \theta }= & {} \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _mt(i,j)\left[ \left( \frac{x_{i+1}^2}{2} - x_{i+1}x_f\right) \right. \nonumber \\&\left. - \left( \frac{x_i^2}{2}-x_ix_f\right) \right] \left[ \frac{y_{i+1}^2}{2} - \frac{y_i^2}{2}\right] \end{aligned}$$

(20)

$$\begin{aligned} I_{\gamma \beta }= & {} \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _mt(i,j)\left[ \left( \frac{x_{i+1}^2}{2} - x_{i+1}x_h\right) \right. \nonumber \\&\left. - \left( \frac{x_i^2}{2}-x_ix_h\right) \right] \left[ \frac{y_{i+1}^2}{2} - \frac{y_i^2}{2}\right] \end{aligned}$$

(21)

$$\begin{aligned} I_{\theta \beta }= & {} \sum \limits _{i=1}^{N_s} \sum \limits _{j=1}^{N_c} \rho _mt(i,j)\nonumber \\&\times \left[ \begin{array}{l} \left( \frac{x_{i+1}^3}{3} - \frac{x_{i+1}^2}{2}(x_f+x_h) + x_{i+1}x_hx_f +1\right) \\ -\left( \frac{x_i^3}{3}-\frac{x_i^2}{2}(x_f+x_h)+x_ix_hx_f \right) \end{array}\right] \nonumber \\&\times [y_{i+1} - y_i] \end{aligned}$$

(22)

where $N_c$ and $N_s$ represent the number of panels in the chord and spanwise directions, respectively, and $t(i,j)$ is the thickness of the relevant panel. This method allows the evaluation of inertia for the expansion of individual panels due to a nonuniform applied temperature distribution.

2.3.4 Thermal expansion

A beam of consistent cross-sectional area under uniform heating conditions can be assumed to expand linearly according to the following relationship:

$$\begin{aligned} L_\mathrm{new} = L(1 + \alpha _m\varDelta T) \end{aligned}$$

(23)

where $L_\mathrm{new}$ is the length of the beam under increase in temperature, $\varDelta T$. $L$ is the original beam length at a reference temperature, $T_\mathrm{ref}$ (288 K). The linear thermal expansion coefficient is defined as $\alpha _m$. The above thermal expansion methodology can be adapted and applied to all the individual panels in the model. Therefore the expansion of each panel becomes a function of the temperature applied to that panel only. The number of panels has to be large enough to capture the details of the applied temperature distribution (Fig. 4). The effects of thermal stresses caused by the temperature gradients are not considered in this analysis. A finite element solution needs to be performed to calculate the thermal stresses present in the analysis.

Fig. 4

Thermal expansion of wing under spike 1 temperature loads with deformation enlarged by 10 %

2.4 Stiffness nonlinearities

The stiffness nonlinearities are introduced in the stiffness term for the control surface degree of freedom ($K_\beta$). The stiffness nonlinearities [20, 49] shown in Fig. 5 can be expressed by a series of equations and solved using a Dormand/Prince routine [10]. The bifurcation behaviours are investigated through a variable step Runge–Kutta time integration. The nonlinearities are defined as:

Fig. 5

Nonlinear structural stiffness characteristics

Free-play:

$$\begin{aligned} M(h) = \left\{ \begin{array}{ll} K_h h + K_h\delta &{} \quad h>\delta \\ 0 &{} \quad -\delta \le h\le \delta \\ K_h h - K_h\delta &{} \quad h<-\delta \\ \end{array}\right. \end{aligned}$$

(24)

Bilinear:

$$\begin{aligned} M(h) = \left\{ \begin{array}{ll} K_{h1} h + (K_{h2} - K_{h1})\delta &{} \quad h>\delta \\ K_{h2} h &{} \quad -\delta \le h\le \delta \\ K_{h1} h - (K_{h2} - K_{h1})\delta &{} \quad h<-\delta \\ \end{array}\right. \end{aligned}$$

(25)

Cubic:

$$\begin{aligned} M(h) = \left\{ \begin{array}{ll} K_h(h^3) &{} \quad {\text {nonlinear hardening}} \\ -K_h(h^3) &{} \quad {\text {nonlinear softening}} \\ \end{array}\right. \end{aligned}$$

(26)

where $h$ represents the degree of freedom of interest, the $K_h$ terms are the slopes of the curves shown in Fig. 5 and $\delta$ is a measure of the dead zone where $2\delta$ is the size of the free-play region. The effects of nonlinearities in the structure can be modelled by updating the stiffness of the control restoring spring ($K_{\beta }$).

3 Results and discussion

The model under consideration uses the parameters as defined in Table 1 [49]:

3.1 Linear system

The linear system was evaluated to obtain a benchmark comparison for the instability speed against the nonlinear responses. The stiffness nonlinearities were coupled with the linear aerodynamic model to determine their effects independent of the nonlinear aerodynamics; the nonlinear aerodynamics and structural dynamics are then coupled.

Figure 6 shows the frequency-damping plots for the hot and cold structures. The flutter velocity of the cold structure is calculated to be 2157.7 ms$^{-1}$. The hot temperature response is obtained by applying the spike 1 temperature distribution to the wing model. The drop in flutter speed with changes in temperature is highlighted in Fig. 6, where the temperature/flutter speed relation becomes clear. An increase in temperature causes a decrease in flutter speed, and a reduction in flutter speed of 257 ms$^{-1}$ is observed. This is highlighted in Fig. 6 since the hot damping ratio approaches zero before the cold damping ratio.

Figure 7 shows the time-marching response at the flutter speed for the hot structure (red), which in this case gives a flutter velocity of 1901.6 ms$^{-1}$ (Fig. 6).

Table 1 Initial parameters of aeroelastic model

At the flutter velocity for the hot structure, the cold structure exhibits a decaying response, as shown in Fig. 7.

The temperature distribution was linearly varied between the various temperature models, as shown in Fig. 3, and the resulting flutter velocities were calculated (Fig. 8). The spike 1 temperature distribution has the lowest flutter speed (Fig. 8), and this is in agreement with Rodgers [34]; therefore it is the only temperature model applied to the structure, because it is the worst case.

3.2 Nonlinear structural dynamics

The response of the system with a stiffness nonlinearity in the control degree of freedom is now analysed. A free-play nonlinearity is implemented followed by bilinear and cubic nonlinearities.

Fig. 6

Frequency and damping ratio of hot and cold structure

Fig. 7

Response of linear system at flutter speed (1901.6 ms$^{-1}$)

Fig. 8

Flutter speed dependency on steady-state temperature

3.2.1 Free-play stiffness

For the free-play nonlinearity the gradient ($K_h$, Eq. 23) was set to twice the stiffness of the control degree of freedom ($K_\beta$) [44], with a dead zone of $\delta = 10^{-4}$ radians, determined from the magnitude of the LCOs (Fig. 7). When a nonlinearity is introduced, the speed at which instabilities occur is altered. This is shown in the bifurcation plot of the system (Fig. 9). Figure 9 shows the response with and without heat. As expected, the bifurcation point has shifted away from the linear stability point as a consequence of the presence of heat. The addition of heat also reduces the number of high-frequency harmonics that are excited in the system’s response. The bifurcation plot displays the values of amplitude of the limit cycle at zero velocity for the nonlinear degree of freedom, i.e. the control surface deflection $\beta$ at $\dot{\beta }=0$. This gives an indication of the number of harmonics present in the system’s simulation, i.e. the number of excited frequencies, hence the system’s complexity. Figure 9 shows that the response is quasi-periodic; the wing no longer oscillates in a smooth sinusoidal pattern, but rather has a number of high-frequency components. This is highlighted in Fig. 10, which shows a close up view of the response for the free-play stiffness. The addition of heat reduces the range of airspeeds at which limit cycle oscillations occur, from 165 to 140 ms$^{-1}$. The bifurcation point occurs at the same velocity where the linear system goes unstable, for the cold case seen in Fig. 9. However unlike the linear system where the amplitude of the response is not bounded, the nonlinearity and heat cause the system to oscillate symmetrically between two bounds, $\pm 1.2(10^{-4})$. A typical phase plot for this response for all degrees of freedom is shown in Fig. 11, the nonlinear degree of freedom, bottom plot of Fig. 11, shows a quasi-periodic nature with a number of high harmonics present (Fig. 12). The frequency content of the signal further suggests the quasi-periodic nature of the response, dominated by a number of frequencies with a low-level broadband spectrum of noise. There are two low-frequency components at 49.4 and 49.6 Hz and some low-amplitude components just above 150 Hz, but the response is dominated by frequencies at around 250, 350 and 450 Hz. These high-frequency components are the 5th, 7th and 9th harmonic terms and present a double mode, i.e. the frequency around 250 Hz has a definite component at 247.1 and 247.8 Hz, followed by a third at 256.6 Hz and a fourth at 258.6 Hz. These final two frequencies are $\sqrt{3}$ multipliers of the fundamental frequencies. The nonlinear region ends at a velocity of 2050 ms$^{-1}$ for the heated model. Hence a stiffening effect is being applied on the nonlinear system by the presence of heat. Bifurcation occurs at a speed of 1905 ms$^{-1}$ (Fig. 9) for the system with free-play stiffness, and this is higher than the flutter velocity predicted by linear theory for the heated system, 1901.6 ms$^{-1}$ (Fig. 6).

Fig. 9

Bifurcation plot for free-play structural stiffness, hot system (top) cold system (bottom)

Fig. 10

Response of heated free-play structural stiffness at an airspeed of 1920 ms$^{-1}$

Fig. 11

Phase plot for the heated free-play stiffness at a velocity of 1920 ms$^{-1}$

Fig. 12

Fast Fourier transform of the heated free-play stiffness at a velocity of 1920 ms$^{-1}$

3.2.2 Bilinear stiffness

A ratio of $K_{h2}/K_{h1}=2$, with $K_{h1} = K_{\beta }$ [44], and $\delta = 10^{-4}$ radians is used for the bilinear nonlinearity. The bifurcation diagram for the hot structure is shown in Fig. 13. The onset of LCOs occurs at 1901 ms$^{-1}$. This deviates slightly from the predicted linear flutter speed (1901.6 ms$^{-1}$) due to the presence of the bilinear nonlinearity in the structure. The bifurcation ends abruptly at 1912 ms$^{-1}$, with an unstable oscillatory behaviour occurring beyond this airspeed. The amplitude of oscillation has a maximum of 0.002 radians at 1912 ms$^{-1}$, slowly growing as the airspeed is increased. The limit cycles are symmetric, but they display a quasi-periodic behaviour. This is highlighted in the typical phase plots for the system’s degrees of freedom in Fig. 14. Figure 14 clearly shows the quasi-periodic nature of the response for the nonlinear states of the system, with the nonlinear state ($\beta$) having a number of high-frequency components in the response.

Fig. 13

Bifurcation plot for the system with bilinear stiffness hot system

Fig. 14

Phase plot for the heated system with bilinear stiffness at 1905 ms$^{-1}$

3.2.3 Cubic stiffness

The hardening effect and softening effect of a cubic nonlinearity are tested for the aeroelastic system under consideration. In the presence of a hardening nonlinearity, the settling time to steady state increases to over 200 s. The response for the hardening cubic stiffness is shown in Fig. 15. Comparing Figs. 15 and 7 shows that for the linear system, the flutter speed reaches a steady state within 50 s, whereas for the hardening cubic stiffness the limit cycle oscillations are not reached until approximately 220 s. The hardening effect on the system with cubic stiffness increases the transient response time. The cubic stiffness increases the magnitude of the response to approximately 1 radian compared to $10^{-4}$ for the free-play and linear responses. This is due to the nature of the nonlinearity, since cubic nonlinearities derive from large amplitude oscillation of flexible wings [20]; however this order of magnitude is physically admissible as control surfaces are typically limited to $30^{\circ }$. The bifurcation plot of the hot system with a hardening cubic stiffness, Fig. 16 (top), displays this behaviour. The corresponding cold bifurcation plot is shown in Fig. 16 (bottom). There is a reduction in the speed at which limit cycle oscillations occur. A drop in the number of harmonics that are excited is observed at any given speed over which limit cycle oscillations are present. The drop in excited harmonics is especially evident at the start of the bifurcation. The effect of heat is to dampen out the higher harmonics, to reduce the rate of growth of the limit cycles as airspeed increases and to reduce the flutter boundary. This was shown for the free-play nonlinearity by comparing Fig. 9 (top) and (bottom) and is made more clear in the cubic nonlinearity by comparing Fig. 16 (top) and (bottom).

Fig. 15

Response of heated cubic structural stiffness at an airspeed of 1903 ms$^{-1}$

Fig. 16

Bifurcation plot for hardening cubic structural stiffness, hot system (top) cold system (bottom)

As a comparison, a system with a softening cubic stiffness was modelled. The softening effect tends to promote the onset of flutter [12]. However this was not observed as the system underwent limit cycle oscillations, as shown in Fig. 17. A stable Hopf limit cycle branch, which increases in limit cycle magnitude with an increase in the airspeed, is present due to the effect of heat on the structure. As shown before, the heat tends to dampen out the effect of instabilities and in this case creates a stable limit cycle branch instead of a subcritical unstable branch following bifurcation. By comparing Figs. 16 (top) and 17 the limit cycles remain constant for the hardening cubic stiffness; however the amplitude increases with flight velocity for softening. The softening cubic stiffness also shows a noticeable shift in the amplitude bounds for the limit cycle oscillations at higher speeds, see Fig. 17. This shift is a second oscillation between two bounds as indicated in Fig. 18. This shift is not observed in the hardening cubic stiffness case (Fig. 15). The softening of the stiffness nonlinearity normally drives the response to an unstable solution; however the heating dampens this out until instability occurs. This is why the limit cycle oscillations grow in magnitude until the onset of flutter (Fig. 17). At the higher speeds, two bifurcations exist, shown in Fig. 17, with bounded magnitudes of $0.5/0.6$ to $-0.4/{-}0.3$ radians and $-0.5/{-}0.6$ to $0.4/0.3$ radians. These bifurcations co-exist, i.e. at a speed greater than 1998 ms$^{-1}$ the wing can oscillate between either bound.

Fig. 17

Bifurcation plot for softening cubic structural stiffness, hot system

Fig. 18

Response for heated softening cubic structural stiffness, at 2015 ms$^{-1}$ (top) at 2013 ms$^{-1}$ (bottom)

The type of stiffness nonlinearity present within the system has a large effect on the response. For bilinear and free-play nonlinearities the response becomes complex and the speeds at which limit cycle oscillations occur are increased, delaying instability. Comparatively cubic nonlinearities increase the magnitude of the response; however they do not produce as chaotic responses as the bilinear and free-play nonlinearities. The next section will analyse the effects of a nonlinearity in the aerodynamics.

3.3 Nonlinear aerodynamics

The previous sections have only used the first-order terms of piston theory aerodynamics. Therefore this section looks at the impact of the nonlinear aerodynamic terms on the response of the three-degree-of-freedom system. Previous studies [1] have looked at the effect of the nonlinear aerodynamic terms on a two-dimensional system. This section extends that analysis to a wing with three degrees of freedom. Figure 19 shows the restoring force of the nonlinear aerodynamics on the system. As is expected the restoring force exhibits a cubic nature. The figure also highlights the hysteretic behaviour of the aerodynamics, since the curve follows a different path with increasing restoring force compared to decreasing.

Fig. 19

The restoring force due to the nonlinear aerodynamics

3.3.1 Nonlinear aerodynamics with linear structural stiffness

To isolate the effect of the nonlinear aerodynamics and understand its influence, the nonlinear aerodynamics are applied to a system without additional complexities. The nonlinear aerodynamics have an equivalent cubic softening effect, resulting in a quicker response time and delaying instability. Figure 20 shows the bifurcation plot for the nonlinear aerodynamic system. As can be seen from Fig. 20 the amplitude of the response increases with increasing flight velocity. Figure 20 shows the increase in the response amplitudes at the higher velocities, similar to the softening stiffness nonlinearity (Fig. 17).

Fig. 20

Bifurcation plot for the nonlinear aerodynamics, hot system

Fig. 21

Response for the system with nonlinear aerodynamics at an airspeed of 1925 ms$^{-1}$

The effect of the nonlinear aerodynamics is demonstrated in Fig. 21. The time before limit cycle oscillations occur is dramatically reduced for the system with nonlinear aerodynamics as seen by comparing Fig. 21 with Figs. 15 (cubic hardening response) and 7 (linear response).

3.3.2 Coupled nonlinear aerodynamics and nonlinear structural dynamics

Here the nonlinear aerodynamics are coupled with the free-play nonlinear stiffness and the steady-state heat model. The velocity at which the limit cycle oscillations begin to occur is increased from 1901 to 1905 ms$^{-1}$. This is shown in the bifurcation plot of Fig. 22. The response decays until a velocity of 1905 ms$^{-1}$ is attained (Fig. 22), the bifurcation speed. By comparing Figs. 22 and 20 after the bifurcation velocity (1905 ms$^{-1}$) the curves are identical. Figure 22 has the characteristic jump at bifurcation associated with piecewise nonlinearities. The magnitude of the response for the nonlinear structural system is low compared to the nonlinear aerodynamics system for these velocities. Therefore at higher speeds the nonlinear aerodynamics dominate the response of the system.

Fig. 22

Bifurcation plot for the system with nonlinear aerodynamics and structural dynamics, hot system

3.4 Sensitivity of response to initial conditions

Previous work on two-dimensional systems indicated that the speed at which the limit cycle oscillations begin is heavily dependent on the initial conditions [38]. The final part of this work is to determine the sensitivity of the initial conditions for the three-degree-of-freedom system. An initial displacement is enforced in the control degree of freedom ($\beta$) to start the time-marching simulations, and the responses are analysed.

Fig. 23

Bifurcation plot for the hot system with cubic stiffness and an initial displacement ($\beta (0) = 1^{\circ }$)

First, a nonlinear cubic stiffness is analysed. The onset speed for the limit cycle oscillations is unchanged; however the early limit cycle oscillation magnitudes are increased when the magnitude of the initial condition is increased. This is illustrated in Fig. 23. By comparing Fig. 16 with Fig. 23 ($\beta (0) = 0^{\circ }$) it can be seen that the speed at which limit cycle oscillations begin to occur is identical. The system is able to dampen out the response due to the initial condition before the LCOs occur. As mentioned in Sect. 3.2.3 the hardening effect of the cubic stiffness increases the time at which the LCOs occur. Therefore the system has more time to remove the effect of any transient behaviour in the system due to the initial condition.

For a free-play stiffness the effect of the initial condition is, on the other hand, to reduce the speed at which the limit cycle oscillations begin. This decreases the flutter speed, creating a less dynamically stable system. This is demonstrated in Fig. 24. With an initial displacement, the response of the system appears to be chaotic in nature, and the LCO onset speed is reduced.

Fig. 24

Bifurcation plot for the hot system with free-play stiffness and an initial displacement ($\beta (0) = 1^{\circ }$)

Fig. 25

Decay and flutter boundary for varying initial conditions with bilinear stiffness, hot system

A sensitivity analysis on the system with a bilinear and free-play stiffness is given in Figs. 25 and 26, respectively. Control deflections of $-5^{\circ } \le \delta \le 5^{\circ }$ were applied, and the response was analysed. Figure 25 shows how the response with a bilinear stiffness varies with control surface deflection. The flutter boundary varies significantly with an initial input in the control deflection, decreasing from 1915 to 1912 ms$^{-1}$ for all control inputs, suggesting that adding a control input has a destabilising effect regardless of the magnitude. As the initial deflection is increased, the speed at which the system decays is reduced. This is in agreement with Tang and Dowell [38].

Fig. 26

Decay and flutter boundary for varying initial conditions with free-play stiffness, hot system

Figure 26 shows how the response with a free-play stiffness varies with control deflection. For the system with a free-play stiffness, the flutter boundary varies depending on the control input (Fig. 26), where the larger the control input, the lower the flutter boundary. The sensitivity plot is not symmetric, meaning that control inputs of the same magnitude but opposite direction do not give the same response. For the free-play stiffness at certain control deflections, the system can swap between a decaying response and a LCO as the airspeed is increased. This is shown in Fig. 26 by the triangles and circles that appear after the decay line, indicating small zones where the system is decaying.

The above results show that having an initial displacement affects the response of the system, through increased chaotic responses and reduced speeds at which LCOs occur. It was shown that due to the hardening effect of the cubic stiffness on the system, the response to a cubic nonlinearity is less affected by initial conditions as it dampens out the response.

4 Conclusions

The aeroelastic response of a three-degree-of-freedom hot wing with a control surface and stiffness nonlinearity has been determined. Three different types of stiffness nonlinearity have been considered: free-play, bilinear and cubic nonlinearities. Aerodynamic nonlinearities arising from piston theory have also been analysed. The resulting equations of motion were solved using a variable step Runge–Kutta method.

For both free-play and cubic nonlinearities, limit cycle oscillations occurred after the flutter speed of the linear system for the hot structure. For the free-play nonlinearity the resulting motion became quasi-periodic. The cubic stiffness nonlinearity contributes a hardening effect to the system; consequently the time at which the limit cycle oscillations become fully developed is increased. The cubic stiffness increased the magnitude of the response significantly; however it excited less harmonics compared to the free-play nonlinearity.

The nonlinear aerodynamics had a softening effect on the structure. This reduced the time required for the limit cycle oscillations to occur. Furthermore, the magnitude of the limit cycle oscillations increased with airspeed.

Finally it was shown that the system is sensitive to initial conditions. Adding an initial control deflection reduced the velocities at which limit cycle oscillations occurred. The initial conditions had the effect of creating a chaotic response. The results presented here add to the work done where chaotic motion and limit cycle oscillations were predicted for a two-dimensional aerofoil with stiffness nonlinearities [15, 33, 38, 50] or aerodynamic nonlinearities [2].