Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets

Abstract

In this paper, a robust continuous guidance law with terminal angle constraint for intercepting maneuvering targets in the presence of autopilot lag is proposed and its finite-time stability is proved. First, assuming that the missile autopilot is sufficiently fast, a composite fast nonsingular terminal sliding mode guidance (CFNTSMG) law is presented. The proposed guidance law is obtained through a combination of fast nonsingular terminal sliding mode control theory and generalized disturbance observer (GDOB). The presented guidance law requires no priori information on target maneuver, which is estimated and compensated online by GDOB. Moreover, no discontinuous term exists in CFNTSMG law and therefore chattering is eliminated effectively. Next, viewing the missile autopilot as an uncertain second-order system, an integrated guidance and control dynamics is formulated and the systematic step-by-step backstepping technique is used to derive a new robust guidance law, which not only holds the advantages of CFNTSMG law, but also is insensitive to autopilot lag. At each backstepping step, novel continuous virtual/real control laws using finite-time control approach are designed and tracking differentiator is used to overcome the ‘explosion of complexity’ problem encountered with traditional backstepping method. Theoretical analysis and numerical simulations demonstrate the effectiveness of the proposed method.

1 Introduction

Proportional navigation guidance (PNG) law has been widely used in missile guidance during the last few decades due to its easy implementation and efficiency for stationary as well as weakly maneuverable targets [1–4]. PNG law issues a missile acceleration command proportional to the inertial line of sight (LOS) angular rate [4]. For the task of intercepting a maneuverable target, however, the performance of PNG law degrades drastically with the increase in target available maneuverability [5]. As for the progress of homing guidance in recent years, controlling the terminal impact angle of a guided missile attracts great attention among control engineers [3, 5–17, 22, 23, 25, 28] since it can improve the overall interception performance, for instance, increasing kill probability, improving penetration capabilities, and reducing the warhead size[6]. Such a requirement is quite important for tactical missiles when intercepting large ships, tanks, ballistic missiles as well as maneuvering aircrafts [7].

Various optimal guidance (OG) laws have been proposed to impose a predefined terminal angle. In [8], a suboptimal guidance law to control the intercept angle was derived for a ballistic reentry vehicle to intercept a non-maneuvering target. Using Swhwartz inequality, a trajectory shaping guidance (TSG) law for imposing an impact angle was proposed in [3] and its analytical solution for first-order lag dynamic system was given in [9]. In order to improve the overall performance of original TSG, a nth-order time-to-go weighted energy cost function is adopted as a performance index [10, 11] to derive OG laws. Reference [12] extends the same formulation to a constant maneuvering target. As OG laws require large control effort at the initial time of terminal guidance phase [3, 8–12], a sinusoidal function weighted OG law was proposed in [13] for the purpose of acceleration command shaping. Although OG laws exhibit good overall performance, these laws need accurate information on target accelerations when intercepting maneuvering targets. Furthermore, time-to-go estimation is another formidable challenge that limits the practical implementation of such OG laws [7].

To enhance the interception performance by minimizing miss distance while imposing a desired terminal angle, sliding mode control (SMC) theory is another powerful tool that can be used to design guidance laws. Based on inertial delay control (IDC) technique, the authors in [14] presented a novel robust second-order SMC-based guidance law to satisfy the terminal LOS angle constraint. Combining backstepping technique and SMC, an impact angle and impact time constraint guidance law was presented in [15] to intercept non-maneuvering targets via LOS angular rate shaping method. Using similar approach as shown in [15], an impact angle constraint guidance law was proposed in [16] for unpowered lifting reentry vehicles against stationary targets. In [17], a SMC-based guidance law that enables imposing a desired terminal angle was presented and its applications in head-on, tail-chase and head-pursuit interception engagement were analyzed.

Note that the above-mentioned guidance laws are Lipshitz continuous and only concern the asymptotic or exponential stability. Besides faster convergent rate, the systems under finite-time convergent (FTC) control laws usually exhibit smaller steady-state tracking errors and better robustness against external disturbance as well as model uncertainty [18, 19]. Moreover, the missile flight time during the terminal guidance phase is generally quite short. For instance, in a space interception, where an agile surface-to-air or air-to-air missile is required to intercept a fast-moving ballistic target, sometimes the lasting time is only several seconds. Consequently, designing guidance laws with finite-time convergence is more desirable [5, 20]. To achieve finite-time stability, terminal sliding mode (TSM) [21]-based guidance laws [7, 22, 23] are some notable works. However, these guidance laws have inherent singularity problem due to the principle of TSM. To avoid this drawback, a nonsingular terminal sliding mode (NTSM) [24]-based guidance law with terminal angle constraint was proposed in [25] to intercept maneuvering targets. This reference, however, has two main limitations: (1) the chattering problem; (2) requiring information on the upper bound of target maneuver. In reality, the target acceleration bound cannot or only very conservative bound can be obtained in advance due to the complexity of the unpredictable target maneuver profiles. Therefore, to guarantee stability of the predefined sliding variable dynamics, a quite large switching gain should be selected, which in turn will increase energy consumption and worsen the undesired chattering phenomenon. Generally, guidance laws that require the upper bound of target maneuver are not practical.

In practical interceptions, the missile autopilot lag always exists and would exhibit significant bad influence on the precision of guidance, especially in the presence of target maneuvers [26–29]. To this end, it is necessary to consider autopilot dynamics in guidance law design to improve the performance of the overall guidance and control system. In [28], the authors studied a dynamic surface control-based impact angle constraint guidance law in the presence of autopilot lag. But the upper bound of target maneuver is still needed and only asymptotical stability is concerned.

To overcome the two mentioned problems of the existing NTSM-based guidance scheme and enhance the guidance performance in the presence of autopilot lag, this paper has presented a new composite guidance law with terminal angle constraint for intercepting maneuvering targets. First, assuming that the autopilot is sufficiently fast, a CFNTSMG law is proposed by using FNTSM control approach [32, 33] and GDOB technique [31]. By effective real-time estimation of GDOB, the proposed CFNTSMG law requires no information on target maneuver and is capable of real implementation. Since no discontinuous term exists, the proposed guidance law is continuous, and therefore chattering is mitigated effectively. Furthermore, time-to-go estimation is also not needed for implementing the proposed guidance law. With the aid of Lypunov method, the finite-time stability of the closed-loop guidance system is established in theory. Next, in order to raise the guidance precision in the presence of autopilot lag, the CFNTSMG law with autopilot lag (CFNTSMGAL), which takes the autopilot dynamics into consideration, is proposed using finite-time control approach and backstepping technique. Moreover, TD is used to avoid repeated analytic differentiation at each backstepping step. Finally, simulations with some comparisons are presented to demonstrate the excellent property of the new guidance law.

The outline of this paper is organized as follows. Section 2 gives some preliminary concepts. In Sect. 3, the presented CFNTSMG law is presented for lag-free missiles. The proposed CFNTSMGAL law is provided in Sect. 4. Finally, some simulation results and conclusions are offered.

2 Preliminary concepts

2.1 Problem formulation

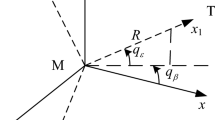
The 2D planar homing engagement geometry between the missile and the target is depicted in Fig. 1, where the subscripts M and T denote the missile and the target, $\gamma _\mathrm{M}$ and $\gamma _\mathrm{T}$ the missile and the target flight path angle, $\lambda$ and $r$ the LOS angle and the missile–target relative range, $V_\mathrm{M}$ and $V_\mathrm{T}$ the missile and the target velocity, and $a_\mathrm{M}$ and $a_\mathrm{T}$ the missile and the target acceleration, which are assumed normal to their corresponding velocities, respectively.

Fig. 1

Homing engagement geometry

Assume that the missile and the target are point masses moving in the plane with constant velocities. The corresponding equations describing the missile–target relative motion dynamics are formulated as

$$\begin{aligned}&{\dot{r}}=V_\mathrm{T} \cos (\gamma _\mathrm{T} -\lambda ) -V_\mathrm{M} \cos (\gamma _\mathrm{M}-\lambda )\end{aligned}$$

(1)

$$\begin{aligned}&{\dot{\lambda }}=\frac{1}{r}\left[ {V_\mathrm{T} \sin \left( {\gamma _\mathrm{T} -\lambda } \right) -V_\mathrm{M} \sin \left( {\gamma _\mathrm{M} -\lambda }\right) }\right] \end{aligned}$$

(2)

$$\begin{aligned}&\dot{\gamma }_\mathrm{M} =\frac{a_\mathrm{M}}{V_\mathrm{M}}\end{aligned}$$

(3)

$$\begin{aligned}&\dot{\gamma }_\mathrm{T} =\frac{a_\mathrm{T}}{V_\mathrm{T}} \end{aligned}$$

(4)

Differentiating Eqs. (1) and (2) with respect to time yields

$$\begin{aligned} \ddot{r}= & {} r{\dot{\lambda }}^{2}+a_{\mathrm{T}r} -a_\mathrm{M} \sin ({\lambda -\gamma _\mathrm{M}})\end{aligned}$$

(5)

$$\begin{aligned} \ddot{\lambda }= & {} -\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{a_{\mathrm{T}\lambda }}{r}-\frac{a_\mathrm{M} \cos (\lambda -\gamma _\mathrm{M})}{r} \end{aligned}$$

(6)

where $a_{\mathrm{T}r} \buildrel \varDelta \over = a_\mathrm{T} \sin (\lambda -\gamma _\mathrm{T}), a_{\mathrm{T}\lambda } \buildrel \varDelta \over = a_\mathrm{T} \cos (\lambda -\gamma _\mathrm{T})$ denote the target and the missile acceleration along and normal to the LOS, respectively.

Assumption 1

[5, 20] During the time horizon of terminal guidance phase, there exist two positive constants $r_{\min }, r_{\max }$ such that $r_{\min } <r<r_{\max }$.

Usually, the acceleration along to missile’s velocity cannot be controlled in terminal guidance phase [5, 28], and therefore only the relative two-degree dynamics between the control input $a_\mathrm{M}$ and the LOS angle $\lambda$, i.e., Eq. (6), is used to design missile guidance laws. Based on Eq. (6), it is easy to verify that the scenarios $\lambda -\gamma _\mathrm{M} =\pm \, \pi /2$, which lead to $\cos (\lambda -\gamma _\mathrm{M})=0$, are singular cases. Under such conditions, the missile has no ability to regulate the LOS angular rate. However, it has been proved in [7] that $\lambda -\gamma _\mathrm{M} =\pm \, \pi /2$ are not stable equilibrium points and hence the guidance system trajectory just across the points $\lambda -\gamma _\mathrm{M} =\pm \, \pi /2$ and will not stay on them. Consequently, the lateral acceleration $a_\mathrm{M}$ can be used to control $\lambda$. Moreover, due to physical limits, the missile achieved acceleration is always bounded and will not go to infinity. Furthermore, in order to remove the dependence of the guidance law on the term $\cos (\lambda -\gamma _\mathrm{M})$, a new variable is introduced as follows

$$\begin{aligned} h=a_\mathrm{M} +a_{\mathrm{T}\lambda } -a_\mathrm{M} \cos (\lambda -\gamma _\mathrm{M}) \end{aligned}$$

(7)

Then, the LOS angular rate dynamics (6) can be rewritten as

$$\begin{aligned} \ddot{\lambda }=-\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{h}{r}-\frac{a_\mathrm{M}}{r} \end{aligned}$$

(8)

Assumption 2

The lumped uncertainty $h$ is piecewise continuous and satisfies

$$\begin{aligned} \left| {\frac{\mathrm{d}^{r}h}{\mathrm{d}t^{r}}}\right| \le \sigma \end{aligned}$$

(9)

where $r$ is a positive integer and $\sigma$ is a positive constant.

Remark 1

The uncertainties considered above can cover many kinds of target maneuvers, for example, constant maneuver, ramp maneuver, periodic maneuver, and higher-order maneuver. It may be noted that it is not required to know the bound $\sigma$.

Let $e=\lambda -\lambda ^{{*}}$ be the LOS angle error, where $\lambda ^{{*}}$ denotes the desired terminal LOS angle. Noting that ${\dot{e}}={\dot{\lambda }}$, then the error dynamics is obtained as

$$\begin{aligned} \ddot{e}=-\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{h}{r}-\frac{a_\mathrm{M}}{r} \end{aligned}$$

(10)

By accepting the intuition that zeroing the LOS angular rate will lead to a perfect interception, the control interest here is to design a guidance law such that both $e$ and ${\dot{e}}$ will converge to a small region around zero in finite time.

2.2 Some lemmas

Before giving the design results, some lemmas, which play important role in the subsequent analysis, are recalled here for convenience.

Lemma 1

[30] Suppose $V(x)$, defined on $U\subset R^{n}$, is a $C^{1}$ smooth positive definite function and $\dot{V}(x)+\beta _1 V^{\eta }(x)+\beta _2 V(x)$ is a negative semi-definite function on $U\subset R^{n}$ for $\eta \in (0,1)$ and $\beta _1 ,\beta _2 \in R^{+}$, then there exists an area $U_0 \subset R^{n}$ such that any $V(x)$ which starts from $U_0 \subset R^{n}$ can reach $V(x)\equiv 0$ in finite time $T_\mathrm{{reach}}$, which is given by

$$\begin{aligned} T_\mathrm{reach} \le \frac{1}{\beta _2 ({1-\eta })}\ln \left[ {\frac{\left( {V^{1-\eta }({x_0})+\beta _1}\right) }{\beta _1}}\right] \end{aligned}$$

(11)

where $V(x_0)$ is the initial value of $V(x)$.

Lemma 2

[30] Suppose $a_1, a_2, \ldots , a_n$ and $0<p<2$ are all positive constants, then the following inequality holds

$$\begin{aligned} ({a_1^2 +a_2^2 +\ldots +a_n^2})^{p}\le ({a_1^p +a_2^p +\ldots +a_n^p})^{2}\nonumber \\ \end{aligned}$$

(12)

3 Design of CFNTSMG

In this section, the proposed CFNTSMG law is presented using FNTSM control theory and GDOB method in the absence of missile autopilot dynamics. The finite-time stability of the closed-loop guidance system is also provided.

3.1 Generalized DOB design

Through some simple manipulations, Eq. (8) can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}({r{\dot{\lambda }}})}{\mathrm{d}t}=-{\dot{r}}{\dot{\lambda }}+h-a_\mathrm{M} \end{aligned}$$

(13)

Motivated by the study of [31], we propose the following GDOB to estimate the lumped uncertainty $h$ in Eq. (13)

$$\begin{aligned} \hat{{h}}^{({j-1})}=\omega _j +l_j r{\dot{\lambda }}, \quad j=0,1,2,\ldots ,r \end{aligned}$$

(14)

where $\hat{{h}}^{(j-1)}$ denotes the estimation of the $(j-1)$th time derivative of $h, l_j >0$ are the observer gains to be designed, and the auxiliary variables $\omega _j$ are defined as

$$\begin{aligned} \dot{\omega }_j= & {} -l_j \left[ {-{\dot{r}}{\dot{\lambda }}-a_\mathrm{M} +\hat{{h}}}\right] +\hat{{h}}^{(j)},\quad \nonumber \\&j=0,1,2,\ldots ,(r-1) \nonumber \\ \dot{\omega }_r= & {} -l_r \left[ {-{\dot{r}}{\dot{\lambda }}-a_\mathrm{M} +\hat{{h}}}\right] \end{aligned}$$

(15)

It follows from Eqs. (14) and (15) that

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\left[ {\hat{{h}}^{(j-1)}}\right] =l_j \tilde{h}+\hat{{h}}^{(j)},\quad j=1,2,\ldots ,r-1 \nonumber \\&\frac{\mathrm{d}}{\mathrm{d}t}\left[ {\hat{{h}}^{\left( {r-1}\right) }}\right] =l_r \tilde{h} \end{aligned}$$

(16)

Let $e_h =\left[ {\tilde{h},\tilde{\dot{h}},\ldots ,\tilde{h}^{(r-1)}}\right] ^{T}$, where $\tilde{h}^{(j)}=h^{(j)}-\hat{{h}}^{(j)}$, be the vector of the GDOB estimation errors. Then one can imply that

$$\begin{aligned} {\dot{e}}_h =Ae_h +Bh^{(r)} \end{aligned}$$

(17)

where

$$\begin{aligned} A=\left[ {{\begin{array}{ccccc} {-l_1}&{}\quad 1&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ {-l_2}&{}\quad 0&{}\quad 1&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {-l_{\left( {r-1}\right) }}&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 1 \\ {-l_r}&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ \end{array}}}\right] , \quad B=\left[ {{\begin{array}{l} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \\ \end{array}}}\right] \end{aligned}$$

(18)

Noting from the definition of $A$, one can easily conclude that the eigenvalues of $A$ can be placed arbitrarily by selecting the observer gains $l_j$ appropriately. Assume that $l_j$ are chosen such that all the eigenvalues of $A$ are placed in the left-half-plane (LHP), then there always exist definite matrices $P$ such that

$$\begin{aligned} A^{T}P+PA=-Q \end{aligned}$$

(19)

for any given positive definite matrices $Q$. The stability as well as performance of GDOB (14) are summarized in the following lemma.

Lemma 3

Under Assumption 2, the GDOB estimation errors are ultimately uniformly bounded (UUB) by

$$\begin{aligned} \Vert e_h\Vert \le \frac{2\sigma \Vert \mathrm{{PB}}\Vert }{\lambda _{\min } (Q)} \end{aligned}$$

(20)

Proof

See “Appendix 1”.

3.2 Guidance law design

In general, the sliding mode controller design consists of two main steps: sliding surface selection and sliding mode control law design. The sliding surface is chosen such that the closed-loop system has satisfactory dynamic behaviors on it while the control law is used to drive the scalar quantity defining the sliding surface to zero in finite time and maintain it thereafter, ultimately achieving exact tracking asymptotically or in finite time. It is known that the NTSM-based control law can afford superior overall properties such as higher precision and faster convergent rate compared with classical linear hyperplane-based sliding mode control [18]. However, traditional NTSM controller has slower convergent rate than linear SMC controller when the system trajectories are far away from the equilibrium points [32, 33]. In this paper, to intercept a maneuvering target at a desired terminal angle with fast convergent rate, a FNTSM surface, which consists of LOS angle tracking error and LOS angular rate, is designed as

$$\begin{aligned} s={\dot{e}}+\alpha _1 e+\alpha _2 \beta (e) \end{aligned}$$

(21)

where $\alpha _1$ and $\alpha _2$ are two positive constants and $\beta (e)$ is governed by

$$\begin{aligned} \beta (e)= & {} \left\{ {{\begin{array}{ll} e^{p/q}, &{}\quad \hbox {if }\bar{{s}}\!=\!0 \hbox { or }\,\bar{{s}}\!\ne \!0,|e|\!\ge \! \mu \\ b_1 e\!+\!b_2 \hbox {sgn}(e)e^{2}, &{}\quad \hbox {if }\,\bar{{s}}\!\ne \! 0,|e|\!<\!\mu \\ \end{array}}} \right. \nonumber \\ \end{aligned}$$

(22)

where $p$ and $q$ are two positive odd integers which satisfy that $1/2<p/q<1, b_1 =(2-p/q)\mu ^{p/q-1}, b_2 =(p/q-1)\mu ^{p/q-2}, \bar{{s}}={\dot{e}}+\alpha _1 e+\alpha _2 e^{p/q}, \mu$ is a small positive constant, and $\hbox {sgn}(\cdot )$ denotes the sign function. The first time derivative of the sliding surface (21) is given by

$$\begin{aligned} \dot{s}=\ddot{e}+\alpha _1 {\dot{e}}+\alpha _2 \dot{\beta } \end{aligned}$$

(23)

where $\dot{\beta }$ is defined as

$$\begin{aligned} \dot{\beta }= & {} \left\{ {{\begin{array}{ll} p/qe^{p/q-1}{\dot{e}}, &{}\quad \hbox {if}\,\bar{{s}}\!=\!0 \hbox { or }\bar{{s}}\!\ne \!0,|e|\ge \mu \\ b_1 {\dot{e}}+2b_2 \hbox {sgn}(e)e{\dot{e}}, &{}\quad \hbox {if}\,\bar{{s}}\!\ne \!0,|e|<\mu \\ \end{array}}} \right. \nonumber \\ \end{aligned}$$

(24)

Remark 2

[32] The choice of $b_1$ and $b_2$ is to make the function $\beta (e)$ and its time derivative continuous. Moreover, the preceding sliding manifold switches from traditional fast TSM to general sliding manifold to avoid singularity problem.

Lemma 4

Considering the LOS angle error dynamics (10) and FNTSM surface (21), if $s=\bar{{s}}=0$ is achieved, then the LOS angular rate and the LOS angle error will converge to zero in finite time.

Proof

See “Appendix 2”.

For sliding surface (21), we propose the following CFNTSMG law

$$\begin{aligned} \left\{ {{\begin{array}{l} a_\mathrm{M} =a_{\mathrm{M}1} +a_{\mathrm{M}2} \\ a_{\mathrm{M}1} =-\,2{\dot{r}}{\dot{\lambda }}+r\alpha _1 {\dot{e}}+r\alpha _2 \dot{\beta } \\ a_{\mathrm{M}2} =k_1 s+k_2 |s|^{\rho }\hbox {sgn}(s)+\hat{{h}} \\ \end{array}}} \right. \end{aligned}$$

(25)

where $k_1 ,k_2 >0, 0<\rho <1$ are design parameter.

Remark 3

It can be observed from Eq. (25) that the proposed guidance law is continuous $(|s|^{\rho }\hbox {sgn}(s)$ is a non-smooth but continuous function) and therefore the undesired chattering is avoided effectively.

3.3 Stability analysis

Theorem 1

Consider the LOS angle error dynamics (10), the sliding surface (21) with guidance law (25), then the sliding variable will converge to the region

$$\begin{aligned} \varOmega= & {} \left\{ |s|\left| |s|\le \varDelta =\min \left( \frac{2\sigma \Vert \mathrm{{PB}}\Vert }{k_1 \lambda _{\min } (Q)},\right. \right. \right. \nonumber \\&\quad \left. \left. \left( {\frac{2\sigma \Vert \mathrm{{PB}}\Vert }{k_2 \lambda _{\min } (Q)}}\right) ^{1/\rho }\right) \right\} \end{aligned}$$

(26)

where $\lambda _{\min } (Q)$ denotes the smallest eigenvalue of the matrix $Q$, in finite time. Furthermore, the LOS angle error and LOS angular rate will converge to the following regions

$$\begin{aligned}&|e|\le \kappa _e = \max \left\{ {\mu ,\frac{\varDelta }{2\alpha _1},\left( {\frac{\varDelta }{2\alpha _2}}\right) ^{q/p}} \right\} \end{aligned}$$

(27)

$$\begin{aligned}&|{{\dot{\lambda }}}|=|{{\dot{e}}}|\le \kappa _{{\dot{e}}} =\varDelta +\alpha _1 \kappa _e +\alpha _2 \kappa _e^{p/q} \end{aligned}$$

(28)

in finite time.

Proof

Considering $V_1 =0.5s^{2}$ as a Lyapunov function candidate for Eq. (21), evaluating the derivative of $V_1$ gives

$$\begin{aligned} \dot{V}_1= & {} s\dot{s}=s\left( {\ddot{e}+\alpha _1 {\dot{e}}+\alpha _2 \dot{\beta }}\right) \nonumber \\= & {} s\left( {-\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{h}{r}-\frac{a_\mathrm{M}}{r}+\alpha _1 {\dot{e}}+\alpha _2 \dot{\beta }}\right) \nonumber \\= & {} s\left[ {\frac{\tilde{h}}{r}-\frac{k_1}{r}s-\frac{k_2}{r}|s|^{\rho }\hbox {sgn}\left( s\right) }\right] \nonumber \\\le & {} \frac{|{\tilde{h}}|}{r}|s|-\frac{k_1}{r}s^{2}-\frac{k_2}{r}|s|^{\rho +1} \end{aligned}$$

(29)

which can be transformed into the following two forms

$$\begin{aligned} \dot{V}_1 \le -\frac{1}{r}\left( {k_1 |s|-|{\tilde{h}}|}\right) |s|-\frac{k_2}{r}|s|^{\rho +1} \end{aligned}$$

(30)

and

$$\begin{aligned} \dot{V}_1 \le -\frac{k_1}{r}s^{2}-\frac{1}{r}\left( {k_2 |s|^{\rho }-|{\tilde{h}}|}\right) |s| \end{aligned}$$

(31)

For Eq. (30), when $|s|>|{\tilde{h}}|/k_1$, one has

$$\begin{aligned} \dot{V}_1 \le -\frac{\bar{{k}}_1}{r}|s|-\frac{k_2}{r}|s|^{\rho +1}\le -\frac{\bar{{k}}_1}{r_{\max }}|s|-\frac{k_2}{r_{\max }}|s|^{\rho +1}\nonumber \\ \end{aligned}$$

(32)

where $\bar{{k}}_1 =k_1 |s|-|{\tilde{h}}|>0$. It follows from Eq. (32) and Lemma 1 that the finite-time stability criteria is satisfied when $|s|>|{\tilde{h}}|/k_1$, that is, the trajectory of the closed-loop system will converge to the region $\varOmega _1 =\left\{ {s\left| {|s|\le |{\tilde{h}}|/k_1} \right. } \right\}$ in finite time. Furthermore, since $\dot{V}_1 \left| {_{|s|=|{\tilde{h}}|/k_1}} \right. \le -k_2 \left( {|{\tilde{h}}|/k_1}\right) ^{\rho +1}/r_{\max } <0, \varOmega _1$ is a positively invariant set of the closed-loop guidance system, which means that $|s|\le |{\tilde{h}}|/k_1$ holds for all $t\in [t_1, t_2)$ if $|s({t_1})|\le |{\tilde{h}}|/k_1$. Similarly, for Eq. (31), one can also conclude that the region $\varOmega _2 =\left\{ {s\left| {|s|\le \left( {|{\tilde{h}}|/k_2}\right) ^{1/\rho }} \right. } \right\}$ can be reached in finite time. Invoking the definition of $e_h$, we have $|{\tilde{h}}|\le \Vert e_h\Vert$. Then, using Lemma 3 leads to the proof of (26).

Next, when $s$ enters the region $\varOmega$, for the case $|e|>\mu$, one has ${\dot{e}}+\alpha _1 e+\alpha _2 e^{p/q}=\phi , |\phi |\le \varDelta$. This expression can be rewritten as ${\dot{e}}+\left( {\alpha _1 -\frac{\phi }{2e}}\right) e+\left( {\alpha _2 -\frac{\phi }{2e^{p/q}}}\right) e^{p/q}=0$, which is still kept in the same form as $\bar{{s}}$ if $\alpha _1 >\phi /(2e)$ and $\alpha _2 >\phi /\left( {2e^{p/q}}\right)$. Then, according to Lemma 4, one can easily conclude that the LOS angle error will converge to the region $|e|\le \max \left\{ {\varDelta /({2\alpha _1}),\left[ {\varDelta /({2\alpha _2})}\right] ^{q/p}} \right\}$ in finite time. Combing the preceding equation with $|e|>\mu$ leads to the proof of Eq. (27). Furthermore, with the sliding mode dynamics (21) and Eq. (26), it shows that the LOS angular rate will converge to the region $|{{\dot{\lambda }}}|=|{{\dot{e}}}|\le |\phi |+\alpha _1 |e|+\alpha _2 |e|^{p/q}\le \kappa _{{\dot{e}}}$ in finite time. This completes the proof.

4 Design of CFNTSMGAL

In the above section, the CFNTSMG law is developed in the absence of missile autopilot dynamics. However, in practice, the acceleration command generated by guidance law is realized via missile autopilot, and the time lag between the acceleration command and the achieved acceleration always exists. Such time lag exhibits significant bad influence on the precision of guidance, and hence considering autopilot dynamics in guidance law design is necessary. As shown in the study of [4, 26, 28], the missile autopilot can be represented by the following uncertain second-order dynamics

$$\begin{aligned} \ddot{a}_\mathrm{M} =-2\xi _{a} \omega _{a} \dot{a}_\mathrm{M} -\omega _{a}^2 a_\mathrm{M} +\omega _{a}^2 a_\mathrm{c} +d_a \end{aligned}$$

(33)

where $a_\mathrm{M}$ is real achieved missile acceleration, $a_\mathrm{c}$ is the acceleration command generated from guidance law, $\xi _{a}$ and $\omega _{a}$ denote damping ratio and natural frequency of the missile autopilot, respectively, and $d_a$ denotes the modeling error and satisfies $|d_a|\le d_{a,\max }$, where $d_{a,\max }$ is a positive constant.

Let $x_1 =s, x_2 =a_\mathrm{M}$ and $x_3 =\dot{a}_\mathrm{M}$, then an integrated guidance and control model can be obtained as

$$\begin{aligned} \dot{x}_1= & {} -\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{h}{r}-\frac{x_2}{r}+\alpha _1 {\dot{e}}+\alpha _2 \dot{\beta } \nonumber \\ \dot{x}_2= & {} x_3 \nonumber \\ \dot{x}_3= & {} -2\xi _a \omega _a x_3 -\omega _a^2 x_2 +\omega _a^2 a_\mathrm{c} +d_a \end{aligned}$$

(34)

Based on the control objective mentioned in Sect. 2 and the results in Sect. 3, the control aim here is to design a control law $a_\mathrm{c}$ such that $x_1$ will converge to a small region around zero in finite time. It can be noted that the time-varying nonlinear system (34) is in a parametric strict feedback form and that backstepping technique is suitable to design a guidance law for this system. In this section, the design of the proposed CFNTSMGAL law is divided into the following three steps.

Step 1 Let $z_1 =x_1$, computing the first time derivative of $z_1$ gives

$$\begin{aligned} \dot{z}_1 =-\frac{2{\dot{r}}{\dot{\lambda }}}{r}+\frac{h}{r}-\frac{x_2}{r}+\alpha _1 {\dot{e}}+\alpha _2 \dot{\beta } \end{aligned}$$

(35)

For Eq. (35), we choose the following virtual control law

$$\begin{aligned} x_2^{*}= & {} -2{\dot{r}}{\dot{\lambda }}\!+\!r\alpha _1 {\dot{e}}\!+\!r\alpha _2 \dot{\beta }\!+\!k_1 z_1 \!+\!k_2 |z_1|^{\rho }\hbox {sgn}(z_1)\!+\!\hat{{h}}\nonumber \\ \end{aligned}$$

(36)

Step 2 Let $z_2 =x_2 -x_2^{*}$, evaluating the first time derivative of $z_2$ gives

$$\begin{aligned} \dot{z}_2 =x_3 -\dot{x}_2^{*} \end{aligned}$$

(37)

For Eq. (37), we choose the following virtual control law

$$\begin{aligned} x_3^{*} =\frac{z_1}{r}-\gamma _1 z_2 -\gamma _2 |z_2|^{\rho }\hbox {sgn}(z_2)+\dot{x}_2^{*} \end{aligned}$$

(38)

where $\gamma _1 ,\gamma _2 >0$ are design parameters.

Step 3 Let $z_3 =x_3 -x_3^{*}$, evaluating the first time derivative of $z_3$ gives

$$\begin{aligned} \dot{z}_3 =-2\xi _a \omega _a x_3 -\omega _a^2 x_2 +\omega _a^2 a_\mathrm{c} +d_a -\dot{x}_3^{*} \end{aligned}$$

(39)

Then, the real CFNTSMGAL acceleration command is obtained as

$$\begin{aligned} a_\mathrm{c}= & {} \omega _a^{-2} \left[ 2\xi _a \omega _a x_3 +\omega _a^2 x_2 +\dot{x}_3^{*} -z_2 -\delta _1 z_3 \right. \nonumber \\&\left. -\delta _2 |z_3|^{\rho }\hbox {sgn}(z_3)\right] \end{aligned}$$

(40)

where $\delta _1 ,\delta _2 >0$ are design parameters.

In reality, $\dot{x}_2^{*}$ and $\dot{x}_3^{*}$ may not be easily acquired due to the complicated forms of $x_2^{*}$ and $x_3^{*}$. Thus, TD [34] is introduced here as an alternative way to obtain the derivative of $x_2^{*}$ and $x_3^{*}$. Taking $x_2^{*}$ as an example, TD is defined as

$$\begin{aligned} \left\{ {{\begin{array}{l} \dot{\hat{{x}}}_2^{*} =\hat{{\dot{x}}}_2^{*} \\ \dot{\hat{{\dot{x}}}}_2^{*} =-r_0 \hbox {sgn}\left( {\hat{{x}}_2^{*} -x_2^{*} +\frac{\hat{{\dot{x}}}_2^{*} \left| {\hat{{\dot{x}}}_2^{*}}\right| }{2r_0}}\right) \\ \end{array}}} \right. \end{aligned}$$

(41)

where $r_0 >0$ is a design parameter and $\hat{{x}}_2^{*}$ and $\hat{{\dot{x}}}_2^{*}$ are the estimations of $x_2^{*}, \dot{x}_2^{*}$, respectively. For properly choosing $r_0, \hat{{x}}_2^{*}$ and $\hat{{\dot{x}}}_2^{*}$ will approach to $x_2^{*}$ and $\dot{x}_2^{*}$, respectively, as fast as possible.

Through the above three steps, the closed-loop guidance and control system can be transformed into the following form

$$\begin{aligned} \dot{z}_1= & {} \frac{\tilde{h}}{r}-\frac{z_2}{r}-\frac{k_1}{r}z_1 -\frac{k_2}{r}|z_1|^{\rho }\hbox {sgn}(z_1) \nonumber \\ \dot{z}_2= & {} \frac{z_1}{r}-\gamma _1 z_2 -\gamma _2 |z_2|^{\rho }\hbox {sgn}(z_2)+z_3 -\tilde{\dot{x}}_2^{*} \nonumber \\ \dot{z}_3= & {} -z_2 -\delta _1 z_3 -\delta _2 |z_3|^{\rho }\hbox {sgn}(z_3)+d_a -\tilde{\dot{x}}_3^{*} \end{aligned}$$

(42)

where $\tilde{\dot{x}}_2^{*} =\hat{{\dot{x}}}_2^{*} -\dot{x}_2^{*}$ and $\tilde{\dot{x}}_3^{*} =\hat{{\dot{x}}}_3^{*} -\dot{x}_3^{*}$ are the differentiator error. Due to the principle of TD, both $\tilde{\dot{x}}_2^{*}$ and $\tilde{\dot{x}}_3^{*}$ are bounded [34]. Suppose $\left| {\tilde{\dot{x}}_2^{*}}\right| \le \varepsilon _2$ and $\left| {\tilde{\dot{x}}_3^{*}}\right| \le \varepsilon _3$, where $\varepsilon _2 , \varepsilon _3$ are two positive constants.

Theorem 2

Consider system (42) with guidance law (40) and TD (51), then the trajectory of the closed-loop system will converge to the region

$$\begin{aligned}&\varTheta = \left\{ {z\left| {z_1 \in \varTheta _1 \cap z_2 \in \varTheta _2 \cap z_3 \in \varTheta _3} \right. } \right\} \nonumber \\&\varTheta _1 =\left\{ z_1 \left| |z_1|\le \min \left( \frac{2\sigma \Vert \mathrm{{PB}}\Vert }{k_1 \lambda _{\min } (Q)},\right. \right. \right. \nonumber \\&\quad \qquad \left. \left. \left( {\frac{2\sigma \Vert \mathrm{{PB}}\Vert }{k_2 \lambda _{\min } (Q)}}\right) ^{1/\rho }\right) \right\} \nonumber \\&\varTheta _2 =\left\{ {z_2 \left| {|z_2|\le \min \left( {\frac{\varepsilon _2}{\gamma _1},\left( {\frac{\varepsilon _2}{\gamma _2}}\right) ^{1/\rho }}\right) } \right. } \right\} \nonumber \\&\varTheta _3 =\left\{ z_3 \left| {|z_3|\le } \right. \min \left( \frac{|d_a|+\left| {\varepsilon _3}\right| }{\delta _1},\right. \right. \nonumber \\&\quad \qquad \left. \left. \left( {\frac{|d_a|+\left| {\varepsilon _3}\right| }{\delta _2}}\right) ^{1/\rho }\right) \right\} \end{aligned}$$

(43)

where $z=[z_1, z_2, z_3]^\mathrm{T}$, in finite time. Moreover, both the LOS angle error and the LOS angular rate will converge to a small region around zero in finite time.

Proof

Considering $V_2 =0.5z^\mathrm{T}z$ as a Lyapunov function candidate for system (42), differentiating $V_2$ with respect to time gives

$$\begin{aligned} \dot{V}_2= & {} z_1 \dot{z}_1 +z_2 \dot{z}_2 +z_3 \dot{z}_3 \nonumber \\= & {} z_1 \left[ {\frac{\tilde{h}}{r}-\frac{z_2}{r}-\frac{k_1}{r}z_1 -\frac{k_2}{r}|z_1|^{\rho }\hbox {sgn}\left( {z_1}\right) }\right] \nonumber \\&+\,z_2 \left[ {\frac{z_1}{r}-\gamma _1 z_2 -\gamma _2 |z_2|^{\rho }\hbox {sgn}(z_2)+z_3 -\tilde{\dot{x}}_2^{*}}\right] \nonumber \\&+\,z_3 \left[ {-z_2 -\delta _1 z_3 -\delta _2 |z_3|^{\rho }\hbox {sgn}\left( {z_3}\right) +d_a -\tilde{\dot{x}}_3^{*}}\right] \nonumber \\= & {} \frac{\tilde{h}z_1}{r}-\frac{k_1}{r}z_1^2 -\frac{k_2}{r}|z_1|^{\rho +1}-\gamma _1 z_2^2 -\gamma _2 |z_2|^{\rho +1}\nonumber \\&-\,z_2 \tilde{\dot{x}}_2^{*} -\delta _1 z_3^2 -\delta _2 |z_3|^{\rho +1}+d_a z_3 -z_3 \tilde{\dot{x}}_3^{*} \nonumber \\\le & {} \frac{\left| {\tilde{h}z_1}\right| }{r}-\frac{k_1}{r}z_1^2 -\frac{k_2}{r}|z_1|^{\rho +1}-\gamma _1 z_2^2 -\gamma _2 |z_2|^{\rho +1}\nonumber \\&+\left| {z_2 \tilde{\dot{x}}_2^{*}}\right| -\delta _1 z_3^2 -\delta _2 |z_3|^{\rho +1}+|d_a z_3|+\left| {z_3 \tilde{\dot{x}}_3^{*}}\right| \nonumber \\ \end{aligned}$$

(44)

When $z$ is out of the region $\varTheta$, using Lemma 2 and similar analysis as shown for Eqs. (31) and (32), Eq. (44) reduces to

$$\begin{aligned} \dot{V}_2\le & {} -\frac{\bar{{k}}_1}{r_{\max }}z_1^2 -\,\frac{\bar{{k}}_2}{r_{\max }}|z_1|^{\rho +1}-\bar{{\gamma }}_1 z_2^2 -\bar{{\gamma }}_2 |z_2|^{\rho +1}\nonumber \\&-\,\bar{{\delta }}_1 z_3^2-\bar{{\delta }}_2 |z_3|^{\rho +1} \nonumber \\\le & {} -\,\frac{\bar{{k}}_1}{r_{\max }}z_1^2 -\bar{{\gamma }}_1 z_2^2 -\bar{{\delta }}_1 z_3^2 -\frac{\bar{{k}}_2}{r_{\max }}|z_1|^{\rho +1}\nonumber \\&-\,\bar{{\gamma }}_2 |z_2|^{\rho +1}-\bar{{\delta }}_2 |z_3|^{\rho +1} \nonumber \\\le & {} -\,\min \left\{ {\frac{\bar{{k}}_1}{r_{\max }},\bar{{\gamma }}_1 ,\bar{{\delta }}_1} \right\} \left( {z_1^2 +z_2^2 +z_3^2}\right) \nonumber \\&-\,\min \left\{ {\frac{\bar{{k}}_2}{r_{\max }},\bar{{\gamma }}_2 ,\bar{{\delta }}_2} \right\} \left( |z_1|^{\rho +1}+|z_2|^{\rho +1}\right. \nonumber \\&\left. +\,|z_3|^{\rho +1}\right) \nonumber \\\le & {} -\,c_1 V_3 -c_2 V_3^{(\rho +1)/2} \end{aligned}$$

(45)

where $c_1 =2\min \left\{ {\bar{{k}}_1 /r_{\max } ,\bar{{\gamma }}_1 ,\bar{{\delta }}_1} \right\} , c_2 =2^{(1+\rho )/2}\min \left\{ {\bar{{k}}_2 /r_{\max } ,\bar{{\gamma }}_2 ,\bar{{\delta }}_2} \right\}$ and $\bar{{k}}_1 ,\bar{{k}}_2 ,\bar{{\gamma }}_1 ,\bar{{\gamma }}_2 ,\bar{{\delta }}_1 ,\bar{{\delta }}_2$ are positive constants. According to Lemma 1, the trajectory of the closed-loop system will converge to the region $\varTheta$ in finite time.

When $s=z_1$ converges to the region $\varTheta _1$, using the results shown in the proof of Theorem 1, one can easily prove that both the LOS angle error and the LOS angular rate will converge to a small region around zero in finite time. This completes the proof.

Remark 4

Furthermore, when $|{z_i}|>1\,(i=1,2,3)$, the linear term $z_i$ will dominate over the corresponding nonlinear term $|{z_i}|^{\rho }\hbox {sgn}(z_i)$ that yields faster asymptotic convergence and the nonlinear term $|{z_i}|^{\rho }\hbox {sgn}(z_i)$ will dominate over the corresponding linear term $z_i$ that yields faster finite-time convergence when $|{z_i}|\le 1$.

5 Simulation studies

In this section, a surface-to-air interceptor is considered in its terminal guidance phase against a maneuvering target. The simulation parameters are given as: (1) missile’s initial position $x_\mathrm{M} (0)=0\,\hbox {m}, y_\mathrm{M} (0)=0\,\hbox {m}$; (2) target’s initial position $x_\mathrm{T} (0)=10{,}000\,\hbox {m}, y_\mathrm{T} (0)=10{,}000\,\hbox {m}$; (3) missile’s velocity $V_\mathrm{M} =500\,\hbox {m/s}$; (4) target’s velocity $V_\mathrm{T} =250\,\hbox {m/s}$; (5) missile’s initial flight path angle $\gamma _\mathrm{M} (0)=\pi /12\,\hbox {rad}$; (6) target’s initial flight path angle $\gamma _\mathrm{T} (0)=\pi \,\hbox {rad}$; (7) desired terminal LOS angle $2\pi /9\,\hbox {rad}$; (8) autopilot parameters are $\xi _a =0.8, \omega _a =10\,\hbox {rad/s}, d_a =10\,\%$ $\omega _a^2 a_\mathrm{c}$; (9) upper bound of missile’s achieved acceleration 200 $\text{ m/s }^{2}$. To test the performance of the proposed guidance law, two different target maneuvers are considered. Case 1: The target performs sudden maneuvers as shown in Fig. 2. Case 2: The target performs weaving maneuvers as $a_\mathrm{T} =80\sin (\pi /10t)\,\hbox {m/s}^{2}$.

Fig. 2

Target maneuver profile in case 1

The design parameters for implementing CFNTSMG and CFNTSMGAL are set as $\alpha _1 =1.5, \alpha _2 =1.5, p=5, q=3, \mu =0.03, k_1 =100, k_2 =400, \rho =0.5, \gamma _1 =\gamma _2 =\delta _1 =\delta _2 =100$. To estimate the lumped uncertainty, a second-order GDOB with zero initial values is used, and all poles of the GDOB are placed at $-10$, that is, $l_1 =20, l_2 =100$. A TD with $r_0 =30$ and zero initial values is adopted to estimate the time derivatives of the virtual control laws.

For better illustration, the finite-time convergent guidance (FTCG) law [5] and the NTSM guidance (NTSMG) law [25] are also employed in simulations for the purpose of comparisons, where the FTCG law is defined as

$$\begin{aligned} a_\mathrm{M} =-N{\dot{r}}{\dot{\lambda }}+f\hbox {sgn}({{\dot{\lambda }}})+\beta |s|^{\eta }\hbox {sgn}({{\dot{\lambda }}}) \end{aligned}$$

(46)

where $N=const>2, f,\beta >0, 0<\eta <1$. The parameters are selected as $N=3, f=80, \beta =30, \eta =0.5$. The NTSMG law is defined as

$$\begin{aligned} a_\mathrm{M}=-2{\dot{r}}{\dot{\lambda }}+\frac{r\kappa }{\alpha }|{{\dot{e}}}|^{2-\alpha } \hbox {sgn}({{\dot{e}}})+K\hbox {sgn}(s) \end{aligned}$$

(47)

where $s=e+b|{{\dot{e}}}|^{\alpha }\hbox {sgn}({{\dot{e}}}), \kappa ,b,K>0, 1<\alpha <2$. The parameters are selected as $\kappa =1, b=1.5, K=400, \alpha =1.5$. From Eqs. (46) and (47), it can be observed that undesired chattering will be excited from the discontinuous terms $f\hbox {sgn}({{\dot{\lambda }}})$ and $K\hbox {sgn}(s)$. To address this problem, the saturation function $\hbox {sat}(x)$ is used to replace the discontinuous sign function, where

$$\begin{aligned} \hbox {sat}(x)=\left\{ {{\begin{array}{l} {\hbox {sgn}(x),\quad |x|>\varepsilon } \\ {x/\varepsilon ,\quad |x|\le \varepsilon } \\ \end{array}}} \right. \end{aligned}$$

(48)

where $\varepsilon$ is a small positive constant and is selected as $0.005$ in simulations.

The simulation results including the 2D interception trajectories, missile achieved accelerations, sliding variable profiles, LOS angle profiles, LOS angular rate profiles, GDOB estimations, obtained by FTCG, NTSMG, CFNTSMG and CFNTSMGAL, are depicted in the following figures. Figure 3 is for case 1, and Fig. 4 is for case 2. The miss distances and interception time obtained by these four different guidance laws under these two cases are summarized in Tables 1 and 2. As shown in Figs. 3a and 4a, the interceptions are achieved at some extent under these four guidance laws. The miss distances obtained by FTCG, NTSMG and CFNTSMG laws, however, are larger than that of CFNTSMGAL law. The reason is that the proposed CFNTSMGAL law can compensate for autopilot lag while FTCG, NTSMG and CFNTSMG laws cannot. Since FTCG law only concerns to regulate the LOS angular rate to zero in finite time, it cannot be used to control the terminal angle (see Figs. 3d and 4d). One can further observe in Figs. 3e and 4e that the performance of the proposed CFNTSMGAL law in driving the LOS angular rate to zero is superior to that of other three guidance laws. From Figs. 3f and 4f, it can also be noted that the GDOB can track the real uncertainty quite faithfully. It should be pointed out one can obtain better transient and estimation performance by using higher-order GDOB.

Fig. 3

Comparison results under these four guidance laws for case 1: a interception trajectories, b missile achieved accelerations, c sliding variable, d LOS angle, e LOS angular rate, and f GDOB estimation

Fig. 4

Comparison results under these four guidance laws for case 2: a interception trajectories, b missile achieved accelerations, c sliding variable, d LOS angle, e LOS angular rate, and f GDOB estimation

Table 1 Miss distances and interception time for case 1

Table 2 Miss distances and interception time for case 2

As the proposed CFNTSMGAL law is an improvement of the existing NTSMG law, some comments on comparison of these laws are stated here. First, implementing the NTSMG law requires the information on the upper bound of target maneuver to choose the switching gain, i.e., $K$ in Eq. (48). Usually, the maximum maneuverability of a pre-designated target is chosen as this upper bound in real applications. However, due to the unpredictability and complicity of target maneuvers, highly conservative bound requires excessive control energy consumption and large chattering will be excited, while lower upper bound will result in guidance performance degradation. As a comparison, the proposed CFNTSMGAL law adopts a GDOB to estimate the lumped uncertainty in missile guidance system, and therefore it requires no knowledge on target maneuvers and is more practical. Besides this, by adopting a backstepping-based autopilot lag compensation scheme, CFNTSMGAL law exhibits better transient phase and more precise interception than NTSMG law.

Next, to better show the characteristic of autopilot dynamics compensation of CFNTSMGAL law, some simulations are performed under different $k_2$ for case 1. The simulation results are given in Fig. 5, where (a) is for CFNTSMG with no autopilot dynamics, (b) is for CFNTSMG with autopilot dynamics, and (c) is for CFNTSMGAL with autopilot dynamics. As shown in Fig. 5, one can see that the sliding variable diverges when the missile is close to the target under CFNTSMG law with autopilot dynamics. As a comparison, the sliding mode variable still converge to a small region around zero in finite time under CFNTSMGAL with autopilot dynamics.

Fig. 5

Sliding mode variable profiles: a CFNTSMG with no autopilot dynamics, b CFNTSMG with autopilot dynamics, and c CFNTSMGAL with autopilot dynamics

Based on the above simulations and analysis, it can be concluded that the proposed CFNTSMGAL law has good overall performance and is capable of real implementation.

6 Conclusions

This paper has presented a new continuous CFNTSMGAL law to intercept maneuvering targets with terminal angle constraint. The proposed approach, compared with other existing impact angle guidance laws, considers the missile autopilot dynamics as well as target maneuvers. By virtue of the GDOB, the presented guidance law requires no information on target maneuver, and thus, the associated drawbacks of standard NTSM algorithm are overcome. The finite-time stability of the closed-loop guidance and control system is also established in theory. Simulation results with some comparisons validate the proposed method. Further works will focus on the acceleration distribution scheme since the proposed guidance law asks high control at the start.

Appendices

Appendix 1: Proof of Lemma 3

Consider the following Lyapunov function candidate

$$\begin{aligned} V=e_h^T Pe_h \end{aligned}$$

(49)

Differentiating Eq. (49) yields

$$\begin{aligned} \dot{V}= & {} e_h^T \left( {A^{T}P+PA}\right) e_h +2e_h^T \mathrm{{PB}}h^{(r)} \nonumber \\\le & {} -\,e_h^T Qe_h +2\sigma \Vert \mathrm{{PB}}\Vert \Vert e_h\Vert \nonumber \\\le & {} -\,\lambda _{\min } (Q)\Vert e_h\Vert ^{2}+2\sigma \Vert \mathrm{{PB}}\Vert \Vert e_h\Vert \nonumber \\\le & {} -\,\Vert e_h\Vert \left( {\lambda _{\min } (Q)\Vert e_h\Vert -2\sigma \Vert \mathrm{{PB}}\Vert }\right) \end{aligned}$$

(50)

It follows from Eq. (50) that $e_h$ is ultimately uniformly bounded (UUB) and its upper bound is obtained as

$$\begin{aligned} \Vert e_h\Vert \le \frac{2\sigma \Vert \mathrm{{PB}}\Vert }{\lambda _{\min } (Q)} \end{aligned}$$

(51)

which completes the proof.

Appendix 2: Proof of Lemma 4

It follows from $s=\bar{{s}}=0$ that ${\dot{e}}=-\alpha _1 e-\alpha _2 e^{p/q}$. Considering $V=0.5e^{2}$ as a Lyapunov function candidate, its time derivative is obtained as $V=e{\dot{e}}=-\alpha _1 e^{2}-\alpha _2 e^{(p+q)/q}=-2\alpha _1 V-2^{(p+q)/(2q)}\alpha _2 V^{(p+q)/(2q)}$. According to $(p+q)/(2q)\in (3/4,1)$ and Lemma 1, one can imply that $e=0$ is achieved in finite time. Furthermore, combining $s=\bar{{s}}=0$ with $e=0$, one can also conclude that ${\dot{\lambda }}={\dot{e}}=0$ is also achieved in finite time. This completes the proof.