1 Introduction

Chaotic systems occur in many real-word scientific and engineering problems. Such systems have complex dynamic behaviors that possess some special features, such as being extremely sensitive to tiny variations of initial conditions, having bounded trajectories in the phase space with a positive leading Lyapunov exponent, and so on. After the pioneering work of Ott et al. [1] and Pecora and Carroll [2], research efforts have investigated chaos control and chaos synchronization problems in many physical chaotic systems [1–22]. Nowadays, different techniques and methods have been proposed to achieve chaos control and chaos synchronization such as sliding mode control [3], active control [4], adaptive control [5], feedback control [6], backstepping method [7], impulsive control [8], \(H_\infty \) approach [9]. However, most of the above-mentioned works on chaos control and synchronization have focused on chaotic system without model uncertainties and external disturbance. But in practical situations, some or all of the system parameters are unknown and even changing from time to time. Moreover, chaotic systems are unavoidably affected by external disturbance. Therefore, the control and synchronization of chaotic systems in the presence of unknown system parameters and external disturbance are an important issue. On the other hand, most of the publications concern on chaos control and synchronization are only valid for some particular chaotic systems. However, from the point of practical applications, it is expected that the control and synchronization scheme can be used for more chaotic systems.

Moreover, some of the above-mentioned control methods and many other existing control approaches need several controllers to realize control or synchronization. From the points of practical applications, it is well known that the controllers to realize control or synchronization must be simple, efficient, and easy to implement. The fewer the number of the designed controllers, the better the control method. Thus, it is desired to design a scalar controller to control or synchronize chaotic systems.

Motivated by the above discussion, the control of general chaotic systems with unknown system parameters and external disturbance is investigated in this paper. Main innovative contributions of this paper are itemized as follows: (a) The control of a class of special chaotic systems is considered. Some robust criteria are proposed based on adaptive control scheme. (b) By introducing proper coordinate transformations, the control of general chaotic systems is studied. A scalar controller to control general chaotic systems is presented via adaptive control. (c) As an example to illustrate the application of the proposed method, the control of the R\(\ddot{o}\)ssler chaotic system is also investigated by using a single input.

This paper is organized as follows: In Sect. 2, we discuss the control of a class of special chaotic systems. The control of general chaotic systems is investigated in Sect. 3. Section 4 includes several numerical examples to demonstrate the effectiveness of the proposed approach; finally, some conclusions are shown in Sect. 5.

2 The control scheme of a class of special chaotic systems

In this section, we consider the the control of the following chaotic systems:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2,\\ \dot{x}_2=x_3,\\ \vdots \\ \dot{x}_n=f(x)^T\theta +g(x)+d(t), \end{array}\right. \end{aligned}$$
(1)

where \(x=(x_1 ,x_2 ,\ldots ,x_n)^T\in R^n\) is the state variable, \(f(x)=(f_1 ,f_2 ,\ldots ,f_m )^T\in R^{m\times 1}\) and \(g(x)\in R\) are functions of \(x\), \(\theta =(\theta _1 ,\ldots ,\theta _m )^T\) is the unknown parameter, \(d(t)\) is the external disturbance.

Remark 1

It is well known that the general strict-feedback system is

(2)

where \(f_i, g_i (i=1,2, \ldots , n-1)\) are smooth functions. Obviously, system (1) is the special case of (2).

Remark 2

There are many famous chaotic systems which can be expressed or transformed into the form (1), such as the Genesio–Tesi system [10], the Duffing system [11].

The Duffing system and Genesio–Tesi system have been studied thoroughly in the literatures [11–16]. Chaos synchronization by driving parameter for two uncoupled identical chaotic double Duffing systems was presented in [11]. The synchronization or anti-synchronization of two uncoupled systems were obtained via replacing two corresponding parameters of the identical systems by the same function of chaotic state variables of a third chaotic system. In paper [12], a new method to control and synchronize chaotic Genesio system was proposed. A nonlinear feedback controller was designed to make the controlled system be stabilized at origin and two Genesio systems be synchronized. In paper [13], the authors considered the stabilization of Genesio–Tesi chaotic system. A dynamic controller was proposed via using the Lyapunov stability theory, and the existence condition of such controllers was derived in terms of linear matrix inequalities (LMIs). The stabilization and synchronization of Genesio–Tesi system were investigated in [14]. A single variable feedback controller was presented via the well-known LaSalle invariance principle. Paper [15] concerned with the problem of synchronization controller design for Genesio–Tesi chaotic systems with plant uncertainties and dead-zone input. Paper [16] studied the chaotic dynamics of fractional-order Genesio–Tesi system. A necessary condition for the occurrence of chaos was theoretically obtained. Further, chaos synchronization of fractional-order Genesio–Tesi system was investigated via two different control strategies.

Obviously, the above results presented in papers [11–16] are under the same assumption that all the system’s parameters are known in advance. It is well known that in practical situations, the values of parameters of chaotic systems is hard to exactly determine in advance. Moreover, the above results are valid for the Duffing system or the Genesio–Tesi system but not for other chaotic systems. In a practical sense, it is desired that the control and synchronization scheme can be used for more chaotic systems. Thus, it is easy to see that compared with those special chaotic systems studied in [11–16] systems (1) have more research values.

In the literatures, the dimensions of most of the chaotic systems are not greater than 4. Based on this consideration, in this section, we only discuss the control of system (1) with \(n=2, 3, 4,\) respectively. Other chaotic systems with \(n\ge 5\) may be discussed in the same way. In the following, we first consider the control of four-dimensional chaotic system by the adaptive control approach and then discuss the three-dimensional and two-dimensional systems.

2.1 The control of four-dimensional systems

The controlled four-dimensional systems are described as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2,\\ \dot{x}_2=x_3,\\ \dot{x}_3=x_4,\\ \dot{x}_4=f(x)^T\theta +g(x)+d(t)+u(t), \end{array}\right. \end{aligned}$$
(3)

where \(x=(x_1, x_2, x_3, x_4)^T\in R^4\) is the state variable, \(f(x)\) \(\in R^{m\times 1}\) and \(g(x)\) \(\in R\) are functions of \(x\), \(\theta =(\theta _1 ,\ldots ,\theta _{m} )^T\) is the unknown parameter, \(d(t)\) is the external disturbance, \(u(t)\) is the controller to be designed.

The control goal considered in this subsection is to design a adaptive controller \(u\) such that \(\lim \limits _{t\rightarrow +\infty } x_i \!=\!0, i= 1, 2, 3, 4.\)

For this end, we introduce the following auxiliary variables:

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 =x_1, \\ z_2 =x_2+c_1z_1 , \\ z_3 =x_3+c_2z_2, \\ z_4=x_4+c_3 z_3, \\ \end{array}} \right. \end{aligned}$$
(4)

where \(c_i>0, i=1, 2, 3\) are constants and satisfy the following inequality constraints:

$$\begin{aligned} \left\{ {\begin{array}{l} c_1-\frac{|c_1 ^2-1|}{2}-\frac{c_1^2 c_2 }{2}>0, \\ c_2 -c_1 -\frac{|c_1 ^2-1|}{2}-\frac{1}{2}| {1-c_2 (c_2 -c_1 )} | >0, \\ c_3 -c_2 -\frac{c_1^2 c_2 }{2}-\frac{1}{2}| {1-c_2 (c_2-c_1 )}| >0. \\ \end{array}} \right. \end{aligned}$$
(5)

Remark 3

Inequalities (5) have many feasible solutions, for example, \(c_1=1, c_2=1.5, c_3=4\) is one of the feasible solutions.

From (4), it is easy to see that \(\lim _{t\rightarrow +\infty } z_i=0\) implies that \(\lim _{t\rightarrow +\infty } x_i=0, i=1, 2, 3 ,4\). Thus, in the following, we will design suitable controller \(u\) such that \(\lim _{t\rightarrow +\infty } z_i=0, i=1, 2, 3 ,4\).

Throughout this paper, we make the following assumption.

Assumption 1

The unknown parameter vector \(\theta \) and the disturbance \(d(t)\) are all bounded, i.e., there exist constants \(\Delta \) and \(d\) such that \(\left\| \theta \right\| \le \Delta \), \( \left| {d(t)} \right| \le d.\)

In order to derive our results, we introduce two Lemmas which will be used in the proof of Theorem 1.

Lemma 1

\(\delta _\theta (\Vert {\hat{\theta }}\Vert )\tilde{\theta }^T\hat{\theta }\le \Delta ^2-\frac{3}{4}\Vert {\tilde{\theta }} \Vert ^2, \) where \(\hat{\theta }\) is the estimated value of \(\theta \), \(\tilde{\theta }=\theta - \hat{\theta }\) and \(\delta _\theta (y)=\delta (\frac{y}{\Delta }),\)

$$\begin{aligned} \delta (y)= \left\{ {\begin{array}{ll} 0, &{} \quad y<1 \\ y-1,&{} \quad y\in \left[ {1,2} \right] \\ 1, &{} \quad y>2 \\ \end{array}} \right. \end{aligned}$$

Proof

By the definition of \( \delta _\theta (y)\), it is easily to obtain

$$\begin{aligned} \delta _\theta (\Vert {\hat{\theta }}\Vert )\tilde{\theta }^T\hat{\theta }&\le \tilde{\theta }^T\hat{\theta }=\tilde{\theta }^T(\theta -\tilde{\theta })\\&\le \Vert {\tilde{\theta }}\Vert \Vert \theta \Vert -\Vert {\tilde{\theta }}\Vert ^2\le \Delta \Vert {\tilde{\theta }}\Vert -\Vert {\tilde{\theta }} \Vert ^2\\&= \Delta \Vert {\tilde{\theta }}\Vert -\frac{1}{4}\Vert {\tilde{\theta }} \Vert ^2-\frac{3}{4}\Vert {\tilde{\theta }} \Vert ^2 \\&= -\left( \Delta -\frac{1}{2}\Vert {\tilde{\theta }} \Vert \right) ^2+\Delta ^2-\frac{3}{4}\Vert {\tilde{\theta }}\Vert ^2\\&\le \Delta ^2-\frac{3}{4}\Vert {\tilde{\theta }} \Vert ^2. \end{aligned}$$

\(\square \)

Lemma 2

\(\delta _\theta (\Vert {\hat{\theta }}\Vert )\tilde{\theta }^T\hat{\theta }\le 0. \)

Proof

Let us consider the following two cases:

  1. (a)

    If \( \Vert {\hat{\theta }}\Vert \le \Delta ,\) then by the definition of \( \delta _\theta (y)\) it is easily to see that \(\delta _\theta (\Vert \hat{\theta }\Vert )=0.\) Therefore, \(\delta _\theta (\Vert \hat{\theta }\Vert ) \tilde{\theta }^T\hat{\theta }=0.\)

  2. (b)

    If \(\Vert {\hat{\theta }}\Vert >\Delta ,\) then \(\delta _\theta (\Vert \hat{\theta }\Vert )>0.\) Thus,

    $$\begin{aligned} \delta _\theta (\Vert \hat{\theta }\Vert )\tilde{\theta }^T\hat{\theta }&= \delta _\theta (\Vert \hat{\theta }\Vert ) (\theta -\hat{\theta })^T\hat{\theta }\\&= \delta _\theta (\Vert \hat{\theta }\Vert )(\theta ^T\hat{\theta }-\Vert {\hat{\theta }} \Vert ^2)\\&\le \delta _\theta (\Vert \hat{\theta }\Vert ) (\Vert \theta \Vert \Vert {\hat{\theta }} \Vert -\Vert {\hat{\theta }}\Vert ^2)\\&= \delta _\theta (\Vert \hat{\theta }\Vert ) \Vert {\hat{\theta }}\Vert (\Vert \theta \Vert -\Vert {\hat{\theta }}\Vert )<0. \end{aligned}$$

\(\square \)

Hence, in any case \(\delta _\theta (\Vert \hat{\theta }\Vert )\tilde{\theta }^T\hat{\theta }\le 0.\) This completes the proof of Lemma 2.

Theorem 1

Under Assumption 1, if the adaptive control law is designed by:

$$\begin{aligned} u(t)&= -g-z_3 -c_3 z_4 +c_3 (c_3 -c_2 )z_3 \nonumber \\&\quad +\,c_3 c_2 (c_2 -c_1 )z_2 +c_3 c_2 c_1 ^2z_1 -f^T\hat{\theta }\nonumber \\&\quad -\,sgn(z_4 )d-c_4z_4 , \end{aligned}$$
(6)

and the parameter estimate law is given as:

$$\begin{aligned} \dot{\hat{\theta }}=fz_4 -\delta _\theta (\Vert {\hat{\theta }}\Vert )\hat{\theta }, \end{aligned}$$
(7)

then \(\lim \limits _{t\rightarrow +\infty } x_i =0, i= 1, 2, 3, 4\), where \(c_4>0\), \(sgn(\cdot )\) denotes the Sign function.

Proof

It follows from Eq.(4) that

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 -c_1 z_1, \\ \dot{z}_2 =z_3 -(c_2 -c_1 )z_2 -c_1 ^2z_1, \\ \dot{z}_3 =z_4 -(c_3 -c_2 )z_3 -c_2 (c_2 -c_1 ) z_2 -c_2 c_1 ^2z_1, \\ \dot{z}_4 =\dot{x}_4+c_3 z_4 -c_3 (c_3 -c_2 )z_3\\ \qquad \,\,\, -\,c_3 c_2 (c_2 -c_1 )z_2 -c_3 c_2 c_1 ^2z_1. \end{array}} \right. \end{aligned}$$
(8)

\(\square \)

Let us construct a Lyapunov function in the form:

$$\begin{aligned} V=\frac{1}{2}z_1^2+\frac{1}{2}z_2^2+\frac{1}{2}z_3 ^2+\frac{1}{2}z_4^2+\frac{1}{2}\tilde{\theta }^T\tilde{\theta }. \end{aligned}$$
(9)

The derivative of \(V\) along the trajectory of system (8) is given by

$$\begin{aligned} \dot{V}&= z_1 \dot{z}_1+z_2\dot{z}_2+z_3\dot{z}_3+z_4\dot{z}_4+\tilde{\theta }^T\dot{\tilde{\theta }} \\&= z_1(z_2-c_1z_1)+z_2[z_3 -(c_2 -c_1 )z_2 -c_1 ^2z_1]\\&\quad +\,z_3 [z_4 -(c_3 -c_2 )z_3 -c_2 (c_2 -c_1 )z_2 -c_2 c_1 ^2z_1]\\&\quad +\, z_4 [ \dot{x}_4 +c_3 z_4 -c_3 (c_3 -c_2 )z_3\\&\quad -\,c_3 c_2 (c_2 -c_1 )z_2 -c_3 c_2 c_1 ^2z_1]+\tilde{\theta }^T\dot{\tilde{\theta }}\\&= z_1z_2-c_1z_1^2+z_2z_3 -(c_2 -c_1 )z_2^2 -c_1 ^2z_1z_2+z_3z_4\\&\quad -\,(c_3 -c_2 )z_3^2 -c_2 (c_2 -c_1 )z_2z_3-c_2 c_1 ^2z_1z_3\\&\quad +\, z_4 [ \dot{x}_4 +c_3 z_4 -c_3 (c_3 -c_2 )z_3\\&\quad -\,c_3 c_2 (c_2 -c_1 )z_2 -c_3 c_2 c_1 ^2z_1]+\tilde{\theta }^T\dot{\tilde{\theta }}\\&\le -c_1z_1^2-(c_2-c_1 )z_2^2-(c_3 -c_2 )z_3^2\\&\quad +\,|c_1^2-1||z_1||z_2|+| c_2c_1^2||z_1 z_3|\\&\quad +\,|1-c_2(c_2-c_1)||z_2 z_3|+z_4 [f^T\theta +g\\&\quad +\,d(t)+u(t)+z_3 +c_3 z_4\\&\quad -\,c_3 (c_3 -c_2 )z_3 -c_3 c_2 (c_2 -c_1 )z_2 -c_3 c_2 c_1 ^2z_1]\\&\quad +\,\tilde{\theta }^T\dot{\tilde{\theta }} \end{aligned}$$

Substituting \(u(t)\) into the above inequality and noting that \(2|ab|\le (a^2+b^2)\), one gets

$$\begin{aligned} \dot{V}&\le -c_1z_1 ^2-(c_2 -c_1 )z_2 ^2-(c_3 -c_2 )z_3 ^2\\&\quad +\,\frac{|c_1 ^2-1|}{2}(z_1 ^2+z_2 ^2) +\frac{c_1^2 c_2}{2}(z_1^2+z_3 ^2) \\&\quad +\,\frac{1}{2}| {1-c_2 (c_2 -c_1 )} | (z_2 ^2+z_3 ^2)-c_4z_4^2\\&\quad +\,z_4[{f^T(\theta -\hat{\theta })+d(t)-sgn(z_4 )d}]+\tilde{\theta }^T\dot{\tilde{\theta }} \\&= -\left[ c_1 -\frac{|c_1 ^2-1|}{2}-\frac{c_1^2 c_2}{2}\right] z_1 ^2-\left[ (c_2 -c_1 )\right. \\&\quad \left. -\,\frac{|c_1 ^2-1|}{2}-\frac{1}{2}|{1-c_2 (c_2 -c_1 )}|\right] z_2 ^2\\&\quad -\,\left[ (c_3 -c_2 )-\frac{c_1^2c_2 }{2}-\frac{1}{2}| {1-c_2 (c_2 -c_1 )}|\right] z_3 ^2\\&\quad -\,c_4z_4^2+z_4 [f^T(\theta -\hat{\theta })\\&\quad +\,d(t)-sgn(z_4 )d]+\tilde{\theta }^T\dot{\tilde{\theta }} \\&= -d_1 z_1 ^2-d_2 z_2 ^2-d_3 z_3 ^2-c_4z_4^2+z_4 [f^T(\theta -\hat{\theta })\\&\quad +\,d(t)-sgn(z_4 )d]+\tilde{\theta }^T\dot{\tilde{\theta }}, \end{aligned}$$

where \(d_1 =c_1 -\frac{|c_1 ^2-1|}{2}-\frac{c_1^2c_2 }{2}>0,d_2 =(c_2 -c_1 )-\frac{|c_1 ^2-1|}{2}-\frac{1}{2}| {1-c_2 (c_2 -c_1 )}| >0, d_3 =(c_3 -c_2 )-\frac{c_1^2{c_2 } }{2}-\frac{1}{2}| {1-c_2(c_2 -c_1 )}| >0.\)

Using the estimate law (7), it follows that

$$\begin{aligned} \dot{V}&\le -d_1 z_1 ^2-d_2 z_2 ^2-d_3 z_3 ^2-c_4z_4^2+z_4 [d(t)\nonumber \\&\quad -\,sgn(z_4 )d]+\delta _\theta (\Vert \hat{\theta }\Vert )\tilde{\theta }^T\hat{\theta }. \end{aligned}$$
(10)

In view of Lemma 1 and note that \(z_4 [d(t)-sgn(z_4 )d]\le 0\), we derive

$$\begin{aligned} \dot{V}&\le -d_1 z_1 ^2-d_2 z_2 ^2-d_3 z_3 ^2-c_4z_4^2-\frac{3}{4}\Vert {\tilde{\theta }}\Vert ^2+\Delta ^2\\&\le -2\min \left\{ {d_1, d_2, d_3, c_4 }\right\} \left( \frac{1}{2}z_1^2+\frac{1}{2}z_2^2+\frac{1}{2}z_3^2\right. \\&\quad \left. +\frac{1}{2}z_4^2\right) -\frac{3}{2}\times \frac{1}{2}\Vert {\tilde{\theta }}\Vert ^2+\Delta ^2\\&= -c_0 V+d_0 , \end{aligned}$$

where \(c_0 =\min \{2\min \{d_1, d_2, d_3, c_4 \},\frac{3}{2}\}, d_0 =\Delta ^2.\) Hence,

$$\begin{aligned} V(t)\le V(0)e^{-c_0 t}+\frac{d_0 }{c_0 }(1-e^{-c_0 t})\le V(0)e^{-c_0 t}+\frac{d_0 }{c_0 }. \end{aligned}$$

From the above expression, it is easy to see that \(V(t)\) is uniformly bounded. On the other hand, by using Lemma 2 and inequality (10) the following is obtained:

$$\begin{aligned} \dot{V}\le -d_1 z_1 ^2-d_2 z_2 ^2-d_3 z_3 ^2-c_4z_4^2. \end{aligned}$$

It is derived from the above inequality that,

$$\begin{aligned} z_1 ^2\le \frac{1}{d_1}(-\dot{V}-d_2 z_2 ^2-d_3 z_3 ^2-c_4z_4^2)\le -\frac{\dot{V}}{d_1}. \end{aligned}$$

Integrating at both sides of the above inequality, from zero to \(t\), and dividing by \(t\), gives

$$\begin{aligned} \frac{1}{t}\int _0^t {z_1 ^2} \hbox {d}t\le -\frac{V(t)-V(0)}{d_1t}. \end{aligned}$$
(11)

Since \(V\) is uniformly bounded, then

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow +\infty } \frac{V(t)-V(0)}{t}=0. \end{aligned}$$

Taking limits at both sides of inequality (11) we get

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow +\infty } \frac{1}{t}\int _0^t {z_1 ^2} \hbox {d}t\le 0. \end{aligned}$$

Keep in mind that \(z_1 ^2\ge 0, \) we have \(\lim _{t\rightarrow \infty } z_1 =0.\) In the same way, we can show \(\lim _{t\rightarrow \infty } z_2 =\lim _{t\rightarrow \infty } z_3=\lim _{t\rightarrow \infty } z_4 =0.\) By using Eq.(4), we have \(\lim _{t\rightarrow +\infty } x_i =0,i= 1, 2, 3, 4, \) which ends the proof of Theorem 1.

Now, let us consider the special case: \(\theta \) is known in advance and \(d(t)=0.\) In this case, it is easy to have the following corollary.

Corollary 1

Suppose \(\theta \) is known in advance and \(d(t)=0\), if the control law is designed by:

$$\begin{aligned} u(t)&= -g-z_3 -c_3 z_4 +c_3 (c_3 -c_2 )z_3 \nonumber \\&\quad +\,c_3 c_2 (c_2-c_1 )z_2 +c_3 c_2 c_1 ^2z_1 -f^T\theta -c_4z_4, \end{aligned}$$
(12)

then \(\lim _{t\rightarrow +\infty } x_i =0, i= 1, 2, 3, 4 \), where \(c_4>0\), \(sgn(\cdot )\) denotes the Sign function.

2.2 The control of three-dimensional systems

The controlled three-dimensional systems are given as:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =x_3 , \\ \dot{x}_3 =f(x)^T\theta +g(x)+d(t)+u(t), \\ \end{array}} \right. \end{aligned}$$
(13)

where \(x=(x_1, x_2, x_3)^T\in R^3\) is the state variable, \(f(x)\in R^{m\times 1}\) and \(g(x)\in R\) are functions of \(x\), \(\theta =(\theta _1 ,\ldots ,\theta _{m} )^T\) is the unknown parameter, \(d(t)\) is the external disturbance, \(u(t)\) is the controller to be designed.

In order to force the states of system (13) to converge to zero, the following auxiliary variables is introduced:

$$\begin{aligned} \left\{ {\begin{array}{l} z_1 =x_1, \\ z_2 =x_2 +z_1 , \\ z_3 =x_3 +c_1 z_2, \\ \end{array}} \right. \end{aligned}$$
(14)

where \(c_1>1\) is a constant.

Obviously \(\lim _{t\rightarrow +\infty } z_i=0\) means that \(\lim _{t\rightarrow +\infty } x_i=0, i=1, 2, 3\). Therefore, in the following, we will design appropriate controller \(u\) such that \(\lim _{t\rightarrow +\infty } z_i=0, i=1, 2, 3\). Similar to Theorem 1, we have Theorem 2.

Theorem 2

Under Assumption 1, if the adaptive control law is designed as:

$$\begin{aligned} u(t)&= -c_1[z_3-(c_1-1)z_2-z_1]-z_2 -c_2 z_3 \nonumber \\&\quad -\,f^T\hat{\theta }-sgn(z_3)d-g, \end{aligned}$$
(15)

and the parameter estimate law is given as:

$$\begin{aligned} \dot{\hat{\theta }}=fz_3 -\delta _\theta (\Vert {\hat{\theta }}\Vert )\hat{\theta }, \end{aligned}$$
(16)

then \(\lim _{t\rightarrow +\infty } x_i =0, i= 1, 2, 3\) where \(c_2>0\), \(sgn(\cdot )\) denotes the Sign function.

Proof

In view of Eq.(14), it follows that

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 -z_1 , \\ \dot{z}_2 =z_3 -(c_1 -1)z_2 -z_1 , \\ \dot{z}_3 =\dot{x}_3 +c_1[ z_3-(c_1 -1)z_2-z_1]. \\ \end{array}} \right. \end{aligned}$$
(17)

\(\square \)

Choose the following Lyapunov function candidate:

$$\begin{aligned} V=\frac{1}{2}z_1 ^2+\frac{1}{2}z_2 ^2+\frac{1}{2}z_3 ^2+\frac{1}{2}\tilde{\theta }^T\tilde{\theta }. \end{aligned}$$

The derivative of \(V\) along the trajectory of (17) is:

$$\begin{aligned} \dot{V}(t)&= z_1\dot{z}_1 +z_2\dot{z}_2 +z_3\dot{z}_3 +\tilde{\theta }^T\dot{\tilde{\theta }}\\&= z_1(z_2-z_1)+z_2[z_3 -(c_1 -1)z_2 -z_1]\\&\quad +\,z_3\{\dot{x}_3 +c_1[ z_3-(c_1 -1)z_2-z_1]\}+\tilde{\theta }^T\dot{\tilde{\theta }}\\&= z_1z_2-z_1^2+z_2 z_3-(c_1 -1)z_2^2-z_1 z_2\\&\quad +\,z_3\{f^T\theta +g+d(t)+u(t)\\&\quad +\,c_1[ z_3-(c_1 -1)z_2-z_1]\}+\tilde{\theta }^T\dot{\tilde{ \theta }}\\&= -z_1^2-(c_1 -1)z_2^2+z_3\{f^T\theta +g+d(t) +u(t)\\&\quad +\,c_1[ z_3-(c_1 -1)z_2-z_1]+z_2\}+\tilde{\theta }^T\dot{\tilde{\theta }}. \end{aligned}$$

Substituting (15) into the above inequality, one gets

$$\begin{aligned} \dot{V}&\le -z_1^2 - (c_1-1)z_2^2-c_2z_3^2 + z_3[f^T(\theta -\hat{\theta })\\&\quad +\,d(t)-sgn(z_3)d]+\tilde{\theta }^T\dot{\tilde{\theta }}. \end{aligned}$$

The remainder is similar to the proof of Theorem 1 and omitted here.

Corollary 2

Suppose \(\theta \) is known in advance and \(d(t)=0\), if the control law is designed by:

$$\begin{aligned} u(t)&= -c_1 z_3 +c_1 (c_1 -1)z_2 +c_1 z_1 -z_2 \nonumber \\&\quad \,-\,c_2 z_3 -f^T\theta -g, \end{aligned}$$
(18)

then \(\lim _{t\rightarrow +\infty } x_i =0, i= 1, 2, 3\), where \(c_2>0\), \(sgn(\cdot )\) denotes the Sign function.

2.3 The control of two-dimensional systems

The controlled two-dimensional systems can be described as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2,\\ \dot{x}_2=f(x)^T\theta +g(x)+d(t)+u(t), \end{array}\right. \end{aligned}$$
(19)

where \(x=(x_1, x_2)^T\in R^2\) is the state variable, \(f(x)\in R^{m\times 1}\) and \(g(x)\in R\) are functions of \(x\), \(\theta =(\theta _1 ,\ldots ,\theta _{m} )^T\) is the unknown parameter, \(d(t)\) is the external disturbance, \(u(t)\) is the controller.

Follow the same line of Theorem 1, we have the following auxiliary variables:

$$\begin{aligned} \left\{ \begin{array}{l} z_1 =x_1,\\ z_2 =x_2 +z_1. \\ \end{array}\right. \end{aligned}$$
(20)

It is easy to see that \(\lim _{t\rightarrow +\infty } z_i=0\) means that \(\lim _{t\rightarrow +\infty } x_i=0, i=1, 2\). Therefore, in the following, we will find appropriate controller \(u\) such that \(\lim _{t\rightarrow +\infty } z_i=0, i=1, 2\).

Theorem 3

Under Assumption 1, if the adaptive control law is designed by:

$$\begin{aligned} u(t)&= -(c_1+1)z_2-f^T\hat{\theta }-sgn(z_2)d-g, \end{aligned}$$
(21)

and the parameter estimate law is given as:

$$\begin{aligned} \dot{\hat{\theta }}=fz_2 -\delta _\theta (\Vert {\hat{\theta }} \Vert )\hat{\theta }, \end{aligned}$$
(22)

then \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2 =0\), where \(c_1>0\), \(sgn(\cdot )\) denotes the Sign function.

Proof

The proof of Theorem 3 is similar to that of Theorem 1, and we omit it here. \(\square \)

3 The control of general chaotic systems

By transforming general chaotic systems into form (1), the control of general chaotic systems is discussed via the mentioned method proposed in the previous sections. In this section, we only discuss the control of the three-dimensional chaotic systems. As for the other chaotic systems, their control schemes can be easily derived in the same way.

Consider the three-dimensional general chaotic systems which is described as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x_1}=f_1(x), \\ \dot{x_2}=f_2(x), \\ \dot{x_3}=f_3(x)\theta +f_4(x)+d(t)+u(t), \\ \end{array}} \right. \end{aligned}$$
(23)

where \(x_1, x_2, x_3\) are state variables, \(x=(x_1, x_2, x_3)^T\), \(f_1(x)\in R, f_2(x)\in R, f_3(x)\in R^{m\times 1}, f_4(x)\in R\), \(\theta =(\theta _1 ,\ldots ,\theta _{m} )^T\) is the unknown parameter, \(d(t)\) is the external disturbance, \(u(t)\) is the controller to be designed.

The main aim of this section is to design proper controller \(u\) such that \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0.\)

Suppose \(f_1(x)\) is a twice differentiable function. In order to use the results obtained in Section 2, we make the following transformation:

$$\begin{aligned} x_1=y_1,\quad f_1(x)=y_2, \quad \dot{f}_1(x)=y_3. \end{aligned}$$

System (23) is then turned into

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{y_1}=y_2, \\ \dot{y_2}=y_3, \\ \dot{y_3}=g_1(x)\theta +g_2(x)+g_3(x,d)+g_4(x, u). \\ \end{array}} \right. \end{aligned}$$
(24)

For systems (23) and (24), we make the following assumptions:

Assumption 2

Suppose \(\lim _{t\rightarrow +\infty } y_1 =\lim _{t\rightarrow +\infty } y_2=\lim _{t\rightarrow +\infty } y_3 =0\) implies \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0.\)

Assumption 3

There exists a constant \(d\) such that \(|g_3(x)d|\le d\).

The following Theorem ensures that the origin of system (24) is globally asymptotically stable, which means that \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0.\)

Theorem 4

Under Assumptions 1–3, if the adaptive control law is designed as:

$$\begin{aligned} g_4(x, u)&= -c_1[z_3-(c_1-1)z_2-z_1]-z_2 -c_2 z_3\nonumber \\&\quad -\,g_1(x)^T\hat{\theta }-sgn(z_3)d-g_2(x), \end{aligned}$$
(25)

and the parameter estimate law is given as:

$$\begin{aligned} \dot{\hat{\theta }}=fz_3 -\delta _\theta (\Vert {\hat{\theta }}\Vert )\hat{\theta }, \end{aligned}$$
(26)

then \(\lim _{t\rightarrow +\infty } x_i =0, i= 1, 2, 3\) where \(z_1 =y_1, z_2 =y_2 +z_1 , z_3 =y_3 +c_1 z_2, \) and \(c_1>1, c_2>0\).

Proof

The proof is straightforward which is omitted here. \(\square \)

In the following, we take the R\(\ddot{o}\)ssler chaotic system as an example to show the application of Theorem 4.

The R\(\ddot{o}\)ssler system is one of the famous chaotic systems, its dynamic system is [17]:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z_1}=-z_2-z_3, \\ \dot{z_2}=z_1+az_2, \\ \dot{z_3}=b+z_3(z_1-c), \\ \end{array}} \right. \end{aligned}$$
(27)

where \(z_1, z_2, z_3\) are state variables, \(a, b, c\) are system’s parameters. If \( a = b = 0.2\) and \(c = 5.7\) system (27) is chaotic.

Let \(x_1=z_2, x_2=z_1, x_3=z_3,\) Eq. (27) can be transformed into:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x_1}=x_2+ax_1, \\ \dot{x_2}=-x_3-x_1, \\ \dot{x_3}=b+x_3(x_2-c). \\ \end{array}} \right. \end{aligned}$$
(28)

Suppose parameters b and c are unknown in advance, and system (28) is affected by external disturbance \(d(t)\). Thus, the controlled system (28) with unknown parameters and external disturbance is rewritten as:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x_1}=x_2+ax_1, \\ \dot{x_2}=-x_3-x_1, \\ \dot{x_3}=b+x_3(x_2-c)+d(t)+u, \\ \end{array}} \right. \end{aligned}$$
(29)

where \(u\) is a controller to be designed.

For the end of designing a scalar controller \(u\) such that \(\lim _{t\rightarrow +\infty } x_i =0, i=1, 2, 3,\) we introduce the following transformation:

$$\begin{aligned} x_1=y_1,\quad x_2+ax_1=y_2, \quad \dot{y}_2=y_3. \end{aligned}$$

By using system (29), it is derived that:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{y_1}=y_2, \\ \dot{y_2}=y_3, \\ \dot{y_3}=\underbrace{-b+cx_3}_{f^T\theta }+ \underbrace{(a^2-1)(x_2+ax_1)-x_3x_2-a(x_1+x_3)}_{g}\\ \qquad -\,d(t)-u. \\ \end{array}} \right. \end{aligned}$$
(30)

In order to get further results, we introduce a Lemma which will be used in the proof of Theorem 5.

Lemma 3

If \(\lim _{t\rightarrow +\infty } y_1 =\lim _{t\rightarrow +\infty } y_2=\lim _{t\rightarrow +\infty } y_3 =0,\) then \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0.\)

Proof

By Noting that

$$\begin{aligned} x_1&= y_1,\quad x_2+ax_1=y_2, \\ y_3&= \dot{y}_2=-x_3-x_1+a(x_2+ax_1), \end{aligned}$$

we know Lemma 3 is obviously true. \(\square \)

According to Lemma 3, it is easy to see that the control problem of system (29) is equivalent to the problem of proving \(\lim _{t\rightarrow +\infty } y_1 =\lim _{t\rightarrow +\infty } y_2=\lim _{t\rightarrow +\infty } y_3 =0.\)

Using the results obtained in Theorem 4, we have Theorem 5.

Theorem 5

Under Assumption 1, if the adaptive control law is designed as:

$$\begin{aligned} u(t)&= c_1[z_3-(c_1-1)z_2-z_1]+z_2 +c_2 z_3\nonumber \\&\quad +\,f^T\hat{\theta }+sgn(z_3)d+g, \end{aligned}$$
(31)

and the parameter estimate law is given as:

$$\begin{aligned} \dot{\hat{\theta }}=fz_3 -\delta _\theta (\Vert {\hat{\theta }}\Vert )\hat{\theta }, \end{aligned}$$
(32)

then \(\lim _{t\rightarrow +\infty } y_i =0, i= 1, 2, 3\) which implies that \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0,\) where \(c_1>1, c_2>0\) and \(z_1=y_1, z_2=y_1+y_2, z_3=y_3+c_1z_2, y_1=x_1, y_2=x_2+ax_1, y_3=-x_3-x_1+a(x_2+ax_1)\).

Proof

The proof is trivial which is omitted here. \(\square \)

Remark 4

The control of R\(\ddot{o}\)ssler system have been discussed extensively in [18–21]. Note that the controllers presented in [18–21] are all vectors; however, the controller proposed in this paper is a scalar. From the points of practical applications it is well known that the controllers must be simple, efficient, and easy to implement. The fewer the number of the designed controllers, the better the control method. Thus, our controller can be readily applied to real-world situations. Furthermore, the control schemes proposed in [18–21] are under the assumption that system’s parameters are known exactly and no external disturbance is affected; however, in this paper, this limitation has been eliminated.

4 Simulation results

In this section, we take the R\(\ddot{o}\)ssler as an example to demonstrate the effectiveness of the proposed design method. The simulation results are carried out using the MATLAB software. The fourth-order Runge–Kutta integration algorithm was performed to solve the differential equations.

Suppose parameters b and c are unknown in advance, and system (28) is affected by external disturbance \(d(t)\), where \(d(t)\)=sin(t). We assume \( a = b = 0.2\) and \(c = 5.7\) such that system (28) is chaotic. The chaotic attractor and the bifurcation diagram of system (28) are shown in Fig. (1).

Fig. 1
figure 1

a The chaotic attractor of system (28). b Bifurcation diagram for increasing c with \(a=b=0.2\)

Full size image

In our simulation, we set \(c_1=2, c_2=1, \Delta =1, d=1\). The adaptive control law is chosen as:

$$\begin{aligned} u(t)&= c_1[z_3-(c_1-1)z_2-z_1]+z_2 +c_2 z_3\nonumber \\&\quad +f^T\hat{\theta }+sgn(z_3)d+g, \end{aligned}$$
(33)

where \(z_1=x_1, z_2=x_1+x_2+0.2x_1, z_3=-x_3-x_1+0.2(x_2+0.2x_1)+2(x_1+x_1+0.2x_1), f^T=(-1, x_3),\hat{\theta }^T=(\hat{b}, \hat{c}), d=1\) and \(g=(0.2^2-1)(x_2+0.2x_1)-x_3x_2-0.2(x_1+x_3)\)

The parameter estimate law is given as:

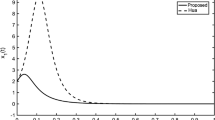
$$\begin{aligned} \dot{\hat{\theta }}=fz_3 -\delta _\theta (\Vert {\hat{\theta }}\Vert )\hat{\theta }. \end{aligned}$$
(34)

Based on (33), (34) and according to Theorem 5, we have \(\lim _{t\rightarrow +\infty } x_1 =\lim _{t\rightarrow +\infty } x_2=\lim _{t\rightarrow +\infty } x_3 =0.\) Let \((x_1(0), x_2(0), x_3(0))= (1, 2, 3), (\hat{b}(0), \hat{c}(0))=(1, 1),\) the corresponding simulation results are shown in Figs. 2, 3 and 4. Figure 2 presents the time response of the state \(x_1, x_2, x_3\). It clearly appears that after a short transient time, the chaotic trajectory stabilized at the origin by the adaptive feedback controllers (33) and the parameters estimation update law (24) in the presence of unknown parameters and external disturbance. The estimate values of unknown parameters \(b\) and \(c\) are given in Fig. 3. One can observe that the identified parameters \(\hat{b}\) and \(\hat{c}\) approach the desired values: \(b=0.2, c=5.7\) in 3 seconds, which means that unknown parameters \(b\) and \(c\) can be estimated in a short time. Fig. 4 depicts the time response of controller \(u(t)\). As one can easily see that \(u(t)\) oscillates between 0.8 and \(-\)1.2 which implies that \(z_i, i=1, 2, 3\) approach 0 after a short transient time. These simulation results have further illustrated the effectiveness of the proposed method.

Fig. 2
figure 2

The time response of states \(x_1, x_2, x_3\)

Full size image
Fig. 3
figure 3

The estimate values of unknown parameters \(b\) and \(c\)

Full size image
Fig. 4
figure 4

The time response of controller \(u\)

Full size image

5 Conclusion

This work investigates the control of general chaotic systems via adaptive controller in the presence of unknown system parameters and external disturbance. We first investigate the control of a class of special chaotic systems and then discuss the control of general chaotic system. By using the appropriate coordinate transformation, some control conditions are derived via the Lyapunov stability theory. In addition, as an example to illustrate the application of the proposed method, the control of the R\(\ddot{o}\)ssler chaotic system is also investigated via a single input. Numerical simulations are given to show the robustness of the controller against unknown parameters and noise disturbance.