1 Introduction

Changes of qualitative structures of the solutions in the nature occur if a parameter passes through a critical point means bifurcation. For any nonlinear dynamic system, a bifurcation phenomenon may originate from an equilibrium (fixed) point with a periodic oscillation, or a limit circle, or a chaotic orbit. However, from the experimental or computational point of perspective, many systems in daily life are illustrated by the discrete-time system which is more suitable for simulation. Certainly, the discrete-time analog inherits the dynamic characteristics of the continuous-time model and the dynamic of discrete-time systems can produce more patterns of bifurcation than those observed in continuous-time models. Meanwhile, various kinds of bifurcation in the discrete-time nonlinear systems such as pitchfork bifurcation [1], flip bifurcation [2], period-doubling bifurcation [3], saddle-node bifurcation [4] and Hopf bifurcation [5, 6] have been researched comprehensively and systematically in theory. Among them, the Hopf bifurcation that gives rise to the closed invariant curves which present some more interesting complex oscillatory behaviors in biological process, social economic, chemical reaction and engineering systems has received increasing interest due to their promising potential application [7–11]. Hence, study on the dynamical properties of periodic solution arising from Hopf bifurcation is tremendously and vigorously done from mathematical and applied point.

Over the years, the logistic map that was first introduced by the population ecologists in the study of population growth of a single species with generations [12] has long served as perhaps the simplest nonlinear discrete-time model, and it has been central in the development and understanding of nonlinear dynamic behaviors. Therefore, the investigation of logistic equation (map) has long been [13–18] and will continue in many field.

However, any mathematical systems are always inevitably affected by some random disturbances such as uncertainty of system parameter, perturbation of external noise and stochastic input. When we investigate the actual population growth and biological process, the incomplete observations including natural disasters, weather changes and technology factors and so forth are unavoidably arousing uncertainties of models. In particular, phenomena that appear in stochastic system at critical value due to the effects of random physical parameters are always unforeseen in the deterministic system and interfere with daily production and life seriously. Therefore, the stochastic system can properly and accurately represent the original systems and the analysis about it will possess more practical significance. Some important results about stochastic logistic map have obtained. For instance, the bifurcation behavior of the externally perturbed logistic map and the noise influence on the bifurcation are analyzed in 1997 [19]. Linz and Lcke [20] have investigated the statistical dynamics of the response of the logistic map toward additively and multiplicatively coupled fluctuating forces for control parameters in the range of the first transcritical and pitchfork bifurcation. In 2007, randomness as fluctuations and uncertainties due to noise and its influence in the nonlinear dynamical behavior of coupled logistic maps are all considered and studied by Marcelo A. Savi [21]. Yang and Gao [22] have researched the behaviors of a logistic map driven by white noise and found that its nondivergent interval decreases with increasing white noise. The influence of additive colored noise near the onset of chaos has been studied for one-dimensional logistic maps by Gutierrez and Iglesias [23]. The effects of noise on each periodic orbit of three different period sequences are investigated for the logistic map by Li [24]. From the previous works about stochastic logistic model, those stochastic systems are all disturbed by the external environmental perturbation. The complicated environment leads to uncertainty in the internal coefficient. This kind of uncertainty is expressed by a random parameter. With the internal random parameters, we can explore the influence of the change of the internal conditions on dynamical behavior in system. So we can avoid some disaster or accident due to internal questions of the systems. Therefore, the dynamic analysis of stochastic discrete-time system with random internal parameter is considered a little attract our interest.

Motivated by the above discussion, taking the lagged logistic system which has a role of cohesion between one-dimensional and high-dimensional logistic model as example in this paper, using the statistical characteristic of random variable, we build a stochastic lagged logistic system with random internal parameter subjected to the given statistics, and the influence of random parameter in the stochastic lagged logistic system on the Hopf bifurcation is investigated by orthogonal polynomial approximation. The organization of this paper is as follows: Transforming the stochastic lagged logistic system with random parameter into its equivalent deterministic one by orthogonal polynomial approximation is obtained in Sect. 2. Section 3 analyzes the Hopf bifurcation of the stochastic lagged logistic system and stability about it. The numerical simulations and analysis of Hopf bifurcation about the stochastic lagged logistic system are shown in Sect. 4. Finally, conclusions are drawn in Sect.  5.

2 Stochastic lagged logistic map with random parameter and its orthogonal polynomial approximation

Considering a two-dimensional deterministic lagged logistic system [25]

$$\begin{aligned} z_{1}(n+1)&= z_{2}(n),\nonumber \\ z_{2}(n+1)&= \bar{\mu }z_{2}(n)(1-z_{1}(n)),\nonumber \\&\qquad (\bar{\mu } \in (0,2.28),\quad z_{1},z_{2}\in (0,1)). \end{aligned}$$
(1)

Obviously, within the scope of system variables, there has only one fixed point in this lagged logistic system \(S(1-1/\bar{\mu },1-1/\bar{\mu })\). For facilitating Hopf bifurcation analysis, applying the coordinate transformation, the fixed point is converted to the origin \(O(0,0)\); then, we have the following logistic system

$$\begin{aligned} x(n+1)&= y(n),\nonumber \\ y(n+1)&= y(n)-(\bar{\mu }-1)x(n)-\bar{\mu }x(n)y(n), \end{aligned}$$
(2)

where \(\bar{\mu }\) is a random parameter which is described as

$$\begin{aligned} \bar{\mu }=\mu +\delta k, \end{aligned}$$
(3)

where \(\mu \) is the deterministic parameter, \(\delta \) is regarded as strength of random disturbance, \(k\) is a random variable defined on nonnegative set integer which obeys density function  \(p_{k}\). So it follows from the orthogonal polynomial approximation that the response of lagged logistic system with random parameter can be expressed by the following Fourier series

$$\begin{aligned} x(n,k)E&= \sum \limits _{i=0}^{M}x_{i}(n)P_{i}(k),\nonumber \\ y(n,k)&= \sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k), \end{aligned}$$
(4)

where \(x_{i}(n)=\sum _{k=0}^{N}p_{k}x(n,k)P_{i}(k)\), \( y_{i}(n)=\sum _{k=0}^{N}\) \(p_{k}y(n,k)P_{i}(k)\), \(P_{i}(k)\) is the \(i\)th standard orthogonal polynomial, \(M\) represents the largest order of the polynomial we retain.

Substituting (4) and (3) into (2), we have

$$\begin{aligned}&\left( \sum \limits _{i=0}^{M}x_{i}(n+1)P_{i}(k)\right) =\sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k),\nonumber \\&\left( \sum \limits _{i=0}^{M}y_{i}(n+1)P_{i}(k)\right) =\sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k)\nonumber \\&\quad -\,(\mu +\delta k-1)\sum \limits _{i=0}^{M}x_{i} (n)P_{i}(k)\nonumber \\&\quad -\,(\mu +\delta k)\left( \sum \limits _{i=0}^{M}x_{i}(n)P_{i} (k)\right) \left( \sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k)\right) .\nonumber \\ \end{aligned}$$
(5)

With the help of cycle recurrence formula of orthogonal polynomial [26]

$$\begin{aligned} kP_{i}(k)=\alpha _{i}P_{i+1}(k) +\beta _{n}P_{i}(k)+\gamma _{i} P_{i-1}(k), \end{aligned}$$
(6)

the stochastic term and the nonlinearity term in the right second equation of system (5) are written as, respectively

$$\begin{aligned}&\delta k \sum \limits _{i=0}^{M}x_{i}(n)P_{i}(k)\nonumber \\&\quad =\delta \sum \limits _{i=0}^{M}x_{i}(n) [\alpha _{i}P_{i+1}(k) +\beta _{n}P_{i}(k)+\gamma _{i} P_{i-1}(k)]\nonumber \\&\quad =\delta \left[ \sum \limits _{i=0}^{M}P_{i}(k) (\gamma _{i+1}x_{i+1}(n)+\beta _{i} x_{i}(n)\right. \nonumber \\&\qquad \left. +\,\alpha _{i-1}x_{i-1}(n))-\,\alpha _{i}x_{i}(n)P_{i+1}(k)\right] , \end{aligned}$$
(7)

and

$$\begin{aligned}&\delta k\left( \sum \limits _{i=0}^{M}x_{i}(n)P_{i}(k)\right) \left( \sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k)\right) \nonumber \\&\quad =\delta k \sum \limits _{i=0}^{M\times 2}S_{i}(n) (P_{i}(k)), \end{aligned}$$
(8)

where \(S_{i}(n)\) which stand for the linear combination of related single polynomials in nonlinearity term are calculated by computer algebraic.

According to Eqs. (7), (8) and (5), the system can be further reduced to

$$\begin{aligned}&\left( \sum \limits _{i=0}^{M}x_{i}(n+1)P_{i}(k)\right) =\sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k),\nonumber \\&\quad \left( \sum \limits _{i=0}^{M}y_{i}(n+1)P_{i}(k)\right) =\sum \limits _{i=0}^{M}y_{i}(n)P_{i}(k)\nonumber \\&\qquad +\,(1-\mu )\sum \limits _{i=0}^{M}x_{i}(n)P_{i}(k)\nonumber \\&\qquad -\,\mu \sum \limits _{i=0}^{2M}S_{i}(n)P_{i}(k)-\delta \sum \limits _{i=0}^{M}\left[ P_{i}(k)(\gamma _{i+1}x_{i+1}(n)\right. \nonumber \\&\left. \qquad +\,\beta _{i}x_{i}(n) +\alpha _{i-1}x_{i-1}(n)) -\alpha _{i}x_{i}(n)P_{i+1}(k)\right] \nonumber \\&\qquad -\,\delta \sum \limits _{i=0}^{2M}\left[ P_{i}(k) (\gamma _{i+1}S_{i+1}(n)+\beta _{i} S_{i}(n)\right. \nonumber \\&\left. \qquad +\,\alpha _{i-1}S_{i-1}(n))-\alpha _{i}S_{i}(n)P_{i+1}(k)\right] , \end{aligned}$$
(9)

where \(x_{-1}(n),x_{M+1},S_{-1}(n),S_{M+1}(n)\) are zero by the principle of approximation.

Multiplying both sides of system (9) by \(P_{i}(k),i=0,1,\ldots ,M\) in sequence and taking expectation with respect to \(k\), according to orthogonal polynomial approximation of discrete random function in the Hilbert spaces and the orthogonality of standard orthogonal polynomials, we can finally get the equivalent deterministic logistic equation. When \(M\rightarrow \infty \), the lagged logistic system with random parameter is strictly equivalent to Eq. (9). In order to facilitate the numerical analysis of this paper, we select \(M=1\) and approximately obtain the equivalent deterministic system of lagged logistic system with random parameter

$$\begin{aligned} x_{0}(n+1)&= y_{0}(n),\nonumber \\ y_{0}(n+1)&= y_{0}(n)+(1-\mu )x_{0}(n)-\mu S_{0}(n)\nonumber \\&\quad -\,\delta (\gamma _{1}x_{1}(n)+\beta _{0}x_{0}(n))-\delta (\gamma _{1} S_{1}(n)\nonumber \\&\quad +\,\beta _{0}S_{0}(n)),\nonumber \\ x_{1}(n+1)&= y_{1}(n),\nonumber \\ y_{1}(n+1)&= y_{1}(n)+(1-\mu )x_{1}(n)-\mu S_{1}(n)\nonumber \\&\quad -\,\delta (\gamma _{2}x_{2}(n)+\beta _{1}x_{1}(n)+\alpha _{0} x_{0}(n))\nonumber \\&\quad -\,\delta (\gamma _{2}S_{2}(n)+\beta _{1}S_{1} (n)+\alpha _{0} S_{0}(n)).\nonumber \\ \end{aligned}$$
(10)

Then, the approximate random response of original stochastic logistic system can be expressed as

$$\begin{aligned} x(n,k)&= x_{0}(n)P_{0}(k)+x_{1}(n)P_{1}(k),\\ y(n,k)&= y_{0}(n)P_{0}(k)+y_{1}(n)P_{1}(k), \end{aligned}$$

and the ensemble mean response of it (EMR) is calculated as

$$\begin{aligned} E[x(n,k)]&= x_{0}(n)E[P_{0}(k)]+x_{1}(n)E[P_{1}(k)],\\ E[y(n,k)]&= y_{0}(n)E[P_{0}(k)]+y_{1}(n)E[P_{1}(k)]. \end{aligned}$$

The strength of random disturbance of the parameter resulting from the uncertainty is small in real model, so in this paper, we suppose that the random intensity \(\delta \) is \(<\)0.1. Meanwhile, we take the initial conditions of system (10) and deterministic system the same as follows, namely

$$\begin{aligned}&x_{0} = x_{0}(0)=0.2,y_{0}=y_{0}(0)=0.1,\\&x_{1}(0) = y_{1}(0)=0. \end{aligned}$$

So we take

$$\begin{aligned} x(0)=(0.2,0)^{T},y(0)=(0.1,0)^{T}. \end{aligned}$$

3 Hopf bifurcation analysis

The influence intensity of prey, environment and pollution cannot be simply described as a kind of environment noise. In this two-dimensional lagged logistic system, the uncertainty can be express as the growth coefficient. At the same time, we know that in this paper, the internal random parameter is increased from zero, and as the mean value and variance of the random variable are larger, the nonuniformity of random parameter measured by experiment or data is more serious. So the Poisson distribution growth coefficient is better to choose. In this paper, we choose the random variable as Poisson distribution with probability density function \(p_{k}\) and the weight orthogonal polynomial as standard Charlier polynomials. So the coefficients \(\alpha _{i},\beta _{i},\gamma _{i}\) are \(1,i+\varepsilon ,\varepsilon i,\), respectively [27], where \(\varepsilon \) is standard deviation of random variable \(k\) and the standard deviation \(\varepsilon \) is equal to 1 in this paper.

3.1 Existence of Hopf bifurcation

We firstly introduce the Hopf bifurcation conditions [28–30] about the discrete-time system as follows:

(H1):

Eigenvalue assignment. The Jacobian matrix of the discrete system has a pair of complex conjugate eigenvalues \(\lambda _{1}(\mu )\) and \(\bar{\lambda }_{1}(\mu )\) with \(|\lambda _{1}(\mu _{c})|=1\) at \(\mu =\mu _{c}\) and the other eigenvalues \(\lambda _{j}(\mu ),j=3,4,\ldots n\), with \(|\lambda _{j}(\mu _{c})|<1\);

(H2):

Transversality condition: \(d|\lambda _{1}(\mu _{c})|/d \mu \ne 0\);

(H3):

Nonresonance condition \(\lambda ^{m}_{1}(\mu _{c})\ne 1\) or resonance condition \(\lambda ^{m}_{1}(\mu _{c})=1,m=3,4,\ldots \).

Let us assume that the solutions of deterministic equivalent lagged logistic system undergo a Hopf bifurcation on some submanifold in parameter space corresponding to a critical value \(\mu =\mu _{c}\).

The Jacobian matrix of system (10) with Poisson coefficient at fixed point \((0, 0, 0,0)\) is

$$\begin{aligned} A&= \left( \begin{array}{cccc}\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 1-\mu -\delta &{}\quad 1&{}\quad -\delta &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ -\delta &{}\quad 0 &{}\quad 1-\mu -2\delta &{}\quad 1 \end{array}\right) . \end{aligned}$$
(11)

Then, the characteristic polynomial of Jacobian matrix A is

$$\begin{aligned} f(\lambda )=\lambda ^{4}+a_{1}\lambda ^{3}+a_{2}\lambda ^{2}+a_{3}\lambda +a_{4}, \end{aligned}$$
(12)

where \(a_{i}(i=1,\ldots ,4)\) are coefficients of Eq. (12), which are shown as follows:

$$\begin{aligned}&a_{1}=-2,\\&a_{2}=3\delta +2\mu -1,\\&a_{3}=-2\mu -3\delta +2,\\&a_{4}=\delta ^{2}+2\mu -3\delta +{\mu }^{2}+3\mu \delta +1. \end{aligned}$$

By the Mathematical software, all eigenvalues are

$$\begin{aligned} \lambda _{1,2}=\frac{1}{2}\pm \frac{\sqrt{5-2\sqrt{5}\delta -6\delta -4\mu }}{2},\end{aligned}$$
(13)
$$\begin{aligned} ~\lambda _{3,4}=\frac{1}{2}\pm \frac{\sqrt{5+2\sqrt{5}\delta -6\delta -4\mu }}{2}. \end{aligned}$$
(14)

If the system (10) occurs Hopf bifurcation, Eq. (12) must exist a pair of conjugate complex roots, that is to say the parameter \(\mu \) must satisfy one of the below conditions

$$\begin{aligned} \mu >\frac{5-2\sqrt{5}\delta -6\delta }{4}~or~\mu >\frac{5+2\sqrt{5} \delta -6\delta }{4}. \end{aligned}$$
(15)

So the eigenvalue’s modules are written as

$$\begin{aligned}&|\lambda _{1}|=|\lambda _{2}|=\sqrt{\mu -1+\frac{1}{2}\sqrt{5} \delta +\frac{3}{2}\delta },\end{aligned}$$
(16)
$$\begin{aligned}&|\lambda _{3}|=|\lambda _{4}|=\sqrt{\mu -1-\frac{1}{2}\sqrt{5} \delta +\frac{3}{2}\delta }. \end{aligned}$$
(17)

Now, discussing when the eigenvalue’s module \(|\lambda _{1}|\) \(=|\lambda _{2}|=1\) or \(|\lambda _{3}|=|\lambda _{4}|=1\), we can get the relations between the bifurcation parameter and the random strength

$$\begin{aligned} \mu _{1}=2-\frac{1}{2}\sqrt{5}\delta -\frac{3}{2}\delta , ~\mu _{2}=2+\frac{1}{2}\sqrt{5}\delta -\frac{3}{2}\delta . \end{aligned}$$
(18)

Substituting all expressions of Eq. (18) into all eigenvalues (13)(14), respectively, for the random strength \(\delta >0\) and small, so there is only one equation \(\mu _{c}=\mu _{1}=2-\frac{1}{2}\sqrt{5}\delta -\frac{3}{2}\delta \) which can satisfy eigenvalue’s module is equal to 1. Then, the expression \(\mu =\mu _{c}\) is substituted into Eq. (12); all eigenvalues are as follows

$$\begin{aligned} \lambda _{1}&= \frac{1}{2}+\frac{\sqrt{3}}{2}I, ~\lambda _{2}=\frac{1}{2}-\frac{\sqrt{3}}{2}I~(I^{2}=-1),\\ \lambda _{3}&= \frac{1}{2}+\frac{\sqrt{-3+4\sqrt{5}\delta }}{2},~ \lambda _{4}=\frac{1}{2} -\frac{\sqrt{-3+4\sqrt{5}\delta }}{2}. \end{aligned}$$

Apparently, the Hopf bifurcation condition (H1) about the system (10) is satisfied. Meantime, the derivative of module \(\lambda _{1}\) at \(\mu =\mu _{c}\) is written as

$$\begin{aligned} d|\lambda _{1}(\mu _{c})|/d\mu&= \frac{1}{\sqrt{-4+2\sqrt{5}\delta + 6\delta +4\mu }}\mid _{\mu =\mu _{c}}\nonumber \\&= \frac{1}{2}\ne 0, \end{aligned}$$
(19)

and

$$\begin{aligned} \lambda _{1}^{m}(\mu _{c})=\left( \frac{1}{2}+\frac{\sqrt{3}}{2}I\right) ^{6}=1. \end{aligned}$$
(20)

It obviously follows that when \(m=6\), the third condition (H3): Resonance condition \(\lambda ^{m}_{1}(\mu _{c})=1\) is satisfied. So all the conditions for the existence of Hopf bifurcation are all set up as \(\mu =\mu _{c}\). The above analysis can be summarized as:

Theorem 1

(Existence of Hopf bifurcation) The equivalent deterministic lagged logistic system occurs Hopf bifurcation at the fixed point \((0,0,0,0)\), when the system parameter \(\mu \) goes by the critical value \(\mu _{c}=2-\frac{1}{2}\sqrt{5} \delta -\frac{3}{2}\delta \).

3.2 Direction and stability of the Hopf bifurcation

In this section, we shall use the Kuznetsov’s normal form method and center manifold theory [31] to investigate the direction and stability of Hopf bifurcation.

Since the fixed point of system (10) is the origin \(O(0,0,0,0)\), the stochastic lagged logistic system can be expressed as

$$\begin{aligned}&X_{n+1}=F_{\nu }(X_{n})=AX_{n}+N(X_{n}),\nonumber \\&N(X_{n})=\frac{1}{2}B(X_{n},X_{n})+\frac{1}{6}C(X_{n},X_{n}, X_{n})\nonumber \\&\qquad \quad \,+\,O(X^{4}_{n}), \end{aligned}$$
(21)

where \(A\) is Jacobian matrix of system (10) at origin point. The multilinear functions \(B:R^{2}\times R^{2}\rightarrow R^{2}\) and \(C:R^{3}\times R^{3}\rightarrow R^{3}\) are, respectively, defined by

$$\begin{aligned}&B_{i}(x,y)=\sum \limits _{j,k=1}^{n}\frac{{\partial }^{2}X_{i}(\xi )}{\partial \xi _{j} \partial \xi _{k}}|_{\xi =0}x_{j}y_{k},~i=1,2,\\&C_{i}(x,y,z){=}\sum \limits _{j,k,l=1}^{n}\frac{{\partial }^{3}X_{i}(\xi )}{\partial \xi _{j} \partial \xi _{k},\partial \xi _{l}}|_{\xi =0}x_{j}y_{k}z_{l},i{=}1,2. \end{aligned}$$

We know that \(N(X_{n})\) of system (10) is described as

$$\begin{aligned} N(X_{n})=\left\{ \begin{array}{ll} N_{1}=0,\\ N_{2}=-\bar{\mu }S_{0}(n)-\delta (S_{0}(n)+S_{1}(n)),\\ N_{3}=0,\\ N_{4}=-\bar{\mu }S_{1}(n)-\delta (S_{0}(n)+2S_{1}(n)),\\ \end{array} \right. \end{aligned}$$

where \(X_{n}=(x_{0}(n),y_{0}(n),x_{1}(n),y_{1}(n))^{T}\). Therefore, \(B(x,x)\) and \(C(x,x,x)\) for the system (10) are

$$\begin{aligned}&B_{i}(\xi ,\eta )\!=\!\sum \limits _{j,k=0}^{4}\frac{{\partial }^{2}(-\bar{\mu }S_{i}(n)\!-\! \delta (S_{i}(n)\!+\!(i\!+\!1)S_{i+1}(n)))}{\partial \xi _{j} \partial \xi _{k}}\nonumber \\&\quad |_{x=0}\xi _{j}\eta _{k},~i=0,1,C_{i}(\xi ,\eta ,\gamma )=0,~i=0,1. \end{aligned}$$
(22)

Meantime, according to the existence of Hopf bifurcation, the eigenvalues of matrix A are \(\lambda _{1,2}(\mu _{c})=\frac{1}{2}\pm \frac{\sqrt{3}}{2}I =e^{\pm i\theta _{0}},~\theta _{0}=\frac{\pi }{3}\). Let \(q \in C^{n}\) be a complex eigenvector corresponding to \(\lambda _{1}\) and \(p \in C^{n}\) be an adjoint eigenvector which satisfy the following properties

$$\begin{aligned}&Aq=e^{i\theta _{0}}q,A\bar{q}=e^{-i\theta _{0}}\bar{q},\nonumber \\&A^{T}p=e^{-i\theta _{0}}p, A^{T}\bar{p}=e^{i\theta _{0}}\bar{p}, \end{aligned}$$
(23)

where vector \(\langle p,q\rangle =\sum _{1=1}^{n}\bar{p}_{i}q_{i}=1\). The \(p,q \in C^{n}\) can be computed by Maple

$$\begin{aligned} q&= \left( 1,\frac{1+\sqrt{3}I}{2},\frac{1+\sqrt{5}}{2}, \frac{(1+\sqrt{5})(1+\sqrt{3}I)}{4}\right) ^{T},\nonumber \\ p&= \frac{1}{\sqrt{15}I}\left( -\frac{(1+\sqrt{3}I)(\sqrt{5}-1)}{4}, \frac{-1+\sqrt{5}}{2},\right. \nonumber \\&\quad \left. -\,\frac{1+\sqrt{3}I}{2},1\right) ^{T}. \end{aligned}$$
(24)

And we also have

$$\begin{aligned} B(q,q)&= (0,-(8+2\sqrt{5})-(8\sqrt{3}+2\sqrt{15} \nonumber \\&-\,\sqrt{15}\delta -\sqrt{3}\delta )I,0,-(8+4\sqrt{5})-(8\sqrt{3}\nonumber \\&+\,4\sqrt{15} -\delta -\sqrt{3}\delta )I)^{T},\nonumber \\ B(q,\bar{q})&= (0,-(8+2\sqrt{5})\nonumber \\&+\,(8\sqrt{3}+2\sqrt{15} -\sqrt{15}\delta -\sqrt{3}\delta )I,\nonumber \\&0,-(8+4\sqrt{5}-2\sqrt{5}\delta -3) +(8\sqrt{3}+4\sqrt{15}\nonumber \\&-\,\delta -\sqrt{3}\delta )I)^{T},\nonumber \\ B(\bar{q},\bar{q})&= (0,-(8+2\sqrt{5})+(8\sqrt{3} +2\sqrt{15}\nonumber \\&-\,\sqrt{15}\delta -\sqrt{3}\delta )I,0,-(8+4\sqrt{5})+(8\sqrt{3}\nonumber \\&+\,4\sqrt{15} -\delta +\sqrt{3}\delta )I)^{T}. \end{aligned}$$
(25)

So the direction coefficient of bifurcation of a closed invariant curve can be calculated by

$$\begin{aligned} a(O)&= Re\left( \frac{e^{- i\theta _{0}}g_{21}}{2}\right) \nonumber \\&\quad -Re \left( \frac{(1-2e^{i\theta _{0}})e^{-2 i\theta _{0}}}{2(1- e^{i\theta _{0})}}g_{20}g_{11}\right) \nonumber \\&\quad -\,\frac{1}{2}|g_{11}|^{2} -\frac{1}{4}g_{02}|^{2}, \end{aligned}$$
(26)

where

$$\begin{aligned} g_{20}&= \langle p,B(q,q)\rangle =\frac{9\sqrt{5}}{5}+7- \frac{\sqrt{5}}{5}\delta \nonumber \\&\quad -\,\left( \frac{3\sqrt{15}}{5}+\frac{7\sqrt{3}}{3}+\frac{\sqrt{15}}{15} \delta \right) I,\nonumber \\ g_{11}&= \langle p,B(q,\bar{q})\rangle =-\frac{9\sqrt{5}}{5}-7 +(\sqrt{5}+2)\delta \nonumber \\&\quad -\,\left( \frac{3\sqrt{15}}{5}+\frac{7\sqrt{3}}{3} -\frac{\sqrt{15}}{15}\delta +\frac{2\sqrt{3}}{3} \delta \right) I,\nonumber \\ g_{02}&= \langle p,B(\bar{q},\bar{q})\rangle =-\frac{9\sqrt{5}}{5}-7 +\frac{\sqrt{5}}{5}\delta \nonumber \\&\quad -\,\left( \frac{3\sqrt{15}}{5}+\frac{7\sqrt{3}}{3} +\frac{\sqrt{15}}{15}\delta \right) I,\nonumber \\ g_{21}\!&= \!\langle p,C(q,q,\bar{q})\rangle {+}2\left\langle p,B(q,(E{-}A)^{-1}B(q,\bar{q}))\right\rangle \nonumber \\&\quad +\,\langle p,B(\bar{q},(e^{2 i\theta }E-A)^{-1}B(q,\bar{q}) \rangle \nonumber \\&\quad +\,\frac{e^{-i\theta _{0}}(1-2e^{ i\theta _{0}})}{1-e^{ i\theta _{0}}}\langle p,B(q,q)\rangle \cdot \langle p,B(q,\bar{q})\rangle \nonumber \\&\quad -\,\frac{2}{1-e^{-i\theta _{0}}}|\langle p,B(q,\bar{q}) \rangle |^{2}\nonumber \\&\quad -\,\frac{e^{i\theta _{0}}}{e^{3i\theta _{0}}-1}|\langle p,B(\bar{q},\bar{q})\rangle |^{2}. \end{aligned}$$
(27)

Substituting Eqs. (24), (26) into (25), when random intensity \(\delta \) is varied from 0 to 0.05, the direction coefficient of bifurcation \(a(O)<0\) is obtained. On the basis of criterion about stability, when the bifurcation parameter \(\mu _{c}=2-\frac{1}{2}\sqrt{5}\delta -\frac{3}{2}\delta \) and the random perturbation intensity of system is a sufficiently small positive real number, the stochastic lagged logistic system occurs the supercritical bifurcation at fixed point \(O(0,0,0,0)\) that is to say the system has a stable limit cycle around the fixed point.

4 Numerical simulations and numerical analysis

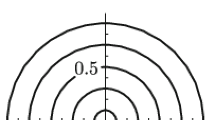
As the random perturbation intensity \(\delta =0.00\), the stochastic lagged logistic system (2) can be degenerated to its original deterministic system. We have known when bifurcation parameter \(\mu _{c}=2\), the system (2) undergoes a Hopf bifurcation at fixed point \((0,0)\). Figure 1 shows the bifurcation phenomenon about the stochastic lagged logistic system when the random intensity \(\delta =0.00,0.005,0.01,0.05\), respectively. By the above theoretical analysis and numerical simulations, the critical value of Hopf bifurcation about the stochastic lagged logistic system is \(\mu _{c}=2-\frac{1}{2}\sqrt{5}\delta -\frac{3}{2}\delta \).

Fig. 1
figure 1

Bifurcation diagrams of deterministic and stochastic lagged logistic system

Full size image

4.1 Hopf bifurcation of the stochastic lagged logistic system

For the strength of random disturbance \(\delta \) is very small, if parameters \(\mu =1.995,\delta =0.001\), the phase trajectories and the time history diagrams of EMR of equivalent deterministic system (10) gradually converge to zero in Fig. 2a, b. We know that the stochastic lagged logistic system does not occur Hopf bifurcation which is illustrated by Fig. 2. Increasing the random intensity to \(\delta =0.005\), the phase trajectories and time history diagrams of system (10) that converge a limit circle are shown in Fig. 3.

Fig. 2
figure 2

Phase portrait (a) and time history diagram (b) for \(\mu =1.995, \delta =0.001\)

Full size image
Fig. 3
figure 3

Phase portrait (a) and time history diagram (b) for \(\mu =1.995, \delta =0.005\)

Full size image

Apparently in Fig. 3, the stochastic lagged logistic system undergoes stochastic Hopf bifurcation. Meantime, when the random intensity \(\delta \) is equal to 0.001, 0.005, respectively, the critical values of bifurcation are 1.997381966, 1.98690983. However, the parameter \(\mu =1.995\) is between the two above critical values. According to the above numerical analysis, we discover that the critical value for Hopf bifurcation in the stochastic lagged logistic system is varying from random intensity.

4.2 The influence of random intensity on Hopf bifurcation

When system parameter \(\mu =1.9\), \(\delta \) is chosen as \(0.00,0.001,0.005\), respectively, the phase trajectories and time history diagrams of EMR converge to zero, which are shown as Fig. 4. Figure 4b, d are local portrait of Fig. 4a, c. As the bifurcation parameter is increasing to \(\mu =2.005\), the phase trajectories and time history diagrams converge to their stable limit cycles which are shown in Fig. 5. Figure 5b is the local portrait of Fig. 5a. From Figs. 4, 5, we find that with the change of bifurcation parameter, the phase trajectories of the deterministic system accord with the phase trajectories of stochastic lagged logistic system. The supercritical bifurcation happens in both two systems.

Fig. 4
figure 4

Phase portrait (a, b) and time history diagram (c) for \(\mu =1.9\)

Full size image
Fig. 5
figure 5

Phase portrait (a, b) and time history diagram (c) for \(\mu =2.005\)

Full size image

Based on theoretical analysis and numerical simulations, we have found that the stochastic lagged logistic system also occurs the Hopf bifurcation with the variation of bifurcation parameter. Comparing to the deterministic system, random intensity obviously affects the bifurcation critical value of its stochastic system, and the bifurcation critical value decreases with the random intensity, that is to say that the Hopf bifurcation point is drifting.

5 Conclusion

The orthogonal polynomial approximation theory of discrete random function is applied to investigate the Hopf bifurcation of stochastic lagged logistic system. We successfully reduce the lagged logistic system with random parameter to its equivalent deterministic system. Through the mathematical analysis, the normal form method and center manifold theory, it is discovered that the critical value of Hopf bifurcation in the stochastic discrete system is influenced by the random intensity and the direction and stability about it is not changed as the random intensity is small. Theoretical results are verified by the numerical simulations. Meanwhile, Hopf bifurcation point is drifting with the changes in random intensity is discussed through the numerical analysis.