Primary parametric resonance–primary resonance response of stiffened plates with moving boundary conditions

Abstract

An approach is presented to investigate the nonlinear vibration of stiffened plates. A stiffened plate is divided into one plate and some stiffeners, with the plate considered to be geometrically nonlinear, and the stiffeners taken as geometrically nonlinear Euler beams. Lagrange equation and modal superposition method are used to derive the dynamic equilibrium equations of the stiffened plate according to the energy of the system. Besides, the effect caused by boundary movement is transformed into equivalent excitations. The primary parametric resonance–primary resonance of the stiffened plate is studied by using homotopy analysis method. Numerical examples for stiffened plates with different thicknesses of the plates are presented to discuss the amplitude–frequency and amplitude–excitation relationship of the primary parametric resonance–primary resonance. In addition, the analysis on how the damping coefficients and the transverse excitations influence amplitude–frequency curves is also carried out. Some nonlinear vibration characteristics of stiffened plates are obtained, which are useful for engineering design.

1 Introduction

Structures consisting of thin plate stiffened by a set of stiffeners are widely used in engineering, such as bridges, aircrafts and ships. Since these structures are subjected to dynamic loads, it is necessary to study the dynamic property of stiffened plates, which can provide references for engineering design.

Nowadays, a lot of methods have been proposed to study the vibration of stiffened plates, including grillage model [1], Rayleigh-Ritz method [2], finite element method [3], finite difference method [4, 5], differential quadrature method [6], meshless method [7] and other methods [8–10]. However, the present study focuses on the linear vibration of stiffened plates. Researches on the nonlinear vibration of stiffened plates are scarce so far. If the amplitude of a plate is much less than its thickness, the linear theory is feasible, if not, the nonlinear theory is essential. The exact solution of nonlinear vibration is difficult to obtain, so the approximate analysis technique is adopted by most researchers. The common methods include Ritz method, Galerkin method, perturbation method, successive approximation method, finite difference method, Runge–Kutta integration method[11–17]. Recently, some researchers propose and develop homotopy analysis method [18, 19], which is suitable to investigate not only weakly nonlinear problems but also strongly nonlinear problems.

In the recent literature, most investigations on the vibration of stiffened plates do not take the damping into account, which cannot reflect the real dynamic characteristics of stiffened plates. Only a few works combine both geometrical nonlinearity and damping: Amabili made an experimental and numerical study of plates with viscous damping and subjected to harmonic excitation [20, 21]. This author studied also numerically circular cylindrical panels with viscous damping [22]. An amplitude equation, based on an approximated harmonic balance method and Galerkin’s procedure, was proposed by Daya et al. [23] to study sandwich beams and plates with central viscoelastic layers. Touze and Amabili built reduced-order models for damped geometrically nonlinear systems [24]. They considered a modal viscous damping. Ribeiro and Petyt [25] used the hierarchical finite element method in an in-depth investigation of the nonlinear response of clamped rectangular plates. Boumediene et al. investigated nonlinear forced vibration of damped plates by an asymptotic numerical method [26].

In the practical engineering, the excitation usually transfers to the plate through the support. For example, if a structure is subjected to the seismic excitation, the displacement of the support is time-varying. This paper deals with the large amplitude vibration of stiffened plates with moving boundary conditions. The effect caused by boundary movement is transformed into equivalent excitations. Besides, the damping of the plate is taken into account as viscoelastic damping. Even if this structural damping is relatively simple, it represents a large part of engineering applications. The strain and kinetic energy of both the plate and stiffeners are established, and then Lagrange’s equation is used to derive the governing equation of motion. Numerical examples for stiffened plates with different thicknesses of the plates are presented to discuss the steady response of the amplitude–frequency relationship of the primary parametric resonance–primary resonance. In addition, the analysis on how the damping coefficients and the transverse excitations influence the dynamic characteristics of stiffened plates is carried out. Some nonlinear vibration characteristics of stiffened plates are obtained, which are useful for engineering design.

2 Derivation of the governing equation

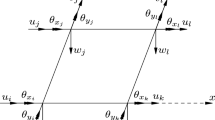
In order to simplify the problem, material nonlinearity is not considered in this paper, and the material of the stiffened plate is isotropic. Consider a stiffened plate in Fig. 1, which is composed of $x$ stiffeners, $y$ stiffeners and one plate. The generally used orthotropic theory is that both $x$ stiffeners and $y$ stiffeners are smeared over the plate. However, this theory has three disadvantages: first, the dynamical differential equation is difficult to formulate because of the non-uniform mass in per unit area; second, the neutral surfaces may not coincide in the orthogonally stiffened directions; third, this theory is inaccurate for the computation of the local effect. This paper deals with the stiffeners and the plate separately, formulates the energy equations respectively and then substitutes the energy equations into Lagrange’s equation. In Ref. [27], the authors studied the nonlinear dynamic response of a stiffened plate with four edges clamped under primary resonance excitation. Thus, the detailed derivation of the governing equation is not given in this paper, which can refer to Ref. [27].

Fig. 1

Structure of a stiffened plate

In Fig. 1, $u$ and $v$ denote the displacements of the middle surface of the plate along the $x$ direction and the $y$ direction, respectively, and $w$ denotes the deflection of the plate. According to Ref. [27], the nonlinear dynamic differential equations can be written in dimensionless form as

$$\begin{aligned}&u_{ij}^*d_{pqij}^{1*} +\frac{1}{2}v_{ij}^*d_{pqij}^{2v*} +\frac{1}{2}w_{ij}^*w_{mn}^*d_{pqijmn}^{4*} =\frac{1}{2}Q_{pq}\nonumber \\ \end{aligned}$$

(1a)

$$\begin{aligned}&\frac{1}{2}u_{ij}^*d_{ijpq}^{2u*} +v_{ij}^*d_{pqij}^{3*} +\frac{1}{2}w_{ij}^*w_{mn}^*d_{pqijmn}^{5*} =\frac{1}{2}Q_{pq}\nonumber \\ \end{aligned}$$

(1b)

$$\begin{aligned}&\frac{\hbox {d}^{2}\left( {w_{ij}^*} \right) }{\hbox {d}\tau ^{2}}\left( {f_{pqij}^{3*} +g_{pqij}^*} \right) \nonumber \\&\qquad +\,w_{ij}^*c_{pqij}^*+u_{ij}^*w_{mn}^*d_{ijpqmn}^{4u*} +v_{ij}^*w_{mn}^*d_{ijpqmn}^{5v*}\nonumber \\&\qquad +\,2w_{ij}^*w_{mn}^*w_{kl}^*d_{pqijmnkl}^{6*} +w_{ij}^*e_{pqij}^*=\frac{1}{2}Q_{pq}\nonumber \\ \end{aligned}$$

(1c)

The expression of each tensor is given in Appendix .

By solving Eqs. (1a) and (1b), the in-plane generalized coordinates $u_{ij}^*$ and $v_{ij}^*$ can be obtained as follows:

$$\begin{aligned}&\left[ {u_{11}^*\;\cdots \;u_{ij}^*\;\cdots \;u_{MN}^*\;v_{11}^*\;\cdots \;v_{ij}^*\;\cdots \;v_{MN}^*} \right] ^{T}\nonumber \\&\quad =\left[ k \right] ^{-1}\left\{ d \right\} \end{aligned}$$

(2)

where $\left[ k \right]$ is the coefficient matrix in Eqs. (1a) and (1b); $\left\{ d \right\}$ is the constant matrix in Eqs. (1a) and (1b).

Substitute $u_{ij}^*$ and $v_{ij}^*$ in Eq. (1c) and obtain the nonlinear differential equation with respect to $w_{ij}^*$. Then, it can be solved according to mathematical methods.

3 Solution procedure

3.1 Displacements of the stiffened plate

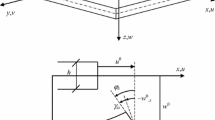
Consider $x=0$ boundary is clamped, and the other three boundaries are simply supported and immovable. The boundary displacements of the stiffened plate are expressed in Fig. 2. Suppose the transverse and rotational displacements are $\delta _1 \left( t \right) \sin \frac{\pi y}{b}$ and $\delta _2 \left( t \right)$ on the boundary $x=a$, respectively. Hence, the boundary conditions should be: $u=v=w={\partial w}/{\partial x}=0$ at $x=0$; $u=v=$0, $w=\delta _1 \left( t \right) \sin \frac{\pi y}{b}$ and ${\partial w}/{\partial x}=\delta _2 \left( t \right)$ at $x=a$; $u=v=w={\partial ^{2}w}/{\partial y^{2}}=0$ at $y=0,b$.

Fig. 2

Boundary displacements of the stiffened plate

The transverse displacement $w\left( {x,y,t} \right)$ of the plate is composed of two parts: one is $w_r \left( {x,y,t} \right)$ which is caused by the boundary movement, the other is $w_s \left( {x,y,t} \right)$ which is caused by the own motion of the plate. Suppose $w_r \left( {x,y,t} \right)$ meets the same boundary conditions as $w\left( {x,y,t} \right)$. Then, the boundary conditions of $w_s \left( {x,y,t} \right)$ are: $u=v=w_{s}={\partial w_s }/{\partial x}=0$ at $x=0,a$; $u=v=w_{s}={\partial ^{2}w_s }/{\partial y^{2}}=0$ at $y=0,b$.

The single-mode assumption neglects all of the coordinates except a single “resonant” coordinate, thus reduces the multi-degree-of-freedom system to a single one. The single-mode approach has been used widely. This is due to the great simplification it introduces in the theory on the one hand, and on the other hand because the error of nonlinear effect, it introduces remains very small for weakly nonlinear vibration [28]. According to the single-mode assumption, the own displacements can take the following forms:

$$\begin{aligned}&u_s \left( {x,y,t} \right) =u_{11}^t \left( t \right) \sin \frac{2\pi x}{a}\sin \frac{\pi y}{b}\end{aligned}$$

(3a)

$$\begin{aligned}&v_s \left( {x,y,t} \right) =v_{11}^t \left( t \right) \sin \frac{\pi x}{a}\sin \frac{2\pi y}{b}\end{aligned}$$

(3b)

$$\begin{aligned}&w_s \left( {x,y,t} \right) =w_{11}^t \left( t \right) \left[ {\sin \left( {\frac{2\pi x}{a}-\frac{\pi }{2}} \right) +1} \right] \sin \frac{\pi y}{b}\nonumber \\ \end{aligned}$$

(3c)

Since there are only the transverse and rotational displacements on the boundary $x=a$, the in-plane displacements caused by boundary movement are 0. Then, the transverse displacement $w_r \left( {x,y,t} \right)$ can be obtained through the method of structure mechanics:

$$\begin{aligned} w_r \left( {x,y,t} \right)&= \left( {\frac{3x^{2}}{a^{2}}-\frac{2x^{3}}{a^{3}}} \right) \delta _1 \left( t \right) \sin \frac{\pi y}{b}\nonumber \\&+\left( {-\frac{x^{2}}{a}+\frac{x^{3}}{a^{2}}} \right) \delta _2 \left( t \right) \sin \frac{\pi y}{b} \end{aligned}$$

(4)

Based on the above analysis, the total displacements of the plate are given by

$$\begin{aligned} u\left( {x,y,t} \right)&= u_{11}^t \left( t \right) \sin \frac{2\pi x}{a}\sin \frac{\pi y}{b}\end{aligned}$$

(5a)

$$\begin{aligned} v\left( {x,y,t} \right)&= v_{11}^t \left( t \right) \sin \frac{\pi x}{a}\sin \frac{2\pi y}{b}\end{aligned}$$

(5b)

$$\begin{aligned} w\left( {x,y,t} \right)&= w_{11}^t \left( t \right) \left[ {\sin \left( {\frac{2\pi x}{a}-\frac{\pi }{2}} \right) +1} \right] \sin \frac{\pi y}{b}\nonumber \\&+\left( {\frac{3x^{2}}{a^{2}}-\frac{2x^{3}}{a^{3}}} \right) \delta _1 \left( t \right) \sin \frac{\pi y}{b}\nonumber \\&+\left( {-\frac{x^{2}}{a}+\frac{x^{3}}{a^{2}}} \right) \delta _2 \left( t \right) \sin \frac{\pi y}{b} \end{aligned}$$

(5c)

3.2 The consideration of damping

Take the damping of the plate into consideration in a viscoelastic type [29], and a non-conservative viscous damping force may be derived from a potential function. The potential function for viscoelastic forces is called the Rayleigh dissipation function, which is given by

$$\begin{aligned} R=\frac{1}{2}\hat{{c}}\int _0^a {\int _0^b {\left( {\dot{u}^{2}+\dot{v}^{2}+\dot{w}^{2}} \right) } } \hbox {d}x\hbox {d}y \end{aligned}$$

(6)

where $\hat{{c}}$ has a different value for each term of the mode expansion.

According to Eqs. (5a)–(5c), Eq. (6) can be written as

$$\begin{aligned} R&= \frac{1}{2}ab\hat{{c}}_{11} \left[ \frac{1}{4}\left( {\dot{u}_{11}^t } \right) ^{2}+\frac{1}{4}\left( {\dot{v}_{11}^t } \right) ^{2}\right. \nonumber \\&+\frac{3}{4}\left( {\dot{w}_{11}^t } \right) ^{2}+\frac{13}{70}\dot{\delta }_1^2 +\frac{a^{2}}{210}\dot{\delta }_2^2 \nonumber \\&\left. {+\frac{1}{2}\dot{w}_{11}^t \dot{\delta }_1 -\frac{\left( {\pi ^{2}+3} \right) a}{12\pi ^{2}}\dot{w}_{11}^t \dot{\delta }_2 -\frac{11a}{210}\dot{\delta }_1 \dot{\delta }_2 } \right] \end{aligned}$$

(7)

where $\hat{{c}}_{11}$ is the damping constants, which can be evaluated from experiments.

The generalized force $Q_j$ with respect to viscoelastic damping can be expressed as:

$$\begin{aligned} Q_j =-\frac{\delta R}{\delta \dot{q}_j } \end{aligned}$$

(8)

where $\dot{q}_j$ is the derivative of the generalized coordinate with respect to time of the $j$th degree of freedom.

Upon neglecting the in-plane damping force, which is an acceptable assumption in most engineering application of thin plates [29]. Taking the transverse damping force into account and according to Eq. (8), the generalized forces with respect to $w_{11}^*$ is expressed as:

$$\begin{aligned} Q_{11} =-\frac{1}{2}ab\hat{{c}}_{11} \left[ {\frac{3}{2}\dot{w}_{11}^t +\frac{1}{2}\dot{\delta }_1^t -\frac{\left( {\pi ^{2}+3} \right) a}{12\pi ^{2}}\dot{\delta }_2 } \right] \end{aligned}$$

(9)

Replacing $w_{11}^t$, $\delta _1$ and $t$ with the dimensionless quantities $w_{11}^*$, $\delta _1^*$ and $\tau$ in Eq. (9), respectively, one obtains

$$\begin{aligned} Q_{11} =-\frac{b}{2a}\sqrt{\frac{D}{\rho h}}\hat{{c}}_{11} \left[ {\frac{3}{2}h\dot{w}_{11}^*+\frac{1}{2}h\dot{\delta }_1^*-\frac{\left( {\pi ^{2}+3} \right) a}{12\pi ^{2}}\dot{\delta }_2 } \right] \nonumber \\ \end{aligned}$$

(10)

where $\delta _1^*={\delta _1 }\big /h$.

3.3 Homotopy analysis method

3.3.1 Differential equation of transverse vibration

According to Eqs. (1a)–(1c), (5a)–(5b) and (10), one can obtain the nonlinear dynamic differential equations as follows:

$$\begin{aligned}&\alpha _1 u_{11}^*+\alpha _2 v_{11}^*+\alpha _3 \left( {w_{11}^*} \right) ^{2}+\alpha _4 \left( {\delta _1^*} \right) ^{2}+\alpha _5 \delta _2^2 \nonumber \\&\qquad +\,\alpha _6 w_{11}^*\delta _1^*+\alpha _7 w_{11}^*\delta _2 +\alpha _8 \delta _1^*\delta _2 =0\end{aligned}$$

(11a)

$$\begin{aligned}&\beta _1 u_{11}^*+\beta _2 v_{11}^*+\beta _3 \left( {w_{11}^*} \right) ^{2}+\beta _4 \left( {\delta _1^*} \right) ^{2}+\beta _5 \delta _2^2 \nonumber \\&\qquad +\,\beta _6 w_{11}^*\delta _1^*+\beta _7 w_{11}^*\delta _2 +\beta _8 \delta _1^*\delta _2 =0\end{aligned}$$

(11b)

$$\begin{aligned}&\gamma _1 \ddot{w}_{11}^*+\gamma _2 \ddot{\delta }_1^*+\gamma _3 \ddot{\delta }_2 +\gamma _4 w_{11}^*+\gamma _5 \delta _1^*+\gamma _6 \delta _2 \nonumber \\&\qquad +\,\gamma _7 u_{11}^*w_{11}^*+\gamma _8 u_{11}^*\delta _1^*+\gamma _9 u_{11}^*\delta _2 \nonumber \\&\qquad +\,\gamma _{10} v_{11}^*w_{11}^*+\gamma _{11} v_{11}^*\delta _1^*\nonumber \\&\qquad +\,\gamma _{12} v_{11}^*\delta _2 +\gamma _{13} \left( {w_{11}^*} \right) ^{3}+\gamma _{14} \left( {w_{11}^*} \right) ^{2}\delta _1^*\nonumber \\&\qquad +\,\gamma _{15} \left( {w_{11}^*} \right) ^{2}\delta _2 +\gamma _{16} w_{11}^*\left( {\delta _1^*} \right) ^{2}+\gamma _{17} w_{11}^*\delta _1^*\delta _2\nonumber \\&\qquad +\,\gamma _{18} w_{11}^*\delta _2^2 +\gamma _{19} \left( {\delta _1^*} \right) ^{3}+\gamma _{20} \left( {\delta _1^*} \right) ^{2}\delta _2 +\gamma _{21} \delta _1^*\delta _2^2 +\gamma _{22} \delta _2^3\nonumber \\&\quad =-\frac{b}{2a}\sqrt{\frac{D}{\rho h}}\hat{{c}}_{11} \left[ {\frac{3}{2}h\dot{w}_{11}^*+\frac{1}{2}h\dot{\delta }_1^*-\frac{\left( {\pi ^{2}+3} \right) a}{12\pi ^{2}}\dot{\delta }_2 } \right] \end{aligned}$$

(11c)

The expressions of $\alpha _1 -\alpha _8$, $\beta _1 -\beta _8$, $\gamma _1 -\gamma _{22}$ are given in Appendix .

To analyze the problem in detail, assume the moving boundary displacements as follows:

$$\begin{aligned}&\delta _1 \left( t \right) =\bar{{\delta }}_1 \cos \left( {\Omega t} \right) \end{aligned}$$

(12a)

$$\begin{aligned}&\delta _2 \left( t \right) =\bar{{\delta }}_2 \cos \left( {\Omega t} \right) \end{aligned}$$

(12b)

where $\bar{{\delta }}_1$ and $\bar{{\delta }}_2$ are the amplitude of the transverse and rotational displacements, respectively; $\Omega$ is the frequency of the excitations.

Replacing the frequency $\Omega$ and time $t$ with dimensionless quantities $\Omega ^{*}$ and $\tau$ in Eqs. (12a) and (12b), respectively, one obtains

$$\begin{aligned}&\delta _1 \left( t \right) =\bar{{\delta }}_1 \cos \left( {\Omega ^{*}\tau } \right) \end{aligned}$$

(13a)

$$\begin{aligned}&\delta _2 \left( t \right) =\bar{{\delta }}_2 \cos \left( {\Omega ^{*}\tau } \right) \end{aligned}$$

(13b)

where $\Omega ^{*}=\Omega a^{2}\sqrt{\frac{\rho h}{D}}$.

Substituting Eqs. (13a) and (13b) into Eqs. (11a)–(11c), solving Eqs. (11a) and (11b), and substituting the expressions of $u_{11}^*$ and $v_{11}^*$ in Eq. (11c), one can obtain the nonlinear dynamic differential equation of transverse vibration as follows:

$$\begin{aligned}&\ddot{w}_{11}^*+p_1 \dot{w}_{11}^*+p_2 w_{11}^*+p_3 \cos \left( {2\Omega ^{*}\tau } \right) w_{11}^*\nonumber \\&\qquad +\,p_4 \cos \left( {\Omega ^{*}\tau } \right) \left( {w_{11}^*} \right) ^{2}+p_5 \left( {w_{11}^*} \right) ^{3}\nonumber \\&\quad =q_1 \cos \left( {\Omega ^{*}\tau } \right) +q_2 \sin \left( {\Omega ^{*}\tau } \right) +q_3 \cos \left( {3\Omega ^{*}\tau } \right) \nonumber \\ \end{aligned}$$

(14)

where the left terms including time-dependent coefficients of the equation are the parametric excitation terms, and the right terms of the equation are the equivalent external excitation terms. The expressions of $p_1 -p_5$, $q_1 -q_3$ are not given in Appendix .

3.3.2 The primary parametric resonance–primary resonance

When the frequency of the parametric excitation is close to twice the natural frequency of the derived system, and the frequency of external excitation is close to the natural frequency of the derived system, the primary parametric resonance–primary resonance may happen. In Eq. (14), $w_{11}^*\left( \tau \right)$ is expressed by $r\left( \tau \right)$, and then, the solution to primary parametric resonance–primary resonance can be written as

$$\begin{aligned} r\left( \tau \right) =\sum _{k=1}^{+\infty } {a_k \cos \left( {k\Omega ^{*}\tau +\theta } \right) } \end{aligned}$$

(15)

where $a_k$ is an unknown real number; $\theta$ is the phase angle.

Before solving Eq. (14) via homotopy analysis method, a nonlinear operator is defined as

$$\begin{aligned}&N\left[ {\phi \left( {\tau ,p} \right) } \right] =\frac{\partial ^{2}\phi \left( {\tau ,p} \right) }{\partial \tau ^{2}}+p_1 \frac{\partial \phi \left( {\tau ,p} \right) }{\partial \tau }\nonumber \\&\quad +\,p_2 \phi \left( {\tau ,p} \right) +p_3 \cos \left( {2\Omega ^{*}\tau } \right) \phi \left( {\tau ,p} \right) \nonumber \\&\quad +\,p_4 \cos \left( {\Omega ^{*}\tau } \right) \left[ {\phi \left( {\tau ,p} \right) } \right] ^{2}+p_5 \left[ {\phi \left( {\tau ,p} \right) } \right] ^{3}\nonumber \\&\quad -\,q_1 \cos \left( {\Omega ^{*}\tau } \right) -q_2 \sin \left( {\Omega ^{*}\tau } \right) -q_3 \cos \left( {3\Omega ^{*}\tau } \right) \nonumber \\ \end{aligned}$$

(16)

where $\phi \left( {\tau ,p} \right)$ is an unknown real number; $\theta$ is a phase angle.

Liao [18] constructed a zeroth-order deformation equation as

$$\begin{aligned} \left( {1-p} \right) L\left[ {\phi \left( {\tau ,p} \right) -r_0 \left( \tau \right) } \right] =p\hbar H\left( \tau \right) N\left[ {\phi \left( {\tau ,p} \right) } \right] \nonumber \\ \end{aligned}$$

(17)

where $p\in \left[ {0,1} \right]$ is an embedding parameter; $L$ is a auxiliary linear operator; $r_0 \left( \tau \right)$ is an initial approximation of $r\left( \tau \right)$; $\hbar$ is a nonzero real number; $H\left( \tau \right)$ is an auxiliary real function.

According to Eq. (15), select auxiliary linear operator as

$$\begin{aligned} L\left[ {\phi \left( {\tau ,p} \right) } \right] =\frac{\partial ^{2}\phi \left( {\tau ,p} \right) }{\partial \tau ^{2}}+\left( {\omega _1^*} \right) ^{2}\phi \left( {\tau ,p} \right) \end{aligned}$$

(18)

where $\omega _1^*$ is the first natural frequency of the derived system, $\left( {\omega _1^*} \right) ^{2}=p_2$.

The initial approximation $r_0 \left( \tau \right)$ can be expressed as

$$\begin{aligned} r_0 \left( \tau \right) =a_0 \cos \left( {\Omega ^{*}\tau +\theta } \right) \end{aligned}$$

(19)

Expand $\phi \left( {\tau ,p} \right)$ in the form of Taylor series as

$$\begin{aligned} \phi \left( {\tau ,p} \right) =r_0 \left( \tau \right) +\sum _{k=1}^{+\infty } {r_k \left( \tau \right) p^{k}} \end{aligned}$$

(20)

where

$$\begin{aligned} r_k \left( \tau \right) =\left. {\frac{1}{k!}\frac{\partial ^{k}\phi \left( {\tau ,p} \right) }{\partial \tau ^{k}}} \right| _{p=0} \end{aligned}$$

(21)

If $\hbar$ and $H\left( \tau \right)$ are appropriate, the series converges when $p=1$. Then, we obtain

$$\begin{aligned} r\left( \tau \right) =r_0 \left( \tau \right) +\sum _{k=1}^{+\infty } {r_k \left( \tau \right) } \end{aligned}$$

(22)

It is bound to be one solution to the primitive equation, which is proved by Liao [18].

Differentiate Eq. (17) m times with respect to $p$ and then setting $p=0$, which is divided by $k$!, and then, we obtain the corresponding kth-order deformation equation as

$$\begin{aligned} L\left[ {r_k \left( \tau \right) -\chi _k r_{k-1} \left( \tau \right) } \right] =\hbar H\left( \tau \right) R_k \left( \tau \right) \end{aligned}$$

(23)

where

$$\begin{aligned}&R_k \left( \tau \right) =\left. {\frac{1}{\left( {k-1} \right) !}\frac{\partial ^{k-1}N\left[ {\phi \left( {\tau ,p} \right) } \right] }{\partial p^{k-1}}} \right| _{p=0}\end{aligned}$$

(24)

$$\begin{aligned}&\chi _k =\left\{ {\begin{array}{ll} 0, &{}\quad k\le 1 \\ 1, &{}\quad k>1 \\ \end{array}} \right. \end{aligned}$$

(25)

In order to follow the principle of expression of solution and coefficient ergodicity [18], the auxiliary real function can be set as

$$\begin{aligned} H\left( \tau \right) =1 \end{aligned}$$

(26)

It can be found that Eq. (24) includes secular terms, which can be expressed as

$$\begin{aligned} R_k \left( \tau \right) =g_0 e^{\pm \mathrm{i}\omega _1^*\tau }+\sum _{n=1}^{M_k } {g_n e^{\pm \mathrm{i}\xi _k \omega _1^*\tau }} \end{aligned}$$

(27)

where $M_{k}$ is a positive integer depending on $k$; $\xi _{k}$ is a real number which is not equal to zero.

In order to eliminate the secular terms, the coefficients of $e^{\pm \mathrm{i}\omega _1^*\tau }$ should be zero. Then, we obtain

$$\begin{aligned} g_0 =0 \end{aligned}$$

(28)

In the following, the primary parametric resonance–primary resonance of Eq. (14) is investigated by setting $k=1$. According to Eq. (27), we obtain

$$\begin{aligned}&R_1 \left( \tau \right) =\ddot{r}_0 +p_1 \dot{r}_0 +p_2 r_0 +p_3 \cos \left( {2\Omega ^{*}\tau } \right) r_0 \nonumber \\&+\,p_4 \cos \left( {\Omega ^{*}\tau } \right) \left( {r_0 } \right) ^{2}+p_5 \left( {r_0 } \right) ^{3}\nonumber \\&-\,q_1 \cos \left( {\Omega ^{*}\tau } \right) {-}q_2 \sin \left( {\Omega ^{*}\tau } \right) {-}q_3 \cos \left( {3\Omega ^{*}\tau } \right) \qquad \end{aligned}$$

(29)

Substituting Eq. (19) in Eq. (29) yields

$$\begin{aligned} R_1 \left( \tau \right)&= e^{\mathrm{i}\Omega ^{*}\tau }\left[ -\frac{1}{2}\left( {\Omega ^{*}} \right) ^{2}a_0 e^{\mathrm{i}\theta }\right. \nonumber \\&+\frac{1}{2}\mathrm{i}p_1 \Omega ^{*}a_0 e^{\mathrm{i}\theta }+\frac{1}{2}p_2 a_0 e^{\mathrm{i}\theta }+\frac{1}{4}p_3 a_0 e^{-\mathrm{i}\theta } \nonumber \\&+\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}+\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}e^{2\mathrm{i}\theta }\nonumber \\&+\left. \frac{3}{8}p_5 \left( {a_0 } \right) ^{3}e^{\mathrm{i}\theta }-\frac{1}{2}q_1 +\mathrm{i}q_2 \right] \nonumber \\&+\,e^{3\mathrm{i}\Omega ^{*}\tau }\left[ \frac{1}{4}p_3 a_0 e^{\mathrm{i}\theta }+\frac{1}{8}p_4 \left( {a_0 } \right) ^{2}e^{2\mathrm{i}\theta }\right. \nonumber \\&+\left. \frac{1}{8}p_5 \left( {a_0 } \right) ^{3}e^{3\mathrm{i}\theta }-\frac{1}{2}q_3 \right] +cn \end{aligned}$$

(30)

where cn is the complex conjugate part to the preceding terms.

In Eq. (14), when the frequency of the parametric excitation is close to twice the natural frequency of the derived system, and the frequency of external excitation is close to the natural frequency of the derived system, the primary parametric resonance–primary resonance may happen. In order to investigate the primary parametric resonance–primary resonance, it is necessary to introduce a detuning parameter $\sigma$, and suppose

$$\begin{aligned} \Omega ^{*}=\omega _1^*+\sigma \end{aligned}$$

(31)

Substituting Eq. (31) in Eq. (30), the solvability condition demands to eliminate the permanent terms, and then, we obtain

$$\begin{aligned}&-\frac{1}{2}\left( {\omega _1^*+\sigma } \right) ^{2}a_0 e^{\mathrm{i}\theta }+\frac{1}{2}\mathrm{i}p_1 \left( {\omega _1^*+\sigma } \right) a_0 e^{\mathrm{i}\theta }\nonumber \\&\quad +\frac{1}{2}\left( {\omega _1^*} \right) ^{2}a_0 e^{\mathrm{i}\theta }+\frac{1}{4}p_3 a_0 e^{-\mathrm{i}\theta }\nonumber \\&\quad +\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}+\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}e^{2\mathrm{i}\theta }\nonumber \\&\quad +\frac{3}{8}p_5 \left( {a_0 } \right) ^{3}e^{\mathrm{i}\theta }-\frac{1}{2}q_1 +\mathrm{i}q_2 =0 \end{aligned}$$

(32)

Set the real and imaginary part to be zero, respectively, and we obtain

$$\begin{aligned}&-\frac{1}{2}\left( {\omega _1^*+\sigma } \right) ^{2}a_0 \cos \theta -\frac{1}{2}p_1 \left( {\omega _1^*+\sigma } \right) a_0 \sin \theta \nonumber \\&\quad +\frac{1}{2}\left( {\omega _1^*} \right) ^{2}a_0 \cos \theta +\frac{1}{4}p_3 a_0 \cos \theta \nonumber \\&\quad +\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}+\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}\cos 2\theta \nonumber \\&\quad +\frac{3}{8}p_5 \left( {a_0 } \right) ^{3}\cos \theta -\frac{1}{2}q_1 =0\end{aligned}$$

(33a)

$$\begin{aligned}&-\frac{1}{2}\left( {\omega _1^*+\sigma } \right) ^{2}a_0 \sin \theta +\frac{1}{2}p_1 \left( {\omega _1^*+\sigma } \right) a_0 \cos \theta \nonumber \\&\quad +\frac{1}{2}\left( {\omega _1^*} \right) ^{2}a_0 \sin \theta -\frac{1}{4}p_3 a_0 \sin \theta \nonumber \\&\quad +\frac{1}{4}p_4 \left( {a_0 } \right) ^{2}\sin 2\theta +\frac{3}{8}p_5 \left( {a_0 } \right) ^{3}\sin \theta +q_2 =0\nonumber \\ \end{aligned}$$

(33b)

Equations (33a) and (33b) are two transcendental equations, and the expressions of $a_{0}$ and $\theta$ cannot be obtained according to these two equations. Therefore, Newton–Raphson method can be used to obtain the non-trivial solutions $a_{0}$ and $\theta$, and then, the amplitude–frequency relationship can also be obtained.

4 Numerical results and discussion

The parameters of the stiffened plates are as follows: $a=1\,\hbox {m}, b=0.6\,\hbox {m}, E=2.1\times 10^{11}\,\hbox {Pa}, \mu =0.3, \rho =7.85\times 10^{3}\,\hbox {kg/m}^{3}, h=0.004\,\hbox {m}$, $A_{x}=A_{y}=2\times 10^{-4}\,\hbox {m}^{2}$, $I_{x}=I_{y}=1\times 10^{-8}\,\hbox {m}^{4}$. Consider both the numbers of $x$ stiffeners and the $y$ stiffeners are three, and the thickness of the plate varies as 0.004, 0.005 and 0.006 m. Then, the influence of damping coefficient and transverse displacement excitation are discussed: (1) Considering the amplitude of the transverse displacement excitation $\bar{{\delta }}_1{\,=\,}0.05\hbox {m}$, the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$ and the damping coefficient $\hat{{c}}_{11} =0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.2\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.5\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, respectively, analyze the amplitude–frequency response $a_{0}-\sigma$ of the primary parametric resonance–primary resonance of the stiffened plates; (2) Considering the damping coefficient $\hat{{c}}_{11} =0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$ and the amplitude of the transverse displacement excitation $\bar{{\delta }}_1 = 0.06$, 0.07, 0.08, 0.09, 0.1 m, respectively, analyze the amplitude–frequency response $a_{0}-\sigma$ of the primary parametric resonance and primary resonance of the stiffened plates. (3) Considering the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$ and the damping coefficient $\hat{{c}}_{11} =0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.2\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.5\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, respectively, analyze the amplitude–excitation $a_{0}-F$ response of the stiffened plates corresponding to $\sigma =1$ ($F$ is the dimensionless amplitude of displacement excitation $\bar{{\delta }}_1$, $F={\bar{{\delta }}_1 }\big /h)$.

4.1 The application of Newton–Raphson method

In this paper, the amplitude–frequency response and amplitude–excitation response are obtained by using Newton–Raphson method. The detailed calculation procedure is introduced in this part.

Equations (33a) and (33b) are two coupled equations with respect to $a_{0}$ and $\theta$. Replace Eqs. (33a) and (33b) with the following expression:

$$\begin{aligned}&f_1 \left( {a_0 ,\theta } \right) =0\end{aligned}$$

(34a)

$$\begin{aligned}&f_2 \left( {a_0 ,\theta } \right) =0 \end{aligned}$$

(34b)

Then, Eqs. (34a) and (34b) can be written as matrix form:

$$\begin{aligned} {\varvec{f}}\left( {a_0 ,\theta } \right) =0 \end{aligned}$$

(35)

The Jacobian matrix corresponding to Eq. (35) is defined as

$$\begin{aligned} {\varvec{f}}^{\prime }\left( {a_0 ,\theta } \right) =\left[ {{\begin{array}{cc} {\frac{\partial f_1 }{\partial a_0 }}&{} {\frac{\partial f_1 }{\partial \theta }} \\ {\frac{\partial f_2 }{\partial a_0 }}&{} {\frac{\partial f_2 }{\partial \theta }} \\ \end{array} }} \right] \end{aligned}$$

(36)

In order to apply Newton–Raphson method to determine amplitude $a_{0}$ and phase angle $\theta$, these two variables are also written as matrix form:

$$\begin{aligned} \varvec{\varLambda } =\left[ {a_0 ,\theta } \right] ^{T} \end{aligned}$$

(37)

The iterative formula of Newton–Raphson method is given by

$$\begin{aligned} \varvec{\varLambda }^{\left( {k+1} \right) }=\varvec{\varLambda }^{\left( k \right) }-\left[ {{\varvec{f}}^{\prime }\left( {\varvec{\varLambda }^{\left( k \right) }} \right) } \right] ^{-1}{\varvec{f}}\left( {\varvec{\varLambda }^{\left( k \right) }} \right) \end{aligned}$$

(38)

As we know, Newton–Raphson method converges rapidly if the initial guess values are close to the solution, otherwise this method may not converge. Here, we choose an initial guess value $\left[ {a_0^0 ,\theta ^{0}} \right] =[1,1]$. If Newton–Raphson method converges in 5 iterations (the error is less than error tolerance $\varepsilon$), this convergence value can be taken as the solution, otherwise the initial guess value is modified as double or half of the previous value, for example, $\left[ {a_0^0 ,\theta ^{0}} \right] =[2,2]$ or $\left[ {a_0^0 ,\theta ^{0}} \right] =[1/2,1/2]$. If some initial guess value makes Newton–Raphson method converge in 5 iterations, the convergence value can be taken as the solution, otherwise the initial guess value is modified repeatedly until convergence.

The calculation flow chart for the application of Newton–Raphson method is illustrated in Fig. 3:

Fig. 3

Calculation flow chart for the application of Newton–Raphson method

4.2 The relationship between damping coefficient and amplitude–frequency response

Figures 4, 5, 6, 7 and 8 show the amplitude–frequency response of the primary parametric resonance–primary resonance of stiffened plates with three different thicknesses of the plate when the amplitude of the transverse displacement excitation $\bar{{\delta }}_1 =0.05\,\hbox {m}$, the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$ and the damping coefficient $\hat{{c}}_{11} =0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.2\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.5\,\hbox {kg}/$ $(\hbox {s}\, \hbox {m}^{2})$, respectively.

Fig. 4

Amplitude–frequency response when damping coefficient is $0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 5

Amplitude–frequency response when damping coefficient is $0.2\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 6

Amplitude–frequency response when damping coefficient is $0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 7

Amplitude–frequency response when damping coefficient is $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 8

Amplitude–frequency response when damping coefficient is $0.5\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

4.3 The relationship between transverse displacement excitation and amplitude–frequency response

Figures 9, 10, 11, 12 and 13 show the amplitude–frequency response of the primary parametric resonance–primary resonance of stiffened plates with three different thicknesses of the plate when the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$, the damping coefficient $\hat{{c}}_{11} =0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, and the amplitude of the transverse displacement excitation $\bar{{\delta }}_1$=0.006, 0.007, 0.008, 0.009, 0.1 m, respectively.

Fig. 9

Amplitude–frequency response when the amplitude of the transverse excitation is 0.06 m

Fig. 10

Amplitude–frequency response when the amplitude of the transverse excitation is 0.07 m

Fig. 11

Amplitude–frequency response when the amplitude of the transverse excitation is 0.08 m

Fig. 12

Amplitude–frequency response when the amplitude of the transverse excitation is 0.09 m

Fig. 13

Amplitude–frequency response when the amplitude of the transverse excitation is 0.1 m

4.4 The relationship between damping coefficient and amplitude–excitation response

Figures 14, 15, 16, 17 and 18 show the amplitude–excitation response of stiffened plates with three different thicknesses of the plate corresponding to $\sigma =1$ when the amplitude of the rotational displacement excitation $\bar{{\delta }}_2 =0.15$ and the damping coefficient $\hat{{c}}_{11} =0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.2\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.3\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, $0.5\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$, respectively.

Fig. 14

Amplitude–excitation response when damping coefficient is $0.1\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 15

Amplitude–excitation response when damping coefficient is $0.2\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 16

Amplitude–excitation response when damping coefficient is $0.3\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 17

Amplitude–excitation response when damping coefficient is $0.4\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

Fig. 18

Amplitude–excitation response when damping coefficient is $0.5\,\hbox {kg}/(\hbox {s}\, \hbox {m}^{2})$

From Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13, it can be observed that (1) all the resonant regions tend to tilt to the right, and thus, the amplitude–frequency response curves have a hardened spring characteristic. (2) The flexural vibration amplitudes increase as the excitation frequency approaches to the linear flexural vibration frequency of the stiffened plates. (3) For each pair of the resonant curves, the upper segment of the right branch is unstable. As $\sigma$ increases from a negative value, $a_{0}$ increases monotonously along the left branch until the peak value, then jumps to the right branch after the peak value. Similarly, as $\sigma$ decreases from a relatively large positive value, $a_{0}$ increases monotonously along the right branch, then jumps to the left branch. (4) The amplitude of $a_{0}$ decreases with the increase in the damping coefficient, while it increases with the increase in the amplitude of the transverse excitation. Both the amplitude of $a_{0}$ and resonant regions decrease with the increase in the thickness of plate. This is because the flexural rigidity of the stiffened plate also increases with the increase in the thickness of plate. Furthermore, the thickness of plate has greater effect on the amplitude of $a_{0}$ than both the damping coefficient and the amplitude of the transverse excitation.

From Figs. 14, 15, 16, 17 and 18, it can be observed that (1) as $F$ increases from zero, $a_{0}$ increases rapidly along the lower solid line, and the solution loses its stability at point A. After point A, the curve exhibits the jumping phenomena, and then, $a_{0}$ increases slowly along the upper solid line. As $F$ decreases from a relatively large value, $a_{0}$ decreases slowly along the upper solid line, and the solution loses its stability at point B. After point B, the curve exhibits the jumping phenomena, and then, $a_{0}$ decreases rapidly along the lower solid line. Points A and B are called the bifurcation points, while the dashed line between points A and B is the unstable solution. Combining both increase and decrease process of $F$, the multi-value behavior of the curves can also be exhibited. (2) As $h$ increases, $a_{0}$ increases within a relatively small values of $F$ and decreases when $F$ is larger than that value.

5 Conclusions

In this work, the nonlinear vibration of stiffened plates with moving boundary conditions has been investigated based on Lagrange equation and the energy principle. The primary parametric resonance–primary resonance of stiffened plates with different thicknesses of the plates is dealt with through numerical examples. Several conclusions can be drawn as follows:

• (1) Almost all perturbation methods are based on such an assumption that a small parameter must exist in an equation. Since homotopy analysis method does not need a small parameter, it has wider application range, which includes not only weakly nonlinear problems but also strongly nonlinear problems.

• (2) Based on Newton–Raphson method, an initial guess value is chosen for trial calculation. If it converges in five iterations (the error is less than error tolerance $\varepsilon$), this convergence value can be taken as the solution, otherwise the initial guess value is modified as double or half of the previous value. This approach can make Newton–Raphson method converge rapidly.

• (3) The amplitude–frequency curve has a hardened spring characteristic; the amplitude decreases with the increase in the damping coefficient, while it increases with the increase in the amplitude of the transverse excitation.

• (4) The flexural rigidity of the stiffened plate increases with the increase in the thickness of the plate; thus, both the amplitudes and resonant regions decrease with the increase in the thickness of the plate.

• (5) Stiffened plates are thin-walled structures. Since the geometrical nonlinearity works, both amplitude–frequency and amplitude–excitation curves exhibit jumping phenomena and multi-value behavior, which are related to geometrical parameters, damping coefficient of stiffened plates, excitation and so on. The geometrical nonlinearity has a significant impact on the dynamic behavior of stiffened plates; thus, it is necessary to take the geometrical nonlinearity into consideration when investigating the mechanical behavior of this type of structures.

• (6) Under the moving boundary conditions, the dynamic system of stiffened plates may exist primary parametric resonance and primary resonance, which can trigger strong vibration, and the structures may be damaged easily. Hence, the stiffened plates should be kept away from the region of primary parametric resonance and primary resonance before performing structural design.

Appendices

Appendix 1

The expression of each tensor in Eq. (1) is given as follows:

$$\begin{aligned} c_{pqij}^*&= \frac{Dh}{2}\int _0^a {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial x^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial x^{2}}\hbox {d}x\hbox {d}y} } \nonumber \\&+\frac{Dh}{2}\int _0^a {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial y^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial y^{2}}\hbox {d}x\hbox {d}y} }\nonumber \\&+\mu Dh\int _0^a {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial x^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial y^{2}}\hbox {d}x\hbox {d}y} } \nonumber \\&+\left( {\mu -1} \right) Dh\int _0^a {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial xy}\frac{\partial ^{2}w_{ij}^d }{\partial xy}\hbox {d}x\hbox {d}y} }\end{aligned}$$

(39)

$$\begin{aligned} d_{pqij}^{1*}&= \frac{Eh^{3}}{2a\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial x}\frac{\partial u_{ij}^d }{\partial x}\hbox {d}x\hbox {d}y} }\nonumber \\&+\frac{Eh^{3}}{4a\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial y}\frac{\partial u_{ij}^d }{\partial y}\hbox {d}x\hbox {d}y} }\end{aligned}$$

(40)

$$\begin{aligned} d_{pqij}^{2v*}&= \frac{-\mu Eh^{3}}{b\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial x}\frac{\partial v_{ij}^d }{\partial y}\hbox {d}x\hbox {d}y} }\nonumber \\&+\frac{Eh^{3}}{2b\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial y}\frac{\partial v_{ij}^d }{\partial x}\hbox {d}x\hbox {d}y} } \end{aligned}$$

(41)

$$\begin{aligned} d_{ijpq}^{2u*}&= \frac{-\mu Eh^{3}}{a\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{ij}^d }{\partial x}\frac{\partial v_{pq}^d }{\partial y}\hbox {d}x\hbox {d}y} }\nonumber \\&+\frac{Eh^{3}}{2a\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial u_{ij}^d }{\partial y}\frac{\partial v_{pq}^d }{\partial x}\hbox {d}x\hbox {d}y} } \end{aligned}$$

(42)

$$\begin{aligned} d_{pqij}^{3*}&= \frac{Eh^{3}}{2b\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial v_{pq}^d }{\partial y}\frac{\partial v_{ij}^d }{\partial y}\hbox {d}x\hbox {d}y} }\nonumber \\&+\frac{Eh^{3}}{4b\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial v_{pq}^d }{\partial x}\frac{\partial v_{ij}^d }{\partial x}\hbox {d}x\hbox {d}y} }\end{aligned}$$

(43)

$$\begin{aligned} d_{pqijmn}^{4*}&= \frac{Eh^{3}}{2\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial x}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial x}\hbox {d}x\hbox {d}y} } \nonumber \\&+\frac{\mu Eh^{3}}{2\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial x}\frac{\partial w_{ij}^d }{\partial y}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} } \nonumber \\&+\frac{Eh^{3}}{2\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial u_{pq}^d }{\partial y}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} }\nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned} d_{ijpqmn}^{4u*}&= \frac{Eh^{4}}{2a\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{ij}^d }{\partial x}\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial x}\hbox {d}x\hbox {d}y} } \nonumber \\&+\frac{\mu Eh^{4}}{2a\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial u_{ij}^d }{\partial x}\frac{\partial w_{pq}^d }{\partial y}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} } \nonumber \\&+\frac{Eh^{4}}{2a\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial u_{ij}^d }{\partial y}\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y}}\nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned} d_{pqijmn}^{5*}&= \frac{\mu Eh^{3}}{2\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial v_{pq}^d }{\partial y}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial x}\hbox {d}x\hbox {d}y} } \\&+\frac{Eh^{3}}{2\left( {1-\mu ^{2}} \right) } \int _0^a {\int _0^b {\frac{\partial v_{pq}^d }{\partial y}\frac{\partial w_{ij}^d }{\partial y}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} } \\&+\frac{Eh^{3}}{2\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial v_{pq}^d }{\partial x}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} }\end{aligned}$$

(46)

$$\begin{aligned} d_{ijpqmn}^{5v*}&= \frac{\mu Eh^{4}}{2b\left( {1-\mu ^{2}} \right) }\int _0^a {\int _0^b {\frac{\partial v_{ij}^d }{\partial y}\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial x}\hbox {d}x\hbox {d}y} } \\&+\frac{Eh^{4}}{2b\left( {1-\mu ^{2}} \right) } \int _0^a {\int _0^b {\frac{\partial v_{ij}^d }{\partial y}\frac{\partial w_{pq}^d }{\partial y}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} } \\&+\frac{Eh^{4}}{2b\left( {1+\mu } \right) }\int _0^a {\int _0^b {\frac{\partial v_{ij}^d }{\partial x}\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial y}\hbox {d}x\hbox {d}y} } \end{aligned}$$

(47)

$$\begin{aligned} d_{pqijmnkl}^{6*}&= \frac{Eh^{4}}{8\left( {1-\mu ^{2}} \right) }\left( {\int _0^a {\int _0^b {\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial x}\frac{\partial w_{kl}^d }{\partial x}\hbox {d}x\hbox {d}y} } } \right. \nonumber \\&+2\int _0^a {\int _0^b {\frac{\partial w_{pq}^d }{\partial x}\frac{\partial w_{ij}^d }{\partial x}\frac{\partial w_{mn}^d }{\partial y}\frac{\partial w_{kl}^d }{\partial y}\hbox {d}x\hbox {d}y} }\nonumber \\&\left. +\int _0^a {\int _0^b {\frac{\partial w_{pq}^d }{\partial y}\frac{\partial w_{ij}^d }{\partial y}\frac{\partial w_{mn}^d }{\partial y}\frac{\partial w_{kl}^d }{\partial y}\hbox {d}x\hbox {d}y} } \right) \end{aligned}$$

(48)

$$\begin{aligned} e_{pqij}^*&= \frac{1}{2}EA_x \left( {d_x } \right) ^{2}h\sum _{k=1}^{N_x } {\left. {\int _0^a {\frac{\partial ^{2}w_{pq}^d }{\partial x^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial x^{2}}\hbox {d}x} } \right| _{y=y_k } } +\nonumber \\&\frac{1}{2}EI_x h\sum _{k=1}^{N_x } {\left. {\int _0^a {\frac{\partial ^{2}w_{pq}^d }{\partial x^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial x^{2}}\hbox {d}x} } \right| _{y=y_k } }\nonumber \\&\frac{1}{2}EA_y \left( {d_y } \right) ^{2}h\sum _{k=1}^{N_y } {\left. {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial y^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial y^{2}}\hbox {d}y} } \right| _{x=x_k } } \nonumber \\&+\frac{1}{2}EI_y h\sum _{k=1}^{N_y } {\left. {\int _0^b {\frac{\partial ^{2}w_{pq}^d }{\partial y^{2}}\frac{\partial ^{2}w_{ij}^d }{\partial y^{2}}\hbox {d}y} } \right| _{x=x_k } } \end{aligned}$$

(49)

$$\begin{aligned} f_{pqij}^{3*}&= \frac{1}{2}\frac{Dh}{a^{4}}\int _0^a {\int _0^b {w_{pq}^d w_{ij}^d \hbox {d}x\hbox {d}y} }\end{aligned}$$

(50)

$$\begin{aligned} g_{pqij}^*&= \frac{DA_x }{2a^{4}}\sum _{k=1}^{N_x } {\left. {\int _0^a {w_{pq}^d w_{ij}^d \hbox {d}x} } \right| _{y=y_k } } \nonumber \\&+\frac{DA_y }{2a^{4}}\sum _{k=1}^{N_y } {\left. {\int _0^b {w_{pq}^d w_{ij}^d \hbox {d}y} } \right| _{x=x_k }} \end{aligned}$$

(51)

Appendix 2

The expressions of $\alpha _1 -\alpha _8$, $\beta _1 -\beta _8$, $\gamma _1 -\gamma _{22}$ in Eq. (11) are given as follows:

$$\begin{aligned} \alpha _1&= \left[ {\frac{\pi ^{2}Ebh}{2a\left( {1-\mu ^{2}} \right) }+\frac{\pi ^{2}Eah}{16b\left( {1+\mu } \right) }} \right] \frac{h^{2}}{a}\end{aligned}$$

(52)

$$\begin{aligned} \alpha _2&= \frac{1}{2}\left[ {\frac{-16\mu Eh}{9\left( {1-\mu ^{2}} \right) }+\frac{8Eh}{9\left( {1+\mu } \right) }} \right] \frac{h^{2}}{b}\end{aligned}$$

(53)

$$\begin{aligned} \alpha _3&= \frac{1}{2}\left[ {-\frac{2\pi ^{2}\mu Eh}{3b\left( {1-\mu ^{2}} \right) }+\frac{\pi ^{2}Eh}{3b\left( {1+\mu } \right) }} \right] h^{2}\end{aligned}$$

(54)

$$\begin{aligned} \alpha _4&= \frac{1}{2}\left[ -\frac{144bEh}{\pi ^{4}a^{2}\left( {1-\mu ^{2}} \right) }+\frac{\left( {\pi ^{2}+30} \right) \mu Eh}{\pi ^{4}b\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {\pi ^{2}+30} \right) Eh}{2\pi ^{4}b\left( {1+\mu } \right) } \right] h^{2}\end{aligned}$$

(55)

$$\begin{aligned} \alpha _5&= \frac{1}{2}\left[ \frac{2\left( {4\pi ^{2}-27} \right) Ebh}{3\pi ^{4}\left( {1-\mu ^{2}} \right) }-\frac{\left( {2\pi ^{2}-15} \right) \mu Ea^{2}h}{2\pi ^{4}b\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. +\frac{\left( {2\pi ^{2}-15} \right) Ea^{2}h}{4\pi ^{4}b\left( {1+\mu } \right) } \right] \end{aligned}$$

(56)

$$\begin{aligned} \alpha _6&= \frac{1}{2}\left[ {-\frac{\pi ^{2}\mu Eh}{3b\left( {1-\mu ^{2}} \right) }+\frac{\pi ^{2}Eh}{6b\left( {1+\mu } \right) }} \right] h^{2}\end{aligned}$$

(57)

$$\begin{aligned} \alpha _7&= \frac{1}{2}\left[ -\frac{2Ebh}{3a\left( {1-\mu ^{2}} \right) }+\frac{\left( {4\pi ^{2}+21} \right) \mu Eah}{72b\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {4\pi ^{2}+21} \right) Eah}{144b\left( {1+\mu } \right) } \right] h\end{aligned}$$

(58)

$$\begin{aligned} \alpha _8&= \frac{1}{2}\left[ -\frac{\left( {\pi ^{2}-18} \right) Ebh}{4\pi ^{4}a\left( {1-\mu ^{2}} \right) }+\frac{\left( {\pi ^{4}+3\pi ^{2}-90} \right) \mu Eah}{3\pi ^{4}b\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {\pi ^{4}+3\pi ^{2}-90} \right) Eah}{6\pi ^{4}b\left( {1+\mu } \right) } \right] h\end{aligned}$$

(59)

$$\begin{aligned} \beta _1&= \frac{1}{2}\left[ {-\frac{16\mu Eh}{9\left( {1-\mu ^{2}} \right) }+\frac{8Eh}{9\left( {1+\mu } \right) }} \right] \frac{h^{2}}{a}\end{aligned}$$

(60)

$$\begin{aligned} \beta _2&= \left[ {\frac{\pi ^{2}Eah}{2b\left( {1-\mu ^{2}} \right) }+\frac{\pi ^{2}Ebh}{16a\left( {1+\mu } \right) }} \right] \frac{h^{2}}{b}\end{aligned}$$

(61)

$$\begin{aligned} \beta _3&= \frac{1}{2}\left[ -\frac{16\pi ^{2}\mu Eh}{15a\left( {1-\mu ^{2}} \right) }+\frac{16\pi ^{2}Eah}{15b^{2}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. +\frac{4\pi ^{2}Eh}{15a\left( {1+\mu } \right) }\right] h^{2} \end{aligned}$$

(62)

$$\begin{aligned} \beta _4&= \frac{1}{2}\left[ \frac{36\left( {\pi ^{2}-12} \right) \mu Eh}{\pi ^{4}a\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. +\frac{\left( {\pi ^{6}+12\pi ^{4}+432\pi ^{2}-5760} \right) Eah}{4\pi ^{4}b^{2}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. +\frac{3\left( {\pi ^{4}+36\pi ^{2}-480} \right) Eh}{4\pi ^{4}a\left( {1+\mu } \right) } \right] h^{2}\end{aligned}$$

(63)

$$\begin{aligned} \beta _5&= \frac{1}{2}\left[ -\frac{\left( {\pi ^{4}-52\pi ^{2}+432} \right) \mu Eah}{4\pi ^{4}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {\pi ^{4}-84\pi ^{2}+720} \right) Ea^{3}h}{2\pi ^{4}b^{2}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {\pi ^{4}-84\pi ^{2}+720} \right) Eah}{8\pi ^{4}\left( {1+\mu } \right) } \right] \end{aligned}$$

(64)

$$\begin{aligned} \beta _6&= \frac{1}{2}\left[ {\frac{2\pi ^{2}Eah}{3b^{2}\left( {1-\mu ^{2}} \right) }+\frac{\pi ^{2}Eh}{6a\left( {1+\mu } \right) }} \right] h^{2}\end{aligned}$$

(65)

$$\begin{aligned} \beta _7&= \frac{1}{2}\left[ {\frac{8\mu Eh}{9\left( {1-\mu ^{2}} \right) }-\frac{40\mu Ea^{2}h}{27\left( {1-\mu ^{2}} \right) b^{2}}-\frac{10Eh}{27\left( {1+\mu } \right) }} \right] h\nonumber \\ \end{aligned}$$

(66)

$$\begin{aligned} \beta _8&= \frac{1}{2}\left[ -\frac{6\left( {7\pi ^{2}-72} \right) \mu Eh}{\pi ^{4}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{2\left( {\pi ^{4}+66\pi ^{2}-720} \right) Ea^{2}h}{\pi ^{4}b^{2}\left( {1-\mu ^{2}} \right) }\right. \nonumber \\&\quad \left. -\frac{\left( {\pi ^{4}+66\pi ^{2}-720} \right) Eh}{2\pi ^{4}\left( {1+\mu } \right) } \right] h\end{aligned}$$

(67)

$$\begin{aligned} \gamma _1&= 2\left[ \frac{3\rho abh}{8}+\frac{3\rho A_x a}{4}\sum _{k=1}^{N_x } {\left. {\sin ^{2}\frac{\pi y}{b}} \right| _{y=y_k } } \right. \nonumber \\&\quad \left. +\,\rho A_y b\sum _{k=1}^{N_y } {\left. {\left( {\cos ^{4}\frac{\pi x}{a}-2\cos ^{2}\frac{\pi x}{a}+1} \right) } \right| _{x=x_k } } \right] \nonumber \\&\qquad h\left( {\frac{1}{a^{2}}\sqrt{\frac{D}{\rho h}}} \right) ^{2}\end{aligned}$$

(68)

$$\begin{aligned} \gamma _2&= 2\left[ {\frac{\rho abh}{8}+\frac{\rho A_x a}{2}\sum _{k=1}^{N_x } {\left. {\sin ^{2}\frac{\pi y}{b}} \right| _{y=y_k } } } \right. \nonumber \\&\qquad -\frac{\rho A_y b}{a^{3}}\sum _{k=1}^{N_y } x^{2}\left( 3a\cos ^{2}\frac{\pi x}{a}-2x\cos ^{2}\frac{\pi x}{a}\right. \nonumber \\&\quad \left. \left. -3a+2x \Big ) \right| _{x=x_k } \right] h\left( {\frac{1}{a^{2}}\sqrt{\frac{D}{\rho h}}} \right) ^{2} \end{aligned}$$

(69)

$$\begin{aligned} \gamma _3&= 2\left[ -\frac{\left( {\pi ^{2}+3} \right) \rho a^{2}bh}{24\pi ^{2}}-\frac{\left( {\pi ^{2}+3} \right) \rho A_x a^{2}}{12\pi ^{2}}\right. \nonumber \\&\quad \times \sum _{k=1}^{N_x } {\left. {\sin ^{2}\frac{\pi y}{b}} \right| _{y=y_k } } \nonumber \\&\qquad -\frac{\rho A_y b}{a^{2}}\sum _{k=1}^{N_y } x^{2}\Big ( a\cos ^{2}\frac{\pi x}{a}-x\cos ^{2}\frac{\pi x}{a}\nonumber \\&\quad \left. -\,2a+x \Big ) \bigg |_{x=x_k } \right] \left( {\frac{1}{a^{2}}\sqrt{\frac{D}{\rho h}}} \right) ^{2}\end{aligned}$$

(70)

$$\begin{aligned} \gamma _4&= 2\left[ {\frac{2\pi ^{4}bD}{a^{3}}+\frac{3\pi ^{4}aD}{8b^{3}}+\frac{\pi ^{4}\mu D}{ab}+\frac{\pi ^{4}\left( {\mu -1} \right) D}{ab}} \right. \nonumber \\&\qquad +\frac{4\pi ^{4}EA_x d_x^2 }{a^{3}}\sum _{k=1}^{N_x } {\left. {\sin ^{2}\frac{\pi y}{b}} \right| _{y=y_k } }\nonumber \\&\qquad +\frac{4\pi ^{4}EI_x }{a^{3}}\sum _{k=1}^{N_x } {\left. {\sin ^{2}\frac{\pi y}{b}} \right| _{y=y_k } } +\frac{4\pi ^{4}EA_y bd_y^2 }{a^{4}}\nonumber \\&\quad \times \sum _{k=1}^{N_y } {\left. {\left( {4\cos ^{4}\frac{\pi x}{a}-4\cos ^{2}\frac{\pi x}{a}+1} \right) } \right| _{x=x_k } }\nonumber \\&\quad +\frac{4\pi ^{4}EI_y b}{a^{4}}\sum _{k=1}^{N_y } \left( 4\cos ^{4}\frac{\pi x}{a}\right. \nonumber \\&\quad \left. \left. \left. -\,4\cos ^{2}\frac{\pi x}{a}+1 \right) \right| _{x=x_k } \right] h\end{aligned}$$

(71)

$$\begin{aligned} \gamma _5&= \left[ {\frac{\pi ^{4}aD}{4b^{3}}} \right. -\frac{\pi ^{4}EA_y d_y^2 }{a^{3}b^{3}}\sum _{k=1}^{N_y } x^{2}\left( 3a\cos ^{2}\frac{\pi x}{a}\right. \nonumber \\&\quad \left. \left. -2x\cos ^{2}\frac{\pi x}{a}-3a+2x \right) \right| _{x=x_k } \nonumber \\&\quad -\frac{\pi ^{4}EI_y }{a^{3}b^{3}}\sum _{k=1}^{N_y } x^{2}\left( 3a\cos ^{2}\frac{\pi x}{a}\right. \nonumber \\&\quad -\left. \left. \left. 2x\cos ^{2}\frac{\pi x}{a}-3a+2x \right) \right| _{x=x_k } \right] h\end{aligned}$$

(72)

$$\begin{aligned} \gamma _6&= \left[ {-\frac{\pi ^{2}\left( {\pi ^{2}+3} \right) a^{2}D}{24b^{3}}} \right. -\frac{\pi ^{2}\mu D}{b}-\frac{\pi ^{2}\left( {\mu -1} \right) D}{b}\nonumber \\&\quad -\frac{\pi ^{4}EA_y d_y^2 }{a^{2}b^{3}}\sum _{k=1}^{N_y } x^{2}\left( a\cos ^{2}\frac{\pi x}{a}\right. \nonumber \\&\quad -\,\left. \left. x\cos ^{2}\frac{\pi x}{a}-a+x \right) \right| _{x=x_k } \nonumber \\&\quad -\frac{\pi ^{4}EI_y }{a^{2}b^{3}}\sum _{k=1}^{N_y } x^{2}\left( a\cos ^{2}\frac{\pi x}{a}\right. \nonumber \\&\quad -\left. \left. \left. x\cos ^{2}\frac{\pi x}{a}-a+x \right) \right| _{x=x_k } \right] \end{aligned}$$

(73)

$$\begin{aligned} \gamma _7&= \left[ {-\frac{4\pi ^{2}\mu Eh}{3\left( {1-\mu ^{2}} \right) b}+\frac{2\pi ^{2}Eh}{3\left( {1+\mu } \right) b}} \right] \frac{h^{3}}{a}\end{aligned}$$

(74)

$$\begin{aligned} \gamma _8&= \left[ {-\frac{\pi ^{2}\mu Eh}{3\left( {1-\mu ^{2}} \right) b}+\frac{\pi ^{2}Eh}{6\left( {1+\mu } \right) b}} \right] \frac{h^{3}}{b}\end{aligned}$$

(75)

$$\begin{aligned} \gamma _9&= \left[ -\frac{2Ebh}{3\left( {1-\mu ^{2}} \right) a}+\frac{\left( {4\pi ^{2}+21} \right) \mu Eah}{72\left( {1-\mu ^{2}} \right) b}\right. \nonumber \\&\quad -\left. \frac{\left( {4\pi ^{2}+21} \right) Eah}{144\left( {1+\mu } \right) b} \right] \frac{h^{2}}{a}\end{aligned}$$

(76)

$$\begin{aligned} \gamma _{10}&= \frac{8\pi ^{2}Eh}{15\left( {1+\mu } \right) a}\frac{h^{3}}{b}\end{aligned}$$

(77)

$$\begin{aligned} \gamma _{11}&= \frac{\pi ^{2}Eh}{6\left( {1+\mu } \right) a}\frac{h^{3}}{b}\end{aligned}$$

(78)

$$\begin{aligned} \gamma _{12}&= \left[ {\frac{8\mu Eh}{9\left( {1-\mu ^{2}} \right) }-\frac{40\mu Ea^{2}h}{27\left( {1-\mu ^{2}} \right) b^{2}}-\frac{10Eh}{27\left( {1+\mu } \right) }} \right] \frac{h^{2}}{b}\nonumber \\ \end{aligned}$$

(79)

$$\begin{aligned} \gamma _{13}&= \frac{Eh}{2\left( {1-\mu ^{2}} \right) }\left[ {\frac{9\pi ^{4}b}{4a^{3}}+\frac{5\pi ^{4}}{8ab}+\frac{105\pi ^{4}a}{64b^{3}}} \right] h^{3}\end{aligned}$$

(80)

$$\begin{aligned} \gamma _{14}&= \frac{3Eh}{8\left( {1-\mu ^{2}} \right) }\left( {\frac{\pi ^{4}}{2ab}+\frac{15\pi ^{4}a}{8b^{3}}} \right) h^{3}\end{aligned}$$

(81)

$$\begin{aligned} \gamma _{15}&= \frac{3Eh}{8\left( {1-\mu ^{2}} \right) }\left[ -\frac{4\pi ^{2}b}{a^{2}}-\frac{12\pi ^{4}+85\pi ^{2}}{144b}\right. \nonumber \\&\quad -\left. \frac{5\pi ^{2}a^{2}\left( {12\pi ^{2}+49} \right) }{192b^{3}} \right] h^{2}\end{aligned}$$

(82)

$$\begin{aligned} \gamma _{16}&= \frac{Eh}{4\left( {1-\mu ^{2}} \right) }\left[ {\frac{27\left( {16\pi ^{4}+45} \right) b}{80\pi ^{2}a^{3}}} \right. \nonumber \\&\quad +\frac{832\pi ^{6}+2016\pi ^{4}-12810\pi ^{2}-279401}{8960\pi ^{2}ab}\nonumber \\&\quad \left. {+\frac{27\left( {832\pi ^{6}-4410\pi ^{2}-133875} \right) a}{17920\pi ^{2}b^{3}}} \right] h^{3}\end{aligned}$$

(83)

$$\begin{aligned} \gamma _{17}&= \frac{Eh}{4\left( {1-\mu ^{2}} \right) }\left[ {-\frac{9\left( {8\pi ^{4}-30\pi ^{2}+135} \right) b}{80\pi ^{2}a^{2}}} \right. \nonumber \\&\quad -\frac{704\pi ^{6}+1848\pi ^{4}+39060\pi ^{2}-1656270}{13440\pi ^{2}b}\nonumber \\&\quad \left. {-\frac{9\left( {704\pi ^{6}+4200\pi ^{4}+13230\pi ^{2}-401625} \right) a^{2}}{17920\pi ^{2}b^{3}}} \right] h^{2}\nonumber \\ \end{aligned}$$

(84)

$$\begin{aligned} \gamma _{18}&= \frac{Eh}{4\left( {1-\mu ^{2}} \right) }\left[ {\frac{3\left( {64\pi ^{4}-240\pi ^{2}+405} \right) b}{320\pi ^{2}a}} \right. \nonumber \\&\quad -\frac{\left( {256\pi ^{6}+2688\pi ^{4}+103320\pi ^{2}-838215} \right) a}{53760\pi ^{2}b}\nonumber \\&\quad \left. {+\frac{3\left( {256\pi ^{6}+52920\pi ^{2}-401625} \right) a^{3}}{71680\pi ^{2}b^{3}}} \right] h\end{aligned}$$

(85)

$$\begin{aligned} \gamma _{19}&= \frac{Eh}{8\left( {1-\mu ^{2}} \right) }\left[ \frac{3\pi ^{4}-15\pi ^{2}-315}{40\pi ^{2}ab}\right. \nonumber \\&\quad \left. +\frac{3\left( {43\pi ^{6}-315\pi ^{2}-9450} \right) a}{280\pi ^{2}b^{3}} \right] h^{3}\end{aligned}$$

(86)

$$\begin{aligned} \gamma _{20}&= \frac{Eh}{8\left( {1-\mu ^{2}} \right) }\left[ {\frac{81\left( {\pi ^{2}-15} \right) b}{\pi ^{4}a^{2}}} \right. \nonumber \\&\quad -\frac{88\pi ^{6}+735\pi ^{4}-3255\pi ^{2}+40950}{140\pi ^{4}b}\nonumber \\&\quad \left. {-\frac{\left( {97\pi ^{8}+630\pi ^{6}+4725\pi ^{4}-23625\pi ^{2}-793800} \right) a^{2}}{560\pi ^{4}b^{3}}} \right] h^{2}\nonumber \\ \end{aligned}$$

(87)

$$\begin{aligned} \gamma _{21}&= \frac{Eh}{8\left( {1-\mu ^{2}} \right) }\left[ {-\frac{243\left( {\pi ^{2}-10} \right) b}{2\pi ^{4}a}} \right. \nonumber \\&\quad -\frac{\left( {49\pi ^{6}+1680\pi ^{4}-17955\pi ^{2}-331750} \right) a}{840\pi ^{4}b}\nonumber \\&\quad \left. {+\frac{\left( {8\pi ^{8}+1890\pi ^{4}+23625\pi ^{2}-396900} \right) a^{3}}{280\pi ^{4}b^{3}}} \right] h\end{aligned}$$

(88)

$$\begin{aligned} \gamma _{22}&= \frac{Eh}{8\left( {1-\mu ^{2}} \right) }\left[ -\frac{3\left( {2\pi ^{4}-57\pi ^{2}+405} \right) b}{4\pi ^{4}}\right. \nonumber \\&\quad -\frac{\left( {\pi ^{6}-30\pi ^{4}+2745\pi ^{2}-23625} \right) a^{2}}{480\pi ^{4}b} \nonumber \\&\quad \left. {-\frac{\left( {\pi ^{8}-315\pi ^{4}+23625\pi ^{2}-198450} \right) a^{4}}{560\pi ^{4}b^{3}}} \right] \end{aligned}$$

(89)

Appendix 3

The expressions of $p_1 -p_5$, $q_1 -q_3$ in Eq. (14) are given as follows:

$$\begin{aligned} p_1&= \frac{1}{\gamma _1 }\left( {-\frac{3b}{4a}\sqrt{\frac{Dh}{\rho }}\hat{{c}}_{11} } \right) \end{aligned}$$

(90)

$$\begin{aligned} p_2&= \frac{\gamma _4 }{\gamma _1 }+p_3 \end{aligned}$$

(91)

$$\begin{aligned} p_3&= \frac{1}{2\gamma _1 }\left[ -\gamma _7 \frac{\alpha _4 \beta _2 -\alpha _2 \beta _4 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 -\gamma _7 \frac{\alpha _5 \beta _2 -\alpha _2 \beta _5 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\bar{{\delta }}_2^2 \right. \nonumber \\&\quad -\,\gamma _7 \frac{\alpha _8 \beta _2 -\alpha _2 \beta _8 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2 -\gamma _8 \frac{\alpha _6 \beta _2 -\alpha _2 \beta _6 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 \nonumber \\&\quad -\,\gamma _8 \frac{\alpha _7 \beta _2 -\alpha _2 \beta _7 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2 -\gamma _9 \frac{\alpha _6 \beta _2 -\alpha _2 \beta _6 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2\nonumber \\&\quad -\,\gamma _9 \frac{\alpha _7 \beta _2 -\alpha _2 \beta _7 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\bar{{\delta }}_2^2 -\gamma _{10} \frac{\alpha _4 \beta _1 -\alpha _1 \beta _4 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h^{2}}\bar{{\delta }}_1^2\nonumber \\&\quad -\,\gamma _{10} \frac{\alpha _5 \beta _1 -\alpha _1 \beta _5 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\bar{{\delta }}_2^2-\gamma _{10} \frac{\alpha _8 \beta _1 -\alpha _1 \beta _8 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2 \nonumber \\&\quad -\,\gamma _{11} \frac{\alpha _6 \beta _2 -\alpha _2 \beta _6 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 -\gamma _{11} \frac{\alpha _7 \beta _2 -\alpha _2 \beta _7 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2\nonumber \\&\quad -\,\gamma _{12} \frac{\alpha _6 \beta _2 -\alpha _2 \beta _6 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2 -\gamma _{12} \frac{\alpha _7 \beta _2 -\alpha _2 \beta _7 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\bar{{\delta }}_2^2 \nonumber \\&\quad \left. {+\,\gamma _{16} \frac{1}{h^{2}}\bar{{\delta }}_1^2 +\gamma _{17} \frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2 +\gamma _{18} \bar{{\delta }}_2^2 } \right] \end{aligned}$$

(92)

$$\begin{aligned} p_4&= \frac{1}{\gamma _1 }\left( -\gamma _7 \frac{\alpha _6 \beta _2 -\alpha _2 \beta _6 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 -\gamma _7 \frac{\alpha _7 \beta _2 -\alpha _2 \beta _7 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\bar{{\delta }}_2 \right. \nonumber \\&\quad -\,\gamma _8 \frac{\alpha _3 \beta _2 -\alpha _2 \beta _3 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 -\gamma _9 \frac{\alpha _3 \beta _2 -\alpha _2 \beta _3 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\bar{{\delta }}_2 \nonumber \\&\quad -\,\gamma _{10} \frac{\alpha _6 \beta _1 -\alpha _1 \beta _6 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 -\gamma _{10} \frac{\alpha _7 \beta _1 -\alpha _1 \beta _7 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\bar{{\delta }}_2\nonumber \\&\quad -\,\gamma _{11} \frac{\alpha _3 \beta _1 -\alpha _1 \beta _3 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 -\gamma _{12} \frac{\alpha _3 \beta _1 -\alpha _1 \beta _3 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\bar{{\delta }}_2 \nonumber \\&\quad +\,\left. \gamma _{14} \frac{1}{h}\bar{{\delta }}_1 +\gamma _{15} \bar{{\delta }}_2 \right) \end{aligned}$$

(93)

$$\begin{aligned} p_5&= \frac{1}{\gamma _1 }\left( {-\gamma _7 \frac{\alpha _3 \beta _2 -\alpha _2 \beta _3 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }-\gamma _{10} \frac{\alpha _3 \beta _1 -\alpha _1 \beta _3 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }+\gamma _{13} } \right) \nonumber \\ \end{aligned}$$

(94)

$$\begin{aligned} q_1&= \frac{1}{\gamma _1 }\left[ {\left( {\Omega ^{*}} \right) ^{2}\left( {\gamma _2 \frac{1}{h}\bar{{\delta }}_1 +\gamma _3 \bar{{\delta }}_2 } \right) -\gamma _5 \frac{1}{h}\bar{{\delta }}_1 -\gamma _6 \bar{{\delta }}_2 } \right] +3q_3\nonumber \\ \end{aligned}$$

(95)

$$\begin{aligned} q_2&= \frac{1}{\gamma _1 }\Omega ^{*}\left[ {\frac{b}{4a}\sqrt{\frac{D}{\rho h}}\hat{{c}}_{11} \bar{{\delta }}_1 -\frac{\left( {\pi ^{2}+3} \right) b}{24\pi ^{2}}\sqrt{\frac{D}{\rho h}}\hat{{c}}_{11} \bar{{\delta }}_2 } \right] \nonumber \\ \end{aligned}$$

(96)

$$\begin{aligned} q_3&= \frac{1}{4\gamma _1 }\left[ {\gamma _8 \frac{\alpha _4 \beta _2 -\alpha _2 \beta _4 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h^{3}}\bar{{\delta }}_1^3 } \right. +\gamma _8 \frac{\alpha _5 \beta _2 -\alpha _2 \beta _5 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2^2 \nonumber \\&\quad +\,\gamma _8 \frac{\alpha _8 \beta _2 -\alpha _2 \beta _8 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 \bar{{\delta }}_2+\gamma _9 \frac{\alpha _4 \beta _2 -\alpha _2 \beta _4 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 \bar{{\delta }}_2 \nonumber \\&\quad +\,\gamma _9 \frac{\alpha _5 \beta _2 -\alpha _2 \beta _5 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\bar{{\delta }}_2^3 +\gamma _9 \frac{\alpha _8 \beta _2 -\alpha _2 \beta _8 }{\alpha _1 \beta _2 -\alpha _2 \beta _1 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2^2\nonumber \\&\quad +\,\gamma _{11} \frac{\alpha _4 \beta _1 -\alpha _1 \beta _4 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h^{3}}\bar{{\delta }}_1^3 +\gamma _{11} \frac{\alpha _5 \beta _1 -\alpha _1 \beta _5 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2^2 \nonumber \\&\quad +\,\gamma _{11} \frac{\alpha _8 \beta _1 -\alpha _1 \beta _8 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 \bar{{\delta }}_2+\gamma _{12} \frac{\alpha _4 \beta _1 -\alpha _1 \beta _4 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h^{2}}\bar{{\delta }}_1^2 \bar{{\delta }}_2 \nonumber \\&\quad +\,\gamma _{12} \frac{\alpha _5 \beta _1 -\alpha _1 \beta _5 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\bar{{\delta }}_2^3 +\gamma _{12} \frac{\alpha _8 \beta _1 -\alpha _1 \beta _8 }{\alpha _2 \beta _1 -\alpha _1 \beta _2 }\frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2^2\nonumber \\&\quad \left. {-\,\gamma _{19} \frac{1}{h^{3}}\bar{{\delta }}_1^3 -\gamma _{20} \frac{1}{h^{2}}\bar{{\delta }}_1^2 \bar{{\delta }}_2 -\gamma _{21} \frac{1}{h}\bar{{\delta }}_1 \bar{{\delta }}_2^2 -\gamma _{22} \bar{{\delta }}_2^3 } \right] \end{aligned}$$

(97)