A new dynamic model for vibration analysis of a ball bearing due to a localized surface defect considering edge topographies

Abstract

When a small initial defect occurs on the races of a ball bearing such as spalls and pits caused by fatigue, the defect will progress around the race in the direction of the ball motion until catastrophic failure happens due to impacts between the ball and the defect edges. Undesirable impulsive excitations can be caused when the orbiting ball strikes the defect edges. The impulse is depended on the shape and sizes of the defect, which can be used to detect and diagnose the defects in bearing systems. To understand characteristics of an impulse caused by a localized surface defect in a ball bearing, a new dynamic model is proposed to investigate the vibration response of a ball bearing due to a localized surface defect on its races, which can consider effects of defect edge topographies. Based on the defect edge topographies and the sizes of the defect, a new contact model for modeling contact relationships between the ball and the defect edges is also developed according to Hertzian elastic contact theory, which can be used to determine changes in the excitations including the time-varying deflection excitation and the time-varying contact stiffness excitation caused by the defect. The proposed model is applied to investigate effects of the defect edge topographies on the contact stiffnesses between the ball and the defect edges, and the vibration response of a ball bearing with a localized surface defect on its races. The results from the proposed model are compared with the available results from the previous models in the literature, which reveals the superiority of the proposed model. It is also shown that numerical results can provide some guidance for the ball bearing defect diagnosis and detection.

1 Introduction

Ball bearing is one of the key components in a variety of industrial machineries due to their carrying capacity and low-friction characteristics. Vibration performances of these machineries are greatly influenced by vibration characteristics of their internal bearings, especially in the presence of various defects [1]. Hence, ball bearing defect diagnosis and detection is one of the important works in industrial maintenance. Although many methods have been proposed for diagnosis and detection of the defects in rolling element bearings, modeling and simulation method is an accurate approach to predict the vibration response of ball bearings [2], which can enhance understanding vibration characteristics of the bearing with various defects.

Many research works have been presented to investigate the vibration response of rolling element bearings with a localized surface defect on their races or rolling elements. Some of the previous works focusing on modeling the force excitations produced by the localized defects are listed in Refs. [3–12]. On the other hand, some research works are interested in simulating the deflection excitations caused by the localized surface defects as shown in Refs. [2, 13–24].

McFadden and Smith [3, 4] used a series of repeated force excitations to model the impulses generated by single and multiple point defects. Tandon and Choudhury [5, 6] used the finite width triangular, rectangular, and half-sine force excitations to describe the impulse generated by a localized surface defect. Kiral and Karagulle [7, 8] described a localized surface defect model as a rectangular force excitation. Sassi et al. [9] formulated the force excitation model for a localized surface defect as sinusoidal and rectangular functions.

References [2, 13–15, 17–21] defined a localized surface defect model as a deflection excitation using rectangular function. Rafsanjani et al. [2] defined a localized surface defect model as a deflection excitation using a rectangular function. In their model, the defect depth is used to define the amplitude of the deflection excitation. References [13–17, 19–21] also used the rectangular deflection excitation model to describe the impulse generated by a localized surface defect. Patil et al. [16] formulated a localized surface defect model as a half-sine deflection excitation wave. Pate et al. [18] also described a localized surface defect model as a rectangular deflection excitation function. In their model, the geometric relationship between the rolling element and the defect is considered. References [10] and [11] analyzed the contact pressure between the rolling element and the defect, but they only considered the constant equivalent contact stiffness between the rolling element and the defect. However, the contact stiffness between the rolling element and the defect varies with the contact position between the rolling element and the defect when the rolling element passes over the defect according to the analysis in Refs. [22–24]. Liu et al. [22] used a finite element method and an experimental method to study effects of the shapes of a localized surface defect on the vibration waveforms of a ball bearing with a localized surface defect on its outer race. In another work [23], they proposed a new localized surface defect model considering the time-varying deflection excitation caused by a localized surface defect for a ball bearing with a localized surface defect on its races. Relationships between the time-varying deflection excitations and the shape and sizes of the defect are considered in their defect model. Moreover, Shao et al. [24] proposed a new method to formulate the time-varying deflection excitation and the time-varying contact stiffness excitation caused by a localized surface defect on the races of a cylindrical roller bearing. In practical, when a small initial spall occurs on the race of the ball bearing, the spall will progress around the race in the direction of the ball motion until catastrophic failure happens due to impacts between the ball and the defect edges [25]. However, in the above works, effects of the defect edge topographies on the vibration response of the ball bearing were not considered.

Several studies have been conducted on studying the spall growth and the spall growth rate of an initial spall on the races of the rolling element bearings based on the experimental and modeling methods. For instance, Lundburg and Palmgren [26] initially discussed the spall growth phenomenon of the rolling bearings. Kotzalas and Harris [27] studied the spall growth on the surfaces of the balls and races of a ball bearing, and they extended the prediction methods of bearing life in Ref. [28] to predict the remaining useful life of the bearing. Xu and Sadeghi [29] proposed a new analytical model to investigate the effect of a dent on the spall initiation and growth in the lubricated contact. Hoeprich [30] studied the randomness inherent to the spall growth and its unknown governing mechanisms based on the spall growth experiments on tapered roller bearings. Rosada et al. [31], Arakere et al. [32], and Forster et al. [33] also proposed a series of experimental and modeling methods to study the spall growth of the bearing materials in their three-part analysis series, which studied three stages of the spall growth of the bearing materials. Branch et al. [34, 35] presented a finite element modeling method to investigate three stages of the spall growth in Refs. [31–33]. Li et al. [36] presented an empirical method to predict spall growth rates of a tapered roller bearing. The above works on the spall growth are focused on the contact stress, fatigue, material microstructure, and plasticity at the edges of the spall defect. Effects of the spall edge topographies on the impulse for the ball bearing were not discussed. Hence, it is helpful to investigate the impulse caused by the spall with different edge topographies for the ball bearing defect diagnosis and detection at its early stage.

The main objective of the present study is to investigate effects of defect edge topographies on the time-varying contact stiffnesses between the ball and the defect edges according to Hertzian elastic contact theory, and the vibration response of the ball bearing with a localized surface defect on its races. The profiles of the propagated defect edges are assumed to be small smooth plane surfaces partly based on the assumptions in Refs. [34] and [35]. The elevation angles and the lengths of the small surfaces at the edges of the defect are used to determine the defect edge topographies. The defect model is formulated partly based on the studies in Refs. [22] and [23], which can consider the time-varying defection excitation and the time-varying contact stiffness excitation caused by the defect with different edge topographies. Relationships between the excitations and the shape and sizes of the defect are established. The time-varying deflection excitation is utilized to describe the additional deflection in the radial and tangential directions caused by the defect, which is an extended model of the radial deflection model in Ref. [23]. The time-varying contact stiffness is used to describe contact deformations at the defect edges when the ball is in contact with the defect edges. The dynamic model of the ball bearing is considered as a two-degree-of-freedom lumped parameter model. It includes effects of the time-varying compliance of the bearing, the damping, the time-varying deflection excitation in the radial and tangential directions, and the time-varying contact stiffness excitation caused by the defect. A fourth-order Runge–Kutta numerical integration method with a fixed time step is adopted to calculate the vibration response of the ball bearing with a localized surface defect on its races. Effects of the defect edge topographies on the time-varying contact stiffnesses between the ball and the defect edges, and the vibration response of the ball bearing are investigated. Numerical results from the proposed model are compared with the available results from the previous models in the literature, which reveals the superiority of the proposed model. It is expected that by applying the proposed method, the relationship between the vibration response of the ball bearing and the defect edge topographies can be obtained, and some guidance for the fault diagnosis and defection of ball bearings can be provided.

2 Problem formulation

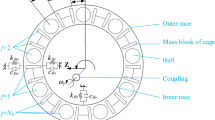
When a localized surface defect occurs on the races of a ball bearing, as shown in Fig. 1, the ball will strike the defect edges when the ball passes over the defect. The periodic impacts arising from the balls against the defect edges will change the topographies of the defect edges due to the plastic deformations at the defect edges. The shapes of the line edges of the defect will be changed according to the analysis in Refs. [34] and [35]. The propagated defect edges are assumed as small smooth plane surfaces in this paper. For instance, a line edge $ab$ of the defect at its initial stage is changed into a small plane surface $a^{\prime }b^{\prime }ef$ as shown in Fig. 2. Figure 2b, c shows the different stages of the small plane surface at the defect edge. Here, it is assumed that the small plane surfaces at the defect edges have same sizes. The changes in the defect edge topographies will affect the contact relationships between the ball and the defect edges. For a healthy race, the contact type between a ball and the race is a ball–ball contact type as shown in Fig. 1a. For a defective race with line defect edges, as shown in Fig. 1a, the contact type between the ball and the defective race becomes a ball–line contact type, which has been discussed in Refs. [22] and [23]. However, when the defect edge topographies are changed due to the impacts between the ball and the defect edges, as shown in Fig. 1a, the contact type between the ball and the defect edges become a ball–plane contact type. It depends on three parameters as follows: (1) the ratio of the defect length to its width, which is defined as $\xi _\mathrm{{d}} =L/B$, where $L$ is the defect length, and $B$ is the defect width; (2) the ratio of the ball size to the defect minimum size, which is defined as $\xi _\mathrm{{bd}} =d/\min (L,B)$, where $d$ is the ball diameter; and (3) the elevation angle $\gamma \,(0< \gamma <\pi /2)$ of the small plane surface as shown in Fig. 2b, c.

Fig. 1

Schematic of a localized surface defect on the race of a ball bearing: a contact positions between the ball and the defect, and b defect location

Fig. 2

Schematic of the contact type between a ball and one defect edge (enlarged view): a line edge, b very small surface edge, and c small surface edge

Fig. 3

Schematic of the contact type between a ball and the small surfaces at defect edges with different topographies: a case 1, b case 2, c case 3, and d case 4

Figure 3 shows effects of the defect edge topographies on the contact types between the ball and the different defect cases. The elevation angle $\gamma$ and the length $l$ of the small surfaces at the defect edges are used to determine the contact types between the ball and the defects. It is assumed that $l$ is larger than Hertzian contact radius in this paper.

For case 1, $\gamma \ge \hbox {arcsin} \left( {{0.5\min \left( {L,B} \right) }/{\sqrt{R^{2}+l^{2}}}} \right) +\arctan \left( {l/R} \right)$ and $\xi _\mathrm{{bd}} >1$, where $R$ is the radius of the ball, as shown in Fig. 3a. The ball is only in contact with the line edges of the defect in considering a case of an early defect stage. For this case, the contact type between the ball and the defect is a ball–line contact type when the ball passes over the defect. It is the early stage of the plastic deformations at the defect edges caused by the periodic impacts arising from the balls against the defect edges for a small localized surface defect.

For case 2, $\min \left( {L,B} \right) /\left( {2R} \right) <\gamma \le \hbox { arcsin }\Big ( 0.5$ $\min \left( {L,B}\right) /{\sqrt{R^{2}+l^{2}}} \Big )+\arctan \left( {l/R} \right)$ and $\xi _\mathrm{{bd}} >1$, as shown in Fig. 3b, the contact type between the ball and the defect depends on the defect parameters $\xi _\mathrm{{d}}$ and $\xi _\mathrm{{bd}}$. The contact type between the ball and the beginning edge of the defect is the ball–line contact type, as well as that between the ball and the ending edge of the defect. It is a ball–plane contact type when the ball is in contact with the small surfaces between the points A and D. It is the middle stage of the plastic deformations at the defect edges caused by the periodic impacts arising from the balls against the defect edges for a small localized surface defect.

For case 3, $\gamma \le \hbox {arcsin}(\hbox {min}(L,B)/(2R))$ and $\xi _\mathrm{{bd}}>1$, as shown in Fig. 3c, the contact type between the ball and the defect is a ball–plane contact type when the ball is in contact with the surfaces between points A and B, and between points C and D. It is a ball–line contact type when the ball makes contact with the beginning edge, the edges at points B and C, and the ending edge of the defect. This case denotes the large plastic deformations at the defect edges. It is the late stage of the plastic deformation at the defect edge caused by the periodic impacts arising from the balls against the defect edges for a small localized surface defect.

For case 4, $\xi _\mathrm{{bd}} \le 1$, or $h_{\max } <H$, as shown in Figs. 1a and 3d, the contact type between the ball and the defect is a ball–line contact type at the points A, B, C, and D; it is the ball–plane contact type when the ball is in contact with the surface between the points A and B, the bottom surface, and the surface between the points C and D of the defect. It is used to describe the plastic deformations at the defect edges caused by the periodic impacts arising from the balls against the defect edges for a large localized surface defect.

For cases 2 and 3, as shown in Fig. 3b, c, the numbers of the contact surfaces are determined by the defect sizes. Here, five different defect types are discussed according to the defect parameters $\xi _\mathrm{{d}}$ and $\xi _\mathrm{{bd}}$.

Figure 4a depicts the first defect type, which denotes a very small defect such as a point defect and a small crack. Thus, effects of the edge topographies of the first defect type can be ignored.

Fig. 4

Schematics of the different localized surface defects: a a small crack, b a small defect with the defect length smaller than its width, c a small defect with the defect length similar to its width, d a small defect with the defect length larger than its width, and e a large defect compared to the ball diameter

Figure 4b plots the second defect type with the length of the defect smaller than its width. The ball only strikes the edges 1 and 4 when the ball passes over the defect, and the numbers of the contact surfaces are 1, 2, and 1, respectively.

For the third defect type with the length of the defect similar to its width, as shown in Fig. 4c, the ball strikes all defect edges 1–4 when the ball passes over the defect, and the numbers of the contact surfaces are 1, 3, 4, 3, and 1, respectively.

Figure 4d gives the fourth defect type with the length of the defect larger than its width. The ball also strikes all defect edges 1–4, and the numbers of the contact surfaces are 1, 3, 2, 3, and 1, respectively.

The fifth defect type is presented in Fig. 4e, the ball strikes the edge 1, the bottom surface of the defect, and the edge 4 when the ball passes over the defect. There is only one contact surface during the entire contact process.

3 Dynamic model of a ball bearing with a localized surface defect

3.1 Localized surface defect model

When a localized surface defect occurs on the races of a ball bearing, an excitation will be generated, which includes the time-varying deflection excitation and the time-varying contact stiffness excitation [23]. Reference [23] presents a time-varying deflection excitation model to describe the additional deflections caused by the defect. In their model, only the radial contact deflections at the defect edges are considered, which are calculated by a static finite element method. However, the time-varying contact stiffness excitation between the ball and the defect is ignored. In this paper, the time-varying deflection excitation, the time-varying contact stiffness excitation, and the defect edge topographies are considered in the proposed model. The contact stiffnesses between the ball and the defect edges are calculated according to Hertzian elastic contact theory.

For a healthy ball bearing, as shown in Fig. 1a, the total contact stiffness $K$ between a ball and the races can be calculated by [37]

$$\begin{aligned} K=\frac{1}{\left[ \frac{1}{K_\mathrm{i}^{1/n} }+\frac{1}{K_\mathrm{o}^{1/n} }\right] ^{n}} \end{aligned}$$

(1)

where $n$ is the load-deflection exponent, $n=1.5$ for a ball bearing; $K_\mathrm{{i}}$ and $K_\mathrm{{o}}$ are the contact stiffnesses between the ball and the inner race, and that between the ball and the outer race, respectively. For a healthy ball bearing, the contact stiffness $K_\mathrm{{h}}$ between the ball and the race can be calculated by [23, 37]

$$\begin{aligned} K_\mathrm{h} =\left( {\frac{\pi ^{2}e^{2}E_\mathrm{{eq}}^{2}\varepsilon }{4.5k^{3}\sum \rho }} \right) ^{0.5} \end{aligned}$$

(2)

in which $\sum \rho$ is the curvature sum; $E_\mathrm{{eq}}$ is the equivalent modulus of elasticity; $k$ and $\varepsilon$ denote the first and second kind of elliptical integral, respectively; and $e$ is the elliptical eccentricity parameter. $\sum \rho ,\,E_\mathrm{{eq}},\, k,\,\varepsilon$, and $e$ can be calculated by the methods presented in Refs. [23] and [37].

When a localized surface defect occurs on the inner race or the outer race of the ball bearing, as shown in Fig. 1a, the contact type between the ball and the defect is no longer a ball–ball contact type since the lined edges of the defect become small surfaces due to the impacts between the ball and the defect edges. Therefore, the contact stiffnesses between the ball and the defect edges cannot be calculated by Eq. (2). In this paper, the small surfaces at the defect edges are assumed as small smooth surfaces as shown in Fig. 1a. As a result, the contact between the ball and one edge of the defect can be considered as a ball–plane contact type. The contact stiffness $K_\mathrm{{p}}$ between the ball and the smooth surface can be calculated by Hertzian elastic contact theory, which is given by [38]

$$\begin{aligned} K_\mathrm{{p}} =\frac{4R^{\frac{1}{2}}}{3\left( {\frac{1-\nu _1^2}{E_1}+\frac{1-\nu _2^2 }{E_2 }} \right) } \end{aligned}$$

(3)

where $R$ is the radius of the ball; $E_{1},\,E_{2}$ are the elastic modulus associated with each contact body; and $\nu _{1},\,\nu _{2}$ are the Poisson’s ratio associated with each contact body.

When the ball makes contact with the small surfaces at the defect edges, the new total contact stiffness $K_\mathrm{{t}}$ between the ball and the races with a localized surface defect cannot be calculated by Eq. (1). Here, a new calculation method is proposed to calculate the new total contact stiffness $K_\mathrm{{t}}$ for a ball bearing with a localized surface defect on its races.

As shown in Fig. 5, the total contact deformation $\delta _\mathrm{tr}$ between the healthy and the defective races can be calculated by

$$\begin{aligned} \delta _\mathrm{tr}&= \delta _\mathrm{hr} + \delta _\mathrm{dr} =\left( \frac{F_\mathrm{r}}{K_\mathrm{h}} \right) ^{2/3}\nonumber \\&\!+\!\left( \frac{F_\mathrm{r} \cos \gamma }{n_\mathrm{s} K_\mathrm{p} }\right) ^{2/3}\cos \gamma ,\quad n_\mathrm{s} \!=\!1, 2, 3,\hbox { and } 4 \end{aligned}$$

(4)

where $\delta _\mathrm{{hr}}$ is the contact deformation between the ball and the healthy race, $\delta _\mathrm{{dr}}$ is the contact deformation between the ball and the defect, $F_\mathrm{{r}}$ is the radial force applied on the ball, and $n_\mathrm{{s}}$ is the numbers of the contact surfaces between the ball and the defect edges. Then, the total contact stiffness $K_\mathrm{{ts}}$ between the ball and the races can be calculated by

$$\begin{aligned} K_\mathrm{ts}&= \frac{1}{{\left[ \left( {\frac{1}{K_\mathrm{h}}}\right) ^{2/3} +\left( {\frac{{({\cos \gamma })}^{5/2}}{n_\mathrm{s} K_\mathrm{p} }} \right) ^{2/3}\right] }^{3/2}},\nonumber \\&\quad n_{s} =1, 2, 3,\hbox { and }4 \end{aligned}$$

(5)

where the subscript $s$ denotes the numbers of the contact surfaces.

Fig. 5

Contact deflections between the ball and the small surface at the defect edges

For the first type of a small defect such as a point defect and a small crack, as the descriptions in Fig. 4, the contact stiffness between the ball and the defect can be considered as a constant $K_{d1}$ [23]. The total deformation between the healthy and the defective races is calculated by

$$\begin{aligned} \delta _\mathrm{tr} =\delta _\mathrm{{hr}} +\delta _\mathrm{{dr}} =\left( {\frac{F_\mathrm{r}}{K_ \mathrm{h}}} \right) ^{2/3}+\left( {\frac{F_\mathrm{r}}{K_{d1} }} \right) ^{1/n_\mathrm{{d}} } \end{aligned}$$

(6)

where $n_\mathrm{{d}}$ denotes the load-deflection exponent for the first defect type, and it depends on the shape and sizes of the defect. Since the sizes of the first defect type are very small, $n_\mathrm{{d}}$ can be assumed to be 1.5 for the first defect type. The total contact stiffness $K_\mathrm{{t0}}$ between the ball and the races with the first type defect can be obtained by a polynomial fitting method according to the load-deflection relationship listed in Eq. (6).

For the first defect type, the contact stiffness $K_\mathrm{{e}}$ between the ball and the races can be defined as

$$\begin{aligned} K_\mathrm{e} =\left\{ \begin{array}{ll} K_\mathrm{{t0}} &{}\quad \left| {\hbox {mod } (\theta _{dj} ,2\pi )-\theta _0 -\theta _\mathrm{e} -0.5\Delta \theta } \right| \\ &{}\qquad \le \theta _\mathrm{e} +0.5\Delta \theta \\ K &{}\quad \hbox { otherwise } \\ \end{array} \right. \end{aligned}$$

(7)

where the operator mod() denotes the modulus after the division arithmetic operation, $\theta _\mathrm{{e}}$ is half of the arc length of the defect in the tangential direction; $K_\mathrm{{t0}}$ is the total contact stiffness between the ball and the races when a first type defect occurs on the surface of the inner race or the outer race; $\Delta \,\theta$ is the arc length of the propagated surface at the defect edges in the tangential direction, which is given by

$$\begin{aligned} \Delta \theta = \left\{ \begin{array}{ll} \hbox {arcsin} \left( {\frac{2l\cos \gamma }{D_\mathrm{i}}} \right) &{}\quad \hbox { defect on inner race} \\ \hbox {arcsin} \left( {\frac{2l\cos \gamma }{D_\mathrm{o}}} \right) &{}\quad \hbox { defect on outer race } \\ \end{array} \right. \end{aligned}$$

(8)

where $D_\mathrm{{i}}$ and $D_\mathrm{{o}}$ are the diameter of the inner race and the outer race, respectively; and $\theta _0$ is the initial angular offset of the defect to the $j$th ball, which is given by

$$\begin{aligned} \theta _0 =\left\{ \begin{array}{ll} \frac{2\pi }{Z}\left( {j-1} \right) +\beta _\mathrm{i} &{}\quad \hbox { defect on inner race} \\ \frac{2\pi }{Z}\left( {j-1} \right) +\beta _\mathrm{o} &{}\quad \hbox { defect on outer race} \\ \end{array} \right. \end{aligned}$$

(9)

where $Z$ is the number of the ball, $\beta _\mathrm{i}$ and $\beta _\mathrm{o}$ are the initial angular offsets of the defect of the first ball when the defect occurs on the inner race and the outer race, respectively; $j$ denotes the $j$th ball, $j$ is 1 to $Z$, and $\theta _{dj}$ is the race contact angle, which is given by

$$\begin{aligned} \theta _{dj} =\left\{ \begin{array}{lll} &{}\frac{2\pi }{Z}\left( {j-1} \right) +\left( {\omega _\mathrm{c} -\omega _\mathrm{r} } \right) t+\beta _\mathrm{i}\\ &{}\quad \hbox { for an inner race contact angle} \\ &{}\frac{2\pi }{Z}\left( {j-1} \right) +\omega _\mathrm{c} t+\beta _\mathrm{o}\\ &{}\quad \hbox { for an outer race contact angle} \\ \end{array} \right. \end{aligned}$$

(10)

where $\omega _\mathrm{c}$ is the rotational speed of the cage, $\omega _\mathrm{r}$ is the rotational speed of the rotor. For the second defect type, the contact stiffness $K_\mathrm{{e}}$ can be described by

$$\begin{aligned} K_\mathrm{e} =\left\{ \begin{array}{ll} K_\mathrm{t1} &{}\quad \theta _0 -\Delta \theta \le \hbox { mod } (\theta _dj,2\pi )\\ &{}\qquad <0.5\theta _\mathrm{{d}} \hbox { and }0.5\theta _\mathrm{{d}} < \hbox { mod }(\theta _dj,2\pi )\\ &{}\qquad \le \theta _\mathrm{d} +\Delta \theta \\ K_\mathrm{t2} &{}\quad \hbox { mod } (\theta _dj,2\pi )=0.5\theta _\mathrm{{d}} \\ K &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(11)

where $K_\mathrm{t1}$ is the total contact stiffness between the ball and the races when the number of the contact surface is 1, $K_\mathrm{t2}$ is the total contact stiffness between the ball and the races when the number of the contact surfaces is 2, $\theta _\mathrm{{d}}$ is the angular position of the defect as follows

$$\begin{aligned} \theta _\mathrm{{d}} =\left\{ \begin{array}{ll} \theta _{0} + \hbox { arcsin }\left( {\frac{L+2l\cos \gamma }{D_\mathrm{i}}} \right) &{} \hbox { defect on inner race} \\ \theta _{0} + \hbox { arcsin }\left( {\frac{L+2l\cos \gamma }{D_\mathrm{o}}} \right) &{} \hbox { defect on outer race} \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(12)

For the third defect type, the contact stiffness $K_\mathrm{{e}}$ can be written as

$$\begin{aligned} K_\mathrm{e} =\left\{ \begin{array}{ll} K_\mathrm{t1} &{}\quad \theta _0 \le \hbox { mod } (\theta _{dj} ,2\pi )\le \theta _0 \hbox { and }\theta _\mathrm{{d}}\\ &{}\qquad \le \hbox { mod } (\theta _{dj} ,2\pi )\le \theta _\mathrm{{d}} \\ K_\mathrm{t3} &{}\quad \theta _0 \!<\!\hbox { mod } (\theta _{dj} ,2\pi )\!<\!0.5\theta _\mathrm{{d}} \hbox { and }0.5\theta _\mathrm{{d}}\\ &{}\qquad < \hbox { mod }(\theta _{dj} ,2\pi )<0.5\theta _\mathrm{{d}}\\ K_\mathrm{t4} &{}\quad \hbox { mod }(\theta _{dj} ,2\pi )=0.5\theta _\mathrm{{d}} \\ K &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(13)

where $K_\mathrm{t3}$ is the total contact stiffness between the ball and the races when the number of the contact surfaces is 3, $K_\mathrm{t4}$ is the total contact stiffness between the ball and the races when the number of the contact surfaces is 4. For the fourth defect type, the contact stiffness $K_\mathrm{{e}}$ can be given by

$$\begin{aligned} K_\mathrm{e} \!=\!\left\{ \begin{array}{ll} K_\mathrm{t1} &{}\quad \theta _0 \!-\!\Delta \theta \!\le \! \hbox { mod } (\theta _dj,2\pi )\le \theta _0\,\;\hbox {and}\,\;\theta _\mathrm{{d}}\\ &{}\qquad \le \hbox { mod } (\theta _dj,2\pi )\le \theta _\mathrm{{d}} +\Delta \theta \\ K_\mathrm{t3} &{}\quad \theta _0 <\hbox { mod } (\theta _dj,2\pi )\le \theta _{1} \hbox { and }\theta _{2}\\ &{}\qquad \le \hbox { mod } (\theta _dj,2\pi )<\theta _\mathrm{{d}} \\ K_\mathrm{t2} &{}\quad \theta _{1} <\hbox { mod } (\theta _dj,2\pi )<\theta _{2} \\ K &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(14)

where $\theta _{1}$ is defined by

$$\begin{aligned} \theta _{1} =\left\{ \begin{array}{ll} &{}\theta _0 +\hbox { arcsin }\left( {\frac{0.5\left( {B+2l\cos \gamma } \right) }{D_\mathrm{i} }} \right) \\ &{}\qquad \hbox { defect on inner race} \\ &{} \theta _0 +\hbox { arcsin }\left( {\frac{0.5\left( {B+2l\cos \gamma } \right) }{D_\mathrm{o} }} \right) \\ &{}\qquad \hbox { defect on outer race } \\ \end{array} \right. \end{aligned}$$

(15)

and $\theta _{2}$ is written as

$$\begin{aligned} \theta _{2} =\left\{ \begin{array}{ll} &{} \theta _\mathrm{{d}} -\hbox { arcsin } \left( {\frac{0.5\left( {B+2l\cos \gamma } \right) }{D_\mathrm{i}}} \right) \\ &{}\qquad \hbox { defect on inner race} \\ &{} \theta _\mathrm{{d}} -\hbox { arcsin } \left( {\frac{0.5\left( {B+2l\cos \gamma } \right) }{D_\mathrm{o} }} \right) \\ &{}\qquad \hbox { defect on outer race} \\ \end{array} \right. \end{aligned}$$

(16)

For the fifth defect type, the contact stiffness $K_\mathrm{{e}}$ can be given by

$$\begin{aligned} K_\mathrm{e} \!=\!\left\{ \begin{array}{ll} K_\mathrm{t1} &{}\quad \theta _0 \!-\!\Delta \theta \!\le \!\! \hbox { mod } (\theta _dj,2\pi ) \!\!<\!\theta _{f1} \hbox { and }\theta _{f2}\\ &{}\qquad <\hbox { mod } (\theta _dj,2\pi )\le \theta _\mathrm{{d}} \!+\!\Delta \theta \\ K_\mathrm{t5} &{}\quad \theta _{f1} \le \hbox { mod } (\theta _dj,2\pi )\le \theta _{f2} \\ K &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(17)

where $K_\mathrm{t5}$ is the contact stiffness between the ball and the bottom surface of the defect, it can be considered as the contact between a ball and a flat smooth surface, and it can be determined by

$$\begin{aligned} K_\mathrm{t5} =\frac{1}{\left[ {\left( {\frac{1}{K_\mathrm{h} }} \right) ^{2/3}+\left( {\frac{1}{K_\mathrm{p}}} \right) ^{2/3}} \right] ^{3/2}} \end{aligned}$$

(18)

and $\theta _{f1}$ is defined by

$$\begin{aligned} \theta _{f1} =\left\{ \begin{array}{ll} &{}\hbox {arcsin} \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H} \right) ^{2}}}{D_\mathrm{i} }} \right) +l\cos \gamma \\ &{}\quad \hbox { defect on inner race} \\ &{}\hbox {arcsin} \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H} \right) ^{2}}}{D_\mathrm{o} }} \right) +l\cos \gamma \\ &{}\quad \hbox { defect on outer race} \\ \end{array} \right. \end{aligned}$$

(19)

where $d$ is the diameter of the ball, $H$ is the defect depth, and $\theta _{f2}$ is given by

$$\begin{aligned} \theta _{f2} =\left\{ \begin{array}{ll} &{}\theta _\mathrm{{d}} -\hbox { arcsin } \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H} \right) ^{2}}}{D_\mathrm{i}}} \right) -l\cos \gamma \\ &{}\quad \hbox { defect on inner race} \\ &{}\theta _\mathrm{{d}} -\hbox { arcsin } \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H} \right) ^{2}}}{D_\mathrm{o}}} \right) -l\cos \gamma \\ &{}\quad \hbox { defect on outer race } \\ \end{array} \right. \end{aligned}$$

(20)

On the other hand, there is an additional deflection due to effects of the presence of the defect with different edge topographies. As shown in Fig. 3, the additional deflection depends on the ratio of the defect length to its width, the ratio of the ball size to the defect minimum size, and the elevation angles of the small surfaces at the defect edges. According to the descriptions in Fig. 3, the maximum of the addition deflection can be obtained. For case 1

$$\begin{aligned} h_{\max 1}&= 0.5d-((0.5d)^{2}-\left( 0.5\min \left( {L,B} \right) \right. \nonumber \\&\left. +\,l\cos \gamma \right) ^{2})^{0.5} \end{aligned}$$

(21)

For case 2

$$\begin{aligned} h_{\max 2}&= 0.5d-((0.5d)^{2}-(0.5\min \left( {L,B} \right) )^{2})^{0.5}\nonumber \\&+\,(0.5\min \left( {L,B} \right) \nonumber \\&+\,\,l\cos \gamma -0.5d\sin \gamma )\tan \gamma \end{aligned}$$

(22)

For case 3

$$\begin{aligned} h_{\max 3}&= 0.5d-((0.5d)^{2}\nonumber \\&-\,\,(0.5\min \left( {L,B} \right) )^{2})^{0.5}+l\sin \gamma \end{aligned}$$

(23)

For case 4

$$\begin{aligned} h_{\max 4} =H \end{aligned}$$

(24)

Then, the time-varying deflection excitation $H^{\prime }$ is given by a piecewise response function, including both the half-sine and the rectangular functions [23], which is defined by

$$\begin{aligned} H^{\prime }=\left\{ \begin{array}{ll} H_1 &{}\quad \xi _\mathrm{{bd}} >>1 \\ H_2 &{}\quad \xi _\mathrm{{bd}} >1 \,\hbox {and}\,\xi _\mathrm{{d}} \le 1 \\ H_3 &{}\quad \xi _\mathrm{{bd}} >1\,\hbox {and}\,\xi _\mathrm{{d}} >1 \\ H_{4} &{}\quad \xi _\mathrm{{d}} \le 1 \\ \end{array} \right. \end{aligned}$$

(25)

where $H_{1},\,H_{2},\,H_{3}$, and $H_{4}$ are the time-varying deflection excitations caused by the first through fifth defect types, respectively, which have been given in Ref. [23]. $H_{1}$ is given by

$$\begin{aligned} H_1 =\left\{ \begin{array}{ll} H &{}\quad \left| {\hbox {mod} (\theta _dj,2\pi )-\theta _0 -\theta _\mathrm{e} -0.5\Delta \theta } \right| \\ &{}\qquad \le \theta _\mathrm{e} +0.5\Delta \theta \\ 0 &{}\quad \hbox { otherwise } \\ \end{array} \right. \end{aligned}$$

(26)

$H_{2}$ is defined by

$$\begin{aligned} H_2 \!=\!\left\{ \begin{array}{ll} h_{\max 2} &{}\, \sin \! \left( {\frac{0.5\pi }{\Delta \theta _2 }\left( {\hbox {mod} (\theta _dj,2\pi )-\theta _0 } \right) } \!\right) \,\theta _0\\ &{}\, \le \hbox { mod } (\theta _dj,2\pi )\le \theta _0 +\Delta \theta _2 \\ 0 &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(27)

$\Delta \theta _2$ is given by

$$\begin{aligned} \Delta \theta _2 =\left\{ \begin{array}{ll} \hbox {arcsin} \left( {\frac{L+2l\cos \gamma }{D_\mathrm{o} }} \right) &{}\quad \hbox {defect on outer race} \\ \hbox {arcsin} \left( {\frac{L+2l\cos \gamma }{D_\mathrm{i} }} \right) &{}\quad \hbox {defect on inner race} \\ \end{array} \right. \end{aligned}$$

(28)

$H_{3}$ is defined by

$$\begin{aligned} H_3 \!=\!\left\{ \begin{array}{ll} h_{\max 3} &{}\, \sin \! \left( {\frac{0.25\pi }{\Delta \theta _1 }\left( {\hbox { mod } \left( {\theta _dj,2\pi } \right) \!-\theta _0 } \right) } \!\right) \,\theta _0\\ &{}\quad \le \hbox { mod } (\theta _dj,2\pi )\le \theta _1 \\ h_{\max 3} &{}\, \theta _1 <\hbox { mod } (\theta _dj,2\pi )<\theta _3 \\ h_{\max 3} &{}\, \sin \! \left( {\frac{0.25\pi }{\Delta \theta _3 }\left( {\hbox {mod} \left( {\theta _dj,2\pi } \right) \!-\theta _0 } \right) } \!\right) \theta _3\\ &{}\quad \le \hbox { mod } (\theta _dj,2\pi )\le \theta _\mathrm{{d}} \\ 0 &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(29)

$\Delta \theta _1$ and $\Delta \theta _3$ are given by

$$\begin{aligned} \Delta \theta _1 =\Delta \theta _{3} =\left\{ \begin{array}{ll} &{}\hbox { arcsin } \left( {\frac{0.5B+l\cos \gamma }{D_\mathrm{o}}} \right) \\ &{}\quad \hbox { defect on outer race} \\ &{} \hbox { arcsin } \left( {\frac{0.5 B+l\cos \gamma }{D_\mathrm{i}}} \right) \\ &{}\quad \hbox { defect on inner race} \\ \end{array} \right. \end{aligned}$$

(30)

$H_{4}$ is defined by

$$\begin{aligned} H_4 =\left\{ \begin{array}{ll} h_{\max 4} &{}\, \sin \left( {0.25\pi /\Delta \theta _4 \left( {\hbox { mod } \left( {\theta _dj,2\pi } \right) -\theta _0 } \right) } \right) \,\theta _0\\ &{}\quad \le \hbox { mod } (\theta _dj,2\pi )<\theta _{f1} \\ h_{\max 4} &{}\, \theta _{f1} \le \hbox { mod } (\theta _dj,2\pi )\le \theta _{f2} \\ h_{\max 4} &{}\, \sin \left( {0.25\pi /\Delta \theta _4 \left( {\hbox { mod } \left( {\theta _dj,2\pi } \right) -\theta _0 } \right) } \right) \,\theta _{f2}\\ &{}\quad <\hbox { mod } (\theta _dj,2\pi )\le \theta _\mathrm{{d}} \\ 0 &{}\quad \hbox { otherwise} \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(31)

$\Delta \theta _4$ is given by

$$\begin{aligned} \Delta \theta _{4} =\left\{ \begin{array}{l} \hbox {arcsin} \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H+l\sin \gamma } \right) ^{2}}+l\cos \gamma }{D_o }} \right) \\ \quad \hbox {defect on outer race} \\ \hbox {arcsin} \left( {\frac{\sqrt{\left( {0.5d} \right) ^{2}-\left( {0.5d-H+l\sin \gamma } \right) ^{2}}+l\cos \gamma }{D_i }} \right) \\ \quad \hbox {defect on inner race} \\ \end{array} \right. \end{aligned}$$

(32)

3.2 Dynamic model of ball bearing

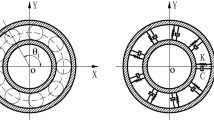
To investigate the vibration characteristics of the ball bearing with a localized surface defect on its races, the contact between the ball and the races is considered as a lumped spring-mass system as shown in Fig. 6. This model was first developed by Sunnersjo [39]. However, in the Sunnersjo’s model, the bearing is only modeled as a lumped spring-mass system; effects of the damping and the defect are ignored. The model is only used to study the vibration response of a rolling element bearing system due to the time-varying compliance. In this paper, the Sunnersjo’s model is extended to include effects of the damping, the time-varying compliance property of the bearing system, and a localized surface defect with different edge topographies on its races. The proposed model can also consider the radial and the tangential deflections at the defect edges, the time-varying deflection excitation and the time-varying contact stiffness excitation caused by the defect, and effects of the different defect edge topographies.

Fig. 6

A lumped spring-mass system of a ball bearing with a localized defect on the races

The governing equations of motion of the two-degree-of-freedom bearing system are written as

$$\begin{aligned} m\ddot{x}+c\dot{x}+K_\mathrm{e} \sum _{j=1}^Z {\lambda _j}\delta _j^{1.5} \cos \theta _{dj}&= Q_x\end{aligned}$$

(33)

$$\begin{aligned} m\ddot{y}+c\dot{y}+K_\mathrm{e} \sum _{j=1}^Z {\lambda _j } \delta _j^{1.5} \sin \theta _{dj}&= Q_y \end{aligned}$$

(34)

where $m$ is the total mass of the inner race and the shaft, $c$ is the damping coefficient, $Q_x$ and $Q_y$ are the components of external force applying on the shaft, $x$ and $y$ are the displacement responses in the $X$- and $Y$-direction, and $\lambda _j$ is the loading zone parameter of the $j$th ball written as

$$\begin{aligned} \lambda _j =\left\{ \begin{array}{ll} 1 &{}\quad \delta _j >0\\ 0 &{}\quad \delta _j \le 0\\ \end{array} \right. \end{aligned}$$

(35)

The total contact deformation of the $j$th ball at any angle $\delta _j$ is given by

$$\begin{aligned} \delta _j =x\cos \theta _j +y\sin \theta _j -C_r -H^{{\prime }} \end{aligned}$$

(36)

where $C_\mathrm{{r}}$ is the internal radial clearance of the ball bearing, $H\prime$ is the time-varying deflection excitation function corresponding to each defect as shown in Eq. (25), $H_{1}$ describes the first defect type, $H_{2}$ is applied to describe the second and third defect types, $H_{3}$ depicts the fourth defect type, and $H_{4}$ describes the fifth defect type.

4 Results and discussion

A fourth-order Runge–Kutta method with a constant time step is applied to calculate the numerical solution from the governing equations of the two-degree-of-freedom model of a ball bearing derived in Sect. 3. The design parameters of a deep-groove ball bearing in Ref. [23], as shown in Table 1, are used. The total mass of the inner race and the shaft is 0.6 kg, and the simulated operating condition is that the shaft rotates at 2,000 rpm and the external radial load of 20 N is applied to the shaft in the $X$-direction. In order to reduce the calculation time and obtain enough points to describe the impulse waveforms caused by the localized surface defects with different edge topographies, the time step for the numerical investigation in this paper is assumed as the time required for 0.0092 $^{\circ }$ of rotation. For the shaft speed of 2,000 rpm, the time step utilized in this numerical solution is $\Delta t={2}\times 10^{-6}\,\hbox {s}$. The initial displacements used for the inner race and the shaft are $x_0 =10^{-6}\,\hbox {m}$ and $y_0 =10^{-6}\,\hbox {m}$, and the initial velocities in the $X$- and $Y$-directions are zero. The sizes and depth of the three different defect cases of interest are listed in Table 2. According to the descriptions in Fig. 3 and the parameters of the ball bearing and the defects in Tables 1 and 2, the value of the elevation angle $\gamma$ of the small plane surface at the defect edge can be from 0.001 rad to 1.571 rad, which is calculated by the method in Fig. 3.

Table 1 Parameters of a deep-groove ball bearing used in the simulation

Table 2 Size and depth of defects studied in this numerical analysis

4.1 Effects of the defect edge topographies on the contact stiffness between the ball and the defect

Figure 7a, b shows the total contact stiffnesses between the healthy outer race and the defective inner race, and those between the healthy inner race and the defective outer race, respectively. As shown in Fig. 7, the total contact stiffnesses between the healthy race and the defective race of the ball bearing increase with the numbers of contact surfaces between a ball and the edges of the defect. It is also shown that the total contact stiffnesses increase as the elevation angle $\gamma$ of the small surface at the edges of the defect increases. Note that the contact stiffness between the ball and the races of the bearing varies with the contact position between the ball and the defect when the ball passes over the defect due to the changes in the numbers of the contact surfaces between the ball and the defect edges.

Fig. 7

Total contact stiffness between the healthy race and the defective race of the ball bearing: a defect on the inner race and b defect on the outer race (line with circle one contact surface; line with triangle two contact surfaces; line with square three contact surfaces; and line with asterisk four contact surfaces)

To verify the proposed method, one ball and the healthy outer race, and one ball and the outer race with a plane surface are modeled using the finite element (FE) analysis method. The contact FE model of the ball and the healthy outer race (ball–ball contact as shown in Fig. 1a), and that of the ball and the outer race with a plane surface (ball–plane contact as shown in Fig. 2b, c) are modeled using three-dimensional solid elements and three-dimensional node-to-surface contact elements that include the elastic Coulomb frictional effect according to the FE modeling method in Ref. [24]. The mesh size in the contact area of the FE model is 0.05 mm. The bottom surface of the outer race is fixed. An external radial load is applied at the center of the top surface of the half ball. The displacements of nodes on the top surface of the half ball in the $Y$-direction are coupled to apply a uniformly distributed load there. The radial contact deformations from the FE model with the healthy outer race for different radial loads are compared with those from Hertzian contact theory, as shown in Table 3. For the contact FE model of the ball and the healthy outer race (ball–ball contact), the differences between the results from the Hertzian contact theory and the FE analysis method are less than 2 %. The radial contact deformations from the FE model with a plane surface for different radial loads are compared with those from Hertzian contact theory, as shown in Table 4. For the contact FE model of the ball and the plane surface (ball–plane contact), the differences between the results from Hertzian contact theory and the FE analysis method are also less than 2 %. Table 5 shows the comparison of radial contact deformations between the ball–ball contact and the ball–plane contact from Hertzian contact theory and the FE analysis method for different radial loads. It is found that the results of the ball–ball contact and those of the ball–plane contact from Hertzian contact theory, and those from the FE analysis method are very different. Table 5 also shows that the radial contact deformations of the ball–ball contact are less than those of the ball–plane contact. Therefore, when the ball first reaches the defect edge, the contact stiffness between the ball and the race will be changed when the ball is in contact with the small surface at the defect edge, which will also cause an impulse.

Table 3 Comparison of radial contact deformations between the ball and the healthy race from Hertzian contact theory and the FE analysis method for different radial loads

Table 4 Comparison of radial contact deformations between the ball and the small surface at the defect edge from Hertzian contact theory and the FE analysis method for different radial loads

Table 5 Comparison of radial contact deformations between the ball–ball contact and the ball–plane contact from Hertzian contact theory and the FE analysis method for different radial loads

4.2 Effects of defect edge topographies on vibration response of the ball bearing

4.2.1 Vibration response comparisons applying different defect models

To verify the proposed model, the time- and frequency-domain vibration response of the inner race of the ball bearing from different defect models is compared. The first defect case on the surface of the outer race of the bearing is investigated. The sizes of the first defect case are given in Table 2. The initial angular position of the defect is assumed to be zero degree. The elevation angle $\gamma$ and the length $l$ of the small surfaces at defect edge are assumed to be 0.4 rad and 0.02 mm. The different defect models include Rafsanjani et al.’s model [2], Patel et al.’s model [18], time-varying deflection excitation model [23], and the proposed model considering both the time-varying deflection excitation and the time-varying contact stiffness excitation. For these four different defect models, the surface areas are assumed to be same, which means the length $L$ and width $B$ of the defect are same, as shown in Fig. 8.

Figure 9a–d shows the time- and frequency-domain acceleration response in the $X$-direction from Rafsanjani et al.’s model, Patel et al.’s model, time-varying deflection excitation model, and the proposed model. Note that the time delay between the impulses caused by the defect is same for the four different models, which is equal to 0.0098 s as shown in Fig. 9a. However, there are significant differences between the waveforms of the acceleration response from the four different models.

Fig. 8

Schematics of the defect size used in vibration response comparisons applying different defect models: a front view of the ball bearing and b top view of the ball bearing

Fig. 9

Comparisons of vibration response in the $X$-direction of the ball bearing with a defect on its outer race using different defect models: a acceleration response from the four different models from 0.117 to 0.137 s, b frequency spectra of acceleration response from the four different models, c closed-up plot of a, and d closed-up plot of b. (line with circle Rafsanjani et al.’s model; line with asterisk Patel et al.’s model; line with inverse triangle time-varying deflection model; line with square the proposed model)

As shown in Fig. 9c, Rafsanjani et al.’s model only describes the time-invariant impulse stage $\hbox {A}_{0}\hbox {A}_{1}\hbox {B}_{1}\hbox {B}_{0}$, since their model used a rectangular function to model the time-invariant deflection excitation caused by the changes in the contact positions between the ball and the defect when the ball passes over the defect as shown in Fig. 1a. Patel et al.’s model also only describes the time-invariant impulse stage $\hbox {A}_{0}\hbox {A}_{2}\hbox {B}_{2}\hbox {B}_{0}$, whose impulse waveform is similar to that from Rafsanjani et al.’s model because they also used a rectangular function to model the time-invariant deflection excitation. However, its amplitude is less than that of Rafsanjani et al.’s model, because Rafsanjani et al.’s model used the defect depth to determine the amplitude of the rectangular function, but that of Patel et al.’s model is determined by the geometry relationship between the ball and the defect. Moreover, the time-varying deflection model can describe the time-varying impulse stage $\hbox {A}_{0}\hbox {B}_{0}$, which used a half-sine function to model the time-varying deflection excitation caused by the changes in the contact positions between the ball and the defect when the ball passes over the defect. According to the descriptions in Sect. 2, when the ball passes over the defect, the impulse caused by the defect is time-varying; the amplitude of the impulse function should be determined by the contact relationship between the ball and the defect; and the impulse excitation includes both the time-varying deflection excitation and the time-varying contact stiffness excitation caused by the changes in the numbers of the contact surfaces between the ball and the defect. However, Rafsanjani et al.’s model, Patel et al.’s model, and the time-varying deflection model only modeled the time-invariant deflection excitation and the time-varying deflection excitation caused by the defect, which cannot describe the impulse caused by the time-varying contact stiffness due to the changes in the numbers of the contact surfaces between the ball and the defect. To overcome this problem, the proposed model considering both the time-varying deflection excitation and the time-varying contact stiffness excitation is proposed in this paper, which is modeled by a piecewise function including the rectangular function and the half-sine function. For the proposed model, the amplitude of the time-varying deflection excitation is determined by the geometry relationship between the ball and the defect, and the value of the time-varying contact stiffness is determined by Hertzian contact theory. As shown in Fig. 9c, the proposed model can describe not only the time-varying impulse stage $\hbox {A}_{0}\hbox {ABB}_{0}$, but also the impulse stages $\hbox {A}_{0}\hbox {A}$ and $\hbox {BB}_{0}$ caused by the time-varying contact stiffnesses due the changes in the numbers of the contact surfaces (from 1 surface to 3 surfaces, and from 3 surfaces to 1 surface) between the ball and the defect edges, as described in Sect. 2.

As shown in Fig. 9c, note that the amplitudes of the acceleration response from Rafsanjani et al.’s model and the proposed model are larger than those from Patel et al.’s model and the time-varying deflection excitation model. Comparisons of the acceleration response from Rafsanjani et al.’s model and the proposed model show that Rafsanjani et al.’s model can only describe the time-invariant impulse caused by the defect, but the proposed model can describe the time-varying impulse and effects of the defect edge topographies which are more close to the real as the analysis in Sect. 2. Comparisons between Patel et al.’s model and the time-varying deflection excitation model show Patel et al.’s model can formulate geometry relationship between the ball and the defect, but it cannot model the time-varying impulse generated by the defect when the ball passes through the defect. The time-varying deflection excitation model can consider effects of both the geometry relationship between the ball and the defect and the deflection impulse, but it cannot consider the time-varying contact stiffness between the ball and the defect.

In addition, comparisons of the frequency spectra of the acceleration response of the inner race of the bearing in the $X$-direction from the four defect models are shown in Fig. 9b, d. Note that the same peak frequencies at 102.20 Hz appear in the frequency spectra from the four models. However, the amplitudes of the peaks are different for the four different models. The amplitude of the frequency spectrum of Rafsanjani et al.’s model is larger than those of the other three models. The amplitude of the proposed model is larger than those of Patel et al.’s model and the time-varying deflection excitation model. The amplitude of the time-varying deflection excitation model is smaller than that of Patel et al.’s model. This occurs because the additional deflection caused by the defect is assumed as the depth of the defect in the Rafsanjani et al.’s model, and both the time-varying deflection excitation and the time-varying contact stiffness excitation are considered in the proposed model, when the ball passes over the defect. However, in Patel et al.’s model and the time-varying deflection excitation model, they only consider the effect of the additional deflection determined by the defect size and ball diameter, which is smaller than those in Rafsanjani et al.’s model and the proposed model. These results show that the proposed model is validation and more accurately for the ball bearing dynamics simulation according to the analysis in Sect. 2. The proposed model can not only describe the time-varying deflection excitation generated by the defect, but also model the time-varying contact stiffness between the ball and the defect with different edge topographies when the ball passes over the defect.

4.2.2 Effects of the defect edge topographies on the waveforms of the acceleration response of the ball bearing

Figures 10, 11, and 12 show effects of the defect edge topographies on the waveforms of the acceleration response in the $X$-direction of the inner race of the ball bearing for the defect cases 1, 2, and 3, respectively. Here, to compare the waveforms of the acceleration responses of the ball bearing caused by different defect, the initial position of the defect is assumed to be zero. Note that the impulses at the points A, B, $\hbox {A}_{1},\hbox { A}_{2},\hbox { A}_{3},\hbox { D}_{1},\hbox { D}_{2}$, and $\hbox {D}_{3}$ caused by the changes in the contact stiffnesses between the ball and the defect edges are also observed in Figs. 10, 11 and 12 for the three studied defect cases, whose reasons are similar with the descriptions in Sect. 4.2.1. Effects of the elevation angle $\gamma$ of the small surface at the defect edge on the acceleration response of the ball bearing for cases 1, 2, and 3 are shown in Figs. 10a, 11a, and 12a, respectively. The amplitude of the acceleration response increases consistently with the elevation angle $\gamma$ for the three different cases. This occurs because the amplitudes of the time-varying deflection excitations and the time-varying contact stiffness excitations caused by the three defect cases increase with the elevation angle $\gamma$ as shown in Eqs. (5), (21) to (23), and Fig. 7, when the elevation angle $l$ is a constant value. Figures 10b, 11b, and 12b plot effects of length $l$ of the small surface at the defect edge on the acceleration response of the three studied defect cases. The amplitude of the acceleration response also increases consistently with the length $l$ for the three different cases. This occurs because the amplitudes of the time-varying deflection excitations caused by the three defect cases increase consistently with the length $l$ as shown in Eqs. (21) and (23) when the elevation angle $\gamma$ is a constant value. Moreover, as shown in Figs. 10b, 11b, and 12b, the differences of the impulses between points $\hbox {A}_{1}$ and $\hbox {B}_{1}$, that between points $\hbox {A}_{2}$ and $\hbox {B}_{2}$, and that between points $\hbox {A}_{3}$ and $\hbox {B}_{3}$ caused by the changes in the contact stiffnesses between the ball and the defect edges decrease as the length $l$ increases for the defect cases 1, 2, and 3. This occurs because the duration of the impulse increases with the arc length of the propagated surface at the defect edges in the tangential direction $\Delta \,\theta$ when the length $l$ increases as shown in Figs. 1 and 2.

Fig. 10

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a first type defect on its outer race using the proposed models from 0.11718 to 0.11726 s: a effect of the elevation angle $\gamma$ and b effect of the length $l$ (line with circle $\gamma =0.40$ rad and $l=0.2L$; line with asterisk $\gamma =0.44$ rad and $l=0.2L$; line with inverse triangle $\gamma =0.48$ rad and $l=0.2L$; line with plus symbol $\gamma =0.40$ rad and $l=0.2L$; line with square $\gamma =0.40$ rad and $l=0.3L$; line with star $\gamma =0.40$ rad and $l=0.4L$)

Fig. 11

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a second defect on its outer race using the proposed models from 0.11718 to 0.11726 s: a effect of the elevation angle $\gamma$ and b effect of the length $l$. (line with circle $\gamma =0.40$ rad and $l=0.2L$; line with asterisk $\gamma =0.44$ rad and $l=0.2L$; line with inverse triangle $\gamma =0.48$ rad and $l=0.2L$; line with plus symbol $\gamma =0.40$ rad and $l=0.2L$; line with square $\gamma =0.40$ rad and $l=0.3L$; line with star $\gamma =0.40$ rad and $l=0.4L$)

Fig. 12

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a third defect on its outer race using the proposed models from 0.11718 to 0.11736 s: a effect of the elevation angle $\gamma$ and b effect of the length $l$. (line with circle $\gamma =0.40$ rad and $l=0.2L$; line with asterisk $\gamma =0.44$ rad and $l=0.2L$; line with inverse triangle $\gamma =0.48$ rad and $l=0.2L$; line with plus symbol $\gamma =0.40$ rad and $l=0.2L$; line with square $\gamma =0.40$ rad and $l=0.3L$; line with star $\gamma =0.40$ rad and $l=0.4L$)

Figures 13 and 15 show effects of time-varying defect edge topographies on waveforms of the acceleration response in the $X$-direction of the inner race of the ball bearing for the defect cases 2, 3, and 4, respectively. In this paper, to describe effects of time-varying defect edge topographies on vibrations of the ball bearing with a localized surface defect on its races, the rates of change of the elevation angle $\gamma$ and the length $l$ of the small surface at the defect edges are assumed to be constant since simulating the rates of the defect edge topographies due to the ball impacts is very complex and beyond the scope of this study. Note that the amplitude of the acceleration response increases consistently with the elevation angle $\gamma$ and the length $l$ of the small surface at the defect edge due to the impacts between the ball and the defect edges for the studied cases. This is because the amplitudes of the time-varying deflection excitation and the time-varying contact stiffness excitation increase with the elevation angle $\gamma$ and the length $l$ of the small surface at the defect edge as analyzed in Eqs. (5), (21) to (23), and Fig. 7. The results from the proposed model considering the time-varying deflection excitation and the time-varying contact stiffness excitation caused by the localized defect with different edge topographies cannot be predicted by the previous localized surface defect models in the literature (Fig. 14).

Fig. 13

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a first defect on its outer race using the proposed models from 0.1172 to 0.1563 s: a effect of the elevation angle $\gamma$ and b effect of the length $l$

Fig. 14

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a third defect on its outer race using the proposed models from 0.1172 to 0.1563 s: a effect of the elevation angle $\gamma$ and b effect of the length $l$

Fig. 15

Effects of defect edge topographies on the acceleration response in the $X$-direction of the ball bearing with a fourth defect on its outer race using the proposed models from 0.1172 to 0.1563 s: a schematic of the fourth defect and b effect of the length $l$

4.2.3 Effects of the defect edge topographies on the statistical measures of the acceleration response of the ball bearing

Statistical measures which can determine the impulsive character of a time-domain signal are widely used in bearing fault diagnosis and detection [7, 8, 40–42]. Here, three different well-known statistical indicators such as root mean square (RMS), crest factor (CF), and kurtosis are applied to investigate effects of the defect edge topographies on the acceleration response in the $X$-direction of the inner race of the ball bearing. These parameters of a discrete signal $s$ are given by [8]

$$\begin{aligned}&\hbox {RMS}=\sqrt{\frac{1}{N_\mathrm{f}}\sum _{i=1}^{N_\mathrm{f}} {s_i^2}}\end{aligned}$$

(37)

$$\begin{aligned}&\hbox {CF}=\frac{\max (s)-\min (s)}{\hbox {RMS}}\end{aligned}$$

(38)

$$\begin{aligned}&\hbox {Kurtosis}=\frac{\sum _{i=1}^{N_\mathrm{f} } {\left( {s_i -\hbox {mean}(s)}\right) ^{4}}}{N_\mathrm{f} \hbox {RMS}^{4}} \end{aligned}$$

(39)

where $N_\mathrm{{f}}$ is the number of samples, $s_\mathrm{{i}}$ is the $i$th data of the discrete signal $s$, max() is the maximum value of the discrete signal $s$, min() is the minimum value of the discrete signal $s$, and mean() is the mean value of the discrete signal $s$.

Figures 16, 17, and 18 show the statistical measures of the acceleration response in the $X$-direction of the inner race of the ball bearing from 0.3 to 0.4 s for the defect cases 1, 2, and 3. According to the parameters in Table 2 and the descriptions in Fig. 3, the range of the elevation angle $\gamma$ can be chosen to be from 0.4 to 0.5 rad in this section. The RMS of the $X$-direction acceleration response for cases 1, 2, and 3 are shown in Figs. 16a, d, g, j, m, 17a, d, g, j, m, and 18a, d, g, j, m, respectively. The RMS increases consistently with the length $l$ and the elevation angle $\gamma$ for the three different cases. This occurs because the amplitude of the acceleration response of the ball bearing increases with the elevation angle $\gamma$ and the length $l$ as shown in Figs. 10, 11, 12, 13, and 14. Figures 16b, e, h, k, n, 17b, e, h, k, n, and 18b, e, h, k, n give the crest factor of the $X$-direction acceleration response of the three studied defect cases. For the three defect cases, the crest factor decreases with the length $l$ because the duration of the impulse waveform increase with the length $l$ as shown in Figs. 10, 11, and 12. It increases as the elevation angle $\gamma$ increases because the duration of the impulse waveform decreases with the elevation angle $\gamma$, and the amplitude of the impulse waveform is affected little by the changes of the elevation angle $\gamma$, as shown in Figs. 10, 11, 12, 13, and 14, when the length $l$ is a constant value for the defect cases 1 and 2. For the defect case 3, it decreases as the elevation angle $\gamma$ increases because of the differences between amplitude of the acceleration response at the contact position at the beginning and ending edges and that at the other locations of the defect as shown in Fig. 12a. The kurtosis of the $X$-direction acceleration response of the three selected defect cases is shown in Figs. 16c, f, i, l o, 17c, f, i, l, o, and 18c, f, i, l, o, respectively. The kurtosis also decreases with the length $l$ for the three defect cases. Moreover, the kurtosis also increases as the elevation angle $\gamma$ increases for the defect cases 1 and 2; it decreases with the elevation angle $\gamma$ for the defect case 3. This occurs because the similar reasons with the crest factors for the three defect cases. The above results show that the vibration level of the ball bearing increases as the defect sizes for the three studied defect cases. The crest factor of the acceleration response will decrease when the defect edges progress along the direction of the ball motion for the defect cases 1, 2, and 3. When the defect edges progress along the direction of the ball motion, the kurtosis of the acceleration response of the ball bearing also decreases for defect cases 1, 2, and 3.

Fig. 16

Statistical measures of the acceleration response of the inner race of the bearing in the $X$-direction for defect case 1: a RMS, b crest factor, c kurtosis, d RMS for $l=0.1L$, e crest factor for $l=0.1L$, f kurtosis for $l=0.1L$, g RMS for $l=0.2L$, h crest factor for $l=0.2L$, i kurtosis for $l=0.2L$, j RMS for $l=0.4L$, k crest factor for $l=0.4L$, l kurtosis for $l=0.4L$, m RMS for $l=0.6L$, n crest factor for $l=0.6L$, and o kurtosis for $l=0.6L$

Fig. 17

Statistical measures of the acceleration response of the inner race of the bearing in the $X$-direction for defect case 2: a RMS, b crest factor, c kurtosis, d RMS for $l=0.1L$, e crest factor for $l=0.1L$, and f kurtosis for $l=0.1L$, g RMS for $l=0.2L$, h crest factor for $l=0.2L$, (i) kurtosis for $l=0.2L$, j RMS for $l=0.4L$, k crest factor for $l=0.4L$, l kurtosis for $l=0.4L$, m RMS for $l=0.6L$, n crest factor for $l=0.6L$, and o kurtosis for $l=0.6L$

Fig. 18

Statistical measures of the acceleration response of the inner race of the bearing in the $X$-direction for defect case 3: a RMS, b crest factor, c kurtosis, d RMS for $l=0.1L$, e crest factor for $l=0.1L$, and f kurtosis for $l=0.1L$, g RMS for $l=0.2L$, h crest factor for $l=0.2L$, i kurtosis for $l=0.2L$, j RMS for $l=0.4L$, k crest factor for $l=0.4L$, l kurtosis for $l=0.4L$, m RMS for $l=0.6L$, n crest factor for $l=0.6L$, and o kurtosis for $l=0.6L$

5 Conclusions

A new ball bearing dynamic model coupled with effects of defect edge topographies is developed to investigate effects of defect edge topographies on the vibration response of a ball bearing with a localized surface defect on its races. According to the shape and sizes of the defect, a new contact model for determining the contact relationships between the ball and the defect edges is proposed based on Hertzian elastic contact theory. The proposed model is applied to investigate effects of defect edge topographies on the contact stiffnesses between the ball and the defect edges, and the vibration response of the ball bearing. The following specific conclusions can be drawn:

• 1. The contact stiffness between the ball and the races of the ball bearing varies with the contact positions between the ball and the defect edges when the ball passes over the defect due to changes in the numbers of the contact surfaces between the ball and the defect edges. The total contact stiffness between the healthy race and the defective race of the ball bearing increases with the numbers of contact surfaces between a ball and the defect edges. The total contact stiffness also increases as the elevation angle $\gamma$ increases.

• 2. The different defect models have significant effect on the pulse waveform of the vibration response of the ball bearing caused by a localized surface defect. Therefore, it is necessary to formulate the localized defect model including effects of the length–width ratio of the defect, the time-varying deflection and the time-varying contact stiffness excitation produced by the defect, and effects of defect edge topographies.

• 3. The impulses caused by changes in the time-varying contact stiffnesses between the ball and the defect edges with different topographies can be described by the proposed model, which cannot be described by the previous deflection excitation models in the literature. The amplitude of the impulse increases with the elevation angle $\gamma$ and the length $l$ of the small surface at the defect edge. Moreover, the proposed method in this paper can be extended to formulate effects of the random defect edge topographies on the vibration response of the ball bearing with a localized surface defect on its races.

• 4. The RMS of the acceleration response of the ball bearing increases consistently with the defect sizes for defect cases 1, 2, and 3. The crest factor and the kurtosis of the acceleration response of the ball bearing will decrease when the defect edges progress along the direction of the ball motion for the defect cases 1, 2, and 3.