1 Introduction

The mechanism analysis and prevention technology for slope hazards have been of concern to engineers, nevertheless, landslides remain a common geological hazard triggered by climatic conditions (e.g. rainwater infiltration) (Petley 2012; Klose et al. 2016; Lin and Wang 2018; Chen et al. 2019). After Terzaghi (1943) verified the presence of the soil arching effect through the trapdoor test, the pile-soil arching effect was an important research topic. The pile-soil arching effect is a phenomenon of stress re-distribution and transfer due to the shear strength of soil during nonuniform displacement of the soil behind the piles (Wang et al. 1974; Bosscher et al. 1986; Kourkoulis et al. 2011). At present, use of anti-sliding piles is considered as an effective reinforcement measure for unstable slopes (Zhang et al. 2016, 2017; Liu et al. 2020). From the perspective of engineering control measures, Zheng et al. (2010) applied the strength-reduction finite element method (FEM) to some design cases of anti-slide piles. By using FEM, the pile-soil interactions were taken into consideration to obtain reasonable resistance in front of pile and the distributions of thrust and resistance, and reasonable lengths of anti-slide piles. Anti-sliding piles can hinder the shear failure of soil along a weak plane and the pile-soil arching effect appears between anti-sliding piles and the reinforced soil (Smethurst et al. 2007; Shubhra et al. 2008; Liang et al. 2014)

The reinforcement effect of pile-soil arch is explored mainly from different aspects such as: the formation process, mechanical modelling, and the axis of the pile-soil arch. Some researchers (Chen et al. 2008; Zou et al. 2008) discussed the vertical pile-soil arching effect and load transfer model for soil between piles and explored the influences of parameters of soil, pile-foundation relative displacement, and pile spacing on the pile-soil arching effect. On the basis of stress condition of the anti-sliding piles under the effect of lateral load, a mathematical analytical expression for the stress at an arbitrary point on the pile and soil can be obtained according to the influence of pile-soil interaction (Li et al. 2010; Ashour et al. 2012). From the perspective of the pile-soil arching effect, Chen et al. (2002) discussed the formation and mechanical behaviour of passive pile groups under the effect of lateral displacement of soil. They also investigated the influence of changes in various parameters (such as shape of arched zone, distribution and shape of piles, and pile-soil relative displacement) on pile-soil interaction. Liang et al. (2002, 2010, 2012, 2014) analysed the main mechanisms of anti-sliding piles in enhancing the stability of the soil slope based on the pile-soil effect. They derived the semi-empirical equations for quantifying the arching effect through three-dimensional finite element model parametric study. And they presented two design examples to discuss optimization design of anti-sliding pile location on slope, dimension of anti-sliding pile (diameter and length), pile spacing between adjacent piles, and reinforcement requirements. Some researchers (Paik et al. 2003; Han et al. 2009; Kousik 2010; Rui et al. 2019; Yang et al. 2019) explored the mechanism of action of the pile-soil arching effect and the load transfer mechanism acting on soil arches between anti-sliding piles for reinforcing slopes and deduced the corresponding method for calculating the stress based on the horizontal pile-soil arching effect between piles. The pile spacing necessary for development of pile-soil arching effect is also assessed and the reasonable pile spacing required under given strength conditions is established by investigating the pile-soil arching effect (Rollins et al. 2006a, b; Liang et al. 2002; Joorabchi et al. 2013; Chen et al. 2020). Based on the reinforcement mechanism of the soil-pile interaction, Ashour et al. (2004, 2012) explored the interaction between piles and the surrounding soil and the bearing capacity of piles and discussed the influences of pile diameter, pile position, and pile spacing on the safety factor of slopes, attaining the optimal effects of the pile position and pile spacing. Li et al. (2010) performed theoretical analysis based on the pile-soil arching effect formed under horizontal force and established a mechanical model of the pile-soil arch and the governing equation for the maximum pile spacing. Zhao et al. (2010) established a calculation model considering the influence of the inclination of slopes on pile spacing based on the inclined arching effect of soil between piles to obtain a formula for pile spacing. The results are based on the assumption that the slope angle is regarded as included angle of the inclined arching. In this study, the mechanical mechanism of the inclined pile-soil arch was discussed along the direction of inclination of the sliding force transferred from a sliding mass to anti-sliding piles, providing a reference for engineering practice when reinforcing slopes with anti-sliding piles.

2 Mechanical behaviour of the inclined pile-soil arch

2.1 Mechanical model of the inclined pile-soil arch

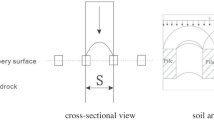
After reinforcing a slope with anti-sliding piles, a reasonable pile-soil arch zone is formed due to the interaction between the anti-sliding piles and soil behind the piles. The sliding force of the slope is transferred to the anti-sliding piles through the pile-soil arch zone to form the pile-soil arching effect. If the sliding force is applied in the horizontal direction, it is supposed to form the horizontal pile-soil arching effect. Generally, the included angle between the sliding force of the slope body and the horizontal plane is nonzero, therefore, it is supposed to form an inclined pile-soil arching effect (Fig. 1). In Fig. 1, F, H, b, L, l, and α refer to the sliding force (kN/m) of the sliding mass per unit width, the length (m) of the free section of the anti-sliding piles, pile width (m), spacing between pile axes (m), clear pile spacing (m), and the included angle between the sliding force and the horizontal direction, respectively.

Fig. 1.
figure 1

Mechanical model of an inclined pile-soil arch: a the pile-soil arch; b the stress on the pile-soil arch

Full size image

According to the stress characteristics of the pile-soil arch, the sliding force of soil behind the piles can be deemed equivalent to the uniformly distributed loads along the pile length. In the analysis, the loads applied to the anti-sliding piles are supposed to be distributed in either triangular or parallelogrammic form (Fig. 2). The basic assumptions made in the following formulation analysis are enumerated: (1) The soil was assumed as elastic and isotropic material with Mohr-Coulomb failure criterion. (2) The soil pressure on the piles is transferred through an inclined pile-soil arch uniformly distributed along the piles. And (3) the shape of pile-soil arch zone between piles is a parabola symmetrical to the middle of span with the inclination angle of pile-soil arch zone set to the inclination angle of sliding force.

Fig. 2.
figure 2

Load distribution on the anti-sliding piles

Full size image

By analysing the stress on the pile-soil arch and the load distribution of anti-sliding piles, the formula governing the inclined pile-soil arch model can be established, thus obtaining the corresponding equation for the arch axis on the pile-soil arch plane.

2.2 Mechanical analysis of the inclined pile-soil arch

According to the working mechanism of reinforcing a slope with anti-sliding piles and the underlying mechanism of the pile-soil arch, it is supposed that the loads applied on the anti-sliding piles are triangularly distributed. Moreover, a mechanical calculation model for the inclined interaction between the inclined pile and soil arch was established (Fig. 3). In Fig. 3, z´, xoy, x´oy´, and \(\alpha\) represent the direction along the pile axis, the inclined pile-soil arch plane, the horizontal plane, and the included angle between xoy and x´oy´, respectively.

Fig. 3.
figure 3

Mechanical calculation model for an inclined pile-soil arch

Full size image

Let

$$q = kz^{\prime}$$
(1)

where, q and k denote the distributed load (kN/m2) arising from the earth pressure applied to the side of the anti-sliding piles and the distribution coefficient (kN/m3) of earth pressure applied along the pile-soil contact surface, respectively.

It is supposed that the earth pressure on the pile side is triangularly distributed. According to the stress characteristics of the inclined pile-soil arch, it can be obtained that:

$$k = \frac{2FL}{{bH^{2} }}$$
(2)

By substituting Eq. (2) into Eq. (1), it can be attained that:

$$q_{{\text{t}}} = \frac{2FL\cos \alpha }{{bH^{2} }}z$$
(3a)

where, \(q_{{\text{t}}}\) refers to the earth pressure applied to the side of the pile-soil arch (this is equivalent to the triangularly distributed load (kN/m2)).

Similarly, it is supposed that the earth pressure on the pile-soil arch is equivalent to the uniformly distributed loads in the form of a parallelogram, and thus it can be attained that:

$$q_{{\text{p}}} = \frac{FL}{{bH}}$$
(3b)

where, \(q_{{\text{p}}}\) represents the earth pressure applied on the anti-sliding piles, which is uniformly distributed in the form of a parallelogram (kN/m2).

According to the theories of elastic mechanics and soil mechanics, it is supposed that, in Fig. 3, the medial axis ADB of the pile-soil arch zone is a quadratic parabola and the soil behind the piles forms a semi-infinite body. By analysing the pile-soil arch zone at the deepest point of the free section of anti-sliding piles, the stresses at an arbitrary point M in the soil on the xoy plane and on vault D on the medial axis of the pile-soil arch zone can be calculated.

(1) The additional stress on point M

Let

$$\left\{ \begin{gathered} a_{1} = \frac{L}{2} + \frac{b}{2} \hfill \\ a_{2} = \frac{L}{2} - \frac{b}{2} \hfill \\ \end{gathered} \right.$$
(4)

Then, the additional stress of pile ① on point M is

$$\sigma_{x}^{1} = \frac{q}{\pi } \left [\arctan \left (\frac{{x - a_{2} }}{y} \right) - \arctan \left (\frac{{x - a_{1} }}{y}\right) - \frac{{y\left (x - a_{2}\right )}}{{y^{2} + \left (x - a_{2} \right )^{2} }} + \frac{{y \left (x - a_{1}\right )}}{{y^{2} + \left(x - a_{1}\right )^{2} }}\right]$$
(5a)
$$\sigma_{y}^{1} = \frac{q}{\pi }\left [\arctan \left (\frac{{x - a_{2} }}{y}\right) - \arctan \left (\frac{{x - a_{1} }}{y}\right) + \frac{{y(x - a_{2} )}}{{y^{2} + (x - a_{2} )^{2} }} - \frac{{y(x - a_{1} )}}{{y^{2} + (x - a_{1} )^{2} }}\right]$$
(5b)
$$\tau_{xy}^{1} = \frac{q}{\pi }\left[\frac{{y^{2} }}{{y^{2} + (x - a_{2} )^{2} }} - \frac{{y^{2} }}{{y^{2} + (x - a_{1} )^{2} }}\right]$$
(5c)

Similarly, the additional stress of pile ② on point M is

$$\sigma_{x}^{2} = \frac{q}{\pi }\left[\arctan \left(\frac{{x + a_{1} }}{y}\right) - \arctan \left(\frac{{x + a_{2} }}{y}\right) - \frac{{y(x + a_{1} )}}{{y^{2} + (x + a_{1} )^{2} }} + \frac{{y(x + a_{2} )}}{{y^{2} + (x + a_{2} )^{2} }}\right]$$
(6a)
$$\sigma_{y}^{2} = \frac{q}{\pi }\left[\arctan \left(\frac{{x + a_{1} }}{y}\right) - \arctan \left(\frac{{x + a_{2} }}{y}\right) + \frac{{y(x + a_{1} )}}{{y^{2} + (x + a_{1} )^{2} }} - \frac{{y(x + a_{2} )}}{{y^{2} + (x + a_{2} )^{2} }}\right]$$
(6b)
$$\tau_{xy}^{2} = \frac{q}{\pi }[\frac{{y^{2} }}{{y^{2} + (x + a_{1} )^{2} }} - \frac{{y^{2} }}{{y^{2} + (x + a_{2} )^{2} }}]$$
(6c)

According to the principle of stress superposition, the stresses on the point M in the soil behind the piles ① and ② are obtained, that is,

$$\begin{aligned} \sigma _{x}^{{12}} = & \frac{q}{\pi }\left\{ {\left[ {\arctan \left( {\frac{{x - a_{2} }}{y}} \right) - \arctan \left( {\frac{{x - a_{1} }}{y}} \right) - \frac{{y(x - a_{2} )}}{{y^{2} + (x - a_{2} )^{2} }} + \frac{{y(x - a_{1} )}}{{y^{2} + (x - a_{1} )^{2} }}} \right]} \right. \\ & \left. { + \left[ {\arctan \left( {\frac{{x + a_{1} }}{y}} \right) - \arctan \left( {\frac{{x + a_{2} }}{y}} \right) - \frac{{y(x + a_{1} )}}{{y^{2} + (x + a_{1} )^{2} }} + \frac{{y(x + a_{2} )}}{{y^{2} + (x + a_{2} )^{2} }}} \right]} \right\} \\ \end{aligned}$$
(7a)
$$\begin{aligned} \sigma _{y}^{{12}} & = \frac{q}{\pi }\left\{ {\left[ {\arctan \left( {\frac{{x - a_{2} }}{y}} \right) - \arctan \left( {\frac{{x - a_{1} }}{y}} \right) + \frac{{y(x - a_{2} )}}{{y^{2} + (x - a_{2} )^{2} }} - \frac{{y(x - a_{1} )}}{{y^{2} + (x - a_{1} )^{2} }}} \right]} \right. \\ &\,\,\, \left. { + \left[ {\arctan \left( {\frac{{x + a_{1} }}{y}} \right) - \arctan \left( {\frac{{x + a_{2} }}{y}} \right) + \frac{{y(x + a_{1} )}}{{y^{2} + (x + a_{1} )^{2} }} - \frac{{y(x + a_{2} )}}{{y^{2} + (x + a_{2} )^{2} }}} \right]} \right\} \\ \end{aligned}$$
(7b)
$$\tau _{{xy}}^{{12}} = \tau _{{yx}}^{{12}} = \frac{q}{\pi }y^{2} \left\{ {\left[ {\frac{1}{{y^{2} + (x - a_{2} )^{2} }} - \frac{1}{{y^{2} + (x - a_{1} )^{2} }}] + [\frac{1}{{y^{2} + (x + a_{1} )^{2} }} - \frac{1}{{y^{2} + (x + a_{2} )^{2} }}} \right]} \right\}$$
(7c)

(2) The self-weight (geostatic) stress on point M

The self-weight (geostatic) stress on point M in soil behind the piles on the xoy plane is

$$\sigma_{x} = K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(8a)
$$\sigma_{y} = K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(8b)
$$\sigma_{z} = \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(8c)

where, \(\sigma_{x}\), \(\sigma_{y}\), and \(\sigma_{z}\) separately refer to the geostatic stresses in the x, y, and z-directions; K0 and \(\gamma\) denote the lateral earth pressure coefficient of soil, and the bulk density (kN/m3) of the sliding mass, respectively.


(3) The total stress on point M

According to the principle of superposition of stresses, the total stress on point M in the soil behind the piles is

$$\sigma_{x}^{M} = \sigma_{x}^{12} + K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(9a)
$$\sigma_{y}^{M} = \sigma_{y}^{12} { + }K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(9b)
$$\sigma_{z}^{M} = \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(9c)

(4) The stress on the vault D on the medial axis of the pile-soil arch zone

By analysing the vertex D (x=0, y, z) on the medial axis ADB of the pile-soil arch zone, it can be found, based on the Mohr-Coulomb strength criterion, that when vault D is at a limit equilibrium state, the stresses on vertex D are

$$\sigma_{x}^{D} = \frac{2q}{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) - \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} + \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right] + K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(10a)
$$\sigma_{y}^{D} = \frac{2q}{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) + \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} - \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right]{ + }K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(10b)
$$\sigma_{z}^{D} = \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(10c)

where, \(\sigma_{x}^{D}\), \(\sigma_{y}^{D}\), and \(\sigma_{z}^{D}\) refer to the geostatic stresses on point D in the x, y, and z-directions, respectively.

Therefore, three principal stresses \(\sigma_{1}^{D}\), \(\sigma_{2}^{D}\), and \(\sigma_{3}^{D}\), and the maximum shear stress \(\tau_{\max }^{D}\) on the vault D can be obtained, that is,

$$\tau_{\max }^{D} = \frac{{\sigma_{1}^{D} - \sigma_{3}^{D} }}{2}$$
(11)

On condition that the vault is in a limit equilibrium state, it can be found, according to the Mohr-Coulomb strength criterion, that

$$\frac{{\sigma_{1}^{D} - \sigma_{3}^{D} }}{2} = \frac{{\sigma_{1}^{D} + \sigma_{3}^{D} }}{2}\tan \phi + c$$
(12)

where, c and ϕ separately denote the cohesion (kPa) and internal friction angle (°) of the sliding mass.

Through analysis on the xoy plane, the principal stresses can be attained:

$$\left. \begin{gathered} \sigma_{1}^{D} \hfill \\ \sigma_{3}^{D} \hfill \\ \end{gathered} \right\} = \frac{{\sigma_{x}^{D} + \sigma_{y}^{D} }}{2} \pm \sqrt {\left(\frac{{\sigma_{x}^{D} - \sigma_{y}^{D} }}{2}\right)^{2} + \left(\tau_{xy}^{D} \right)^{2} }$$
(13a)
$$\tau_{xy}^{D} = \tau_{yx}^{D} = 0$$
(13b)

By substituting Eqs. (13a and b) into Eq. (12) and combining the result with Eqs. (10a, b, c), it can be found that:

$$\frac{{{2}q}}{\pi }\left(\frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }} - \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }}\right) = \frac{2q}{\pi }\left[arctan\left( {\frac{{a_{1} }}{y}} \right) - arctan\left( {\frac{{a_{2} }}{y}} \right)\right]\tan \phi + K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)\tan \phi + c$$
(14)

2.3 Active surface of the pile-soil arch zone

According to the assumptions of the inclined pile-soil arch formed when reinforcing slopes with anti-sliding piles, the active surface of the pile-soil arch zone is parallel to the direction of the sliding force F, thus forming the inclined plane xoy. By decomposing Eqs. (10a, b, c) in the horizontal plane x´oy´, the stresses on the inclined pile-soil arch in the horizontal direction can be obtained, that is,

$$\sigma_{{x^{\prime}}}^{D} = \sigma_{x}^{D} = \frac{2q}{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) - \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} + \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right] + K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)$$
(15a)
$$\sigma_{{y^{\prime}}}^{D} = \frac{2q\cos \alpha }{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) + \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} - \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right]{ + }K_{0} \gamma \left( {z\cos \alpha - y\sin \alpha } \right)\cos \alpha$$
(15b)
$$\sigma_{{z^{\prime}}}^{D} = \gamma \left( {z\cos \alpha - y\sin \alpha } \right)\cos \alpha$$
(15c)

After decomposing the sliding force of the sliding mass into the horizontal force, the horizontal pile-soil arching effect (x´oy´) formed by the horizontal component was analysed. When the earth pressure along the pile-soil contact surface is triangularly distributed, it can be obtained that:

$$q_{{\text{t}}} = \frac{{2FL\cos^{2} \alpha }}{{bH^{2} }}z$$
(16a)

Similarly, when the earth pressure along the pile-soil contact surface is uniformly distributed in the form of parallelogram, it can be attained that:

$$q_{{\text{p}}} = \frac{FL\cos \alpha }{{bH}}$$
(16b)

Therefore, the total stress on the x´oy´ plane when the earth pressure is triangularly distributed can be calculated as

$$\sigma_{{x^{\prime}}}^{D} = \frac{2q\cos \alpha }{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) - \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} + \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right] + K_{0} \gamma z\cos \alpha$$
(17a)
$$\sigma_{{y^{\prime}}}^{D} = \frac{2q\cos \alpha }{\pi }\left[\arctan \left(\frac{{a_{1} }}{y}\right) - \arctan \left(\frac{{a_{2} }}{y}\right) + \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }} - \frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }}\right] + K_{0} \gamma z\cos \alpha$$
(17b)
$$\sigma_{{z^{\prime}}}^{D} = \gamma z\cos \alpha$$
(17c)

Similarly, the total stress on the x´oy´ plane when the earth pressure is uniformly distributed in the form of parallelogram is also obtained.

By substituting Eqs. (17a, b) into Eq. (13) and combining Eq. (12), it can be found that:

$$\frac{{{2}q\cos \alpha }}{\pi }\left(\frac{{ya_{2} }}{{y^{2} + a_{2}^{2} }} - \frac{{ya_{1} }}{{y^{2} + a_{1}^{2} }}\right) = \frac{2q\cos \alpha }{\pi }\left[arctan\left( {\frac{{a_{1} }}{y}} \right) - arctan\left( {\frac{{a_{2} }}{y}} \right)\right]\tan \phi + K_{0} \gamma z\cos \alpha \tan \phi + c$$
(18)

2.4 Analysis of the axes of the pile-soil arch zone

It is supposed that the lower arch axis A´D´B´ and the medial axis ADB of the pile-soil arch zone both take the form of a quadratic parabola. The corresponding lower arch axis A´D´B´ at the inner side arch foot of the pile-soil arch zone was analysed, that is,

$$y = - \frac{4r}{{l^{2} }}x^{2} + r$$
(19)

where, r refers to the distance (m) from the vault D´ of the arch axis A´D´B´ to the point o.

Based on the limit equilibrium condition of the soil at the pile-soil interface at the lower arch foot of the pile-soil arch zone, it can be obtained that:

$$\tau_{\max } = \frac{{Fl^{2} }}{8rbH}$$
(20)

According to the limit equilibrium equation for the soil, the distance from the vault D´ of the lower arch axis to the point o can be calculated, that is,

$$y\left( {x = 0} \right) = r = \frac{{Fl^{2} }}{{4\left( {Fl\tan \phi - 2cbH} \right)}}$$
(21)

By substituting Eq. (21) into Eq. (19), the equation for the arch axis A´D´B´ of the pile-soil arch zone becomes

$$y = - \frac{F}{{\left( {Fl\tan \phi - 2cbH} \right)}}x^{2} + \frac{{Fl^{2} }}{{4\left( {Fl\tan \phi - 2cbH} \right)}}$$
(22a)

Similarly, the equation for the arch axis for formation of the horizontal pile-soil arching effect due to the horizontal components of the sliding force is as follows:

$$y^{\prime} = - \frac{F\cos \alpha }{{\left( {Fl\tan \phi \cos \alpha - 2cbH} \right)}}x^{{\prime}{2}} + \frac{{Fl^{2} \cos \alpha }}{{4\left( {Fl\tan \phi \cos \alpha - 2cbH} \right)}}$$
(22b)

2.5 Calculation of pile spacing

The analysis was performed by substituting the equation for the lower arch axis of the pile-soil arch zone into the limit equilibrium equation for the soil at the vault.

Let

$$Y = \frac{1}{y}$$
(23)

The vault D´ of the lower arch axis was analysed. By substituting Eq. (21) into Eq. (23), it can be found that:

$$Y = \frac{{4\left( {Fl\tan \phi - 2cbH} \right)}}{{Fl^{{2}} }}$$
(24)

Substituting Eq. (23) into Eq. (14),

$$\frac{{{2}q}}{\pi }\left(\frac{{Y^{2} a_{2} }}{{1 + Y^{2} a_{2}^{2} }} - \frac{{Y^{2} a_{1} }}{{1 + Y^{2} a_{1}^{2} }}\right) = \frac{2q}{\pi }[arctan\left( {a_{1} Y} \right) - arctan\left( {a_{2} Y} \right)]Y\tan \phi + \left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)Y - K_{0} \gamma \sin \alpha \tan \phi$$
(25)

By Taylor-series expansion of Eq. (25) and simplified calculation based on the first term, it can be found that:

$$\frac{2q}{\pi }\left( {a_{1} - a_{2} } \right)\left( {1 + \tan \phi } \right)Y^{2} + \left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)Y - K_{0} \gamma \sin \alpha \tan \phi = 0$$
(26)

It is supposed that the relationship between the clear pile spacing and the pile width is as follows:

$$l = nb$$
(27)

By substituting Eq. (27) into Eq. (4), it can be found that:

$$\left\{ \begin{gathered} a_{1} = \frac{n + 2}{2}b \hfill \\ a_{2} = \frac{n}{2}b \hfill \\ \end{gathered} \right.$$
(28)

By substituting Eqs. (24 and 28) into Eq. (26), it can be found that:

$$\begin{gathered} K_{0} \gamma \sin \alpha \tan \phi Fl^{3} - \left[ {\frac{64(1 + \tan \phi )\cos \alpha }{{\pi H^{2} }}z\tan^{2} \phi F^{2} + 4\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)F\tan \phi } \right]l^{2} { + } \hfill \\ \left[ {\frac{{{256}(1 + \tan \phi )\cos \alpha }}{\pi H}z\tan \phi Fc + 8\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)cH} \right]bl - \frac{256(1 + \tan \phi )\cos \alpha }{\pi }zc^{2} b^{2} = 0 \hfill \\ \end{gathered}$$
(29)

Let

$$\left\{ \begin{gathered} A_{1} = K_{0} \gamma \sin \alpha \tan \phi F \hfill \\ A_{2} = \frac{64(1 + \tan \phi )\cos \alpha }{{\pi H^{2} }}z\tan^{2} \phi F^{2} + 4\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)F\tan \phi \hfill \\ A_{3} = \frac{{{256}(1 + \tan \phi )\cos \alpha }}{\pi H}z\tan \phi Fc + 8\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)cH \hfill \\ A_{4} = \frac{256(1 + \tan \phi )\cos \alpha }{\pi }zc^{2} \hfill \\ \end{gathered} \right.$$
(30)

Substituting Eqs. (27 and 30) into Eq. (29), then

$$b = \frac{{A_{2} n^{2} { - }A_{3} n + A_{4} }}{{A_{1} n^{3} }}$$
(31)

Similarly, when the earth pressure along the pile-soil contact surface is uniformly distributed in the form of a parallelogram, it can be found that:

$$b = \frac{{A_{{{2}2}} n^{2} { - }A_{{{3}3}} n + A_{{4{4}}} }}{{A_{{1}} n^{3} }}$$
(32)

where,

$$\left\{ \begin{gathered} A_{{{2}2}} = \frac{{{32}(1 + \tan \phi )}}{\pi H}\tan^{2} \phi F^{2} + 4\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)F\tan \phi \hfill \\ A_{{{3}3}} = \frac{{{128}(1 + \tan \phi )}}{\pi }\tan \phi Fc + 8\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)cH \hfill \\ A_{{4{4}}} = \frac{{{128}(1 + \tan \phi )}}{\pi }c^{2} H \hfill \\ \end{gathered} \right.$$
(33)

Similarly, Taylor approximation was conducted after substituting Eq. (23) into Eq. (18). By doing so, the relationship between the clear pile spacing and the pile width for formation of the horizontal pile-soil arching effect can be found. When the earth pressure along the pile-soil contact surface is triangularly distributed, it can be found that:

$$n = \frac{{A_{3}^{\prime } + \sqrt {\left( {A_{3}^{\prime } } \right)^{2} - 4A_{2}^{\prime } A_{4}^{\prime } } }}{{2A_{2}^{\prime } }}$$
(34)

where,

$$\left\{ \begin{gathered} A_{2}^{\prime } = \frac{{{64}(1 + \tan \phi )\cos^{{2}} \alpha }}{{\pi H^{2} }}z\tan^{2} \phi F^{2} + 4\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)F\tan \phi \hfill \\ A_{3}^{\prime } = \frac{{{256}(1 + \tan \phi )\cos^{{2}} \alpha }}{\pi H}z\tan \phi Fc + 8\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)cH \hfill \\ A_{4}^{\prime } = \frac{{{256}(1 + \tan \phi )\cos^{{2}} \alpha }}{\pi }zc^{2} \hfill \\ \end{gathered} \right.$$
(35)

On condition that the earth pressure along the pile-soil contact surface is distributed in the form of a parallelogram, then

$$n = \frac{{A_{{{3}3}}^{\prime } + \sqrt {\left( {A_{{3{3}}}^{\prime } } \right)^{2} - 4A_{{{2}2}}^{\prime } A_{{4{4}}}^{\prime } } }}{{2A_{{{2}2}}^{\prime } }}$$
(36)

where,

$$\left\{ \begin{gathered} A_{{2{2}}}^{\prime } = \frac{{{32}(1 + \tan \phi )}}{\pi H}\tan^{2} \phi F^{2} + 4\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)F\tan \phi \hfill \\ A_{{{3}3}}^{\prime } = \frac{{{128}(1 + \tan \phi )}}{\pi }\tan \phi Fc + 8\left( {K_{0} \gamma z\cos \alpha \tan \phi + c} \right)cH \hfill \\ A_{{4{4}}}^{\prime } = \frac{{{128}(1 + \tan \phi )}}{\pi }c^{2} H \hfill \\ \end{gathered} \right.$$
(37)

2.6 Conditions for the formation of an inclined pile-soil arch

According to the positional relationship of the vault of the arch axis A´D´B´ of the pile-soil arch, the formation condition of the pile-soil arch was attained by substituting y≥0 into Eq. (21) for the lower arch axis of the pile-soil arch, that is,

$$n \ge \frac{2cH}{{F\tan \phi }}$$
(38a)

or

$$c \le \frac{Fn\tan \phi }{{2H}}$$
(38b)

Similarly, it is feasible to attain the condition for formation of a horizontal pile-soil arch through calculation based on the horizontal pile-soil arch, that is,

$$n \ge \frac{2cH}{{F\cos \alpha \tan \phi }}$$
(39a)

or

$$c \le \frac{Fn\cos \alpha \tan \phi }{{2H}}$$
(39b)

3 Discussion and analysis of the pile-soil arching effect

3.1 Illustration result

To verify the proposed pile spacing calculation method and conditions for the formation of an inclined pile-soil arch, we analysed case study data to perform a comparison (Smethurst et al. 2007; Ashour et al. 2012; Liang et al. 2010, 2014; Chen, et al. 2020). The piles at the instrumented section are 10 m long, 0.6 m diameter bored concrete piles constructed at a spacing of 2.4 m. A point force of 60 kN was applied in the analysis at two-thirds the depth of the failing mass to increase the factor of safety to 1.3. The soil strength parameters used in design, which are given in Table 1.

Table 1. Design landslide and anti-sliding pile parameters (Smethurst et al. 2007; Ashour et al. 2012; Liang et al. 2010, 2014; Chen et al. 2020)
Full size table

According to the characteristics of a landslide and designed safety factor, it can be found that the sliding force was 100 kN/m. The inclination of the sliding mass was 0° (horizontal arching), and 24° (slope angle), and 36° (angle of design failure surface at anti-sliding pile), respectively. The lateral earth pressure coefficient, K0 was taken to be 0.42. By substituting the relevant parameters into Eqs. (31–37), the pile spacing was calculated (Table 2).

Table 2. Calculated pile spacing
Full size table

As shown in Table 2, the calculated results when the inclination of sliding force was 0 degree were similar to those of Smethurst et al. (2007), Ashour et al. (2012), Liang et al. (2010, 2014), and Chen et al. (2020). And the calculated pile spacing increased with the increasement of inclination of sliding force. Therefore, the case study showed that the calculation equation of pile spacing is reasonable.

3.2 Analysis of the pile-soil arching effect

By analysing published case study data (Li et al. 2010), the calculation method was verified, and the influence of the inclined pile-soil arching effect was investigated. The characteristics of landslides are described as follows: the front edge has a width of 120 m, the back edge has a width of 80 m, the sliding surface has a length and area of 130–190 m and about 2.07 × 104 m2, respectively, and the volume of the sliding mass of about 37.3 × 104 m3. The sliding soil in the landslide is a gravelly silty clay and the landslide is reinforced with anti-sliding piles. The section (z´ = 9.0 m) with the strongest pile-soil arching effect was analysed to find a maximum clear pile spacing of 4.85 m against a designed clear pile spacing of 4.0 m (salient parameters of the landslide and anti-sliding piles are listed in Table 3).

Table 3. Landslide and anti-sliding pile parameters
Full size table

According to the characteristics of a landslide and designed safety factor, it can be found that the sliding force and inclination of the sliding mass were about 869.6 kN/m and 20°, respectively. By taking the pile width b to be 2 m and substituting the relevant parameters into Eqs. (31–37), the pile-soil arching effect was analysed (Table 4).

Table 4. Calculated pile-soil arching effect
Full size table

As shown in Table 4, the calculated results when the earth pressure along the pile-soil contact surface was triangularly distributed were similar to those when the earth pressure was distributed in the form of a parallelogram. The clear pile spacing calculated for generation of the inclined pile-soil arching effect can satisfy the arching requirement and the practical cohesion of the sliding mass could also satisfy the maximum cohesion required for arching. The clear pile spacing calculated according to the horizontal arching failed to satisfy the condition for horizontal arching. The clear pile spacing obtained through the proposed method was 4.32 m and that for inclined arching was 3.92 m, which was consistent with the designed clear pile spacing (4 m) in previous research. Therefore, the proposed method of calculation was deemed feasible and it was reasonable to calculate and analyse the slope reinforcement slope with anti-sliding piles according to the inclined pile-soil arching effect. According to the theoretical analysis, the influences of various factors (e.g. the value and inclination of the sliding force, cohesion and friction angle of the sliding mass, and pile width) on the pile-soil arching effect were separately calculated.

3.2.1 The effect of the sliding force of the sliding mass

The calculated results pertaining to the influence of the sliding force (value and inclination) of the sliding mass on the pile-soil arch are shown in Figs. 4 and 5.

Fig. 4.
figure 4

Relationships between sliding force and the parameters of the pile-soil arch: a parameter n versus sliding force F; b cohesion for arching c versus sliding force F; c clear pile spacing l versus sliding force F

Full size image
Fig. 5.
figure 5

Relationships between the inclination of sliding force and the parameters of the pile-soil arch: a parameter n versus inclination of the sliding force α; b cohesion for arching c versus inclination of the sliding force α; c clear pile spacing l versus inclination of the sliding force α

Full size image

As shown in Fig. 4a, b, with increased sliding force, the ratio n of the clear pile spacing to the pile width reduced and then stabilised while the cohesion required for arching calculated on the basis of an inclined pile-soil arch decreased, then gradually stabilised: however, the cohesion calculated for horizontal arching was lower than the actual value. The calculated results showed that the arching condition was satisfied according to the inclined pile-soil arch while it failed when undertaking the analysis based on horizontal arching. On condition that the sliding force exceeded 3500 kN/m, the calculated results according to the inclined pile-soil arch and horizontal arching both failed to satisfy the arching condition. As shown in Fig. 4c, the clear pile spacing calculated according to the inclined pile-soil arch was greater than that calculated based on horizontal arching and the calculated results under horizontal arching action and an inclined pile-soil arch were similar when the sliding force exceeded 2000 kN/m.

It can be seen from Fig. 5a, b that, with increasing inclination of the sliding force, the ratio n of the clear pile spacing to the pile width calculated according to the inclined pile-soil arch rose while n calculated according to the horizontal arching was constant. Moreover, as the inclination of the sliding force increased, the cohesion required for arching calculated on the basis of an inclined pile-soil arch increased while that calculated based on horizontal arching decreased and was lower than the actual value. The calculated results indicated that the inclined pile-soil arch could satisfy the arching condition while the horizontal arching failed to satisfy it. As shown in Fig. 5c, the clear pile spacing calculated when the earth pressure was distributed in the form of a parallelogram was greater than that when the earth pressure was triangularly distributed for an inclined pile-soil arch.

3.2.2 The influences of mechanical parameters of the sliding mass

The calculated results concerning the influences of the mechanical parameters of the sliding mass (such as the cohesion and internal friction angle) on the pile-soil arch are displayed in Figs. 6 and 7.

Fig. 6.
figure 6

Relationships between soil cohesion and the parameters of the pile-soil arch: a parameter n versus cohesion c; b the change in arching condition, c; c clear pile spacing l versus cohesion c

Full size image
Fig. 7.
figure 7

Relationships between the internal friction angle of the sliding mass and the parameters of the pile-soil arch: a parameter n versus internal friction angle ϕ; b cohesion for arching c versus internal friction angle ϕ; c clear pile spacing l versus internal friction angle ϕ

Full size image

As shown in Figs. 6a, b, with increasing cohesion, the ratio n of the clear pile spacing to the pile width increased. At the same time, the cohesion required for arching calculated according to the inclined pile-soil arch with the earth pressure distributed in the form of a parallelogram increased, which conformed to the arching condition. By contrast, the cohesion calculated based on horizontal arching was lower than the actual value. The calculated results revealed that the results obtained according to the inclined pile-soil arch could satisfy the arching condition while those according to the horizontal arching could not. It is shown in Fig. 6c that the clear pile spacing calculated according to the inclined pile-soil arch exceeded that based on horizontal arching, therefore, the cohesion of the sliding mass greatly influenced the pile-soil arch.

As shown in Figs. 7a, b, c, the ratio n of the clear pile spacing to the pile width decreased with the growth of the internal friction angle of soil. The values of n and the clear pile spacing calculated according to the inclined pile-soil arch were similar to those calculated on the assumption of horizontal arching when the internal friction angle of the sliding mass was greater than 15°. The calculated results obtained according to the inclined pile-soil arch and horizontal arching both failed to satisfy the arching condition at a low internal friction angle; at a large internal friction angle, the calculated results on the basis of an inclined pile-soil arch could satisfy the arching condition while those calculated based on the horizontal arching failed to satisfy it. It is shown in Fig. 7c that the clear pile spacing calculated according to the assumption of horizontal arching exceeded that calculated based on the inclined pile-soil arch at a low internal friction angle. At a large internal friction angle, the calculated results under the two modes were similar.

3.2.3 The influence of the pile width

By analysing the influence of the pile width on the pile-soil arching effect, a reasonable pile width can be calculated (Fig. 8).

Fig. 8.
figure 8

Relationships between the pile width and the parameters of the pile-soil arch: a parameter n versus pile width b; b cohesion for arching c versus pile width b; c clear pile spacing l versus pile width b

Full size image

As shown in Figs. 8a, b, c, the ratio n of the clear pile spacing to the pile width and the clear pile spacing both increased with increasing pile width. When the pile width was less than 1 m, the calculated results failed to satisfy the arching condition for an inclined pile-soil arch and horizontal arching. The calculated results attained according to the inclined pile-soil arch with the applied earth pressure distributed in the form of a parallelogram were larger than those based on other modes.

4 Conclusions

Based on the pile-soil arching effect, a mechanical calculation model of the inclined pile-soil arch was established to analyse a soil landslide reinforced with anti-sliding piles. The main conclusions of the present study can be obtained as follows:

  1. (1)

    The pile-soil interaction is a spatial problem. A mechanical calculation model of the inclined pile-soil arch was established to analyse the behaviour of a slope reinforced with anti-sliding piles based on the inclined pile-soil arching effect. The case study showed that the calculation equation of pile spacing is reasonable.

  2. (2)

    The analytical solutions for the pile width when the earth pressure in the pile side was distributed in triangular and parallelogrammic forms were attained based on the inclined pile-soil arching effect. Moreover, the equations for the inclined and horizontal arching and the arching conditions under the two modes were derived. The result showed that the calculated result obtained based on the inclined pile-soil arch was more reasonable than that according to the assumption of horizontal arching.

  3. (3)

    The inclined pile-soil arching effect was affected by the sliding force and mechanical parameters of the sliding mass as well as the pile width. The analysis of a case study showed that the calculated results attained according to the inclined pile-soil arch and horizontal arching both failed to satisfy the arching condition when the sliding force exceeded 3500 kN/m; on condition that the pile width was less than 1 m, the calculated results obtained according to the inclined pile-soil arch and horizontal arching both failed to satisfy the arching condition. The clear pile spacings calculated according to the inclined pile-soil arch and horizonal arching were similar when the internal friction angle exceeded 15°; the lower the sliding force or the larger the angle of inclination of the sliding force, the greater the required clear pile spacing; the greater the cohesion or the lower the internal friction angle of the sliding soil mass, the greater the required clear pile spacing. The analytical results are expected to provide a technical reference for slope reinforcement with anti-sliding piles.