1 Introduction

Scaling is an important issue in ecology, meteorology, biology and hydrology. Flood scaling can be expressed by a power law as \(Q_{T} = \alpha_{T} A^{{\theta_{T} }}\), where QT is the flood quantile of T-year return period flood, A is the drainage area, log(αT) is the intercept parameter and θT is the scaling exponent (Gupta et al. 1996; Medhi and Tripathi 2015). Since at-site flood frequency analysis is hindered for ungauged basins (Medhi and Tripathi 2015), flood scaling is widely used in regional flood frequency analysis (RFFA) where observed data are deficient.

Flood quantiles were generally used in flood scaling by developing regression relationships between flood quantiles and basin attributes (Han et al. 2012; Furey et al. 2016). Haddad et al. (2011) and Han et al. (2012) obtained regression relationships between flood quantiles and basin slope, drainage density and stream slope. In the regression equation, some other basin attributes were also included, such as basin width and rainfall duration (Galster et al. 2006; Ayalew et al. 2014; Van et al. 2000; Furey and Gupta 2005). For all of these basin attributes, drainage area is the most widely used to analyze flood scaling effect (Jothityangkoon and Sivapalan 2001; Ishak et al. 2011; Furey and Gupta 2007), which can be used to predict flood quantiles without observed data. On this basis, flood is seemed to exhibit simple scaling if the scaling exponent is constant. If the scaling exponent changes with return period, it is called multiscaling (Gupta and Dawdy 1995). Ogden and Dawdy (2003) analyzed peak discharge scaling in small watersheds in Goodwin Creek Experimental Watershed (GCEW) and found that the flood quantiles in all sub-basins exhibited simple scaling. Furey et al. (2016) developed a nested mixed-effects linear (NMEL) model to connect event-based scaling with quantile-based scaling in GCEW further and found that scaling slopes of event-to-event peak discharges were on average equivalent to the mean scaling slope of annual peak quantiles, which was also supportive of the result of Ogden and Dawdy (2003).

However, previous flood scaling studies were under stationary assumption which means the distribution of flood extreme value keeps invariable over time. In recent decades, climate variation and anthropogenic activities have changed regional flood mechanism and many river basins showed hydrological nonstationarity (Villarini et al. 2009, 2010, 2012; Li et al. 2014a, b, c; Xiong and Guo 2004; Cong and Xiong 2012; Gu et al. 2014), which makes the assumption of stationarity be questioned. Milly et al. (2008) considered that stationarity was dead and could not be revived. So flood frequency analysis (FFA) under stationary hypothesis seems to be no longer effective and accurate enough. In this case, nonstationarity was considered in flood frequency analysis. Vogel et al. (2011) combined two-parameter lognormal model and exponential trend model to analyze the trend of annual maximum streamflows in USA and variation in flood quantile. Liu et al. (2014) presented the nonstationary generalized extreme value (NSGEV) distribution and used it to investigate the risk of Niangziguan Springs discharge decreasing to zero by defining the GEV parameters as functions of time. Zeng et al. (2014) employed mixed distribution to fit the nonstationary flood series in North China. All of the above studies showed that nonstationary flood frequency analysis was more accurate and flexible. In addition, GAMLSS (Generalized Additive Model in Location, Scale and Shape), which was proposed by Rigby and Stasinopoulos (2005), was used for nonstationary flood frequency analysis in many researches due to its high degree of flexibility. Villarini et al. (2009) applied GAMLSS to annual maximum peak discharge records for Little Sugar Creek by modeling the parameters of the selected parametric distribution as a smooth function of time via cubic splines. Villarini et al. (2012) studied the relation between NAO (North Atlantic Oscillation) and annual maximum daily discharge with Gumbel distribution in GAMLSS. López and Francés (2013) and Gu et al. (2014) used GAMLSS to address the modeling of nonstationary time series with the parameters of the selected distributions as a function of time only and climate indices and reservoir index, respectively. However, few studies analyzed design flood quantiles and return period under nonstationarity. There are two common methods to calculate the return periods of hydrological extreme value event, i.e., expected waiting time (EWT) proposed by Wigley (1988, 2009) and expected number of exceedances (ENE) proposed by Parey et al. (2007). In order to make FFA under nonstationarity, Salas and Obeysekera (2014) extended EWT to nonstationary condition and applied it to analyze hydrological series with upward or downward trend, finding that the result was more reliable. Cooley (2013) also extended both EWT and ENE to hydrological extreme series. Du et al. (2015) used ENE to calculate flood return periods and risk under nonstationarity.

Flood scaling under nonstationarity must be carried out due to climate change or land surface change. In Daqinghe River basin, a mass of hydraulic structures were built after 1980s, and the land surface also changed a lot during this period (Gong et al. 2012; Li and Tan 2015; Deng et al. 2016). Changing land surface and land use may influence runoff process. Li (2011) found land use change in Zijingguan sub-watershed in Daqinghe River basin leads to the decrease in runoff. Fu (2010) also presented transformation of land use had effect on flood peak and flood volume. Therefore, Daqinghe River basin was selected as study region to analyze nonstationary flood scaling in order to identify if flood scaling was applicative under changing environment.

The aims of this paper are to (1) identify the trend and change points of AMFP series of the eight sub-watersheds in Daqinghe River basin; (2) make flood frequency analysis based on the reconstructed stationary series and observed nonstationary series, respectively; (3) analyze flood scaling and the effect of changing environment on scaling exponent; (4) find the possible influence factor of scaling exponent. The novelty of this paper is to analyze flood scaling under stationary and nonstationary conditions by using reconstructed flood data and observed nonstationary flood data, respectively, and compare the changes in scaling exponent.

2 Study area

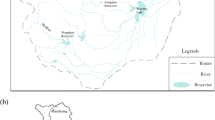
Daqinghe River basin, which is located in the middle of Haihe River Basin, lies between 113°39′ and 117°34′E longitude and 38°10′–40°102′N latitude. The drainage area of Daqinghe River basin is 43,060 km2, in which mountains and plains account for 43.3% and 56.7%, respectively. The basin is in a temperate continental semiarid monsoon climate. The annual mean temperature is 12.5 °C, and the average annual temperature in mountain and plain is 7.6 °C and 13.1 °C, respectively. The average annual precipitation is about 500–600 mm, about 80% of which is in the flood season.

In recent decades, many hydraulic structures have been built in Daqinghe River basin, which has changed the natural conditions of the river flow. For example, Wangkuai reservoir in Daqinghe River basin was built in June 1958 and completed in September 1960. It has a control drainage area of 3770 km2 and total storage capacity of 1.389 billion m3. In this drainage area, more than 6000 check dams were built, which were used for soil and water conservation. Xidayang reservoir was built in January 1958 and completed in January 1960, which has a control drainage area of 4420 km2, and the total storage capacity is 1.137 billion m3. Hengshanling reservoir, Longmen reservoir and Angezhuang reservoir have total storage capacity of 0.303 billion m3, 0.24 billion m3 and 0.127 billion m3, respectively.

3 Data and methods

3.1 Data

In this study, eight mesoscale sub-watersheds of Daqinghe River basin, including Wangkuai reservoir (WK), Angezhuang reservoir (AGZ), Hengshanling reservoir (HSL), Xidayang reservoir (XDY), Longmen reservoir (LM), Fuping station (FP), Zhangfang station (ZF) and Zijingguan station (ZJG), are selected as the study area to analyze flood scaling under nonstationarity (Fig. 1). Fuping station is located in the upstream of Wangkuai reservoir, and Zijingguan station is located in the upstream of Zhangfang station. Other sub-watersheds are all non-nested. Hourly rainfall and corresponding flood data which occurred in the flood season (June to September) are used for flood scaling analysis in this study. The drainage area and data length of the sub-watersheds are listed in Table 1, and the AMFP series are shown in Fig. 2. Moreover, the land use in Daqinghe River basin in different periods (Fig. 3) was selected to analyze the influence of environmental change on flood scaling.

Fig. 1
figure 1

Daqinghe River basin and location of study sub-watersheds

Full size image
Table 1 Drainage area and data length of the eight sub-watersheds
Full size table
Fig. 2
figure 2

AMFP series of eight sub-watersheds in Daqinghe River basin

Full size image
Fig. 3
figure 3

Land use in Daqinghe River basin in 1970, 1980 and 2000

Full size image

3.2 Detection of nonstationarity in AMFP series

Nonstationarity in hydrological series caused by climate change and anthropogenic activities has made traditional stationary assumption be questioned which is the basis of flood frequency analysis. For analyzing flood scaling in Daqinghe River basin, the trend and change point of AMFP series of the eight sub-watersheds should be tested to identify the nonstationarity. In this paper, two widely used nonparametric trend test methods, Mann–Kendall test (Mann 1945; Kendall 1975) and Spearman test (Spearman 1904), were used to detect the trend of the AMFP series. And the test statistics of the two methods are UK and T, respectively. Nonparametric Pettitt test (Pettitt 1979) was applied to check the change point of the series. All of these nonparametric tests were selected with a significance level \(\alpha = 0.05\).

3.3 Flood frequency analysis under nonstationarity

Due to nonstationarity in AMFP series, they need to be reconstructed to conduct flood frequency analysis. Traditionally, flood series are always reconstructed based on the past or current environmental conditions according to the change point in the series. However, it can only reflect the past or current condition and cannot predict future flood frequency. Time-varying moment model, which presents the nonstationarity of flood series by setting distribution parameter varying over covariates like time, can effectively reflect the trend of time series and estimate future flood frequency (López and Francés 2013). So flood frequency analysis is conducted based on both reconstructed series and nonstationary AMFP series, and we compared the results of two methods.

3.3.1 Reconstructed AMFP series based on rainfall–runoff relation

Due to the trend and change points in AMFP series, the time series need reconstruction based on relationship between precipitation and runoff to get stationary AMFP series (Deng et al. 2016). The procedure is: (1) selecting enough flood events and corresponding precipitation events; (2) calculating average rainfall depth P, antecedent rainfall depth Pa and total runoff depth R; (3) establishing rainfall–runoff relationship before and after the change point, respectively (Fig. 4); (4) reconstructing AMFP series based on the relationship between P + Pa and R before and after the change point.

Fig. 4
figure 4

Rainfall–runoff relationship before and after the change point. Red line and blue line refer to rainfall–runoff relationship before and after the change point, respectively. R1 and R2 refer to the runoff depth corresponding to the same precipitation P + Pa before and after the change point

Full size image

In this paper, antecedent rainfall depth Pa can be calculated by:

$$P_{a,t + 1} = K_{a} (P_{a,t} + P_{t} )$$
(1)

where Pa,t+1 and Pa,t are antecedent rainfall depth at time t + 1 and t. Ka is dissipation coefficient of soil moisture. We considered the soil moisture at the first day of flood season every year, which is Pa,1, was 0. Then, we can calculate P + Pa according to observed rainfall data at time t.

The magnitude to revise runoff depth after the change point based on rainfall–runoff relationship before the change point can be calculated by:

$$\beta_{1} = (R_{1} - R_{2} )/R_{1}$$
(2)

where R1 and R2 refer to the runoff depth corresponding to the same precipitation event before and after the change point. Similarly, the magnitude to revise runoff depth before the change point based on rainfall–runoff relationship after the change point is calculated by:

$$\beta_{2} = (R_{1} - R_{2} )/R_{2}$$
(3)

Then annual maximum flood volume can be revised based on the two magnitudes, and AMFP series can be reconstructed according to the linear relationship between annual maximum flood volume and AMFP.

3.3.2 GAMLSS

GAMLSS was chosen as a fitting tool to analyze flood frequency based on observed nonstationary AMFP series. GAMLSS was proposed by Rigby and Stasinopoulos (2005), which can regress the relationship between explanatory variables and response variables with its series of distribution family of continuous or discrete distributions with highly skewness and kurtosis. Herein, we provide a brief introduction to the main theory of GAMLSS model. The GAMLSS model assumes that independent observations \(y_{t}\) for t = 1,2,…,n follow a probability (density) function \(f(y_{t} |\theta^{t} )\) where \(\theta_{t} = (\theta_{t1} ,\theta_{t2} , \ldots,\, \theta_{tp} )\) is a vector of p parameters at time t. In most situations, distribution with less than or equal to p = 4 parameters is applied because it is accurate and flexible enough to model series. While the first two parameters \(\mu_{i}\) and \(\sigma_{i}\) are also known as location and scale parameters, let \(y = (y_{1} ,y_{2} , \ldots ,y_{n} )^{T}\) be the n-length vector of response variable and \(\theta_{k} = (\theta_{1k} ,\theta_{2k} , \ldots ,\theta_{nk} )^{T}\) be the vector of kth parameter where \(k = 1,2, \ldots ,p\). Let \(g_{k} ( \cdot )\) be monotonic link functions relating \(\theta_{k}\) and explanatory variables \(X_{k}\) through semi-parametric additive models given by:

$$g_{k} (\theta_{k} ) = \eta_{k} = X_{k} \beta_{k} + \sum\limits_{j = 1}^{{J_{k} }} {Z_{jk} \gamma_{jk} }$$
(4)

where \(\eta_{k}\) and θk are n-length vectors, \(\beta_{k} = (\beta_{1k} ,\beta_{2k} , \ldots ,\beta_{Ikk} )^{T}\) is a regression parameter of length \(I_{k}\), Xk is an explanatory matrix of order \(n \times I_{k}\), Zjk is a fixed design matrix of order \(n \times q_{jk}\) and \(\gamma_{jk}\) is a qjk–dimensional random variable following normal distribution.

When considering function relating parameters and time t, the explanatory matrix \(X_{k}\) can be also given by:

$$X_{k} = \left[ {\begin{array}{*{20}c} 1 & t & \ldots & {t^{{I_{k} - 1}} } \\ 1 & t & \ldots & {t^{{I_{k} - 1}} } \\ \ldots & \ldots & \ldots & {t^{{I_{k} - 1}} } \\ 1 & t & \ldots & {t^{{I_{k} - 1}} } \\ \end{array} } \right]_{{n \times I_{k} }}$$
(5)

In GAMLSS, the likelihood function of regression parameter \(\beta\) is given by:

$$L(\beta_{1} ,\beta_{2} ) = \prod\limits_{t = 1}^{n} {f(y_{t} |\beta_{1} ,\beta_{2} )}$$
(6)

For choosing the best-fit model and penalizing model overfitting, global deviation (GD) and Generalized Akaike Information Criterion (GAIC) can be used, and GAIC includes Akaike Information Criterion (AIC; Akaike 1974) and Schwarz Bayesian Criterion (SBC; Schwarz 1978). Moreover, the quality of fitting is examined by computing the visual investigation of the residual QQ plot and worm plot. For a detailed discussion, readers can consult Rigby and Stasinopoulos (2005).

3.3.3 Return period under nonstationarity

There are two interpretations of return period in traditional flood frequency analysis. The first is expected waiting time (EWT) proposed by Wigley (1988, 2009) which assumes that X is the year of the first occurrence of an extreme event that exceeds the given flood quantile zp. The second is the expected number of exceedances (ENE) proposed by Parey et al. (2007) whose assumption is that the expected number of exceedances in T-years is 1. In traditional stationary hydrological frequency analysis, the distribution of extreme events doesn’t change over time. So the return period of both interpretations can be easily received by T = 1/p where p means exceedance probability. As for nonstationary condition, due to p changing over time, we cannot calculate return period T as easily as stationary condition. In this case, Salas and Obeysekera (2014) extended EWT to nonstationary condition and applied it to analyze hydrological series with upward or downward trend, finding that the result was more reliable. Meanwhile, Cooley (2013) applied EWT and ENE to nonstationary hydrological extreme series and investigated flood quantiles corresponding to the given return period under nonstationarity. Because the nonstationarity in flood series cannot sustain over time, Shi et al. (2016) presented the trend duration concept and simplify the EWT definition under nonstationarity to calculate nonstationary return period. In this paper, EWT definition was applied for flood frequency analysis based on GAMLSS.

3.4 Flood scaling

According to the results of flood frequency analysis based on both reconstructed stationary AMFP series and nonstationary AMFP series, the flood scaling effect can be analyzed by:

$$Q_{T} = \alpha_{T} A^{{\theta_{T} }}$$
(7)

Take the logarithm on both sides of the equation, and it becomes:

$$\log Q_{T} = \theta_{T} \log A + \log \alpha_{T}$$
(8)

where QT is the flood quantiles at return period T, A is the drainage area, θT and αT are the flood scaling exponent and scaling intercept, respectively, which can be calculated by linear regression of log QT and log A. By analyzing the scaling exponents at different return periods of both reconstructed stationary AMFP series and nonstationary AMFP series, it can be seen if the flood in Daqinghe River basin exhibits simple scaling or multiscaling. Comparing the variation in scaling exponents of reconstructed AMFP series under the environmental conditions before and after change point, we can analyze the influence of environmental variation on flood scaling.

4 Results and discussion

4.1 Trend and change point of AMFP series

Mann–Kendall and Spearman test were used to examine the trend of the AMFP series with significance level \(\alpha = 0.05\) and the critical values Uα/2 = 1.96 and tα = 1.676, respectively. Then, the nonparametric Pettitt and Brown–Forsythe tests were applied for the detection of change points of the AMFP series. The results of trend test and change point test are listed in Tables 2 and 3 and Fig. 5, respectively.

Table 2 Results of trend test by nonparametric Mann–Kendall and Spearman test
Full size table
Table 3 Results of change points test by nonparametric Pettitt and Brown–Forsythe tests (“—” means that no significant change point was identified)
Full size table
Fig. 5
figure 5

Change point analysis by nonparametric Pettitt test. X-axis refers to year, and y-axis refers to frequency P

Full size image

It can be seen that all of the AMFP series show downward trend, four of which show significant downward trend. Because continuous heavy rainstorm occurred in whole Daqinghe River basin in 1963 and 1996, which therefore caused catastrophic floods in these two years, 1963 and 1996 were neglected in change point analysis. According to Fig. 4 and Table 3, it is displayed that no significant change point was detected in Angezhuang. HSL exhibited change points at 1971 and 1979, while Longmen and XDY exhibited change points at 1979 and around 1990. Other sub-watersheds present a statistically significant change point in 1979. Considering the situation of Daqinghe River basin, there were a mass of hydraulic structures built around 1980s, and the land use and land cover also changed during this period (Li and Feng 2010; Li et al. 2014b; Chen and Li 2011). So the change point of the AMFP series for Daqinghe River basin is initially regarded as 1979. For confirming the most possibly change point, eight AMFP series were separated before and after 1979 and diagnosed trend, respectively. According to Table 4, separated AMFP series showed no significant trend. It meant that 1979 was reasonable to be regarded as change point, which also agrees with the previous research (Gong et al. 2012; Li and Tan 2015; Deng et al. 2016). Therefore, the AMFP series are no longer stationary in the study area.

Table 4 Trend analysis of separated AMFP series before and after 1979
Full size table

4.2 Flood frequency analysis based on reconstructed AMFP series

Flood frequency analysis based on the reconstructed stationary AMFP series under the environmental conditions before and after the change point (1979) was conducted, respectively, and the flood quantiles at given return periods of the two AMFP series are shown in Fig. 6. Most flood quantiles for reconstructed series under the environmental conditions after 1979 are lower than those before 1979 (Table 5). The reason is that the AMFP series decrease obviously after the change point (1979) as a result of change in land use, land cover and construction of hydraulic structures. Therefore, for the same rainfall P + Pa, there will be less runoff R after 1979 than before 1979.

Fig. 6
figure 6

Flood quantiles at given return periods based on reconstructed series under the environmental conditions (a) before 1979 and (b) after 1979

Full size image
Table 5 Change of flood quantiles at given return periods based on reconstructed series under the environmental conditions after 1979 relative to that before 1979
Full size table

4.3 Flood frequency analysis based on observed nonstationary AMFP series

Based on the observed AMFP series, GAMLSS was employed for nonstationary flood frequency analysis by simulating the distributions of the AMFP series. In GAMLSS, five common two-parameter distributions, which included log normal distribution (LOGNO), gamma distribution (GA), Gumbel (GU), Weibull (WEI) and normal (NO), were selected as candidates to choose the best-fit distributions of the AMFP series. In this paper, time t was selected to be the only covariate to analyze flood frequency under nonstationarity based on the observed AMFP series, and only the link function between t and distribution parameters was considered. In GAMLSS, we set μ and σ constant and time varying, which means we fit four model for every series (constant μ and σ, time-varying μ and constant σ, constant μ and time-varying σ, time-varying μ and σ). The fitting model with the smallest AIC (Akaike 1974) and SBC (Schwarz 1978) was considered as the best-fit model which is displayed in Table 6.

Table 6 Summary of the best-fit models of the AMFP series
Full size table

The best-fit distribution of Longmen was GA, and the best-fit distribution of Xidayang was WEI, while LOGNO fitted other six sub-watersheds best. For a satisfactory fit of model, all the observations in worm plot should fall inside the two elliptic curves. For QQ plots, the observations should lie next to the 1:1 line. According to the QQ plots and worm plots of residuals of eight best-fit models (Figs. 7, 8), the results of GAMLSS model were credible. Because distribution parameter μ reflects mean value and σ reflects variance, σ of all the best-fit models was constant and μ was various which can reflect trend of AMFP series. The parameters of the best-fit distributions of Angezhuang and Hengshanling were constant. So two sub-watersheds showed no significant nonstationarity in flood frequency analysis according to GAMLSS model, which also agreed with the result of above trend analysis. However, the location parameters μ of the other six AMFP series which relate to the mean all showed a negative correlation with time t, and scale parameters remain constant. The results of GAMLSS proved that flood in Daqinghe River basin displayed a decreasing trend. For comparison with the flood quantiles based on reconstructed series, 1956 was deemed to be the first year of flood frequency analysis based on observed nonstationary AMFP. The results of flood quantiles at given return periods based on observed nonstationary AMFP series are listed in Fig. 9.

Fig. 7
figure 7

QQ plot of the residuals of eight best-fit models with GAMLSS model

Full size image
Fig. 8
figure 8

Worm plot of the residuals of eight best-fit models with GAMLSS model

Full size image
Fig. 9
figure 9

Flood quantiles at given return periods based on observed nonstationary AMFP series

Full size image

It could be seen that the flood quantiles at given return period are much smaller than the results which are based on reconstructed AMFP series shown in Tables 4 and 5, which also means that the AMFP series have decreasing trend. For the six sub-watersheds which showed nonstationarity, the flood quantiles at larger return periods are much smaller than the results based on reconstructed series. However, the flood quantiles show little variability at small return period, i.e., 20 and 10.

4.4 Flood scaling

Flood scaling is the relation between flood peak and basin area in similar hydrological regions. In this study, the identification of similarity of the eight selected sub-watersheds was not done, because Feng et al. (2013) classified these areas into the same hydrological response units. And Wei et al. (2014) pointed out that these eight sub-watersheds were still in the same hydrological response unit after land surface change.

In this paper, drainage area A was selected as the basin attribute to analyze flood scaling effect by establishing the correlation between drainage areas A and flood quantiles of T-year return period flood QT. According to the results of flood frequency analysis based on reconstructed series and observed nonstationary series, the regression relationship in the eight sub-watersheds can be obtained. Figures 10 and 11 show the flood scaling of stationary reconstructed series under the environmental conditions before and after 1979, respectively.

Fig. 10
figure 10

Flood scaling based on stationary reconstructed series under the environmental conditions before 1979 at return periods of (a) 500, (b) 200, (c) 100, (d) 50, (e) 20, (f) 10 years, respectively

Full size image
Fig. 11
figure 11

Flood scaling based on stationary reconstructed series after 1979 at return periods of (a) 500, (b) 200, (c) 100, (d) 50, (e) 20, (f) 10 years, respectively

Full size image

Due to no significant trend in Angezhuang and Hengshanling sub-watersheds in trend analysis and nonstationary flood frequency analysis by GAMLSS model, and the parameters of probability distribution functions are constant, so the flood quantiles corresponding to given return periods remain unchanged. Therefore, Angezhuang and Hengshanling were neglected in nonstationary flood scaling effect analysis. Figure 12 displays flood scaling based on observed nonstationary AMFP series.

Fig. 12
figure 12

Flood scaling based on observed nonstationary series at return periods of (a) 500, (b) 200, (c) 100, (d) 50, (e) 20, (f) 10 years, respectively

Full size image

The results of flood scaling exponents based on stationary reconstructed and observed nonstationary AMFP series are listed in Table 7. For stationary AMFP series, reconstructed series under the environmental conditions before and after 1979 have significant flood scaling effect. For reconstructed series under the environmental conditions before 1979, flood scaling exponent θT ranges from the minimum 0.3999 to the maximum 0.5585, and for reconstructed series under the environmental conditions after 1979, θT ranges from 0.4299 to 0.5712. For both series, flood scaling exponent θT decreases slightly with the decrease in return period T. Besides, the flood scaling exponents of reconstructed series under the environmental conditions before 1979 are slightly smaller than those after 1979 at the same return period.

Table 7 Summary of flood scaling exponents based on stationary and nonstationary AMFP series
Full size table

As for flood scaling based on observed nonstationary AMFP series, the result is very different. The scaling exponents are much larger than that of stationary reconstructed AMFP series. The maximum flood scaling exponent is 0.7670, and the minimum is 0.5603. Moreover, scaling exponents based on observed nonstationary AMFP series have a significant decreasing trend with the decrease in return period which also shows similar properties comparing with the result from the reconstructed series.

All of the flood scaling exponents, θT, increase with the increase in return period T. The possible reason is that more rainfall, which causes larger flood peak, will make the whole basin closer to saturation. And the relation between the flood peak and drainage area is close to linearity. Therefore, the flood scaling exponents increase and become close to 1. Eight rainfall–flood events were selected to analyze the relation between scaling exponent and rainfall which are shown in Table 8 and Fig. 13. It is found that scaling exponent θ displayed positive correlation with rainfall. And the Pearson correlation coefficient between θ and maximum 1-h rainfall is 0.724 which means they show strong correlation. So it is reasonable to consider that the increase in scaling exponent with return periods can be attributed to the increasing rainfall.

Table 8 Maximum 1-h, 3-h rainfall and scaling exponents of rainfall–flood events
Full size table
Fig. 13
figure 13

Relation between scaling exponents and rainfall of selected events

Full size image

Also we can see that the flood scaling exponents of reconstructed series under the environmental conditions before 1979 are slightly smaller than those after 1979 at the same return period. And the change of flood quantiles varies between different sub-watersheds (Table 9 and Fig. 14). Change ratio of flood quantiles of XDY and WK is 5.78% and 5.55%, respectively, while FP and LM reach 15.03% and 15.04% whose drainage areas are smaller than XDY and WK. Because the drainage area decreases from ZF to HSL, it is found that the change ratio and change on unit area exhibit upward trend with the decrease in drainage area. So the changing environment seemed to influence flood more on smaller sub-watersheds than larger ones. For confirming this, the land use of eight sub-watersheds before and after environmental changing (1970 and 1980) was analyzed. The area of grass and forest, which is considered to have significant influences on flood (Li 2011; Fu 2010), is shown in Table 10. The area of forest and grass of ZF and ZJG changed much more than other sub-watersheds. However, Fu (2010) found that the land use changing in ZJG, especially changing between forest and grass, influenced little on flood peak. So the changing in flood of ZJG and ZF, which is located in the downstream of ZJG, is considered not affected by land use changing. The land use changing of other sub-watersheds between 1970 and 1980 is shown in Fig. 15.

Table 9 Change ratio of flood quantiles based on reconstructed series under the environmental conditions after 1979 than that before 1979
Full size table
Fig. 14
figure 14

Change of flood quantiles under the environmental conditions after 1979 relative to that before 1979 of eight sub-watersheds

Full size image
Table 10 Grass and forest area of eight sub-watersheds in 1970 and 1980
Full size table
Fig. 15
figure 15

Change ratio of area of forest and grass from 1970 to 1980 of six sub-watersheds

Full size image

It can be seen that all the sub-watersheds show the increase in forest area and the decrease in grass area from 1970 to 1980. And it has been found in previous research that the increasing forest area and the decreasing grass area may cause the decrease in runoff (Gong et al. 2012). Moreover, the change ratio of forest and grass increases as the drainage area decreases, which causes the decrease in flood in smaller sub-watersheds more than that in larger ones. Therefore, the flood quantile scatters become “slant” and scaling exponent θ increases after 1979.

5 Conclusions

In this paper, flood data of eight sub-watersheds of Daqinghe River basin were applied to analyze flood scaling effect under nonstationarity, and the following conclusions can be obtained:

  1. (1)

    Nonparametric Mann–Kendall and Spearman tests were used to examine the presence of trends of the AMFP series, and it was found that the AMFP series of all the sub-watersheds had downward trend. Moreover, the nonparametric Pettitt and Brown–Forsythe tests were applied to detect the change points of the AMFP series, and the change points were all in the year of 1979.

  2. (2)

    The AMFP series were reconstructed under the environmental condition before and after the change point (1979) based on the relationship between rainfall P + Pa and runoff R to achieve stationary series. On the basis of the flood quantiles calculated by reconstructed flood peak series, flood scaling between flood peak and catchment area was analyzed, and the scaling exponent decreased with the decrease in return period.

  3. (3)

    Flood frequency analysis used the observed nonstationary series directly by GAMLSS to calculate flood quantiles. The flood scaling exponent showed the decreasing trend with the decrease in return period, and it is much larger than that obtained from reconstructed stationary series. Due to downward trend and change point in AMFP series, flood scaling results by observed nonstationary series and reconstructed series under the environmental condition before change point (1979) were not applicative for FFA. Reconstructed series under the environmental condition after 1979 may be more suitable to FFA for designing hydraulic structures and flood risk analysis.

  4. (4)

    Significant flood scaling effect could be found under both stationarity and nonstationarity. In this paper, the scaling exponents of flood quantiles of reconstructed AMFP series in Daqinghe River basin were around 0.5. Since the results of scaling analysis should provide significant information for design flood calculation in ungauged basins, we highly recommend the power law under the current environmental conditions, which is the result obtained by the reconstructed stationary flood series under the environmental condition after the change point.

Although we analyzed the relations between land use change and scaling exponent, the physical mechanism of quantile-based flood scaling remains unclear. Event-based flood scaling needs to be analyzed in future research. Through establishing a distributed hydrological model in this study area, the event-based flood processes could be simulated, and how the scaling exponent is influenced by rainfall characteristics, land use change and soil moisture could be addressed by flood modeling in the future work. Then a function between scaling exponent and the driven factors can be built, and it could be used to provide significant information in other ungauged basins for design flood calculation.