Scour hole depth prediction around pile groups: review, comparison of existing methods, and proposition of a new approach

Abstract

A dataset of 365 laboratory tests for scour hole depth (SHD) around pile groups (PGs) under unidirectional aligned flow is compiled, and the performances of the existing equations are comparatively evaluated on the dataset using several statistical indices. A formulation based on a correction of HEC-18 equation provides the best estimate with a correlation factor of 0.58. The test durations of the considered data ranged between 4 and 389 h. A time factor (K _t ) is proposed to take into account the temporal variation of the SHD around different PGs. Among the datasets, 51 long-duration experiments are scrutinized to show the temporal variation of scour depth toward equilibrium state. The time duration for these tests is up to 16 days. The proposed K _t factor for PGs has a superior performance compared to existing single-pier time factors. Subsequently, the equilibrium scour depths are calculated by extrapolation of scour depths reported at the end of the experiments using the K _t equation. The results showed that only 27–93% of the equilibrium scour depths were obtained at the end of the experimental measurements. Finally, a new equation for prediction of equilibrium SHD around PGs is proposed, which has 10% less prediction error than the existing equations. This comprehensive comparative study is a significant step forward in the correct estimation of current-induced SHD around PG foundations of hydraulic and coastal structures.

1 Introduction

Scour hole formation around the foundations of hydraulic and marine structures is one of the main risks of structural instability and damage. Scour hole develops when structures are placed on erodible beds and exposed to current and waves. The formation of scour around river and marine structures such as bridges, jacket-type offshore platforms, subsea templates, and jetties can pose a threat to their design life structural performance. Therefore, an accurate estimation of the scour depth around the base of the foundation for a safe design of marine and river structures has to be considered. Pile groups and complex foundations are widely used as the foundation to support river and marine structures in coastal and ocean engineering. Pile group foundations are commonly considered for bridges and causeways across rivers, estuaries, and tidal inlets, jetties and piers, jacket-type offshore oil platforms, offshore wind turbines, and elevated buildings in beaches.

Scour studies around bridge piers started in the late 1950s, and various design methods and formulae have been developed for estimating local scour depth in the vicinity of bridge piers (Melville 1997; Melville and Coleman 2000; Simarro et al. 2011). Melville (1997) comprehensively investigated the effective parameters in the pier and abutment scour and presented empirical relations, called K-factors. A comparison of existing empirical equations for single-pier scour is given by Qi et al. (2016).

While a substantial amount of knowledge has been accumulated about the scour and flow structures around single piers over the last decades, comparatively little is known about the scour and flow field around pile groups (Ataie-Ashtiani and Beheshti 2006; Zounemat-Kermani et al. 2009; Beheshti and Ataie-Ashtiani 2016b). Salim and Jones (1998) studied the scour around submerged and un-submerged pile groups and presented equations for the effect of pile spacing and attack angle in pile groups. Zhao and Sheppard (1998) investigated the effect of flow skew angle on local scour in pile groups. Ataie-Ashtiani and Beheshti (2006) conducted an experimental study on pile groups and derived a correction factor to predict the maximum local scour in pile groups. Amini et al. (2012) evaluated the commonly used equations to estimate the local scour depth in a group of piles for different spacing, arrangements, and submergences. The performance of sacrificial piles in front of pile groups was studied by Wang et al. (2016a, b).

Knowledge about scour mechanisms around pile groups has been limited to few investigations. Sumer et al. (2005) described two scour mechanisms for pile groups: first, the mechanisms causing local scour in individual piles and, second, those causing a global scour over the entire area of the pile group caused by horseshoe vortices and contracted flow between piles. Another relevant process, which is important for scouring at piles inline with the flow, is the sheltering effect, as discussed by Ataie-Ashtiani and Aslani-Kordkandi (2013), which reduces scour hole in the downstream piles. It should be noted that in this study the combined effect of local and global scour around pile groups is considered.

While in river engineering applications, scour is studied under the action of current alone, in coastal and marine environments it is necessary to investigate scour under influence of wave with or without current. The focus of this study is current-alone scour experiments.

A review of the previous studies showed that the existing methods for local scour prediction provided widely different estimates for different configurations of pile groups. Moreover, the observed scour depths exhibited a considerable degree of data scatter. Whether the data scatter and unrealistic prediction of the scour depth are due to the lack of existing data or inadequacy of the proposed methods has remained to be determined. In this paper, a comprehensive dataset on pile group scour gathered from the literature was reported. The main objective of this paper is to investigate the equilibrium scour depth of pile groups. For this purpose, in this study an equation is given which considers the effect of time on the estimation of scour hole depth around pile groups, and a factor which considers the time development of scour is used to extrapolate the raw and uncorrected data with durations of 4–389 h to the equilibrium scour depth.

2 Dimensional analysis

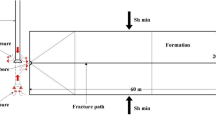
A schematic of a PG setup is shown in Fig. 1. PG scour hole depth, y _s, is in general a function of flow and sediment characteristics, and PG geometry and arrangement. Based on the dimensional analysis performed by Ataie-Ashtiani and Beheshti (2006) and Ataie-Ashtiani et al. (2010), Lança et al. (2013a) and Moreno et al. (2015), the functional relationship for pile group scour can be presented as:

$$\frac{{y_{\text{s}} }}{{b_{\text{p}} }} = f\left( {\frac{V}{{V_{\text{c}} }}{\text{ or }}\frac{{u_{*} }}{{u_{{*{\text{c}}}} }} ,\varvec{F}_{r} ,\frac{y}{{b_{\text{p}} }}{\text{ or }}\frac{y}{W},m,n,\frac{{S_{n} }}{{b_{\text{p}} }},\frac{{S_{m} }}{{b_{\text{p}} }},K_{\text{s}} ,\frac{{b_{\text{p}} }}{{d_{50} }},\frac{{V_{t} }}{{b_{\text{e}} }}{\text{ or }}\frac{{V_{t} }}{{b_{\text{p}} }}} \right).$$

(1)

Here y _s = scour depth, b _p = pile width, b _e = equivalent width for single pile that produces the same scour as the pile group, V = depth-averaged approach flow velocity, V _c = depth-averaged critical velocity for initiation of sediment motion, u _*  = bed shear velocity (u _*c is related to V _c through boundary layer variations of velocity), u _*c = critical bed shear velocity, F _r  = flow Froude number = V/(gy)^0.5, y = approach flow depth, m = number of piles inline with flow, n = number of piles perpendicular to the flow, S _n  = center-to-center spacing of adjacent piles perpendicular to the flow, S _m  = center-to-center spacing of piles inline with flow, K _s = shape factor for the individual pile within the pile group or the entire pile group, d ₅₀ = median sediment size, W = projected width of pile group, t = time, and f = functional relationship. Some of these parameters are shown in Fig. 1 that shows a 2 × 3 (n × m) pile group arrangement located in a channel with the width B _flume. The symbol S is used for center-to-center spacing of adjacent piles for the case when the spacing is the same in both directions, and a few researchers use G for gap spacing of adjacent piles in scour equations. The streamlines between upstream piles are contracted, and the horseshoe vortices that form in front of the upstream piles interfere with each other in the space between the two piles (Ataie-Ashtiani and Aslani-Kordkandi 2012). In the wake region between inline piles, sheltering effect reduces streamwise velocity (Ataie-Ashtiani and Aslani-Kordkandi 2013). Figure 2 shows sample photographs of two pile group scour experiments based on Baratian (2007) and Hajzaman (2008) experiments; in both cases, a general scour hole is observed between piles. In Fig. 2b, the spacing of piles is in the order of pile diameter, and if a rectangular round-nose solid pier is circumscribed around the pile group, the resulting scour of the solid pier will be the same as the pile group.

Fig. 1

Schematic of pile group: a plan and b upstream view

Fig. 2

Scour hole shape around PGs after the end of the experiments and dewatering the flume with arrows showing flow direction for experiments of: a Baratian (2007) and b Hajzaman (2008)

The location of maximum scour depth for pile groups consisting of two or more piles inline with the flow generally occurs in the leading, upstream pile, as evidenced by tandem piers experiments done by Wang et al. (2016a, b) which shows the sheltering effect of upstream pile. In a rare case belonging to Lança et al. (2013a), reinforcement of horseshoe vortices caused a greater scour depth at the downstream piers for four inline piles of the same diameter. This study considered the maximum scour depth whether it occurs in front of upstream pier or one of the downstream piers. It is known that SHD will vary in space and time in a pile group, and the measurement of SHD is not necessarily consistent between such varied pile group arrangements since the location of maximum scour hole measured in each experiment is not the same, and although it might be important for design purposes to know the location of it, this study does not specify the location of maximum scour.

3 Database

The database for pile group local scour experiments includes 365 laboratory data that are compiled from previous studies for unidirectional flow with zero angle of attack for approach flow. The list of data sources for data with known and unknown test duration are given in Table 1, which includes 338 and 27 data, respectively. The electronic supplementary file contains the database used in this study.

Table 1 Data sources for pile group scour

From the data with known time duration, there are 60 experiments for which time development of SHD was measured. These are listed in Table 1, along with the test duration and PG configuration in terms of n × m.

Most of the experiments are run in clear-water scour condition, except for three live-bed experiments. Most of the experiments have identical spacing between piles in both directions, while 41 data have nonuniform spacing. Most of the experiments are done using circular piles except for eight experiments with square piles.

The ranges of non-dimensional parameters with breakdown over important sources are given in Table 2. The values of flow intensity, as indicated by V/V _c, are calculated with different equations by each investigator. In order to gain uniformity, V/V _c values were calculated with the equation of Beheshti and Ataie-Ashtiani (2008), and it was found that they fall in the range 0.47 ≤ V/V _c ≤ 1.02. Also, spacing between piles falls in the range 1 ≤ S _n /b _p ≤ 11. The non-dimensional time parameters V _t /b _pg and t/t ₉₀ are also reported in Table 2; here b _pg is equivalent width of pile group calculated with HEC-18 method, and t ₉₀ is the time required to reach 90% of equilibrium scour depth calculated with the equation of Sheppard et al. (2011).

Table 2 Non-dimensional range of parameters

Different arrangements of pile groups for all experiments according to the number of piles in both directions (n × m) are drawn in Fig. 3. The configurations with time record of SHD development are also marked in Fig. 3.

Fig. 3

Arrangements of pile groups used in this study in the form n × m, underlined for configurations with available time record of SHD development (in some experiments, square piles were used)

The criteria for data selection are done as follows. According to Chiew and Melville (1987), effect of sediment size can be eliminated for b/d ₅₀ > 50 which holds for all experiments. The criterion for non-rippling sediments is d ₅₀ < 0.7 mm based on Chiew and Melville (1987) which is violated in certain experiments of Smith (1999) and Ataie-Ashtiani and Beheshti (2006); however, this matter was inconsequential because the ripples were observed only at the downstream of the test section.

In order to eliminate the effect of the contraction scour, Chiew and Melville (1987) suggest that the projected width of the pier (pile group in this study) should be at most 10% of flume width, B _flume. This condition is approximately satisfied for data of this study.

Another criterion states that the experiments should have reasonable time durations, and very short durations are not desirable because clear-water scour is a slow process (Simarro et al. 2011). However, in this study all gathered data including the data with durations as short as 4 h (data from Gao et al. 2013; Martin-Vide et al. 1998; and Oliveto et al. 2004) are retained. As can be seen in the following sections, these short-duration experiments highlight the need for extrapolation of data to an equilibrium state in providing empirical equations.

Assuming that the HEC-18 can estimate the equilibrium scour depth accurately for designing the foundation depth, the difference between the observed scour depths from short-time tests and estimated ones based on design formula of HEC-18 can show that the equilibrium scour depth for that pier, sediment, and flow conditions is not achieved and this observed scour depth could not be used in foundation design. For data of Ataie-Ashtiani and Beheshti (2006) and Amini et al. (2012) with test duration of 7–8 h, the ratio of predicted scour depth to observed scour depth, y _s(HEC)/y _s(obs), was in the range 0.7–0.9, whereas for data of Lança et al. (2013a) with test duration of 166–389 h, the ratio was roughly 1.7. This discrepancy shows that test duration of 24 h produces half of the scour depth for tests lasting several days and that time parameter is an important variable in the pile group scouring.

Sufficiency of test duration can also be obtained by checking the condition V _t /b _pg = 10⁶ which is required for reaching 90% of equilibrium scour (Franzetti and Radice (2015), where b _pg is equivalent width of pile group calculated with HEC-18 method. The parameter V _t /b _pg is calculated in Table 2 which shows that this criterion is not met for some of the data sources. Another method for checking duration sufficiency is calculation of t/t ₉₀, where t ₉₀ is the time required for reaching 90% of equilibrium scour obtained by the formulas given in Sheppard et al. (2011). Comparison of t/t ₉₀ values in Table 2 shows that some experiments have insufficient duration.

In the following section, we first evaluate the existing scour equations based on the raw data gathered from different studies. The plots between predicted and observed scour depths show a scattering in results. This can partly be related to the different time durations in different experiments. Next, we provide a time factor, indicating the effect of time on scour development, based on different time development records of scour experiments conducted on several pile group arrangements by different researchers. By using this time factor, all measured scour depths are extrapolated to equilibrium scour depth.

4 Existing equations

Equation of HEC-18 (Arneson et al. 2012) calculates PG scour by substituting b _e = K _Smn W in single-pier equation of HEC-18. Here K _Smn is a factor that accounts for pile group configuration; the expression of K _Smn is given in Table 3. The single-pier equation of HEC-18 can be expressed by (assuming plane bed conditions and fine sediments):

$$\frac{{y_{\text{s}} }}{y} = 2.2K_{\text{s}} \left( {\frac{{b_{\text{e}} }}{y}} \right)^{0.65} \varvec{F}_{r}^{0.43}$$

(2)

Table 3 Existing equations for SHD estimation around PGs

Coleman (2005) calculates PG scour by substituting b _e calculated from HEC-18 in single-pier equation of Melville and Coleman (2000). The single-pier equation of Melville and Coleman (2000) can be expressed by Eq. (3):

$$y_{\text{s}} = K_{\text{s}} K_{\text{y,be}} K_{d50} K_{\text{I}} K_{t}$$

(3)

In Eq. (3), K _y,be = factor for flow depth and pier size, K _y,be = (b _e y)^0.5 for 0.7 < b _e/y < 5; K _d50 = sediment size factor, K _d50 = 1 for b _e/d ₅₀ > 25; K _I = flow intensity factor, for clear-water scour condition and uniform sediment K _I = V/V _c; and K _t  = the time factor.

Equation of FDOT (Sheppard and Renna 2005) calculates the SHD in PGs by substituting b _e = K _s K _Smn W in the FDOT single-pier expression. K _Smn for FDOT equation is given in Table 3. The single-pier equation of FDOT for clear-water scour condition and for single pier having width b _e can be written as Eq. (4):

$$\begin{aligned} \frac{{y_{\text{s}} }}{{b_{\text{e}} }} & = 2.5\tanh \left[ {\left( {\frac{y}{{b_{\text{e}} }}} \right)^{0.4} } \right] \times \left\{ {1 - 1.75\left[ {\ln \left( {\frac{V}{{V_{\text{c}} }}} \right)} \right]^{2} } \right\} \\ & \quad \times \,\left[ {\frac{{{{b_{\text{e}} } \mathord{\left/ {\vphantom {{b_{\text{e}} } {d_{50} }}} \right. \kern-0pt} {d_{50} }}}}{{0.4\left( {{{b_{\text{e}} } \mathord{\left/ {\vphantom {{b_{\text{e}} } {d_{50} }}} \right. \kern-0pt} {d_{50} }}} \right)^{1.2} + 10.6\left( {{{b_{\text{e}} } \mathord{\left/ {\vphantom {{b_{\text{e}} } {d_{50} }}} \right. \kern-0pt} {d_{50} }}} \right)^{ - 0.13} }}} \right] \\ \end{aligned}$$

(4)

The three above-mentioned equations are marked as “Widely used” in Table 3 due to their popularity. Equations of Salim and Jones (1998), Ataie-Ashtiani and Beheshti (2006), Amini et al. (2012) and Beheshti et al. (2013) are corrections for HEC-18 equation. Ataie-Ashtiani and Beheshti (2006) has also proposed a correction for Coleman’s (2005) equation, as given in Table 3 and marked as “Correction” type. A comparison of several machine learning equations for scour around PGs is given by Beheshti and Ataie-Ashtiani (2016a).

Note that HEC-18 and FDOT methods are capable of calculating scour depth for complex piers consisting of a column, pile cap, and PG. Here we consider the special case of PG without considering relevant bed-level adjustments.

Some of the machine learning approaches used for PG scour are given by Ghaemi et al. (2013), which used multiple linear regression and model tree approaches. The relevant equations are given in Table 4.

Table 4 Ranking of equations via comparison of statistical indices on raw data

5 Evaluation of scour equations based on raw data

In this section, the performance of 12 scour equations mentioned in the “Existing Equations” section are evaluated based on the raw data. Comparisons are made based on statistical indices. The 365 data with known or unknown durations are considered.

The basis for comparison using the statistical indices is as follows: 1) for root-mean-square error (RMSE), percent error (%|ε|), and mean absolute error (MAE), a value of zero indicates a good performance and large positive values are undesirable; 2) for coefficient of correlation (ρ), coefficient of determination (R ²), also known as Nash–Sutcliffe efficiency factor, and Willmott’s index of agreement (I _a), a value of 1 is desirable and smaller values close to 0 as well as negative values for R ² are undesirable. Discrepancy ratio (DR) of 1 shows unbiased model, whereas DR < 1 shows underprediction and DR > 1 shows overprediction behavior.

It should be mentioned that Coleman’s (2005) method was originally developed as an envelope curve, while HEC-18 is a central predictor; therefore, the comparison here may be regarded as unfair. However, since these equations do not indicate what amounts of overdesign have been incorporated into them, the authors can only directly compare these equations.

The values of statistical indices for existing equations are given in Table 4, which also ranks equations from best to worst. These values are evaluated based on the raw database. Comparison of RMSE shows that the poorest equation in terms of RMSE and R ² is FDOT and Coleman (2005) equations, with R ² = −0.4 for FDOT and R ² = 0.12 for Coleman (2005) equations. Negative values of R ² mean that the model performs worse than average of observations. The best equations in term of the smallest RMSE and highest R ² are Ataie-Ashtiani and Beheshti (2006) and Beheshti et al. (2013) equations with R ² = 0.58. Inspecting the values of discrepancy ratio shows that equations such as Howard and Etemad-Shahidi (2014) with DR ≤ 0.93 suffer from underprediction, while equations of Coleman (2005) and FDOT with DR ≥ 1.2 suffer from overprediction. The rest of the equations with DR in the range 1.00 ≤ DR ≤ 1.12 are unbiased or tend to overpredict slightly. Willmott’s index of agreement (I _a), which shows the best behavior for I _a = 1, shows superior performance of Ataie-Ashtiani and Beheshti (2006) correction on Coleman (2005) equation with I _a = 0.88 and the worst performance for Salim and Jones (1998) with I _a = 0.59. In terms of correlation coefficient, the best equation has ρ = 0.80 and worse equation is Coleman (2005) with ρ = 0.47. In terms of percent error (%|ε|), equation of FDOT with 51% error and equation of Ataie-Ashtiani and Beheshti (2006) correction on HEC-18 with 20% error are the worst and best equations, respectively. HEC-18 equation has 25% error which is relatively good compared to other equations. The authors suggest using the first five rows of equations in Table 4 for design purposes because these equations have the best ranking.

Scatter plots of predicted vs. observed values of scour depth for six selected equations are shown in Fig. 4. Comparison is made by counting the number of predictions close to perfect agreement line, and points within and outside ±20% error lines. Non-dimensional scour depth (y _s/W) is used for plots. Inspecting these plots shows that Ataie-Ashtiani and Beheshti (2006) based on HEC-18 has the most number of predictions that lie within ±20% error lines, with 64% of predictions within the two bounds, while for FDOT equation, only 23% of predictions fall between the two bounds. The most severe case of overprediction belongs to FDOT with 69% of prediction above +20% error line. The most severe case of underprediction belongs to equation of Amini et al. (2012), with 38% of predictions lying below −20% error line. Based on these comparisons, the method of Ataie-Ashtiani and Beheshti (2006) is the best with highest performance based on the raw data.

Fig. 4

Scatter plots of predicted versus observed values of non-dimensional scour depth (y _s/W) for raw data using equations of: a HEC-18, b Coleman (2005), c FDOT, d Ataie-Ashtiani and Beheshti (2006)—correction on HEC-18, e Amini et al. (2012) and f Beheshti et al. (2013)

To our knowledge, a similar comparative study of equations of the current-induced SHD around pile groups has not been done before, considering the wealth of database, varieties of methods, and the diversities of statistical indexes.

6 Time factor

Wide range of test times in different reported experiments makes it a difficult task to compare scour depth equations based on these data. A time factor K _t is obtained to account for the effect of time on development of scour depth. K _t is defined as the fraction of equilibrium scour depth obtained at time t or K _t  = y _s(t)/y _s,e. Here y _s(t) = scour depth at time t and y _s,e = equilibrium scour depth.

Although several equations for K _t have been proposed for single piers in previous research papers, the subject has not been studied for SHD around PGs. Single-pier equations for K _t are given by Franzetti et al. (1982), Melville and Chiew (1999), and others are listed in Table 5. These K _t equations are modified for use in PGs by substituting b = b _pg where b _pg is calculated with HEC-18 equation.

Table 5 Summary of existing equations for time factor, K _t

The value of y _s,e can be achieved by one of the following methods: (1) continuing scour experiments for infinite time, which is impractical; (2) estimating y _s,e with an empirical relationship, such as the work of Coleman (2005); (3) using the scour at the end of experiment (y _s,end) for data with extra long duration and setting y _s,e = y _s,end; and (4) extrapolating scour depth to infinite time for data with available record of time development of SHD. Based on Table 1, only 60 data with record of SHDs versus time can be used for the last method.

Data of 55 experiments have recorded scour depths to allow good fitting. The equation of Lança et al. (2013a) with five unknowns (a ₁, a ₂, t ₁, t ₂, and t ₃) and an additional unknown of y _s,e, named Kt-6p herein, is considered in our work for extrapolation of PG scour data. Kt-6p has the advantage of considering three phases of scour for each term, with the first term related to short-term scour and the last term related to long-term scour.

The task is to extrapolate 55 data with available record of time development. Lança et al. (2013a) fitted Kt-6p equation to their experiments, including the 30 experiments of aligned flow. The extrapolation was recalculated in this study, and the y _s,e values are adopted in the database. The original fitted values of y _s,e were found to be correct except for an instance of excessive value of y _s,e and an instance of overly small value of y _s,e even smaller than y _s,end.

For the remaining 25 data with known time duration, equilibrium values were obtained by extrapolation using Kt-6p. Details of fitting Kt-6p equation for 6 data with durations between 65 h ≤ t _end ≤ 310 h are given in Table 6. The R ² values are close to 1, except for data of Smith (1999) which have lower values of fitting R ², because in these live-bed experiments scour depth has oscillations, with intervals of partial refilling of the scour hole during the experiment. The fitted curves for observed scour depths versus time are drawn in Fig. 5. Defining K _t  = y _s,end/y _s,e, for the 55 data time factor falls in the range 0.8 ≤ K _t  ≤ 1, with an average of K _t  = 0.92.

Table 6 Extrapolated y _s,e values calculated by fitting Kt-6p equations to six experiments with available record of time development

Fig. 5

Fitting Kt-6p equation to six experiments with record of time development of SHD

For the remaining 283 data with known time and scour depth at the end of the experiments, equilibrium scour depths are found by using the relationship y _s,e = y _s,end/K _t (t _end). All of the equations in Table 7 can be used for obtaining K _t . Application of Kt-6p equation for this purpose requires construction of expressions for a ₁, a ₂, t ₁, t ₂, and t ₃ based on pile geometry and flow characteristics. The best K _t equation is found by considering week-long experiments (t _end = 24–390 h and the corresponding measured value of y _s,e) and checking whether it is possible to successfully obtain y _s,end by extrapolation from a truncated time t _p and the corresponding value of scour depth, y _s,p, usually in the range t _p = 8–24 h. Comparing the measured and extrapolated y _s,end by means of percent absolute error value (%|ε|) and coefficient of determination R ² shows the best method, as done in Table 7.

Table 7 Average value of coefficient of determination (R ²) and percent error on y _s,end (%|ε|) for existing and presented time equations

A new equation for time development factor, K _t , is also developed here, with the difference that the proposed equation is specific for the problem of PG rather than single piers. Two K _t factors are proposed. The average value of R ² for fitting each of the proposed K _t equations for 55 records is given in Table 7. The equation which uses b = b _pg is given in Eq. (5), hereinafter known as Kt-PS1p equation. In Eq. (5) b _pg is calculated with HEC-18 equation (Arneson et al. 2012). Here a ₁ and a ₂ are functions of d ₅₀/b _pg. Note that b _pg is calculated with HEC-18 equation.

$$\begin{aligned} K_{t} & = 1 - \exp \left( { - a_{1} \left( {{{V_{t} } \mathord{\left/ {\vphantom {{V_{t} } {b_{\text{pg}} }}} \right. \kern-0pt} {b_{\text{pg}} }}} \right)^{{a_{2} }} } \right) \\ a_{1} & = 0.133\left( {{{d_{50} } \mathord{\left/ {\vphantom {{d_{50} } {b_{\text{pg}} }}} \right. \kern-0pt} {b_{\text{pg}} }}} \right)^{0.192} ,\quad a_{2} = 0.053\left( {{{d_{50} } \mathord{\left/ {\vphantom {{d_{50} } {b_{\text{pg}} }}} \right. \kern-0pt} {b_{\text{pg}} }}} \right)^{ - 0.289} \\ \end{aligned}$$

(5)

The second equation which uses b = b _p is given in Eq. (6), hereinafter known as Kt-PS2p equation. Here a ₁ and a ₂ are functions of pile numbers in each direction and pile spacing.

$$\begin{aligned} K_{t} & = 1 - \exp \left( { - a_{1} \left( {{{Vt} \mathord{\left/ {\vphantom {{Vt} {b_{p} }}} \right. \kern-0pt} {b_{p} }}} \right)^{{a_{2} }} } \right) \\ a_{1} & = 0.110m^{ - 0.439} n^{ - 0.716} \left( {{{{\text{S}}_{n}^{\prime } } \mathord{\left/ {\vphantom {{{\text{S}}_{n}^{\prime } } {{\text{b}}_{\text{p}} }}} \right. \kern-0pt} {{\text{b}}_{\text{p}} }}} \right)^{0.297} ,\quad a_{2} = 0.113m^{0.420} n^{0.313} \left( {{{S_{n}^{\prime } } \mathord{\left/ {\vphantom {{S_{n}^{\prime } } {b_{\text{p}} }}} \right. \kern-0pt} {b_{\text{p}} }}} \right)^{ - 0.085} \\ \end{aligned}$$

(6)

Table 7 compares K _t equations for all data, as well as long-duration and medium-duration data separately, as defined by long-duration (100 h ≤ t _end ≤ 390 h) and medium-duration (17 h ≤ t _end ≤ 75 h) tests. It can be seen that Kt-MCp has better performance on medium-duration data than on long-duration data. More recent equations of Kt-Lp, Kt-Cp, and Kt-SMp (refer to Table 5 for abbreviated names) perform better on long-duration data than on medium-duration data. This may be due to the fact that the equation of Melville and Chiew (1999) was mainly built on experiments with durations of <100 h, whereas equation of Cheng et al. (2016) was built on longer-duration tests, many of which lasted more than 100 h. For long-duration data, Kt-PS2p has the best performance with R ² = 0.94, and the best equation in existing equations is the Kt-Lp. For medium-duration data, the best equation is Kt-MCp and Kt-PS2p, which both have R ² = 0.87, indicating the capability of Kt-MCp equation on shorter-duration data. For all data combined, the best equation is Kt-PS2p with R ² = 0.91 and 6.08% error on y _s,end, while the best existing equation is Kt-Lp with R ² = 0.88 and 7.20% error on y _s,end, indicating that Kt-PS2 is superior to the best existing equation.

In order to assess the performance of K _t equations on long-duration data, plots of several individual experiments with records of time development of SHD are drawn in Fig. 6, along with different K _t equations superimposed. In this figure, the position of truncation time is also marked with an arrow, in which all K _t curves are forced to pass through the pivot point, except for Kt-6p curve. In Fig. 6a–c, it can be seen that Kt-PS2p and Kt-Lp equations have excellent performance, while equations such as Kt-MCp fail to follow the trend of scour after the point of pivot and attain its equilibrium value, which is the underprediction of the observed value. In Fig. 6d, it can be seen that Kt-Lp equation struggles to follow the trend of data, underpredicting scour depths before pivot point and overpredicting them after the pivot point. Similar comparison for medium-duration data is done in Fig. 7, showing that Kt-MCp is the best existing equation, and Kt-PS2p has at most 5% error which shows good performance.

Fig. 6

Plot of time development of SHD compared to time equations for long-duration tests of: a Moreno et al. (2014) run PG; b Lança et al. (2013a) run 3; c same, run 53 and d Smith (1999), run 7

Fig. 7

Plot of time development of SHD compared to time equations for medium-duration experiments of: a Shrestha (2015), run s2r6; b Nouri et al. (2013), run 2; c Amini et al. (2012), run 1–3 and d Ataie-Ashtiani and Beheshti (2006), run 62

Having established that Kt-PS2 equation has reasonable performance for extrapolating data, the next step is to combine K _t values from this equation with y _s,end for 283 data with known time duration to find the equilibrium scour depth from the equation K _t (t _end) = y _s,end/y _s,e. For experiment of Martin-Vide et al. (1998), the value of y _s,e/y _s,end = 1.25 was used. Computed K _t values for Kt-PS2 equation fall in the range 0.27 ≤ K _t  ≤ 0.93 with an average of K _t  = 0.52. In comparison, Kt-MC equation (Melville and Chiew 1999) produces K _t values in the range 0.72 ≤ K _t  ≤ 1 with an average of K _t  = 0.9. There is great discrepancy between the two equations here. However, the proposed Kt-PS2 equation is unique in considering the parameters of pile group, and therefore, the K _t values by this equation are adopted for the rest of the paper. A scatter plot of K _t versus t _end for 282 experiments is plotted in Fig. 8, showing the general increase in K _t as t _end increases.

Fig. 8

Scatter plots of K _t versus t calculated over 282 experiments for equations of: a Kt-PS2; b Kt-MC, in which histogram of t at top and histograms of K _t on the right side

Since most successful design relationships need to predict equilibrium scour depth, this concern is addressed by extrapolating data. But how can one trust the equation, it will be seen that the K _t formula is validated against long-term data which assure its reliability.

7 Prediction of equilibrium scour depth

In this section, a new equation for prediction of equilibrium scour depth around pile groups is proposed. The distribution of 338 raw data as reported by previous researchers and the equilibrium values is plotted in Fig. 9. For raw data, the average value of non-dimensional scour depth is y _s/W = 1.36 with standard deviation of 0.54. For extrapolated data, the average value of non-dimensional equilibrium scour depth is y _s,e/W = 2.57 with standard deviation of 1.27. The increase in standard deviation is also evident in Fig. 9, which shows that extrapolated data have a broader distribution with more scatter compared to the narrower distribution of raw data.

Fig. 9

Histogram of non-dimensional scour depth for raw scour depths (black bars) and equilibrium scour depths (gray bars)

Correction factors are presented that can be combined with HEC-18 or FDOT equations. The first type of correction factor is defined as K _Smn  = b _e/W, where b _e is the equivalent width of pile group that when combined with a scour equation would produce the same scour depth as observed scour depth. The second type of correction factor is defined as K _PG = y _s,e/y _s,W. Here y _s,W is scour depth of single pier having width of W calculated from an equation.

An inspection of K _PG values with y _s,W calculated with FDOT method was done to screen outliers. Inspection showed that for data of Gao et al. (2013), the range of this parameters is 3.5 ≤ K _PG ≤ 9.23, while for all other data sources, the range of this parameter is 0.4 ≤ K _PG ≤ 2.9, where y _s,W is calculated with FDOT method. This means that the extrapolation of data of Gao et al. (2013) resulted in excessive increase of scour depths. This can be attributed to short duration of their tests (4 h). Simarro et al. (2011) have pointed out that short-duration data are not suitable for extrapolation. Therefore, data of Gao et al. (2013) are eliminated from database used for fitting an equation for equilibrium scour depth.

The correction for HEC-18 equation is given of K _PG type as given in Eq. (7), hereinafter known as Present Study 1 equation. This equation is found by applying a natural logarithm transform on data and using model tree (M5′) command in Weka software (Witten et al. 2005). The resulting equation is a piecewise linear function with two sub-functions, divided based on non-dimensional spacing of piles. The proposed equation is a central predictor, unlike equation of Coleman (2005) which is an envelope or design curve.

$$\begin{aligned} K_{\text{PG}} & = 2.548m^{ - 0.357} n^{ - 0.134} \left( {\frac{{S_{n}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.255} \left( {\frac{{S_{m}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.019} \times \left( {\frac{{d_{50} }}{{b_{\text{p}} }}} \right)^{ - 0.095} \left( {\frac{y}{{b_{\text{p}} }}} \right)^{ - 0.199} \, \\ & \quad {\text{for }}\frac{{S_{n}^{\prime } }}{{b_{\text{p}} }} \le 1.58;\quad {\text{Otherwise:}} \\ \end{aligned}$$

$$K_{\text{PG}} = 3.041m^{ - 0.229} n^{ - 0.745} \left( {\frac{{S_{n}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.22} \left( {\frac{{S_{m}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.072} \left( {\frac{{d_{50} }}{{b_{\text{p}} }}} \right)^{ - 0.183} \left( {\frac{y}{{b_{\text{p}} }}} \right)^{ - 0.409}$$

(7)

The division is based on S _n ′/b _p = 1.58, differentiating between the case of a single row of piles (n = 1) or nearly touching piles (S _n /b _p ≈ 1, n ≥ 2) from the rest of the database. The first and second partitions contain 150 and 143 data points, respectively. In Eq. (7), S _n ′ (or S _m ′) is modified version of S _n (or S _m ), with the difference that for the case of n = 1 (or m = 1) when S _n (or S _m ) is undefined, we set S _n ′ = b _p (or S _m ′ = b _p), and the primed or modified quantities are used since for a single row of piles the value of S _n is undefined; however, S _n ′ is always defined even for a single row of piles, and this circumvents the appearance of zero term in equations or the need to substitute S _n with S _m . Equation (7) considers the effect of spacing in both directions. A note about using y/b _p in Eq. (7) is needed. Since HEC-18 equation already considers the effect of y/b, the justification for using this factor in K _PG equation is that the shallowness coefficient of used data has the sufficient range (0.7 < y/b < 25 from Table 2) to merit inclusion in K _PG factor, compared to range of y/b used in similar studies such as the work of Cheng et al. (2016).

Despite the popular use of HEC-18 equation, there might be concern about the lack of the sediment size representation, e.g., b/d ₅₀, in this equation. Recent studies have demonstrated the importance of incorporating the influence of b/d ₅₀ in scour equations mainly because of higher values of this ratio in laboratory experiments compared to field observations. FDOT equation has the advantage of considering effects of pier size and flow shallowness (b/y), sediment size scale (b/d ₅₀), and flow intensity (V/V _c). Since FDOT equation is also a function of b/d ₅₀ and V/V _c, there is no need to consider these parameters separately in K _t formula. V _c was once calculated with FDOT equation and another time calculated as average of FDOT, Melville and Coleman (2000) and Beheshti and Ataie-Ashtiani (2008) equations. However, the first approach was found to be better.

The correction factor for FDOT formula that is of K _Smn type is given in Eq. (8), hereinafter known as Present Study 2 equation. Here K _Smn is only a function of pile group configuration.

$$K_{Smn} = 3.726m^{ - 0.561} n^{ - 0.429} \left( {\frac{{S_{n}^{\prime } }}{{b_{\text{p}} }}} \right)^{0.936} \left( {\frac{{S_{m}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.053} \quad {\text{for}}\quad \frac{{S_{n}^{\prime } }}{{b_{\text{p}} }} \le 1.3;\quad {\text{Otherwise:}}$$

$$K_{Smn} = 3.784m^{ - 0.221} n^{ - 1.045} \left( {\frac{{S_{n}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.331} \left( {\frac{{S_{m}^{\prime } }}{{b_{\text{p}} }}} \right)^{ - 0.026}$$

(8)

The first and second partitions contain 129 and 164 data points, respectively. The scatter plot of predicted vs. observed values for the proposed equations (Present Study 1 and 2) is illustrated in Fig. 10a, b, and scatter plots for two existing equations, namely HEC-18 and Ataie-Ashtiani and Beheshti (2006), based on HEC-18 are drawn in Fig. 10c, d. The performance of Present Study 1 equation is relatively good, since 79% of predictions fall between ±20% error lines, whereas for HEC-18 and Ataie-Ashtiani and Beheshti (2006) equations, at least 70% of predictions fall under −20% error line, showing that the equations that previously worked very well on raw data show poor performance when they are used for predicting equilibrium SHD. Figure 10 also shows extrapolated data of Gao et al. (2013) which are not included in the analysis but are nevertheless shown here to demonstrate that this data source consists of outliers.

Fig. 10

Scatter plots of predicted versus observed values of non-dimensional equilibrium scour depth for extrapolated data using equation of: a Present study 1 based on HEC-18; b present study 2 based on FDOT; c HEC-18 and d Ataie-Ashtiani and Beheshti (2006)—correction on HEC-18

It is possible to compare the estimated final scour depths by Eqs. (7) and (8) with observed depths for long-duration tests only. This can be done by looking at blue crosses (×) in Fig. 10 which belong to long-duration tests of Lança et al. (2013a, b), which have undergone no extrapolation using the proposed Kt equation. The figure shows good agreement between observations and predictions for these data. However, Eqs. (7) and (8) are derived using both long- and short-duration data. Therefore in Fig. 10, the x-axis of “observed values” is in fact extrapolation of measured observed values using K _t equation with K _t values in the range of 27–93%. Figure 10 shows that Eqs. (7) and (8) have reasonable accuracy for predicting scour of short-duration experiments.

Comparing equations on equilibrium data quantitatively using several statistical indices is done. For most existing equations, we have negative value of coefficient of determination R ², whereas the Present Study 1 equation has R ² = 0.81 (R ² calculated based on y _s/W). Also in terms of percent error (%|ε|), Present Study 1 equation has 11% less error than the best existing equation. Comparing the values of discrepancy ratio shows that all existing equations tend to underpredict with DR < 0.91, while the presented equation has DR close to unity. Values of correlation coefficient are also favorable for Present Study 1 equation, with ρ = 0.90, whereas other equations have 0.34 ≤ ρ ≤ 0.77. Present Study 2 equation works similar to Present Study 1 equation.

A box plot for showing the distribution of error residuals on equilibrium scour depth for different equations is displayed in Fig. 11. The box length, which includes 50% of data, is centered at zero error for Present Study equation, but for all other equations, the box falls under the zero residual line. The box length is smallest in the proposed equation. The distance between whiskers, which shows difference between maximum positive and negative error, is nearly similar for all equations. Correction factor of HEC-18 (Present Study 1 equation) works slightly better than that of FDOT (Present Study 2 equation).

Fig. 11

Box charts for residual error on equilibrium scour depths

8 Conclusion

In this study, maximum scour depth (y _s) around PGs (pile groups) was investigated. A database of 365 laboratory data points was assembled in an electronic supplement. Also, 12 existing equations for prediction of scour depth around pile groups were explained, and their equations were given in table form. Comparison of existing equations on the scour depth data showed better performance for correction of Ataie-Ashtiani and Beheshti (2006) on HEC-18 (Hydraulic Engineering Circular No. 18) with R ² = 0.58 and 20% error compared to other existing equations, while the worst equation was found to be FDOT (Florida Department of Transportation) (Sheppard and Renna 2005) with R ² = −0.4 and 51% error.

For considering the effect of time, extrapolation techniques were used to convert the reported scour depths by researchers, or raw data, into equilibrium data. From 338 data with known time duration, 55 experiments have durations of at least 24 h and record of time development of scour; extrapolation to equilibrium value was done by an equation of Lança et al. (2010).

A list of time factor equations (K _t ) available in the technical literature for evolution of scour were assembled, and their performance was assessed over 55 records of SHD versus time for PGs, with equation of Lança et al. (2013a) having the best performance (R ² = 0.87). Also a new K _t was proposed which considers the effect of pile group arrangement and has better performance over time records (R ² = 0.90). Using the proposed equation, SHDs for 283 data with known time duration were extrapolated to equilibrium value, with an average value of K _t  = 0.52.

After extrapolation, the average value of y _s/W = 1.36 for raw data increased to y _s,e/W = 2.57 for equilibrium data (W is the projected width of pile group). A new equation based on model trees was used to fit a new equation for estimation of equilibrium SHD (scour hole depth) around PGs. The proposed equation is a correction factor for HEC-18 and FDOT equations based on model trees which is made of two sub-functions that consider the effect of pile group parameters, sediment size, and flow shallowness. Whereas the existing equations suffer from severe underprediction of equilibrium scour depth, with at least 29% error and a near zero and R ² = 0.20, the proposed correction for HEC-18 has satisfactory performance with R ² = 0.81 and 18% error.