1 Introduction

The occurrence of earthquakes is characterized by extreme randomness. They are of highly stochastic nature in both the spatial and the temporal domains. As a result, very little progress has been achieved so far in accurate prediction of future earthquakes, both spatially and temporally. However, it has been observed from the earthquake history that while some regions are more susceptible to earthquakes, others are seismically relatively inactive. This leads us to the possibility that although it is virtually impossible to pinpoint the time and location of a future earthquake exactly, it might still be possible to predict the long-term seismic hazard for a region from its past recorded earthquakes (Anagonos and Kiremidjian 1988; Sadeghian 2007). Seismic hazard assessment is often based on statistical analysis of the seismic history of a study region. Many of these assessments are purely probabilistic, such as (1) estimation of seismic hazard parameters for different recurrence time interval based on the Gutenberg and Richter distribution (Gutenberg and Richter 1944) and (2) models based on Poissonian seismicity models (e.g., Cornell 1968; Gardner and Knopoff 1974; Kijko and Seflevoll 1981; Brillinger 1982; Araya and Der Kiureghian 1986; Anagonos and Kiremidjian 1988; Kagan and Jackson 1991). Seismicity modeling of an area mainly depends on past seismicity in terms of their location, occurrences and magnitude of the event (Kramer 1996; Mohanty and Verma 2013). However, above-discussed models analyze the seismicity with the assumption that the earthquake occurrences are independent in space and time. Moreover, these methods of seismicity analyses may not be suitable where a large region is considered. However, seismic rebound model can be used for the relatively small regions (Lomnitz and Nava 1983). In this context, other stochastic modeling techniques such as Markov model can be applied for the seismicity assessment of the small regions. This is in contrast to the Poisson model, which describes the dependency in a sequence of events. The Markovian property states that in the process accompanying a series of past events, the next event is only depend on current event and not on the previous ones. Many researchers have discussed the application of Markov chains for seismic hazard assessment. Following paragraph enlists the literature related to different stochastic modeling of earthquake process. This statistical approach is applied for the estimation of seismic hazards of the Northeastern India.

A number of probabilistic earthquake occurrence models are currently used for seismic hazard assessment. Among the most important ones are the Poisson models (Cornell 1968; Gardner and Knopoff 1974) and the Markov to semi-Markov models (Cluff et al. 1980; Herrera et al. 2006; Altinok and Kolcak 1999; Nava et al. 2005). It is observed that while the Poisson model applies to regions characterized by moderate frequent earthquakes, other models such as the Markov and semi-Markov models describe the sequences of events more adequately in regions with large infrequent earthquakes (Anagonos and Kiremidjian 1988). In the past, many researchers have suggested and emphasized the use of different models specific to different parts of the world with special focus on seismicity analysis. A few of them include the elastic-rebound model (Reid 1910; Richter 1958), seismic migration (Richter 1958; Mogi 1968) and the Markov models (Vere-Jones and Davies 1966; Knopoff 1971; Vagliente 1973; Veneziano and Cornell 1974; Lomitz-Adler 1983; Patwardhan et al. 1980), the time predictable or slip predictable model (Shimazaki and Nakata 1980), the seismic gap concept number (Fedotov 1965; Mccann and Nishenko 1979; Kagan and Jackson 1991) and Poissonian seismicity models (Brillinger 1982; Lomnitz and Nava 1983). Many other statistical methods have also been reported in the literature which are link with pattern recognition (i.e., based on the detection of seismic spatiotemporal variations). An application of pattern recognition for seismicity analysis is presented by Keilis-Borok and Kossobokov (1990) where subjective weights are assigned to the past seismic activity in order to determine times of increased probability (TIP) for strong earthquakes. A similar study by Agnew and Jones (1991) reports that at short time scales, some large earthquakes are preceded by smaller earthquakes which occur in the zones very close to the source of the great event. A detail description about different stochastic models and their application in seismic hazard analysis is discussed in a review article by Anagonos and Kiremidjian (1988).

In addition, Tsapanos and Papadopoulou (1999) used a discrete Markov model in order to model the occurrence of great earthquakes. Nava et al. (2005) proposed Markov model on the basis of transition probabilities of seismicity patterns. There is a growing literature on the application of different stochastic models for earthquake data analysis and pitfalls. In particular, Markov models have been used in many earthquake-related problems such as earthquake prediction (Di Luccio et al. 1997; Console 2001; Console et al. 2002), modeling seismic aftershocks and foreshocks (AI-Hajjar and Blanpain 1997; Felzer et al. 2004) and cluster analysis of earthquake catalogs (Ebel et al. 2007; Wu 2011). Several authors have also used semi-Markov models for earthquake data analysis (Altinok and Kolcak 1999; Sadeghian 2012; Votsi et al. 2012). A recent study by Alvarez (2005) describes the application of Weibull semi-Markov process through a new parametric estimation method. Later on, Garavaglia and Pavani (2009) presented a similar type of study based on a mixture of exponential and Weibull distribution for seismicity analysis. However, these papers do not discuss much on analysis and evaluation of obtained results. Patwardhan et al. (1980) discussed some advantages of semi-Markov models in comparison with other models with proper explanation. The assessment of usefulness and suitability of different stochastic model to different regions is progressively examined and reported by many researchers (Anagonos and Kiremidjian 1988; Herrera et al. 2006; Votsi et al. 2012). Recent application of Markov models and other statistical techniques for the seismic hazard analysis of Turkey is reported by Ünal et al. (2014). However, observation from past literature suggests that it is very difficult to answer that which is the best model among all stochastic models used for seismic hazard analysis (Anagonos and Kiremidjian 1988). The suitability of the Markov models for earthquake occurrence analysis can be explained due to the fact that the energies accumulated under faults are freed when an earthquake occurs; the time and magnitude of the earthquake within a specified region depend on the previous earthquake in the region. Some advantages of Markov models are relatively easy to derive (or infer) from successional data and modest computation requirement, and it does not require deep insight into the mechanisms of dynamic change; however, essential parameters of dynamic changes are described in transition probability matrix. Moreover, it has been noted that the transition probabilities (i.e., transitions from one state to other) in Markov models are difficult to obtain from limited data. Such models are primarily suitable to plate boundaries and characterized by high seismic activity (Anagonos and Kiremidjian 1988). Present study is focused to analyze seismicity of Northeast (NE) India which is a seismically one of the most active regions. High seismicity in the NE India is due to its location at the boundary of Indian and Eurasian plates.

In the present study, two Markov models are used to estimate the long-term and short-term predictions of a seismically active region in the temporal domain. Further, these models are applied to NE India. Finally, the limitations of the models are discussed in the context of incomplete datasets. It is also valuable in earthquake prediction to determine the occurrence probability of major earthquakes by making use of data obtained from precursory phenomena up to the time of the evaluation. In this study, the time evolution of the state determined by earthquakes and precursory phenomena was modeled using Markov chains. Various probabilities suitable for earthquake prediction were derived from the transition probability of the Markov chain with a chosen length of memory time. Earthquake time series data from 1897 to 2009 in NE India have been used for stochastic generation of occurrence of future large earthquakes using the transition matrix approach of the Markov chain process.

Study area is shown over the seismic zonation map of India in Fig. 1. This article is structured in total six sections. A detailed literature review on related topics is discussed in the introduction section (i.e., Sect. 1). Section 2 describes the tectonic and seismic activity in the study area followed by seismicity data description, and source zones identification is presented in Sect. 3. Detailed methodological description is presented in Sect. 4. Results and discussion are described in Sect. 5, and finally, paper is concluded in Sect. 6.

Fig. 1
figure 1

Map showing the four seismic zones of India (after IS: 1893 (part I) 2002). The NE India lies in the seismic zone V. Study area is marked in the black box

Full size image

2 Study area and its seismotectonic setting

In the present study region, NE India covers the area between 20°N and 31°N latitudes and, 85°E and 97°E longitudes (Figs. 1, 2). The Northeastern India is one of the seismically most active regions of the world. According to the Seismic Zonation Map of India (SZMI) published by Bureau of Indian Standards (BIS, IS: (Part 1) 2002), the present study region lies in the highest zone V (Fig. 1).

Fig. 2
figure 2

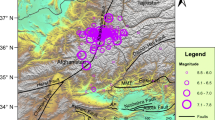
The seismotectonic setup of the Northeast (NE) India. DF Dhubri Fault, JGF Jangipur-Gaibandha Fault, DBF Debagram-Bogra Fault, PF Pingla Fault, EHZ Eocene Hinge Zone, MCT Main Central Thrust, MBT Main Boundary Thrust, MFT Main Frontal Thrust, NT Naga Thrust, DT Disang Thrust, DF Dauki Fault, KF Kulsi Fault, DhF Dudhnoi Fault, SF Sylhet Fault, LT Lohit Thrust, DKF Dhansiri Kopili Fault, MT Mishmi Thrust, KNF Katihar-Nailphamari Fault, TF Tista Fault, MaT Mat Fault, SSF Shan-Shagaing Fault, EBTZ Eastern Boundary Thrust Zone (modified after GSI 2000; after Vaccari et al. 2011; Mohanty et al. 2013)

Full size image

Global Seismic Hazard Assessment Programme (GSHAP) also demarcated the Northeast Indian region in the high seismic risk zone with expected peak ground acceleration (PGA) of the order of 0.35–0.4 g (Bhatia et al. 1999). The occurrence of three great earthquakes like 1897 Shillong plateau earthquake M = 8.7, 1934 Bihar Nepal earthquake with M = 8.3 and 1950 Upper Assam earthquake M = 8.7 signifies the possibility of great earthquakes in future from this region. The significant tectonic features of these regions are Eastern Himalaya region, Shillong plateau and Mikri hills, Arakan-Yoma subduction zone, Brahmaputra valley and Bengal basin [Geological Survey of India (GSI), 2000) (Fig. 2).

The complex Himalayan structure consists of the Main Central Thrust (MCT), the Main Boundary Thrust (MBT), Main Frontal Thrust (MFT) and their subsidiary thrusts, faults, folds and minor lineaments. An oblique subduction is found in the Burmese arc (Nandy 2001). The Indo Myanmar arc is sidelined with Patkoi–Naga–Manipur–China hills and marked by the Arkan Yoma region forming the eastern boundary thrust. The structures of the Himalayan arc and the Indo Myanmar arc connect to form the Assam syntaxis. The Assam syntaxis outlined with Mishmi thrust, Lohit thrust, Po Chu Fault and Tidding suture forms a prominent tectonic intricacy. The Shillong plateau and Mikir Hills constitute the western portion of the region. The Assam valley zone or the Brahmaputra basin lies on the Northern side edged by the Naga thrust on the south eastern flank. Kopili Fault is etched on middle of the Brahmaputra basin. Dauki Fault underlined the Shillong plateau from the south. The high seismicity of the region is accounted by the presence of different activities of thrusting and strike slip. Major earthquakes in the NE Indian region are listed in Table 1 which indicates the seismotectonic implications of the region.

Table 1 List of major earthquakes (M w  ≥7) in the study region (NE India)
Full size table

3 Database and source zoning

For the assessment of the occurrence of earthquakes in the study region, a composite catalog of NE India has been prepared for the period 1897–2009. Earthquake catalog has been compiled from different sources for the study region with M w >3. The completeness of the catalog is analyzed using Gutenberg–Richter frequency magnitude relation (Kramer 1996), where cutoff magnitude is estimated at 4. The sources for earthquake catalog include United States Geological Survey (USGS), International Seismological Center (ISC), Harvard Seismology (Dziewonski et al. 1981; Ekstrom et al. 2005), Indian Meteorological Department (IMD), Bapat et al. (1983) and Chandra (1992). Different sources report earthquakes in different magnitude scales, and all magnitudes have been converted to moment magnitude (M w ) using universal relationships (Scordilis 2006; Hanks and Kanamori 1979) as in Mohanty et al. (2014) and Mohapatra et al. (2014). In addition, declustering (removal of aftershock and foreshock) has been carried out to have independent events only (Knopoff and Gardner 1972; Gardner and Knopoff 1974). Seismicity distribution and annual occurrence of earthquakes are shown in Figs. 3 and 4, respectively. It can be observed that the data prior to 1960 are less compared to post 1960 which is obvious. Based on the quantitative analysis of seismicity, it is decided to use the entire data that are available in the first model, while for the second model, only data post 1960 are used. This decision is based on the kind of qualities, on which two models are designed to calculate. Several moderate-to-large earthquakes can be seen from the seismicity plot shown in Fig. 3, and it clearly reveals the high seismic activity of the region.

Fig. 3
figure 3

Three source zones [Zone 1 Arakan-Yoma Zone (AYZ), Zone 2 Himalayan Zone (HZ), and Zone 3 Shillong Plateau Zone (SPZ)] of NE India show intense earthquake activity for the period 1897–2009

Full size image
Fig. 4
figure 4

Recorded earthquake magnitudes versus their year of occurrence

Full size image

The seismicity map shows that most of the events fall in the tectonic domains of Eastern Himalaya, Assam shelf and Meghalaya plateau of the region. Based on seismicity and tectonic characteristics, the study area is divided into three source zones (Fig. 3), namely Zone 1: Arakan-Yoma Zone (AYZ), Zone 2: Himalayan Zone (HZ) and Zone 3: Shillong Plateau Zone (SPZ). Similar zoning has also been adopted by Mohanty and Walling (2008a, b) and Mohapatra et al. (2014). The Arakan-Yoma Range is characterized by the subduction zone, developed by the junction of the Indian Plate and the Eurasian Plate. It shows a dense clustering of earthquake events and the 1908 eastern boundary earthquake. The Himalayan tectonic zone depicts the subduction zone and the Assam syntaxis. This zone consists of two important thrust of the Himalayan region such as MCT and the MBT. The 1950 Assam earthquake, 1934 Bihar earthquake and the 1951 Upper Himalayan earthquake all with M w >8 are the major earthquakes from this zone (Seeber and Armbruster 1981). The 1897 Shillong earthquake occurred with M w >8.5 in the Shillong Plateau zone area, and it shows the prominent tectonic feature, the Dauki Fault (Chen and Molnar 1990) and major portion of the Eocene Hinge Zone (EHZ).

4 Methodology and analysis

A Markov is characterized by discrete states and time intervals in which the successive state occupancy is governed by a transition probability (Patwardhan et al. 1980). Many natural processes, for instance, day-to-day changes in weather, are Markovian. The use of the Poisson process to interpret the earthquake occurrences is still debatable (Knopoff 1964; Singh and Sanford 1972; Smalley et al. 1987; Wang and Kuo 1998). The Markov processes can be used to describe the periodic behavior of earthquakes.

In Markovian estimation, the transition matrix represents the distribution of a Markov chain at the next step if its current state is given. In other words, it is the probability of going from ith to jth state (Howard 1971). The probability of going from ith to jth state in r steps is

$$p^{r} (i,j) = P(X_{n + r} = j|X_{n} = i)$$
(1)

where \(p^{r} (i,j)\) is not the same as the rth power of p(i, j), and it is independent of n.

Moreover, the r-step transition probabilities are also independent of the past, i.e.,

$$P(X_{n + r} = j|X_{n} = i,X_{n - 1} = i_{n - 1} , \ldots ,X_{0} = i_{0} ) = P(X_{n + r} = j|X_{n} = i)$$
(2)

4.1 Basic postulates of a Markov model for earthquake prediction

The Markov models used for earthquake prediction work provide two important fundamental postulates:

  1. 1.

    The sequence of occurrences of earthquakes in a particular area is a stochastic process in time.

  2. 2.

    A stochastic process has Markov property such that the conditional probability distribution of future states of the process, for given present state and all past states, depends only upon the present state and not on any past states, and it is conditionally independent of the past states.

4.2 Explanation of the two Markov models

The present work discusses two models, one for the prediction of a large earthquake within a definite time span in the future and another model for the prediction of earthquakes falling within different magnitude ranges, just following an earthquake whose magnitude is known.

4.2.1 Model 1 for estimation of at least one large earthquake within a finite period

The first step in this model is to create class intervals of earthquake magnitudes, which should be properly chosen, so that ideally there is no such class for which there is not even a single earthquake with magnitude falling within its range. For example, choosing classes with magnitude ranges less than the minimum earthquake magnitude or greater than the maximum earthquake magnitude, than that is recorded in the available data, will be a meaningless class. The classes that have been chosen for this study, consistent with the data, are (M < 5), (5 ≤ M < 6), (6 ≤ M < 7) and (M ≥ 7) (see Table 2). Next, the total time length L, of which the dataset consists of, is divided into equal time intervals. If N be the total number of time intervals, and Δt be the time interval, then

$$N = L/\varDelta t$$
(3)
Table 2 Magnitude classification for state analysis
Full size table

In each time interval, there will be either no earthquake recorded, or a finite number of them. The earthquake with the highest magnitude, in each time interval, is selected. If there are no earthquakes recorded in a particular time interval, then the highest magnitude in that interval is taken to be “zero.” A state is then assigned to that interval depending upon which class interval, as already defined, the magnitude belongs to the corresponding states will be numbered 1, 2, 3 and 4 (see Table 2).

Continuing in the above way for all the N time intervals, the Markov chain is built up. Each element can assume an integer value from the set S = {1, 2, 3, and 4}. One can then use this Markov chain to create the transition probability matrix P (4 × 4), where the matrix element corresponding to ith row and jth column is denoted by p ij .

p ij is defined as the transition probability from state i to state j, where i and j are state variables belonging to S. p ij is calculated in the following manner.

$$p_{ij} = \frac{{{\text{Total}}\,{\text{number}}\,{\text{of}}\,{\text{transitions}}\,{\text{from}}\,{\text{state}}\,i\,{\text{to}}\,{\text{state}}\,j}}{{{\text{Total}}\,{\text{number}}\,{\text{of}}\,{\text{transition}}\,{\text{from}}\,{\text{state}}\,i}}$$
(4)

where \(\sum\nolimits_{j = 1}^{4} {p_{ij} = 1}\).

The matrix P is the most important quantity for all further analysis. The next task will be to choose an earthquake magnitude for the area under analysis, above which all earthquakes are to be considered damaging. Again, this has to be done very carefully as choosing a magnitude higher than the highest recorded earthquake will be meaningless. Similarly, choosing a magnitude too low will put even the smallest of earthquakes in the risk category, thereby rendering this method useless. In this study, the magnitude of 6.0 is taken as the lower limit for a destructive earthquake.

The transition probability matrix P is used to follow the evolution of the system through successive intervals of time. Here, an assumption is invoked that the occurrences of earthquakes can be modeled as a Markov process. Thus, it is possible to calculate the probability of occurrence of a particular state in a particular time interval in the future, if the present state is given. Suppose it is required to predict the system over n time intervals, then it means that the total time for which the prediction is being made is nΔt. Again if the initial state is i(0), the probability X that the system will evolve through the following sequence of n states denoted by Y = {i(1), i(2), …, i(n)} is given by

$$X = \, \left( {p_{i\left( 0 \right)i(1)} } \right)\left( {p_{i\left( 1 \right)i(2)} } \right)\left( {p_{i\left( 2 \right)i(3)} } \right) \ldots \left( {p_{{i\left( {n - 1} \right)i(n)}} } \right)$$
(5)

where the elements of set Y belong to the set S.

The probability of occurrence of at least one damaging earthquake over n time intervals is denoted by H, and the probability of occurrence of no damaging earthquake over n time intervals is denoted by H C.

Then,

$$H = 1\hbox{-}H^{C}$$
(6)

Then, the task reduces to compute H C. If no damaging earthquake is to occur over n time intervals, then it implies that the system is free to evolve through all those possible states where the highest permissible earthquake magnitude is below the limit set as damaging. It means that, the elements of set Y are no longer free to assume any value from set S. Instead, they can only assume the values 1 and 2, in this particular study. Thus, in this case

$$H^{c} = \sum\limits_{i(1) = 1}^{2} {\sum\limits_{i(2) = 1}^{2} { \cdots \sum\limits_{i(n) = 1}^{2} X } }$$
(7)

Hence, the probability of occurrence of at least one damaging earthquake within a total time of nΔt, the initial state being given (state 1 in this case), is estimated.

4.2.2 Model 2 for forecasting earthquake probabilities of different magnitude ranges following an earthquake

The first part of this model is similar to the previous model. It involves proper choice of class intervals of earthquake magnitudes. The classes that have been chosen for this study are (M < 5), (5 ≤ M < 6), (6 ≤ M < 7) and (M ≥ 7), but the process of building up the Markov chain is different in this case. Each earthquake is considered and categorized into the class to which it belongs. Accordingly, each earthquake is assigned a state, consistent with the last model (see Table 2).

Hence, in this case, the length of the Markov chain is equal to the total number of recorded earthquakes. As discussed before, each element can assume an integer value from the set S = {1, 2, 3, 4} and similar to the previous model, the Markov chain is used to create the transition probability matrix P, with elements corresponding to ith row and jth column denoted by p ij . p ij denotes the transition probability from state i to state j. It is calculated in the similar manner as in Eq. 1.

Given the state of the last earthquake in the area, one can predict the chances of occurrences of earthquakes belonging to the different magnitude classes which would follow immediately after it. It should be noted that this model cannot give an upper bound to the time of occurrence of the following earthquake. The matrix given above is a N × N transition probability matrix P with elements p ij , and it represents the N 2 transition probabilities that describe a Markov process.

To calculate the probability of occurrence of a state j, the probability is being denoted by X (i(r) = j), at the rth stage of evolution in the future, where the initial state being is i(0). Now it is required to calculate the probability of its evolution through any arbitrary sequence of states of length r.

Let this sequence be \(Y^{{\prime }} = \{ i^{{\prime }} \left( 1 \right),i^{{\prime }} \left( 2 \right), \ldots , \, i^{{\prime }} \left( {r - 1} \right), \, j\}\)

The probability X’ that the system will evolve through this sequence of r state is

$$X^{{\prime }} = \left( {p_{{i\left( 0 \right) \, i^{{\prime }} (1)}} } \right)\left( {p_{{i^{{\prime }} \left( 1 \right) \, i^{{\prime }} (2)}} } \right)\left( {p_{{i^{{\prime }} \left( 2 \right) \, i^{{\prime }} (3)}} } \right) \ldots \left( {p_{{i^{{\prime }} \left( {r - 1} \right) \, j}} } \right)$$
(8)

Therefore, X(i(r) = j) is given by the sum of X′ over all possible sequences of length r terminating with state j.

$$X\left( {i\left( r \right) \, = \, j} \right) = \sum\limits_{i'(1) = 1}^{4} {\sum\limits_{i'(2) = 1}^{4} \ldots \sum\limits_{i'(r - 1) = 1}^{4} {X^{\prime } } }$$
(9)

As it is evident that when r = 1, Eq. (9) reduces simply to Eq. (7).

In addition, analysis of the uncertainties in the transition probability values and robustness of the model are carried out. To find the robustness of the model to uncertainties in the transition probabilities, we have changed the transitional probability values by a maximum of ±5 %, while ensuring that the row sums of the transition probability equal to 1. A precise flowchart describing the steps involved in the present study is shown in Fig. 5.

Fig. 5
figure 5

Flowchart representing the steps involved in the present study

Full size image

5 Results and discussion

5.1 Model I

In the present study, the earthquakes of M w  ≥ 6.0 are considered as potentially damaging earthquakes for all the three zones. The time interval ∆t is fixed as 0.5 years. The probability of occurrence of at least one damaging earthquake within a period of 0.5, 1, 1.5 years, and up to a period of 25 years for each zone has been estimated. The obtained results are presented in Fig. 6. It is clear that H values for the Arakan-Yoma zone (Zone 1) show the highest probability of occurrence of at least one earthquake (M > 6) in comparison with the other two zones. It reaches a value of 0.8 within 2 years, 0.9 within 3 years and 0.96 within 4 years of elapsed time from the last recorded data in that zone. It indicates that Zone 1 has a very high risk of experiencing a damaging earthquake in the near future. On the other hand, the Shillong Plateau (Zone 3) shows a slow rate of increment in the H values. It only reaches 0.7 at 15 years and 0.9 after the end of 25 years. Thus, this region has less risk than other two regions of experiencing a damaging earthquake within a considerable period of time in the future.

Fig. 6
figure 6

Plots of predicted H values versus the number of years elapsed since the last occurrences of M w  >6 for all the three zones

Full size image

The Himalayan zone (Zone 2) shows a much higher rate of increment in H values, which is comparable to the Arakan-Yoma zone, although it is slightly less. The risk faced by the Shillong Plateau (Zone 3) can be best termed as “moderate,” with the H value taking almost 15 years to reach 0.7. All the three lines in Fig. 6 should theoretically approach H = 1 asymptotically and that is coming clearly in present case (Fig. 6). The line for Zone 3 will also eventually do so, but the time taken in this case to achieve the desired is outside the scales set in the graph. The results obtained give a very clear picture of the relative seismicity of the three zones. Consequently, it is possible to get an idea about the long-term seismic risks faced by each of the three zones under analysis.

5.2 Model II

In this analysis, the post 1960 earthquake data have been used for Zones 1 and 2; however, for Zone 3, the data after 1980 is used. The earthquake magnitude classification is same as discussed in the previous model I (see Table 2). Given the magnitude of the last recorded earthquake in a region, model II can be used to estimate the probabilities of the successive earthquake which will fall in different magnitude classes. The results obtained by applying the model II for all three zones are shown in Table 3.

Table 3 Transition probabilities of earthquake falling within different magnitude ranges for the three zones: (a), (b) and (c) corresponding to the transition matrices for Zone 1, Zone 2 and Zone 3, respectively
Full size table

For all the three regions, the p 1j values show a decreasing trend with the highest value for j = 1 and the lowest for j = 4. This is completely in agreement with the fact that a low-magnitude earthquake (State 1) is the most likely to be followed by another low-magnitude earthquake and is the least likely to be followed by a very high magnitude earthquake, for all the three zones.

The p 2j values are showing slightly different behavior. The p 22 value is greater than the p 21 value for the Zones 1 and 2, and going up very slightly for Zone 1 and Zone 2. However, for Zone 3, the p 21 value is greater than the p 22. After that the p 2j values decline rapidly to a small value for j = 3, for all the zones and decrease further for j = 4. This suggests that if any of the zones experience a State 2 earthquake, then it is most likely to be followed by another State 2 or a State 1 earthquake. The chances of State 2 are slightly more than State 1 in Zones 1 and 2; however, it is different for Zone 3. The chances that a State 3 or a State 4 earthquake will follow a State 2 earthquake are very low for all the three zones.

The p 3j values are even more interesting, and they reflect a few important things. They decrease rapidly for all zones from j = 2 to j = 4, except for Zone 3 where it remains constant while going from j = 1 to j = 3 (for post 1980 data in Zone 3). But while going from j = 1 to j = 2, they become twice for Zone 1 and remain constant for Zone 2 and Zone 3. However, the increase in p 32 value for Zone 1 can easily be explained by the unusually high seismicity of the area, predicted using model 1.

As far as the p 4j values are concerned, there are no State 4 earthquakes recorded in Zone 2 (in post 1960 data) and Zone 3 (in post 1980 data). Hence, for these two zones, p 4j is 0 for j = 1, 2, 3, 4. In Zone 1, p 4j  = 0.33 for j = 1, 0.67 for j = 2 and 0 otherwise, which are perfectly reasonable. This means that in Zone 1, a State 4 earthquake will most likely be followed by a State 2 earthquake or a State 1 earthquake, but no State 3 or State 4 earthquakes. The probability of State 2 earthquake follow is twice the probability of State 1 earthquake.

In addition, we have analyzed the variation of a particular p ij with number of steps (r = 10). The obtained results show the Markov chain to be ergodic; i.e., \(\mathop {\lim}\nolimits_{r \to \infty} p_{ij}^{(r)} = \pi_{j}\), where the π j elements (independent of i) are known as stationary probabilities, that depend on the relative occurrence ratios of the states. For example, results (i.e., values of p ij for i = 1 and j = 1) for each step for Zone 1 are shown in Fig. 7, where it can be seen that the probability values approach their limiting values. The accuracy of the two models is highly limited by the length of the dataset. This is mainly due to the fact that the process is being modeled by its very random nature and hence unpredictable with complete accuracy. The two models only aim to predict the results with a certain probability. It has already been stated beforehand that the two models are aimed at predicting two entirely different quantities. Hence, the underlying methodologies of the two models are different too. This difference determines to what extent the accuracy of each method will depend on the accuracy and length of the available data. These aspects are briefly discussed below.

Fig. 7
figure 7

Variation in the values of transition probability (p 11) with respect to number of steps (r) for Zone 1

Full size image

The first model is aimed at calculating the probability of occurrence of at least one major earthquake within a definite period of time in the future. In this study, it has been tried to achieve a prediction over a time length of the earthquake data. Hence, in a way it was required, due to the constraints to use whatever data were available also before 1960. It turns out that the accuracy of the results obtained using this model is less susceptible to data incompleteness. It is because incompleteness in a way leads to a much smaller length of data prior to 1960 compared to that recorded later. Another motivation for doing it is that, because the data before 1960 records earthquakes only magnitude above 5, on an average, there will be quite large gaps between recorded data points. Hence, if Δt is chosen carefully, one can fill in the gaps with multiple states of 1, which is with low-magnitude earthquakes, and there by averaging out the effects of having only large magnitude earthquakes. In this work, Δt was taken to be equal to 0.5 years. However, one must not forget that this is merely an approximation equivalent to any other standard data completeness technique. Better results can be obtained if better methods are employed to complete the gaps in the data. In this study, all that has been tried is to make a qualitative prediction of a large earthquake hitting the area under consideration in the long run. Hence, the inaccuracies that creep in due to data incompleteness are not so important because their effects are averaged out in the long run.

The second model on the other hand is much more sensitive to inaccuracies in the available data. It was initially tested with the entire data that was available, and it produced meaningless results. However, all such ambiguities vanished as soon as the model was tested with the post 1960 data for Zones 1 and 2, and post 1980 data for Zone 3. A plausible explanation for this is that this model tries to predict short-term behavior immediately following the occurrence of an earthquake falling in any arbitrary class interval as discussed previously. Hence, if the data are inaccurate or incomplete, this method will fail altogether. On the other hand, accurate and dense data will produce very good results. In other words, short-term predictions are highly sensitive to inaccuracies in the data because they do not get averaged out over small time scales.

In this study, analysis of uncertainties associated with the transition probability values and robustness of the model is presented for Zone 1. Steps involved in this analysis have been presented in Fig. 5.

Now, for example, P for Zone 1 is taken as (see Table 3):

$$P = \left[ {\begin{array}{*{20}c} {0.6955} & {0.2789} & {0.0231} & {0.0024} \\ {0.4668} & {0.5098} & {0.0215} & {0.0020} \\ {0.3125} & {0.6250} & {0.0625} & {0.0000} \\ {0.3333} & {0.6667} & {0.0000} & {0.0000} \\ \end{array} } \right]$$

Now, limiting multistep transition probability matrix, Φ (Howard 1971), is obtained as

$$\varPhi = \left[ {\begin{array}{*{20}c} {0.6005} & {0.3742} & {0.0232} & {0.0022} \\ {0.6005} & {0.3742} & {0.0232} & {0.0022} \\ {0.6005} & {0.3742} & {0.0232} & {0.0022} \\ {0.6005} & {0.3742} & {0.0232} & {0.0022} \\ \end{array} } \right]$$

As mentioned earlier, we have changed the transitional probability values by a maximum of ±5 %, while ensuring that the row sums of the transition probability equal to 1. Now, new transition probability matrix (say P′) is obtained as

$$P^{{\prime }} = \left[ {\begin{array}{*{20}c} {0.7104} & {0.2654} & {0.0220} & {0.0023} \\ {0.4901} & {0.4872} & {0.0208} & {0.0019} \\ {0.3281} & {0.6125} & {0.0595} & {0.0000} \\ {0.3495} & {0.6505} & {0.0000} & {0.0000} \\ \end{array} } \right]$$

Corresponding limiting multistep transition probability matrix, Φ′ (Howard 1971), is given by

$$\varPhi^{{\prime }} = \left[ {\begin{array}{*{20}c} {0.6236} & {0.3520} & {0.0223} & {0.0021} \\ {0.6236} & {0.3520} & {0.0223} & {0.0021} \\ {0.6236} & {0.3520} & {0.0223} & {0.0021} \\ {0.6236} & {0.3520} & {0.0223} & {0.0021} \\ \end{array} } \right]$$

Now, for robustness testing of the model, we have estimated the Mean Absolute Percentage Error (MAPE) between Φ (element of one row, i.e., limiting multistep transition probability vectors) and Φ′ (element of one row, i.e., limiting multistep transition probability vectors). It is obtained as ~4 %, which suggests that the error is very less, and hence, it can be concluded that obtained model is robust.

Moreover, we analyzed the robustness of the results by looking into the number of observations. The number of observations in each row of transition probability matrix P for Zone 1 is 821, 512, 33 and 3, respectively. As the occurrences of higher magnitude earthquakes are less, the worst-case possibility is with the occurrence of higher magnitude (M > 7). For example, the number of observations in the fourth row of transition probability matrix for Zone 1 is obtained as: p 4j  = [1 2 0 0]; i.e., for i = 4 and j = 1, 2, 3 and 4. Thus, the worst case may be possible as change from state 4 (i = 4, j = 1) to States 3 and/or 4 (i = 4, j = 3 and/or 4).

6 Conclusions

A probabilistic seismic hazard assessment based on the two first-order Markov models has been carried out for NE India. This approach is based on the data of past earthquake events over a long period time from 1897 to 2009. On the basis of the geology, active tectonics, homogeneous instrumental catalog, historical seismicity and three major possible seismic sources in NE India are identified. These major source zones are Zone 1: Arakan-Yoma Zone (AYZ), Zone 2: Himalayan Zone (HZ) and Zone 3: Shillong Plateau Zone (SPZ). Both the Markov models are applied to all the three source zones, and seismic hazard level is predicted for each of the zones. Model I predicts the long-term risks in the region of experiencing at least one major earthquake (M w  ≥ 6), and Model II predicts the immediate short-term risks which reflects that only the case r = 1 is considered. Moreover, analysis of the results obtained up to r = 10 is shown in Fig. 7, which suggests the probability values approach their limiting values.

In the present work, a comparative analysis of the predictions using the two Markov models has been performed. Model I predicts that Zone 1 is the most prone to experience a hazardous earthquake among all the three zones in the near future. The probability of it being hit by one dangerous earthquake is 0.8 for 2 years and 0.9 for 3 years of elapsed time from the last recorded data. Zone 2 also faces a similar risk but on the slightly lower side. The probability of it being hit by one dangerous earthquake is 0.7 for 3 years and 0.9 for 5 years of elapsed time. Zone 3 faces a moderate risk of being hit by a major earthquake. The results of this model are not correlated with those of model 2 beyond 5 years, because the later model essentially predicts the immediate short-term events. The predictions of model I shows Zone 1 is the most seismically hazardous zone, followed closely by Zone 2 and Zone 3.

Comparison of these results with that of Mohanty and Walling (2008a) shows that the findings are consistent. It is reported that the seismicity of Zone 1 is the highest followed by Zone 2 where as Zone 3 suffers less risk than Zone 1 and Zone 2. The results of model 1 also bear close resemblance with their predictions on the return periods of earthquakes of different magnitudes. The return periods predicted by Mohanty and Walling (2008a) for the three zones for 6 magnitude earthquake are roughly 0.7, 10 and 30 years, respectively. For a 6.5 magnitude earthquake, the return periods are roughly 1, 20 and 100 years, respectively, for the three zones. These results are completely in agreement with current results which achieve highest probabilities of occurrence of a dangerous earthquake for Zone 1, closely followed by Zone 2; however, the risk is less for Zone 3.

The results of Model I can also be compared with the findings of Mohanty and Walling (2008a) regarding the probabilities of occurrence of different magnitude earthquakes with different return periods of 50 and 100 years. The results show that the probabilities of occurrence 6 and above magnitude earthquakes decrease monotonically from Zone 1 to Zone 3. This is again consistent with the predictions of Model I in which it also achieved the same decreasing order for the three zones over a time period of 25 years. Hence, it can be concluded that the predictions of model I are correct under reasonable limits.

On the other hand, from the predictions of model II, it is found that p 14 = 0 and p 24 = 0 for all the zones except Zone I for which they have small values of 0.0024 and 0.0020, respectively. Although it is expected that these values will be small, nonzero values for Zone I confirm the prediction of the previous model that it is indeed the seismically most active region among all the three zones. As far as Zone 3 is concerned, p 4j  = 0 for state j = 1, 2, 3, 4 means that there was not even a single State 4 earthquake recorded in these zones. This again confirms the relatively low seismicity of these two regions as predicted by the last model. However, model I also predicted 98.9 % chance that Zone 2 will experience at least one major earthquake (State 3 or State 4) within 10 years. The complete absence of any State 4 earthquake over 48 years, in this region, thus requires an explanation. It is clear from Table 3 (Zone 2) that State 3 earthquakes have been recorded in Zone 2, as p 3j  ≠ 0 for j = 1, 2, 3. Hence, it leads to the prediction that Zone 2 is more susceptible to seismic hazards for State 3 earthquakes (magnitude range 6–7), than from State 4 earthquakes (magnitude range ≥7). The duration without experiencing any State 4 earthquake for Zone 2 has also been investigated through model I. To do this, the probability of occurrence of at least one State 4 earthquake in this zone within 5, 10, 15…up to 50 years was calculated, keeping the same Δt = 0.5 years and using the entire dataset available for the zone. The results are presented in Table 4.

Table 4 Probability of at least one State 4 earthquake in Zone 2
Full size table

The results in Table 4 clearly reveal that the probability that Zone 2 will experience at least one State 4 earthquake is only 0.76 in 25 years. It goes up to 0.9 in 40 years and 0.93 in 45 years, which is roughly the length of the time interval for the data that were available after 1960 for this zone. This essentially means that the probability that Zone 2 will experience at least one State 4 earthquake within roughly 50 years is quite high. Hence, the total absence of any State 4 earthquake in Zone 2 over the last 48 years makes it especially vulnerable to the same (M w  ≥7) in the immediate vicinity.

The results of Model II are also consistent with the findings reported by Mohanty and Walling (2008a). Their histograms of earthquake distribution of different magnitude ranges for the three zones show that the number of earthquakes of magnitude 5 is the highest for all the three zones. The number comes down significantly for magnitude 6 earthquakes; while for magnitude 7 earthquakes, only Zone 1 has a few recorded events and for other zones, they are virtually nonexistent. For magnitude 8 and higher earthquakes, there is no recorded event for any of the zones. These explain, to a great extent, the very low transition probabilities for the higher magnitude earthquakes as predicted by Model II.

From the comparative study of both Markov I and Markov II models, a qualitative conclusion can be drawn that Markov I model has an advantage over using Markov II model as the former is least affected by the uncertainties in the recording of smaller magnitudes which are very common in pre-instrumental earthquake catalogs. It is better to use Markov I model in seismic hazard assessment because it deals with higher magnitude earthquakes which generally cause extreme destruction at the site. Nevertheless, both the Markovian models used in this context yield satisfactory results for NE India.

In the present study, the accuracy of the results obtained by Markov models is tested by analyzing the uncertainties in the values. The error values are in the acceptable range. A recent study by Ünal et al. (2014) also suggests that the results obtained using Markov model are superior to those from null hypothesis (i.e., that the system is memory-less and behaves in a Poissonian way).