1 Introduction

The frequency-size distribution of earthquakes has attracted interest from many researchers starting with its first discussion by Ishimoto and Iida (1939) followed by Gutenberg and Richter (1944) which is one of the most common magnitude–frequency relations used in seismology. The Gutenberg–Richter law is effective with high accuracy for small and moderate magnitudes, but for small space–time volumes provides highly uncertain and sometimes unstable estimates because of the power-law character of the earthquake size distribution and insufficient instrumental and historical earthquake records for relatively small seismic regions (McCaffrey 1997; Holt et al. 2000). The law depends on the size of the catalogue and reveals no information about maximum magnitude.

The largest earthquake in a region is an important parameter in earthquake hazard assessment and disaster management. These large events contribute significantly to the total deformation, and the long return period events with low probability of occurrence are not easily captured by the classical distributions. The seismic hazard assessment exercises may fail to capture the very long return period events due to relatively short catalogue data available and may fail to model the tail portion of the occurrence models, for example with a Poisson model. The general methodologies to assess the largest magnitude are based on a seismotectonic modelling using past earthquake data and tectonics of the region. The absence of a well-documented earthquake cycle is a considerable impediment to quantifying seismic risk correctly. It is thus of special importance to develop statistical methods that analyse as closely as possible the range of its extreme values or the tail of the distributions in addition to the whole of the distributions. Several investigations (Bird and Kagan 2004; Cosentino et al. 1977; Kagan 1991, 1996, 1999, 2002a, b; Kijko and Sellevoll 1989, 1992; Knopoff et al. 1982; Main et al. 1999; Ogata and Katsura 1993; Pisarenko and Sornette 2003, 2004; Utsu 1999; Wu 2000; Pisarenko and Rodkin 2007) were conducted in the past for finding a suitable description of the tail of the magnitude frequency distribution. For the large event distribution Pacheco and Sykes (1992) suggested visual inspection, Sornette et al. (1996) pointed out Monte-Carlo simulations, Kagan (1997, 1999) and Kagan and Schoenberg (2001) suggested Maximum likelihood estimation of the proposed Pareto distribution tapered by an exponential distribution. Several parametric families, such as Gamma distributions (Main and Burton 1984; Kagan 1994, 1997), modified Pareto distribution (Kagan and Schoenberg 2001) and Weibull distributions (Laherrere and Sornette 1998) were suggested for earthquake moment distributions including the tail range, but none of these models could be universally accepted. One of the best known modifications of the G–R distribution (Kagan 1997; Kagan and Schoenberg 2001; Bird and Kagan 2004) was multiplication of the power law distribution of seismic moments (which corresponds to the modified G–R distribution of magnitudes) by an exponential taper.

To look into the behaviour of large events the Himalaya region has been taken as a case study. The Himalayan tectonic zone, where Indian plate drives under the Eurasian plate, rapidly releases strain over large areas generating great earthquakes with long intervals. The Himalayan arc extends over a distance of about 2900 km and has experienced five great earthquakes (1505, 1803, 1897, 1934 and 2015) with magnitudes exceeding 8 (M w) and numerous magnitudes 7 (M w). In the present study, theoretical distributions of earthquake size, especially dealing with large return periods of earthquakes, have been considered for testing various distributions.

1.1 Seismic Hazard Assessment Approaches

The distribution of earthquake magnitude in a given period of time can be described by a recurrence low. The following section describes the classical approach using the G–R distribution along with three of the probability distributions being used in the present study namely: Pareto, Truncated Pareto, and Tapered Pareto distributions.

1.2 Classical Approach

The classical approach relates the cumulative occurrence rate of earthquakes. Usually the G–R distribution indicated a linear relationship on a log linear plot between earthquake magnitude M and the total number of events N(M) greater than equal to M. The completeness is considered with bounded G–R distribution. If the catalogue completeness threshold is constant in time, we can analyse two distributions a temporal sequence of earthquake numbers and earthquake size. Usually the temporal distribution of the number of events follows memoryless distribution, i.e., all events are independent of other events (Molchan and Podgaetskaya 1973; Kijko and Graham 1998). The density function, n(M), defining the occurrence rate of earthquakes per unit magnitude at magnitude M can be defined as

$$ n(M)\; = \; - \frac{{{\text{d}}N(M)}}{{{\text{d}}M}} = N(M_{\hbox{min} } )\; \times \;\beta \; \times \;{\text{e}}^{{ - \beta \left( {M - M_{\hbox{min} } } \right)}} , $$
(1)

where M min is lower threshold magnitude and N(M min) is the cumulative rate of occurrence of earthquakes with magnitude M ≥ M min and β = b × ln 10 where b is the seismicity constant in the G–R distribution. In reality, the earthquake magnitude for a seismic source has to be characterised by an upper bound. Thus, a truncation of the density function of Eq. (1) is necessary in practical hazard analysis applications. The corresponding density function n(M) becomes

$$ n(M) = N(M_{\hbox{min} } )\; \times \;\beta \; \times \;{\text{e}}^{{ - \beta \left( {M - M_{\hbox{min} } } \right)}} H\left( {M_{\hbox{max} } - M} \right), $$
(2)

where H(·) is the Heaviside step function. To have correct number of earthquakes with magnitude greater than or equal to M min, this needs to be normalised by \( (1 - {\text{e}}^{{ - \beta (M_{\hbox{max} } - M_{\hbox{min} } )}} ) \)

$$ n(M)\; = \;\frac{{N(M_{\hbox{min} } )\; \times \;\beta \; \times \;{\text{e}}^{{ - \beta (M - M_{\hbox{min} } )}} H\left( {M_{\hbox{max} } - M} \right)}}{{1 - {\text{e}}^{{ - \beta (M_{\hbox{max} } - M_{\hbox{min} } )}} }}. $$
(3)

The corresponding cumulative distribution function is obtained as

$$ N(M)\; = \;N(M_{\hbox{min} } )\frac{{{\text{e}}^{ - \beta \; \times \;M} - e^{{ - \beta \; \times \;M_{\hbox{max} } }} }}{{{\text{e}}^{{ - \beta \; \times \;M_{\hbox{min} } }} - e^{{ - \beta \; \times \;M_{\hbox{max} } }} }}H(M_{\hbox{max} } - M). $$
(4)

In the relationship given by Eq. (4), the occurrence rate N(M) reduces exponentially to zero as M approaches M max, but the total number N(M min) of earthquakes with magnitudes greater than or equal to the threshold magnitude M min remains unaltered. This model is therefore termed as the modified Gutenberg–Richter or exponential recurrence model.

Some seismic sources are seen to produce more frequent earthquakes in a narrow range of magnitude around M max than that described by the exponentially decaying model of Eqs. (3) and (4). For such cases, characteristic recurrence model described by Aki (1983) and Schwartz and Coppersmith (1984) may be considered as more appropriate. Youngs and Coppersmith (1985) proposed the characteristic earthquake model for certain faults which experience the large earthquakes. The density function for the characteristics recurrence model can be defined as

$$ n\left( M \right) = \left\{ {\begin{array}{*{20}l} {N\left( {{\text{M}}_{ \hbox{min} } } \right)\beta {\text{e}}^{{ - \beta \left( {M - M_{ \hbox{min} } } \right)}} , } \hfill & {M_{ \hbox{min} } \le M \le M_{\text{ch}} } \hfill \\ {n_{\text{c}} = N\left( {M_{ \hbox{min} } } \right)\beta e^{{ - \beta \left( {M^{\prime } - M_{min} } \right)}} , } \hfill & {M_{\text{ch}} < M \le M_{ \hbox{max} } } \hfill \\ \end{array} } \right., $$
(5)

where \( M_{\text{ch}} = M_{ \hbox{max} } - 1 \) and \( M^{\prime } = M_{\text{ch}} - 0.5. \) The corresponding cumulative distribution function can be written as

$$ N\left( M \right) = \left\{ {\begin{array}{*{20}l} {N\left( {M_{ \hbox{min} } } \right)\left[ {e^{{ - \beta \left( {M - M_{ \hbox{min} } } \right)}} - {\text{e}}^{{ - \beta \left( {M_{\text{ch}} - M_{ \hbox{min} } } \right)}} } \right] + n_{\text{c}} } \hfill & {M_{ \hbox{min} } \le M \le M_{\text{ch}} } \hfill \\ {n_{\text{c}} \times \left( {M_{ \hbox{max} } - M} \right),} \hfill & {M_{\text{ch}} < M \le M_{ \hbox{max} } } \hfill \\ \end{array} } \right.. $$
(6)

The characteristic recurrence model is supported theoretically as well as by observations by Swan et al. (1980), Papageorgiou and Aki (1983) and others.

1.3 Pareto Distribution

The classical approach of Gutenberg and Richter (1944) shows a power-law decay of magnitude size. The Pareto distribution is used to describe a phenomenon which exhibit power-law decay of sizes above a minimum threshold size. The Pareto distribution (Coles 2001) is useful to study the tail of the distribution of the earthquake events with magnitude above a predefined threshold. The Pareto distribution allows fitting efficiently the seismic moment–frequency distribution only in the tail portion which contains reliable moment and occurrence times of the extreme largest events. Therefore, even an incomplete seismicity containing reliable seismic moment and times of the largest events becomes useful to estimate seismic hazard parameters together with the Pareto distribution (Kagan 1993).

Statistical tests of whether a Pareto or some other distribution best describes the tail of a given empirical distribution are discussed by Kagan (2002a) and Clauset et al. (2009). The earthquake magnitude is related to the scalar seismic moment M 0 as (Hanks and Kanamori 1979)

$$ M = \left( {\frac{2}{3}} \right)\log_{10} M_{0} - 10.7 , $$
(7)

where \( M_{0} = a \mu d \) expressed in dyne-cm units (where \( \mu \) is an average shear elastic coefficient of the crust, d is the average slip of the earthquake over a surface d of rupture). The G–R distribution translated from magnitude to seismic moment using Eq. (7) and the number \( N\left( {M_{0} } \right) \) of earthquakes with seismic moment above \( M_{0} \) becomes

$$ N\left( {M_{0} } \right)\sim M_{0}^{ - \beta } , $$
(8)

where β = 2/3 × b is the index parameter of the distribution. Introducing the appropriate threshold seismic moment \( M_{0t} \), one obtains the complementary of the distribution function of Pareto for seismic moments:

$$ \bar{F}\left( {M_{0} } \right) = \left( {\frac{{M_{0} }}{{M_{0t} }}} \right)^{ - \beta } ,\;\;M_{0t} \le M_{0} . $$
(9)

The Tails function \( \bar{F}\left( {M_{0} } \right) \) as having power-law tails. This description is especially useful when describing and modelling processes with large deviations, a situation where one is primarily interested in the largest possible observations. In seismology, the Pareto distribution describes the distribution of the seismic moment released in earthquakes as a power-law.

1.4 Truncated Pareto distribution

The Pareto distribution is unbounded; however, each seismic source zone can release only limited energy, implicating that the Pareto distribution must be modified for large seismic moments. This problem is solved by introducing an additional parameter called the maximum moment \( M_{0U} \) into the distribution. Anderson and Luco (1983) proposed a truncation from above at \( M_{0U} \) of either the cumulative distribution, or its density distribution.

For the Pareto distribution with truncation at both ends, the probability density is

$$ f\left( {M_{0} } \right)\; = \;\frac{{M_{0U}^{\beta } M_{0t}^{\beta } }}{{M_{0U}^{\beta } - M_{0t}^{\beta } }} M_{0}^{ - 1 - \beta } ,\;\; M_{0t} \le M_{0} \le M_{0U} , $$
(10)

and the Tail function is

$$ \bar{F}\left( {M_{0} } \right)\; = \;\frac{{\left( {{\raise0.7ex\hbox{${M_{0t} }$} \!\mathord{\left/ {\vphantom {{M_{0t} } {M_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${M_{0} }$}}} \right)^{\beta } - \left( {{\raise0.7ex\hbox{${M_{0t} }$} \!\mathord{\left/ {\vphantom {{M_{0t} } {M_{0U} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${M_{0U} }$}}} \right)^{\beta } }}{{1 - \left( {{\raise0.7ex\hbox{${M_{0t} }$} \!\mathord{\left/ {\vphantom {{M_{0t} } {M_{0U} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${M_{0U} }$}}} \right)^{\beta } }} ,\; \; M_{0t} \le M_{0} \le M_{0U} . $$
(11)

Similar considerations led to the use of the Tapered Pareto distribution by Jackson and Kagan (1999), Vere-Jones et al. (2001) and Kagan and Schoenberg (2001).

1.5 Tapered Pareto distribution

The Tapered distribution has an exponential taper applied to the cumulative number of events with seismic moment larger than \( M_{0} \). The corresponding Tail function becomes

$$ \bar{F}\left( {M_{0} } \right) = \left( {{\raise0.7ex\hbox{${M_{0t} }$} \!\mathord{\left/ {\vphantom {{M_{0t} } {M_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${M_{0} }$}}} \right)^{\beta } \exp \left( {\frac{{M_{0t} - M_{0} }}{{M_{0x} }}} \right),\;\; M_{0t} \le M_{0} < M_{0x} . $$
(12)

The corresponding probability density function is

$$ f\left( {M_{0} } \right)\; = \;\left[ {\frac{\beta }{{M_{00} }}\; + \;\frac{1}{{M_{0x} }}} \right]\left( {{\raise0.7ex\hbox{${M_{0t} }$} \!\mathord{\left/ {\vphantom {{M_{0t} } {M_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${M_{0} }$}}} \right)^{\beta } { \exp }\left( {\frac{{M_{0t} - M_{0} }}{{M_{0x} }}} \right), $$
(13)

where \( M_{0x} \) is the seismic moment for the largest earthquake event. Some researchers (Jackson and Kagan 1999; Vere-Jones et al. 2001; Kagan and Schoenberg 2001) have proposed that earthquake sizes may be well described by a Tapered Pareto distribution which has small exponential tails but is otherwise similar to the Pareto distribution.

2 Parameter estimation of distributions

In the present study, the parameters β and N(M min) of Eq. (4) are estimated using available data on past earthquakes. The parameter β for a part of the catalogue with the minimum magnitude of completeness M c can then be evaluated using the maximum likelihood method (Aki 1965; Utsu 1965) as \( \left( {\bar{M} - M_{\text{c}} } \right)^{ - 1} \) where \( \bar{M} \) is the average of all the available magnitudes greater than or equal to M C during the period of completeness. Kijko and Smit (2012) have extended the Aki-Utsu b value estimator for magnitude grouped data. If \( M_{\text{C}}^{1} ,{\kern 1pt} \;M_{\text{C}}^{2} , \ldots ,M_{\text{C}}^{S} \) are the minimum magnitudes of completeness for periods \( t_{1} ,\;t_{2} , \ldots ,t_{S} \) with number of events in various intervals as \( n_{1} ,\;n_{2} , \ldots ,n_{S} \), respectively, then the generalised Aki-Utsu \( \beta \)-value estimator is given by

$$ \beta = \left( {\frac{{r_{1} }}{{\beta_{1} }} + \frac{{r_{2} }}{{\beta_{2} }} + \cdots + \frac{{r_{S} }}{{\beta_{S} }}} \right)^{ - 1} , $$
(14)

where \( r_{i} = n_{i} /N \) with N as the total number of events in all the intervals of completeness and \( \beta_{i} \) is the classic Aki-Utsu estimator for ith interval. Kijko and Smit (2012) have given an expression for the maximum likelihood estimator of occurrence rate, \( N(M_{\hbox{min} } ) \) of events with magnitude equal to or greater than M min as

$$ N(M_{\hbox{min} } )\; = \;\frac{N}{{\sum\nolimits_{i = 1}^{S} {t_{i} \exp \left[ { - \beta (M_{C}^{i} - M_{\hbox{min} } )} \right]} }}. $$
(15)

If M min is the minimum magnitude of completeness for the entire duration of the catalogue, then there is only one interval with \( M_{l}^{1} = M_{\hbox{min} } \) and t 1 = T for which the relation of Eq. (15) gives \( N(M_{\hbox{min} } ) = N/T \), as expected.

Pareto distribution has one parameter β for estimation and the maximum likelihood estimator method has been used to estimate β. For Pareto distribution the log-likelihood function for n observations of the seismic moment is

$$ l_{o} = n\left[ {\beta \log \left( {M_{0t} } \right) + \log \beta } \right] - \left( {1 - \beta } \right)\mathop \sum \limits_{i}^{n} \log M_{0t} . $$
(16)

The maximum likelihood equation of \( \beta \) (Deemer and Votaw 1955; Aki 1965; Kagan 2002a) is

$$ \hat{\beta } = \frac{n}{{\mathop \sum \nolimits_{i}^{n} \log \left( {\frac{{M_{0i} }}{{M_{0t} }}} \right)}}, $$
(17)

with standard error \( \sigma_{\beta } = \frac{{\hat{\beta }}}{\sqrt n } \) The Pareto distribution has no upper limit of seismic moment and incorporates the maximum moment \( M_{0u} \) in Truncated Pareto distribution. For the Truncated Pareto distribution the log-likelihood function for n observations of the seismic moment is

$$ l_{o} = n\beta \log M_{0t} + n\log \beta - (1 + \beta )\log M_{0i} - \log \left( {1 - \left( {\frac{{M_{0t} }}{{M_{0u} }}} \right)^{\beta } } \right). $$
(18)

The maximum likelihood equation of \( \hat{\beta } \) for Truncated Pareto distribution (Kagan 2002a) is

$$ \frac{1}{{\hat{\beta }}} - \frac{{\log \left( {M_{0u} /M_{0t} } \right)}}{{\left( {M_{0u} /M_{0t} } \right)^{{\hat{\beta }}} - 1}} - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \log \left( {\frac{{M_{0i} }}{{M_{0t} }}} \right) = 0. $$
(19)

β value is estimated by solving it iteratively. The standard error of \( \hat{\beta } \) equation is

$$ \sigma_{\beta } = \frac{{1 - \left( {M_{0t} /M_{0u} } \right)^{\beta } }}{{\sqrt {n\left[ {\left( {1 - \left( {M_{0t} /M_{0u} } \right)^{\beta } } \right)^{2} \hat{\beta }^{ - 2} - \left( {M_{0t} /M_{0u} } \right)^{\beta } \left( {\log \left( {M_{0u} /M_{0t} } \right)} \right)^{2} } \right]} }}. $$
(20)

To estimate \( M_{0u} \), Pisarenko (1991) and Kijko and Graham (1998) proposed a method based on statistical moment of Truncated Pareto distribution which is

$$ \hat{M}_{0u} = M_{0n} \left\{ {1 + \frac{1}{n\beta }\left[ {\left( {M_{0n} /M_{0t} } \right)^{\beta } - 1} \right]} \right\}. $$
(21)

The log likelihood equation of Tapered Pareto distribution is

$$ l_{o} = n\beta \log M_{0t} + \frac{I}{{M_{0x} }}\left( {nM_{0t} - \mathop \sum \limits_{i = 1}^{n} M_{0i} } \right) - \beta \mathop \sum \limits_{i = 1}^{n} { \log }M_{0i} + \mathop \sum \limits_{i = 1}^{n} { \log }\left( {\frac{\beta }{{M_{0i} }} + \frac{1}{{M_{0x} }}} \right). $$
(22)

Maximum likelihood equations of \( M_{0} \) x and \( \beta \) for Tapered Pareto distribution are

$$ \mathop \sum \limits_{i = 1}^{n} \frac{1}{{\beta \; + \;\theta M_{0} i}} + \mathop \sum \limits_{i = 1}^{n} \log \left( {\frac{{M_{0t} }}{{M_{0i} }}} \right) = 0, $$
(23)
$$ \mathop \sum \limits_{i = 1}^{n} \frac{{M_{0i} }}{{\beta + \theta M_{0} i}}\; + \;\mathop \sum \limits_{i = 1}^{n} M_{0i} - M_{0t} = 0, $$
(24)

where \( \theta = \frac{1}{{M_{0x} }} \). For both Tapered and Truncated Pareto distribution, the maximum likelihood equation of β is determined by the Eqs. (23) and (24) by iteration. To look into the behaviour of large events using the above said distributions, their application has been tested by taking the Himalaya region as case study.

3 The Himalayas: A Case Study

The Himalayan front is seismically one of the most active regions of the world and has experienced both great to moderate earthquakes in the recent past. The Himalayan tectonic zone, being a collision plate boundary, is manifested with a number of north-dipping thrusts that are exposed at the surface. During the past few decades the Himalayan region has been studied fairly extensively in terms of present deformation and the seismicity is mostly attributed to the continent–continent collision where the Indian plate is underthrusting the Eurassian plate. India has been thrusting underneath Tibet since ~55 Ma (Besse and Courtillot 1988; Dewey et al. 1989). India’s convergence into Asia is approximately 18 mm/years (Wang et al. 2001). Out of 36 mm/year (SSE) India–Sunda plate motion, about ~16 mm/year motion is accommodated in Indo-Burmese Fold and Thrust Belt, both as normal convergence (~6 mm/year) and active slip (~7–11 mm/year) in this region (Barman et al. 2017). A global GPS measurement was done and published in http://gsrm2.unavco.org/model/velocities/GEM_GSRM_VelocityViewer.html where it is shown that the convergence rate across the Himalaya is well estimated with 13–16 mm/year. This is significantly lower than that claimed by many authors (Bilham et al. 1997; Kundu et al. 2014; Ader et al. 2012). The accumulated strain energy is being released in the form of major earthquakes. The catalogue on the occurrence of earthquakes from Himalayan region has been compiled for its use in the proposed modelling to estimate the various probabilities of occurrence.

4 Data and Resources

The published earthquake information has been used to compile earthquake catalogue for the present study. In addition to the catalogue compiled by I. D. Gupta (personal communication) for the period 1255–2015, the main sources of non-instrumental and historical data considered for periods prior to 1890 are Baird-Smith (Baird Smith 1843a, b), Oldham (1883), Milne (1911), Lee et al. (1976), and Quittmeyer and Jacob (1979). For the consideration of early instrumental data for the period from 1890 to 1964 Gutenberg and Richter (1954), Gutenberg (1956) and Rothe (1969) are considered. Some data have also been added from improved publications also namely Abe (1981), Abe and Noguchi (1983a, b), Pacheco and Sykes (1992), Engdahl and Villaseñor (2002), Ambraseys (2000), Ambraseys and Douglas (2004), and Martin and Szeliga (2010). The instrumental data for 1964–2015 have been collected from the website of International Seismological Centre (ISC) http://www.isc.ac.uk/of UK, National Earthquake Information Centre (NEIC) of USGS http://earthquake.usgs.gov/earthquake/search/and additional data have been taken from Indian Meteorological Department (IMD).

The compiled catalogue is available in local magnitude Richter’s scale M L, surface wave magnitude M s, Body wave magnitude m b, and moment magnitude M w. For the homogenization, all magnitudes of pre instrumental data are converted into moment magnitude M w, by using empirical conversion relations (Gutenberg 1956; Chung and Bernreuter 1981; Hanks and Kanamori 1979). For instrumental data the Scordilis (2006) conversion relation has been used. Scordilis (2006) has developed the conversion relations from new M S and m b to M W using a very large worldwide database from ISC, NEIC and CMT catalogues for the period 1965–2003.

The window method is used for removing foreshocks and aftershock proposed by the Uhrhammer (1986). Initially 9050 earthquake events were present in the catalogue and after declustering the catalogue we had 5220 independent earthquake events. The seismicity thus obtained was plotted along with the tectonic of the Himalaya region.

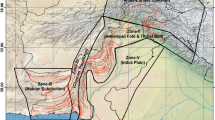
The division of the study area into seismotectonic segments which are homogeneous parts of the seismic source zones is one of the basic requirements for the application of the estimation procedure for seismic hazard parameters. The Himalaya region (26°–38°N and 68°–98°E) is seismically very active and highly complicated from a seismotectonic point of view. The entire Himalayas has been divided into five seismic source zones based on seismotectonic, seismicity distribution, topography variations, and various constraints that were considered in previous studies (Sharma 2003; Sharma and Lindholm 2012; Shanker and Sharma 1997; Sharma and Arora 2005). The five seismic source zones along the tectonic feature of area are as follows:

Seismic Source Zone I 30.92°–36.13°N and 73.71°–79.91°E

Seismic Source Zone II 27.85°–33.09°N and 77.44°–84.39°E

Seismic Source Zone III 26.27°–30.71°N and 82.17°–87.76°E

Seismic Source Zone IV 26.06°–29.94°N and 87.12°–91.09°E

Seismic Source Zone V 26.94°–30.92°N and 91.09°–96.63°E

The seismic source zones SSZ I to SSZ V are shown in Fig. 1 which also shows the main regional features and epicentres of M w ≥4.0 that have occurred during the period 1255–2015.

Fig. 1
figure 1

Characterization of 5 seismic source zones in the Himalaya regions on the basis of seismicity and tectonics. The epicentral distribution of independent earthquakes of M W ≥ 5.0 that occurred during the period 1255–2015 are also shown in the figure along with seismic source zones

Full size image

The number of observed events for all seismic source zones along with the cumulative number of events in each seismic source zone is shown in Fig. 2.

Fig. 2
figure 2

Distribution of number of events with respect to magnitude in each seismic source zone and magnitude of completeness estimated for all seismic source zones as defined in Fig. 1

Full size image

Further, the magnitude of completeness estimated for the five seismic source zones using Woessner and Wiemer (2005) methods is shown in Fig. 2. The magnitudes of completeness for the five seismic source zones are presented in Table 1. This has been used for further estimation of parameters. The periods of completeness for different magnitude ranges has been estimated by the Stepp (1972) Method.

Table 1 Parameters of G–R distribution for all seismic source zones
Full size table

5 Application of Probability Distributions

As a practical consideration, we simply used five statistical probability models for illustrating the of earthquake occurrence. In the present study, the Tail distribution functions of the Pareto, the Truncated Pareto and the Tapered Pareto distributions are expressed by Eqs. (9), (11), and (12), respectively. For the purpose of comparison with the modified G-R distribution and the characteristics recurrence distribution, Eqs. (4) and (6) have been normalised by \( N(M_{\hbox{min} } \le M < M{}_{\hbox{max} }) \), which gives the complementary of the distribution function of the magnitude. Then the complementary of the distribution function or tail function for modified G–R may be written as

$$ \overline{F} \left( M \right) = \frac{{{\text{e}}^{ - \beta \; \times \;M} - {\text{e}}^{{ - \beta \; \times M_{\hbox{max} } }} }}{{{\text{e}}^{{ - \beta \; \times \;M_{\hbox{min} } }} - {\text{e}}^{{ - \beta \; \times \;M_{\hbox{max} } }} }}H\left( {M_{\hbox{max} } - M} \right), $$
(25)

and for the characteristic recurrence distribution as

$$ \bar{F}\left( M \right) = \left\{ {\begin{array}{*{20}l} {\left[ {{\text{e}}^{{ - \beta \left( {M - M_{ \hbox{min} } } \right)}} - {\text{e}}^{{ - \beta \left( {M_{\text{ch}} - M_{ \hbox{min} } } \right)}} } \right] + \beta {\text{e}}^{{ - \beta \left( {M^{\prime } - M_{\hbox{min} } } \right)}} } \hfill & {M_{ \hbox{min} } \le M \le M_{\text{ch}} } \hfill \\ {\beta {\text{e}}^{{ - \beta \left( {M^{\prime } - M_{ \hbox{min} } } \right)}} \times \left( {M_{ \hbox{max} } - M} \right), } \hfill & {M_{\text{ch}} < M \le M_{ \hbox{max} } } \hfill \\ \end{array} } \right.. $$
(26)

These probabilistic distributions have been considered for five seismogenic sources to revisit the return periods of large earthquakes for each seismic source zone.

In the present study the Chi Square test has been used to distinguish between the probability distributions. The Pareto, Truncated Pareto, and Tapered Pareto distribution are applied to describe the probability of occurrence of seismic moment for each seismic source zone. Then the results are compared with the modified G–R and the Characteristic earthquake recurrence models.

The modified G–R distribution uses two parameters: β and \( N(M_{ \hbox{min} } ) \) for estimating the probability of earthquake occurrence. To estimate the values of β and \( N(M_{ \hbox{min} } ) \) for each seismic source zone, the maximum likelihood method has been applied and the values of parameters of the G–R distribution are presented in Table 1. The highest and the lowest values of \( N(M_{ \hbox{min} } ) \) have been observed for SSZ V and SSZ II, respectively, which clearly indicates the seismic source zones having the most and least seismic activity within the study area.

Further, the CDF has been estimated using Eqs. (4) and (6) for the modified G–R and the characteristics recurrence models, respectively. While the modified G–R model decays smoothly (say after magnitude 7), the characteristic model shows different behaviour for higher magnitude as shown in Fig. 3. Figure 3 shows that, for each seismic source zone, the modified G–R distribution yields the lowest probability of occurrence of earthquake events while the characteristic distribution estimates the highest for large earthquakes events.

Fig. 3
figure 3

Cumulative rate of occurrence using the modified G–R and the charecteristics recurrence models for each seismic source zone. Observed data is also plotted for each seismic source zone

Full size image

The Pareto distribution has only one parameter β , which has been estimated using maximum likelihood method along with its standard error \( \sigma_{\beta } \) for all seismic source zones using Eq. (17). The β values thus estimated are given in Table 2. The Truncated Pareto uses two parameters: β and \( M_{0U} \) for estimation of probability of occurrence of earthquake events. The maximum likelihood estimates of the values of β and \( M_{0U} \) for truncated Pareto distribution for each seismic source zones have been estimated using Eqs. (19) and (21) and the same are also reported in Table 2. The Tapered Pareto distribution also uses two parameters: β and \( M_{0x} \), and these two can be estimated by solving maximum likelihood equations of β and \( M_{0x} \) as given in Eqs. (23) and (24), respectively. The values of different parameters used in Pareto, Truncated Pareto, and Tapered Pareto distributions are shown in Table II for all seismic source zones.

Table 2 Parameters of Pareto, Truncated Pareto and Tapered Pareto distribution for all seismic source zones
Full size table

The β estimation for the Pareto distribution resulted in relatively higher values than the Truncated and Tapered Pareto distribution for most of the seismic source zones. Table 2 shows that the β parameter of the Pareto distribution is highest for SSZ V and the estimated upper seismic moment using the Truncated Pareto is larger than the Tapered Pareto for all five seismic source zones.

The probability of occurrence of seismic events or the Tail functions of the Pareto, the Truncated Pareto, and the Tapered Pareto Distributions have been estimated using Eqs. (9), (11), and (12), respectively, for all seismic source zones and are shown in Fig. 4. Figure 4 reveals that the modified G–R yields the lowest probabilities of occurrence while the Characteristic distribution estimates are on the higher side. One of the conspicuous interpretations made from Fig. 4 is the linearity of Pareto distribution on log–log scale showing that it is not capturing the behaviour of other distributions at higher magnitudes as shown in the Fig. 4.

Fig. 4
figure 4

Probability of occurrence with respect to seismic moment for SSZ1, SSZ2, SSZ3, SSZ4, and SSZ5 using various distributions

Full size image

The performance of Chi Square test on five distributions for all the seismic source zones has been carried out, and permitted acceptance of all considered probabilistic distributions for further use.

The probability of occurrence of large earthquake events, i.e., 6, 7 and 8 (M w) as defined by their seismic moments was estimated in different seismic source zones using the Pareto, Truncated Pareto, and Tapered Pareto distributions. The probabilities are comparable for the three distributions at magnitude 6, but it differs for magnitude 8 viz. while the Pareto gives 0.0013, 0.0024, 0.035, 0.000112, and 0.00052, respectively, for seismic source zone SSZ I to SSZ V, the Tapered Pareto gives 0.000563, 0.0013, 0.0012, 0.0.000131, and 0.000397, respectively, for seismic source zone SSZ I to SSZ V and Truncated Pareto gives values in between. The results are given in Table 3.

Table 3 Probability of occurrence for SSZ I, SSZ II, SSZ III, SSZ IV, and SSZ V using the Pareto, Truncated Pareto and Tapered Pareto distributions for magnitude 6, 7 and 8 (M w)
Full size table

One of the conspicuous conclusions obtained is that due to the high seismicity in SSZ V, there is a continuous release of strain energy and hence, the probability of occurrence of a large event is the least here. On the other hand, SSZ III possesses the highest susceptibility of occurrence of a large event. However, the results tend to vary when a different set of distributions has been applied.

For seismic source zone SSZ I, the result shows that the Pareto distribution yields higher probability of occurrence at seismic moment 2E+26 dyne-cm (6.8 M). However, for more than 2E+26 dyne-cm (6.8 M w) the characteristics model shows higher probability (see Fig. 4). The large earthquakes are of magnitude 8.5 and 8 which occurred in 1555 (Kashmir) and 1905 (Kangra), respectively. The seismicity includes activity along the Herat fault north of Kabul, the Chaman fault, and the mountain range in the Pamir Knot with thrust type of faulting. Seismic source zone SSZ II includes the MBT, and the Indus Suture zone and the probability of occurrence for all earthquake events is the highest when estimated using the Pareto Distribution and the lowest for the modified G–R distribution (Fig. 4). The observed largest magnitude is 8.2, which occurred in 1505.

In the seismic source zone SSZ III the largest event was the Nepal–Bihar Earthquake (magnitude 8.1) which occurred in 1934. Recently, a large earthquake of magnitude 7.8 occurred on 25th April 2015 in Nepal. The probability of occurrence estimated by the Pareto Distribution is observed to be higher for all magnitude ranges, and the modified G–R distribution yields the lowest value of the same (Fig. 4). For seismic source zone SSZ IV, the largest event of magnitude 6.8 occurred in 1951. The probability of occurrence estimated by the characteristic distribution is the highest while the modified G–R distribution shows the lowest value of probability of occurrence for entire seismic moment range (Fig. 4).

The seismic source zone SSZ V is the most seismically active region in the Himalayan belt and includes the junction of three plates, namely the Indian plate, Eurasian plate, and Burmese plate. This has experienced great earthquakes of magnitude M w 8.1 in 1897 (Assam), and the probability of occurrence estimated by Characteristic distribution is on the higher side as compared to other distributions for large seismic moment values. The modified G–R distribution shows the lowest value of probability of occurrence for same values (Fig. 4). The modified G–R distribution and the Tapered Pareto distribution show comparable probability of occurrence for all events. The Chi Square test shows the Tapered Pareto distribution is most appropriate one for all seismic source zones viz., SSZ I to SSZ V.

6 Conclusion

There are several statistical distribution models which are used to describe earthquake occurrence. Due to short catalogues it is difficult to select any particular distribution which follows realistic trends as per the size and the return periods, especially in case of large earthquakes. Himalayas are one of the cases where multiple collisions and existence of great earthquakes with large return periods implicates testing of such statistical distributions which considers the large return periods. It is thus of special importance to use statistical methods that analyse as closely as possible the range of its extreme values or the tail of the distributions rather than the whole of the distributions. In the present study, an attempt has been made to compare different distribution of seismic moment for earthquakes in Himalayan region. The whole Himalaya region has been divided into five seismic source zones. The probability of occurrence in Himalaya region has been estimated using the Pareto, the Truncated Pareto, and the Tapered Pareto, and compared with the modified G–R, and the characteristic recurrence distribution using an updated and reliable earthquake catalogue for the period 1255–2015. For each seismic source zone, Chi Square test performed to set the selection criteria of the best fit distribution. The results show that the Tapered Pareto distribution better describes seismicity for each of the seismic source zones. The earthquake occurrence is a complex phenomenon in itself and interaction of sources during pre and post-earthquake along with the assumption that each event considered is an independent event are some of the factors which necessarily implicate fitting of different distributions. The distribution for estimating the probability of occurrence in all seismic source zones considered using various distribution models is informative and useful from engineering point of view. The differences in the probabilities estimated using the different distributions will have bearing on the ultimate results of seismic hazard assessment exercises and hence it is recommended to use different statistical models which fit best in the individual seismic source zones in Himalayas.