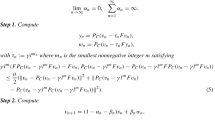1 Introduction

Throughout this paper, assume that C is a nonempty, convex and closed subset of the real Hilbert space H with the inner product \(\langle , \rangle\) and the norm \(\Vert . \Vert\). Let \(F: {H} \rightarrow {H}\) be a Lipschitz continuous operator. The object of our investigation is the following variational inequality problem (shortly, VI(C, F)):

Find \({{x}^{*}}\in C\) such that

$$\begin{aligned} \langle Fx^*, x - x^*\rangle \ge 0 \ \ \forall x \in C. \end{aligned}$$
(1)

We denote the solution set of VI(C, F) by Sol(C, F).

Many problems in various fields such as physic, economics, engineering, optimization theory can be led to variational inequalities. Iterative methods for solving these problems have been proposed and analyzed (see, for example, Facchinei and Pang (2003), Gibali et al. (2017), Kassay et al. (2011), Kinderlehrer and Stampacchia (1980), Konnov (2001) and references therein). One of the most famous methods for solving VI(C, F) is the extragradient method introduced by Korpelevich (1976). In this method, one needs to calculate two projections onto C at each iteration. This may affect the efficiency of the method when finding a projection onto a closed and convex set C is not an easy problem.

In recent years, many authors are interested in the extragradient method and improved it in various ways, see, e.g. Anh et al. (2020), Censor et al. (2011a, b, 2012b), Reich, Thong and Dong et al. (2021), Reich, Thong and Cholamjiak et al. (2021), Thong and Hieu (2018), Thong and Vuong (2021), Yang et al. (2018), Yang (2021) and references therein. The subgradient extragradient method, proposed by Censor et al. (2012a) for solving VI(C, F) in real Hilbert spaces is one of these modifications.

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H,\\ y_n=P_C(x_n-\lambda Fx_n),\\ T_n=\{x\in H: \langle x_n-\lambda Fx_n-y_n,x-y_n\rangle \le 0\},\\ x_{n+1}=P_{T_n}(x_n-\lambda Fy_n), \end{array}\right. } \end{aligned}$$
(2)

where \(\lambda \in (0,\dfrac{1}{L}),\) and L is a Lipschitz constant of F. This method replaces two projections onto C by one projection onto C and one onto a half-space. The sequence \(\{x_n\}\) generated by (2) converges weakly to an element of Sol(C, F) provided that Sol(C, F) is nonempty.

Kraikaew and Seajung (2014) used the subgradient extragradient method and Halpern method to introduce an algorithm for solving VI(C, F) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0\in H,\\ y_n=P_C(x_n-\lambda Fx_n),\\ T_n=\{x\in H: \langle x_n-\lambda Fx_n-y_n,x-y_n\rangle \le 0\},\\ z_n=P_{T_n}(x_n-\lambda Fy_n),\\ x_{n+1}=\alpha _nx_0+(1-\alpha _n)z_n, \end{array}\right. } \end{aligned}$$
(3)

where \(\lambda \in (0,\dfrac{1}{L}), \{\alpha _n\}\subset (0,1), \alpha _n\rightarrow 0, \sum _{n=1}^\infty \alpha _n =+\infty .\) They proved that the sequence \(\{x_n\}\) generated by (3) converges strongly to \(P_{Sol(C,F)}x_0\) if F is monotone and L-Lipschitz continuous. The main disadvantage of Algorithms (2), (3) is a requirement to know the Lipschitz constant of F or at least to know some its estimation.

Very recently, Yang (2021) proposed a modification of subgradient extragradient method with step size rule using the inertial-type method as follows: Given \(\lambda _0>0, \mu <\mu _0\in (0,1)\). Let \(x_0, x_1\in H\) be arbitrary

$$\begin{aligned} w_n&=x_n+\alpha _n(x_n-x_{n-1}),\\ y_n&=P_C(w_n-\lambda _n Fw_n),\\ T_n&:=\{x\in H : \langle w_n-\lambda _n Fw_n-y_n,x-y_n\rangle \le 0 \},\\ x_{n+1}&=P_{T_n}(w_n-\lambda _n Fy_n),\\ \lambda _{n+1}&={\left\{ \begin{array}{ll} \min \{\mu \dfrac{\Vert w_n-y_n\Vert ^2+\Vert x_{n+1}-y_n\Vert ^2}{2\langle Fw_n-Fy_n, x_{n+1}-y_n\rangle }, \lambda _n\} &{}\text { if } \langle Fw_n-Fy_n,z_n-y_n\rangle > 0,\\ \lambda _n &{}\text { otherwise}. \end{array}\right. } \end{aligned}$$

Under the pseudomonotonicity and sequential weak continuity of the mapping, the convergence of the algorithm was established without the knowledge of the Lipschitz constant of the mapping.

Motivated and inspired by the above mentioned works, and by the ongoing research in these directions, in this paper, we suggest a new iterative scheme for finding the minimum-norm solution to VI(C, F) (1). It is worth pointing out that the proposed algorithm does not require the prior knowledge of the Lipschitz-type constant of the variational inequality mapping and only requires to compute one projection onto a feasible set per iteration as well as without the assumption on the weakly sequential continuity of the mapping. Moreover, the convergence rate is obtained under strong pseudomonotonicity and Lipschitz continuity assumptions of the variational inequality mapping.

The paper is organized as follows. In Sect. 2, we recall some basic definitions and results. In Sect. 3, we present and analyze the convergence of the proposed algorithms. Finally in Sect. 4, we present some numerical experiments to illustrate the performance of the proposed method.

2 Preliminaries

Lemma 2.1

([Cottle and Yao (1992), Lemma 2.1]) Consider the problem VI(C, F) with C being a nonempty, closed, convex subset of a real Hilbert space H and \(F : C \rightarrow H\) being pseudo-monotone and continuous. Then, \(x^*\) is a solution of VI(C, F) if and only if

$$\begin{aligned} \langle Fx, x - x^*\rangle \ge 0 \ \ \forall x \in C. \end{aligned}$$

Lemma 2.2

Let H be a real Hilbert space. Then the following results hold:

  1. (i)

    \(\Vert x+y\Vert ^2=\Vert x\Vert ^2+2\langle x,y\rangle +\Vert y\Vert ^2 \ \forall x,y\in H;\)

  2. (ii)

    \(\Vert x+y\Vert ^2\le \Vert x\Vert ^2+2\langle y,x+y\rangle \ \forall x,y\in H.\)

Definition 2.1

Let \(T:C\rightarrow H\) be an operator, where C is a closed and convex subset of a real Hilbert space H. Then

  • T is called L-Lipschitz continuous with \(L>0\) if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L \Vert x-y\Vert \ \ \ \forall x,y \in C. \end{aligned}$$

  • T is called monotone if

    $$\begin{aligned} \langle Tx-Ty,x-y \rangle \ge 0 \ \ \ \forall x,y \in C. \end{aligned}$$

  • T is said to be pseudo-monotone if

    $$\begin{aligned} \langle Tx,y-x \rangle \ge 0 \Longrightarrow \langle Ty,y-x \rangle \ge 0. \end{aligned}$$

    It is called \(\delta\)-strongly pseudo-monotone if there is \(\delta > 0\) such that

    $$\begin{aligned} \langle Tx,y-x \rangle \ge 0 \Longrightarrow \langle Ty,y-x \rangle \ge \delta \Vert y - x\Vert ^2. \end{aligned}$$

  • T is said to be weakly sequentially continuous if, for each sequence \(\{x_n\}\) in C, \(\{x_n\}\) converges weakly to a point \(x\in C\), then \(\{Tx_n\}\) converges weakly to Tx.

  • T is called weakly closed on C if for any \(\{x_n\} \subset C,\) \(x_n \rightharpoonup x,\) and \(T(x_n) \rightharpoonup y,\) then \(T(x) = y.\)

  • T is said to have \(*\)-property on C, if the function \(\Vert T(x)\Vert\) is weakly lower-semicontinuous (w.l.s.c.) on C,  i.e., for any \(\{x_n\} \subset C,\) \(x_n \rightharpoonup x,\)

    $$\begin{aligned} \Vert T(x)\Vert \le \liminf _{n\rightarrow \infty }\Vert T(x_n)\Vert . \end{aligned}$$

A relation between the weakly sequential continuity, weak closedness and \(*\)-property are revealed in the following simple statement.

Lemma 2.3

  1. (i)

    Any weakly sequentially continuous operator is weakly closed and have the \(*\)-property.

  2. (ii)

    A weakly closed operator, mapping bounded subsets into bounded subsets, is weakly sequentially continuous.

  3. (iii)

    An operator having the \(*\)-property and mapping bounded subsets into bounded subsets is not necessarily weakly sequentially continuous, and hence is not necessarily weakly closed.

Proof

i. Suppose T is weakly sequentially continuous on C. Then it is weakly closed by definition. Further, let \(C \ni x_n \rightharpoonup x,\) then \(T(x_n) \rightharpoonup T(x),\) and due to the weak lower continuity of the norm, one gets \(\Vert T(x)\Vert \le \liminf _{n\rightarrow \infty }\Vert T(x_n)\Vert ,\) which means the \(*\)-property of T.

ii. Assume that T is weakly closed and maps bounded subsets into bounded subsets. Let \(x_n \rightharpoonup x,\) than the sequence \(\{x_n\}\) is bounded, hence, the set \(\{T(x_n)\}\) is also bounded. Let \(\zeta\) be a weak cluster point of \(\{T(x_n)\}.\) There exists a weakly convergent subsequence \(T(x_{n_k}) \rightharpoonup \zeta .\) Since \(x_{n_k} \rightharpoonup x,\) by the weak closedness of T,  one gets \(\zeta = T(x).\) Thus, \(T(x_n) \rightharpoonup T(x).\)

iii. Let H be a real Hilbert space with an orthonormal basis \(\{e_n\}\) and C be a closed ball centered at 0 with radius \(r:= \sqrt{2}.\) Define the operator \(T: C \rightarrow H\) by \(T(x) := \Vert x\Vert x.\) Obviously, T maps bounded subsets into bounded subsets. Further, T has the \(*\)-property. Indeed, let \(x_n \rightharpoonup x,\) then \(\Vert T(x)\Vert = \Vert x\Vert ^2 \le \left( \liminf _{n\rightarrow \infty }\Vert x_n\Vert \right) ^2 \le \liminf _{n\rightarrow \infty }\Vert x_n\Vert ^2 = \liminf _{n\rightarrow \infty }\Vert T(x_n)\Vert\). On the other hand, T is not weakly sequentially continuous. Indeed, let \(x_n = e_n + e_1.\) Then \(x_n \rightharpoonup e_1,\) and for \(n \ge 2\), \(T(x_n) = \sqrt{2}(e_n + e_1) \rightharpoonup \sqrt{2}e_1 \ne T(e_1) = 2 e_1\).

Lemma 2.4

(Saejung and Yotkaew (2012)) Let \(\{a_n\}\) be a sequence of nonnegative real numbers, \(\{\alpha _n\}\) be a sequence of real numbers in (0, 1) with \(\sum _{n=1}^\infty \alpha _n=\infty\) and \(\{b_n\}\) be a sequence of real numbers. Assume that

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\alpha _n b_n\ \ \forall n\ge 1. \end{aligned}$$

If \(\limsup _{k\rightarrow \infty } b_{n_k} \le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying \(\liminf _{k\rightarrow \infty }(a_{n_k+1}-a_{n_k})\ge 0\) then \(\lim _{n\rightarrow \infty }{a_n} = 0\).

Definition 2.2

(Ortega and Rheinboldt (1970)) Let \(\{x_n\}\) be a sequence in H.

  1. (i)

    \(\{x_n\}\) is said to converge R-linearly to \(x^*\) with rate \(\rho \in [0, 1)\) if there is a constant \(c>0\) such that

    $$\begin{aligned} \Vert x_n-x^*\Vert \le c\rho ^n \ \ \forall n\in \mathbb {N}. \end{aligned}$$
  2. (ii)

    \(\{x_n\}\) is said to converge Q-linearly to \(x^*\) with rate \(\rho \in [0, 1)\) if

    $$\begin{aligned} \Vert x_{n+1}-x^*\Vert \le \rho \Vert x_n-x^*\Vert \ \ \forall n\in \mathbb {N}. \end{aligned}$$

3 Main results

In this work, we assume the following conditions:

Condition 1

The feasible set C is nonempty, closed, and convex.

Condition 2

The mapping \(F:H\rightarrow H\) is L-Lipschitz continuous, pseudomonotone on H. However, the information of L is not necessary to be known.

Condition 3

The solution set Sol(C, F) is nonempty.

The proposed algorithm is of the form:

Algorithm 3.1

  • Initialization: Let \(\{\alpha _n\}\) be a sequence of nonnegative real numbers satisfying \(\sum _{n=1}^\infty \alpha _n <+\infty\). Let \(\theta >0\), \(\tau _1>0\), \(\mu \in (0,1)\) and \(x_0,x_1\in H\) be arbitrary. We assume that \(\{\theta _n\}\), \(\{\epsilon _n\}\) and \(\{\gamma _n\}\) are three positive sequences such that \(\{\theta _n\}\subset [0,\theta )\) and \(\epsilon _n=o(\gamma _n)\), i.e., \(\lim _{n\rightarrow \infty }\dfrac{\epsilon _{n}}{\gamma _n}=0\), where \(\{\gamma _n\}\subset (0,1)\) satisfies the following conditions:

    $$\begin{aligned} \lim _{n\rightarrow \infty }\gamma _n=0, \quad \sum _{n=1}^\infty \gamma _n=\infty . \end{aligned}$$

    Iterative Steps: Calculate \(x_{n+1}\) as follows:

    • Step 1. Given the iterates \(x_{n-1}\) and \(x_n\) \((n\ge 1)\), choose \(\theta _n\) such that \(0\le \theta _n\le \bar{\theta }_n\), where

      $$\begin{aligned} \begin{aligned} \bar{\theta }_n= {\left\{ \begin{array}{ll} \min \bigg \{\theta , \frac{\epsilon _n}{\Vert x_n-x_{n-1}\Vert }\bigg \}&{}\text {if} \ x_n \ne x_{n-1}, \\ \theta &{}\text { otherwise}. \end{array}\right. } \end{aligned} \end{aligned}$$
      (4)

      Step 2. Set \(u_n=(1-\gamma _n)(x_n+\theta _n(x_n-x_{n-1}))\) and compute

      $$\begin{aligned} q_n=P_C(u_n-\tau _n Fu_n). \end{aligned}$$

      Step 3. Compute

      $$\begin{aligned} x_{n+1}=P_{T_n}(u_n-\tau _nFq_n), \end{aligned}$$

      where \(T_n:=\{x\in H| \langle u_n-\tau _nFu_n-q_n,x-q_n\rangle \le 0 \}.\)

    • Update

      $$\begin{aligned} \begin{aligned} \tau _{n+1}:= {\left\{ \begin{array}{ll}\min \{\mu \frac{\Vert u_n-q_n\Vert ^2+\Vert x_{n+1}-q_n\Vert ^2}{2\langle Fu_n-Fq_n,x_{n+1}-q_n\rangle },\tau _n+\alpha _n\}\ \text { if } \langle Fu_n-Fq_n,x_{n+1}-q_n\rangle > 0,\\ \tau _n+\alpha _n \text { otherwise. } \end{array}\right. } \end{aligned} \end{aligned}$$
      (5)

      Set \(n:=n+1\) and go to Step 1.

Remark 3.1

As noted in Liu and Yang (2020), the sequence generated by (5) is allowed to increase from iteration to iteration. Hence, our results in this work are different from those in Yang et al. (2018), Yang (2021).

Lemma 3.5

(Liu and Yang (2020)) Assume that Condition 2 holds. Let \(\{\tau _n\}\) be the sequence generated by (5). Then

$$\begin{aligned} \lim _{n\rightarrow \infty } \tau _n=\tau \text { with } \tau \in \bigg [ \min \left\{ \tau _1,\dfrac{\mu }{L}\right\} ,\tau _1+\alpha \bigg ], \end{aligned}$$

where \(\alpha =\sum _{n=1}^\infty \alpha _n\). Moreover

$$\begin{aligned} 2\langle Fu_{n}-Fq_{n},x_{n+1}-q_n\rangle \le \dfrac{\mu }{\tau _{n+1}}(\Vert u_{n}-q_{n}\Vert ^2+\Vert x_{n+1}-q_n\Vert ^2). \end{aligned}$$
(6)

Theorem 3.1

Assume that Conditions 1–3 hold. If the mapping \(F:H\rightarrow H\) satisfies the \(*\)-property then the sequence \(\{x_n\},\) generated by Algorithm 3.1, converges strongly to an element \(z\in Sol(C,F)\), where \(z=P_{Sol(C,F)}(0)\).

Proof

To improve readability, we split the proof of our main theorem into some parts.

Claim 1.

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le \Vert u_n-z\Vert ^2 -(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert x_{n+1}-q_n\Vert ^2. \end{aligned}$$

Since \(z\in C\subset T_n\) and \(P_{T_n}\) is firmly nonexpansive, see, for example Reich and Shafrir (1987), we have

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2=&\ \Vert P_{T_n}(u_n-\tau _n Fq_n)-P_{T_n}z\Vert ^2\le \langle x_{n+1}-z,u_n-\tau _n Fq_n-z\rangle \\ =&\ \dfrac{1}{2}\Vert x_{n+1}-z\Vert ^2+\dfrac{1}{2}\Vert u_n-\tau _n Fq_n-z\Vert ^2-\dfrac{1}{2}\Vert x_{n+1}-u_n+\tau _n Fq_n\Vert ^2\\ =&\ \dfrac{1}{2}\Vert x_{n+1}-z\Vert ^2+\dfrac{1}{2}\Vert u_n-z\Vert ^2+\dfrac{1}{2}\tau ^2_n \Vert Fq_n\Vert ^2- \langle u_n-z,\tau _n Fq_n \rangle \\&- \dfrac{1}{2}\Vert x_{n+1}-u_n\Vert ^2-\dfrac{1}{2}\tau ^2_n \Vert Fq_n\Vert ^2-\langle x_{n+1}-u_n, \tau _n Fq_n\rangle \\ =&\ \dfrac{1}{2}\Vert x_{n+1}-z\Vert ^2+\dfrac{1}{2}\Vert u_n-z\Vert ^2 -\dfrac{1}{2}\Vert x_{n+1}-u_n\Vert ^2-\langle x_{n+1}-z, \tau _n Fq_n\rangle . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le \Vert u_n-z\Vert ^2 -\Vert x_{n+1}-u_n\Vert ^2-2\langle x_{n+1}-z, \tau _n Fq_n\rangle . \end{aligned}$$
(7)

Since z is the solution of VI, we have \(\langle Fz,x-z\rangle \ge 0\) for all \(x\in C\). By the pseudomontonicity of F on C we have \(\langle Fx,x-z\rangle \ge 0\) for all \(x\in C\). Taking \(x:=q_n\in C\) we get

$$\begin{aligned} \langle Fq_n,z-q_n\rangle \le 0. \end{aligned}$$

Thus,

$$\begin{aligned} \langle Fq_n,z-x_{n+1}\rangle =&\langle Fq_n,z-q_{n}\rangle +\langle Fq_n,q_n-x_{n+1}\rangle \le \langle Fq_n,q_n-x_{n+1}\rangle . \end{aligned}$$
(8)

From (7) and (8) we obtain

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le& \ \Vert u_n-z\Vert ^2-\Vert x_{n+1}-u_n\Vert ^2+2\tau _n\langle Fq_n,q_n-x_{n+1}\rangle \\ =& \ \Vert u_n-z\Vert ^2-\Vert x_{n+1}-q_n\Vert ^2-\Vert q_{n}-u_n\Vert ^2-2\langle x_{n+1}-q_n,q_{n}-u_n \rangle \\&+2\tau _n\langle Fq_n,q_n-x_{n+1}\rangle \\ =& \ \Vert u_n-z\Vert ^2-\Vert x_{n+1}-q_n\Vert ^2-\Vert q_{n}-u_n\Vert ^2 +2\langle u_n-\tau _n Fq_n-q_n,x_{n+1}-q_n\rangle . \end{aligned}$$
(9)

Since \(q_n=P_{T_n}(u_n-\tau _n Fu_n)\) and \(x_{n+1}\in T_n\) we have

$$\begin{aligned} \begin{aligned} 2\langle u_n-\tau _n Fq_n-q_n,&x_{n+1}-q_n\rangle \\&=2\langle u_n-\tau _n Fu_n-q_n,x_{n+1}-q_n\rangle +2\tau _n \langle Fu_n-Fq_n,x_{n+1}-q_n\rangle \\&\le 2\tau _n \langle Fu_n-Fq_n,x_{n+1}-q_n\rangle . \end{aligned} \end{aligned}$$
(10)

It follows from (6) that

$$\begin{aligned} 2\tau _n\langle Fu_n-Fq_n,x_{n+1}-q_n\rangle \le \mu \dfrac{\tau _n}{\tau _{n+1}}\Vert u_n-q_n\Vert ^2+\mu \dfrac{\tau _n}{\tau _{n+1}}\Vert q_n-x_{n+1}\Vert ^2. \end{aligned}$$
(11)

Combining (10) and (11), we obtain

$$\begin{aligned} 2\langle u_n-\tau _n Fq_n-q_n,x_{n+1}-q_n\rangle \le \mu \dfrac{\tau _n}{\tau _{n+1}}\Vert u_n-q_n\Vert ^2+\mu \dfrac{\tau _n}{\tau _{n+1}}\Vert q_n-x_{n+1}\Vert ^2. \end{aligned}$$
(12)

Substituting (12) into (9) we obtain

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le \Vert u_n-z\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert x_{n+1}-q_n\Vert ^2. \end{aligned}$$

Claim 2. The sequence \(\{x_n\}\) is bounded. Indeed, we have

$$\begin{aligned} \begin{aligned} \Vert u_n-z\Vert&=\Vert (1-\gamma _n)(x_n+\theta _n(x_n-x_{n-1}))-z\Vert \\&=\Vert (1-\gamma _n)(x_n-z)+(1-\gamma _n)\theta _n(x_n-x_{n-1})-\gamma _n z\Vert \\&\le (1-\gamma _n)\Vert x_n-z\Vert +(1-\gamma _n)\theta _n\Vert x_n-x_{n-1}\Vert +\gamma _n \Vert z\Vert \\&=(1-\gamma _n)\Vert x_n-z\Vert +\gamma _n [ (1-\gamma _n)\dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert +\Vert z\Vert ]. \end{aligned} \end{aligned}$$
(13)

On the other hand, since (4) we have

$$\begin{aligned} \dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert \le \dfrac{\epsilon _n}{\gamma _n}\rightarrow 0, \end{aligned}$$

which implies that \(\lim _{n\rightarrow \infty }\bigg [ (1-\gamma _n)\dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert +\Vert z\Vert \bigg ]=\Vert z\Vert\), hence there exists \(M>0\) such that

$$\begin{aligned} (1-\gamma _n)\dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert +\Vert z\Vert \le M. \end{aligned}$$
(14)

Combining (13) and (14) we obtain

$$\begin{aligned} \Vert u_n-z\Vert \le (1-\gamma _n)\Vert x_n-z\Vert +\gamma _n M. \end{aligned}$$

Moreover, we have \(\lim _{n\rightarrow \infty }(1-\mu \dfrac{\tau _n}{\tau _{n+1}})=1-\mu >\dfrac{1-\mu }{2}\), hence there exists \(n_0\in \mathbb {N}\) such that \(1-\mu \dfrac{\tau _n}{\tau _{n+1}}>0 \ \ \forall n\ge n_0.\) By Claim 1 we obtain

$$\begin{aligned} \Vert x_{n+1}-z\Vert \le \Vert u_n-z\Vert \ \ \forall n\ge n_0. \end{aligned}$$
(15)

Thus

$$\begin{aligned} \Vert x_{n+1}-z\Vert &\le(1-\gamma _n)\Vert x_n-z\Vert +\gamma _n M\\&\le \max \{\Vert x_n-z\Vert , M \}\le ...\le \max \{\Vert x_{n_0}-z\Vert ,M\}. \end{aligned}$$

Therefore, the sequence \(\{x_n\}\) is bounded.

Claim 3.

$$\begin{aligned} (1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2&+(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert x_{n+1}-q_n\Vert ^2\\ \le& \ \Vert x_n-z\Vert ^2-\Vert x_{n+1}-z\Vert ^2+\gamma _n M_1. \end{aligned}$$

Indeed, we have \(\Vert u_n-z\Vert \le (1-\gamma _n)\Vert x_n-z\Vert +\gamma _n M\), this implies that

$$\begin{aligned} \begin{aligned} \Vert u_n-z\Vert ^2&\le (1-\gamma _n)^2\Vert x_n-z\Vert ^2+2\gamma _n(1-\gamma _n)M \Vert x_n-z\Vert +\gamma _n^2M^2\\&\le \Vert x_n-z\Vert ^2+\gamma _n [2(1-\gamma _n)M \Vert x_n-z\Vert +\gamma _n M^2]\\&\le \Vert x_n-z\Vert ^2+\gamma _n M_1, \end{aligned} \end{aligned}$$
(16)

where \(M_1:=\max \{2(1-\gamma _n)M \Vert x_n-z\Vert +\gamma _n M^2:\ \ n\in \mathbb {N}\}\). Substituting (16) into Claim 1 we get

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2&\le \Vert x_n-z\Vert ^2+\gamma _n M_1-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert x_{n+1}-q_n\Vert ^2. \end{aligned}$$

Or equivalently

$$\begin{aligned} (1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2+(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert x_{n+1}-q_n\Vert ^2\\ \le \Vert x_n-z\Vert ^2-\Vert x_{n+1}-z\Vert ^2+\gamma _n M_1. \end{aligned}$$

Claim 4.

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le& \ (1-\gamma _n)\Vert x_n-z\Vert ^2+\gamma _n\bigg [2(1-\gamma _n)\Vert x_n-z\Vert \dfrac{\theta _n}{\gamma _n} \Vert x_n-x_{n-1}\Vert \\&+\theta _n \Vert x_n-x_{n-1}\Vert \dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert +2 \Vert z\Vert \Vert u_n-x_{n+1}\Vert +2 \langle -z,x_{n+1}-z \rangle \bigg ], \end{aligned}$$

\(\forall n\ge n_0.\) Indeed, using Lemma 2.2 ii) and (15) we get

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le& \ \Vert u_n-z\Vert ^2\ \ \forall n\ge n_0 = \Vert (1-\gamma _n) (x_n-z)\\&+(1-\gamma _n) \theta _n (x_n-x_{n-1})-\gamma _n z\Vert ^2\ \ \forall n\ge n_0 \\ \le&\ \Vert (1-\gamma _n)(x_n-z)+(1-\gamma _n)\theta _n (x_n-x_{n-1})\Vert ^2\\ &+2\gamma _n \langle -z,u_n-z\rangle \ \ \forall n\ge n_0\\ \le&\ (1-\gamma _n)^2\Vert x_n-z\Vert ^2+2(1-\gamma _n)\theta _n\Vert x_n-z\Vert \Vert x_n-x_{n-1}\Vert\\ &+\theta _n^2\Vert x_n-x_{n-1}\Vert ^2+2\gamma _n \langle -z,u_n-x_{n+1} \rangle \\ &+2 \gamma _n\langle -z,x_{n+1}-z \rangle \ \ \forall n\ge n_0 \\ \le&\ (1-\gamma _n)\Vert x_n-z\Vert ^2+\gamma _n\bigg [2(1-\gamma _n)\Vert x_n-z\Vert \dfrac{\theta _n}{\gamma _n} \Vert x_n-x_{n-1}\Vert \\&+\theta _n \Vert x_n-x_{n-1}\Vert \dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert \\&+2 \Vert z\Vert \Vert u_n-x_{n+1}\Vert +2 \langle -z,x_{n+1}-z \rangle \bigg ]\ \ \forall n\ge n_0. \end{aligned}$$

Claim 5. \(\{\Vert x_n-z\Vert ^2\}\) converges to zero.

Indeed, by Lemma 2.4 it suffices to show that \(\limsup _{k\rightarrow \infty }\langle -z, x_{n_k+1}-z\rangle \le 0\) and \(\limsup _{k\rightarrow \infty }\Vert u_{n_k}-x_{n_k+1}\Vert \le 0\) for every subsequence \(\{\Vert x_{n_k}-z\Vert \}\) of \(\{\Vert x_n-z\Vert \}\) satisfying

$$\begin{aligned} \liminf _{k\rightarrow \infty }(\Vert x_{n_k+1}-z\Vert -\Vert x_{n_k}-z\Vert )\ge 0. \end{aligned}$$

For this purpose, suppose that \(\{\Vert x_{n_k}-z\Vert \}\) is a subsequence of \(\{\Vert x_n-z\Vert \}\) such that \(\liminf _{k\rightarrow \infty }(\Vert x_{n_k+1}-z\Vert -\Vert x_{n_k}-z\Vert )\ge 0.\) Then

$$\begin{aligned} \liminf _{k\rightarrow \infty }(\Vert x_{n_k+1}-z\Vert ^2-\Vert x_{n_k}-z\Vert ^2)=\liminf _{k\rightarrow \infty }[(\Vert x_{n_k+1}-z\Vert -\Vert x_{n_k}-z\Vert )\\(\Vert x_{n_k+1}-z\Vert +\Vert x_{n_k}-z\Vert )]\ge 0. \end{aligned}$$

By Claim 3 we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }&\bigg [(1-\mu \dfrac{\tau _{n_k}}{\tau _{{n_k}+1}})\Vert u_{n_k}-q_{n_k}\Vert ^2+(1-\mu \dfrac{\tau _{n_k}}{\tau _{{n_k}+1}})\Vert x_{n_k+1}-q_{n_k}\Vert ^2\bigg ]\\&\le \limsup _{k\rightarrow \infty }\bigg [ \Vert x_{n_k}-z\Vert ^2-\Vert x_{{n_k}+1}-z\Vert ^2+\gamma _{n_k} M_1\bigg ]\\&\le \limsup _{k\rightarrow \infty }\bigg [ \Vert x_{n_k}-z\Vert ^2-\Vert x_{n_k+1}-z\Vert ^2\bigg ]+\limsup _{k\rightarrow \infty }\gamma _{n_k} M_1\\&=- \liminf _{k\rightarrow \infty }\bigg [ \Vert x_{n_k+1}-z\Vert ^2-\Vert x_{_{n_k}}-z\Vert ^2\bigg ]\\&\le 0. \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert q_{n_k}-u_{n_k}\Vert =0 \text { and } \lim _{k\rightarrow \infty } \Vert x_{n_k+1}-q_{n_k}\Vert =0. \end{aligned}$$

Thus

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert x_{n_k+1}-u_{n_k}\Vert =0. \end{aligned}$$
(17)

Now, we show that

$$\begin{aligned} \Vert x_{n_k+1}-x_{n_k}\Vert \rightarrow 0\,\, \text { as }\,\, k\rightarrow \infty . \end{aligned}$$
(18)

Indeed, using \(\lim _{n\rightarrow \infty }\gamma _n=0\) we have

$$\begin{aligned} \begin{aligned} \Vert x_{n_k}-u_{n_k}\Vert&=\Vert (1-\gamma _{n_k})(x_{n_k}+\theta _{n_k}(x_{n_k}-x_{n_k-1}))-x_{n_k}\Vert \\&=\Vert \theta _{n_k}(x_{n_k}-x_{n_k-1})-\gamma _{n_k}(x_{n_k}+\theta _{n_k}(x_{n_k}-x_{n_k-1}))\Vert \\&\le \theta _{n_k} \Vert x_{n_k}-x_{n_k-1}\Vert +\gamma _{n_k}\Vert x_{n_k}+\theta _{n_k}(x_{n_k}-x_{n_k-1})\Vert \\&=\gamma _{n_k}\dfrac{\theta _{n_k}}{\gamma _{n_k}} \Vert x_{n_k}-x_{n_k-1}\Vert +\gamma _{n_k}\Vert x_{n_k}+\theta _{n_k}(x_{n_k}-x_{n_k-1})\Vert \rightarrow 0. \end{aligned} \end{aligned}$$
(19)

From (17) and (19), we get

$$\begin{aligned} \Vert x_{n_k+1}-x_{n_k}\Vert \le \Vert x_{n_k+1}-u_{n_k}\Vert +\Vert x_{n_k}-u_{n_k}\Vert \rightarrow 0. \end{aligned}$$

Since the sequence \(\{x_{n_k}\}\) is bounded, it follows that there exists a subsequence \(\{x_{n_{k_j}}\}\) of \(\{x_{n_k}\}\), which converges weakly to some \(z^*\in H\), such that

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle -z,x_{n_k}-z\rangle =\lim _{j\rightarrow \infty }\langle -z,x_{n_{k_j}}-z\rangle =\langle -z,z^*-z\rangle . \end{aligned}$$
(20)

Using (19), we get

$$\begin{aligned} u_{n_k} \rightharpoonup z^* \text { as } k\rightarrow \infty , \end{aligned}$$

Using (17), we obtain

$$\begin{aligned} x_{n_k} \rightharpoonup z^* \text { as } k\rightarrow \infty . \end{aligned}$$

Now, we show that \(z^*\in Sol(C,F)\). Indeed, since \(q_{n_k}=P_C(u_{n_k}-\tau _{n_k}Fu_{n_k})\), we have

$$\begin{aligned} \langle u_{n_k}-\tau _{n_k} Fu_{n_k}-q_{n_k},x-q_{n_k}\rangle \le 0 \ \ \forall x\in C, \end{aligned}$$

or equivalently

$$\begin{aligned} \dfrac{1}{\tau _{n_k}}\langle u_{n_k}-q_{n_k},x-q_{n_k}\rangle \le \langle Fu_{n_k},x-q_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$

Consequently

$$\begin{aligned} \dfrac{1}{\tau _{n_k}}\langle u_{n_k}-q_{n_k},x-q_{n_k}\rangle +\langle Fu_{n_k},q_{n_k}-u_{n_k}\rangle \le \langle Fu_{n_k},x-u_{n_k}\rangle \ \ \forall x\in C. \end{aligned}$$
(21)

Being weakly convergent, \(\{u_{n_k}\}\) is bounded. Then, by the Lipschitz continuity of F, \(\{Fu_{n_k}\}\) is bounded. As \(\Vert u_{n_k}-q_{n_k}\Vert \rightarrow 0\), \(\{q_{n_k}\}\) is also bounded and \(\tau _{n_k} \ge \min \{\tau _1,\dfrac{\mu }{L}\}\). Passing (21) to limit as \(k\rightarrow \infty\), we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Fu_{n_k},x-u_{n_k}\rangle \ge 0\ \ \forall x\in C. \end{aligned}$$
(22)

Moreover, we have

$$\begin{aligned} \langle Fq_{n_k},x-q_{n_k}\rangle =\langle Fq_{n_k}- Fu_{n_k},x-u_{n_k}\rangle +\langle Fu_{n_k},x-u_{n_k}\rangle +\langle Fq_{n_k},u_{n_k}-q_{n_k}\rangle . \end{aligned}$$
(23)

Since \(\lim _{k\rightarrow \infty }\Vert u_{n_k}-q_{n_k}\Vert =0\) and F is L-Lipschitz continuous on H, we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert Fu_{n_k}-Fq_{n_k}\Vert =0 \end{aligned}$$

which, together with (22) and (23) implies that

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Fq_{n_k},x-q_{n_k}\rangle \ge 0. \end{aligned}$$

Next, we choose a sequence \(\{\epsilon _k\}\) of positive numbers decreasing and tending to 0. For each k, we denote by \(N_k\) the smallest positive integer such that

$$\begin{aligned} \langle Fq_{n_j},x-q_{n_j}\rangle +\epsilon _k \ge 0 \ \ \forall j\ge N_k. \end{aligned}$$
(24)

Since \(\{ \epsilon _k\}\) is decreasing, it is easy to see that the sequence \(\{N_k\}\) is increasing. Furthermore, for each k, since \(\{q_{N_k}\}\subset C\) we can suppose \(Fq_{N_k}\ne 0\) (otherwise, \(q_{N_k}\) is a solution) and, setting

$$\begin{aligned} v_{N_k} = \dfrac{Fq_{N_k}}{\Vert Fq_{N_k}\Vert ^2 }, \end{aligned}$$

we have \(\langle Fq_{N_k}, v_{N_k}\rangle = 1\) for each k. Now, we can deduce from (24) that for each k

$$\begin{aligned} \langle Fq_{N_k}, x+\epsilon _k v_{N_k}-q_{N_k}\rangle \ge 0. \end{aligned}$$

From F is pseudomonotone on H, we get

$$\begin{aligned} \langle F(x+\epsilon _k v_{N_k}), x+\epsilon _k v_{N_k}-q_{N_k}\rangle \ge 0. \end{aligned}$$

This implies that

$$\begin{aligned} \langle Fx, x-q_{N_k}\rangle \ge \langle Fx-F(x+\epsilon _k v_{N_k}), x+\epsilon _k v_{N_k}-q_{N_k} \rangle -\epsilon _k \langle Fx, v_{N_k}\rangle . \end{aligned}$$
(25)

Now, we show that \(\lim _{k\rightarrow \infty }\epsilon _k v_{N_k}=0\). Indeed, since \(u_{n_k}\rightharpoonup z^{*}\) and \(\lim _{k\rightarrow \infty }\Vert u_{n_k}-q_{n_k}\Vert =0,\) we obtain \(q_{N_k}\rightharpoonup z^{*} \text { as } k \rightarrow \infty\). By \(\{q_n\}\subset C\), we obtain \(z^*\in C\). Since F has \(*\)-property, we have

$$\begin{aligned} 0 < \Vert Fz^*\Vert \le \liminf _{k\rightarrow \infty }\Vert Fq_{n_k}\Vert . \end{aligned}$$

Since \(\{q_{N_k}\}\subset \{q_{n_k}\}\) and \(\epsilon _k \rightarrow 0\) as \(k \rightarrow \infty\), we obtain

$$\begin{aligned} 0 \le \limsup _{k\rightarrow \infty } \Vert \epsilon _k v_{N_k} \Vert = \limsup _{k\rightarrow \infty } \left( \dfrac{\epsilon _k}{\Vert Fq_{n_k}\Vert }\right) \le \dfrac{\limsup _{k\rightarrow \infty }\epsilon _k }{\liminf _{k\rightarrow \infty }\Vert Fq_{n_k}\Vert }=0, \end{aligned}$$

which implies that \(\lim _{k\rightarrow \infty } \epsilon _k v_{N_k} = 0.\)

Now, letting \(k\rightarrow \infty\), then the right-hand side of (25) tends to zero by F is uniformly continuous, \(\{u_{N_k}\}, \{v_{N_k}\}\) are bounded and \(\lim _{k\rightarrow \infty }\epsilon _k v_{N_k}=0\). Thus, we get

$$\begin{aligned} \liminf _{k\rightarrow \infty }\langle Fx,x-q_{N_k}\rangle \ge 0. \end{aligned}$$

Hence, for all \(x\in C\) we have

$$\begin{aligned} \langle Fx, x-z^*\rangle =\lim _{k\rightarrow \infty } \langle Fx, x-q_{N_k}\rangle =\liminf _{k\rightarrow \infty } \langle Fx, x-q_{N_k}\rangle \ge 0. \end{aligned}$$

By Lemma 2.1, we get

$$\begin{aligned} z^*\in \mathrm{Sol(C,F)}. \end{aligned}$$

Since (20) and the definition of \(z=P_{Sol(C,F)}(0)\), we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle -z,x_{n_k}-z\rangle =\langle -z,z^*-z\rangle \le 0. \end{aligned}$$
(26)

Combining (18) and (26), we have

$$\begin{aligned} \begin{aligned} \limsup _{k\rightarrow \infty }\langle -z,x_{n_k+1}-z\rangle&\le \limsup _{k\rightarrow \infty }\langle -z,x_{n_k}-z\rangle \\&=\langle -z,z^*-z\rangle \\&\le 0. \end{aligned} \end{aligned}$$
(27)

Hence, by (27), \(\lim _{n\rightarrow \infty }\dfrac{\theta _n}{\gamma _n}\Vert x_n-x_{n-1}\Vert =0\), \(\lim _{k\rightarrow \infty }\Vert x_{n_k+1}-u_{n_k}\Vert =0\), Claim 5 and Lemma 2.4, we have \(\lim _{n\rightarrow \infty }\Vert x_n-z\Vert =0,\) which was to be proved.

Remark 3.2

It should be noted that if the operator F is monotone, the \(*\) property is redundant, see Denisov et al. (2015), Vuong (2018).

4 Convergence Rate

In this section we establish a convergence rate for the so-called relaxed inertial subgradient extragradient method. Actually, we consider the following modification of Algorithm 3.1:

Algorithm 4.2

Let \(\{\alpha _n\}\) be a sequence of nonnegative real numbers which satisfies \(\sum _{n=1}^\infty \alpha _n <+\infty\). Given \(\theta \in [0,1), \gamma \in (0,\dfrac{1}{2}), \ \mu \in (0,1)\) and \(\tau _1>0\), Let \(x_0,x_1\in H\) be arbitrary. Let

$$\begin{aligned} u_n&=x_n+\theta (x_n-x_{n-1}),\\ q_n&=P_C(u_n-\tau _n Fu_n),\\ z_n&=P_{T_n}(u_n-\tau _nFq_n), \end{aligned}$$

where \(T_n:=\{x\in H| \langle u_n-\tau _nFu_n-q_n,x-q_n\rangle \le 0 \}\),

$$\begin{aligned}x_{n+1}=(1-\gamma )x_n+\gamma z_n.\end{aligned}$$

Update

$$\begin{aligned} \tau _{n+1}:= {\left\{ \begin{array}{ll} \min \{\mu \dfrac{\Vert u_n-q_n\Vert ^2+\Vert z_n-q_n\Vert ^2}{2\langle Fu_n-Fq_n,z_n-q_n\rangle },\tau _n+\alpha _n\} \text { if } \langle Fu_n-Fq_n,z_n-q_n\rangle > 0,\\ \tau _n+\alpha _n \text {otherwise}. \end{array}\right. } \end{aligned}$$

Throughout this section, the operator F is assumed to be L-Lipschitz continuous on H and \(\delta\)-strongly pseudo-monotone on C. We now prove that the iterative sequence generated by Algorithm 4.2 converges strongly to the unique solution of problem (VI) with an R-linear rate.

Theorem 4.2

Assume that \(F: H\rightarrow H\) is L-Lipschitz continuous on H and \(\delta\)-strongly pseudo-monotone on C. Let \(\theta \in \bigg [0,\dfrac{\delta }{L+\delta }\bigg )\), \(\mu \in \bigg (\dfrac{\theta }{1+\theta }\dfrac{L}{\delta },\dfrac{1-\theta }{1+\theta }\bigg )\) and \(\tau _1 >\dfrac{\mu }{L}\). Then the sequence \(\{x_n\}\) generated by Algorithm 4.2 converges in norm with an R-linear convergence rate to the unique element z in Sol(C,F).

Proof

Since \(\langle Fz,q_n-z\rangle \ge 0\), the \(\delta\)-strong pseudo-monotonicity of F on C yields the inequality

$$\begin{aligned} \langle Fq_n,q_n-z\rangle \ge \delta \Vert q_n-z\Vert ^2. \end{aligned}$$

This implies that

$$\begin{aligned} \langle Fq_n,z-z_n\rangle = \langle Fq_n,z-q_n \rangle +\langle Fq_n,q_n-z_n\rangle \le -\delta \Vert q_n-z\Vert ^2+\langle Fq_n,q_n-z_n\rangle . \end{aligned}$$
(28)

Now, using (28) and a similar argument as in Claim 1 of Theorem 3.1, we get

$$\begin{aligned} \Vert z_n-z\Vert ^2\le& \ \Vert u_n-z\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert z_n-q_n\Vert ^2-2\delta \tau _n\Vert q_n-z\Vert ^2\\ \le& \ \Vert u_n-z\Vert ^2-(1-\mu \dfrac{\tau _n}{\tau _{n+1}})\Vert q_n-u_n\Vert ^2-2\delta \tau _n\Vert q_n-z\Vert ^2. \end{aligned}$$

Since \(\theta <\dfrac{\delta }{L+\delta }\), it follows that

$$\begin{aligned} \dfrac{\theta }{1+\theta }\dfrac{L}{\delta }<\dfrac{1-\theta }{1+\theta } \end{aligned}$$

therefore there always exists

$$\begin{aligned} \mu \in \bigg (\dfrac{\theta }{1+\theta }\dfrac{L}{\delta },\dfrac{1-\theta }{1+\theta }\bigg ). \end{aligned}$$

From \(\mu <\dfrac{1-\theta }{1+\theta },\) one finds \(\dfrac{1-\mu }{2}>\dfrac{\theta }{1+\theta }\) and \(\mu >\dfrac{ \theta }{1+\theta }\dfrac{L}{\delta }\) implies that \(\delta \dfrac{\mu }{L}>\dfrac{\theta }{1+\theta }\). Fix \(\epsilon \in \bigg (\dfrac{\theta }{1+\theta }, \min \bigg \{\dfrac{1-\mu }{2},\delta \dfrac{\mu }{L}\bigg \}\bigg )\). We have

$$\begin{aligned} \lim _{n\rightarrow \infty }(1-\mu \dfrac{\tau _n}{\tau _{n+1}})=1-\mu >2\epsilon \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\delta \tau _n=\delta \tau \ge \delta \min \bigg \{\tau _1,\dfrac{\mu }{L}\bigg \} =\delta \dfrac{\mu }{L}> \epsilon . \end{aligned}$$

Therefore, there exists \(N\in \mathbb {N}\) such that for all \(n\ge N\), we get

$$\begin{aligned} \Vert z_n-z\Vert ^2 \le& \ \Vert u_n-z\Vert ^2-2\epsilon \Vert q_n-u_n\Vert ^2-2\epsilon \Vert q_n-z\Vert ^2\\ \le& \ \Vert u_n-z\Vert ^2-\epsilon \Vert u_n-z\Vert ^2\\=& \ (1-\epsilon )\Vert u_n-z\Vert ^2. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2&=\Vert (1-\gamma )x_n+\gamma z_n-z\Vert ^2\\&=\Vert (1-\gamma )(x_n-z)+\gamma (z_n-z)\Vert ^2\\&= (1-\gamma )\Vert x_n-z\Vert ^2+\gamma \Vert z_n-z\Vert ^2-(1-\gamma )\gamma \Vert x_n-z_n\Vert ^2\\&=(1-\gamma )\Vert x_n-z\Vert ^2+\gamma \Vert z_n-z\Vert ^2-\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2\\&\le (1-\gamma )\Vert x_n-z\Vert ^2+\gamma (1-\epsilon )\Vert u_n-z\Vert ^2-\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2\ \forall n\ge N. \end{aligned}$$

We also have

$$\begin{aligned} \Vert u_n-z\Vert ^2&=\Vert (1+\theta )(x_n-z)-\theta (x_{n-1}-z)\Vert ^2\\&=(1+\theta )\Vert x_n-z\Vert ^2-\theta \Vert x_{n-1}-z\Vert ^2+\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2&\le (1-\gamma )\Vert x_n-z\Vert ^2+\gamma (1-\epsilon )[(1+\theta )\Vert x_n-z\Vert ^2-\theta \Vert x_{n-1}-z\Vert ^2\\ &\quad+\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2]-\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2\ \forall n\ge N\\&\le (1-\gamma (1-(1-\epsilon )(1+\theta )))\Vert x_n-z\Vert ^2-\gamma (1-\epsilon )\theta \Vert x_{n-1}-z\Vert ^2\\&\quad +\gamma (1-\epsilon )\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2-\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2 \ \forall n\ge N\\&\le (1-\gamma (1-(1-\epsilon )(1+\theta )))\Vert x_n-z\Vert ^2+\gamma (1-\epsilon )\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2\\ &\quad-\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2\ \forall n\ge N. \end{aligned}$$

Since \(\gamma \in (0,\dfrac{1}{2}),\) it implies \(\dfrac{1-\gamma }{\gamma }>1\). Hence, we obtain

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2+\Vert x_{n+1}-x_n\Vert ^2&\le\Vert x_{n+1}-z\Vert ^2+\dfrac{1-\gamma }{\gamma }\Vert x_{n+1}-x_n\Vert ^2\\&\le (1-\gamma (1-(1-\epsilon )(1+\theta )))\Vert x_n-z\Vert ^2\\&\quad +\gamma (1-\epsilon )\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2 \ \forall n\ge N. \end{aligned}$$

This follows that

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2&+\Vert x_{n+1}-x_n\Vert ^2\le (1-\gamma (1-(1-\epsilon )(1+\theta )))\bigg [\Vert x_n-z\Vert ^2\\ &+\dfrac{1}{(1-\gamma (1-(1-\epsilon )(1+\theta ))))}\gamma (1-\epsilon )\theta (1+\theta )\Vert x_n-x_{n-1}\Vert ^2\bigg ]\ \forall n\ge N. \end{aligned}$$

We now show that

$$\begin{aligned} 1-\gamma (1-(1-\epsilon )(1+\theta ))\in (0,1) \end{aligned}$$

and

$$\begin{aligned} \dfrac{1}{1-\gamma (1-(1-\epsilon )(1+\theta ))}\gamma (1-\epsilon )\theta (1+\theta )\in (0,1). \end{aligned}$$

Indeed, since \(\epsilon \in (\dfrac{\theta }{1+\theta }, \min \bigg \{\dfrac{1-\mu }{2},\delta \dfrac{\mu }{L}\bigg \})\), this implies that \(\epsilon >\dfrac{\theta }{1+\theta }\), or, \(1-\epsilon <\dfrac{1}{1+\theta }\) that is \((1-\epsilon )(1+\theta )<1\), hence \(1-\gamma (1-(1-\epsilon )(1+\theta ))\in (0,1)\). It is easy to see that

$$\begin{aligned} \dfrac{1}{1-\gamma (1-(1-\epsilon )(1+\theta ))}\gamma (1-\epsilon )\theta (1+\theta )\in (0,1). \end{aligned}$$

Therefore, we deduce

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2+\Vert x_{n+1}-x_n\Vert ^2\le (1-\gamma (1-(1-\epsilon )(1+\theta )))[\Vert x_n-z\Vert ^2+\Vert x_n-x_{n-1}\Vert ^2]\ \forall n\ge N. \end{aligned}$$

Letting \(a_n:=\Vert x_n-z\Vert ^2+\Vert x_n-x_{n-1}\Vert ^2\) and \(\xi :=(1-\gamma (1-(1-\epsilon )(1+\theta )))\), we get

$$\begin{aligned} \Vert x_{n+1}-z\Vert ^2\le a_{n+1}\le \xi a_n\le \xi ^{n-N+1}a_N=\dfrac{\xi }{\xi ^N}a^N \xi ^n. \end{aligned}$$

Thus, the sequence \(\left\{ x_n \right\}\) converges R-linearly to z, as desired.

Remark 4.3

It should be emphasized that we obtain the linear convergence rate of Algorithm 4.2 instead of the strong convergence as in Shehu et al. (2021).

Remark 4.4

In Theorem 4.2, the \(*\)- property of F is not assumed.

5 Numerical Illustrations

In this section, we present some numerical experiments in solving variational inequality problems. In the first example, we compare the proposed algorithm with three well-known algorithms including Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021), and the subgradient extragradient algorithm (SEGM) of Censor et al. (2012a) and illustrate the convergence of the proposed algorithm. In the second example, we compare the proposed algorithm with Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021) and [Shehu et al. (2021), Algorithm 1]. In the last example, we compare the proposed algorithm with Algorithm 3.1 of Yang (2021) and [Shehu et al. (2021), Algorithm 1]. All the numerical experiments are performed on an HP laptop with Intel(R) Core(TM)i5-6200U CPU 2.3GHz with 4 GB RAM. The programs are written in Matlab 2015a.

Remark 5.5

We usually choose \(\alpha _n=\theta _0\) for Algorithm 3.1 of Yang (2021) because \(\alpha _n\) and \(\theta _n\) have similar roles in their algorithm as well as in our proposed algorithm. Similarly, we take \(\lambda =\tau _0\) for the subgradient extragradient algorithm of Censor et al. (2012a).

In the numerical experiments, we choose parameters as follows:

$$\begin{aligned} &\text{Proposed algorithm:} \ \theta _0=0.5, \theta _n= {\left\{ \begin{array}{ll} \min \{\theta _0, \frac{\gamma _n^2}{\Vert x_n-x_{n-1}\Vert } \} &\text { if } x_n \ne x_{n-1},\\ \theta _0 &\text {otherwise}. \end{array}\right. }\\&\text{Algorithm 3.1:} \ \alpha _n=\theta _0=0.5. \end{aligned}$$

Example 1

Assume that \(F:\mathbb {R}^m \rightarrow \mathbb {R}^m\) is defined by \(F(x) = Mx + q\) with \(M = NN^T + S + D\), N is an \(m\times m\) matrix, S is an \(m\times m\) skew-symmetric matrix, D is an \(m\times m\) diagonal matrix, whose diagonal entries are positive (so M is positive definite), q is a vector in \(\mathbb {R}^m\), and

$$\begin{aligned} C:=\{x \in \mathbb {R}^m: x_i \ge -1, i=1,\cdots ,m\}. \end{aligned}$$

It is clear that F is monotone and Lipschitz continuous with the Lipschitz constant \(L =\Vert M\Vert\). For \(q = 0\), the unique solution of the corresponding variational inequality is \(x^*=0\).

For the experiment, all entries of B, S and D are generated randomly from a normal distribution with mean zero and unit variance. The process is started with the initial \(x_0=(1,..., 1)^T \in \mathbb {R}^m\) and \(x_1 =0.9x_0\). To terminate algorithms, we use the condition \(D_n =\Vert x_n-x^*\Vert ^2 \le \epsilon\) with \(\epsilon =10^{-6}\) or the number of iterations \(\ge\) 2000 for all algorithms. We choose \(\mu =0.5\) for the proposed algorithm, Algorithms 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021) and \(\gamma _n=\frac{1}{n+1}\) for the proposed algorithm. Case 1: We take \(\lambda =\frac{0.7}{\Vert M\Vert }\) for the subgradient extragradient algorithm of Censor et al. (2012a) and \(\tau _0=\frac{0.7}{\Vert M\Vert }\) for Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021) and the proposed algorithm. The numerical results are described in Table 1 and Figs. 1 and 2.

Table 1 Numerical results obtained by other algorithms
Full size table
Fig. 1
figure 1

Comparison of all algorithms with \(m=50\)

Full size image
Fig. 2
figure 2

Comparison of all algorithms with \(m=100\)

Full size image

Case 2: We take \(\lambda =\frac{0.9}{\Vert M\Vert }\) for the subgradient extragradient algorithm of Censor et al. (2012a) and \(\tau _0=\frac{0.9}{\Vert M\Vert }\) for Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021) and the proposed algorithm. The numerical results are described in Table 2 and Figs. 3 and 4.

Table 2 Numerical results obtained by other algorithms
Full size table
Fig. 3
figure 3

Comparison of all algorithms with \(m=50\)

Full size image
Fig. 4
figure 4

Comparison of all algorithms with \(m=100\)

Full size image

Tables 1 and 2 and Figs. 1–4 give the errors of the proposed algorithm, algorithm of Censor et al. (2012a), Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021) as well as their execution times. They show that the proposed algorithm is less time consuming and more accurate than those of Yang et al. (2018), Yang (2021), Censor et al. (2012a).

In Fig. 5 we illustrate the convergence rate of the proposed algorithm for different choices of the \(\theta\) with \(\lambda =\frac{0.7}{\Vert M\Vert }, \mu =0.5, m=50\) and \(\gamma _n=\frac{1}{n+1}\).

Fig. 5
figure 5

Convergence rate of the proposed algorithms for different choice of the \(\theta\)

Full size image

In Fig. 6 we illustrate the convergence rate of the proposed algorithm for different choices of the \(\gamma _n\) with \(\lambda =\frac{0.7}{\Vert M\Vert }, \mu =0.5, m=50\) and \(\theta =0.5\).

Fig. 6
figure 6

Convergence rate of the proposed algorithm for different choice of the \(\gamma _n\)

Full size image

Figures 5 and 6 show that the rate of convergence of the proposed algorithm in general depends strictly on the convergent rate of sequence of \(\gamma _n\) and \(\theta\).

Example 2

In the second example, we study an important Nash–Cournot oligopolistic market equilibrium model, which was proposed originally by Murphy et al. (1982) as a convex optimization problem. Later, Harker reformulated it as a monotone variational inequality in Harker (1984). We provide only a short description of the problem, for more details we refer to Facchinei and Pang (2003), Harker (1984), Murphy et al. (1982). There are N firms, each of them supplies a homogeneous product in a non-cooperative fashion. Let \(q_i \ge 0\) be the ith firm’s supply at cost \(f_i(q_i)\) and p(Q) be the inverse demand curve, where \(Q \ge 0\) is the total supply in the market, i.e., \(Q =\sum _{i=1}^{N} q_i\). A Nash equilibrium solution for the market defined above is a set of nonnegative output levels \((q_1^*,q_2^*,...q_N^*)\) such that \(q_i^*\) is an optimal solution to the following problem for all \(i= 1,2 ..... N\):

$$\begin{aligned} \max _{q_i \ge 0} {q_i p (q_i + Q_i^*) - f_i (q_i)} \end{aligned}$$
(29)

where

$$\begin{aligned} Q_i^* = \sum _{j=1, j\not = i}^N q_j^*. \end{aligned}$$

A variational inequality equivalent to (29) is (see Harker (1984))

$$\begin{aligned} \text {find} \quad (q_1^*,q_2^*,...q_N^*) \in \mathbb {R}^N_{+} \quad \text {such that} \quad \langle F(q^*), q-q^*\rangle \ge 0 \quad \forall q \in \mathbb {R}^N_{+}, \end{aligned}$$

where \(F(q^*) = (F_1(q^*), F_2 (q^*), ... F_N(q^*))\) and

$$\begin{aligned} F_i(q^*) = f_i'(q_i^*) -p \left( \sum _{j=1}^{N} q_j^*\right) - q_i^*p' \left( \sum _{j=1}^{N} q_j^*\right) . \end{aligned}$$

As in the classical example of the Nash-Cournot equilibrium Harker (1984), Murphy et al. (1982), we consider an oligopoly with N firms, each with the inverse demand function p and the cost function \(f_i\) take the form

$$\begin{aligned} p(Q) = 5000 ^{1/1.1} Q^{-1/1.1} \quad \text {and} \quad f_i(q_i) = c_i q_i +\frac{\beta _i}{\beta _i + 1} L_i^{\frac{-1}{\beta _i}} q_i^{\frac{\beta _i+1}{\beta _i}}. \end{aligned}$$

Each entry of \(c_i, L_i\) and \(\beta _i\) are drawn independently from the uniform distributions with the following parameters

$$\begin{aligned} c_i \sim \mathscr U (1,100), \quad L_i \sim \mathscr U (0.5,5), \quad \beta _i \sim \mathcal U (0.5, 2). \end{aligned}$$

We choose \(\mu =0.5, \tau =\tau _0=0.01\) for the proposed algorithm, Algorithm 1 of Yang et al. (2018), Algorithm 3.1 of Yang (2021), \(\gamma _n=\frac{1}{n+1}\) for the proposed algorithm and \(\theta = 0.9, \rho _n = \rho = 0.4\) for Shehu et al. [Shehu et al. (2021), Algorithm 1]. The process is started with the initial \(x_0=10*(1,..., 1)^T \in \mathbb {R}^N\) and \(x_1 =0.9*x_0\) and stopping conditions is \(\text {Residual} := \Vert u_n - q_n\Vert \le 10^{-10}\) or the number of iterations \(\ge\) 200 for all algorithms. The numerical results are described in Table 3 and Figs. 7 and 8.

Table 3 Numerical results are obtained by other algorithms
Full size table
Fig. 7
figure 7

Comparison of all algorithms with \(N=500\)

Full size image
Fig. 8
figure 8

Comparison of all algorithms with \(N=1000\)

Full size image

Example 3

Consider the following fractional programming problem:

$$\begin{aligned} \min f(x)=\frac{x^TQx+a^Tx+a_0}{b^Tx+b_0} \end{aligned}$$

subject to \(x \in X:=\{x \in \mathbb {R}^m: b^Tx+b_0>0\}\), where Q is an \(m \times m\) symmetric matrix, \(a, b \in \mathbb {R}^m\), and \(a_0, b_0 \in \mathbb {R}\). It is well known that f is pseudoconvex on X when Q is positive-semidefinite. We consider the following cases:

Case 1:

$$\begin{aligned} Q = \begin{pmatrix} 5 &{} -1 &{} 2 &{} 0 \\ -1 &{} 5 &{} -1 &{} 3 \\ 2 &{} -1 &{} 3 &{} 0\\ 0 &{} 3 &{} 0 &{} 5 \end{pmatrix}, a= \begin{pmatrix} 1\\ -2\\ -2\\ 1 \end{pmatrix}, b= \begin{pmatrix} 2\\ 1\\ 1\\ 0 \end{pmatrix}, a_0=-2, b_0=4. \end{aligned}$$

We minimize f over \(C := \{x \in \mathbb {R}^4 : 1 \le x_i \le 10, i = 1,\cdots , 4\} \subset X\). It is easy to verify that Q is symmetric and positive definite in \(\mathbb {R}^4\) and consequently, f is pseudo-convex on X.

We choose \(\mu =0.5, \tau =\tau _0=0.5\) for the proposed algorithm and Algorithm 3.1 of Yang (2021), \(\theta = 0.9, \rho _n = \rho = 0.4, \alpha _n = \frac{1}{n\sqrt{n}}\) for [Shehu et al. (2021), Algorithm 1] and \(\alpha _n = \frac{1}{n\sqrt{n}}, \gamma _n=\frac{1}{\gamma '(n+\gamma '')},\) where \(\gamma ' = 10^6, \; \gamma '' = 10^5\) for the proposed algorithm.

The process is started with the initial \(x_0=(20,-20, 20,-20)^T\) and \(x_1 =0.9*x_0\) and stopping conditions is \(\text {Residual} := \Vert u_n - q_n\Vert \le 10^{-10}\) or the number of iterations \(\ge\) 1000 for all algorithms. The numerical results are described in Fig. 9 and Table 4.

Fig. 9
figure 9

Comparison of all algorithms

Full size image
Table 4 Numerical results obtained by other algorithms
Full size table

Case 2: In the second experiment, we make the problem even more challenging. Let matrix \(A:\mathbb {R}^{m \times m} \rightarrow \mathbb {R}^{m \times m}\), vectors \(c, d,y_0 \in \mathbb {R}^m\) and \(c_0,d_0\) be generated from a normal distribution with mean zero and unit variance. We put \(e=(1,1,\cdots ,1)^T \in \mathbb {R}^m, Q=A^TA+I, a:=e+c, b:=e+d, a_0=1+c_0, b_0=1+d_0\). We minimize f over \(C := \{x \in \mathbb {R}^m : 1 \le x_i \le 10, i = 1,\cdots , m\} \subset X\). Because Matrix Q is symmetric and positive definite in \(\mathbb {R}^m\), f is pseudo-convex on X.

The process is started with the initial \(x_0:=m*y_0\) and \(x_1 =0.9*x_0\), stopping conditions and parameters as in Case 1. The numerical results are described in Figs. 10 and 11 and Table 5.

Table 5 Numerical results obtained by other algorithms
Full size table
Fig. 10
figure 10

Comparison of all algorithms with \(m=30\)

Full size image
Fig. 11
figure 11

Comparison of all algorithms with \(m=50\)

Full size image