1 Introduction

Modern societies depend on the continuous and proper functioning of critical infrastructure networks such as transportation, telecommunications, electric power, natural gas, and water distribution, among others. Such infrastructure networks provide the fundamental services that support the economic productivity, security, and quality of life of citizens. However, infrastructure networks are subject to be affected by different types of disruptive events, including random failures, malevolent attacks, and natural disasters. Hence, for several years, the United States, as well as many countries around the globe, have been interested in effectively preparing for and responding in a timely manner to such disruptive events (e.g., “secure, functioning, and resilient critical infrastructures” (White House 2013)). Therefore, it is increasingly important to not only protect current infrastructure networks against disruption, but to be able to restore them once they have been disrupted.

Several works in the literature have studied the restoration problem of an infrastructure network. They provide methods and algorithms with different objectives to restore the functionality of an infrastructure network following the occurrence of a disruptive event (e.g., Xu et al. 2007; Yan and Shih 2009; Matisziw et al. 2010; Nurre et al. 2012; Aksu and Ozdamar 2014; Vugrin et al. 2014; Kamamura et al. 2015; Fang et al. 2016; Hu et al. 2016; Fang and Sansavini 2017; Fu et al. 2017). However, infrastructure networks are not isolated from each other, but rather they rely on one another in different ways for their proper functioning. Hence, they exhibit interdependency, where two infrastructure networks are said to be interdependent if there is a bidirectional relationship between them through which the state of each infrastructure is dependent on the state of the other (Rinaldi et al. 2001). Rinaldi et al. (2001) classified the interdependencies between infrastructure networks into four categories: (i) physical interdependency, an output from an infrastructure network is an input to another one and vice versa, (ii) cyber interdependency, if an infrastructure network depends on information transmitted through an information infrastructure, (iii) geographical interdependency, if two infrastructure networks are affected by the same local disruptive event, and (iv) logical interdependency, all other types of interdependencies. In this paper, the authors consider the physical interdependency among different infrastructure networks. However, the work in this paper could be extended to consider other types of interdependencies such as geographical interdependency, which could be incorporated in this work by considering the co-location of disrupted components from multiple interdependent infrastructure networks. Moreover, other types of interdependencies (i.e., cyber and logical) could be incorporated as well as long as they can be described in a similar manner by the logic discussed in this work.

Rinaldi (2004) categorized the models and techniques that consider interdependencies among infrastructure networks into six broad categories: (i) aggregate supply and demand tools (e.g., Lee et al. 2007; Min et al. 2007; Caschili et al. 2015), (ii) dynamic simulations (e.g., Hernandez-Fajardo and Dueñas-Osorio 2013; Zhang et al. 2016), (iii) agent-based models (e.g., Panzieri et al. 2004; Oliva et al. 2010), (iv) physics-based models (e.g., An et al. 2003; Unsihuay et al. 2007), (v) population mobility models (e.g., Casalicchio et al. 2009), and (vi) Leontief input-output models (e.g., Haimes and Jiang 2001; Reed et al. 2009). The model proposed in this paper falls in the aggregate supply and demand tools category by Rinaldi (2004), which evaluates the total demands, in the form of services or commodities, for an infrastructure network in a region and the ability to supply them. In addition, it is classified as a network-based approach according to a similar categorization by Ouyang (2014) for the approaches of modeling and simulation in infrastructure networks considering their interdependencies. The network-based approach (Ouyang 2014) describes the infrastructures as networks of nodes, links, and inter-links (i.e., nodes represent the different components of the infrastructures, links represent the physical relationship between the nodes, and inter-links represent the interdependencies among different infrastructures).

Interdependencies across critical infrastructure networks can improve their operational efficiency since they generally lead to greater centralization of control, hence they play a significant role in the continuous, reliable operation of infrastructure network (Rinaldi et al. 2001). However, the proliferation of interdependencies among infrastructure networks may potentially cause them to be highly vulnerable to disruption. Consequently, if the operability of an infrastructure network is affected by the occurrence of a disruptive event, this could lead to cascading inoperability in some or all dependent infrastructure networks due to their interdependencies (Little 2002; Wallace et al. 2003; Buldyrev et al. 2010; Eusgeld et al. 2011). The high vulnerability of the infrastructure networks, due to their increased interdependencies, has been shown through several recent worldwide events, including the 1998 Canada ice storm (Chang et al. 2007), the 2001 US World Trade Center attack (Mendonça and Wallace 2006), the 2003 North American blackout (U.S.-Canada Power System Outage Task Force 2004), and the 2010 Chile earthquake and tsunami (Wen et al. 2011), among others. Therefore, it is crucial for decision makers to account for interdependencies between infrastructure networks when preparing the plans for their recoverability to obtain a realistic analysis of their performance (Holden et al. 2013). In addition, performing restoration activities for each infrastructure network independently could lead to improper utilization of available resources, wasted time, and may even cause further disruptions when improperly scheduled (Baidya and Sun 2017). As a result, the restoration of such interdependent infrastructure networks following a disruptive event has become more challenging for decision makers as the increase in interdependency among infrastructure networks magnifies the complexity associated with planning for their post-disruption recovery and operation.

The National Infrastructure Protection Plan (DHS 2013) highlights the importance of addressing the risks associated with the interdependencies among different infrastructure networks as being “essential to enhancing critical infrastructure security and resilience”. Hence, it is important to have resilient infrastructure networks accounting for the interdependencies between them, thus the motivation of this paper. The Infrastructure Security Partnership (2011) defined resilient infrastructure networks as the infrastructure networks that would “prepare for, prevent, protect against, respond or mitigate any anticipated or unexpected significant threat or event” and “rapidly recover and reconstitute critical assets, operations, and services with minimum damage and disruption”.

This paper addresses the interdependent networks restoration problem (INRP). INRP seeks to find the minimum-cost restoration strategy of a system of interdependent networks following the occurrence of a disruptive event that enhances its resilience considering the availability of time and resources. The goal of this paper is to help decision makers plan for recovery following the occurrence of a disruptive event, to procure strategies that center not only on recovering the system promptly, but also such that the weighted average performance of the system is maximized during the recovery process (i.e., enhancing its resilience). Accordingly, to solve the INRP, the authors propose a resilience-driven multi-objective optimization model, formulated using mixed-integer programming (MIP). Hence, the primary objective of this work is to: (i) prioritize the restoration of the disrupted components for each infrastructure network, and (ii) assign and schedule the prioritized networks components to the available work crews, such that the resilience of the system of interdependent infrastructure networks is enhanced considering a reduction in the performance of disrupted components based on multiple different disruption scenarios and taking into consideration the physical interdependency among networks. By studying the resilience of the interdependent infrastructure networks in this work, the authors unveil the effects on their performance of both the magnitude of the disruptive event (i.e., network vulnerability) and the trajectory of recovery of their disrupted components (i.e., network recoverability). Note that in this paper we focus on improving the resilience of the system through actions that are made only after a disaster has occurred, as this mimics a plethora of realistic situations where disasters occur unexpectedly, and where all the decision center on actions that can recover the system efficiently. However, the proposed post-disaster model could be easily extended to also consider mitigation actions, such as retrofitting components or increasing the availability of resources.

This paper builds upon initial work by Almoghathawi et al. (2019), which assumes (i) a binary status of the networks components (i.e., either fully disrupted or undisrupted), (ii) a restoration with a non-preemptive recovery process (i.e., work crews cannot switch between components during restoration), and (iii) completion dependence between nodes in interdependent networks (i.e., a dependent node cannot function unless the node or nodes that it depends on are completely functioning). This paper addresses these limitations and also explores recovery strategies based on different assumptions and considerations related to the assignment of the available work crews and the functionality of disrupted networks components.

The remainder of the paper is organized as follows. Section 2 provides brief background about the restoration of interdependent networks, including an overview of network resilience and some of the most relevant works in the literature. Section 3 presents the proposed optimization model to solve the INRP, including notation, assumptions, objectives, and constraints used. In Section 4, an illustrative example is presented through a system of interdependent infrastructure networks in Shelby County, TN, affected by hypothetical earthquakes of different magnitude. Different considerations for the recovery process of the disrupted networks components are discussed in Section 5. Finally, Section 6 provides concluding remarks and suggests some relevant ideas for future work.

2 Background

In this section, the authors discuss the most relevant works in the literature that study the restoration of interdependent networks. Moreover, the authors give an overview regarding the resilience of networks.

2.1 Interdependent Network Restoration

The literature has recently addressed the restoration problem of interdependent networks. Accordingly, several approaches have been developed that could best be described with two groups: (i) infrastructure-specific approaches, which consider the physics of different infrastructures (e.g., DC power flow model) and hence could be applied on these infrastructure networks only, and (ii) general approaches, which could be applied to any system of interdependent infrastructure networks.

As for the infrastructure-specific approaches for the interdependent network restoration, Coffrin et al. (2012) studied the problem of restoring two physically interdependent infrastructure networks, power and gas networks. They integrated two network-specific flow models (i.e., a linearized DC flow model for the power network and a maximum flow model for the gas network) using MIP with the objective of maximizing the weighted sum of interdependent demand over the restoration time horizon and solved them using a randomized adaptive decomposition approach. The proposed models aim to find: (i) the set of disrupted components to be restored, and (ii) the restoration order of the selected disrupted components. However, the proposed model did not consider different restoration durations for the disrupted networks components in addition for being developed for specific types of infrastructure networks. Baidya and Sun (2017) provided an optimization-based restoration strategy that aims to prioritize the restoration activities between two physically interdependent networks, power system and communication networks, considering their physics-based properties. The proposed approach is formulated using MIP with the objective of activating every node in both networks with the minimum number of activation/energization of branches. Tootaghaj et al. (2017) focused on the cascading disruptions impact on the physically interdependent power grid and communication network considering disruptions in power networks only. Accordingly, they proposed a two-phase recovery approach: (i) avoid further cascade, for which they formulate the minimum cost flow assignment problem using linear programming (LP) with the objective of finding a DC power flow setting that stops the cascading failure at minimum cost, and (ii) provide a recovery schedule, for which they formulate the recovery problem using MIP with the objective of maximizing the total amount of delivered power over the recovery horizon and solve it using two heuristic approaches: a shadow-pricing heuristic and a backward algorithm.

Regarding the general approaches for setting up the restoration of interdependent networks, Lee et al. (2007) proposed an interdependent layer network model using MIP that accounts for different interdependencies among the infrastructure networks. The objective of the model is to minimize the flow costs along with the slack costs but not including the cost associated with the restoration process of the disrupted components. Moreover, it focuses only on determining the set of disrupted components (i.e., links) of the interdependent infrastructure networks that need to be recovered to restore the performance of each of the infrastructure networks to the functionality level prior to the occurrence of a disruptive event. Hence, the proposed model does not specify the time at which they need to be restored (i.e., the prioritizing of the restoration process for the disrupted components) or which work crew is assigned to restore which disrupted component. In addition, the model assumes binary status of network components (i.e., disrupted or not disrupted). On the other hand, Gong et al. (2009) focused only on the scheduling problem of a predetermined set of disrupted components for interdependent infrastructure networks with predefined due dates for them. They provided a multi-objective restoration planning model, using MIP, to find the optimal restoration schedule for disrupted components and solved it using a logic-based benders decomposition approach. The objective of the model is to minimize the weighted sum of the cost, tardiness, and makespan that are associated with the restoration process of the disrupted components. Cavdaroglu et al. (2013) and Sharkey et al. (2015) integrated the two approaches by Lee et al. (2007) and Gong et al. (2009) by providing a MIP model that integrates: (i) determining the set of disrupted components (i.e., links) to be restored, along with (ii) assigning and scheduling them to work crews, and solved it using a suggested heuristic solution method. The objective of this model is to minimize the total cost of flow, unsatisfied demand, and installation and assignment that is associated with the full restoration of a set of infrastructure networks accounting for the interdependencies among them. However, they assumed binary status of network components (i.e., disrupted or not disrupted) which could be restored with a non-preemptive recovery process. Holden et al. (2013) proposed an extended network-flow approach to simulate the performance of a set of infrastructure networks at a local scale (i.e., community scale) considering the physical interdependency among them. Hence, they provided an optimization model using LP that aims to find the optimal performance of the infrastructure networks such that the total cost associated with production, storage, commodity flow, discharge, and shortage (i.e., unsatisfied demand) is minimized. However, the proposed approach does not explicitly discuss what are the set of disrupted networks components, their restoration durations, and their restoration priorities. Also, the approach does not consider the availability of the work crews; hence determine their restoration schedule. Di Muro et al. (2016) studied the recovery problem of the system of physically interdependent networks in the presence of cascading failures to mitigate its breakdown. They considered restoring the disrupted network components (i.e., nodes) that are located at the boundary of the largest connected component (i.e., functional network) and reconnect them to it considering the probability of recovery that halts the cascade for interdependent networks. They developed a stochastic model for the competition between the cascading failures and the restoration strategy for the disrupted components and solved it theoretically using random node percolation theory. However, they considered a random recovery strategy for the disrupted nodes. In addition, they have not considered the availability of work crews. González et al. (2016) studied the interdependent network design problem considering their physical and geographical interdependencies. They formulated an MIP model to determine: (i) the set of disrupted components to be restored, and (ii) the order of their restoration, with the objective of minimizing the overall cost associated with preparing geographical locations, restoration of disrupted components, unbalance from disconnection, and flow. However, the model does not specify which work crews should restore particular disrupted components. Moreover, they assumed binary status of network components (i.e., disrupted or not disrupted). Zhang et al. (2018) provided an optimization model that determines the optimal allocation of restoration resources for a set infrastructure networks that are physically interdependent such that its resilience is enhanced. The proposed model aims to: (i) allocate limited resources to interdependent infrastructure networks, and (ii) determine the optimal budget for restoration following a specific disruptive event, solved using a genetic algorithm approach. However, their work focuses only on the allocation of restoration resources (i.e., budget) for a set of infrastructure networks following a disruptive event.

In this paper, the authors propose a general resilience-driven multi-objective optimization model to solve the INRP using MIP with the objectives of: (i) maximizing the resilience of the system of interdependent infrastructure networks, and (ii) minimizing the total costs associated with the restoration process (i.e., flow, restoration, and disruption costs). The proposed model expands on Almoghathawi et al. (2019), by not only considering: (i) binary status of the networks components (i.e., either fully disrupted or undisrupted), (ii) complete dependence between nodes (i.e., a dependent node cannot be functioning unless the node or nodes that it depends on are completely functioning), and (iii) non-preemptive recovery process, but also considering: (iv) partial disruptions for the disrupted network components, (v) partial recovery of the disrupted network components considering their different restoration rates which allows for a preemptive recovery process, and (vi) partial dependence between nodes (i.e., a dependent node could be partially functioning if the node or nodes it depends on are partially functioning as well). Furthermore, the proposed optimization model takes into account the availability of the time and network-specific resources (i.e., a set of available resources or work crews or that are specific to each network). Different recovery strategies are explored considering different assumptions for work crews and disrupted component functionality. The proposed optimization model focuses on maximizing the resilience of the interdependent infrastructure networks to retain their performance level prior to the disruption. Hence, the disrupted networks components might: (i) not be all restored, especially if they do not influence the resilience of the other networks, or (ii) restored partially, if they could be functioning partially. Next section gives and overview regarding network resilience and how it can be quantified.

2.2 Network Resilience

Resilience is generally defined as the ability of an entity or system to withstand, adapt to, and recover from a disruptive event in a timely manner (Barker et al. 2017). Resilience has been quantified by several different approaches that exist in the literature (Hosseini et al. 2016), including: the normalized shaded area underneath the performance function curve of a system (Cimellaro et al. 2010), topological measures (Rosenkrantz et al. 2009), the ratio of the probability of failure and recovery (Li and Lence 2007), among others. In this paper, the authors consider the paradigm proposed by Henry and Ramirez-Marquez (2012) to describe and quantify the resilience of a system or a network based on its performance, as shown in Fig. 1, which is considered by several papers in the literature (e.g., Barker et al. 2013; Baroud et al. 2014; Pant et al. 2014). In this work, the proposed model aims to maximize the weighted average performance of the system between the occurrence of a disruptive event and when the system has been fully recovered, in addition to procuring a quick recovery. Thus, the proposed model seeks to determine the distribution, crew assignment, and recovery strategies that maximize the performance of the system immediately after a disruptive event (i.e., minimizing the effects of such event) and during its recovery process. That is, the proposed model determines the set of post-disruption actions that would lead to the maximum resilience achievable, as it simultaneously seeks to reduce the damage propagation effects and the recoverability of the system.

Fig. 1
figure 1

Illustration of decreasing network performance, (φ), across different transition states over time (adapted from Henry and Ramirez-Marquez (2012))

Full size image

Figure 1 shows three transition states with regard to the operation within a network: (i) the original state, S0, which is the state of the network from time t0 until the occurrence of a disruptive event, ej at time te, (ii) the disrupted state, Sd, which is the state resulted following the maximum disruption that occurred during the period (te, td) and will last until the recovery process starts at time ts, and (iii) the recovered state, Sf, which is the state of the network upon the completion of the recovery process at time tf, which is not necessarily be same as S0 as it could be lower or higher than S0. The performance of the network (e.g., flow, connectivity, unsatisfied customers, or delay) across these different states over time is measured by the function φ(t), which describes the behavior of the network: (i) prior to the occurrence of a disruptive event, φ(t0), (ii) after being disrupted, φ(td), and (iii) after being recovered to a desired level, φ(tf). Note that the performance of the system (network) following a disruptive event, φ(td), could decrease as a result of the disruption (e.g., flow, connectivity, utilization of asset), as illustrated in Fig. 1 (Henry and Ramirez-Marquez 2012).

Henry and Ramirez-Marquez (2012) define network resilience, denoted by Я, as the time dependent ratio of the recovered performance of the network over the maximum loss in its performance following a disruptive event, ej, from a set J of possible disruptive events (i.e., Я(t) = Recovery(t)/Loss(td), td < t). Hence, Я(t) quantifies the resilience of the network at time t, td < t < tf, as shown in Fig. 1. There are two primary dimensions of the system (network) resilience: (i) vulnerability, or the magnitude of damage to a network caused by a disruptive event (Jönsson et al. 2008), and (ii) recoverability, or the speed at which a disrupted network recovers to a desired level of performance following the occurrence of a disruptive event (Rose 2007).

Hence, network resilience can be demonstrated when the performance of the network at S0, φ(t0), is affected by a disruptive event, ej, at time te. Starting at this time, the network performance degrades until time td. Then, the network will stay at the disrupted state Sd, which has an associated performance level of φ(td), until the restoration process commences at time ts. The restoration process continues until the network reaches the desired state Sf, which has an associated performance level of φ(tf). Thus, the resilience at time t (i.e., ts < t < tf), Я(t), for networks with decreasing performance when disrupted depicted in Fig. 1, can be mathematically represented by Eq. (1), where φ(t| ej) − φ(td| ej) represent the recovery of the network performance at time t, and φ(to) − φ(td| ej) represent the loss of the network performance up to time td. Hence, Eq. (1) considers both the vulnerability and recoverability of the network. That is, the numerator of Eq. (1) shows the speed of network recovery to a desired level of performance (i.e., recoverability), and the denominator of Eq. (1) presents the magnitude of loss to the network caused by ej, (i.e., vulnerability).

(1)

According to Eq. (1), the value of the network resilience, Яφ(t| ej), at time t given the occurrence of a disruptive event, ej, is between 0 and 1 (i.e., Яφ(t| ej) ∈ [0, 1]), where Яφ(t| ej) = 1 indicates the network is fully resilient. In this work, the authors consider the flow as the measure for the performance of networks. Hence, the performance of the networks in or study decreases following the occurrence of a disruptive event, as shown in Fig. 1. That is, the maximum flow of an interdependent infrastructure network from its multiple supply nodes to its multiple demand nodes is considered to be the function by which the network performance is measured, and its resilience is determined, using Eq. (1).

3 Optimization Model

In this paper, the authors propose a multi-objective resilience-driven optimization model for solving the INRP using MIP, aiming to maximize the resilience of the collective set of networks while minimizing the costs associated with the restoration process.

3.1 Assumptions

There are several assumptions and considerations for the proposed optimization model to solve the INRP:

  • Each infrastructure network consists of a set of components (used to generally refer to nodes and links) that are subjected to be partially or completely disrupted.

  • Each disrupted component in each infrastructure network can be restored with different restoration rates (i.e., recovery durations are not fixed for all disrupted components).

  • Each disrupted component in each infrastructure network could be partially recovered according to their restoration rates, which allow for a preemptive recovery process. Accordingly, different work crews can work to restore the same disrupted network component at different time periods.

  • A single work crew can work on restoring a disrupted network component at a time.

  • Each supply node, demand node, and link in each infrastructure network has a known supply capacity, demand, and flow capacity, respectively.

  • The flow costs through each link, disruption (i.e., unmet demand) costs, and restoration costs for disrupted components in each infrastructure network are known and fixed.

  • The physical interdependence among different infrastructure networks is considered. That is, for a node in an infrastructure network to be operational, it requires a specific node from another infrastructure network to also be operational. Consequently, the proposed model considers cascading effects as a result of such interdependency. However, cascading disruptions that occur during the restoration process are not considered in this work and are considered for future work. Hence, the model could be extended to consider failures propagation time to capture such cascading disruption.

  • The model allows for partial interdependencies considering the partial status of disruption or the partial recovery of a disrupted component, where a node could be functioning partially if the other node upon which it depends is also functioning partially. However, the case where partially functional components might cause cascading effects on dependent components is not considered. On the other hand, if it is known in advance that a component would fail as a direct consequence of another node failing due to its partial functionality, then such could be incorporated in the proposed model through the interdependency parameter.

  • The number of available work crews for each infrastructure network (i.e., infrastructure-specific resources) for the restoration of its disrupted components is known and could be different from one infrastructure network to another, where each work crew in each infrastructure network can work on a single disrupted component at a time.

  • Regardless of the extent of disruption, the network flows are under control (but subject to functionality constraints).

3.2 Notation

The sets, parameters, and decision variables of the proposed optimization model to solve the INRP are shown in Tables 1, 2, and 3, respectively.

Table 1 Sets of the restoration model
Full size table
Table 2 Parameters of the restoration model for network k ∈ K
Full size table
Table 3 Decision variables of the restoration model for network k ∈ K at time t ∈ T
Full size table

As shown in Table 1, Rk represents the available work crews for each infrastructure network for restoration. In this work, the transition of a work crew from one disrupted component to another in two consecutive time periods is not considered, though the model could be extended to account for such behavior.

The restoration rates of nodes and links, \( {\gamma}_{it}^k \) and \( {\delta}_{ijt}^k \), respectively, represent the percentage of recovery of each component that can be accomplished during time period t ∈ T. Moreover, as stated in Table 2, terms \( {a}_i^k \) and \( {b}_{ij}^k \)refer to the number of units in node i ∈ Nk and link(i, j) ∈ Lk, respectively, which can work independently from each other. Consequently, the status of nodes and links is represented by the operational units in each one of them. That is, if a network component has more than one unit, it could be functioning partially depending on the number of operational units in that component following a disruption in two cases: (i) if it is not completely disrupted, or (ii) after a partial recovery. On the other hand, in case if a disrupted network component cannot be operational unless it is fully recovered, the number of units in this network component is assumed to be one, since the component cannot be functioning partially.

The amount of unmet demand at node \( i\in {N}_d^k \) in network k ∈ K at time t ∈ T is determined by the flow reaching to that demand point. Moreover, the number of operational units in node i ∈ Nk and link (i, j) ∈ L′k in network k ∈ K at time t ∈ T is determined by the their status (i.e., \( {y}_{it}^k \) and \( {z}_{ijt}^k \)), respectively. Furthermore, the proposed model considers the capacity of disrupted components based on which the flow through such components is affected. If a component is completely disrupted, its capacity is reduced to 0 (i.e., no flow can go thought this component until it is restored). Accordingly, the model tries to retain the optimal configuration of the network prior to the occurrence of the disruptive event with the goal of enhancing the resilience measure of the system of networks to a desired level with the minimum cost associated with the restoration process. Hence, there could be some disrupted components that are not restored if they have no influence on the resilience of the system or their restoration cost is higher than what they could save in flow cost. As a result, the flow from a supply node to a demand node could go through a different route than the route used prior to disruption and may change at any point during the restoration.

3.3 Objectives

The proposed mathematical model for solving the INRP focuses on optimizing two main objectives: (i) maximizing a measure of resilience for the collective set of networks, and (ii) minimizing the total costs associated with the restoration process. The two objectives are explained in more detail in the following sections.

3.3.1 Resilience Objective

The authors assume that resilience is a function of unmet demand, \( {q}_{it}^k \), or the extent to which demand in node i of network k is not being met at time t considering a reduction in performance of disrupted networks components; hence network performance is based on multiple different disruption scenarios. Accordingly, slacks represent the loss in the maximum flow, and reducing them to a desired level represents a means to measure the effectiveness of the restoration process. Hence, the first objective function, the resilience of the system of interdependent infrastructure networks, is represented mathematically by Eq. (2), where \( {\mu}_t^k \) is the weight of network k ∈ K at time t ∈ T. Moreover, \( {Q}_o^k \) refers to the total original slacks at all demand nodes in network k ∈ K at time t0 and \( {Q}_d^k \)refers to the total slacks at all demand nodes in network k ∈ K at time td following a disruptive event, ej, as shown in Fig. 1. Hence, \( \left({Q}_d^k-{\sum}_{i\in {N}_d^k}{q}_{it}^k\right) \) represents the recovery of network k ∈ K at time t ∈ T and \( \left({Q}_d^k-{Q}_0^k\right) \) represents the total loss in network k ∈ K following a disruptive event.

$$ \max\ \sum \limits_{k\in K}\sum \limits_{t=1}^{\tau }{\mu}_t^k\left[\frac{Q_d^k-{\sum}_{i\in {N}_d^k}{q}_{it}^k}{Q_d^k-{Q}_o^k}\right] $$
(2)

Equation (2) represents an improvement to the resilience-driven objective function from Almoghathawi et al. (2019) and Almoghathawi and Barker (2019), in which the dynamics of recovery was not captured.

3.3.2 Cost Objective

Three different costs associated with the restoration process are considered in the optimization model for solving the INRP: (i) flow cost, (ii) disruption cost (i.e., penalties of unmet demand), and (iii) restoration cost. The flow cost is a unitary cost for the flow through link (i, j) ∈ Lk in network k ∈ K. The disruption cost is a unitary cost of unmet demand at node \( i\in {N}_d^k \) in network k ∈ K. The restoration cost is a fixed cost for restoring node i ∈ N′k and link (i, j) ∈ L′k in network k ∈ K based on their restoration rates, \( {\gamma}_{it}^k \) and \( {\delta}_{ijt}^k \), respectively. Hence, the system cost (second objective function) can be represented mathematically by Eq. (3).

$$ \min \sum \limits_{k\in K}\sum \limits_{t\in T}\left(\sum \limits_{\left(i,j\right)\in {L}^k}{f}_{ij}^k{x}_{ij t}^k+\sum \limits_{i\in {N}_d^k}{p}_{it}^k{q}_{it}^k+\sum \limits_{r\in {R}^k}\left[\sum \limits_{i\in {N}_k^{\prime }}{g}_{it}^k{\gamma}_{it}^k{v}_{it}^{kr}+\sum \limits_{\left(i,j\right)\in {L}^{\prime k}}{h}_{ij t}^k{\delta}_{ij t}^k{w}_{ij t}^{kr}\right]\right) $$
(3)

Not explicitly considered in the cost objective is the travel cost of work crews (e.g., from optimal resource location sites (Mooney et al. 2019)). However, the current model could be extended to consider it, by keeping track of the origin and destination of each work crew.

3.4 Constraints

Several sets of constraints are considered in the proposed optimization model for solving the INRP: (i) network flow constraints, (ii) restoration constraints, (iii) interdependence constraints, (iv) logical link constraints for the network flow with restoration, and (v) constraints governing the nature of the decision variables. All sets of constraints are explained and formulated in the following sections.

3.4.1 Network Flow Constraints

For each infrastructure network, the flow conservation at each of its (i) supply nodes,\( i\in {N}_s^k \), (ii) transshipment nodes, \( i\in {N}^k\backslash \left\{{N}_s^k,{N}_d^k\right\} \), and (iii) demand nodes, \( i\in {N}_d^k \) is represented by constraints (4),(5), and (6), respectively. Constraints (7) ensure that the flow through link (i, j) ∈ Lk in network k ∈ K at time t ∈ T does not exceed its capacity. Constraints (8) ensure that the amount of slack or unmet demand, \( {q}_{it}^k \), at node \( i\in {N}_d^k \) in network k ∈ K at time t ∈ T does not exceed the required demand at that node.

$$ \sum \limits_{\left(i,j\right)\in {L}^k}{x}_{ijt}^k-\sum \limits_{\left(j,i\right)\in {L}^k}{x}_{jit}^k={u}_{it}^k,\forall i\in {N}_s^k,k\in K,t\in T $$
(4)
$$ \sum \limits_{\left(i,j\right)\in {L}^k}{x}_{ijt}^k-\sum \limits_{\left(j,i\right)\in {L}^k}{x}_{jit}^k=\mathbf{0},\forall i\in {N}^k\backslash \left({N}_s^k\cup {N}_d^k\right),k\in K,t\in T $$
(5)
$$ \sum \limits_{\left(i,j\right)\in {L}^k}{x}_{ijt}^k-\sum \limits_{\left(j,i\right)\in {L}^k}{x}_{jit}^k-{q}_{it}^k=-{d}_i^k,\forall i\in {N}_d^k,k\in K,t\in T $$
(6)
$$ {x}_{ij t}^k-{c}_{ij}^k\le \mathbf{0},\forall \left(i,j\right)\in {L}^k,k\in K,t\in T $$
(7)
$$ {q}_{it}^k-{d}_i^k\le \mathbf{0},\forall i\in {N}_s^k,k\in K,t\in T $$
(8)

In this work, we consider a single link between any two nodes in a network (i.e., in each direction). That is, a multigraph scenario is not considered where there exists more than one link between the same two nodes and some of which could be redundant. However, they could be incorporated in the proposed model by creating duplicates of the relevant nodes and links, and then create a one-to one interdependency between those two nodes.

3.4.2 Restoration Constraints

Work crew r ∈ Rk in infrastructure network k ∈ K can work on the restoration of a single disrupted network component, node i ∈ N′k or link (i, j) ∈ L′k, as shown in constraints (9). Constraints (10) and (11) ensure that for network k ∈ K, only a single work crew is assigned to work on the restoration of node i ∈ N′k and link (i, j) ∈ L′k, respectively, at time t ∈ T. The recovery status of node i ∈ N′k and link (i, j) ∈ L′k in network k ∈ K is determined by constraints (12) and (13), respectively, which represent the status of the disrupted components after the occurrence of a disruptive event along with the recovery progress of these disrupted components by the available work crews in that network.

$$ \sum \limits_{i\in {N}^{\prime k}}{v}_{it}^{kr}+\sum \limits_{\left(i,j\right)\in {L}^{\prime k}}{w}_{ijt}^{kr}\le \mathbf{1},\forall k\in K,t\in T,r\in {R}^k, $$
(9)
$$ \sum \limits_{r\in {R}^k}{v}_{it}^{kr}\le \mathbf{1},\forall i\in {N}^{\prime k},k\in K,t\in T $$
(10)
$$ \sum \limits_{r\in {R}^k}{w}_{ijt}^{kr}\le \mathbf{1},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(11)
$$ {y}_{it}^k\le {y}_{i\mathbf{0}}^k+\sum \limits_{r\in {R}^k}\sum \limits_{l=\mathbf{1}}^t{\gamma}_{il}^k{v}_{il}^{kr},\forall i\in {N}^{\prime k},k\in K,t\in T $$
(12)
$$ {z}_{ij t}^k\le {z}_{ij\mathbf{0}}^k+\sum \limits_{r\in {R}^k}\sum \limits_{l=\mathbf{1}}^t{\delta}_{ij l}^k{w}_{ij l}^{kr},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(13)

3.4.3 Interdependence Constraints

The physical interdependence among the different infrastructure networks is captured by constraints (14). This set of constraints ensure that for a node \( \overline{i}\in {N}^{\overline{k}} \) in network \( \overline{k}\in K \) to be operational at time t ∈ T, node i ∈ Nk in network k ∈ K must be operational at time t ∈ T as well, where \( \left(\left(i,k\right),\left(\overline{i},\overline{k}\right)\right)\in \varPsi \).

$$ {y}_{\overline{i}t}^{\overline{k}}-{y}_{it}^k\le \mathbf{0},\forall \left(\left(i,k\right),\left(\overline{i},\overline{k}\right)\right)\in \varPsi, t\in T $$
(14)

In this work considerate is assumed that for a dependent node to be operational, the other node or nodes upon which it depends must be operational. However, the proposed model could be easily generalized by adding a new parameter that captures all different cases of interdependencies (González et al. 2016): (i) a node can be operational if the other node or set of nodes that it depends on is operational, (ii) a node can be operational if at least one of the nodes that it depends on is operational, (iii) a node can be operational if a specific node or group of nodes from the set of the nodes that it depends on is operational, and (iv) a node depends partially on the functionality of a set of nodes.

3.4.4 Logical Link Constraints of Network Flow to Restoration

The number of operational units, \( {\alpha}_{it}^k \) and \( {\beta}_{ijt}^k \), in node i ∈ N′k and link (i, j) ∈ L′k in network k ∈ K at time t ∈ T, respectively, are based on their operational state and determined by constraints (15) and (16), respectively. For example, in a transportation network, if a highway has four lanes, then the number of units in this highway will be four where each lane represents 25% of that highway. So, if the highway is completely disrupted and then recovered 50%, then two lanes will be operational. However, if it is 60% recovered, then again still two lanes will be working until the link is 75% recovered such that a third lane will then be available, and so on. Hence, the amount of supply at node \( i\in {N}_s^k \) in network k ∈ K could be affected by how many units are operational at that node, as governed by constraints (17). Also, the flow through link (i, j) ∈ Lk in network k ∈ K is determined by the capacity of the link as well as the number of the operational units in the nodes at both ends on that link as shown in constraints (18) and (19). Furthermore, the capacity of link (i, j) ∈ L′k in network k ∈ K is determined by the number of the operational units in the link itself which is captured by constraints (20).

$$ {a}_i^k{y}_{it}^k\ge {\alpha}_{it}^k,\forall i\in {N}^{\prime k},k\in K,t\in T $$
(15)
$$ {b}_{ij}^k{z}_{ij t}^k\ge {\beta}_{ij t}^k,\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(16)
$$ {u}_{it}^k-{s}_i^k\left({\alpha}_{it}^k/{a}_i^k\right)\le \mathbf{0},\forall i\in {N}_s^k,k\in K,t\in T $$
(17)
$$ {x}_{ij t}^k-{c}_{ij}^k\left({\alpha}_{it}^k/{a}_i^k\right)\le \mathbf{0},\forall \left(i,j\right)\in {L}^k,i\in {N}^k,k\in K,t\in T $$
(18)
$$ {x}_{ij t}^k-{c}_{ij}^k\left({\alpha}_{jt}^k/{a}_j^k\right)\le \mathbf{0},\forall \left(i,j\right)\in {L}^k,j\in {N}^k,k\in K,t\in T $$
(19)
$$ {x}_{ij t}^k-{c}_{ij}^k\left({\beta}_{ij t}^k/{b}_{ij}^k\right)\le \mathbf{0},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(20)

3.4.5 Constraints on the Nature of Decision Variables

For infrastructure network k ∈ K, the amount of supply, \( {s}_{it}^k \), slack for unmet demand, \( {sl}_{it}^k \), and flow through link (i, j) ∈ Lk, \( {x}_{ijt}^k \), must be non-negative at time t ∈ T, as shown in constraints (21), (22), and (23), respectively. Constraints (24) and (25) represent the status of node i ∈ N′k and link (i, j) ∈ L′k in network k ∈ K at time t ∈ T, respectively, which is continuous depending on the magnitude of damage occurred at each one of them and their recovery progress. The number of operational units in node i ∈ Nk and link (i, j) ∈ L′k in network k ∈ K at time t ∈ T must be non-negative integer, see constraints (26) and (27), respectively. Finally, constraints (28) and (29) represent the binary restoration variables for node i ∈ N′k and link (i, j) ∈ L′k in network k ∈ K at time t ∈ T, respectively.

$$ {u}_{it}^k\ge \mathbf{0},\forall i\in {N}_s^k,k\in K,t\in T $$
(21)
$$ {q}_{it}^k\ge \mathbf{0},\forall i\in {N}_s^k,k\in K,t\in T $$
(22)
$$ {x}_{ijt}^k\ge \mathbf{0},\forall \left(i,j\right)\in {L}^k,k\in K,t\in T $$
(23)
$$ \mathbf{0}\le {y}_{it}^k\le \mathbf{1},\forall i\in {N}^k,k\in K,t\in T $$
(24)
$$ \mathbf{0}\le {z}_{ijt}^k\le \mathbf{1},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(25)
$$ {\alpha}_{it}^k\in \left\{\mathbf{0}\right\}\cup {\mathbb{Z}}^{+},\forall i\in {N}^k,k\in K,t\in T $$
(26)
$$ {\beta}_{ijt}^k\in \left\{\mathbf{0}\right\}\cup {\mathbb{Z}}^{+},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T $$
(27)
$$ {v}_{it}^{kr}\in \left\{\mathbf{0},\mathbf{1}\right\},\forall i\in {N}^{\prime k},k\in K,t\in T,r\in {R}^k $$
(28)
$$ {w}_{ijt}^{kr}\in \left\{\mathbf{0},\mathbf{1}\right\},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T,r\in {R}^k $$
(29)

4 Illustrative Example

In this section, the proposed optimization model to solve the INRP is illustrated through a realistic, well-known case in the literature, system of interdependent infrastructure networks in Shelby County, TN, in the United States. This county, which contains the city of Memphis, is constantly under earthquake hazard due to its proximity to the New Madrid Seismic Zone. Hence, in this example, we study the restoration strategies of such system considering the impact on it by multiple hypothetical earthquakes.

4.1 Data

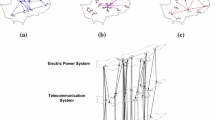
The system of networks considered in this paper consists of two interdependent infrastructure networks in Shelby County, TN: water and power. The topologies used were adapted from González et al. (2016) and Hernandez-Fajardo and Dueñas-Osorio (2011). In particular, there are 256 network components that form this system of interdependent networks (i.e., 109 nodes and 147 links). The water network is composed of 49 nodes and 71 links, while the power network is composed of 60 nodes and 76 links. The two infrastructure networks are shown in Fig. 2.

Fig. 2
figure 2

Graphical representations of the, a power, b water, and c interdependent water and power networks in Shelby County, TN (adapted from González et al. 2016)

Full size image

4.2 Experiment

This work explores the four different magnitudes for hypothetical earthquake scenarios in Shelby County, TN presented by González et al. (2016), Mw ∈ {6, 7, 8, 9}, considering the different failure probabilities of each component (node or link) in the system of interdependent networks with each hypothetical earthquake scenario. Accordingly, the average number of the disrupted network components, as well as their percentage of the total number of components for the system of interdependent infrastructure networks, for each hypothetical earthquake scenario, considering 1000 disaster realizations for each magnitude, are shown in Table 4.

Table 4 Disruption size considering different magnitudes for hypothetical earthquake scenarios
Full size table

In this work, the demands at node \( i\in {N}_d^k \) in network k ∈ K is assumed proportional to the population surrounding it (González et al. 2016). Also, the unitary flow cost and fixed restoration cost for link (i, j) ∈ Lk and (i, j) ∈ Lk, respectively, are assumed proportional to their lengths. Moreover, the cost of unmet demand (i.e., disruption cost) in node \( i\in {N}_d^k \) is considered to be greater than the maximum feasible total flow and restoration costs to set the priorities for the restoration strategy of the proposed model (i.e., satisfying the unmet demand first). In addition, the number of units in each of the network components is considered to be equal 1, (i.e., \( {a}_i^k \), \( {b}_{ij}^k \) =1). That is, a disrupted network component will not be operational unless it is fully restored. It is assumed that μk = 1/ ∣ K∣, τ = 18, Rk = 6, and \( {\gamma}_{it}^k,{\delta}_{ijt}^k\sim U\left(0,1\right) \). Naturally, the chosen values of the parameters considered in this work could easily accommodate other assumptions to reflect more realistic operating and accounting scenarios. The proposed optimization model was solved using Python 2.7 with Gurobi 7.5. Figure 3 illustrates the improvement of the interdependent network resilience measure throughout the restoration process for the four different hypothetical earthquake scenarios from Table 4.

Fig. 3
figure 3

Network resilience with hypothetical earthquakes of different magnitudes

Full size image

As stated earlier in Section 2.1, the proposed optimization model for solving the INRP focuses on enhancing the resilience of the interdependent infrastructure networks to regain their performance level prior to the disruption. Hence, the disrupted networks components might: (i) not all be restored, especially if they do not influence the resilience of the other networks, or (ii) restored partially, if they could be functioning partially. This point is illustrated in Fig. 4 for the example of the system of interdependent infrastructure networks in Shelby County, TN, considering different magnitudes of hypothetical earthquakes, Mw ∈ {6, 7, 8, 9}. Figure 4 shows: (i) the cumulative number of restored components over the restoration time horizon, and (ii) the percentage of the number of restored components to the number of disrupted components, for a disaster realization for each hypothetical earthquake scenario. Observed from Fig. 4 is that not all the disrupted components are restored for the system of interdependent infrastructure networks (i.e., 4 components are restored (40.0%) with Mw = 6, 19 components are restored (70.4%) with Mw = 7, 36 components are restored (72.0%) with Mw = 8, and 56 components are restored (67.5%) with Mw = 9).

Fig. 4
figure 4

Restored network components over time in terms of a magnitude (bars) and b percentage (lines) with hypothetical earthquakes of different magnitudes

Full size image

5 Exploring Different Recovery Considerations

As shown in Section 3.1, the proposed optimization model for solving the INRP takes into account some assumptions and considerations related to the assignment of work crews and the functionality of network components. However, this section offers some extensions, considerations, and strategies to those assumptions and considerations, that could be incorporated in the proposed optimization model.

5.1 Recovery Acceleration

In the proposed optimization model, it is assumed that only a single work crew can work on restoring a disrupted component at time t ∈ T. However, since some network components could be critical and have high influence on their performance (or the performance of other networks), having multiple work crews working on restoring them at the same time could help in expediting the restoration process for the components themselves as well as their networks. In addition, the number of work crews that can work at the same time could differ from one time to another according to the criticality and the need as determined by decision makers. Hence, to allow for such consideration, constraints (10) and (11) are replaced by constraints (30) and (31), respectively, where \( {\theta}_i^k \) is the maximum number of work crews allowed to work at the same time on node i ∈ N′k in network k ∈ K at t ∈ T. Similarly, \( {\rho}_{ij}^k \) is the maximum number of work crews allowed to work at the same time on link (i, j) ∈ L′k in network k ∈ K at t ∈ T.

$$ \sum \limits_{r\in {R}^k}{v}_{it}^{kr}\le {\theta}_{it}^k,\forall i\in {N}^{\prime k},k\in K,t\in T $$
(30)
$$ \sum \limits_{r\in {R}^k}{w}_{ijt}^{kr}\le {\rho}_{ijt}^k,\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T\kern0.5em $$
(31)

Figure 5 shows the improvements of the resilience of the interdependent networks with the recovery progress considering two scenarios where (i) a single work crew (referred to as “one WC”), and (ii) multiple work crews (or “multiple WCs”) can work on node i ∈ N′k or link (i, j) ∈ L′k in network k ∈ K at time t ∈ T. For illustrative purposes, each disrupted network component is assumed to have the option of having any number of the available work crews to work on its restoration at the same time at any time, that is \( {\theta}_{it}^k \) and \( {\rho}_{ijt}^k \) are equal to the number of the available work crews in network k ∈ K (i.e., \( {\theta}_{it}^k \), \( {\rho}_{ijt}^k \)= κ). Moreover, four different magnitudes for hypothetical earthquake scenarios are considered (i.e., Mw ∈ {6, 7, 8, 9}) as shown in Fig. 5. As it can be observed from Fig. 5, the difference in the resilience measure of the interdependent networks between the two work crew assignment strategies reduces as the disruption is larger. Hence, though assigning multiple work crews to the same disrupted network component could aid in faster recovery, there are more critical network components that need to be restored to achieve a higher level of resilience. Therefore, different work crews are assigned to different disrupted network components, not the same component.

Fig. 5
figure 5

Network resilience considering different work crew scenarios with hypothetical earthquakes of magnitude a Mw= 6, b Mw= 7, c Mw= 8, and d Mw= 9

Full size image

5.2 Network Components Functionality

Recall that \( {a}_i^k \)and \( {b}_{ij}^k \) represent the number of units in node i ∈ Nk and link (i, j) ∈ Lk in network k ∈ K, respectively. Such numbers of units could be one or multiple depending on the nature of the network and the functionality of its components. Accordingly, the number of unit in a network component could be one if the network component cannot be operational until it is completely restored. On the other hand, there could be multiple units in a network component if the component can be functioning partially following a disrupted event if it is not completely disrupted or after a partial recovery. While the initial illustration in Fig. 3 assumed that the number of units in each component was 1, it could be assumed that \( {a}_i^k,{b}_{ij}^k\sim U\left(1,4\right) \) such that they could be functioning partially when they are partially disrupted or partially recovered. Although the values of these parameters (i.e., for \( {a}_i^k \) and \( {b}_{ij}^k \)) are considered for illustrative purpose, other assumptions could be captured by the proposed model to reflect a more realistic network scenario. Figure 6 shows the improvement in the resilience of the interdependent networks with the recovery progress considering two assumptions: (i) \( {a}_i^k,{b}_{ij}^k=1 \), “one unit”, and (ii) \( {a}_i^k,{b}_{ij}^k\sim U\left(1,4\right) \), “multiple units”, for node i ∈ Nk and link (i, j) ∈ Lk in network k ∈ K, respectively. In this work, we consider one scenario for the number of multiple units considered for nodes and links (i.e., the number of multiple units for any component is not changing from time to time, rather it is considered the same throughout the whole study).

Fig. 6
figure 6

Network resilience considering different recovery (i.e., number of units) assumptions with hypothetical earthquakes of magnitude a Mw= 6, b Mw= 7, c Mw= 8, and d Mw= 9

Full size image

As shown in Fig. 6, considering partial functioning of the disrupted networks components results in a better level of resilience for the of the system of interdependent networks through the recovery time horizon. However, the two different assumptions reach to the level of having a fully resilient system of interdependent networks at the same time. It should be noted that the notion of a “units” is a function of the type of network not a recovery strategy, and that the illustration in Fig. 6 may not be appropriate for actual water and electric power networks.

5.3 Recovery Task Assignment

As discussed in Section 5.1, the proposed optimization model for solving the INRP assures that only one work crew is working to restore node i ∈ N′k or link (i, j) ∈ L′k in network k ∈ K at time t ∈ T. However, there could be different work crews working on the same network component at different time periods, especially when the restoration rate and cost are specific to the work crew. To illustrate this idea, the authors consider work crew-based restoration costs and rates shown in Table 5.

Table 5 Modified restoration parameters for work crew r ∈ Rk in network k ∈ K
Full size table

To assign restoration tasks of a network component that requires multiple time periods for its restoration to the same work crew, new assignment variables must be added. These decision variables are used to assign the recovery tasks of node i ∈ Nk or link (i, j) ∈ Lk in network k ∈ K to the available work crews. Hence, \( {\hat{v}}_i^{kr} \) is a binary variable that equals 1 if node i ∈ N′k in network k ∈ K is assigned to work crew r ∈ Rk; and 0 otherwise. Similarly, \( {\hat{w}}_{ijl}^{kr} \) is a binary variable that equals 1 if link (i, j) ∈ L′k in network k ∈ K is assigned to work crew r ∈ Rk; and 0 otherwise. As such, constraints (32)–(35) are added to the proposed model.

$$ {v}_{it}^{kr}\le {\hat{v}}_i^{kr},\forall i\in {N}^{\prime k},k\in K,t\in T,r\in {R}^k $$
(32)
$$ {w}_{ij t}^{kr}\le {\hat{w}}_{ij}^{kr},\forall \left(i,j\right)\in {L}^{\prime k},k\in K,t\in T,r\in {R}^k $$
(33)
$$ \sum \limits_{r\in {R}^k}{\hat{v}}_i^{kr}\le \mathbf{1},\forall i\in {N}^{\prime k},k\in K $$
(34)
$$ \sum \limits_{r\in {R}^k}{\hat{w}}_{ij}^{kr}\le \mathbf{1},\forall \left(i,j\right)\in {L}^{\prime k},k\in K $$
(35)

Though only a single work crew can work on node i ∈ N′k or link (i, j) ∈ L′k in network k ∈ K at time t ∈ T (i.e., the original assumption of the proposed optimization model), two strategies are considered for the work crew assignment: (i) the same work crew works on the same disrupted network component at any time (referred to as “same WC”), and (ii) different work crews could work on the same disrupted network component at different time periods (or “different WCs”). Figure 7illustrates the improvement in the resilience of the interdependent networks with the recovery progress for these two strategies considering \( {\gamma}_{it}^{kr},{\delta}_{ijt}^{kr}\sim U\left(0,1\right) \). The resilience measure for the system of interdependent networks is very similar for both strategies, as shown in Fig. 7, and that is due to the number of units being equal to 1 (i.e., \( {a}_i^k \), \( {b}_{ij}^k \) =1). That is, a disrupted network component will not be operational unless it is fully restored. However, since the authors are considering different restoration rates for different work crews, which result in different restoration cost for the disrupted network components accordingly, the restoration cost for both strategies are compared. Hence, Fig. 8 shows the restoration cost for both strategies, normalized by the lowest restoration cost (i.e., considering the original assumption, different work crews, of the proposed optimization model), where the steady state of the cost indicates that the system of interdependent networks has reached the maximum level of resilience (i.e., Я = 1 for the example). Considering different work crews to restore a network component at different time periods could result in a lower restoration cost due to the different recovery rates of the available work crews, as shown in Fig. 8. The difference in the restoration cost between the two strategies for work crew assignment reduces as the disruption worsens, which is due to the size of the disruption (i.e., number of disrupted network components) and the number of available work crews during the recovery process.

Fig. 7
figure 7

Network resilience considering different work crew (WC) assignment strategies with hypothetical earthquakes of magnitude a Mw= 6, b Mw= 7, c Mw= 8, and d Mw= 9

Full size image
Fig. 8
figure 8

Normalized restoration cost considering different work crew (WC) assignment strategies with hypothetical earthquakes of magnitude a Mw= 6, b Mw= 7, c Mw= 8, and d Mw= 9

Full size image

In general, the variation in the improvement of the interdependent network resilience measure depends on: (i) the status (i.e., disruption size) of the disrupted networks components as well as their networks, (ii) the nature of the interdependency among the infrastructure networks, (iii) the number of available work crews for each infrastructure network, and (iv) and variation in the restoration rates for the work crews; hence the variation in restoration costs of the disrupted networks components.

5.4 Recovery Process

There are two different cases for the recovery process of the disrupted network component regarding the work crews: (i) preemptive recovery, and (ii) non-preemptive recovery. The proposed optimization model for solving the INRP considers the preemptive recovery process, where a work crew can move from one disrupted component to another in different time periods without having achieved full restoration of the previous disrupted component (e.g., a work crew can work on the restoration of node i ∈ N′k in network k ∈ K at time t ∈ T and then work on the restoration of node j ∈ N′k in network k ∈ K at time t + 1 ∈ T). However, for a non-preemptive recovery process, a work crew is not allowed to move from a disrupted component to another unless they complete the restoration of the previous one. To consider a non-preemptive recovery process with the assumption that the disrupted network components need to reach a desired level of functionality, new parameters are added to represent the recovery durations of the disrupted components to reach a desired level of recovery. Hence, \( {m}_i^k \) is the recovery duration for node i ∈ N′k in network k ∈ K (i.e., \( {m}_i^k=\left\lceil \left({\zeta}_i^k-{y}_{i0}^k\right)/{\gamma}_{it}^{kr}\right\rceil \)) where \( {\zeta}_i^k\in \left[0,1\right] \) is the desired level of functionality for node i ∈ N′k in network k ∈ K (i.e., \( {\zeta}_i^k\ge {y}_{i0}^k \)). Likewise, \( {n}_{ij}^k \) is the recovery duration for link (i, j) ∈ L′k in network k ∈ K (i.e., \( {n}_{ij}^k=\left\lceil \left({\eta}_{ij}^k-{z}_{ij0}^k\right)/{\delta}_{ij t}^{kr}\right\rceil \)) where \( {\eta}_{ij}^k\in \left[0,1\right] \) is the desired level of functionality for link (i, j) ∈ L′k in network k ∈ K (i.e., \( {\eta}_{ij}^k\ge {z}_{ij0}^k \)). That is, the recovery duration of a disrupted component represents the required number of time periods that a work crew needs to work on the restoration of that disrupted component until it reaches a desired level of recovery based on the restoration rate per time period (i.e., the percentage of recovery of that disrupted component that can be accomplished during time period t by that work crew). For example, if the desired level of recovery is 100%, the status of the disrupted component after a disruption is 0%, and the restoration rate is 25%, the recovery duration of that disrupted component is 4 time periods [(100–0)/25]=4, and so on. Since the proposed optimization model is dealing with time periods for the restoration duration of the disrupted components, the recovery durations for the disrupted nodes and links (i.e., \( {m}_i^k \) and \( {n}_{ij}^k \), respectively) are rounded up to the nearest integer value. Moreover, constraint (9) is replaced by constraint (36) with the consideration of the recovery tasks assignment constraints in Section 5.3.

$$ \sum \limits_{i\in {N}^{\prime k}}\sum \limits_{l=t}^{\mathbf{\min}\left\{\tau, t+{m}_i^k-\mathbf{1}\right\}}{v}_{il}^{kr}/{m}_i^k+\sum \limits_{\left(i,j\right)\in {L}^{\prime k}}\sum \limits_{l=t}^{\mathbf{\min}\left\{\tau, t+{n}_{ij}^k-\mathbf{1}\right\}}{w}_{ij l}^{kr}/{n}_{ij}^k\le \mathbf{1},\forall k\in K,t\in T,r\in {R}^k $$
(36)

Similar to the result in Section 5.3, the interdependent network resilience measure is very similar for the two different recovery process assumptions due to the number of units being equal to 1 (i.e., \( {a}_i^k \), \( {b}_{ij}^k \) =1). Figure 9 shows the restoration cost considering the two different cases for the recovery process (preemptive and non-preemptive recovery processes) normalized by the restoration cost resulting from the original preemptive assumption. Hence, considering a preemptive recovery assumption during the recovery process could lead to a lower restoration cost over time, as shown in Fig. 9. Moreover, the difference in the restoration cost of the two assumptions by the work crew is small as each of the disrupted network components in this example has one unit only (i.e., a disrupted network component cannot be operational unless it is completely restored).

Fig. 9
figure 9

Normalized restoration cost considering different assumptions for the recovery process with hypothetical earthquakes of magnitude a Mw= 6, b Mw= 7, c Mw= 8, and d Mw= 9

Full size image

On the other hand, when the disrupted network components have multiple units each (i.e., they can be functioning partially), the difference in the restoration cost could be substantial. In addition, the resilience measure for the system of interdependent networks could be different when considering preemptive and non-preemptive assumptions since the disrupted network components could be functioning partially or have some partial recovery.

6 Concluding Remarks

This paper explores the interdependent network restoration problem (INRP), which seeks to find the minimum-cost restoration strategy of a system of interdependent networks following the occurrence of a disruptive event that enhances its resilience considering the availability of time and resources, and then proposes an optimization model to solve this problem. In particular, the proposed model: (i) prioritizes the restoration of the disrupted components for each infrastructure network, and (ii) assigns and schedule the prioritized networks components to the available work crews, such that the resilience of the system of interdependent infrastructure networks is enhanced considering the physical interdependency among them. Moreover, the proposed optimization model provides the status of the disrupted network components over the recovery trajectory (i.e., the percentage of a disrupted component that is recovered at the end of each time period). In addition, in case a disrupted component can function partially, the proposed model provides the percentage of its functionality depending on the nature of the disrupted component.

The proposed optimization model for solving the INRP considers: (i) partial disruptions for the disrupted network components, (ii) partial recovery of the disrupted network components, and (iii) partial dependence between nodes in different networks. Furthermore, four different recovery strategies considering different assumptions regarding work crew assignment and recovery process have been explored. These strategies include: (i) recovery acceleration (i.e., assigning more than one work crew to restore the same disrupted component at the same time), (ii) network component functionality (i.e., recovering a disrupted component partially), (iii) recovery tasks assignment (i.e., assigning the same work crew to recover a disrupted component at any time), and (iv) recovery process (i.e., considering a preemptive or non-preemptive recovery process).

The proposed optimization model is illustrated with a realistic system of interdependent power and water infrastructure networks in Shelby County, TN. These interdependent infrastructure networks are located in the New Madrid Seismic Zone, which puts them at risk of earthquake hazards. Accordingly, different magnitudes for hypothetical earthquake scenarios of magnitudes, Mw ∈ {6, 7, 8, 9}, are considered to study the restoration strategies of such system considering the impact on it by the multiple hypothetical earthquake scenarios. Since the proposed optimization model focuses on enhancing the resilience of the system of interdependent networks to retain their performance level prior to the disruption, not all the disrupted networks components might be restored. In addition, different recovery strategies could have different impacts on the improvement of the resilience of set of the interdependent networks along with the recovery progress or the restoration cost of the disrupted components. Moreover, several other factors could affect the progress of improvement for the resilience of the system of interdependent infrastructure networks, the recovery time of the system, and the total cost associated with the recovery process: (i) the disruption size, (i.e., number of disrupted components in each infrastructure network), (ii) the nature of the interdependencies among the infrastructure networks, (iii) the recovery durations of the disrupted components and (iv) the number of available work crews for each infrastructure network during the restoration process (i.e., the number of available work crews, the restoration rate of each work crew). Furthermore, the available time and budget for the restoration process can decide the maximum level of resilience that the system of interdependent infrastructure networks can reach.

As for future work, the proposed model could be extended to consider the location of facilities from which work crews dispatch to the locations of their assigned disrupted networks components. That is, finding the optimal location of these facilities from a set of candidate sites considering the cost of establishing such facilities along with the travel distance and cost for the work crews. In addition, the proposed model considers the physical interdependency among infrastructure networks. However, other types of interdependency could be considered such as geographical interdependency. Geographical interdependency could be incorporated in the proposed model by considering the preparation of spaces that are shared by disrupted components from multiple interdependent infrastructure networks prior to the commencement of their restoration activities. Furthermore, instead of assigning the same weight to each infrastructure network to determine the resilience of the system of interdependent networks, a new method could be utilized for trading off one infrastructure network versus another and their weights could be adjusted accordingly. We will explore restoration priorities, including a sensitivity analysis of network and component weights, as well as exploring component importance measures for focusing restoration efforts (Almoghathawi and Barker 2019). Moreover, the proposed model could be extended to quantify objectives related not just to infrastructure resilience but also to the economic impact on multiple industries (Darayi et al. 2017) or the resilience of the communities that interact with these infrastructure networks. Additionally, the proposed model and recovery strategies could be extended to account for cascading disruptions that could be resulted from partially disrupted network components. Finally, a solution approach for the proposed model could be developed provide optimal -or near optimal- results in a faster time, particularly for very large-scale systems of interdependent networks. Finally, studying the vulnerability of the components in each infrastructure network could help in identifying those that are critical to reinforce or protect prior to any disruption, thus potentially leading a shorter time to achieve full resilience as well as a lower cost associated with the restoration process. Therefore, a tradeoff between the vulnerability and restoration of the interdependent infrastructure networks could be studied to find the optimal strategy for investment.