1 Introduction

Due to technological advancement in recent years, robotic manipulators have been extensively used in various areas, such as industrial manipulators, aerospace manipulators and so on. For industrial applications like loading and unloading workpieces, assembling parts and sorting goods, the requirements for the trajectory tracking accuracy and control performance of robotic manipulators are constantly increasing. In order to meet these demands, it is necessary to realize the precise motion control of the manipulator, which has attracted great attention from the academic and engineering circles [1,2,3,4]. However, designing a fast tracking controller for a robotic manipulator remains challenging due to the uncertainty of the manipulator system, input saturation and prescribed tracking error constraints.

The robotic manipulator system is characterized by inherent nonlinearity and physical constraints of components, which brings great difficulty for tracking controller design. Lots of good schemes have been proposed such as PID control [5], feedback linearization [6], model predictive control [7], sliding mode control [8,9,10,11,12], optimal control [13, 14] and robust control [15]. Among these control strategies, sliding mode control is widely used because of its robustness to external disturbances. However, the linear sliding manifold can only achieve asymptotic convergence of the system state, which means that high gains are required to achieve rapid state convergence. Because of this issue, some nonlinear sliding mode surfaces are proposed such as terminal sliding mode [16], nonsingular terminal sliding mode [17] and fast nonsingular terminal sliding mode [18, 19]. [18] proposed a fast nonsingular terminal sliding mode controller with a disturbance observer for permanent magnet linear motors. In [19], an integral fast nonsingular terminal sliding mode surface was introduced for robotic manipulators and proposed a novel backstepping sliding mode controller. It should be pointed out that the finite-time stability of [18] and [19] is proved by using the Lyapunov method. Recently, a so-called fixed-time sliding mode controller is proposed in the literature [20,21,22]. The biggest difference between the fixed-time stability and the finite-time stability is the settling time of the closed-loop system. To be more specific, the settling time of the finite-time stability depends on the initial conditions and will change when different initial conditions are selected. However, the settling time of the fixed-time stability is not affected by initial conditions, which implies that the settling time of the fixed-time stability is bounded and only depends on the design parameters. Paper [20] proposed an integral fixed-time sliding mode control algorithm for permanent magnet synchronous motor with a disturbance estimation compensation. The speed tracking error was proved to be fixed-time stable based on the Lyapunov method. In [21] a fixed-time disturbance observer-based tracking controller was presented for the n-DOF manipulators and Barrier Lyapunov Function was used to ensure the prescribed performance of the tracking errors. A fault-tolerant fixed-time trajectory tracking control scheme was introduced for marine surface vessels in [22]. The aforementioned results can ensure the fixed-time stability of the closed-loop system, but all controllers are designed based on the system model. It should be pointed out that for robotic manipulators, the nominal parts of the system model may not be available. Therefore, how to design a fixed-time controller for a robotic manipulator with system uncertainty is still a problem to be solved.

Dynamic uncertainty always appears in robotic manipulator systems, which will cause great problems when designing a trajectory tracking controller. Therefore, the influence of uncertainty on the design of industrial manipulator controllers cannot be ignored. The dynamic uncertainty indicates that we cannot obtain the accurate mathematical model of the system for controller design and how to improve the tracking performance of the uncertain robotic manipulator is still a challenge for the research community. On purpose to handle the uncertainty of mechanical systems, many approaches had been put forward such as fuzzy control [23, 24] and neural networks control [25, 26]. Owing to its universal approximation property, neural networks have been extensively used to approximate unknown dynamics. Considering the system uncertainty and time-varying output constraints, [27] proposed a model-based control scheme and an adaptive neural networks control scheme for robotic manipulators. Paper [28] used neural networks to handle the system uncertainty and input dead zone, both the state-feedback controller and output-feedback controller were introduced. However, only asymptotic convergence or uniformly ultimately bounded is achieved in [26,27,28]. Therefore, designing a fixed-time neural adaptive controller for an uncertain manipulator system is the purpose of this paper.

Although much great progress has been made in trajectory tracking controller design for robotic manipulators, most control schemes are developed due to the hypothesis that controllers are working in good conditions. However, many control systems are subjected to physical limitations and how to handle these constraints of the system in the controller design process has become a hot research issue. Limited by the physical properties of components, input saturation always appears in mechanical systems. Therefore, it is inevitable to reckon input saturation nonlinearity in concrete applications. Controller design with input saturation for nonlinear systems had been considered by researchers and many great methods had been proposed. For uncertain mobile robot systems with input saturation, [29] proposed a novel adaptive neural controller and used a dynamic system to compensate input saturation. Tracking errors of the system were proved to be asymptotically convergent. In [30], an auxiliary system was employed to reduce the influence of input saturation and a fuzzy controller was introduced for nonstrict-feedback stochastic nonlinear systems under input saturation. [31] presented a neural controller for a pure-feedback stochastic MIMO nonlinear system with input saturation and full state constraints. The proposed controller decreased the influence of input saturation by citing an asymmetric smooth model and achieved a smooth saturation limitation. By applying smooth hyperbolic functions, [32] proposed a boundary controller for flexible manipulators subject to input saturation. According to the above literature, nearly no study has tackled the fixed-time anti-saturation control problem for robotic manipulators.

For many practical systems, it is necessary to design a reasonable controller to make the trajectory tracking error satisfies performance requirements, such as realizing the tracking error convergence to an arbitrarily small residual set, error convergence speed not less than a preset value, and the maximum overshoot less than a certain constant. In order to design a controller to achieve the above performance requirements, Bechlioulis and Rovithakis [33] first proposed a prescribed performance controller for nonlinear systems. By introducing performance function, the prescribed performance control method can specify the transient performance and steady-state performance of trajectory tracking error and have been successfully extended to a variety of different applications such as quadrotor [34], DC converter system [35], rigid satellite [36], space manipulators [37] and other fields [38,39,40,41]. However, the existing prescribed performance control results cannot guarantee the fixed-time stability of tracking error, and cannot meet the requirements of the control accuracy and convergence time of the manipulator system subject to input saturation.

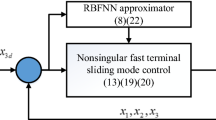
In this paper, an adaptive neural fixed-time sliding mode controller is created for a class of uncertain robotic manipulators subject to input saturation and prescribed constraints. An auxiliary nonlinear dynamic system is introduced to handle the input saturation nonlinearity, RBF NNs are used to approximate the closed-loop dynamic uncertainty and the performance of trajectory tracking error is ensured by a performance function. Compared with former results, the advantages of our controller are

  1. 1.

    A novel auxiliary nonlinear dynamic system is constructed to deal with the influence of input saturation. Different from the auxiliary system proposed in [29] and [30], the fixed-time stability of the auxiliary system state is proved by using the Lyapunov method.

  2. 2.

    A neural adaptive fixed-time sliding mode control method is proposed based on auxiliary dynamic system and performance function. Under the physical limitation, the proposed scheme can ensure the trajectory tracking error satisfies the prescribed performance and converge to a smaller neighborhood of the origin within a fixed time.

  3. 3.

    RBF NNs are used to approximate the uncertainty of the closed-loop system. Different from most neural controllers that update all weight elements online [25,26,27,28], this paper uses the norm of the weight matrix as adaptive parameter. Therefore, the parameter that need to be adjusted is decreased to one, which can reduce the calculation burden.

The remaining parts are ordered as the following arrangements: Sect. 2 provides some lammes and control objective of this article. The adaptive neural fixed-time tracking control approach is designed and stability discussion is introduced in Sec. 3. Simulation results are shown in Sect. 4 to verify the good performance of the present controller. Moreover, in Sect. 5, we complete this paper with some conclusions.

1.1 Notations

In this paper, \(Sig^\alpha (\zeta )=\left[ \vert \zeta _1 \vert ^\alpha \mathrm{sign} (\zeta _1),\vert \zeta _2 \vert ^\alpha \mathrm{sign}(\zeta _2),\dots ,\vert \zeta _n \vert ^\alpha \mathrm{sign}(\zeta _n)\right] ^T\) and \(D^\alpha (\zeta )=\mathrm{diag}\left\{ \vert \zeta _1 \vert ^\alpha ,\vert \zeta _2 \vert ^\alpha ,\dots ,\vert \zeta _n \vert ^\alpha \right\} \) where \(\alpha >0\) and \(\zeta =\left[ \zeta _1,\zeta _2,\dots ,\zeta _n\right] ^T\). \(\vert \zeta _i \vert \) and \(\Vert \zeta \Vert \) denote the absolute value and Euclidean norm, respectively. \(\Vert A \Vert _F\) represents the Frobenius norm and \(\lambda _\mathrm{min}(A)\), \(\lambda _\mathrm{max}(A)\) denote the minimum eigenvalue and maximum eigenvalue of matrix A, respectively.

2 Problem Formulation

2.1 Dynamic Model of Robotic Manipulator

The dynamics of n-link robotic manipulator system in joint space can be expressed as

$$\begin{aligned} M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)=u(v)+\tau _d \end{aligned}$$
(1)

where \( M(q)\in \mathcal {R}^{n \times n} \) denotes the inertia matrix. \( C(q,\dot{q})\in \mathcal {R}^{n \times n} \) represents the Coriolis and centrifugal matrix. \( G(q)\in \mathcal {R}^{n} \) represents the gravity force. q, \(\dot{q}\), \(\ddot{q}\in \mathcal {R}^{n} \) are the vectors of the manipulator position, velocity and acceleration, respectively. \( \tau _d\in \mathcal {R}^{n} \) represents external disturbance which is upper bounded by \(\Vert \tau _d \Vert \le \tau _d^*\). In this paper, we assume that \(\tau _d^*\) is unknown. \( u(v)\in \mathcal {R}^{n} \) represents manipulator input subject to saturation nonlinearity and can be expressed as

$$\begin{aligned} u(v)= {\left\{ \begin{array}{ll} \mathrm{sign}(v)u_\mathrm{max} &{} \text {if } \Vert v \Vert \ge u_\mathrm{max}\\ v &{} \text {if } \Vert v \Vert < u_\mathrm{max} \end{array}\right. } \end{aligned}$$
(2)

where v denotes the designed control input. The constant \(u_\mathrm{max}\) denotes the given bound of saturation nonlinearity. Define \( \varDelta u = u(v)-v \) and assume that \( \Vert \varDelta u \Vert \le U \) where U is a known constant.

In this paper, assume that M(q), \(C(q,\dot{q})\) and G(q) in (1) are totally unknown, which means that the nominal values and the actual values of the system dynamics cannot be used in the controller design process. Thus, to facilitate the design of the controller, a designed positive diagonal matrix \(M_0\) is introduced and equation (1) can be rewritten as

$$\begin{aligned} M_0\ddot{q}=u(v)+\tau _d-\left( M(q)-M_0\right) \ddot{q}-C(q,\dot{q})\dot{q}-G(q) \end{aligned}$$
(3)

2.2 Preliminaries

In order to design a fixed-time controller for the robotic manipulator system (1), some useful definitions and lemmas are presented in this subsection.

Definition 1

[42] Consider the following nonlinear system

$$\begin{aligned} \dot{x}(t)=g(t,x),\quad x(0)=x_0 \end{aligned}$$
(4)

where \(x\in \mathcal {R}^{n}\) and \(g \in \mathcal {R}^+ \times \mathcal {R}^{n} \rightarrow \mathcal {R}^{n}\) are nonlinear functions. The origin of the system (4) is said to be fixed-time stable if for any initial condition \(x_0\), the system state reach the origin at \(T(x_0)\), i.e. \(\lim _{t \rightarrow T(x_0)} x(t)=0\) and there exists a constant \(T_\mathrm{max} \in \mathcal {R}^+\) such that \(T(x_0) \le T_\mathrm{max}\).

Lemma 1

[43] For a selected Lyapunov function V(x) such that

$$\begin{aligned} \dot{V}(x)=-\alpha V^{\frac{m}{n}}(x)-\beta V^{\frac{p}{q}}(x) \end{aligned}$$
(5)

where \(\alpha \), \(\beta \) are positive constants and m, n, p, q are odd integers satisfying \(m>n\), \(p<q\). Then, the origin of (4) is fixed-time stable and the settling time is

$$\begin{aligned} T<\frac{1}{\alpha }\frac{n}{m-n}+\frac{1}{\beta }\frac{q}{q-p} \end{aligned}$$
(6)

Lemma 2

[44] For a selected Lyapunov function V(x) such that

$$\begin{aligned} \dot{V}(x)=-\alpha V^{\frac{m}{n}}(x)-\beta V^{\frac{p}{q}}(x)+\varsigma \end{aligned}$$
(7)

where \(\alpha \), \(\beta \), \(\varsigma \) are positive constants and m, n, p, q are odd integers satisfying \(m>n\), \(p<q\). Then, the origin of (4) is practical fixed-time stable and the settling time is

$$\begin{aligned} T<\frac{1}{\alpha \delta }\frac{n}{m-n}+\frac{1}{\beta \delta }\frac{q}{q-p} \end{aligned}$$
(8)

where \(0<\delta <1\). The residual set of (7) is given by

$$\begin{aligned} x \in \left\{ V(x) \le \mathrm{min} \left\{ \left( \frac{\varsigma }{(1-\delta )\alpha }\right) ^\frac{n}{m},\left( \frac{\varsigma }{(1-\delta )\beta }\right) ^\frac{q}{p}\right\} \right\} \end{aligned}$$
(9)

Lemma 3

[45] For any \(a > 1\) we have the following inequality

$$\begin{aligned} \sum _{i=1}^{N} y_i^a \ge N^{1-a}\left( \sum _{i=1}^{N} y_i \right) ^a \end{aligned}$$
(10)

and if \(0<a \le 1\) we have

$$\begin{aligned} \sum _{i=1}^{N} y_i ^a \ge \left( \sum _{i=1}^{N} y_i \right) ^a \end{aligned}$$
(11)

where N is a positive constant and \(y_i>0\).

Lemma 4

[45] For any \(a\ge 0\), \(b>0\) and \(c>0\), the following inequality holds

$$\begin{aligned} a^c(b-a) \le \frac{1}{1+c}\left( b^{1+c}-a^{1+c}\right) \end{aligned}$$
(12)

Lemma 5

[45] For any \(a>0\), \(b \le a\) and \(c>1\), the following inequality holds

$$\begin{aligned} (a-b)^c \ge b^c - a^c \end{aligned}$$
(13)

2.3 RBF NNs

In this article, RBF NNs are used to approximate the unknown dynamics of the manipulator. According to Park and Sandberg [46], a continuous unknown function f(Z) approximated by RBF NNs can be written as

$$\begin{aligned} f(Z)=w^{*T}\phi (Z)+\epsilon \end{aligned}$$
(14)

where \(w^{*} \in \mathcal {R}^{p_1 \times m_1}\) denotes the ideal weight matrix. \(\phi (Z)=\left[ \phi _1(Z),\phi _2(Z),\ldots ,\phi _{p_1}(Z)\right] ^T\) is the basis function vector and \(\phi _i(Z)\) for \(i=1,2,\ldots ,p_1\) are Gaussian functions, such that \(\phi _i(Z)=\exp \left( \frac{-\Vert Z-\xi _i \Vert ^2}{\eta _i^2}\right) \) where Z represents the input of RBF NNs, \(\xi _i\) and \(\eta _i\) represent the receptive field center and width of the Gaussian function, respectively. \(\epsilon \) denotes the approximation error and \(\Vert \epsilon \Vert \le \epsilon ^*\) with \(\epsilon ^* \ge 0\).

2.4 Control Objective

In this article, the control objective is to design an adaptive neural fixed-time sliding mode trajectory tracking control approach for a class of uncertain robotic manipulators to achieve the following requirements

  1. 1.

    Under the effect of input saturation, the system output q tracks the desired trajectory \(q_d\) in fixed time.

  2. 2.

    Tracking error will satisfy the prescribed performance requirements and all signals in the closed-loop system are fixed-time stable.

3 Controller Development

In this section, the adaptive neural fixed-time sliding mode control approach is designed for the robotic system (1). A novel fixed-time auxiliary dynamic system is designed to deal with input saturation. The prescribed performance method is used to make tracking error satisfies the prescribed constraints. All signals in the closed-loop system are proved to be fixed-time stable.

3.1 Prescribed Performance and Error Transformation

Considering system dynamics (3), define \(x_1=q\) and \(x_2=\dot{q}\), thus equation (3) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1 =x_2\\ M_0\dot{x}_2 =u(v) + \tau _d +f(Z) \end{array}\right. } \end{aligned}$$
(15)

where \(f(Z)=-\left( M(x_1)-M_0\right) \dot{x}_2- C(x_1,x_2)x_2-G(x_1)\). Let \(z_1=x_1-q_d\) and \(z_2=x_2-\dot{q}_d\) where \(z_1=\left[ z_{11},z_{12},\dots ,z_{1n}\right] ^T\) denotes angular tracking error and \(z_2=\left[ z_{21},z_{22},\dots ,z_{2n}\right] ^T\) denotes angular velocity error. Assuming that \(z_1\) satisfies the prescribed performance such as

$$\begin{aligned} -k_{1i}\sigma _i(t)<z_{1i}<k_{2i}\sigma _i(t) \quad i=1,2,\dots ,n \end{aligned}$$
(16)

where \(k_{1i}\) and \(k_{2i}\) are positive design constants and \(\sigma _i(t)\) is the performance function which can be written as

$$\begin{aligned} \sigma _i(t)=(\sigma _i(0)-\sigma _i(\infty ))e^{-\varpi _it}+\sigma _i(\infty ) \end{aligned}$$
(17)

where \(\sigma _i(0)>\sigma _i(\infty )>0\) and \(\varpi _i>0\) are designed parameters that based on the performance requirements. We can see from (17) that the performance function \(\sigma _i(t)\) is exponential decreasing and the decreasing rate is adjustable by \(\varpi _i\).

In order to achieve trajectory tracking control with prescribed performance, a performance transformation method is introduced to transform the constrained error \(z_{1i}\) into an equivalent unconstrained error \(S_{1i}\). Define

$$\begin{aligned} z_{1i}=\sigma _i(t)T_{1i}(S_{1i}) \end{aligned}$$
(18)

where \(T_{1i}(S_{1i})\) is a smooth and strictly increasing function with \(\lim _{S_{1i} \rightarrow -\infty }T_{1i}(S_{1i})=-k_{1i}\) and \(\lim _{S_{1i} \rightarrow +\infty }T_{1i}(S_{1i})=k_{2i}\). In this paper we choose the trasnformed function \(T_{1i}(S_{1i})\) as

$$\begin{aligned} T_{1i}(S_{1i})=\frac{k_{2i}e^{S_{1i}}-k_{1i}e^{-S_{1i}}}{e^{S_{1i}} +e^{-S_{1i}}} \end{aligned}$$
(19)

From (18) and (19), the transformed unconstrained error can be expressed as

$$\begin{aligned} S_{1i}=\frac{1}{2}\ln \frac{k_{1i}+\frac{z_{1i}}{\sigma _i(t)}}{k_{2i} -\frac{z_{1i}}{\sigma _i(t)}} \end{aligned}$$
(20)

Differentiating (20) along time we have

$$\begin{aligned} \dot{S}_{1i}=h_i\left( z_{2i}-\frac{\dot{\sigma }_i(t)}{\sigma _i(t)}z_{1i}\right) \end{aligned}$$
(21)

where \(h_i=\frac{1}{2\sigma _i(t)}\frac{k_{1i}+k_{2i}}{\left( k_{1i}+\frac{z_{1i}}{\sigma _i(t)}\right) \left( k_{2i}-\frac{z_{1i}}{\sigma _i(t)}\right) }\) and \(h_i>0\). Thus the vector form of (21) can be given as

$$\begin{aligned} \dot{S}_1=H\left( z_2-\varPsi z_1\right) \end{aligned}$$
(22)

where \(S_1=\left[ S_{11},S_{12},\dots ,S_{1n}\right] ^T\), \(H=\mathrm{diag}\left\{ h_1,h_2,\dots ,h_n\right\} \) and \(\varPsi =\mathrm{diag}\left\{ {\frac{\dot{\sigma }_1(t)}{\sigma _1(t)},\frac{\dot{\sigma }_2(t)}{\sigma _2(t)},}\right. \left. {\dots ,\frac{\dot{\sigma }_n(t)}{\sigma _n(t)}}\right\} \). Define \(S_2=z_2-\varPsi z_1\),thus (22) can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{S}_1=HS_2\\ \dot{S}_2=\dot{z}_2-\dot{\varPsi }z_1-\varPsi z_2 \end{array}\right. } \end{aligned}$$
(23)

3.2 Fixed-time Auxiliary Nonlinear Dynamic System

How to design a fixed-time auxiliary dynamic system to handle the effect of input saturation is the main difficulty in this part. Therefore, to solve this problem, we propose the following auxiliary system

$$\begin{aligned} \begin{aligned} \dot{\hbar }=-H_1 Sig^\frac{m_1}{n_1}(\hbar )-H_2 Sig ^\frac{p_1}{q_1}(\hbar )-UM_0^{-1}\mathrm{sign}(\hbar )+M_0^{-1}(u(v)-v) \end{aligned} \end{aligned}$$
(24)

where \(\hbar \) is the state parameter of the auxiliary dynamic system, \(H_1\) and \(H_2\) are designed diagonal matrices, \(m_1\), \(n_1\), \(p_1\), \(q_1\) are odd integers satisfying \(m_1>n_1\), \(p_1<q_1\).

Theorem 1

Considering the auxiliary nonlinear dynamic system (24), the system state \(\hbar \) is fixed-time stable and the settling time \(T_1\) satisfies

$$\begin{aligned} \begin{aligned} T_1<\frac{1}{n^\frac{n_1-m_1}{2n_1}2^\frac{m_1+n_1}{2n_1}\lambda _\mathrm{min}(H_1)}\frac{2n_1}{m_1-n_1}+\frac{1}{2^\frac{p_1+q_1}{2q_1}\lambda _\mathrm{min}(H_2)}\frac{2q_1}{q_1-p_1} \end{aligned} \end{aligned}$$
(25)

Proof

Choosing the Lyapunov function candidate as

$$\begin{aligned} V_1=\frac{1}{2}\hbar ^T\hbar \end{aligned}$$
(26)

taking the time derivative of (26) and combine with (24) we have

$$\begin{aligned} \begin{aligned} \dot{V}_1=-\hbar ^TH_1 Sig^\frac{m_1}{n_1}(\hbar )-\hbar ^TH_2Sig^\frac{p_1}{q_1}(\hbar )-\hbar ^TUM_0^{-1}\mathrm{sign}(\hbar )+\hbar ^TM_0^{-1}(u(v)-v) \end{aligned} \end{aligned}$$
(27)

From some basic mathematical derivation, it can be seen that \(\hbar ^TUM_0^{-1}\mathrm{sign}(\hbar )-\hbar ^TM_0^{-1}(u(v)-v) \ge 0\), thus we have

$$\begin{aligned} \begin{aligned} \dot{V}_1\le -n^\frac{n_1-m_1}{2n_1}2^\frac{m_1+n_1}{2n_1}\lambda _\mathrm{min}(H_1)V_1^\frac{m_1+n_1}{2n_1}-2^\frac{p_1+q_1}{2q_1}\lambda _\mathrm{min}(H_2)V_1^\frac{p_1+q_1}{2q_1} \end{aligned} \end{aligned}$$
(28)

Based on Lemma 1, the fixed-time convergence of the system state \(\hbar \) is guaranteed and the settling time of the dynamic system can be estimated as (25).

3.3 Fixed-time Sliding Mode Controller Design

The fixed-time sliding mode controller is now designed for manipulator system (1) in this subsection. Considering the transformed errors \(S_1\), \(S_2\) and the auxiliary dynamic system state \(\hbar \), the nonsingular fixed-time sliding mode surface is formulated as

$$\begin{aligned} s=S_2+\Lambda _1Sig^\frac{m_2}{n_2}(S_1)+\Lambda _2\varphi (S_1)-\hbar \end{aligned}$$
(29)

where \(\Lambda _1\) and \(\Lambda _2\) are designed positive matrix, \(m_2\) and \(n_2\) are odd integers satisfying \(m_2>n_2\). \(\varphi (S_1)=\left[ \varphi _1(S_{11}),\varphi _2(S_{12}),\dots ,\varphi _n(S_{1n})\right] ^T\) is expressed as

$$\begin{aligned} \varphi _i(S_{1i})= {\left\{ \begin{array}{ll} \vert S_{1i} \vert ^\frac{p_2}{q_2}\mathrm{sign}(S_{1i}) &{} \text {if } s_{1i}=0, \text { or }\\ &{}\quad s_{1i} \ne 0, \vert S_{1i} \vert > \mu \\ l_1S_{1i}+l_2S_{1i}^2\mathrm{sign}(S_{1i}) &{} \text {if } s_{1i} \ne 0, \vert S_{1i} \vert \le \mu \end{array}\right. } \end{aligned}$$
(30)

where \(s_1=\left[ s_{11},s_{12},\dots ,s_{1n}\right] ^T\) and \(s_1\) is defined as \(s_1=S_2+\Lambda _1Sig^\frac{m_2}{n_2}(S_1)+\Lambda _2Sig^\frac{p_2}{q_2}(S_1)\). \(l_1=\left( 2-\frac{p_2}{q_2}\right) \mu ^{\frac{p_2}{q_2}-1}\), \(l_2=\left( \frac{p_2}{q_2}-1\right) \mu ^{\frac{p_2}{q_2}-2}\) where \(p_2\) and \(q_2\) are odd integers satisfying \(p_2<q_2\) and \(\mu \) is a small positive constant.

Theorem 2

Considering the sliding mode surface (29), if \(s=s_1=0\) is achieved, then the transformed error \(S_1\) is fixed-time stable and the settling time is

$$\begin{aligned} \begin{aligned} T_2<&\frac{1}{n^\frac{n_1-m_1}{2n_1}2^\frac{m_1+n_1}{2n_1}\lambda _\mathrm{min}(H_1)}\frac{2n_1}{m_1-n_1}+\frac{1}{2^\frac{p_1+q_1}{2q_1}\lambda _\mathrm{min}(H_2)}\frac{2q_1}{q_1-p_1}\\&+\frac{1}{\alpha _0 n^{\frac{n_2-m_2}{2n_2}}2^\frac{m_2+n_2}{2n_2}}\frac{2n_2}{m_2-n_2}+\frac{1}{\beta _0 2^\frac{p_2+q_2}{2q_2}}\frac{2q_2}{q_2-p_2} \end{aligned} \end{aligned}$$
(31)

Proof

Choosing the Lyapunov function candidate

$$\begin{aligned} V_2=\frac{1}{2}\sum _{i=1}^{n}S_{1i}^2 \end{aligned}$$
(32)

when \(s=s_1=0\), it indicates that

$$\begin{aligned} S_{2i}+\Lambda _{1i}\vert S_{1i}\vert ^\frac{m_2}{n_2}\mathrm{sign}(S_{1i})+\Lambda _{2i}\vert S_{1i}\vert ^\frac{p_2}{q_2}\mathrm{sign}(S_{1i})-\hbar _i=0 \end{aligned}$$
(33)

Based on Theorem 1 we have \(\hbar _i\) is fixed-time stable, thus (33) can be expressed as

$$\begin{aligned} S_{2i}=-\Lambda _{1i}\vert S_{1i}\vert ^\frac{m_2}{n_2}\mathrm{sign}(S_{1i})-\Lambda _{2i}\vert S_{1i}\vert ^\frac{p_2}{q_2}\mathrm{sign}(S_{1i}) \end{aligned}$$
(34)

Take the time derivative of equation (32), we have

$$\begin{aligned} \dot{V}_2=\sum _{i=1}^{n}S_{1i}\dot{S}_{1i} \end{aligned}$$
(35)

Combine with (23) and (34), (35) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{V}_2=\,&\sum _{i=1}^{n}S_{1i}h_i\left( -\Lambda _{1i}\vert S_{1i} \vert ^\frac{m_2}{n_2}\mathrm{sign}(S_{1i})-\Lambda _{2i}\vert S_{1i} \vert ^\frac{p_2}{q_2}\mathrm{sign}(S_{1i})\right) \\ \le&-\alpha _0\sum _{i=1}^{n} (S_{1i}^2) ^{\frac{m_2+n_2}{2n_2}}-\beta _0\sum _{i=1}^{n}(S_{1i}^2) ^{\frac{p_2+q_2}{2q_2}} \end{aligned} \end{aligned}$$
(36)

where \(\alpha _0=\mathrm{min}\left\{ h_1\Lambda _{11},h_2\Lambda _{12},\dots ,h_n\Lambda _{1n}\right\} \) and \(\beta _0=\mathrm{min}\left\{ h_1\Lambda _{21},h_2\Lambda _{22},\dots ,h_n\Lambda _{2n}\right\} \). Based on Lemma 3, we have

$$\begin{aligned} \begin{aligned} \dot{V}_2\le -\alpha _0n^\frac{n_2-m_2}{2n_2}2^{\frac{m_2+n_2}{2n_2}}V_2^\frac{m_2+n_2}{2n_2}-\beta _02^{\frac{p_2+q_2}{2q_2}}V_2^\frac{m_2+q_2}{2q_2} \end{aligned} \end{aligned}$$
(37)

Thus, based on Lemma 1 the fixed-time convergence of the transformed error \(S_1\) is guaranteed and the settling time can be estimated as (31).

Now the fixed-time controller is designed based on (29). Derivate (29) along time, we get

$$\begin{aligned} \dot{s}=\dot{S}_2+\frac{m_2}{n_2}\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)\dot{S}_1+\Lambda _2\dot{\varphi }(S_1)-\dot{\hbar } \end{aligned}$$
(38)

Multipulting \(M_0\) and considering (23) (24), (38) can be expressed as

$$\begin{aligned} \begin{aligned} M_0\dot{s}=&M_0\dot{x}_2-M_0\ddot{q}_d-M_0\dot{\varPsi }z_1-M_0 \varPsi z_2 +\frac{m_2}{n_2}M_0H\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)S_2+M_0\Lambda _2\dot{\varphi }(S_1)\\&+M_0H_1Sig^\frac{m_1}{n_1}(\hbar )+M_0H_2Sig^\frac{p_1}{q_1}(\hbar )+U\mathrm{sign}(\hbar )-u(v)+v \end{aligned} \end{aligned}$$
(39)

Combine with (15) and use RBF NNs to approximate the system uncertainties f(Z). Thus (39) can be written as

$$\begin{aligned} \begin{aligned} M_0\dot{s}=\,&v + \tau _d + w^{*T}\phi (Z)+\epsilon -M_0\ddot{q}_d-M_0\dot{\varPsi }z_1-M_0 \varPsi z_2+\frac{m_2}{n_2}M_0H\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)S_2 \\&+M_0\Lambda _2\dot{\varphi }(S_1)+M_0H_1Sig^\frac{m_1}{n_1}(\hbar )+M_0H_2Sig^\frac{p_1}{q_1}(\hbar )+U\mathrm{sign}(\hbar ) \end{aligned} \end{aligned}$$
(40)

Remark 1

Based on (15) considering unknown function \(f(Z) \in \mathcal {R}^{n}\), the ideal weight matrix \(w^* \in \mathcal {R}^{p_1 \times n}\). Thus, the totally number of the estimate parameters are \(np_1\). Considering \(\Vert w^* \Vert _F\) is an unknown constant and define \(\Vert w^* \Vert _F^2 = k_N\theta ^*\) where \(k_N>0\). Thus we can estimate \(\theta ^*\) instead of the weight matrix \(w^*\), and the estimate number is decreased from \(np_1\) to one, which can reduce the calculation burden.

Assuming that \(\hat{\theta }\), \(\hat{\tau }_d\) are the estimate of \(\theta ^*\) and \(\tau _d^*\) respectively. \(\tilde{\theta }\) and \(\tilde{\tau }_d\) are defined as \(\tilde{\theta }=\theta ^*-\hat{\theta }\) and \(\tilde{\tau }_d=\tau _d^*-\hat{\tau }_d\). Then, the adaptive neural fixed-time controller can be written as

$$\begin{aligned} \begin{aligned} v=&-K_1Sig^\frac{m_3}{n_3}(s)-K_2Sig^\frac{p_3}{q_3}(s)+M_0\ddot{q}_d+M_0\dot{\varPsi }z_1+M_0 \varPsi z_2\\&-\frac{m_2}{n_2}M_0H\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)S_2-M_0\Lambda _2\dot{\varphi }(S_1)-M_0H_1Sig^\frac{m_1}{n_1}(\hbar )\\&-M_0H_2Sig^\frac{p_1}{q_1}(\hbar )-U\mathrm{sign}(\hbar )-\frac{k_N}{2}\hat{\theta }s\phi ^T(Z)\phi (Z)-\hat{\tau }_d \mathrm{sign}(s) \end{aligned} \end{aligned}$$
(41)

where \(K_1\) and \(K_2\) are controller gain matrix and \(m_3\), \(n_3\), \(p_3\), \(q_3\) are odd integers satisfying \(m_3>n_3\), \(p_3<q_3\). The adaptive laws of \(\hat{\theta }\) and \(\hat{\tau }_d\) are developed as

$$\begin{aligned}&\dot{\hat{\theta }}=\frac{k_N}{2}s^Ts\phi ^T(Z)\phi (Z) -r_1\hat{\theta }^\frac{m_3}{n_3}-r_2\hat{\theta }^\frac{p_3}{q_3} \end{aligned}$$
(42)
$$\begin{aligned}&\dot{\hat{\tau }}_d=k_d\Vert s \Vert -r_3\hat{\tau }_d^\frac{m_3}{n_3}-r_4\hat{\tau }_d^\frac{p_3}{q_3} \end{aligned}$$
(43)

where \(k_d\), \(r_1\), \(r_2\), \(r_3\) and \(r_4\) are positive numbers.

3.4 Stability Analysis

Theorem 3

For uncertain robotic manipulator dynamic system (1) with the transformed error dynamic system (23) and auxiliary nonlinear dynamic system (24). If the fixed-time sliding mode surface is chosen as (29) and (30), and the controller is designed as (41) with the adaptive laws (42) and (43), then we have the following statements:

  1. 1.

    The fixed-time sliding mode surface s will converge to a small neighborhood of zero in fixed time.

  2. 2.

    The transformed error \(S_1\) is bounded in fixed time which means that the tracking error \(z_1\) will converge to the neighborhood of the equilibrium in fixed time and satisfy the prescribed performance.

  3. 3.

    All signals in the closed-loop system are fixed-time stable subject to input saturation.

Proof

Considering the following Lyapunov Function

$$\begin{aligned} V_3=\frac{1}{2}s^T M_0 s+\frac{1}{2}\tilde{\theta }^2+\frac{1}{2k_d}\tilde{\tau }_d^2 \end{aligned}$$
(44)

Taking time derivative of \(V_3\) we have

$$\begin{aligned} \dot{V}_3=s^TM_0\dot{s}-\tilde{\theta }\dot{\hat{\theta }}-\frac{1}{k_d}\tilde{\tau }_d\dot{\hat{\tau }}_d \end{aligned}$$
(45)

Combine with (40), (42) and (43), we get

$$\begin{aligned} \begin{aligned} \dot{V}_3&=s^T\left( {v-M_0\ddot{q}_d-M_0\dot{\varPsi }z_1-M_0 \varPsi z_2+\frac{m_2}{n_2}M_0H\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)S_2}\right. \\&\quad \left. {+M_0\Lambda _2\dot{\varphi }(S_1)+M_0H_1Sig^\frac{m_1}{n_1}(\hbar )+M_0H_2Sig^\frac{p_1}{q_1}(\hbar )+U\mathrm{sign}(\hbar )}\right) \\&\quad +s^T\tau _d+s^T\left( w^{*T}\phi (Z)+\epsilon \right) -\frac{1}{k_d}\tilde{\tau }_d\left( k_d\Vert s \Vert -r_3\hat{\tau }_d^\frac{m_3}{n_3}-r_4\hat{\tau }_d^\frac{p_3}{q_3}\right) \\&\quad -\tilde{\theta }\left( \frac{k_N}{2}s^Ts\phi ^T(Z)\phi (Z)-r_1\hat{\theta }^\frac{m_3}{n_3}-r_2\hat{\theta }^\frac{p_3}{q_3}\right) \end{aligned} \end{aligned}$$
(46)

Considering the following inequalities

$$\begin{aligned} \begin{aligned}&s^T\tau _d \le \tau _d^*\Vert s \Vert \\&s^Tw^{*T}\phi (Z)\le \frac{k_N}{2}\theta ^*s^Ts\phi ^T(Z)\phi (Z)+\frac{1}{2}\\&s^T\epsilon \le \frac{1}{2} s^Ts + \frac{1}{2} \epsilon ^{*2} \end{aligned} \end{aligned}$$
(47)

thus (46) can be given as

$$\begin{aligned} \begin{aligned} \dot{V}_3 \le&s^T\left( {v-M_0\ddot{q}_d-M_0\dot{\varPsi }z_1-M_0 \varPsi z_2+\frac{m_2}{n_2}M_0H\Lambda _1D^{\frac{m_2-n_2}{n_2}}(S_1)S_2+M_0\Lambda _2\dot{\varphi }(S_1)}\right. \\&\left. {+M_0H_1Sig^\frac{m_1}{n_1}(\hbar )\!+\!M_0H_2Sig^\frac{p_1}{q_1}(\hbar )+U\mathrm{sign}(\hbar )}\right) \!+\!\tau _d^*\Vert s \Vert +\frac{k_N}{2}\theta ^*s^Ts\phi ^T(Z)\phi (Z)\\&+\frac{1}{2}+\frac{1}{2} s^Ts + \frac{1}{2} \epsilon ^{*2}-\frac{1}{k_d}\tilde{\tau }_d\left( k_d\Vert s \Vert -r_3\hat{\tau }_d^\frac{m_3}{n_3}-r_4\hat{\tau }_d^\frac{p_3}{q_3}\right) \\&-\tilde{\theta }\left( \frac{k_N}{2}s^Ts\phi ^T(Z)\phi (Z)-r_1\hat{\theta }^\frac{m_3}{n_3}-r_2\hat{\theta }^\frac{p_3}{q_3}\right) \\ \end{aligned} \end{aligned}$$
(48)

Substituting (41) into (48), we have

$$\begin{aligned} \begin{aligned} \dot{V}_3 \le&-s^TK_1Sig^\frac{m_3}{n_3}(s)-s^TK_2Sig^\frac{p_3}{q_3}(s)+\frac{1}{2}+\frac{1}{2}s^Ts +\frac{1}{2} \epsilon ^{*2}\\&+ r_1\tilde{\theta }\hat{\theta }^\frac{m_3}{n_3} +r_2\tilde{\theta }\hat{\theta }^\frac{p_3}{q_3} +\frac{r_3}{k_d}\tilde{\tau }_d\hat{\tau }_d^\frac{m_3}{n_3}+ \frac{r_4}{k_d}\tilde{\tau }_d\hat{\tau }_d^\frac{p_3}{q_3} \end{aligned} \end{aligned}$$
(49)

Based on Lemmaes 4 and 5, we can get

$$\begin{aligned} \begin{aligned}&\tilde{\theta }\hat{\theta }^\frac{m_3}{n_3} \le \frac{n_3}{m_3+n_3}\left( 2\theta ^{*\frac{m_3+n_3}{n_3}}-(\tilde{\theta }^2)^\frac{m_3+n_3}{2n_3}\right) \\&\tilde{\theta }\hat{\theta }^\frac{p_3}{q_3} \le \frac{q_3}{p_3+q_3}\left( 2\theta ^{*^\frac{p_3+q_3}{q_3}}-(\tilde{\theta }^2)^\frac{p_3+q_3}{2q_3}\right) \\&\tilde{\tau }_d\hat{\tau }_d^\frac{m_3}{n_3} \le \frac{n_3}{m_3+n_3}\left( 2\tau _d^{*\frac{m_3+n_3}{n_3}}-(\tilde{\tau }_d^2)^\frac{m_3+n_3}{2n_3}\right) \\&\tilde{\tau }_d\hat{\tau }_d^\frac{p_3}{q_3} \le \frac{q_3}{p_3+q_3}\left( 2\tau _d^{*^\frac{p_3+q_3}{q_3}}-(\tilde{\tau }_d^2)^\frac{p_3+q_3}{2q_3}\right) \\ \end{aligned} \end{aligned}$$
(50)

Thus (49) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{V}_3 \le&-\lambda _\mathrm{min}(K_1)n^\frac{n_3-m_3}{2n_3}2^\frac{m_3+n_3}{2n_3}\left( \frac{1}{2}s^Ts\right) ^\frac{m_3+n_3}{2n_3}-2^\frac{m_3+n_3}{2n_3}\frac{r_1n_3}{m_3+n_3}\left( \frac{1}{2}\tilde{\theta }^2\right) ^\frac{m_3+n_3}{2n_3}\\&-2^\frac{m_3+n_3}{2n_3}k_d^\frac{m_3-n_3}{2n_3}\frac{r_3n_3}{m_3+n_3}\left( \frac{1}{2k_d}\tilde{\tau }_d^2\right) ^\frac{m_3+n_3}{2n_3}-\lambda _\mathrm{min}(K_2)2^\frac{p_3+q_3}{2q_3}\left( \frac{1}{2}s^Ts\right) ^\frac{p_3+q_3}{2q_3}\\&-2^\frac{p_3+q_3}{2q_3}\frac{r_2q_3}{p_3+q_3}\left( \frac{1}{2}\tilde{\theta }^2\right) ^\frac{p_3+q_3}{2q_3}-2^\frac{p_3+q_3}{2q_3}k_d^\frac{p_3-q_3}{2q_3}\frac{r_4q_3}{p_3+q_3}\left( \frac{1}{2k_d}\tilde{\tau }_d^2\right) ^\frac{p_3+q_3}{2q_3}\\&+\frac{1}{2}s^Ts+F \end{aligned} \end{aligned}$$
(51)

where

$$\begin{aligned} \begin{aligned} F=&\frac{1}{2}+\frac{1}{2} \epsilon ^{*2}+\frac{2r_1n_3}{m_3+n_3}\theta ^{*^\frac{m_3+n_3}{n_3}}+\frac{2r_2q_3}{p_3+q_3}\theta ^{*^\frac{p_3+q_3}{q_3}}\\&+\frac{2r_3n_3}{k_d(m_3+n_3)}\tau _d^{*\frac{m_3+n_3}{n_3}}+\frac{2r_4q_3}{k_d(p_3+q_3)}\tau _d^{*^\frac{p_3+q_3}{q_3}} \end{aligned} \end{aligned}$$

Based on Lemma 3, we have

$$\begin{aligned} \dot{V}_3 \le -3^\frac{n_3-m_3}{2n_3}CV_3^\frac{m_3+n_3}{2n_3}-DV_3^\frac{p_3+q_3}{2q_3}+F \end{aligned}$$
(52)

where

$$\begin{aligned} \begin{aligned} C=&\mathrm{min}\left\{ \frac{\lambda _\mathrm{min}(K_1)n^\frac{n_3-m_3}{2n_3}2^\frac{m_3+n_3}{2n_3}-1}{\left( \lambda _\mathrm{max}(M_0)\right) ^\frac{m_3+n_3}{2n_3}},2^\frac{m_3+n_3}{2n_3}\frac{r_1n_3}{m_3+n_3},2^\frac{m_3+n_3}{2n_3}k_d^\frac{m_3-n_3}{2n_3}\frac{r_3n_3}{m_3+n_3}\right\} \\ D=&\mathrm{min}\left\{ \frac{\lambda _\mathrm{min}(K_2)2^\frac{p_3+q_3}{2q_3}-1}{\left( \lambda _\mathrm{max}(M_0)\right) ^\frac{p_3+q_3}{2q_3}},2^\frac{p_3+q_3}{2q_3}\frac{r_2q_3}{p_3+q_3},2^\frac{p_3+q_3}{2q_3}k_d^\frac{p_3-q_3}{2q_3}\frac{r_4q_3}{p_3+q_3}\right\} \\ \end{aligned} \end{aligned}$$
(53)

From Lemma 2, we have s, \(\tilde{\theta }\) and \(\tilde{\tau }_d\) are fixed-time stable and can converge to a small neighborhood of zero by choosing suitable parameters. The residual set is

$$\begin{aligned} V_3 \le \mathrm{min} \left\{ \left( \frac{F}{3^\frac{n_3-m_3}{2n_3}C(1-\delta )}\right) ^\frac{2n_3}{m_3+n_3},\left( \frac{F}{D(1-\delta )}\right) ^\frac{2q_3}{p_3+q_3}\right\} \end{aligned}$$
(54)

and the settling time is

$$\begin{aligned} T_3<\frac{1}{3^\frac{n_3-m_3}{2n_3}C\delta }\frac{2n_3}{m_3-n_3}+\frac{1}{D\delta }\frac{2q_3}{q_3-p_3} \end{aligned}$$
(55)
Fig. 1
figure 1

Trajectory tracking performance of \(q_1\)

Full size image
Fig. 2
figure 2

Trajectory tracking performance of \(q_2\)

Full size image
Fig. 3
figure 3

Trajectory tracking error of \(q_1\)

Full size image
Fig. 4
figure 4

Trajectory tracking error of \(q_2\)

Full size image
Fig. 5
figure 5

Transformed error \(S_{11}\)

Full size image
Fig. 6
figure 6

Transformed error \(S_{12}\)

Full size image
Fig. 7
figure 7

Sliding mode surface \(s_1\)

Full size image
Fig. 8
figure 8

Sliding mode surface \(s_2\)

Full size image
Fig. 9
figure 9

Control input of \(u_1\)

Full size image
Fig. 10
figure 10

Control input of \(u_2\)

Full size image
Fig. 11
figure 11

Auxiliary dynamic system state \(\hbar \)

Full size image
Fig. 12
figure 12

Norm estimation of RBF NNs weight matrix

Full size image

Remark 2

It can be seen that s, \(\tilde{\theta }\) and \(\tilde{\tau }_d\) are bounded and converge to a small neighborhood of zero from (54). Considering \(\tilde{\theta }=\theta ^*-\hat{\theta }\), \(\tilde{\tau }_d=\tau _d^*-\hat{\tau }_d\) and the boundedness of \(\theta ^*\) and \(\tau _d^*\), then we have \(\hat{\theta }\) and \(\hat{\tau }_d\) are bounded. When s is converge to a small neighborhood of zero, it implies that \(S_1\), \(S_2\) are bounded. Thus from (20), it is easy to find that \(z_1\) and \(z_2\) are bounded. Therefore, we can conclude that the output q will track the desired trajectory \(q_d\) successfully with input saturation and perscribed constraints, and all signals in the closed-loop system are fixed-time stable.

Remark 3

The main challenge of this paper is to use the sliding mode method to design a fixed-time prescribed performance controller that meets the performance requirements and construct a fixed-time auxiliary dynamic system to deal with input saturation nonlinearity. Unlike most prescribed performance controllers that achieve uniformly ultimately bounded [36,37,38], fixed-time stability is proved by using the Lyapunov method. Compared with [29] and [30], a fixed-time auxiliary dynamic system is designed to deal with input saturation and only one neural parameter needs to be adjusted online, which can reduce the calculation burden.

4 Simulation

Simulation results on a 2-DOF robotic manipulator with input saturation are shown in this section to illustrate the effectiveness of the adaptive neural fixed-time controller proposed in this paper.

The simulation model of the manipulator is chosen from Ge et al [47], details are as follows

$$\begin{aligned}&M(q)=\begin{bmatrix} p(1)+p(2)+2p(3)\mathrm{cos}(q_2) &{}\quad p(2)+p(3)\mathrm{cos}(q_2)\\ p(2)+p(3)\mathrm{cos}(q_2) &{}\quad p(2)\\ \end{bmatrix}\\&C(q,\dot{q})=\begin{bmatrix} -p(3)\dot{q}_2\mathrm{sin}(q_2) &{}\quad -p(3)(\dot{q}_1+\dot{q}_2)\mathrm{sin}(q_2)\\ p(3)\dot{q}_1\mathrm{sin}(q_2) &{}\quad 0\\ \end{bmatrix}\\&G(q)=\begin{bmatrix} p(4)g\mathrm{cos}(q_1)+p(5)g\mathrm{cos}(q_1+q_2)\\ p(5)g\mathrm{cos}(q_1+q_2) \end{bmatrix}\\&\tau _d=\begin{bmatrix} 0.3\mathrm{sin}(t)\\ 0.3\mathrm{sin}(t) \end{bmatrix} \end{aligned}$$

where \( p=\left[ 2.9\quad 0.76\quad 0.87\quad 3.04\quad 0.87\right] kgm^2\) and \(g=9.8m/s^2\) . The RBF NNs are constructed by using \(5^4\) nodes with the center evenly laying on \([-1 \quad 1] \times [-1 \quad 1] \times [-1 \quad 1] \times [-1 \quad 1]\) and the width of Gaussian function are selected as \(\eta _1=3\) and \(\eta _2=5\).

Performance function is designed as

$$\begin{aligned} \sigma _i(t)=(1.5-0.02)e^{-t}+0.02,\quad i=1,2 \end{aligned}$$
(56)

and the tracking errors are required to satisfy (16) where \(k_{11}=1\), \(k_{12}=0.8\), \(k_{21}=0.8\) and \(k_{22}=1\). The design parameters are chosen as \(M_0=\mathrm{diag}\left\{ 2 \quad 4\right\} \) \(H_1=H_2=\mathrm{diag}\left\{ 10 \quad 10\right\} \), \(\Lambda _1=\mathrm{diag}\left\{ 5 \quad 3\right\} \), \(\Lambda _2=\mathrm{diag}\left\{ 5 \quad 4\right\} \) and \(K_1=K_2=\mathrm{diag}\left\{ 8 \quad 8\right\} \). \(m_1=21\), \(n_1=17\), \(p_1=11\), \(q_1=17\), \(m_2=23\), \(n_2=17\), \(p_2=17\), \(q_2=23\), \(m_3=37\), \(n_3=29\), \(p_3=31\), \(q_3=33\). \(\mu =0.1\), \(k_N=5\), \(k_d=15\), \(r_1=r_2=3\) and \(r_3=r_4=0.9\). The desired trajectory \(q_{d}=\left[ 0.6+0.5\mathrm{cos}(t),0.3+0.8\mathrm{sin}(t)\right] ^T\) with the initial position and velocity are selected as \(q_1=1.4rad\), \(q_2=0.8rad\), \(\dot{q}_1=\dot{q}_2=0rad/s\) respectively. The input saturation is set as \(u_\mathrm{max}=50Nm\) and \(t \in \left[ 0,20\right] \).

Simulation results are shown from Figs. 1, 2, 3, 4, 5, 6, 7,8, 9, 10, 11 and 12. Figs. 1 and 2 show the manipulator joint trajectory tracking performance. From these two figures, we can see that the joint angular can track the desired trajectory successfully. The tracking error of the two joints will converge to a small region of zero in fixed time and satisfy the prescribed performance requirements, which can be seen in Figs. 3 and 4. The transformed errors \(S_{11}\) and \(S_{12}\) are shown in Figs. 5 and 6 which are converged to the neighborhood of zero. The convergence of sliding mode surfaces \(s_1\) and \(s_2\) can be seen in Figs. 7 and 8. Control inputs are presented in Figs. 9 and 10. We can see that the actual control input \(u_1\) and \(u_2\) are within the limit of input saturation while the designed control input \(v_1\) and \(v_2\) exceed the limit amplitude. Therefore, it indicates that by introducing the fixed-time auxiliary dynamic system, the influence of input saturation nonlinearity is handled successfully. The auxiliary dynamic system state \(\hbar \) is shown in Figs. 11 and 12 shows the estimated value of \(\hat{\theta }\).

From Figs. 1, 2, 3, 4, 5, 6, 7,8, 9, 10, 11 and 12 it is easy to see that the adaptive fixed-time neural sliding mode controller proposed in this paper can make the manipulator track the desired trajectory successfully when considering system uncertainty, input saturation and prescribed constraints. Thus the simulation results verify the effectiveness of our proposed fixed-time trajectory tracking controller.

5 Conclusions

In this paper, the sliding mode based fixed-time adaptive neural trajectory tracking controller for uncertain robotic manipulators under input saturation, external disturbances and prescribed constraints is constructed. The prescribed performance method is utilized to deal with the prescribed constraints of trajectory tracking error. The effect of input saturation is tackled successfully by employing a novel fixed-time auxiliary nonlinear dynamic system and the fixed-time sliding mode surface is introduced for controller design. RBF NNs are constructed to approximate the system uncertainty. Different from most neural controllers that adjust all weight parameters, in this paper, only one parameter is needed to be updated online by estimating the norm of the weight matrix. Furthermore, by using the Lyapunov synthesis, all signals in the closed-loop system are illustrated to be fixed-time stable. Finally, simulation works show the feasibility and effectiveness of the fixed-time neural tracking controller proposed in this article.

For future studies, how to achieve fixed-time stability when only position measurement is available is one research direction. Meanwhile, the convergence time of the fixed-time stability depends on the control parameters and how to ensure the stability of the system within a given time constant is another research direction in the future.