1 Introduction

Over the past few decades, neural network is a hot topic of research. It has attracted many scholars due to its wide range of practical applications in various fields including associative memory, signal processing, pattern recognition, artificial intelligence, combinational optimization, and so on [1,2,3,4,5,6,7,8]. In the beginning, most of the works in neural networks were mainly in real valued neural networks (RVNNs) and complex valued neural networks (CVNNs) [6, 9,10,11,12,13]. Continuous development of real and complex valued neural networks are certain, due to their limitations to deal with the problems of multi dimensional data. For instance, when issue on detection of symmetry is encountered, RVNNs may not be useful, whereas CVNNs can solve such problems [3]. CVNNs have also limitations when dealing with three and four dimensional data. Therefore, we have to use high dimensional numbers. Quaternion number being an extension of complex number, is a special case of clifford algebra introduced by British Mathematician William Rowan Hamilton in the year 1843. As compared to real numbers and complex numbers, commutativity of multiplication does not hold in quaternions, due to this the quaternions did not receive much attention of the researchers earlier. But recently, researchers have started working in this direction due to its wide range of potential applications in various fields like computer graphics, array processing, three/four dimensional data modelling, color image processing, attitude control, predication of 3-D wind processing [14,15,16,17].

Quaternion valued neural network (QVNN) is an extension of CVNN. In QVNNs, the states, activation functions and the connection weights take values in quaternions with unique superiority to deal with multi dimensional data. For the image compression [18], three neurons are needed for the transmission of one colour signal, whereas for QVNN one quaternion neuron can transmit one colour through three channels. Therefore, QVNNs store large amount of data in lesser number of neurons. More precisely, QVNNs perform better to deal with the problems of optimization and estimation as compared to RVNNs and CVNNs [19,20,21].

As an important kind of dynamical behaviour, synchronization of neural networks has been an interesting topic of research in recent years. This is widely applied in various aspects viz., secure communication [22], image encryption [23], medicine [24], synchronization of local brain region in patient with Parkinson’s disease [25]. However, most of the works are limited to attain synchronization in infinite time, including projective synchronization [26], adaptive synchronization [27, 28], exponential synchronization [29] and asymptotical synchronization [30]. These types of synchronization rarely satisfy the synchronization condition unless the time is infinite. Therefore, the method in which the synchronization within finite time is of great interest rather than synchronization in infinite time [31,32,33,34,35,36]. However, the drawback of finite-time synchronization is that it depends wholly on initial conditions. More precisely, larger the initial synchronization error, bigger will be the settling time. But in actual applications of the neural networks, it is not always possible to find the initial conditions of the system explicitly. To overcome this drawback, A. Polyakov proposed the fixed-time synchronization [37]. Here, synchronization is achieved in a fixed time irrespective of any initial conditions i.e., the uniform upper bound of finite time stability is independent of initial values. Some important applications of fixed time synchronization are found in power system [38] and rigid spacecraft [39]. Thus it is fruitful to focus on fixed time stability/ synchronization of non linear systems. Recent works on the fixed time synchronization can be found in the articles [38,39,40,41,42,43]. These works are mainly on the RVNNs and CVNNs. Till date a few results are available on the fixed-time synchronization of QVNNs [44,45,46,47,48,49]. In most of these works, the neural network models have been considered without time delay or discrete delay or time varying delay [45, 46, 49]. In this article, we have purposed mixed time varying delay neural networks model which is more general. As far as, the synchronization of QVNNs with both time varying and distributed delay is still an open and challenging problem.

Since time delays are generally time varying in nature, therefore it is inescapable in dynamical system due to limited transmission velocity between the neurons. In presence of time delay dynamical behaviours of QVNNs become more complex and more general. Time delay may lead to performance degradation, for example, oscillation, instability, bifurcation etc. On the other hand due to existence of vast parallel pathways with different axon sizes and lengths, it is more rational way to introduce continuously distributed delay into neural networks model [50, 51]. Few important practical applications for the system with distributive delay can be found in the research articles [52, 53].

Taking into account of all the above discussions, this article aims to study the fixed time synchronization between the identical drive-response systems of QVNN (1) with mixed time varying delays. This is obtained by using the criterion of fixed time stability of error system. For the fixed time stabilty, the synchronization of drive-response systems is established within fixed time. Some major contributions of this scientific contribution are listed as follows.

  1. (1)

    It is the first time the fixed time synchronization of QVNNs is discussed with mixed time varying delays.

  2. (2)

    The controllers are deigned in such a way that the settling time is independent of the delay terms.

  3. (3)

    Converting the QVNN into four real parts and by using some suitable controllers along with Lyapunov function, the synchronization within fixed time is achieved.

The rest of the article is organized as follows: Section 2 contains model description and prerequisite, section 3 contains main theoretical results, section 4 includes a numerical example for validation of theoretical results, which is followed by the section 5 as conclusion.

Notations: \(\mathbb {R},\mathbb {C},\mathbb {Q} \) are real field, complex field and quaternion skew field, respectively. \(\mathbb {R}^{n\times m},\mathbb {C}^{n\times m}\) and \(\mathbb {Q}^{n\times m}\) denote the \( n\times m \) matrices where entries are from the \(\mathbb {R},\mathbb {C} \text { and } \mathbb {Q}\), respectively.

2 Model Description and Preliminaries

The quaternion numbers form a class of hypercomplex numbers composed of one real and three imaginary parts. A quaternion number is 4-D vector space over \( \mathbb {R} \). Let \(q\in \mathbb {Q} \), then it can be written as

$$\begin{aligned} q=q^R+q^Ii+q^Jj+q^Kk, \end{aligned}$$

where \( q^R,q^I,q^J,q^K\in \mathbb {R} \). The unit components of quaternion numbers obey the Hamilton rules i.e., the units \( i,j \text { and } k \) satisfy the following:

\( ij=-ji=k, jk=-kj=i, ki=-ik=j, ~~i^2=j^2=k^2=ijk=-1\).

This shows that multiplication in quaternions is non commutative. Conjugate of the quaternion number is \( q^* \text { or } \bar{q} =q^R-q^Ii-q^Jj-q^Kk,\) and the modulus value |q| is defined as \( |q|=\sqrt{q.q^{*}} =\sqrt{(q^R)^2+(q^I)^2+(q^J)^2+(q^K)^2}.\)

If \( q_1,q_2\in \mathbb {Q}\), where \(q_1=q_1^{R}+q_1^{I}i+q_1^{J}j+q_1^{K}k\in \mathbb {Q}\) and \(q_2=q_2^{R}+q_2^{I}i+q_2^{J}j+q_2^{K}k\in \mathbb {Q}\). The addition \(q_1+q_2\) and multiplication \( q_1.q_2 \) are defined as

$$\begin{aligned} q_1+q_2=&\, (q_1^{R}+q_2^{R})+(q_1^{I}+q_2^{I})i+(q_1^{J}+q_2^{J})j+(q_1^{K}+q_2^{K})k,\\ q_1.q_2=&\, (q_1^{R}q_2^{R}-q_1^{I}q_2^{I}-q_1^{J}q_2^{J}-q_1^{K}q_2^{K})+(q_1^{R}q_2^{I}+q_1^{I}q_2^{R}+q_1^{J}q_2^{K}-q_1^{K}q_2^{J})i\\&+(q_1^{R}q_2^{J}+q_1^{J}q_2^{R}-q_1^{I}q_2^{K}+q_1^{K}q_2^{I})j+(q_1^{R}q_2^{K}+q_1^{K}q_2^{R}+q_1^{I}q_2^{J}-q_1^{J}q_2^{I})k. \end{aligned}$$

The model of QVNN with mixed time varying delay is considered as

(1)

where \(p=1,2,\ldots ,n\); \(z(t) = [z_{1}(t), z_{2}(t),\ldots ,z_{n}(t)]^{T} \in \mathbb {Q}^{n}\) is the state vector of the neural networks with n neurons at time \(t; C=\text {diag}\{c_1,c_2,\ldots ,c_n\}\in \mathbb {R}^{n\times n}\) is the self-feedback connection weights matrix with \(c_i>0\) for \(i=1,2,\ldots ,n\); and \(D=(d_{ij})_{n\times n}\in \mathbb {Q}^{n\times n}\) for \(i=1,2,\ldots ,n\), \(j=1,2,\ldots ,n\), are the connection weight matrices; \(f_i(.), g_i(.)\) and \(h_i(.)\) are the activation functions for \(i=1,2,\ldots ,n\) of suitable dimensions; \(I_i(t)\) for \(i=1,2,\ldots ,n\), denote the external inputs. \(\tau _{1}(t)\) and \(\tau _{2}(t)\) are the time varying delays.

The following assumptions will be used frequently.

Assumption 1

Each of the activation functions can be written as

$$\begin{aligned} F_p(z_p(t))=F^R_p(z^R_p(t))+F^I_p(z^I_p(t))+F^J_p(z^J_p(t))+F^K_p(z^K_p(t)), \end{aligned}$$
(2)

where \(F_p=f_p,g_p,h_p\) for \(p=1,2,\ldots ,n\); \(z_p^\gamma \in \mathbb {R}\) for \(\gamma =R,I,J,K\); \(p=1,2,\ldots ,n.\)

Assumption 2

Each of the four components of every activation function satisfies the Lipschitz condition i.e., for \(x_1,x_2 \in \mathbb {R}\), \(\exists \) constants \(l^1_p,l^2_p,l^3_p\in \mathbb {R}\), such that

$$\begin{aligned}&|f^\gamma _p(x_1)-f^\gamma _p(x_2)|\le l^1_p|x_1-x_2|,\\&|g^\gamma _p(x_1)-g^\gamma _p(x_2)|\le l^2_p|x_1-x_2|,\\&|h^\gamma _p(x_1)-h^\gamma _p(x_2)|\le l^3_p|x_1-x_2|. \end{aligned}$$

Remark 1

The activation functions are absolutely inherent components of the neural networks which influence the dynamical behaviour of the designed neural networks. From both the assumptions, the existence and uniqueness of the solution of model (1) can be guaranteed due to continuity and Lipschitz condition of the activation functions [54].

The system (1) with the Assumption 1 can be written in four real valued systems as

(3)

The corresponding slave system is given by

(4)

Let us define the error term as \(\varepsilon _p(t)=s_p(t)-z_p(t).\)

Then from Eqs. (3) and (4), we get

(5)

Let the controllers be defined as

$$\begin{aligned} U_p^\gamma (t)=&-\xi _{1p} \varepsilon _p^\gamma (t)-sign (\varepsilon _p^\gamma (t))\bigg (\xi _{2p}^\gamma |\varepsilon _p^\gamma (t-\tau _{1}(t))|+\xi _{3p}^\gamma \int _{t-\tau _{2}(t)}^t|\varepsilon _p^\gamma (s)|ds\nonumber \\&+\xi _{4p}|\varepsilon _p^\gamma (t)|^\alpha +\xi _{5p}|\varepsilon _p^\gamma (t)|^\beta \bigg ), \end{aligned}$$
(6)

where \(\xi _{4p}>0\), \(\xi _{5p}>0\), \(0< \alpha <1\), \(\beta >1\). \(\xi _{1p}\), \(\xi _{2p}^\gamma \) and \(\xi _{3p}^\gamma \) are the parameters those are to be defined later.

Remark 2

The controller in the present article is designed in such a way that it contains the linear and non linear terms. Non linear term plays significant role in the rate of synchronization. Also the settling time obtained is independent of the delays.

Some definitions and lemmas used in this article are described below.

Definition 1

([37]) The origin of the system (5) is said to achieve finite time stability, if there exists a function \(T:\mathbb {R}^{n}\rightarrow \mathbb {R}_{+} \cup \{0\}\) called settling time function such that \(\lim _{t\rightarrow T(\varepsilon _0)}\Vert \epsilon (t)\Vert =0 \) and \(\epsilon (t)=0\) for all \(t\ge T(\varepsilon _0)\). Here, \(\varepsilon _0\) is the initial value of the system (5).

Definition 2

([37]) The origin of the system (5) is called fixed time stable if it is finite time stable and the settling time function is bounded i.e., there exists a positive constant \(\mathcal {C}\) such that \(T(\varepsilon _{0})<\mathcal {C}\) for all \(\varepsilon _{0} \in \mathbb {Q}^{n}\).

Remark 3

From the definitions of finite-time and fixed-time stabilities, it can be seen that in finite time stability, the settling time depends on initial conditions i.e., for every change in initial conditions we will have different settling time expressions. Whereas in fixed time stability, the settling time is invariant of initial conditions i.e., the settling time expression is independent of initial conditions.

Lemma 1

[55] Let \(V(.):\mathbb {R}^{n}\rightarrow \mathbb {R}_{+} \cup \{0\}\) is a continuous and radially unbounded function. If e(t) is any solution of expression (5), then the origin of the system (5) is fixed time stable provided

  1. (i)

    \(V(e(t))=0 \) iff \(e(t)=0\);

  2. (ii)

    for some \(k_1,k_2,k_3>0,\)

    $$\begin{aligned} \dot{V}(t)\le -k_1V^{\alpha }(e(t))-k_2V^{\beta }(e(t))-k_3V(e(t)), 0<\alpha < 1 \text { and } \beta >1. \end{aligned}$$

The settling time expression is given by \(T_{set}^1 = \frac{1}{k_3(1-\alpha )}ln(1+\frac{k_3}{k_1})+\frac{1}{k_3(\beta -1)}ln(1+\frac{k_3}{k_2})\).

Lemma 2

[37] If \(V(.):\mathbb {R}^{n}\rightarrow \mathbb {R}_{+}\) is a continuous and radially unbounded function and e(t) is any solution of (5), then the origin of the system (5) is fixed time stable provided

  1. (i)

    \(V(e(t))=0 \) iff \(e(t)=0\);

  2. (ii)

    for some \(k_1,k_2>0,\)

    $$\begin{aligned} \dot{V}(t)\le -k_1V^{\alpha }(e(t))-k_2V^{\beta }(e(t)), 0<\alpha < 1 \text { and } \beta >1. \end{aligned}$$

The settling time expression is given by \(T_{set}^2 = \frac{1}{k_1(1-\alpha )}+\frac{1}{k_2(\beta -1)}\).

Lemma 3

[49] let \(z_{i}\ge 0\) for \(i=1,2,\ldots ,n\); \(0<p\le 1\) and \(q >1\). Then the following inequality holds.

$$\begin{aligned} \sum _{i=1}^{n}z_{i}^{p}\ge \left( \sum _{i=1}^{n}z_{i}\right) ^{p}, \sum _{i=1}^{n}z_{i}^{q} \ge n^{1-q}\left( \sum _{i=1}^{n}z_{i}\right) ^{q}{.} \end{aligned}$$

3 Main Results

Theorem 1

The system (5) with the Assumption 2 and the controllers (6) gains fixed time stability if it satisfies the following conditions:

Here, the expression of settling time expression is \(T_{set}^1=\frac{1}{c(1-\alpha )}\ln \left( 1+\frac{c}{\min _{p}(\xi _{4p})}\right) +\frac{1}{c(\beta -1)}\ln \left( 1+\frac{c}{\min _{p}(\xi _{5p})(4n)^{1-\beta }}\right) \),

where .

Proof

Consider the Lyapunov functional as

$$\begin{aligned} V(t)=\sum _{i=1}^4V_i(t), \end{aligned}$$
(7)

where \(V_1(t)=\sum _{i=1}^n|\varepsilon _p^R(t)|\), \(V_2(t)=\sum _{i=1}^n|\varepsilon _p^I(t)|\), \(V_3(t)=\sum _{i=1}^n|\varepsilon _p^J(t)|\), \(V_4(t)=\sum _{i=1}^n|\varepsilon _p^K(t)|\).

Then the dinni derivative of \(V_1(t)\) along the trajectories of the considered system is given by

Similarly,

Merging these four inequalities, we have

(8)

By using Lemma 1 and Lemma 3, we obtain

Corollary 1

The system (5) with the Assumption 2 and the controllers (6) achieves fixed time stability with the same sufficient conditions as in Theorem 1. The settling time obtained in this case is given by

$$\begin{aligned} T_{set}^2=\frac{1}{\min _{p}(\xi _{4p})(1-\alpha )}+\frac{1}{\min _{p}(\xi _{5p})(4n)^{1-\beta }(\beta -1)}. \end{aligned}$$
(9)

Proof

Define the Lyapunov functional as

$$\begin{aligned} V(t)=\sum _{p=1}^{n}(|\varepsilon _p^R(t)|+|\varepsilon _p^I(t)|+|\varepsilon _p^J(t)|+|\varepsilon _p^K(t)|). \end{aligned}$$

Calculating the derivative of V(t) along the trajectories of given system as calculated in Theorem 1 in equation (8), and using Lemma 1 and Lemma 3, we obtain

$$\begin{aligned} \dot{V}(t)\le -\min _{p}(\xi _{4p})V^\alpha (t)-\min _{p}(\xi _{5p})(4n)^{1-\beta }V^{\beta }(t), \end{aligned}$$

and the corresponding settling time is given by expression (9).

Remark 4

Our considered model is more general and more complex as compared to the existing models to achieve the fixed time synchronization of QVNNs. If we take the connection weights matrix \(D=0\) in the model (1), then we will get the model used in [46] which is without distributed delay. Again by taking the connection weight matrices \(B=0\) and \(D=0\) in (1), we get the model of [49] which is without delay term. But in actual implementation of neural networks, the delay is an inescapable quantity.

4 Numerical Example

In this section a drive is made to validate the efficiency and effectiveness of the proposed method while applying it during synchronization of two identical QVNNs with mixed time delays.

Example 1

Consider QVNN as given in (1) for \(n=2\) as

$$\begin{aligned} \dot{z}(t) = -Cz(t)+Af(z(t))+Bg(z(t-\tau _{1}(t)))+D\int _{t-\tau _{2}(t)}^{t}h(z(s))ds+ I(t), \end{aligned}$$
Fig. 1
figure 1

Plot of trajectories of \(z_1^R(t)\) and \(s_1^R(t)\), \(z_1^I(t)\) and \(s_1^I(t)\), \(z_1^J(t)\) and \(s_1^J(t)\), \(z_1^K(t)\) and \(s_1^K(t)\) for the master-slave systems (3) and (4) without controllers

Full size image
Fig. 2
figure 2

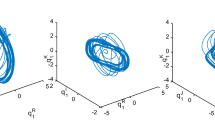
Plots of the trajectories of \(e_1^R(t)\), \(e_1^I(t)\), \(e_1^J(t)\), \(e_1^K(t)\) and \(e_2^R(t)\), \(e_2^I(t)\), \(e_2^J(t)\), \(e_2^K(t)\) for the solution e(t) of the error system (5)

Full size image

where \(z=z^{R}+z^{I}i+z^{J}j+z^{K}k,\)

$$\begin{aligned} A= & {} \begin{pmatrix} 1+2.2\bar{i}+2\bar{j}-1\bar{k} &{} -2-3.5\bar{i}+2.5\bar{j}-3\bar{k}\\ -2+1.5\bar{i}+1\bar{j}+1.5\bar{k} &{} 0.5-1.5\bar{i}+0.5\bar{j}-1\bar{k} \end{pmatrix},\\ B= & {} \begin{pmatrix} 0.5-1.5\bar{i}+2\bar{j}+-2\bar{k} &{} 1+1\bar{i}-2\bar{j}-1.5\bar{k}\\ 3-\bar{i}+1\bar{j}-2\bar{k} &{} 0.5-\bar{i}+3\bar{j}-2\bar{k}\\ \end{pmatrix},\\ D= & {} \begin{pmatrix} 0.3+2\bar{i}+1\bar{j}+.5\bar{k} &{} -1-0.3\bar{i}+2\bar{j}-1\bar{k}\\ -1-0.2\bar{i}+3\bar{j}-1\bar{k} &{} 1+0.5\bar{i}-1\bar{j}+1.5\bar{k}\\ \end{pmatrix},\\ C= & {} diag[1.5,1.4], I=(1.2-1.2\bar{i}+1.3\bar{j}+1.4\bar{k}, 1.4\\&+1.3\bar{i}+1.4\bar{j}-1.3\bar{k})^{T},\\ \tau _{1}(t)= & {} \tau _{2}(t)=cos^{2}(t), \end{aligned}$$

and let us take the activation functions as

$$\begin{aligned} f_{j}(z_{j}^{\gamma })=tanh(z_{j}^{\gamma }),\; g_{j}(z_{j}^{\gamma })=tanh(z_{j}^{\gamma }),\; h_{j}(z_{j}^{\gamma })=tanh(z_{j}^{\gamma }), \end{aligned}$$

for \(j=1,2\) and \(\gamma =R,I,J,K.\)

Let us consider the initial conditions as

\(z_{1}(0)=80+70\bar{i}+60\bar{j}+50\bar{k}\), \(z_{2}(0)=40+30\bar{i}+20\bar{j}+10\bar{k}\), \(s_{1}(0)= 10+20\bar{i}+30\bar{j}+40\bar{k}, s_{2}(0)=50+60\bar{i}+70\bar{j}+80\bar{k}\).

For this case, the trajectories of the system without controllers are shown through Fig. 1 which clearly show its non-synchronization. Again, the Assumption (2) with the above considered activation functions hold for \(l^1_{p}=1 = l^2_{p} = l^3_{p}\). Now, considering \(\xi _{11}=12, \xi _{12}=14, \alpha =0.5, \beta =1.5, \xi _{21}=20, \xi _{22}=20,\xi _{31}=20,\xi _{32}=20,\xi _{4p}=10,\xi _{5p}=20 \) for \(p=1,2\), the controller functions become

$$\begin{aligned} U_{1}^{\gamma }(t)=&-12\varepsilon _{1}^{\gamma }(t)-sign(\varepsilon _{1}^{\gamma }(t))[20\varepsilon _{1}^{\gamma }(t-cos^{2}(t))+20\int _{t-cos^{2}(t)}^{t}|\varepsilon _{1}^{\gamma }(s)|ds\\ {}&+10|\varepsilon _{1}^{\gamma }(t)|^{0.5}+20|\varepsilon _{1}^{\gamma }(t)|^{1.5}],\\ U_{2}^{\gamma }(t)=&-14\varepsilon _{2}^{\gamma }(t)-sign(\varepsilon _{2}^{\gamma }(t))[20\varepsilon _{2}^{\gamma }(t-cos^{2}(t))+20\int _{t-cos^{2}(t)}^{t}|\varepsilon _{2}^{\gamma }(s)|ds\\ {}&+10|\varepsilon _{2}^{\gamma }(t)|^{0.5}+20|\varepsilon _{2}^{\gamma }(t)|^{1.5}]. \end{aligned}$$

The synchronization of the trajectories of the systems with control functions are depicted through Fig. 2. The settling times are calculated as \(T_{set}^1=0.4464\) and \(T_{set}^2=0.6656\). Therefore, the settling time obtained by Lemma 1 gives more accurate result as compared to that given by Lemma 2.

Remark 5

The settling time using Lemma 1 is less as compared to that using Lemma 2. A general comparison of the two settling time expressions is given in [46]. Lemma 2 is used to prove synchronization results in [49, 58] which gives more conservative results.

Remark 6

QVNNs store large amount of data in lesser number of neurons as compared to the CVNNs and RVNNs. In [56], the proposed neural network needs 144 neurons to store 12 \(\times \) 12 pixel colour figure, however the corresponding CVNNs should have 432 neurons to store the same. Also, in [57], this has been shown that the storage capacity of the CVNNs is larger than that of the RVNNs.

5 Conclusion

This article has investigated the fixed time synchronization of QVNNs with mixed time varying delays. To achieve the desired synchronization, a set of sufficient conditions is derived through designing a new controller and a proper choice of Lyapunov function. Two different lemmas have been used for getting two different settling time expressions. The theoretical results are validated through a given numerical example. To overcome the non-commutativity of quaternions, QVNNs have been decomposed into four equivalent RVNNs, which have supported to open a good scope of doing research in QVNNs as in RVNNs. In QVNNs the pre-defined time stability and the effect of time varying impulses on finite or fixed time stability may be a good area of research in near future.