Synchronization in Quaternion-Valued Neural Networks with Delay and Stochastic Impulses

Abstract

A class of global exponential synchronization problem for delayed quaternion-valued neural networks with stochastic impulses has been investigated in this paper, where the impulses arouse time and strength both are randomly. Firstly, the delayed quaternion-valued model with stochastic impulses was fain to separate to four real-valued parts in consideration of the fact that noncommutativity character of quaternion multiplication. Then, a new criterion was obtained to achieve the global exponential synchronization via building an appropriate classically Lyapunov candidate function and utilizing the method of comparison principle and reduction to absurdity. Finally, in order to verify the validity of the proposed theorem, a given numerical example is provided.

1 Introduction

The quaternion is a class of hyper-complex number, that was first proposed by the Irish Scientist Hamilton [9] in 1843 and could be regarded as a four-dimension space extension of real-valued and complex-valued. In the past few years, the application fields of quaternion-valued neural networks(QVNNs) was continuously developing and enriching accompanied by the constantly deepened quaternion algebra theoretical research and rapid development of neural networks [2, 3, 5]. Especially the [19] which fits the quaternion perfectly because all of the four elements of quaternion own each corresponding real meaning unlike the normal case just the three imaginary parts be used. Relative to the dynamic behaviour of QVNNs [26, 30, 42], the synchronization although is the hotspot of research recent years in the nonlinear systems, which means that the whole network nodes have a same collective conduct. Nowadays, a variety of synchronization have been studied in QVNNs [6, 18, 24]; such as phase synchronization [7], quasi-synchronization [17], Mittag-Leffler synchronization [38] etc. The global exponential synchronization has gained widespread attraction and an analogous about delay quaternion-valued memristive neural networks has been researched in [35]. It follows that the results of global exponential synchronization with time delays is rare in QVNNs. It is urgent to enrich, develop and perfect the content of aforementioned in the field of QVNNs.

Resolving the time delay is always a key and tricky problem in the research of global exponential synchronization with time delays in QVNNs. Due to the speed limit of signal propagation, the wear rate of the equipment, the capacity constraints in series systems etc., especially the limited switching speed and limited transmission speed of neuron amplifiers in neural networks, which made the trend of many systems not only related to the current state, but also depends on the past state. Thus, time delays widely exists in both artificial and biological neural systems. It has made a great difficulty to analyze and synthesize the control system and often leads the synchronization system out of synchronous property. It thus appears that, the study of time delays is essential to the synchronization of QVNNs. Generally, the problem often discussed in the study of synchronized delays in QVNNs is whether the system is delay-dependent or not. And the major approach of dealing with the delay-dependent usually adopts the Lyapunov–Krasovskii (L-K) method to construct the Lyapunov candidate functions, while just could resolve the small and little change delays. In contrast, there are many approaches to deal with the delay-independent, such as the Lyapunov–Razumikhin (L-R) method, the M matrix method and the method by utilizing the major matrix inequalities to deal with the derivative of Lyapunov candidate functions. The characteristic is obviously contrast to the former, which could deal with the unknown and large-scale delays. There are many results about synchronization with delay-independent and delay-dependent in QVNNs [4, 22, 25, 28]. Yet, QVNNs with delay-independent are less discussed that we need to improve in the next few years.

During the process of signal transmission, the signal may jump abruptly at some discrete moment, which is called the impulse. This phenomenon widely exists in nature, such as the closing of switch in a circuit system, timed fishing of population ecosystems and the frequency modulation system in communication and etc. Through the above analysis of impulses, the impulses system is playing an important role in the research of dynamical behavior and application. In the past, a host of studies have investigated the impulsive system, for example [12, 23, 27, 31, 40, 43]. According to [1, 10], the receptor has received a signal of stimulus where from the external environment or the body, the neural network will accept the electrical impulses, where the impulsive effects occur naturally. Due to the superiority and capacity of quaternion valued, the quaternion valued impulses neural networks(QVINNs) has widely aroused researchers’ concern, and many dynamics behaviors and application results are posted in following literatures [16, 24, 39]. We also know that neural networks can made the system stable, asymptotically stable, synchronized or exponentially synchronized by some stochastic disturbances. Therefore, the dynamic behavior analysis of stochastic neural networks becomes more and more important. There are many achievements about stochastic disturbances in NNs [31,32,33].

Just use the fixed impulses can not always model completely and ideally due to the practical complex environment accompanied by time varying, stochastic factors and others. And with the effects of stochastic and impulsive neural network model should describe the evolution of the system more accurately. A new research about the combination of stochastic and impulses has been proposed. Limited works of neural networks with the stochastic impulses has been done, such as [13, 14, 21]. In [11, 34], Tang and He had been discussed the synchronization and stability of network with the strengths of impulses occur according to probabilities, which had opened up a new fields in NNs with impulses and gave us a new impulse generator form in the neural network. Inspired by the aforementioned researches, this paper focused on exploring the global exponential synchronization of delayed QVNNs with stochastic impulses. The main contributions of this paper can be listed as follows: (1) for the first time, we try to investigate synchronization problem of the delayed QVNNs with stochastic impulses wherein the strength is probabilistic; (2) a novel inequality condition about the synchronization of delayed QVNNs with stochastic impulses has been proposed by utilizing the method of comparison principle and reduction to absurdity; (3) a new condition with the LMI of global exponential synchronization is delay-independent regardless of the value of the delay bounded, but related to the rate of convergence.

The structure of remaining article consist of five section as follows. Section 2 introduces the preliminaries and the main model of the delayed QVNNs with stochastic impulses. Section 3, we prove the main theorem and the new condition with the globally exponential synchronization. In Sect. 4, a specific illustrative example is presented to verify the reasonableness of the obtained theorem. Last in Sect. 5, with the conclusions are given.

Notations: ${\mathbb {R}}$, ${\mathbb {Q}}$ represents the field of real-valued and quaternion-valued, respectively. $\mathbb {R}^{n\times m}$, $\mathbb {Q}^{n\times m}$ separately stands for $n\times m$ dimensional real-valued, quaternion-valued matrices with the entries elements from $\mathbb {R}$ and $\mathbb {Q}$. Simply, when $m=1$, $\mathbb {R}^{n}$ and $\mathbb {Q}^{n}$ stands for the $1\times n$ column vector of real-valued and quaternion-valued, respectively. The notations $\bar{A}$, $A^T$ and $A^*$ stands for the conjugate, the transpose, and the conjugate transpose of matrix A, respectively; $A=A^*$ means that the self-conjugate matrix A is denoted as Hermitian in quaternion field. $SC_n(Q)$ denote the set of whole quaternion self-conjugate matrix of order n. Let $A\in SC_n(Q)$, if $x^*Ax>0(\geqslant 0)$ for any $0\ne x=(x_1,\ldots ,x_n)^T\in \mathbb {Q}^{n\times 1}$, then A represent quaternion positive(semi-positive) matrix. The set of whole quaternion positive(semi-positive) matrix of order n denote as $SC_n^{>}(Q)$($SC_n^{\geqslant }(Q)$). $\mathbb {R}_+$ and $\mathbb {Z}_+$ denote the positive real-valued and integer set $\triangleq {1,2,3,\ldots }$, respectively. $\Vert \cdot \Vert$ means the Euclidean norm of vector or matrix. PC(n) refers to the class of piecewise right continuous function $\phi : [t_0-\tau ,+\infty )\rightarrow \mathbb {Q}^n$ where the norm defined by $\Vert \phi (t)\Vert _{\tau }= \sup _{-\tau \le s \le 0}\Vert \phi (t+s)\Vert$.

2 Model Description and Preliminaries

Generally, a quaternion $a \in \mathbb {Q}$ could be stated as follows:

$$\begin{aligned} m=m_0+m_1 i+m_2 j+m_3k, \end{aligned}$$

where $m_0$, $m_1$, $m_2$ and $m_3$ are the real coefficients, i, j and k represent the standard imaginary units in $\mathbb {Q}$, which obey the Hamilton rules:

$$\begin{aligned} \left\{ \begin{aligned}&i^2=j^2=k^2=-1,\ i j=- j i=k,\\&j k=-k j=i,\ k i=-i k= j. \end{aligned} \right. \end{aligned}$$

Apparently, the quaternion does not satisfy commutative rule of multiplication according to the Hamilton rules. Next, we will introduce some basic operations in the field of quaternion. For any two quaternion m and $\nu =\nu _0+\nu _1 i+\nu _2 j+\nu _3k$, the sum and product of m and $\nu$ are defined as:

$$\begin{aligned} m+\nu =(m_0+\nu _0)+(m_1+\nu _1) i+(m_2+\nu _2) j+(m_3+\nu _3)k, \end{aligned}$$

and

$$\begin{aligned} m\nu&=(m_0\nu _0-m_1\nu _1-m_2\nu _2-m_3\nu _3)+(m_0\nu _1+m_1\nu _0+m_2\nu _3-m_3\nu _2)i \\&\quad +(m_0\nu _2-m_1\nu _3+m_2\nu _0+m_3\nu _1)j+(m_0\nu _3+m_1\nu _2-m_2\nu _1+m_3\nu _0)k. \end{aligned}$$

In addition, the modulus of $\nu \in \mathbb {Q}$ denoted by $|\nu |$, and $|\nu |=(\nu \bar{\nu })^{1/2}=\sqrt{((\nu ^R)^2+}$ $\overline{(\nu ^I)^2+(\nu ^J)^2+(\nu ^K)^2}$. Furthermore, let vector $\gamma =(\gamma _1, \gamma _2, \dots , \gamma _n)^T \in \mathbb {Q}^n$, where $\gamma (t)=\gamma _p^R(t)+ i \gamma _p^I(t)+ j \gamma _p^J(t)+k \gamma _p^K(t),\ p\in \mathbb {Z}_+$. Let $|\gamma |=(|\gamma _1|,|\gamma _2|,\dots ,|\gamma _n|)^T$ be the modulus of ${|\gamma |}$. The norm of $\gamma$ is defined as $|\gamma |=\sqrt{\sum _{p=1}^n(\gamma ^R_p)^2+(\gamma ^I_p)^2+}$ $\overline{(\gamma ^J_p)^2+(\gamma ^K_p)^2}$ .

2.1 Model Formulation and Basic Lemmas

Considering the following QVNNs with time-varying delay:

$$\begin{aligned} \frac{d\chi _p(t)}{dt}=&-c_p\chi _p(t)+\sum _{q=1}^{n}a_{pq}f_q(\chi _q(t)) \nonumber \\&+\sum _{q=1}^{n}b_{pq}g_q(\chi _q(t-\tau (t)))+u_p(t), \ t\ge 0, \end{aligned}$$

(1)

where $p\in \{1,2,\dots ,n\}\!\!:=T$, $\chi _p(t)\in \mathbb {Q}$ define as the state variable of the pth neuron at time t, $c_p \in \mathbb {R}^+$ is the element of self-feedback connection weight coefficient matrix; $A=(a_{pq})_{n\times n}\in \mathbb {Q}^{n\times n}$ is a non-delayed connection weight matrices at time t from neuron q to neuron p and $B=(b_{pq})_{n\times n}\in \mathbb {Q}^{n\times n}$ refers to the delayed connection weight matrices; $f_q(\chi _q(t))\in \mathbb {Q}$ represent the activation functions without time-varying delays, and $g_q(\chi _q(t-\tau (t)))\in \mathbb {Q}$ with $q\in T$ denote functions with time-varying delays. $\tau (t)$ refers to the time-varying delay; $u_p(t) \in \mathbb {Q}$ represents the external control input with $p\in T$.

To overcome the challenge of the non-commutativity property of quaternion multiplication, we take $\chi _q=\chi _q^R +i\chi _q^I + j\chi _q^J +k\chi _q^K$, $u_q(t)=u_q^R(t)+i u_q^I(t)+j u_q^J(t)+ku_q^K(t)$ where $\chi _q^v$, $u_q^v \in \mathbb {R}$, $v\in \{R,I,J,K\}:= E$ and $q\in T$, then activation function $f_q(\chi _q)$ and $g_q(\chi _q)$ can be expressed as:

$$\begin{aligned} f_q(\chi _q)=f_q^R(\chi _q^R)+i f_q^I(\chi _q^I)+j f_q^J(\chi _q^J)+kf_q^K(\chi _q^K), \end{aligned}$$

and

$$\begin{aligned} g_q(x_q)=g_q^R(\chi _q^R)+i g_q^I(\chi _q^I)+j g_q^J(\chi _q^J)+kg_q^K(\chi _q^K), \end{aligned}$$

where $f_q^v,\ g_q^v: \mathbb {R}^4\rightarrow \mathbb {R},\ q\in T$.

By employing the assumption above and together with Hamilton rules, the QVNNs system (1) can be regarded as four real-valued systems as follows:

$$\begin{aligned}&\left\{ \begin{aligned} \dot{\chi }_p^R(t)=&-c_p\chi _p^R(t)+\sum _{q=1}^n[a_{pq}^Rf_q^R(\chi _q^R(t))-a_{pq}^If_q^I(\chi _q^I(t)) \\&-a_{pq}^Jf_q^J(\chi _q^J(t))-a_{pq}^Kf_q^K(\chi _q^K(t))]\\&+\sum _{q=1}^n[b_{pq}^Rg_q^R(\chi _{q}^R(t-\tau (t)))-b_{pq}^Ig_q^I(\chi _{q}^I(t-\tau (t)))\\&-b_{pq}^Jg_q^J(\chi _{q}^J(t-\tau (t)))-b_{pq}^Kg_q^K(\chi _{q}^K(t-\tau (t)))]+u_p^R(t), \\ \dot{\chi }_p^I(t)=&-c_p\chi _p^I(t)+\sum _{q=1}^n[a_{pq}^If_q^R(\chi _q^R(t))+a_{pq}^Rf_q^I(\chi _q^I(t))\\&-a_{pq}^Kf_q^J(\chi _q^J(t))+a_{pq}^Jf_q^K(\chi _q^K(t))]\\&+\sum _{q=1}^n[b_{pq}^Ig_q^R(\chi _{q}^R(t-\tau (t)))+b_{pq}^Rg_q^I(\chi _{q}^I(t-\tau (t)))\\&-b_{pq}^Kg_q^J(\chi _{q}^J(t-\tau (t)))+b_{pq}^Jg_q^K(\chi _{q}^K(t-\tau (t)))]+u_p^I(t),\\ \end{aligned} \right. \\&\left\{ \begin{aligned} \dot{\chi }_p^J(t)=&-c_p\chi _p^J(t)+\sum _{q=1}^n[a_{pq}^Jf_q^R(\chi _q^R(t))+a_{pq}^Kf_q^I(\chi _q^I(t))\\&+a_{pq}^Rf_q^J(\chi _q^J(t))-a_{pq}^If_q^K(\chi _q^K(t))]\\&+\sum _{q=1}^n[b_{pq}^Jg_q^R(\chi _{q}^R(t-\tau (t)))+b_{pq}^Kg_q^I(\chi _{q}^I(t-\tau (t)))\\&+b_{pq}^Rg_q^J(\chi _{q}^J(t-\tau (t)))-b_{pq}^Ig_q^K(\chi _{q}^K(t-\tau (t)))]+u_p^J(t),\\ \dot{\chi }_p^K(t)=&-c_p\chi _p^K(t)+\sum _{q=1}^n[a_{pq}^Kf_q^R(\chi _q^R(t))-a_{pq}^Jf_q^I(\chi _q^I(t))\\&+a_{pq}^If_q^J(\chi _q^J(t))+a_{pq}^Rf_q^K(\chi _q^K(t))]\\&+\sum _{q=1}^n[b_{pq}^Kg_q^R(\chi _{q}^R(t-\tau (t)))-b_{pq}^Kg_q^I(\chi _{q}^I(t-\tau (t)))\\&+b_{pq}^Ig_q^J(\chi _{q}^J(t-\tau (t)))+b_{pq}^Rg_q^K(\chi _{q}^K(t-\tau (t)))]+u_p^K(t).\\ \end{aligned} \right. \end{aligned}$$

Let $A=A^R+i A^I+j A^J+kA^K$, $B=B^R+i B^I+j B^J+kB^K$, $\chi (t)=\chi ^R(t)+i \chi ^I(t)+j \chi ^J(t)+k \chi ^K(t)=(\chi _1(t), \chi _2(t), \dots , \chi _n(t))^T \in \mathbb {Q}^n$, $C=\mathrm{diag}(c_1, c_2, \dots , c_n)$, $U(t)=U^R(t)+i U^I(t)+ j U^J(t)+k U^K(t)=(u_1(t),u_2(t), \dots , u_n(t))^T\in \mathbb {Q}^n$, $f(\chi (t))=f^R(\chi ^R)+i f^I(\chi ^I)+j f^J(\chi ^J)+k f^K(\chi ^K)=(f_1(\chi _1(t)), f_2(\chi _2(t)), \dots , f_n(\chi _n(t)))^T \in \mathbb {Q}^n$ and $g(\chi (t-\tau (t)))=g^R(\chi ^R(t-\tau (t)))+i g^I(\chi ^I(t-\tau (t))))+j g^J(\chi ^J(t-\tau (t))))+k g^K(\chi ^K(t-\tau (t))))=(g_1(\chi _1(t-\tau (t))), g_2(\chi _2(t-\tau (t))), \dots , g_n(\chi _n(t-\tau (t))))^T \in \mathbb {Q}^n$. Then the QVNNs system (1) could be rewritten as

$$\begin{aligned} \dot{\chi }(t)=-C\chi (t)+Af(\chi (t))+Bg(\chi (t-\tau (t)))+U(t), \ t\ge 0. \end{aligned}$$

(2)

By employing quaternion multiplication with the non-commutativity, the delayed system (2) of vector form can be subsequently rewritten into four parts as follows:

$$\begin{aligned}&\left\{ \begin{aligned} \dot{\chi }^R(t)=&-C\chi ^R(t)+A^Rf^R(\chi ^R(t))-A^If^I(\chi ^I(t)) \\&-A^Jf^J(\chi ^J(t))-A^Kf^K(\chi ^K(t))]\\&+B^Rg^R(\chi ^R(t-\tau (t)))-B^Ig^I(\chi ^I(t-\tau (t))) \\&-B^Jg^J(\chi ^J(t-\tau (t)))-B^Kg^K(\chi ^K(t-\tau (t)))]+U^R(t), \\ \dot{\chi }^I(t)=&-C\chi ^I(t)+A^Rf^I(\chi ^I(t))+A^If^R(\chi ^R(t)) \\&+A^Jf^K(\chi ^K(t))-A^Kf^J(\chi ^J(t))] \\&+B^Rg^I(\chi ^I(t-\tau (t)))+B^Ig^R(\chi ^R(t-\tau (t))) \\&+B^Jg^K(\chi ^K(t-\tau (t)))-B^Kg^J(\chi ^J(t-\tau (t)))]+U^I(t),\\ \end{aligned} \right. \\&\left\{ \begin{aligned} \dot{\chi }^J(t)=&-C\chi ^J(t)+A^Rf^J(\chi ^R(t))-A^If^K(\chi ^K(t)) \\&+A^Jf^R(\chi ^R(t))+A^Kf^I(\chi ^I(t))]\\&+B^Rg^J(\chi ^J(t-\tau (t)))-B^Ig^K(\chi ^K(t-\tau (t)))\\&+B^Jg^R(\chi ^R(t-\tau (t)))+B^Kg^I(\chi ^I(t-\tau (t)))]+U^J(t), \\ \dot{\chi }^K(t)=&-C\chi ^K(t)+A^Rf^K(\chi ^I(t))+A^If^J(\chi ^J(t))\\&-A^Jf^I(\chi ^I(t))+A^Kf^R(\chi ^R(t))]\\&+B^Rg^K(\chi ^K(t-\tau (t)))+B^Ig^J(\chi ^J(t-\tau (t)))\\&-B^Jg^I(\chi ^I(t-\tau (t)))-B^Kg^I(\chi ^I(t-\tau (t)))]+U^K(t). \end{aligned} \right. \end{aligned}$$

For convenience, let $\tilde{C}=\mathrm{diag}(C,C,C,C)$, $\tilde{U}=\mathrm{diag}(U^R,U^I,U^J,U^K)$, $\tilde{\chi }(t)$= $((\chi ^R(t))^T, (\chi ^I(t))^T, (\chi ^J(t))^T,(\chi ^K(t))^T)^T$, $\tilde{f}(\tilde{\chi }(t))=((f^R(\chi ^R(t))^T, (f^I(\chi ^I(t)))^T, (f^J(\chi ^J(t)))^T, (f^K(\chi ^K(t)))^T)^T$, $\tilde{g}(\tilde{\chi }(t-\tau (t)))=((g^R(\chi ^R(t-\tau (t)))^T, (g^I(\chi ^I(t-\tau (t))))^T, (g^J(\chi ^J(t-\tau (t))))^T, (g^K(\chi ^K(t-\tau (t))))^T)^T$,

$$\begin{aligned} \tilde{A}=\begin{bmatrix} A^R &{}-A^I &{}-A^J &{}-A^K \\ A^I &{}A^R &{}-A^K &{}A^J\\ A^J &{}A^K &{}A^R &{}-A^I \\ A^K &{}-A^J &{}A^I &{}A^R \end{bmatrix},~~\tilde{B}=\begin{bmatrix} B^R &{}-B^I &{}-B^J &{}-B^K \\ B^I &{}B^R &{}-B^K &{}B^J\\ B^J &{}B^K &{}B^R &{}-B^I \\ B^K &{}-B^J &{}B^I &{}B^R \end{bmatrix}, \end{aligned}$$

then the system (2) can be written in the following compact form:

$$\begin{aligned} \dot{\tilde{\chi }}(t)=-\tilde{C}\tilde{\chi }(t)+\tilde{A}\tilde{f}(\tilde{\chi }(t))+\tilde{B}\tilde{g}(\tilde{\chi }(t-\tau (t)))+\tilde{U}(t), \ t\ge 0. \end{aligned}$$

(3)

To study the synchronization of QVNNs, the driven system can be chosen as:

$$\begin{aligned} \dot{\tilde{y}}(t)=-\tilde{C}\tilde{y}(t)+\tilde{A}\tilde{f}(\tilde{y}(t))+\tilde{B}\tilde{g}(\tilde{y}(t-\tau (t))),\ t\ge 0, \end{aligned}$$

(4)

where $\tilde{y}(t)\in \mathbb {Q}^n$ denotes the state vector of driven system, $\tilde{g}(\tilde{y}(t-\tau (t)))\in \mathbb {Q}^n$ and $\tilde{f}(\tilde{y}(t))$ refers to the activation function of above driven system with and without time-varying delay, respectively.

Let the error denote as $\tilde{e}(t)=\tilde{\chi }(t)-\tilde{y}(t)$. Subsequently, error dynamics system can be modeled as:

$$\begin{aligned} \dot{\tilde{e}}(t)=&-\tilde{C}\tilde{e}(t)+\tilde{A}\tilde{f}(\tilde{e}(t))+\tilde{B}g(\tilde{e}(t-\tau (t)))+\tilde{U}(t), \ t\ge 0, \end{aligned}$$

(5)

where $\tilde{f}(\tilde{e}(t))=\tilde{f}(\tilde{\chi }(t))-\tilde{f}(\tilde{y}(t))$ and $\tilde{g}(\tilde{e}(t-\tau (t)))=\tilde{g}(\tilde{\chi }(t-\tau (t)))-\tilde{g}(\tilde{y}(t-\tau (t)))$. The initial function of error system (5) is given by

$$\begin{aligned} \tilde{e}(s)=\psi (s), s\in [-\tau ,0], \end{aligned}$$

where $\psi (s)\in PC([-\tau ,0], \mathbb {Q}^n)$, with its norm define as $\Vert \psi (s)\Vert _{\tau }=\sup _{-\tau \le s\le 0}|\psi (s)|$. Under the stochastic impulsive control laws, the error dynamics system (3) can be rewritten as:

$$\begin{aligned} \left\{ \begin{aligned} \dot{\tilde{e}}(t)=&-\tilde{C}e(t)+\tilde{A}\tilde{f}(e(t))+\tilde{B}\tilde{g}(e(t-\tau (t))), \ t\ne t_k,\\ \tilde{e}(t_k)=&\tilde{e}(t_k^-)+\xi _k\tilde{e}(t_k^-), \ k\in \mathbb {Z}_+, \end{aligned} \right. \end{aligned}$$

(6)

where $t_k$ is impulsive instant that satisfies $0=t_0<t_1<\dots<t_k<\dots$, and $\lim _{k\rightarrow \infty }t_k=+\infty$, $\tilde{e}(t_k)=\tilde{e}(t_k^+)=\lim _{t\rightarrow t_k^+}\tilde{e}(t_k)$, $\xi _k\in (-1,0)$ is the stochastic impulsive control gain that satisfies

$$\begin{aligned} \xi _k=\sum _{i=1}^\mu \alpha _{\{\xi _k=\varpi _i\}}\varpi _i, \ i=1, 2, \dots , \mu , \end{aligned}$$

in which $\alpha _{\{\xi _k=\varpi _i\}}$ are the functions of indicator:

$$\begin{aligned} \alpha _{\{\xi _k=\varpi _i\}}=\left\{ \begin{aligned}&1,\ \xi _k=\varpi _i,\\&0,\ \xi _k\ne \varpi _i,\\ \end{aligned} \right. \end{aligned}$$

Prob $\{\xi _k=\varpi _i\}=\mathbb {E}\{\alpha _{\{\xi _k=\varpi _i\}}\}=\alpha _i \ (i=1,2,\dots , \mu )$ and $\sum _{i=1}^\mu \alpha _i=1$. The expression of $\alpha _{\{\xi _k=\varpi _i\}}$ is similar to the method of describing time-varying delays in [8].

($\mathbf {H_1}$). The average impulsive interval of the impulsive sequence $\{t_1,t_2,\dots \}$ on the interval (t, Q) is equal to $T_a$ if there exists a positive number $M_0>0$ such that

$$\begin{aligned} \aleph (Q,t)\ge \frac{Q-t}{T_a}-M_0, \end{aligned}$$

where $\aleph (Q,t)$ is the number of the synchronizing impulsive sequence.

($\mathbf {H_2}$). For any $\chi =(\chi _1, \chi _2, \dots , \chi _n)^T$, $\widetilde{\chi }=(\widetilde{\chi }_1, \widetilde{\chi }_2, \dots , \widetilde{\chi }_n)^T\in \mathbb {Q}^{n}$, there exist positive vectors $l_q^v,\ g_q^v \in \mathbb {R}$ such that

$$\begin{aligned}&|f_q^v(\chi _q^v(t))-f_q^v(\widetilde{\chi }_q^v(t))|\le l_q^v|\chi _q^v(t)-\widetilde{\chi }_q^v(t)|, \\&|g_q^v(\chi _q^v(t))-g_q^v(\widetilde{\chi }_q^v(t))|\le g_q^v|\chi _q^v(t)-\widetilde{\chi }_q^v(t)|. \end{aligned}$$

where $f_q^v(\chi _q^v(t))$, $g_q^v(\chi _q^v(t))\in \mathbb {R}$, $v\in \{R,I,J,K\}:= E$ and $q\in T$, let $L_f=\mathrm{diag}(l_1^{\max },l_2^{\max }, \dots , l_n^{\max })$, $L_g=\mathrm{diag}(g_1^{\max },g_2^{\max }, \dots , g_n^{\max })$ where $l_p^{\max }\triangleq {\max }{\{l_p^{R},l_p^{I},l_p^{J},l_p^{K}}\}(g_p^{\max }\triangleq {\max }{\{g_p^{R},g_p^{I},g_p^{J},g_p^{K}}\})$. Then, easily derive following:

$$\begin{aligned}&|f(\chi (t))-f(\widetilde{\chi }(t))|\le L_f|\chi (t)-\widetilde{\chi }(t)|, \\&|g(\chi (t))-g(\widetilde{\chi }(t))|\le L_g|\chi (t)-\widetilde{\chi }(t)|. \end{aligned}$$

Remark 1

It is important to emphasize the reason why the impulses of error system (6) is stochastic, because it is more fitted to the actual situation to compare the general fixed impulsive control and fixed impulsive strengths [39, 44]; and have a great importance of future research. Here we choose the binomial distribution as the distribution function of $\alpha$ which expectation also is $\alpha _i$ at $\xi _k=\varpi _i$.

Before moving upon, we introduce the following definition and lemma.

Definition 1

[29] If there exist a constant $M\ge 1$ and $\epsilon >0$, then the time-varying system with delay and stochastic impulses in (1) is globally exponentially synchronized to (4), such that:

$$\begin{aligned} \sum \limits _{i=1}^n|\tilde{e}_p(t))|\le M\Vert \phi (t)\Vert _{\tau } e^{-\epsilon t}, \end{aligned}$$

where $\epsilon >0$ is a unique solution of

$$\begin{aligned} \epsilon - \omega +\beta e^{\epsilon \tau }=0. \end{aligned}$$

Lemma 1

[37] Let x, $y \in \mathbb {Q}^n$, $\epsilon \in \mathbb {R}$ be a positive constant, and positive definite Hermitian matrix $S \in \mathbb {Q}^{n\times n}$, then the subsequent inequality holds:

$$\begin{aligned} yx+x^*y^* \le \epsilon \bar{x}S^{-1}x+\frac{1}{\epsilon }yS\bar{y}. \end{aligned}$$

Lemma 2

[37] If $V(\tilde{e}(t))=\tilde{e}^*(t)P\tilde{e}(t)$ and $P \in SC_n^{>}(Q)$, then for any $\tilde{e}(t) \in \mathbb {Q}^{4n}$,

$$\begin{aligned} 0<\lambda _{\min }(P)|\tilde{e}(t)|^2\le V(\tilde{e}(t))\le \lambda _{\max }(P)|\tilde{e}(t)|^2. \end{aligned}$$

Lemma 3

[41] Let $0<\tau (t)\le \tau$ and function $\mu (t)$, $\mu (t-\tau (t)) \in PC([t_0-\tau , +\infty ]; \mathbb {R}^n)$ and $\Xi (t,\mu (t),\mu (t-\tau (t)))$: $\mathbb {R}^+ \times \mathbb {R} \times \mathbb {R} \mapsto \mathbb {R}$ be nondecreasing in $\mu (t-\tau (t))$ for each fixed $(t, \mu (t))$ and $I_k(\mu (t))$ : $\mathbb {R} \mapsto \mathbb {R}$ be nondecreasing in $\mu (t)$. Supposed that $\mu _1(t)$, $\mu _2(t)$ satisfy

$$\begin{aligned} \left\{ \begin{array}{lr} D^+\mu _1(t)\le \Xi (t,\mu _1(t),\mu _1(t-\tau (t))),&{}\ t \ne t_k\\ \mu _1(t_k^+)\le I_k(\mu _1(t_k^-)), \ \ \ \ K\in \mathbb {N}_+, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{lr} D^+\mu _2(t)> \Xi (t,\mu _2(t),\mu _2(t-\tau _(t))),&{}\ t \ne t_k\\ \mu _2(t_k^+)\ge I_k(\mu _2(t_k^-)), \ \ \ \ K\in \mathbb {N}_+, \end{array} \right. \end{aligned}$$

Then $\mu _1(t)\le \mu _2(t)$ for $t_0-\tau \le t \le t_0$ which can implies that $\mu _1(t) \le \mu _2(t)$ for $t>0$, where $D^+\mu _i(t)=\overline{\lim }_{h\rightarrow 0^+}((\mu _i(t+h)-\mu (t))/h)(i=1,2)$.

3 Stochastic Impulsive Synchronization

Theorem 1

If the assumptions $(H_1)-(H_2)$ hold, and there exists positive constants $\epsilon _1$, $\epsilon _2$, three positive definite Hermitian matrix (equivalent $\in SC_n^{>}(Q)$) P, $S_1$ and $S_2 \in \mathbb {Q}^{4n\times 4n}$, then the response system of QVNNs with time-varying delays and stochastic impulse neural network (3) will be globally synchronized to the driven system (4) if the following inequalities holds as:

$$\begin{aligned}&\begin{bmatrix} \prod _{11} &{} P\tilde{A} &{} P\tilde{B} \\ \bigstar &{} -\epsilon _1S_1 &{}0 \\ \bigstar &{}\bigstar &{} -\epsilon _2S_2\end{bmatrix} \le 0, \end{aligned}$$

(7)

$$\begin{aligned}&\epsilon _2L_g S_2L_g \le \beta P, \end{aligned}$$

(8)

$$\begin{aligned}&\alpha +\frac{2\ln (1+\xi _k)}{T_a} +\beta (1+\xi _k)^{-2M_0}>0, \end{aligned}$$

(9)

where $\prod _{11}=-P\tilde{C}-\tilde{C}^*P+\frac{1}{\epsilon _1}L_f S_1L_f-\alpha P$, $\omega =\alpha +\frac{2ln(1+\xi _k)}{R}$, $\xi _k=\sum _{i=1}^\mu \alpha _i\varpi _i$, then the delayed QVNNs with stochastic impulse in (4) could be globally exponentially synchronized to (3):

$$\begin{aligned}&\sum _{p=1}^n\Vert \tilde{e}_p(t)\Vert \le \Vert \phi (t)\Vert _{\tau } e^{-\epsilon t}, \end{aligned}$$

and $\epsilon >0$ is a unique solution of

$$\begin{aligned} \epsilon -\omega +\beta e^{\epsilon \tau }=0. \end{aligned}$$

Proof

By constructing the suitable Lyapunov candidate function as follows:

$$\begin{aligned} \begin{aligned} V(t)=\tilde{e}^*(t)P\tilde{e}(t). \end{aligned} \end{aligned}$$

Calculating the right-upper Dini derivative of V(t) for any $t\in [t_{k-1},t_k),\ k\in \mathbb {Z}_+$, we obtain

$$\begin{aligned} D^+V(t)&=\tilde{e}^*(t)P\dot{\tilde{e}}(t)+\dot{\tilde{e}}^*(t)P\tilde{e}(t)\nonumber \\&=\tilde{e}^*(t)P[-\tilde{C}\tilde{e}(t)+\tilde{A}\tilde{f}(\tilde{e}(t))+\tilde{B}\tilde{g}(\tilde{e}(t-\tau (t)))]\nonumber \\&\quad +[-\tilde{C}\tilde{e}(t)+\tilde{A}\tilde{f}(\tilde{e}(t))+\tilde{B}\tilde{g}(\tilde{e}(t-\tau (t)))]^*P\tilde{e}(t)\nonumber \\&=\tilde{e}^*(t)(-P\tilde{C}-\tilde{C}^*P)\tilde{e}(t)+\tilde{e}^*(t)P\tilde{A}\tilde{f}(\tilde{e}(t))\nonumber \\&\quad +\tilde{e}^*(t)P\tilde{B}\tilde{g}(\tilde{e}(t-\tau (t)))+\tilde{f}^*(\tilde{e}(t))\tilde{A}^*P\tilde{e}(t) \nonumber \\&\quad +\tilde{g}^*(\tilde{e}(t-\tau (t)))\tilde{B}^*P\tilde{e}(t). \end{aligned}$$

(10)

Using Lemma 1, it follows from ($H_2$) that

$$\begin{aligned}&\tilde{e}^*(t)P\tilde{A}\tilde{f}(\tilde{e}(t))+\tilde{f}^*(\tilde{e}(t))\tilde{A}^*P\tilde{e}(t)\nonumber \\&\quad \le \frac{1}{\epsilon _1}\tilde{e}^*(t)P\tilde{A}S_1^{-1}\tilde{A}^*P\tilde{e}(t)+\epsilon _1\tilde{f}^*(\tilde{e}(t)) S_1\tilde{f}(\tilde{e}(t))\nonumber \\&\quad \le \frac{1}{\epsilon _1}\tilde{e}^*(t)P\tilde{A}S_1^{-1}\tilde{A}^*P\tilde{e}(t)+\epsilon _1\tilde{e}^*(t)L_f S_1L_f \tilde{e}(t). \end{aligned}$$

(11)

Similarly, we have

$$\begin{aligned}&\tilde{e}^*(t)P\tilde{B}\tilde{g}(\tilde{e}(t-\tau (t)))+\tilde{g}^*(\tilde{e}(t-\tau (t)))\tilde{B}^*P\tilde{e}(t)\nonumber \\&\le \frac{1}{\epsilon _2}\tilde{e}^*(t)P\tilde{B}S_2^{-1}\tilde{B}^*P\tilde{e}(t)+\epsilon _2\tilde{f}^*(\tilde{e}(t-\tau (t))) S_2\tilde{f}(\tilde{e}(t-\tau (t)))\nonumber \\&\le \frac{1}{\epsilon _2}\tilde{e}^*(t)P\tilde{B}S_2^{-1}\tilde{B}^*P\tilde{e}(t)+\epsilon _2\tilde{e}^*(t-\tau (t))L_g S_2L_g \tilde{e}(t-\tau (t)). \end{aligned}$$

(12)

Substituting (11) and (12) into (10), it is able to deduce that

$$\begin{aligned} D^+V(t)&=\tilde{e}^*(t)(-P\tilde{C}-\tilde{C}^*P+\epsilon _1 L_f S_1L_f \\&\quad +\frac{1}{\epsilon _1}P\tilde{A}S_1^{-1}\tilde{A}^*P+\frac{1}{\epsilon _2}P\tilde{B}S_2^{-1}\tilde{B}^*P)\tilde{e}(t) \\&\quad +\epsilon _2\tilde{e}^*(t-\tau (t))L_g S_2L_g \tilde{e}(t-\tau (t)). \end{aligned}$$

It follows from (7) and (8) that

$$\begin{aligned} D^+V(t)\le \alpha V(t)+\beta V(t-\tau (t)). \end{aligned}$$

Due to the better property of the binomial distribution function:

Prob$\{\xi _k=\varpi _i\}=\mathbb {E}\{\alpha _{\{\xi _k=\varpi _i\}}\}=\alpha _i \ (i=1,2,\dots , \mu )$, then substitute $\mathbb {E}\{\alpha _{\{\xi _k=\varpi _i\}}\}=\alpha _i$ into above Dini-derivative, then easily gained the expected form:

$$\begin{aligned} D^+\mathbb {E}V(t)&=\mathbb {E}\alpha V(t)+\mathbb {E}\beta V(t-\tau (t). \end{aligned}$$

On the other hand, when $t=t_k$, $k\in \mathbb {Z}_+$, we have

$$\begin{aligned} \begin{aligned} V(t_k)&=\tilde{e}^*(t_k)P\tilde{e}(t_k)\\&=(1+\xi _k)^2\tilde{e}^*(t_k^-)P\tilde{e}(t_k^-)\\&=(1+\xi _k)^2V(t_k^-).\\ \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \mathbb {E}V(t_k^+)&= \mathbb {E}(1+\xi _k)^2V(t_k^-)\\&=(1+\xi _k)^2\mathbb {E}V(t_k^-).\\ \end{aligned} \end{aligned}$$

For arbitrary $\iota >0$, let z(t) be the unique solution of the following delayed impulsive system

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}(t)&=\alpha z(t)+\beta z(t-\tau (t))+\iota ,\ t \ne t_k,\\ z(t_k)&=(1+\xi _k)^2z(t_k^-),\ k\in \mathbb {Z}_+,\\ z(s)&=\lambda _{\max }(P)\Vert \psi (s)\Vert ^2_{\tau }, \ -\tau <s\le 0. \end{aligned} \right. \end{aligned}$$

(13)

Based on the variation of parameters [20] for the formula, the solution of system (13) that

$$\begin{aligned} z(t)=Z(t,0)l(0)+\int _0^tZ(t,s)[\beta z(t-\tau (t))+\iota ]ds, \end{aligned}$$

(14)

where $Z(t,s)(t>s\ge 0)$ is the fundamental solution matrix of the below linear system with impulses which can be estimated as

$$\begin{aligned} \left\{ \begin{array}{lr} \ \ \dot{r}(t)=\alpha r(t), \ t\ne t_k \\ r(t_k^+)=(1+\xi _k)^2 r(t_k^-), \ k\in \mathbb {Z}_+. \end{array} \right. \end{aligned}$$

Therefore, it yields that

$$\begin{aligned} Z(t,s)&={e}^{\alpha (t-s)}\mathop {\varPi }\limits _{s<t_k\le t}(1+\xi _k)^2. \nonumber \\&\le {e}^{\alpha (t-s)}(1+\xi _k)^{2{\aleph (t,s)}} \nonumber \\&=(1+\xi _k)^{-2M_0}{e}^{(\alpha +\frac{2ln(1+\xi _k)}{T_a})(t-s)} \nonumber \\&=(1+\xi _k)^{-2M_0}{e}^{\omega (s-t)} , \end{aligned}$$

(15)

let $\omega =\alpha +\frac{2ln(1+\xi _k)}{T_a}$, $\bar{\delta }= (1+\xi _k)^{-2M_0}\lambda _{\max }(P)\Vert \psi (s)\Vert ^2_{\tau }$. One gets from (14) and (15) that

$$\begin{aligned} z(t)&\le \bar{\delta }{e}^{\omega t}+\int _0^t(1+\xi _k)^{-2M_0}{e}^{\omega (t-s)}[\beta z(s-\tau (s)) +\iota ]ds, \ \forall t\ge 0. \end{aligned}$$

(16)

Let

$$\begin{aligned} \Upsilon (\lambda )=\lambda +\omega +\beta (1+\xi _k)^{-2M_0}{e}^{\lambda \tau }. \end{aligned}$$

Due to Definition 1 of the unique solution existence and (9), one has $\Upsilon (0)=\omega +\beta (1+\xi _k)^{-2M_0}<0$. Since $\Upsilon (+\infty )=+\infty$ and $\dot{\Upsilon }(\lambda )=1+\tau \beta (1+\xi _k)^{-2M_0}{e}^{\lambda \tau }>0$. Therefore, there exists a unique solution $\lambda >0$, which make the following equality holds:

$$\begin{aligned} \Upsilon (\lambda )=\lambda +\omega +\beta (1+\xi _k)^{-2M_0}{e}^{\lambda \tau }=0. \end{aligned}$$

From above equation, it can be derived for $t\in [-\tau , 0]$ that

$$\begin{aligned} z(t)&=(1+\xi _k)^{-2M_0}\lambda (P)\Vert \psi _p(s)\Vert ^2_{\tau }\\&\le \bar{\delta }<\bar{\delta }{e}^{-\lambda t}+\frac{\iota }{W}, \end{aligned}$$

where $W=-\omega (1+\xi _k)^{2M_0}-\beta$ and in the next content, it is easy to use the method of “reduction to absurdity” to prove below equality hold for any $t\ge 0$

$$\begin{aligned} z(t)<\bar{\delta }{e}^{-\lambda t}+\frac{\iota }{W}. \end{aligned}$$

(17)

and the specific proof process as follows. Suppose that (17) dose not true, so there exists a $\tilde{t}>0$ such that:

$$\begin{aligned} l(\tilde{t})\ge \bar{\delta }{e}^{-\lambda \tilde{t}}+\frac{\iota }{W} \end{aligned}$$

(18)

and

$$\begin{aligned} z(t)<\bar{\delta }{e}^{-\lambda t}+\frac{\iota }{W}, \ t<\tilde{t}. \end{aligned}$$

(19)

Substituting (16) and (19) into (18) and we get

$$\begin{aligned} z(\tilde{t})&\le e^{\omega \tilde{t}} \{\bar{\delta }+\int _0^{\tilde{t}}(1+\xi _k)^{-2M_0}e^{-\omega s}[\beta z(s-\tau (s))+\iota ]ds\}\nonumber \\&< e^{\omega \tilde{t}} \{\bar{\delta }+\frac{\iota }{W}+\int _0^{\tilde{t}}(1+\xi _k)^{-2M_0}e^{-\omega s}[\beta (\bar{\delta }{e}^{-\lambda (s-\tau (s))}+\frac{\iota }{W})+\iota ]ds\}\nonumber \\&< e^{\omega \tilde{t}} \{\bar{\delta }+\frac{\iota }{W}+\bar{\delta }\beta e^{\lambda \tau }(1+\xi _k)^{-2M_0}\int _0^{\tilde{t}}e^{-(\omega +\lambda )s}ds\nonumber \\&\quad + (1+\xi _k)^{-2M_0}(\frac{\iota \beta }{W}+\iota )\int _0^{\tilde{t}}e^{-\omega s}ds\} \nonumber \\&= e^{\omega \tilde{t}} \{\bar{\delta }+\frac{\iota }{W}-\bar{\delta }(\omega +\lambda )\int _0^{\tilde{t}}e^{-(\omega +\lambda ) s}ds\nonumber \\&\quad +(1+\xi _k)^{-2M_0}\frac{\iota (\beta +W)}{W}\int _0^{\tilde{t}}e^{-\omega s}ds\}\nonumber \\&=\bar{\delta }e^{-\lambda \tilde{t}}+\frac{\iota }{W}. \end{aligned}$$

(20)

Obviously, (20) contradicts with the (18), it derivative the (17) holds. Let $\iota \rightarrow 0$ and by using the Lemma 2. It is true that

$$\begin{aligned} \lambda _{min}(P)|\tilde{e}(t)|^2\le V(\tilde{e}(t))=\tilde{e}^*(t)P\tilde{e}(t)&\le z(t) <\bar{\delta }{e}^{-\lambda t}, \ t\ge 0. \end{aligned}$$

Finally, we obtained that as follows: $|\tilde{e}(t)|\le \sqrt{\frac{\lambda _{\max }(P)}{\lambda _{\min }(P)}(1+\xi _k)^{-2M_0}\Vert \psi (s)\Vert ^2_{\tau }}e^{-\frac{\lambda }{2} t}$.

Therefore, this completes the proof. $\square$

Remark 2

Theorem 1 constructed a general quadric Lyapunov candidate function, then obtained the synchronization criterion by utilized the method of comparison principle and reduction to absurdity; The method of stochastic impulsive control is superior to the general continuous control ways [15, 36] and have stronger robust, also reduces the cost to a great extent. In addition, a synchronization criteria for delay-independent LMI over quaternion fields are obtained, it can derive that the delay of the system does not affect the property of the system, but affected by the synchronization rate, Therefore the results of this paper can be extended to QVNNs with fuzzy delay and large scale delay [4].

In what follows, there was considered the delayed of QVNNs with the fixed impulses strength $\varpi _1$, $\alpha =1$ and $\mu =1$.

Corollary 1

Suppose these assumptions (H1) and (H2) is true, then the delayed impulsive neural network in (6) will be globally exponentially synchronized to $\hat{\chi }(t)$, if the subsequent inequalities holds:

$$\begin{aligned}&\begin{bmatrix} \prod _{11} &{} P\tilde{A} &{} P\tilde{B} \\ \bigstar &{} \frac{1}{\epsilon _1}S_1 &{}0 \\ \bigstar &{}\bigstar &{} \frac{1}{\epsilon _2}S_2\end{bmatrix}\le 0, \end{aligned}$$

(21)

$$\begin{aligned}&\frac{1}{\epsilon _2}L_g S_2L_g\le \beta P, \end{aligned}$$

(22)

$$\begin{aligned}&\omega -\beta >0, \end{aligned}$$

(23)

where $\omega =-(\alpha +\frac{2ln(1+\xi _1)}{R})$, $\xi _1=\varpi _1$ (that is to say the impulse strength is a definite value) and $\prod _{11}=-P\tilde{C}-\tilde{C}^*P+\frac{1}{\epsilon _1}L_f S_1L_f-\alpha P$, then the QVSINN with time-varying delays in (5) can be globally exponentially synchronized to (4):

$$\begin{aligned} \sum _{p=1}^n\tilde{e}_p^*(t)\tilde{e}_p(t)\le \delta e^{-\epsilon t}, \end{aligned}$$

where $\delta =\sup _{-\tau \le s\le 0}||\psi (s)\Vert ^2$ and $\epsilon >0$ is a unique solution of

$$\begin{aligned} \epsilon -\omega +\beta e^{\epsilon \tau }=0. \end{aligned}$$

Remark 3

In addition, an analogous synchronization criteria for delay-independent LMI over quaternion fields are obtained by the Corollary 1. It is obvious that the difference between Corollary 1 and Theorem 1 is the fixed impulses and stochastic impulses; and compared to the inequality of two former, the stochastic impulses strength $\xi _k$ just affected the exponential $\omega$ numerical valued by the formulation of system (16), so the impulses strength determines the rate of convergence and the stochastic impulses is more flexible than the fixed one.

4 Numerical Example

Consider the delayed QVNNs with stochastic impulse system which given as:

$$\begin{aligned} \frac{d{\chi }_p(t)}{dt}=&-c_p\chi _p(t)+\sum _{q=1}^{2}a_{pq}f_q(\chi _q(t)) \nonumber \\&+\sum _{q=1}^{2}b_{pq}g_q(\chi _q(t-\tau (t)))+u_p(t), \ t\ge 0,p=1,2 \end{aligned}$$

(24)

where $\chi =\chi ^R+i \chi ^I+j \chi ^J+k\chi ^K$, $d=[1.5;1.4]$ and $\tau (t)=0.32+0.68\frac{\exp (t)}{1+\exp (t)}$, $u_1=1.2-i1.2+j1.3+k1.4$, $u_2=1.4+i1.3+j1.4-k1.3$; $C=\begin{bmatrix} 1.5 \\ 1.4 \end{bmatrix}$; $A=A^R+i A^I+j A^J+kA^K$; $B=B^R+i B^I+j B^J+kB^K$; $A^R=\begin{bmatrix} 0.5 &{} 1 \\ 3 &{} 0.5 \end{bmatrix}$, $A^I=\begin{bmatrix} 2.2 &{} -3.5 \\ 1.5 &{} -1.5 \end{bmatrix}$, $A^J=\begin{bmatrix} 2 &{} 2.5 \\ 1 &{} 0.5 \end{bmatrix}$,

$A^K=\begin{bmatrix} -1 &{} -3 \\ 1.5 &{} -1 \end{bmatrix}$; $B^R=\begin{bmatrix} 1 &{} -2 \\ -2 &{} 0.5 \end{bmatrix}$, $B^I=\begin{bmatrix} -1.5 &{} 1 \\ -1 &{} -1 \end{bmatrix}$,

$B^J=\begin{bmatrix} 2 &{} -2 \\ 1 &{} 3 \end{bmatrix}$, $B^K=\begin{bmatrix} -2 &{} -1.5 \\ -2 &{} -2 \end{bmatrix}$;

and set the neuron activation function as: ${L_f}_p(\chi _p^\mu )=\tanh (\chi _p^\mu )$, ${L_g}_p(\chi _p^\mu )=\tanh (\chi _p^\mu )$,

it implies that Lipschitz coefficient ${L_f}_p^\mu ={L_g}_p^\mu =1$, where $p=1,2$ and $\mu =R,I,J,K$;

Above initial condition is taken as below:

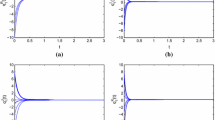
$\chi _1(0)=2.2+i0.2-j1.1-k3.8$, $\chi _2(0)=4.3+i0.1+j1.2-k 1.4$, $\tilde{\chi }_1(0)=-0.1+i0.7-j1.0-k3.0$, $\tilde{\chi }_2(0)=0.9+i2.0+j2-k0.5$; and consider that case with $\alpha _1=0.7$, $\alpha _2=0.3$, $\varpi _1=-0.35$, $\varpi _2=-0.16$ (Figs. 1, 2).

And then by using the Yalmip toolbox, we can resolve the LMI and get the $P^R=\begin{bmatrix} 0.7344 &{} 0.15 \\ -0.15 &{} 0.7488 \end{bmatrix},$ and $P^I=\begin{bmatrix} 0 &{} 0.6005 \\ -0.6005 &{} 0 \end{bmatrix}$, $P^J=\begin{bmatrix} 0 &{} 0.410 \\ -0.410 &{} 0 \end{bmatrix}$, $P^K=\begin{bmatrix} 0 &{} 0.102 \\ -0.102 &{} 0 \end{bmatrix}$; $\alpha = -1.0195$, $\beta = 0.8472$, and the Fig. 3 refers to the synchronization errors and confirmed the effectiveness of the Theorem 1.

Fig. 1

The needle figure of impulses strength

Fig. 2

Synchronization of errors without stochastic impulses

Fig. 3

Synchronization of errors with $\alpha _1=0.2$, $\alpha _2=0.8$

Fig. 4

Synchronization of errors with $\alpha _1=0.3$, $\alpha _2=0.7$

5 Conclusions

The synchronization problem of delayed QVNNs under stochastic impulse effect is investigated in the present paper, where the impulses arouse time and impulse strength all is stochastic. By constructing the suitable Lyapunov candidate function, and utilizing the method of comparison principle and reduction to absurdity, a synchronization criterion with delay-independent has been obtained in the form of LMI in quaternion fields; the LMI could be dealt with the Yalmip toolbox in MATLAB. While this paper just considered the stabilization problem of stochastic impulses, the stochastic disturbance problem had not been considered all through, which is our future works.

Fig. 5

Unsynchronization figure when selected unsuitable $\alpha$ and $\beta$