1 Introduction

Due to hysteresis is an important nonlinear phenomenon which exists widely in practical systems, nonlinear systems with hysteresis have been one of the rigorous challenging and worthy research for control [1]. The properties, such as, inaccuracies, oscillations and instability affected by the non-differentiability of hysteresis may gradually deteriorate the system performance [2, 3]. Recently, numerous adaptive control schemes have been developed to control uncertain nonlinear systems with unknown backlash-like hysteresis. In [4, 5], an adaptive state feedback control and an adaptive fuzzy output feedback control were designed for a class of uncertain nonlinear systems preceded by unknown backlash-like hysteresis, respectively. Note that the controllers designed in [4,5,6] are based on the backlash-like hysteresis. There are other hysteresis patterns needed to be analyzed. The authors in [7] developed an adaptive neural output feedback control scheme for nonlinear systems with unknown Prandtl–Ishlinskii (PI) hysteresis. Additionally, there exist some methods of control and tracking for this hysteresis system, such as adaptive robust output feedback control and robust adaptive backstepping control, etc. [8,9,10,11].

In some cases, the states of a control system are usually unmeasurable, whereas the system outputs are measurable at sampling instants. In particular, for a networked control system (NCS), its outputs are usually acquired by data acquisitions at sampling instants. Therefore, the design of sampled-data observers is more significant and challenging than that of traditional observers. For a continuous linear system, observer can be designed on the basis of its accurate discretization model. However, for a continuous nonlinear system, it is usually difficult to obtain its accurate discretization model. Therefore, the design method cannot be extended to continuous nonlinear systems. Recently, researchers have paid great enthusiasm on sampled-data observer design for nonlinear systems, and developed three categories of design method, such as design based on approximate discretization models [12, 13], continuous design and corresponding discretization [14, 15], and continuous and discrete design [16,17,18,19,20,21]. Inspired by Chen and Ge [7], we try to extend sampled-data observer design for nonlinear systems with unknown hysteresis by the third method. Because when the sampling-data observer adopts this method, the sampling-data can be directly utilized to update the observer without discretizing the nonlinear system.

In practical engineering applications, nonlinearities and uncertainties are usually contained in an amount of systems. In addition, unmatched time-varying disturbances are unavoidable, with which the whole system will be unstable [22,23,24]. To this end, RBFNNs and fuzzy logic systems possessing superior approximation and adaptability were employed to compensate the uncertainties and the unmatched time-varying disturbances [25,26,27,28].

Following the previous references, few results are combined with sampled-data observers, although researches on control and application of hysteresis have been carried out in recent years. In this paper, we consider sampled-data observer design for a class of nonlinear systems with unknown hysteresis and unknown unmatched disturbance based on RBFNNs. The main contributions of this paper are summarized as follows. (1) We investigate a sampled-data nonlinear system and present sufficient conditions such that the considered system is UUB. (2) Continuous observers are designed for a class of nonlinear systems with unknown hysteresis and unknown disturbances, which are approximated by RBFNNs. The sampled measurements are used to update the observer whenever they are available. (3) By constructing a Lyapunov–Krasovskii function, sufficient conditions are derived to guarantee that the observation errors are UUB. Compared with [7], the ways of process of the hysteresis and the disturbances are different, the restriction on the constant control gain parameter is relaxed, and the problem of parameter selection is solved.

The rest of this paper is organized as follows. In Sect. 2, the problem statement, some assumptions, and the control objective are described. Section 3 describes the design procedure of the adaptive sampled-data observer by using RBFNNs. In Sect. 4, an example is used to illustrate the validity of the proposed design methods. Some conclusions are given in Sect. 5.

2 Problem Formulations and Preliminaries

In this paper, our purpose is to design an adaptive sampled-data observer for the following system

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\dot{x}}_1}(t) = {x_2}(t) + {f_1}({{\bar{x}}_1}(t)) +{d_1 }({{\bar{x}}_1}(t),t),\\ \ \ \ \ \ \ \ \ \vdots \end{array}\\ {{{\dot{x}}_{n - 1}}(t) = {x_n}(t) + {f_{n - 1}}({{\bar{x}}_{n - 1}}(t)) }+{d_{n-1} }({{\bar{x}}_{n-1}}(t),t),\\ {{{\dot{x}}_n}(t) = b\omega (u(t)) + {f_n}({{\bar{x}}_n}(t)) }+{d_n }({{\bar{x}}_{n}}(t),t),\\ {y(t) = {x_1}({t_k}),\mathrm{{ }}t \in [{t_k},{t_{k + 1}}),\mathrm{{ }}k \ge 0,} \end{array}} \right. \end{aligned}$$
(1)

where \(x(t) = [{x_1}(t),{x_2}(t), \ldots , {x_n}(t)] \in {R^n}\) (\({\bar{x}_i}(t) = {[{x_1}(t),{x_2}(t), \ldots , {x_i}(t)]^T} \in {R^i}, (i = 1,2, \ldots , n\))) is the state vector of the system, the input \(u(t)\in {R}\), the system output \(y(t) \in R\) is sampled at time instant \({t_k}\), where \(\mathrm{{\{ }}{t_k}\mathrm{{\} }}\) is a strictly increasing sequence and satisfies \({\lim _{k \rightarrow \infty }}{t_k} = \infty \), T is the sampling period, and \(T\mathrm{{ = }}{t_{k + 1}} - {t_k}\). \({f_i}({\bar{x}_i}(t))\)\((i = 1, 2, \ldots , n)\) are known smooth nonlinear functions, \({d_i }({{\bar{x}}_i}(t),t)\in R\)\((i = 1, 2, \ldots , n)\) denote unknown time-varying unmatched disturbances, \(b \in R\)\((b \ne 0)\) represents an unknown but bounded constant control gain, \(\omega (u(t))\in {R}\) represents an unknown PI hysteresis, whose model is given by [29]

$$\begin{aligned} \begin{aligned} \omega (u(t)) = P[u](t)&= {p_0}u(t) - \int _0^{r_1} {p(r){F_r}[u](t)dr},\\&={p_0}u(t)+{d_0}(u(t)), \end{aligned} \end{aligned}$$
(2)

where r is a threshold, p(r) is a given density function and satisfies \(p(r) > 0\) and \(\int _0^\infty r p(r)dr < \infty \), \({p_0} = \int _0^{r_1} p (r)dr\) is a constant and depends on the density function, and \(r_1\) denotes the upper limit of the integration. Let \(f_r: R \rightarrow R\) be defined by

$$\begin{aligned} {f_r}(u(t),\omega (u(t)) ) = \max \left( {u(t) - r,\min (u(t) + r,\omega (u(t)) )} \right) . \end{aligned}$$

The play operator \({F_r}[u]({t})\) is given by

$$\begin{aligned} \begin{array}{l} {F_r}[u](0) = {f_r}\left( {u(0),0} \right) , \\ {F_r}[u](t) = {f_r}\left( {u(t),{F_r}[u]({t_i})} \right) , \end{array} \end{aligned}$$

with \({t_i} < t \le {t_{i + 1}}\) and \(0 \le i \le N - 1\), where \(0 = {t_0}< {t_1}< \cdots < {t_N} = {t_E}\) is a partition of \([0, {t_E}]\) such that the function u(t) is monotone on \((t_i, t_{i+1}]\), and \(C[0,{t_E}]\) is a set of bounded continuous functions on \([0,{t_E}]\). For any input \(u(t) \in C[0,{t_E}]\), the play operator is Lipschitz continuous [29].

The system (1) can also be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\dot{x}}_1}(t) = {x_2}(t) + {f_1}({{\bar{x}}_1}(t)) +{d_1 }({{\bar{x}}_1}(t),t),\\ \ \ \ \ \ \ \ \ \vdots \end{array}\\ {{{\dot{x}}_{n - 1}}(t) = {x_n}(t) + {f_{n - 1}}({{\bar{x}}_{n - 1}}(t)) }+{d_{n-1} }({{\bar{x}}_{n-1}}(t),t),\\ {{{\dot{x}}_n}(t) = {b_0}u(t) + b{d_0}(u(t)) + \delta (u(t))}+ {f_n}({{\bar{x}}_n}(t))\\ \qquad \qquad +{d_n }({{\bar{x}}_{n}}(t),t),\\ {y(t) = {x_1}({t_k}), t \in [{t_k},{t_{k + 1}}),\mathrm{{ }}k \ge 0,} \end{array}} \right. \end{aligned}$$
(3)

where \(\delta (u(t)) = (b{p_0} - {b_0})u(t)\) and \({b_0}\) is a design parameter.

We make the following assumptions to facilitate analysis.

Assumption 1

([6]) There exist constants \({l_{i1}}\)\((i = 1,2, \ldots , n)\) such that the following inequalities

$$\begin{aligned} \begin{aligned}&\left| {{f_i}({{\bar{x}}_i}(t)) - {f_i}({{\hat{\bar{ x}}}_i}(t))} \right| \le {l_{i1}}(\left| {{x_1}(t) - {{\hat{x}}_1}}(t) \right| + \cdots + \left| {{x_i}(t) - {{\hat{x}}_i}(t)} \right| ), \end{aligned} \end{aligned}$$
(4)

hold.

Assumption 2

For the nonlinear system (3), the input \(u(t) \in C[0,{t_E}]\), thus, there exists an unknown positive constant \({\sigma _0}\) such that \(\left| { \delta (u(t))} \right| \le {\sigma _0}\).

Remark 1

Although the parameter b is unknown, we can select the design parameter \({b_0}\) to approach \(b{p_0}\). In other words, the design parameter \({b_0}\) should be selected appropriately to achieve better state estimation performance.

The following lemmas are needed, which can be found in [7, 30].

Lemma 2.1

([30]) Let \(M \in {R^{n \times n}}\) and \(\gamma \) denote a positive definite matrix and a positive real number, respectively. The vector function \(\varphi (t) \) is defined on the interval \([0,\gamma ]\) and is integrable. Then, we have

$$\begin{aligned} {\left[ {\int _0^\gamma {\varphi (s)ds} } \right] ^T}M\left[ {\int _0^\gamma {\varphi (s)ds} } \right] \le \gamma \left[ {\int _0^\gamma {\varphi {{(s)}^T}M\varphi (s)ds} } \right] . \end{aligned}$$

Lemma 2.2

([7]) Let f(Z) be a continuous function on a compact set \(\Omega \), which can be approached by a RBFNN, that is,

$$\begin{aligned} \hat{f}(Z) = {\hat{W}^{T}}S(Z) + \varsigma , \end{aligned}$$

where \(Z = {[{z_1},{z_2}, \ldots , {z_m}]^T} \in \Omega \subset {R^m}\) and \(\hat{W} \subset {R^q}\) are the input vector and the weight of the RBFNN, respectively, \(S(Z) = {[{S_1}(Z),{S_2}(Z), \ldots , {S_q}(Z)]^T} \in {R^q}\) is the basis function vector, and \(\varsigma >0\) is the approximation error. The optimal weight \({W^*}\) of RBFNN is given by

$$\begin{aligned} {W^*} = \arg \mathrm{{ }}\mathop {\min }\limits _{\hat{W} \in {\Omega }} \left[ {\mathop {\sup }\limits _{Z \in {R^q}} \left| {\hat{f}(Z|\hat{W}) - f(Z)} \right| } \right] . \end{aligned}$$

By using the optimal weight, we have

$$\begin{aligned} f(Z) = {W^{*T}}S(Z) + {\varsigma ^*}, \left| {{\varsigma ^*}} \right| \le \bar{\varsigma }, \end{aligned}$$

where \({\varsigma ^*}\) is the optimal approximation error, and \(\bar{\varsigma }> 0\) is the upper bound of the approximation error.

Lemma 2.3

([31]) There exist real numbers \(c_1\), \(c_2\) and real-valued function \(\Delta (x,y)>0\) such that the following inequality holds:

$$\begin{aligned} \left| {x}\right| ^{c_1}\left| {y}\right| ^{c_2}\le \frac{c_1}{c_1+c_2}\Delta (x,y)\left| {x}\right| ^{c_1+c_2}+\frac{c_2}{c_1+c_2}\Delta ^{-\frac{c_1}{c_2}}(x,y) \left| {y}\right| ^{c_1+c_2}. \end{aligned}$$

For a sampled-data nonlinear system, we give the definition of UUB and sufficient conditions of UUB.

Definition 1

For the following sampled-data nonlinear system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = g\left( {x(t),\mathrm{{ }}x(t_k)} \right) ,\\ x(t_{k+1})=\lim _{t\rightarrow t_{k+1}^-}x(t_k),\mathrm{{ }}t \in [{t_k},\mathrm{{ }}{t_{k + 1}}),\mathrm{{ }}k \ge 0, \end{array} \right. \end{aligned}$$
(5)

where \(x(t)\in R^n\) is the state of the system, and \(g(\cdot )\) is a continuous function with \(g(0)=0\). Denote the solution to (5) with respect to the initial conditions \(x_0\) as x(t). If there exists a constant \(b_1>0\) and a constant \(T'(x_0, b_1)\) such that

$$\begin{aligned} |x(t)|<b_1, \forall t > {t_0} + T'(x_0,{b_1}), \end{aligned}$$

then, the system (5) is UUB.

Lemma 2.4

For the nonlinear sampled-data system (5), if there exists a Lyapunov function V(x(t)) defined on the interval \([{t_0},\infty )\) such that

$$\begin{aligned} \begin{aligned} \frac{{dV(x(t))}}{{dt}} \le - {\alpha _1}V(x(t)) + {\beta _1}V(x({t_k})) + C,\ t \in [{t_k},{t_{k + 1}}), \end{aligned} \end{aligned}$$
(6)

and

$$\begin{aligned} \alpha _1>\beta _1, \end{aligned}$$

hold, where \({\alpha _1}\), \({\beta _1}\) and C are three positive real numbers, then it is UUB. Moreover, we have \({\lim _{k \rightarrow \infty }}V(x(t)) \le \frac{2- {\alpha _2}}{{1- {\alpha _2}}}\frac{C}{{{\alpha _1}}}\).

Proof

Multiplying \({e^{{\alpha _1}t}}\) on both sides of the inequality (6), we have

$$\begin{aligned} \frac{{d({e^{{\alpha _1}t}}V(x(t)))}}{{dt}} \le {e^{{\alpha _1}t}}{\beta _1}V(x({t_k})) + C{e^{{\alpha _1}t}},\ t \in [{t_k},{t_{k + 1}}). \end{aligned}$$

Then,

$$\begin{aligned} V(x(t)) \le&[(1 - \frac{{{\beta _1}}}{{{\alpha _1}}}){e^{ - {\alpha _1}(t-t_k)}} + \frac{{{\beta _1}}}{{{\alpha _1}}}]V(x({t_k}))+\frac{C}{{{\alpha _1}}}, t \in [{t_k},{t_{k+ 1}}). \end{aligned}$$
(7)

Let \(t=t_{k+1}\), we can obtain

$$\begin{aligned} V(x(t_{k+1})) \le \alpha _2V(x({t_k})) + \frac{C}{{{\alpha _1}}} \end{aligned}$$
(8)

where \({\alpha _2} = (1 - \frac{{{\beta _1}}}{{{\alpha _1}}}){e^{ - {\alpha _1}T}} + \frac{{{\beta _1}}}{{{\alpha _1}}}\). Since \(\alpha _1>\beta _1\), we have \(\alpha _2<1\). From (8), it follows that

$$\begin{aligned} V(x(t_k)) \le {\alpha _2}^kV(x({t_0})) + \frac{{1 - {\alpha _2}^k}}{{1 - {\alpha _2}}}\frac{C}{{{\alpha _1}}}. \end{aligned}$$
(9)

Substituting (9) into (7) results in

$$\begin{aligned} V(x(t)) \le {\alpha _2}^kV(x({t_0}))+\frac{{2- {\alpha _2}- {\alpha _2}^k}}{{1 - {\alpha _2}}}\frac{C}{{{\alpha _1}}},\ t \in [{t_k},{t_{k+ 1}}). \end{aligned}$$

Thus, \({\lim _{t \rightarrow \infty }}V(x(t)) \le \frac{2- {\alpha _2}}{{1 - {\alpha _2}}}\frac{C}{{{\alpha _1}}}\), and the sampled-data nonlinear system (5) is UUB. \(\square \)

3 Adaptive Sampled-Data Observer Design

Since the play operator \({F_r}[u](t)\) is continuous and the density function is integrable, it is concluded that the PI model is continuous. In order to design the adaptive sampled-data observer, we use RBFNNs to approximate the unknown time-varying unmatched disturbances \({\nu _i}{d_i }({{\bar{x}}_{i}}(t),t)\)\((i = 1,2, \ldots , n)\) and unknown function \({\nu _0}b{d_0}(u(t))\).

According to Lemma 2.2, we have

$$\begin{aligned}&{W^{*T}}S\left( {u(t)} \right) + \varsigma _0^* = {\nu _0}b{d_0}\left( {u(t)} \right) ,\end{aligned}$$
(10)
$$\begin{aligned}&\theta _{i}^{{{^*}^T}}\varphi _i ({{ \bar{x}}_i}(t))+{\varsigma _i}^*=\nu _i{d_i }({{\bar{x}}_i}(t),t), \end{aligned}$$
(11)

where \({\nu _i} > 0\) (\(i=0,1,\ldots ,n\)) are some design parameters.

Then, substituting (10) and (11) into the system (3), we have

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\dot{x}}_1}(t) = {x_2}(t) + {f_1}({{\bar{x}}_1}(t))+\frac{1}{{{\nu _1}}}\theta _{1}^{{{^*}^T}}\varphi _1 ({{ \bar{x}}_1}(t))+\frac{1}{{{\nu _1}}}{\varsigma _1}^*,\\ \ \ \ \ \ \ \ \ \vdots \end{array}\\ {{{\dot{x}}_{n - 1}}(t) = {x_n}(t) + {f_{n - 1}}({{\bar{x}}_{n - 1}}(t)) }+\frac{1}{{{\nu _{n-1}}}}\theta _{n-1}^{{{^*}^T}}\varphi _{n-1} ({{ \bar{x}}_{n-1}}(t))\\ \qquad \quad \qquad + \frac{1}{{{\nu _{n-1}}}}{\varsigma _{n-1}}^*,\\ {{{\dot{x}}_n}(t) = {b_0}u(t) + {f_n}({{\bar{x}}_n}(t))}+\frac{1}{{{\nu _n}}}\theta _{n}^{{{^*}^T}}\varphi _n ({{ \bar{x}}_n}(t))+ \frac{1}{{{\nu _n}}}{\varsigma _n}^*\\ \qquad \quad \quad + {\frac{1}{{{\nu _0 }}}{W}^{*T}S(u(t))}+{\frac{1}{{{\nu _0 }}}{\varsigma _0 }^* }+ \delta (u(t)),\\ {{y}(t) = {x_1}({t_k}),\mathrm{{ }}t \in [{t_k},{t_{k + 1}}),\mathrm{{ }}k \ge 0,} \end{array}} \right. \end{aligned}$$
(12)

where \({\varsigma _i ^*}\) (\(i=0,1,\ldots ,n\)) are the optimal approximation errors, \(\varphi _i ({{ \bar{x}}_i}(t))\)\((i = 1,2, \ldots , n)\) and S(u(t)) are some basis function vectors, and which are selected such that the following conditions

$$\begin{aligned} \left| {{\varphi _i}(\bar{ x_i}(t)) - {\varphi _i}({{\hat{\bar{ x}}}_i}(t))} \right| \le {l_{i2}}(\left| {{x_1}(t) - {{\hat{x}}_1}}(t) \right| + \cdots + \left| {{x_i}(t) - {{\hat{x}}_i}(t)} \right| ), \end{aligned}$$
(13)

hold for some positive real numbers \({l_{i2}}\)\((i = 1,2, \ldots , n)\).

Let \({D_i} = \frac{1}{{{\nu _i}}}{\varsigma _i}^* \), \((i = 1,2, \ldots , n - 1)\) and \({D_n} = \delta (u(t)) + \frac{1}{{{\nu _n}}}{\varsigma _n}^*+{\frac{1}{{{\nu _0 }}}{\varsigma _0 }^* } \). Then, the system (12) can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\dot{x}}_1}(t) = {x_2}(t) + {f_1}({{\bar{x}}_1}(t))+ {D_1}+\frac{1}{{{\nu _1}}}\theta _{1}^{{{^*}^T}}\varphi _1 ({{\bar{x}}_1}(t)),\\ \ \ \ \ \ \ \ \ \vdots \end{array}\\ {{{\dot{x}}_{n - 1}}(t) = {x_n}(t) + {f_{n - 1}}({{\bar{x}}_{n - 1}}(t)) + {D_{n-1}}}+\frac{1}{{{\nu _{n-1}}}}\theta _{n-1}^{{{^*}^T}}\varphi _{n-1} ({{\bar{x}}_{n-1}}(t)),\\ {{{\dot{x}}_n}(t) = {b_0}u(t) + {f_n}({{\bar{x}}_n}(t)) + {D_n}}+ {\frac{1}{{{\nu _0 }}}{W}^{*T}S(u(t))}\\ \qquad \quad \quad +\frac{1}{{{\nu _n}}}\theta _{n}^{{{^*}^T}}\varphi _n ({{\bar{x}}_n}(t)),\\ {{y}(t) = {x_1}({t_k}),t \in [{t_k},{t_k}{{_ + }_1}),k \ge 0.} \end{array}} \right. \end{aligned}$$
(14)

From Assumption 2 and definitions of \({D_i}\) and \({D_n}\), we can obtain that \(\left| {{{ D}_i}} \right| \le {\sigma _i}_1\) with \({\sigma _i}_1 > 0, (i = 1,2, \ldots , n).\)

Now, we present the following dynamical system to estimate the unknown states of the nonlinear sampled-data system (14).

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {{\dot{\hat{x}}}_1}(t) = {{\hat{x}}_2}(t) + {f_1}({{\hat{\bar{x}}}_1}(t)) + \Gamma {k_1}{e_1}({t_k})+\frac{1}{{{\nu _1}}}\hat{\theta }_{1}^{{^T}}\varphi _1 ({\hat{\bar{x}}_1}(t)),\\ \ \ \ \ \ \ \ \ \vdots \end{array}\\ {{{\dot{\hat{x}}}_{n - 1}}(t) = {{\hat{x}}_n}(t) + {f_{n - 1}}({{\hat{\bar{x}}}_{n - 1}}(t)) + \Gamma ^{n-1} {k_{n - 1}}{e_1}({t_k})}\\ \qquad \qquad \quad +\frac{1}{{{\nu _{n-1}}}}\hat{\theta }_{n-1}^{{^T}}\varphi _{n-1} ({\hat{\bar{x}}_{n-1}}(t)),\\ {{{\dot{\hat{x}}}_n}(t) = {b_0}u(t) + {f_n}({{\hat{\bar{x}}}_n}(t)) +\Gamma ^n {k_n}{e_1}({t_k})}\\ \qquad \quad \quad + {\frac{1}{{{\nu _0 }}}{{\hat{W}}^T}{S}(u(t))}+\frac{1}{{{\nu _n}}}\hat{\theta }_{n}^{{^T}}\varphi _n ({\hat{\bar{x}}_n}(t)),\\ \hat{x}_i(t_{k+1})=\lim _{t\rightarrow t_{k+1}^-}\hat{x}_i(t), \ t \in [t_k, t_{k+1}), k \ge 0, \end{array}} \right. \end{aligned}$$
(15)

where \({e_1}({t_k})={x_1}({t_k})-{{\hat{x}}_1}({t_k})\), and \({\hat{x}_i}(t)\), \({\hat{\bar{x}}_i}(t)\), \(\hat{W}\), \(\hat{\theta }_i\), \((i = 1,2, \ldots , n)\) are the estimates of \({x_i}(t)\), \({\bar{x}_i}(t)\), \(W^*\), \(\theta ^*_i\), respectively. \(\Gamma \ge 1 \), \({k_i}>0\) (\(k=1, 2, \ldots , n\)) are the design parameters.

From (14)–(15), the estimation error can be obtained.

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{e}}_1}(t) = {e_2}(t) + {{\tilde{f}}_1} - \Gamma {k_1}{e_1}(t_k) + {D_1}+\frac{1}{{{\nu _1}}}\theta _1^{{{^*}^T}}{{\tilde{\varphi }}_1}\\ \qquad \qquad +\frac{1}{{{\nu _1}}}\tilde{\theta }_{1}^{{^T}}\varphi _1 ({\hat{\bar{x}}_1}(t)),\\ \ \ \ \ \ \ \ \ \vdots \\ {{\dot{e}}_{n - 1}}(t) = {e_n}(t) + {{\tilde{f}}_{n - 1}} - \Gamma ^{n-1}{k_{n - 1}}{e_1}(t_k)+ {D_{n - 1}}\\ \qquad \qquad \quad +\frac{1}{{{\nu _{n-1}}}}\theta _{n-1}^{{{^*}^T}}{{\tilde{\varphi }}_{n-1}}+\frac{1}{{{\nu _{n-1}}}}\tilde{\theta }_{n-1}^{{^T}}\varphi _{n-1} ({\hat{\bar{x}}_{n-1}}(t)),\\ {{\dot{e}}_n}(t) = {{\tilde{f}}_n} - \Gamma ^n{k_n}{e_1}(t_k) + {\frac{1}{{{\nu _0}}}{{\tilde{W}}^T}S(u(t))} + {D_n}\\ \qquad \qquad \quad +\frac{1}{{{\nu _n}}}\theta _n^{{{^*}^T}}{{\tilde{\varphi }}_n}+\frac{1}{{{\nu _n}}}\tilde{\theta }_{n}^{{^T}}\varphi _n ({\hat{\bar{x}}_n}(t)),\\ t \in [{t_k},{t_k}{{_ + }_1}),k \ge 0, \end{array} \right. \end{aligned}$$
(16)

where \({e_i}(t) = {x_i}(t) - {\hat{x}_i}(t)\), \({\tilde{f}_i} = {f_i}({\bar{x}_i}(t)) - {f_i}({\hat{\bar{x}}_i}(t))\), \({\tilde{\varphi }_i} = {\varphi }_i({\bar{x}_i}(t)) - {\varphi }_i({\hat{\bar{x}}_i}(t))\), \(\tilde{W} = {W^*} - \hat{W}\), \({{\tilde{\theta }}_i} = {\theta _i}^* - {{\hat{\theta }}_i}\). Consider the following coordinate transformation

$$\begin{aligned} {\vartheta _i}(t) = \frac{{{e_i}(t)}}{{{\Gamma ^{i-1 }}}}, i=1,2, \ldots , n. \end{aligned}$$

After transformation, the system (16) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} {{{\dot{\vartheta }}_1}(t) = \Gamma {\vartheta _2}(t) - \Gamma {k_1}{\vartheta _1}(t) + \Gamma {k_1}\left( {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right) } \\ \qquad \quad \quad + \frac{{{{\tilde{f}}_1}}}{{{\Gamma ^0 }}} + \frac{{{D_1}}}{{{\Gamma ^0 }}} + \frac{1}{{{\nu _1}{\Gamma ^0 }}}\theta _1^{*T}{{\tilde{\varphi }}_1} + \frac{1}{{{\nu _1}{\Gamma ^0 }}}\tilde{\theta }_1^T{\varphi _1}\left( {{{\hat{\bar{x}}}_1}(t)} \right) ,\\ \ \ \ \ \ \ \ \ \vdots \\ {{{\dot{\vartheta }}_{n - 1}}(t) = \Gamma {\vartheta _n}(t) - \Gamma {k_{n-1}}{\vartheta _1}(t)}+ \Gamma {k_{n-1}}({\vartheta _1}(t)-\\ \qquad \quad {\vartheta _1}({t_k})) + \frac{{{{\tilde{f}}_{n - 1}}}}{{{\Gamma ^{n - 2}}}}+ \frac{{{D_{n - 1}}}}{{{\Gamma ^{n - 2}}}}+ \frac{1}{{{\nu _{n-1}}{\Gamma ^{n - 2}}}}\theta _{n - 1}^{*T}{{\tilde{\varphi }}_{n - 1}} \\ \qquad \quad \quad + \frac{1}{{{\nu _{n-1}}{\Gamma ^{n - 2}}}}\tilde{\theta }_{n - 1}^T{\varphi _{n - 1}}\left( {{{\hat{\bar{x}}}_{n - 1}}(t)} \right) ,\\ {{{\dot{\vartheta }}_n}(t) = - \Gamma {k_{n}}{\vartheta _1}(t) + \Gamma {k_{n}}\left( {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right) }\\ \qquad \qquad \quad + \frac{{{{\tilde{f}}_n}}}{{{\Gamma ^{n-1 }}}} + \frac{{{D_n}}}{{{\Gamma ^{n-1 }}}}+ {\frac{1}{{{\nu _0}{\Gamma ^{n-1 }}}}{{\tilde{W}}^T}S(u(t))}\\ \qquad \qquad \quad + \frac{1}{{{\nu _n}{\Gamma ^{n-1 }}}}\theta _n^{*T}{{\tilde{\varphi }}_n}+ \frac{1}{{{\nu _n}{\Gamma ^{n-1 }}}}\tilde{\theta }_n^T{\varphi _n}\left( {{{\hat{ \bar{x}}}_n}(t)} \right) ,\\ {t \in [{t_k},{t_{k + 1}}),k \ge 0,} \end{array} \right. \end{aligned}$$
(17)

We can also obtain the following compact form of the system (17).

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\vartheta } = \Gamma A\vartheta + \tilde{F} + \Gamma \tilde{K} + \tilde{W}_\lambda + \tilde{D} + {\tilde{\Phi }}+\tilde{D}_\lambda ,\\ t \in [{t_k},{t_k}{{_ +}_1}),k \ge 0, \end{array} \right. \end{aligned}$$
(18)

where \(\vartheta = {[{\vartheta _1}(t),{\vartheta _2}(t), \ldots , {\vartheta _n}(t)]^T}\), \(\hat{k} = {({k_1},{k_2}, \ldots , {k_n})^T}\), \(\tilde{K}\mathrm{{ = }}\hat{k}({\vartheta _1}(t) - {\vartheta _1}({t_k}))\), \(\tilde{F} = {[\frac{{{{\tilde{f}}_1}}}{{{\Gamma ^0 }}}, \frac{{{{\tilde{f}}_2}}}{{{\Gamma ^1}}}, \ldots , \frac{{{{\tilde{f}}_{n}}}}{{{\Gamma ^{n-1}}}}]^T}\),

\(\tilde{W}_\lambda = {\left[ {\begin{array}{*{20}{c}} 0\\ \vdots \\ 0\\ {{\frac{1}{\nu _0{\Gamma ^{n-1 }} }{{\tilde{W}}^T}{S}(u(t))} } \end{array}} \right] ^{n \times 1}}\), \(A = \left[ {\begin{array}{*{20}{c}} { - {k_1}}&{}1&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ { - {k_{n - 1}}}&{}0&{} \cdots &{}1\\ { - {k_n}}&{}0&{} \cdots &{}0 \end{array}} \right] \), \(\tilde{D} = {[\frac{{{D_1}}}{{{\Gamma ^0 }}},\frac{{{D_2}}}{{{\Gamma ^1}}}, \ldots , \frac{{{D_n}}}{{{\Gamma ^{n-1}}}}]^T}\), \(\tilde{\Phi }= [\frac{1}{{{\nu _1}{\Gamma ^0 }}}\theta _1^{{{^*}^T}}{{\tilde{\varphi }}_1},\frac{1}{{{\nu _2}{\Gamma ^1}}}\theta _2^{{{^*}^T}}{{\tilde{\varphi }}_2}, \ldots , \frac{1}{{{\nu _n}{\Gamma ^{n-1}}}}\times \theta _n^{{{^*}^T}}{{\tilde{\varphi }}_n}]^T\), \(\tilde{D}_\lambda = [\frac{1}{{{\nu _1}{\Gamma ^0 }}}\tilde{\theta }_{1}^{{^T}}\varphi _1 ({\hat{\bar{x}}_1}(t)),\frac{1}{{{\nu _2}{\Gamma ^1}}}\tilde{\theta }_{2}^{{^T}}\varphi _2 ({\hat{\bar{x}}_2}(t)), \ldots , \frac{1}{{{\nu _n}{\Gamma ^{n-1}}}}\tilde{\theta }_{n}^{{^T}}\times \varphi _n ({\hat{\bar{x}}_n}(t))]^T\), and the gains \({k_i} > 0\)\((i = 1,2, \ldots , n)\) are chosen such that the polynomial \(H(s) = {s^n} + {k_1}{s^{n - 1}} + \cdots + {k_{n - 1}}s + {k_n}\) is Hurwitz. Thus, there exists a symmetric positive definite matrix P \((P\mathrm{{ = }}{P^T} > 0)\) such that the following matrix inequality holds,

$$\begin{aligned} {A^T}P + PA \le - I. \end{aligned}$$
(19)

The adaptive laws of the weights \({\hat{W}}\) and \({\hat{\theta }_i}\) are designed as follows,

$$\begin{aligned} {\dot{\hat{ W}}}= & {} {\Lambda _0}\left( - {{S}(u(t)){e_1}({t_k})\chi _0 + {\ell _0}{{\hat{W}}}} \right) ,\end{aligned}$$
(20)
$$\begin{aligned} {{\dot{ \hat{\theta }} }_i}= & {} {\Lambda _i}\left( { - \varphi _i ({\hat{\bar{x}}_i}(t)){e_1}({t_k}){\chi _i} + {\ell _i}{{\hat{\theta }}_i}} \right) , i = 1,2, \ldots , n, \end{aligned}$$
(21)

where \({\Lambda _0} = {\Lambda _0}^T > 0\), \({\Lambda _i} = {\Lambda _i}^T > 0\) are some constant diagonal design matrices, and \({\ell _0} > 0\), \({\ell _i} > 0\), \({\chi _0}>0\), \({\chi _i}>0\) are some parameters to be designed.

Next, we give the definition of adaptive sampled-data observer of the nonlinear system (1).

Definition 2

For the nonlinear system (1), design the system (15), and the adaptive laws of the weights (20) and (21), if there exist two positive real numbers \(\delta _0\) and \(T_1>0\), such that

$$\begin{aligned} \Vert e(t)\Vert <\delta _0, t>T_1, \end{aligned}$$

then, the system (15) with the adaptive laws (20) and (21) is called an adaptive sampled-data observer of the system (1).

Theorem 1

Consider the system (1) with conditions (4) and (13). If \({k_i} > 0 (i = 1,2, \ldots , n)\) are selected such that the condition (19) holds, and the sampling period T, the parameters \(\phi \), \(\Delta _1\), \(\Delta _2\), \({\ell _0}\), \({\ell _i}\) satisfy the following conditions

$$\begin{aligned} \begin{aligned}&T \le \min \left\{ { \frac{{\frac{1}{2} - {{\bar{p}}_2}\phi }}{\Gamma }, \frac{1}{{\phi + L_0 + 6{L_1}}},\sqrt{\frac{{\frac{1}{2}{{\bar{p}}_3}\phi }}{{(L_0 + 6{L_1})\bar{k}{\Gamma ^2}}}}, } \right. \\&\left. { \sqrt{\frac{1}{{4(L_0 + 6{L_1})}} }, \sqrt{\frac{{\frac{{\ell _i}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}} - \frac{1}{2}{\lambda _{\max }}(\Lambda {{_i}^{ - 1}})\phi }}{{\left( {L_0 + 6{L_1}} \right) \frac{{{\eta _0}^2}}{{{\nu _1}^2}} }}}} \right\} , \end{aligned} \end{aligned}$$
(22)

and

$$\begin{aligned} \phi \le \min \left\{ {\frac{1}{{{{2\bar{p}}_2}}},\frac{{\ell _0} - \frac{2}{{{\Delta _1}}} - \frac{2}{{{\Delta _2}}}}{{{\lambda _{\max }}(\Lambda {{_0}^{ - 1}})}},\frac{{\ell _i} - \frac{2}{{{\Delta _1}}} - \frac{2}{{{\Delta _2}}}}{{{\lambda _{\max }}(\Lambda {{_i}^{ - 1}})}}} \right\} , \end{aligned}$$
(23)

and

$$\begin{aligned} \begin{aligned} {\ell _0} - \frac{2}{{{\Delta _1}}} - \frac{2}{{{\Delta _2}}}> 0, {\ell _i} - \frac{2}{{{\Delta _1}}} - \frac{2}{{{\Delta _2}}}> 0, \end{aligned} \end{aligned}$$
(24)

then, the state observation error system (18) is UUB, or, the system (15)–(20)–(21) is an adaptive sampled-data observer of the system (1), where \(L_0=24\Gamma {{\bar{p}}_1}n\bar{k}\), \(L_1=\frac{{{\Delta _2}}}{2}{\upsilon _0}^2{{\bar{\chi }}^2}+{\frac{{{\Delta _2}}}{2}}{\eta _0}^2{{\bar{\chi }}^2}\), \({\upsilon _0} = \left\| {{S}(u(t))} \right\| \), \({\eta _i} = \left\| {\varphi ({\hat{\bar{x}}_i}(t))} \right\| \), \({\eta _0} = \max ({\eta _i})\), \(\underline{\nu }= \min ({\nu _0}, \nu _i)\)\(\bar{\chi }= \max ({\chi _0}, \chi _i)\), \({\bar{p}_1} = {\lambda _{\max }}({P^T}P)\), \({\bar{p}_2} = {\lambda _{\max }}(P)\), \({\bar{p}_3} = {\lambda _{\min }}(P)\), \(\bar{k} = \max ({k_i}^2)\), \(\bar{l} =\max \left( {\sqrt{\sum \limits _{i = 1}^n {i{l_{i1}}^2} }, \sqrt{\sum \limits _{i = 1}^n {i{l_{i2}}^2} }} \right) \).

Proof

Consider the following Lyapunov–Krasovskii functional

$$\begin{aligned} V(t) = {V_1}(t) + {V_2}(t)+ {V_3}(t)+ \Gamma ^2{V_4}(t) , \end{aligned}$$
(25)

where \({V_1}(t) = {\vartheta ^T}P\vartheta \), \({V_2}(t) =\frac{1}{2} {{{\tilde{W}}}^T{\Lambda _0}^{ - 1}{{\tilde{W}}}}\), \({V_3}(t)=\frac{1}{2}\sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}} {\Lambda _i}^{ - 1}{\tilde{\theta }_i}\), \({V_4}(t) = \int _{t - T}^t {\int _\tau ^t {\left[ {{\vartheta _1}{{(s)}^2} + {\vartheta _2}{{(s)}^2}} \right] } } dsd\tau ,\ t \in [{t_{k0}},\infty ), \) and \( {k_0} = \min \{ k:T < {t_k}\} \).

Then, along the trajectory of the system (18), the derivative of \({V_1}(t)\) is given as follows:

$$\begin{aligned} {\dot{V}_1}(t)=&\Gamma {\vartheta ^T}({A^T}P + PA)\vartheta + 2{\vartheta ^T}P(\tilde{F} + \Gamma \tilde{K} + \tilde{D} + {\tilde{\Phi }}+ \tilde{D}_\lambda + \tilde{W}_\lambda )\nonumber \\ \le&- \Gamma {\vartheta ^T}\vartheta + 2{\vartheta ^T}P\tilde{F} + 2\Gamma {\vartheta ^T}P\tilde{K} + 2{\vartheta ^T}P\tilde{D}+ 2{\vartheta ^T}P{\tilde{\Phi }}\nonumber \\&+2{\vartheta ^T}P\tilde{D}_\lambda +2{\vartheta ^T}P\tilde{W}_\lambda . \end{aligned}$$
(26)

Based on Assumption 1 and Lemma 2.3, the following inequalities hold.

$$\begin{aligned} 2{\vartheta ^T}P\tilde{F}\le & {} 2\left\| \vartheta ^T \right\| \left\| P \right\| \bar{l}\sqrt{\sum \limits _{i = 1}^n {\frac{{\left| {{x_i}(t) - {{\hat{x}}_i}(t)} \right| }^2}{{{\Gamma ^{2(i - 1)}}}}} }\nonumber \\\le & {} 2\bar{l}\sqrt{{{\bar{p}}_1}} {\left\| \vartheta \right\| ^2},\end{aligned}$$
(27)
$$\begin{aligned} 2{\vartheta ^T}P\tilde{\Phi }\le & {} 2\left\| {{\vartheta ^T}} \right\| \left\| P \right\| \left\| {\tilde{\Phi }} \right\| \le 2\bar{l}\sqrt{{{\bar{p}}_1}} \frac{{{\varpi _0}}}{{{\underline{\nu }}}}{\left\| \vartheta \right\| ^2},\end{aligned}$$
(28)
$$\begin{aligned} 2{\vartheta ^T}P\tilde{D}_\lambda\le & {} 2\left\| {{\vartheta ^T}} \right\| \left\| P \right\| \left\| {{{\tilde{D}}_\lambda }} \right\| \nonumber \\\le & {} \frac{{{\Delta _1}{\eta _0}^2{{\bar{p}}_1}}}{{{\underline{\nu }}^2}}{\left\| \vartheta \right\| ^2} + \frac{1}{{{\Delta _1}}}\sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}},\end{aligned}$$
(29)
$$\begin{aligned} 2{\vartheta ^T}P\tilde{W}_\lambda\le & {} 2\left\| {{\vartheta ^T}} \right\| \left\| P \right\| \left\| {\tilde{W}_\lambda } \right\| \nonumber \\\le & {} \frac{{{\Delta _1}{\upsilon _0}^2{{\bar{p}}_1}}}{{{{\underline{\nu }} ^2}}}{\left\| \vartheta \right\| ^2} + \frac{1}{{{\Delta _1}}} {{{\left\| {{{\tilde{W}}}} \right\| }^2}} ,\end{aligned}$$
(30)
$$\begin{aligned} 2{\vartheta ^T}P\tilde{D}\le & {} 2\left\| {{\vartheta ^T}} \right\| \left\| P \right\| \left\| {\tilde{D}} \right\| \le 4{{\bar{p}}_1}{\left\| \vartheta \right\| ^2} + \frac{1}{{4}}\sum \limits _{i = 1}^n {\sigma _{i1}^2},\end{aligned}$$
(31)
$$\begin{aligned} 2\Gamma {\vartheta ^T}P\tilde{K}= & {} 2\Gamma {\vartheta ^T}P{\hat{k}}({\vartheta _1}(t) - {\vartheta _1}({t_k}))\nonumber \\\le & {} 4\Gamma {\bar{p}_1}n\bar{k}{({\vartheta _1}(t) -{\vartheta _1}({t_k}))^2} + \frac{\Gamma }{4}{\left\| \vartheta \right\| ^2}, \end{aligned}$$
(32)

where \({\varpi _i} = \left\| {\theta {{_i^*}^T}} \right\| \), \({\varpi _0} = \max ({\varpi _i})\).

According to Lemma 2.1, we can obtain

$$\begin{aligned}&{\left| {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right| ^2}= {\left| {\int _{{t_k}}^t {{{\dot{\vartheta }}_1}(s)ds} } \right| ^2} \le (t - {t_k}) \int _{{t_k}}^t {{{\left| {{{\dot{\vartheta }}_1}(s)} \right| }^2}ds} \nonumber \\&\quad \le (t - {t_k})\int _{{t_k}}^t\left[ {\Gamma {\vartheta _2}(s) - \Gamma {k_1}{\vartheta _1}({t_k})+ \frac{{{{\tilde{f}}_1}}}{{{\Gamma ^0 }}} + \frac{{{ D_1}}}{{{\Gamma ^0 }}}+ \frac{1}{{{\nu _1}{\Gamma ^0 }}}\theta _1^{*T}{{\tilde{\varphi }}_1}} \right. \nonumber \\&\qquad \quad \left. { + \frac{1}{{{\nu _1}{\Gamma ^0 }}}\tilde{\theta }_1^T{\varphi _1}\left( {{{\hat{\bar{x}}}_1}(s)} \right) } \right] ^2ds\nonumber \\&\quad \le 6\Gamma ^2(t - {t_k})\int _{{t_k}}^t\left[ {{\vartheta _2}{{(s)}^2} + \frac{(1 + \frac{{{\varpi _0}^2}}{{{\nu _1}^2}}){l_1}^2}{\Gamma ^2}{\vartheta _1}{{(s)}^2}+ \bar{k}{\vartheta _1}{{({t_k})}^2} } \right. \nonumber \\&\qquad \quad \left. {+ \frac{1}{{{\Gamma ^2}}}\sum \limits _{i = 1}^n {\sigma _{i1}^2} +\frac{{{\eta _0}^2}}{{{\nu _1}^2}\Gamma ^2}\sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}}} \right] ds, t \in [{t_k},{t_{k + 1}}), k \ge k_0, \end{aligned}$$
(33)

where \({l_1} = \max \left( {{l_{11}}, {l_{12}}} \right) \), \(\Gamma \ge \sqrt{\left( {1 + \frac{{{\varpi _0}^2}}{{{\nu _1}^2}}} \right) {l_1}^2 } \).

It follows from (32) and (33) that,

$$\begin{aligned} 2\Gamma {\vartheta ^T}P\tilde{K}&\le \frac{\Gamma }{4}{\left\| \vartheta \right\| ^2}+ L_0{\Gamma ^2}\bar{k}{(t - {t_k})^2}{\vartheta _1}{({t_k})^2} \nonumber \\&\quad +L_0{\Gamma ^2}(t - {t_k})\int _{{t_k}}^t {\left[ {{\vartheta _1}{{(s)}^2} + {\vartheta _2}{{(s)}^2}} \right] ds} \nonumber \\&\quad + L_0\frac{{{\eta _0}^2}}{{{\nu _1}^2}}{(t - {t_k})^2}\sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}}+L_0{(t - {t_k})^2}\sum \limits _{i = 1}^n {{\sigma _{i1}}^2} , \nonumber \\&\quad t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned}$$
(34)

From (26)–(31), and (34), we have

$$\begin{aligned} {{\dot{V}}_1}(t)&\le - \frac{5}{8}\Gamma {\left\| \vartheta \right\| ^2}+ L_0{\Gamma ^2}\bar{k}{(t - {t_k})^2}{\vartheta _1}{({t_k})^2}\nonumber \\&\quad +L_0{\Gamma ^2}(t - {t_k})\int _{{t_k}}^t {\left[ {{\vartheta _1}{{(s)}^2} + {\vartheta _2}{{(s)}^2}} \right] ds}\nonumber \\&\quad +\left( {L_0\frac{{{\eta _0}^2}}{{{\nu _1}^2}}{(t - {t_k})^2} + \frac{1}{{{\Delta _1}}}} \right) \sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}}\nonumber \\&\quad +\left( {L_0{(t - {t_k})^2}+\frac{1}{4}} \right) \sum \limits _{i = 1}^n {{\sigma _{i1}}^2}+ \frac{1}{{{\Delta _1}}}{{{\left\| {{{\tilde{W}}}} \right\| }^2}},\nonumber \\&\quad t \in [{t_k},{t_{k + 1}}), k \ge k_0, \end{aligned}$$
(35)

where \(\Gamma \ge 8(2\bar{l}\sqrt{{{\bar{p}}_1}}(1 + \frac{{{\varpi _0}}}{{{\nu _1}}})+4{{\bar{p}}_1}+ \frac{{{\Delta _1}{\upsilon _0}^2{{\bar{p}}_1}}}{{{{\underline{\nu }} ^2}}}+\frac{{{\Delta _1}{\eta _0}^2{{\bar{p}}_1}}}{{{\underline{\nu }}^2}})\).

In order to deal with \({\tilde{W}}\) and \({\tilde{\theta }_i}\), the derivatives of \({V_2}(t)\) and \({V_3}(t)\) are given as follows.

$$\begin{aligned} {\dot{V}_2}(t)= & {} {{{\tilde{W}}}^T{\Lambda _0}^{ - 1}{{\dot{ \tilde{ W}}}}} = - {{{\tilde{W}}}^T{\Lambda _0}^{ - 1}{{\dot{ \hat{ W}}}}},\end{aligned}$$
(36)
$$\begin{aligned} {\dot{V}_3}(t)= & {} \sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}{\Lambda _i}^{ - 1}{{\dot{ \tilde{\theta }} }_i}} = -\sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}{\Lambda _i}^{ - 1}{{\dot{\hat{\theta }} }_i}} . \end{aligned}$$
(37)

Substituting (20)–(21) into (36)–(37) results in

$$\begin{aligned} {{\dot{V}}_2}(t)+{{\dot{V}}_3}(t)&= - {{{\tilde{W}}}^T\left( { - {S}(u(t)){\vartheta _1}({t_k}){\chi _0} + {\ell _0}{{\hat{W}}}} \right) }\nonumber \\&\quad -\sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}\left( { - \varphi ({\hat{\bar{x}}_i}(t)){\vartheta _1}({t_k}){\chi _i} + {\ell _i}{{\hat{\theta }}_i}} \right) }\nonumber \\&=- {{\tilde{W}}}^T\left( {- {S}(u(t)){\vartheta _1}(t){\chi _0} + {S}(u(t))({\vartheta _1}(t) -{\vartheta _1}({t_k})){\chi _0}} \right. \nonumber \\&\quad \left. {+ {\ell _0}{{\hat{W}}}} \right) -\sum \limits _{i = 1}^n \tilde{\theta }_i^{^T}\left( {- \varphi ({\hat{\bar{x}}_i}(t)){\vartheta _1}(t){\chi _i}+\varphi ({\hat{\bar{x}}_i}(t))({\vartheta _1}(t)-} \right. \nonumber \\&\quad \left. { {\vartheta _1}({t_k})){\chi _i} + {\ell _i}{{\hat{\theta }}_i}} \right) , \end{aligned}$$
(38)

where \({e_1}({t_k}) = {\vartheta _1}({t_k})\). Then, according to \({\tilde{W}} = {W}^* - {\hat{W}}\), \({{\tilde{\theta }}_i} = {\theta _i}^* - {{\hat{\theta }}_i}\) and Lemma 2.3, we have

$$\begin{aligned}&2{{\tilde{W}}}^T{\hat{W}}+2\tilde{\theta }_i^{^T}{{\hat{\theta }}_i}\nonumber \\&\quad = {\left\| {{{\tilde{W}}}} \right\| ^2} + {\left\| {{{\hat{W}}}} \right\| ^2} - {\left\| {{W}^*} \right\| ^2}+{\left\| {{{\tilde{\theta }}_i}} \right\| ^2} + {\left\| {{{\hat{\theta }}_i}} \right\| ^2} - {\left\| {{\theta _i}^*} \right\| ^2}\nonumber \\&\quad \ge {\left\| {{{\tilde{W}}}} \right\| ^2} - {\left\| {{W}^*} \right\| ^2}+{\left\| {{{\tilde{\theta }}_i}} \right\| ^2} - {\left\| {{\theta _i}^*} \right\| ^2},\end{aligned}$$
(39)
$$\begin{aligned}&{{\tilde{W}}}^T{S}(u(t)){\vartheta _1}(t){\chi _0}+\sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}\varphi ({\hat{\bar{x}}_i}(t)){\vartheta _1}(t){\chi _i}}\nonumber \\&\quad \le L_1{\left\| \vartheta \right\| ^2} + \frac{1}{{2{\Delta _2}}}{{{\left\| {{{\tilde{W}}}} \right\| }^2}}+\frac{1}{{2{\Delta _2}}}\sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}} ,\end{aligned}$$
(40)
$$\begin{aligned}&\qquad \quad -{{\tilde{W}}}^T{S}(u(t))\left( {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right) {\chi _0}\nonumber \\&\quad \le \frac{{{\Delta _2}}}{2}{\upsilon _0}^2{\bar{\chi }^2}{\left( {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right) ^2} + \frac{1}{{2{\Delta _2}}} {{{\left\| {{{\tilde{W}}}} \right\| }^2}},\end{aligned}$$
(41)
$$\begin{aligned}&-\sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}\varphi ({\hat{\bar{x}}_i}(t))({\vartheta _1}(t) - {\vartheta _1}({t_k})){\chi _i}}\nonumber \\&\quad \le \frac{{{\Delta _2}}}{2} {\eta _0}^2{{\bar{\chi }}^2}{({\vartheta _1}(t) - {\vartheta _1}({t_k}))^2} + \frac{1}{{2{\Delta _2}}}\sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}} , \end{aligned}$$
(42)

Considering (33), (41), and (42), we have

$$\begin{aligned}&- {{{\tilde{W}}}^T{S}(u(t))\left( {{\vartheta _1}(t) - {\vartheta _1}({t_k})} \right) } {\chi _0} - \sum \limits _{i = 1}^n {\tilde{\theta }_i^{^T}\varphi ({\hat{\bar{x}}_i}(t))}\times \nonumber \\&\qquad ({\vartheta _1}(t) - {\vartheta _1}({t_k})){\chi _i} \nonumber \\&\quad \le 6L_1\Gamma ^2\bar{k}{(t - {t_k})^2}{\vartheta _1}{({t_k})^2}+6L_1{(t - {t_k})^2}\sum \limits _{i = 1}^n {{\sigma _{i1}}^2}\nonumber \\&\qquad \quad + 6L_1\Gamma ^2(t - {t_k}) \int _{{t_k}}^t {\left[ {{\vartheta _1}{{(s)}^2} + {\vartheta _2}{{(s)}^2}} \right] ds}+ \frac{1}{{2{\Delta _2}}} {{{\left\| {{{\tilde{W}}}} \right\| }^2}}\nonumber \\&\qquad \quad +\left( {6L_1\frac{{{\eta _0}^2}}{{{\nu _1}^2}}{{(t - {t_k})}^2} + \frac{1}{{2{\Delta _2}}}} \right) \sum \limits _{i = 1}^n {{{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}}, \nonumber \\&t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned}$$
(43)

Based on (38)–(43), we have

$$\begin{aligned}&{{\dot{V}}_2}(t)+{{\dot{V}}_3}(t)\nonumber \\&\quad \le \frac{1}{8}\Gamma {\left\| \vartheta \right\| ^2} + 6L_1\Gamma ^2\bar{k}{(t - {t_k})^2}{\vartheta _1}{({t_k})^2}+ 6L_1\Gamma ^2(t - {t_k})\nonumber \\&\qquad \quad \times \int _{{t_k}}^t {\left[ {{\vartheta _1}{{(s)}^2} + {\vartheta _2}{{(s)}^2}} \right] ds}- \sum \limits _{i = 1}^n\left( {\frac{{{\ell _i}}}{2} - \frac{1}{{{\Delta _2}}}-6L_1\frac{{{\eta _0}^2}}{{{\nu _1}^2}}} \right. \nonumber \\&\qquad \quad \left. {\times \,(t - {t_k})^2} \right) {{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}- {\left( {\frac{{{\ell _0}}}{2} - \frac{1}{{{\Delta _2}}}} \right) {{\left\| {{{\tilde{W}}}} \right\| }^2}}+6L_1{(t - {t_k})^2}\times \nonumber \\&\sum \limits _{i = 1}^n {{\sigma _{i1}}^2}+ {\frac{{{\ell _0}}}{2}{{\left\| {{W}^*} \right\| }^2}}+\sum \limits _{i = 1}^n {\frac{{{\ell _i}}}{2}{{\left\| {{\theta _i}^*} \right\| }^2}}, \nonumber \\&t \in [{t_k},{t_{k + 1}}), k \ge k_0, \end{aligned}$$
(44)

where \(\Gamma \ge 8{L_1}\).

Note that when \(t \in [{t_k},{t_{k + 1}})\), we have \(t-T < {t_k}\). Thus, from (35) and (44), it follows that

$$\begin{aligned}&{{\dot{V}}_1}(t) + {{\dot{V}}_2}(t) + {{\dot{V}}_3}(t)\nonumber \\&\quad \le - \frac{1}{2}\Gamma {\left\| \vartheta \right\| ^2} + \left( {L_0 + 6L_1} \right) \bar{k}\Gamma ^2{T^2}{\vartheta _1}{({t_k})^2}\nonumber \\&\qquad \quad + (L_0 + 6L_1){ \Gamma ^2}T\int _{t - T}^t {[{\vartheta _1}{(s)^2}+{\vartheta _2}{{(s)}^2}]ds}\nonumber \\&\qquad \quad - \sum \limits _{i = 1}^n {\left( {\frac{{{\ell _i}}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}}-(L_0+ 6L_1)\frac{{{\eta _0}^2}}{{{\nu _1}^2}}{T^2}} \right) {{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}\nonumber }\\&\qquad \quad - {\left( {\frac{{{\ell _j}}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}}} \right) {{\left\| {{{\tilde{W}}}} \right\| }^2}}+\left( {(L_0 + 6L_1){T^2}+\frac{1}{4}} \right) \sum \limits _{i = 1}^n {{\sigma _{i1}}^2}\nonumber \\&\qquad \quad +{\frac{{{\ell _0}}}{2}{{\left\| {{W}^*} \right\| }^2}}+\sum \limits _{i = 1}^n {\frac{{{\ell _i}}}{2}{{\left\| {{\theta _i}^*} \right\| }^2}} ,t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned}$$
(45)

Further, the derivative of \(V_4(t)\) is given by

$$\begin{aligned} {{\dot{V}}_4}(t)&= T({\vartheta _1}{(t)^2}+{\vartheta _2}{(t)^2})-\int _{t - T}^t {({\vartheta _1}{(s)^2}+{\vartheta _2}{{(s)}^2})ds},\nonumber \\&t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned}$$
(46)

Next, for \(n \ge 2\), we have

$$\begin{aligned} \begin{aligned} {\dot{V}_4}(t)&\le T{\left\| \vartheta \right\| ^2} - \int _{t - T}^t {\left[ {{\vartheta _1}{(s)^2}+{\vartheta _2}{{(s)}^2}} \right] ds},\\&t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned} \end{aligned}$$
(47)

Substituting (45) and (47) into (25), we have

$$\begin{aligned}&\dot{V}(t) = {{\dot{V}}_1}(t) + {{\dot{V}}_2}(t) + {{\dot{V}}_3}(t) +\Gamma ^2 {{\dot{V}}_4}(t)\nonumber \\&\quad \le - ( \frac{1}{2} - T\Gamma )\Gamma {\vartheta ^T}(t)\vartheta (t) + \left( {L_0 + 6L_1} \right) \bar{k}\Gamma ^2{T^2}{\vartheta _1}{({t_k})^2}\nonumber \\&\qquad \quad + \left( {(L_0 + 6L_1){\Gamma ^2}T-\Gamma ^2} \right) \int _{t - T}^t {[{\vartheta _1}{(s)^2}+{\vartheta _2}{{(s)}^2}]ds}\nonumber \\&\qquad \quad - \sum \limits _{i = 1}^n {\left( {\frac{{{\ell _i}}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}}-(L_0 + 6L_1)\frac{{{\eta _0}^2}}{{{\nu _1}^2}}{T^2}} \right) {{\left\| {{{\tilde{\theta }}_i}} \right\| }^2}}\nonumber \\&\qquad \quad - {\left( {\frac{{{\ell _0}}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}}} \right) {{\left\| {{{\tilde{W}}}} \right\| }^2}}+\left( {(L_0 + 6L_1){T^2}+\frac{1}{4}} \right) \sum \limits _{i = 1}^n {{\sigma _{i1}}^2} \nonumber \\&\qquad \quad + {\frac{{{\ell _0}}}{2}{{\left\| {{W}^*} \right\| }^2}}+\sum \limits _{i = 1}^n {\frac{{{\ell _i}}}{2}{{\left\| {{\theta _i}^*} \right\| }^2}}, t \in [{t_k},{t_{k + 1}}), k \ge k_0, \end{aligned}$$
(48)

Note that

$$\begin{aligned} \begin{aligned} {V_4}(t) \le T\int _{t - T}^t {({\vartheta _1}{(s)^2}+{\vartheta _2}{{(s)}^2})} ds, t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned} \end{aligned}$$
(49)

Then, from (48) and (49), we can obtain

$$\begin{aligned}&\dot{V}(t)\le - \frac{1 - 2T\Gamma }{{{2{\bar{p}}_2}}}{V_1}(t)- \frac{{2\left( {\frac{{\ell _0}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}}} \right) }}{{{\lambda _{\max }}(\Lambda {{_0}^{ - 1}})}}{V_2}(t)\nonumber \\&\quad - \frac{{2\left( {\frac{{\ell _i}}{2} - \frac{1}{{{\Delta _1}}} - \frac{1}{{{\Delta _2}}} - \left( {L_0 + 6L_1} \right) \frac{{{\eta _0}^2}}{{{\nu _1}^2}} {T^2}} \right) }}{{{\lambda _{\max }}(\Lambda {{_i}^{ - 1}})}}{V_3}(t)\nonumber \\&\quad - \frac{{\left( {1 - \left( {L_0 + 6L_1} \right) T} \right) }}{T}{\Gamma ^2}{V_4}(t)+ \frac{{\left( {L_0 + 6L_1} \right) \bar{k}{\Gamma ^2}{T^2}}}{{{{\bar{p}}_3}}}{V_1}({t_k})\nonumber \\&\quad +\left( {(L_0 + 6L_1){T^2}+\frac{1}{4}} \right) \sum \limits _{i = 1}^n {{\sigma _{i1}}^2}+ {\frac{{{\ell _0}}}{2}{{\left\| {{W}^*} \right\| }^2}}+\sum \limits _{i = 1}^n {\frac{{{\ell _i}}}{2}{{\left\| {{\theta _i}^*} \right\| }^2}},\nonumber \\&t \in [{t_k},{t_{k + 1}}), k \ge k_0. \end{aligned}$$
(50)

Since the sampling period T, and the parameters \(\phi \), \(\Delta _1\), \(\Delta _2\), \({\ell _0}\), \({\ell _i}\) satisfy the conditions (22)–(24), then,

$$\begin{aligned} \begin{aligned} \frac{d}{{dt}}V(t) \le - \phi V(t) + \frac{\phi }{2}V({t_k}) + {{C_1}}, t \in [{t_k},{t_{k + 1}}), k \ge k_0, \end{aligned} \end{aligned}$$
(51)

where \({C_1} =\frac{1}{2}\sum \limits _{i = 1}^n {{{\sigma _{i1}}^2}} + {\frac{{{\ell _0}}}{2}{{\left\| {{W}^*} \right\| }^2}}+\sum \limits _{i = 1}^n {\frac{{{\ell _i}}}{2}{{\left\| {{\theta _i}^*} \right\| }^2}}\). In order to ensure the error system is UUB, the corresponding high-gain design parameter \(\Gamma \) should be chosen such that

$$\begin{aligned}&\Gamma \ge \max \left\{ {1, \sqrt{\left( {1 + \frac{{{\varpi _0}^2}}{{{\nu _1}^2}}} \right) {l_1}^2}, 8L_1,} \right. \\&\left. {8\left( {2\bar{l}\sqrt{{{\bar{p}}_1}} (1 + \frac{{{\varpi _0}}}{{{\nu _1}}}) + 4{{\bar{p}}_1} + \frac{{{\Delta _1}{\upsilon _0}^2{{\bar{p}}_1}}}{{{\underline{\nu }}^2}} + \frac{{{\Delta _1}{\eta _0}^2{{\bar{p}}_1}}}{{{\underline{\nu }}^2}}} \right) } \right\} . \end{aligned}$$

Since \({\phi _1}=(1 - \frac{1}{2}){e^{ - \phi T}} + \frac{1}{2} < 1\). From the differential inequality (51) and Lemma 2.4, we have

$$\begin{aligned} V(t) \le {\phi _1}^kV(t_0) + \frac{{2- {\phi _1}-{\phi _1}^k}}{{1- {\phi _1}}}\frac{C_1}{\phi }. \end{aligned}$$

Thus, we obtain that the system (18) is UUB, i.e., \({\lim _{t \rightarrow \infty }}V(t) \le \frac{{{(2- \phi _1)C_1}}}{{(1 - {\phi _1})\phi }}\). On the one hand, \( \mathop {\lim }\limits _{t \rightarrow \infty } {V_1}(t) \le \mathop {\lim }\limits _{t \rightarrow \infty } V(t) \le \frac{{{(2- \phi _1)C_1}}}{{(1 - {\phi _1})\phi }}\), on the other hand, \({V_1}(t) \ge {{\bar{p}}_3}{\vartheta ^T}\vartheta \ge \frac{{{{\bar{p}}_3}{e^T}e}}{{{\Gamma ^{2(n - 1)}}}}\). Thus, we have

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } {e^T}e \le \frac{{{(2- \phi _1)C_1{\Gamma ^{2(n - 1)}}}}}{{(1 - {\phi _1})\phi {{\bar{p}}_3} }}, \end{aligned}$$

This completes the proof. \(\square \)

Remark 2

The design method can be extended to nonlinear systems with other hysteresis inputs and may not necessarily limited to the system described by (1). On the one hand, \(C_1\) in (3) is determined by the parameters \(\sigma _{i1}\), \({\ell _0}\), \({\ell _i}\). Note that the value of the parameters \(\sigma _{i1}\), \( {\ell _0},\)\({\ell _i} \) can be adjusted. Thus, a small value of \(C_1\) can be guaranteed. On the other hand, we can properly select the design parameters \(\Gamma \), \({k_i}\), \({l_{i1}}\), \({l_{i2}}\), \({\upsilon _0}\), \({\eta _i}\), \({\nu _0}\), \({\nu _i}\), \({\ell _0}\), \({\ell _i}\), \({ \chi _0 }\), \({ \chi _i }\), \({\Delta _1}\) and \({\Delta _2}\). Then, based on these parameters, the sampling period T and \(\phi \) can be found such that the error system converges to a relatively small neighborhood of the origin.

Remark 3

In [7], the estimation state \(\hat{x}(t)\) is introduced into the RBFNNs to approximate the hysteresis and the uncertainties. Therefore, the considered nonlinear system not only has the unknown state x(t) but also the estimation state \(\hat{x}(t)\). Whereas, in this paper, we only use the system state x(t) to approximate the hysteresis and the disturbances. Thus, the considered nonlinear system (12) only has x(t) but not \(\hat{x}(t)\). Moreover, compared with [7], we relaxed the restriction on the constant control gain parameter b by using the approximation formulation (10), and solved the problem of parameter selection by introducing the high gain parameter \(\Gamma \).

4 Simulation Example

In this section, a simulation example will be demonstrated the effectiveness of the proposed scheme.

Example 1

Consider the nonlinear system with unknown hysteresis and unknown unmatched disturbance

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1}(t) = {x_2}(t),\\ {{\dot{x}}_2}(t) = b\omega (u(t)) + f(\bar{x}(t)) +d({{\bar{x}}}(t),t),\\ y(t) = {x_1}({t_k}), t \in [{t_k},{t_{k + 1}}), k \ge 0, \end{array} \right. \end{aligned}$$

where \(f(\bar{x}(t)) =-3 \sin ({x_1}(t))\) and \(d({{\bar{x}}}(t),t)=0.1\sin (x_1)e^{-0.1x_2}\). The PI hysteresis out \(\omega (u(t))\) is determined by (2) and the density function is chosen as \(p(r) = 0.8{e^{ - 0.067{{(r - 1)}^2}}}\). We choose \(R\mathrm{{ = }}100\) as the upper limit of integration.

Considering (15), the adaptive sampled-data observer is constructed as

$$\begin{aligned} \left\{ \begin{array}{llll} {{\dot{\hat{ x}}}_1}(t) = {{\hat{x}}_2}(t) +\Gamma {k_1}{e_1}({t_k}),\\ {{\dot{\hat{ x}}}_2}(t) = {b_0}u(t)-3\sin ({{\hat{x}}_1})+\Gamma ^2 {k_2}{e_1}({t_k})+ {\frac{1}{{{\nu _0}}}{{\hat{W}}^T}S(u(t))} \\ \quad \qquad \quad +\frac{1}{{{\nu _1}}}\hat{\theta }^{{^T}}\varphi ({\hat{\bar{x}}}(t)),\\ \hat{y}(t) = {{\hat{x}}_1}({t_k}),\mathrm{{ }}t \in [{t_k},{t_{k + 1}}),\mathrm{{ }}k \ge 0,\\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{l} {S}(u(t)) = [\frac{4}{{1 + {e^{ - u(t)}}}} - 2.5, \frac{5}{{1 + {e^{ - u(t)}}}} - 3]^T\\ \varphi ({\hat{\bar{x}}}(t)) = \exp \left[ { - \frac{{{{({{\hat{x}}_1} - 6 + 2l)}^2}}}{2}} \right] \times \exp \left[ { - \frac{{{{({{\hat{x}}_2} - 3 + l)}^2}}}{4}} \right] , l = 1,\mathrm{{ }} \ldots , 5. \end{array} \right. \end{aligned}$$
Fig. 1
figure 1

Trajectory of \(\left\| {\hat{W} } \right\| \)

Full size image
Fig. 2
figure 2

Trajectory of \(\left\| {\hat{\theta }} \right\| \)

Full size image
Fig. 3
figure 3

Estimation of \({x_1}\) of the nonlinear system

Full size image
Fig. 4
figure 4

Estimation of \({x_2}\) of the nonlinear system

Full size image
Fig. 5
figure 5

Trajectories of the errors \(e_1(t)\) and \(e_2(t)\)

Full size image
Fig. 6
figure 6

Trajectory of the Lyapunov function V(t)

Full size image

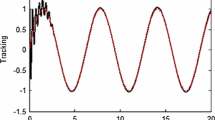
where \({e_1}({t_k})=x_1({t_k}) - {{\hat{x}}_1}({t_k})\), and the update laws of the weights are given by (20) and (21). In the following simulation, we choose \(\Gamma =2\), \({k_1}={k_2}=1.5\), \(u(t)=(12\cos (3t)-4)/(1 + 6t)\)\(+\cos (2t)\), \({b_0}=1\), \(\nu _0=0.8\), \(\nu _1=1.5\), \({\Lambda ^1 _{0}}={\Lambda ^2 _{0}}={\Lambda _{l}}=0.004\), \({\ell ^1 _{0}}={\ell ^2 _{0}}={\ell _{l}}=0.05\), \({\chi ^1 _{0}}=60\), \({\chi ^2 _{0}}=55\), \({\chi _{l}}=(0.5,40,0.5,60,0.5)\) and \({\Delta _1}={\Delta _2}=100\). The initial conditions \(({x_1}(0),{x_2}(0))= (-1,1)\), \(({\hat{x}_1}(0),{\hat{x}_2}(0))=(1,3)\), \(({{\hat{W}}^1_{0}}(0), {{\hat{W}}^2_{0}}(0))=(0.05, 0.05)\) and \({{\hat{\theta }}_l}(0)=(0,0.01,\)\(0,-0.05,0)\). By simple computation, we have \(P=[0.8482, -0.5093; -0.5093, 1.0689]\), \(\lambda _{\max }(P)=1.4797\) and \(\lambda _{\min }(P)=0.4374\). The sampling period T is given as \(T=0.1s\). Figures 1 and 2 illustrate the trajectories of \(\left\| {\hat{W}} \right\| \) and \(\left\| {\hat{\theta }} \right\| \), respectively. In Figs. 3 and 4, the state estimation results of two unmeasurable states are presented, respectively. The trajectories of the state estimate errors and Lyapunov function V(t) are depicted in Figs. 5 and 6, respectively.

5 Conclusion

In this paper, a novel adaptive sampled-data observer design based on RBFNNs was proposed for nonlinear systems with unknown PI hysteresis and unknown unmatched disturbances. Firstly, RBFNNs were designed to approximate the unknown time-varying unmatched disturbances and unknown hysteresis of the systems. Then, a sampled-data observer was constructed to estimate the unmeasured states, and the learning laws of the weights of RBFNNs were also given. Based on a Lyapunov function and the corresponding sufficient conditions, we demonstrated that the observer errors were UUB. Finally, the effectiveness of the design scheme was verified by the illustrative simulation case. In the future, the developed adaptive sampled-data observer design method will be extended to the MIMO nonlinear systems with hysteresis and multiple uncertainties.