Distributed Pinning Impulsive Control for Inner–Outer Synchronization of Dynamical Networks on Time Scales

Abstract

In this paper, inner–outer synchronization problem of dynamical networks on time scales is studied. This kind of network synchronization means that two dynamical networks can achieve inner/outer synchronization simultaneously. By designing suitable distributed pinning impulsive controllers, the inner–outer synchronization target is realized. Based on the Lyapunov function method and the mathematical induction approach, two sufficient criteria are given for inner–outer synchronization of two networks with identical and non-identical topologies. Due to the structure of time scales, the derived results can be applied to study the inner–outer synchronization problems of continuous/discrete networks and networks on hybrid time domains. A numerical simulation example is given to illustrate the effectiveness of the derived results.

1 Introduction

It is well known that many practical systems in some fields, such as science, nature and engineering, can be described by models of complex networks [1,2,3,4,5,6,7,8,9]. As an interesting and important collective behavior of complex dynamical networks, synchronization inside a network, which is also called “inner synchronization”, has attracted considerable attention over the past years [10,11,12,13,14,15,16]. Besides, another kind of synchronization, named “outer synchronization” between two networks, was first proposed in [17]. In reality, the phenomenon of outer synchronization between two networks does exist in our lives, such as prey-predator communities [17] and AIDS [18]. Since then, a great number of results about outer synchronization between two networks have been obtained [19,20,21,22]. Unfortunately, outer synchronization between two networks dose not ensure that each network can achieve inner synchronization and vice versa. Moreover, the inner/outer synchronization problems of two networks are always studied separately. Then, a natural question is that can inner/outer synchronization between two dynamical networks be achieved simultaneously? To overcome this problem, this paper proposes a kind of network synchronization, called inner–outer synchronization.

Almost all of existing results were about continuous or discrete networks, and they were usually studied separately. However, different nodes in some networks can communicate with each other on an arbitrary time domain, so it is meaningful and necessary to study both continuous and discrete networks under a unform framework. In 1988, the time-scale theory was introduced by Stefan Hilger to unify the theory of difference equations and differential equations. To date, complex dynamical networks on time scales have received continued attention [23,24,25,26,27,28,29,30]. However, to the best of our knowledge, the existing results are only about inner synchronization of networks on time scales, therefore, numerous network synchronization problems on time scales remain to be further solved, such as achieving outer network synchronization on time scales, achieving inner and outer synchronization between two networks on time scales simultaneously, etc.

Recently, inner or outer network synchronization problems have been investigated with different control schemes, such as adaptive distributed control [31, 32], distributed impulsive control [33,34,35,36,37], pinning control [38,39,40], pinning impulsive control [30, 41], etc. In [41], the authors proposed a new control strategy, named pinning impulsive control, to solve stabilization problem of nonlinear time-varying time-delay dynamical networks. In [30], a different pinning impulsive control strategy was proposed to solve the synchronization problem of linear dynamical networks on time scales, in which the number of the nodes to be controlled at impulsive instants can be various. By designing an adaptive pinning impulsive controller, the outer synchronization problem between drive and response networks was investigated in [19].

Motivated by the aforementioned discussions, by designing proper distributed pinning impulsive controllers, this paper investigates the inner–outer synchronization problems of two dynamical networks with identical and non-identical topologies, which have never been studied before. The main contributions can be summarized as follows:

• (i) Different from the results in [23,24,25,26,27,28, 30], this paper first investigates inner–outer synchronization problem of dynamical networks on time scales, which means inner synchronization and outer synchronization can be achieved simultaneously. Moreover, by the proposed control strategies, inner synchronization and outer synchronization can be realized separately.

• (ii) Compared with the pinning impulsive control strategy in [30], the designed controllers here allow each distributed controller to use information from its neighboring nodes, which are more feasible to implement in some practical applications. In addition, the designed control schemes here require that only parts of nodes be chosen to be controlled at each impulsive instant, hence they can further reduce the control cost.

• (iii) The derived results are of generality, since they can be also applied to investigate the inner–outer synchronization problems of continuous/discrete networks and networks on hybrid time domains.

This paper is organized as follows: In Sect. 2, we recall some preliminary knowledge. In Sect. 3, the inner–outer synchronization problem of two dynamical networks on time scales is formulated. By designing suitable distributed pinning impulsive controllers, two inner–outer synchronization criteria for two dynamical networks with identical and non-identical topologies on time scales are given in Sect. 4. In Sect. 5, we give an illustrative simulation example, which is followed by a brief conclusion in Sect. 6.

Notations. In the sequel, the following notations will be used: $\mathbf {R}_{+}$, $\mathbf {Z}$, $\mathbf {N}$, $\mathbf {N_{+}}$ represent the set of all non-negative real numbers, the set of all integer numbers, the set of all natural numbers and the set of all positive integer numbers, respectively; $\mathbf {R}^{n}$ denotes the $n-$dimensional Euclidean space with the Euclidean norm $\parallel \cdot \parallel$; $\sharp M$ denotes the number of elements of a finite set M; $\overline{M}$ denotes the complementary set of the set M; $\mathbf {0}$ represents the null vector with proper dimension; the Kronecker product of matrices $X\in \mathbf {R}^{m\times n}$ and $Y\in \mathbf {R}^{p\times q}$ is denoted as $X\otimes Y\in \mathbf {R}^{mp\times nq}$; exp(z) represents the usual exponential function $e^{z}$. A matrix A satisfying $A>0$ means that it is positive definite.

2 Preliminaries

A time scale $\mathbf {T}$ is an arbitrary nonempty closed subset of the set of real numbers $\mathbf {R}$. When $t>\inf \mathbf {T}$, the backward jump operator $\rho :\mathbf {T}\rightarrow \mathbf {T}$ is defined as $\rho (t)=\sup \{s\in \mathbf {T}:s<t\}$; when $t<\sup \mathbf {T}$, the forward jump operator $\sigma :\mathbf {T}\rightarrow \mathbf {T}$ is defined as $\sigma (t)=\inf \{s\in \mathbf {T}:s>t\}$. If $\rho (t)<t$, t is said to be left-scattered; if $\rho (t)=t$, t is said to be left-dense; if $\sigma (t)>t$, t is said to be right-scattered; if $\sigma (t)=t$, t is said to be right-dense. The graininess function $\mu :\mathbf {T}\rightarrow \mathbf {R_{+}}$ is defined by $\mu (t):=\sigma (t)-t.$ Assume $g:\mathbf {T}\rightarrow \mathbf {R}$, if for any $\varepsilon >0$, there exists a constant $\delta >0$ and a neighborhood $U_{\mathbf {T}}(=U\bigcap \mathbf {T})$ of t, such that $\mid g(\sigma (t))-g(s) -\delta [\sigma (t)-s]\mid \le \varepsilon |\sigma (t)-s|,s\in U_{\mathbf {T}},$ then g is said to be $\varDelta$-differentiable at t, and the derivative is defined as $g^{\varDelta }(t)$.

Definition 1

[42] A function $g:\mathbf {T}\rightarrow \mathbf {R}$ is called rd-continuous provided it is continuous at right-dense points and its left-sided limits exist (finite) at left-dense points. The set of all rd-continuous functions $g:\mathbf {T}\rightarrow \mathbf {R}$ is denoted as $C_{rd}(\mathbf {T,\mathbf {R}})$.

Definition 2

[42] A function $q:\mathbf {T}\rightarrow \mathbf {R}$ is called regressive, if for all $t\in \mathbf {T}^{\kappa }, 1+\mu (t)q(t)\ne 0$, where the set $\mathbf {T}^{\kappa }$ is defined by the formula: $\mathbf {T}^{\kappa }=\mathbf {T}\setminus (\rho (\sup \mathbf {T}),\sup \mathbf {T}]$ if $\sup \mathbf {T}<\infty$ and left-scattered, and $\mathbf {T}^{\kappa }=\mathbf {T}$ if $\sup \mathbf {T}=\infty$. $\mathcal {R}=\mathcal {R} (\mathbf {T})=\mathcal {R}(\mathbf {T},\mathbf {R})$ denotes the set of all regressive and rd-continuous functions. A function $q:\mathbf {T}\rightarrow \mathbf {R}$ is called positive regressive, if for all $t\in \mathbf {T}^{\kappa },1+\mu (t)q(t)>0$. $\mathcal {R^{+}}=\mathcal {R^{+}}(\mathbf {T}) =\mathcal {R^{+}}(\mathbf {T},\mathbf {R})$ denotes the set of all positive regressive and rd-continuous functions.

Definition 3

[42] If $q\in \mathcal {R}$, then the exponential function is defined as $e_{q}(t,s)=\exp (\displaystyle {\int _{s}^{t}\xi _{\mu (\tau )}(q(\tau ))\varDelta \tau })$, where $s,t\in \mathbf {T}$, $\displaystyle {\xi _\mu (p) =\frac{1}{\mu } \log (1+\mu p)}$ if $\mu \ne 0$, $\xi _\mu (p)=p$ if $\mu =0$.

Lemma 1

[42] Let $g\in C_{rd}(\mathbf {T},\mathbf {R})$ and $q\in \mathcal {R^{+}}$. Then, for all $t\in \mathbf {T}$, $z^{\varDelta }(t)\le q(t)z(t)+g(t)$ implies that $z(t)\le z(t_{0})e_{q}(t,t_{0}) +\displaystyle {\int ^{t}_{t_{0}}}e_{q}(t,\sigma (s))g(s)\varDelta s$.

Lemma 2

[43] Let $U=(a_{ij})_{N\times N}$, $M\in \mathbf {R}^{n\times n}$, $x=(x_{1}^{T},\ldots ,x_{N}^{T})^{T}$, $y=(y_{1}^{T},\ldots ,y_{N}^{T})^{T}$, where $x_{i}=(x_{i1},\ldots ,x_{in})^{T}\in \mathbf {R}^{n}$ and $y_{i}=(y_{i1},\ldots ,y_{in})^{T}\in \mathbf {R}^{n}.$ If $U=U^{T}$, and each row sum of  U is zero, then

$$\begin{aligned} x^{T}(U\otimes M)y=-\displaystyle {\sum _{1\le i<j\le N}} a_{ij}(x_{i}-x_{j})^{T}M(y_{i}-y_{j}). \end{aligned}$$

3 Problem Statement

Consider the following two dynamical networks:

$$\begin{aligned} x^{\varDelta }_{i}(t)= & {} Ax_{i}(t)+\alpha \displaystyle {\sum _{j=1}^{N}}c_{ij}\varGamma x_{j}(t)+u_{i}, \end{aligned}$$

(1)

$$\begin{aligned} y^{\varDelta }_{i}(t)= & {} By_{i}(t)+\beta \displaystyle {\sum _{j=1}^{N}}d_{ij} \varGamma y_{j}(t)+v_{i}, \end{aligned}$$

(2)

where $i=1,2,\ldots ,N$; $t\in {\mathbf {T}}$, $\mathbf {T}$ is a time scale with $\sup \mathbf {T}=\infty$ and $\mu (t)\le \mu$, where $\mu (t)$ is the graininess function, and $\mu \ge 0$ is a constant; $x_{i}(t)=(x_{i1}(t),\ldots ,x_{in}(t))^{T} \in \mathbf {R}^{n}$, $y_{i}(t)=(y_{i1}(t),\ldots ,y_{in}(t))^{T}\in \mathbf {R}^{n}$ are the state vectors; matrices A, $B\in \mathbf {R}^{n\times n}$; $u_{i}$ and $v_{i}$ are the control inputs; $\varGamma =diag\{\alpha _{1}, \ldots ,\alpha _{n}\}>0$ is the matrix describing the inner-coupling between the subsystems at time t; $C=(c_{ij})_{N\times N}$, $D=(d_{ij})_{N\times N}$ are the coupling configuration matrices with zero-sum rows, and are defined as follows: if there is a connection from node j to node $i(i\ne j)$, $c_{ij}>0$, $d_{ij}>0$, otherwise $c_{ij}=0$, $d_{ij}=0$; $\alpha >0$, $\beta >0$ are the coupling strengthes.

Remark 1

According to the structure of time scales, different types of networks can be formulated. For example, when $\mathbf {T}=\mathbf {R}$ or $\mathbf {Z}$, networks (1) and (2) can be transformed into the following continuous or discrete forms:

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}_{i}(t) = Ax_{i}(t)+\alpha \displaystyle {\sum _{j=1}^{N}}c_{ij} \varGamma x_{j}(t)+u_{i},\\ \dot{y}_{i}(t) = By_{i}(t)+\beta \displaystyle {\sum _{j=1}^{N}}d_{ij} \varGamma y_{j}(t)+v_{i},~t\in \mathbf {R}. \end{array}\right. \\&\left\{ \begin{array}{l} \varDelta x_{i}(k) = Ax_{i}(k)+\alpha \displaystyle {\sum _{j=1}^{N}}c_{ij} \varGamma x_{j}(k)+u_{i},\\ \varDelta y_{i}(k) = By_{i}(k)+\beta \displaystyle {\sum _{j=1}^{N}}d_{ij} \varGamma y_{j}(k)+v_{i},~k\in \mathbf {Z}. \end{array}\right. \end{aligned}$$

Except for the continuous and discrete networks, other forms can be also formulated by networks (1) and (2), such as systems on nonuniform discrete time domains and systems with a mixed time.

Let $e_{i}(t)=y_{i}(t)-x_{i}(t)$. The existing results are mainly focused on two cases: (i) inner synchronization of a single dynamical network. (ii) outer synchronization between two dynamical networks without centering on inner synchronization of each network. Our goal is to design proper distributed pinning impulsive controllers that ensure networks (1) and (2) can achieve inner–outer synchronization. The definition of inner–outer synchronization for networks (1) and (2) is given as follows.

Definition 4

Networks (1) and (2) are said to be inner–outer synchronized if there exist suitable controllers, such that for all $i,j=1,2,\ldots ,N$, $\displaystyle {\lim _{t\rightarrow \infty }}\parallel x_{i}(t)-x_{j}(t)\parallel =0$, $\displaystyle {\lim _{t\rightarrow \infty }}\parallel y_{i}(t)-y_{j}(t)\parallel =0$, and $\displaystyle {\lim _{t\rightarrow \infty }}\parallel e_{i}(t)\parallel =0$.

Remark 2

It is obvious that only if the states trajectories of network (1) and error network converge to equilibriums, inner synchronization of network (2) can be achieved. Therefore, the main objective is to design proper controllers to guarantee inner synchronization of network (1) and outer synchronization between networks (1) and (2). Similarly, it is also feasible to design suitable controllers that ensure inner synchronization of network (2) and outer synchronization between networks (1) and (2). These two strategies are analogous, so we only consider the first case in this paper.

To ensure that networks (1) and (2) can achieve inner–outer synchronization, the distributed pinning impulsive controllers are designed as follows:

$$\begin{aligned} u_{i}= & {} \left\{ \begin{array}{l} \displaystyle {\sum _{k=0}^{\infty }}q_{1,k}\big (x_{i}(t) -\displaystyle {\sum _{j=1}^{N}}c_{ij}x_{j}(t)\big )\delta (t-t_{k}),~i\in \mathcal {D}_{k},\\ 0,~i\notin \mathcal {D}_{k}, \end{array}\right. \end{aligned}$$

(3)

$$\begin{aligned} v_{i}= & {} \left\{ \begin{array}{lcr} \displaystyle {\sum _{k=0}^{\infty }}\Big [q_{1,k}\big (y_{i}(t) -\displaystyle {\sum _{j=1}^{N}}d_{ij}y_{j}(t)\big )+q_{2,k}e_{i}(t)\Big ] \delta (t-t_{k}),i\in \mathcal {D}_{k},\\ 0,~i\notin \mathcal {D}_{k}, \end{array}\right. \end{aligned}$$

(4)

where $k\in \mathbf {N}$, the constants $q_{1,k}$ and $q_{2,k}$ are the impulsive control gains to be determined, and $\delta (\cdot )$ is the Dirac delta function; the impulsive instant sequence $\{t_{k}\}$ satisfies $\{t_{k}\}\in {\mathbf {T}}$, $0=t_{0}<t_{1}<\cdots<t_{k}<t_{k+1}<\cdots$, and $\displaystyle {\lim _{k\rightarrow \infty }}t_{k}=\infty$; the index set $\mathcal {D}_{k}$ is defined as follows: if the nodes $x_{i}$ and $y_{i}$ are chosen to be controlled at $t_{k}$, then $i\in \mathcal {D}_{k}$ and $\sharp \mathcal {D}_{k}=l_{k}$, where $l_{k}\le N$.

Remark 3

In the distributed pinning impulsive control schemes (3) and (4), each node is allowed to utilize the information from its neighboring nodes, and only $l_{k}$ nodes need to be controlled at each impulsive instant, so the designed controllers (3) and (4) are practically more feasible to implement than those control strategies in [30, 35, 36].

By the controller (3), network (1) can be transformed into the following form:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\varDelta }_{i}(t) = Ax_{i}(t)+\alpha \displaystyle {\sum _{j=1}^{N}}c_{ij} \varGamma x_{j}(t),~t\ne t_{k},\\ \varDelta x_{i}(t_{k}) = q_{1,k}(x_{i}(t_{k})-\displaystyle {\sum _{j=1}^{N}} c_{ij}x_{j}(t_{k})),~i\in \mathcal {D}_{k}, \end{array}\right. \end{aligned}$$

(5)

and by the controllers (3) and (4), the error network is formulated as follows:

$$\begin{aligned} \left\{ \begin{aligned} e^{\varDelta }_{i}(t)&= By_{i}(t)-Ax_{i}(t)+\displaystyle {\sum _{j=1}^{N}} \big [\beta d_{ij}\varGamma y_{j}(t)-\alpha c_{ij}\varGamma x_{j}(t)\big ],~t\ne t_{k},\\ \varDelta e_{i}(t_{k})&= q_{1,k}(y_{i}(t_{k}) -\displaystyle {\sum _{j=1}^{N}}d_{ij}y_{j}(t_{k}))+q_{2,k}e_{i}(t_{k})\\&\quad -q_{1,k}(x_{i}(t_{k})-\displaystyle {\sum _{j=1}^{N}}c_{ij}x_{j}(t_{k})), ~i\in \mathcal {D}_{k}, \end{aligned}\right. \end{aligned}$$

(6)

where $\varDelta x_{i}(t_{k})=x_{i}(t_{k}^{+})-x_{i}(t_{k}^{-})$, $\varDelta e_{i}(t_{k})=e_{i}(t_{k}^{+})-e_{i}(t_{k}^{-})$. In this paper, we assume that for all $k\in \mathbf {N}$, $x_{i}(t_{k}^{-})=x_{i}(t_{k})$, $y_{i}(t_{k}^{-})=y_{i}(t_{k})$, which clearly yield $e_{i}(t_{k}^{-})=e_{i}(t_{k})$.

Let $x=(x^{T}_{1},\ldots ,x^{T}_{N})^{T}$, $e=(e^{T}_{1}, \ldots ,e^{T}_{N})^{T}$ and $\vartheta =(\upsilon _{ij})_{Nn\times Nn}$ be a diagonal matrix with $\upsilon _{ii}$ equaling 1 if $i\in \mathcal {D}_{k}$ and $\upsilon _{ii}$ equaling 0 otherwise. Then, $x=x_{\mathcal {D}_{k}}+x_{\overline{{\mathcal {D}}}_{k}}$, $e=e_{\mathcal {D}_{k}}+e_{\overline{{\mathcal {D}}}_{k}}$, where $x_{\mathcal {D}_{k}}=\vartheta x$, $e_{\mathcal {D}_{k}}=\vartheta e$. By this decomposition, systems (5) and (6) can be rewritten as the following forms.

$$\begin{aligned}&\left\{ \begin{aligned} x^{\varDelta }(t)&=(I_{N}\otimes A+\alpha (C\otimes \varGamma ))x(t)\\&=\varPhi _{1}x(t),t\ne t_{k},\\ \varDelta x_{\mathcal {D}_{k}}(t_{k})&=q_{1,k}\vartheta (I_{Nn}-C\otimes I_{n})x(t_{k})\\&=q_{1,k}\varPhi _{3}x(t_{k}), \end{aligned}\right. \end{aligned}$$

(7)

$$\begin{aligned}&\left\{ \begin{aligned} e^{\varDelta }(t)&=[I_{N}\otimes B+\beta (D\otimes \varGamma )]e(t)\\&\quad +[I_{N}\otimes (B-A)+\beta (D\otimes \varGamma )-\alpha (C\otimes \varGamma )]x(t)\\&=\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t),t\ne t_{k},\\ \varDelta e_{\mathcal {D}_{k}}(t_{k})&=q_{1,k}\vartheta ((C-D)\otimes I_{n})x(t_{k})\\&\quad +\vartheta \big [q_{1,k}(I_{Nn}-D\otimes I_{n})+q_{2,k}I_{Nn}\big ]e(t_{k})\\&=q_{1,k}(\varPhi _{4}-\varPhi _{3})x(t_{k})+(q_{1,k}\varPhi _{4}+q_{2,k}\vartheta )e(t_{k}), \end{aligned}\right. \end{aligned}$$

(8)

where $\varPhi _{1}=I_{N}\otimes A+\alpha (C\otimes \varGamma )$, $\varPhi _{2}=I_{N}\otimes B+\beta (D\otimes \varGamma )$, $\varPhi _{3}=\vartheta (I_{Nn}-C\otimes I_{n})$ and $\varPhi _{4}=\vartheta (I_{Nn}-D\otimes I_{n})$.

For simplifying the presentation, in the sequel, we let $H^{\star }=H^{T}H$ and $H^{*}=H^{T}+H$ for any matrix H.

4 Main Results

In this section, by the controllers (3) and (4), we firstly study the inner–outer synchronization problem of networks (1) and (2) with non-identical topologies (i.e. $C\ne D)$. A sufficient condition is given as follows:

Theorem 1

Networks (1) and (2) can achieve inner–outer synchronization by the controllers (3) and (4), if there exist three positive constants $\theta$, $\gamma$, $\varepsilon$, two sets of positive constants $\{\eta _{k}\}$ and $\{b_{k}\}$, $k\in \mathbf {N}$, such that the following inequalities hold:

$$\begin{aligned}&(\varPhi ^{T}_{1}\varOmega )^{*}+\mu \varPhi ^{T}_{1}\varOmega \varPhi _{1} +\frac{1+\mu +\mu \theta }{\theta }(\varPhi _{2} -\varPhi _{1})^{\star }-\varepsilon \varOmega \le 0, \end{aligned}$$

(9)

$$\begin{aligned}&\varPhi _{2}^{*}+\mu (1+\theta )\varPhi _{2}^{\star } +(\theta -\varepsilon )I_{Nn}\le 0, \end{aligned}$$

(10)

$$\begin{aligned}&(q_{1,k}\varPhi _{3}+I_{Nn})^{T}\varOmega (q_{1,k}\varPhi _{3}+I_{Nn})\nonumber \\&\quad +\left( q^{2}_{1,k}+\frac{q_{1,k}}{\theta }\right) (\varPhi _{4}-\varPhi _{3})^{\star } -\eta _{k}\varOmega \le 0, \end{aligned}$$

(11)

$$\begin{aligned}&(1+\theta q_{1,k})(q_{1,k}\varPhi _{4}+q_{2,k}\vartheta +I_{Nn})^{\star } -\eta _{k}I_{Nn}\le 0, \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle {\frac{b_{k}}{b_{k+1}}}\eta _{k}e_{\varepsilon }(t_{k+1},t_{k}) exp(\gamma (t_{k+1}-t_{k}))\le 1, \end{aligned}$$

(13)

where $\varPhi _{i}(i=1,\ldots ,4)$ are given in (8), $\varOmega =U\otimes I_{n}$, and

$$\begin{aligned} U=\left( \begin{array}{cccc} N-1 &{} -1 &{} \cdots &{} -1 \\ -1 &{} N-1 &{} \cdots &{} -1 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ -1 &{} -1 &{} \cdots &{} N-1 \\ \end{array}\right) _{N\times N}. \end{aligned}$$

Proof

Construct the Lyapunov function $V(t)=V_{1}(t)+V_{2}(t)$, where $V_{1}(t)=x^{T}(t)\varOmega x(t)$, $V_{2}(t)=e^{T}(t)e(t)$. When $t\ne t_{k}$, by calculating the $\varDelta -$derivative of $V_{i}(t)~(i=1,2)$ along the trajectories of systems (7) and (8), we have from Theorem 1.20 in [42] that

$$\begin{aligned} V^{\varDelta }_{1}(t)= & {} {{(x^{T}(t))^{\varDelta }\varOmega x(\sigma (t)) +x^{T}(t)\varOmega x^{\varDelta }(t)}} \\= & {} {{(x^{T}(t))^{\varDelta }\varOmega (x(t)+\mu (t)x^{\varDelta }(t)) +x^{T}(t)\varOmega x^{\varDelta }(t)}} \\= & {} x^{T}(t)\varOmega x^{\varDelta }(t)+(x^{T}(t))^{\varDelta }\varOmega x(t) +\mu (t)(x^{\varDelta }(t))^{T}\varOmega x^{\varDelta }(t) \\= & {} x^{T}(t)\varOmega \varPhi _{1}x(t)+x^{T}(t)\varPhi ^{T}_{1}\varOmega x(t) +\mu (t)x^{T}(t)\varPhi ^{T}_{1}\varOmega \varPhi _{1}x(t), \\ V^{\varDelta }_{2}(t)= & {} e^{T}(t)e^{\varDelta }(t)+(e^{T}(t))^{\varDelta }e(t) +\mu (t)(e^{\varDelta }(t))^{T}e^{\varDelta }(t) \\= & {} e^{T}(t)\big [\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t)\big ] \\&+\,\big [\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t)\big ]^{T}e(t) +\mu (t)\big [\varPhi _{2}e(t) \\&+\,(\varPhi _{2}-\varPhi _{1})x(t)\big ]^{T}\big [\varPhi _{2}e(t) +(\varPhi _{2}-\varPhi _{1})x(t)\big ] \\= & {} e^{T}(t)(\varPhi _{2}+\varPhi ^{T}_{2})e(t)+2e^{T}(t)(\varPhi _{2}-\varPhi _{1})x(t) \\&+\,\mu (t)\big [e^{T}(t)\varPhi ^{T}_{2}\varPhi _{2}e(t)+2e^{T}(t) \varPhi ^{T}_{2}(\varPhi _{2}-\varPhi _{1})x(t) \\&+\,x^{T}(t)(\varPhi _{2}-\varPhi _{1})^{T}(\varPhi _{2}-\varPhi _{1})x(t)\big ]. \end{aligned}$$

According to the fact that $x^{T}y+y^{T}x\le \theta x^{T}x+\frac{1}{\theta }y^{T}y$, where $\theta >0$, and by (9)-(10), we can get

$$\begin{aligned} V^{\varDelta }(t)\le \varepsilon V(t). \end{aligned}$$

(14)

From (7), (8), and (11), (12) we can get

$$\begin{aligned} V(t^{+}_{k})= & {} x^{T}(t^{+}_{k})\varOmega x(t^{+}_{k}) +e^{T}(t^{+}_{k})e(t^{+}_{k}) \nonumber \\= & {} x^{T}(t_{k})(q_{1,k}\varPhi _{3}+I_{Nn})^{T} \varOmega (q_{1,k}\varPhi _{3}+I_{Nn})x(t_{k}) \nonumber \\&+\,q^{2}_{1,k}x^{T}(t_{k})(\varPhi _{4}-\varPhi _{3})^{T}(\varPhi _{4}-\varPhi _{3})x(t_{k}) \nonumber \\&+\,e^{T}(t_{k})(q_{1,k}\varPhi _{4}+q_{2,k}\vartheta +I_{Nn})^{T}(q_{1,k}\varPhi _{4} \nonumber \\&+\,q_{2,k}\vartheta +I_{Nn})e(t_{k})+2q_{1,k}x^{T}(t_{k})(\varPhi _{4}-\varPhi _{3})^{T} \nonumber \\&\times \,(q_{1,k}\varPhi _{4}+q_{2,k}\vartheta +I_{Nn})e(t_{k}) \nonumber \\\le & {} \eta _{k}V(t_{k}). \end{aligned}$$

(15)

By Lemma 1, (14) and (15), we can get that for all $t\in (t_{k},t_{k+1})_{\mathbf {T}}$,

$$\begin{aligned} V(t)\le & {} e_{\varepsilon }(t,t^{+}_{k})V(t^{+}_{k}) \\\le & {} \eta _{k}e_{\varepsilon }(t,t^{+}_{k})V(t_{k}). \end{aligned}$$

Since $\varepsilon >0$, we have

$$\begin{aligned} e_{\varepsilon }(t,t^{+}_{k})=e_{\varepsilon }(t,\sigma (t_{k})) \le e_{\varepsilon }(t,t_{k}). \end{aligned}$$

Thus,

$$\begin{aligned} V(t)\le \eta _{k}e_{\varepsilon }(t,t_{k})V(t_{k}). \end{aligned}$$

For $t=t_{k+1}$, if $t_{k+1}$ is left dense, then

$$\begin{aligned} V(t_{k+1})\le & {} \displaystyle {\lim _{t\rightarrow t^{-}_{k+1}}} \eta _{k}e_{\varepsilon }(t,t_{k})V(t_{k}) \\= & {} \eta _{k}e_{\varepsilon }(t_{k+1},t_{k})V(t_{k}). \end{aligned}$$

If $t_{k+1}$ is left scattered, then

$$\begin{aligned} V(t_{k+1})= & {} V(\rho (t_{k+1}))+\mu (\rho (t_{k+1}))V^{\varDelta }(\rho (t_{k+1})) \\\le & {} \big [1+\varepsilon \mu (\rho (t_{k+1}))\big ]V(\rho (t_{k+1})) \\= & {} e_{\varepsilon }(t_{k+1},\rho (t_{k+1}))V(\rho (t_{k+1})) \\\le & {} \eta _{k}e_{\varepsilon }(\rho (t_{k+1}),t_{k}) e_{\varepsilon }(t_{k+1},\rho (t_{k+1}))V(t_{k}) \\= & {} \eta _{k}e_{\varepsilon }(t_{k+1},t_{k})V(t_{k}). \end{aligned}$$

Thus, for all $t\in (t_{k},t_{k+1}]_{\mathbf {T}}$,

$$\begin{aligned} V(t)\le \eta _{k}e_{\varepsilon }(t,t_{k})V(t_{k}). \end{aligned}$$

(16)

Let $\gamma _{0}=exp(\gamma t_{1})\sup _{t \in [0,t_{1}]_{\mathbf {T}}}V(t)$. Then, for all $t\in [0,t_{1}]_{\mathbf {T}}$, we have $V(t)\le \gamma _{0}exp(-\gamma t)$.

For $t\in (t_{1},t_{2}]_{\mathbf {T}}$, by (13) and (16) we can get

$$\begin{aligned} V(t)\le & {} \eta _{1}e_{\varepsilon }(t,t_{1})V(t_{1}) \\\le & {} \gamma _{0}\eta _{1}exp(-\gamma t_{1})e_{\varepsilon }(t,t_{1}) \\\le & {} \gamma _{0}e_{\varepsilon }(t,t_{1})\displaystyle {\frac{b_{2} exp(-\gamma t_{2})}{b_{1}e_{\varepsilon }(t_{2},t_{1})}} \\= & {} \displaystyle {\frac{b_{2}\gamma _{0}exp(-\gamma t_{2})}{b_{1} e_{\varepsilon }(t_{2},t)}}. \end{aligned}$$

Next, by the mathematical induction approach, we will prove that for all $t\in (t_{k},t_{k+1}]_{\mathbf {T}}$, $k\in \mathbf {N_{+}}$,

$$\begin{aligned} V(t)\le \displaystyle {\frac{b_{k+1}\gamma _{0} exp(-\gamma t_{k+1})}{b_{1}e_{\varepsilon }(t_{k+1},t)}}. \end{aligned}$$

(17)

Suppose for all $t\in (t_{k},t_{k+1}]_{\mathbf {T}}$ and $k\le m$ ($m\in \mathbf {N_{+}}$), (17) holds. For $k=m+1$ and $t\in (t_{m+1},t_{m+2}]_{\mathbf {T}}$, by (13) and (16), we can get

$$\begin{aligned} V(t)\le & {} \eta _{m+1}e_{\varepsilon }(t,t_{m+1})V(t_{m+1}) \\\le & {} \displaystyle {\frac{b_{m+1}}{b_{1}}}\gamma _{0}\eta _{m+1} exp(-\gamma t_{m+1})e_{\varepsilon }(t,t_{m+1}) \\\le & {} \gamma _{0}e_{\varepsilon }(t,t_{m+1})\displaystyle {\frac{b_{m+2} exp(-\gamma t_{m+2})}{b_{1}e_{\varepsilon }(t_{m+2},t_{m+1})}} \\= & {} \displaystyle {\frac{b_{m+2}\gamma _{0}exp(-\gamma t_{m+2})}{b_{1} e_{\varepsilon }(t_{m+2},t)}}. \end{aligned}$$

Thus, for all $t\in (t_{k},t_{k+1}]_{\mathbf {T}}$, $k\in \mathbf {N_{+}}$, (17) holds, which implies

$$\begin{aligned} V(t)\le & {} \displaystyle {\frac{b_{k+1}\gamma _{0} exp(-\gamma t_{k+1})}{b_{1}e_{\varepsilon }(t_{k+1},t)}} \\\le & {} \displaystyle {\frac{b_{k+1}\gamma _{0}exp(-\gamma t_{k+1})}{b_{1}}} \\\le & {} \displaystyle {\frac{b_{k+1}\gamma _{0}exp(-\gamma t)}{b_{1}}}, \end{aligned}$$

and hence we can get $\displaystyle {\lim _{t\rightarrow \infty }}V(t)=0$.

By Lemma 2 we have, for all $i,j=1,2,\ldots ,N$,

$$\begin{aligned}&\displaystyle {\sum _{1\le i<j\le N}}\parallel x_{i}(t)-x_{j}(t))\parallel ^{2} +\displaystyle {\sum _{i=1}^{N}}\parallel e_{i}(t)\parallel ^{2} \\&\qquad =\displaystyle {\sum _{1\le i<j\le N}}(x_{i}(t) -x_{j}(t))^{T}(x_{i}(t)-x_{j}(t))+e^{T}(t)e(t) \\&\qquad =x^{T}(t)(U\otimes I_{2})x(t)+e^{T}(t)e(t) \\&\qquad = V(t) \end{aligned}$$

which implies $\displaystyle {\lim _{t\rightarrow \infty }}\parallel x_{i}(t)-x_{j}(t)\parallel =0$ and $\displaystyle {\lim _{t\rightarrow \infty }}\parallel e_{i}(t)\parallel =0$ for all $i,j=1,2,\ldots ,N$. The proof is thus completed. $\square$

The result in Theorem 1 is concerned with two networks with non-identical topologies (i.e. $C\ne D)$. For networks (1) and (2) with identical topologies (i.e. $C=D)$, a sufficient condition can be similarly obtained if the inequality (9)–(13) are changed into the corresponding forms.

Theorem 2

Networks (1) and (2) can achieve inner–outer synchronization by the controllers (3) and (4), if there exist three positive constants $\theta$, $\gamma$, $\varepsilon$, two sets of positive constants $\{\eta _{k}\}$ and $\{b_{k}\}$, $k\in \mathbf {N}$, such that the following inequalities hold:

$$\begin{aligned}&(\varPhi ^{T}_{1}\varOmega )^{*}+\mu \varPhi ^{T}_{1}\varOmega \varPhi _{1} +\frac{1+\mu +\mu \theta }{\theta }(\varPhi _{2} -\varPhi _{1})^{\star }-\varepsilon \varOmega \le 0, \end{aligned}$$

(18)

$$\begin{aligned}&\varPhi _{2}^{*}+\mu (1+\theta )\varPhi _{2}^{\star } +(\theta -\varepsilon )I_{Nn}\le 0, \end{aligned}$$

(19)

$$\begin{aligned}&(q_{1,k}\varPhi _{3}+I_{Nn})^{T}\varOmega (q_{1,k} \varPhi _{3}+I_{Nn})-\eta _{k}\varOmega \le 0, \end{aligned}$$

(20)

$$\begin{aligned}&(1+\theta q_{1,k})(q_{1,k}\varPhi _{3}+q_{2,k}\vartheta +I_{Nn})^{\star } -\eta _{k}I_{Nn}\le 0, \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle {\frac{b_{k}}{b_{k+1}}}\eta _{k}e_{\varepsilon } (t_{k+1},t_{k})exp(\gamma (t_{k+1}-t_{k}))\le 1, \end{aligned}$$

(22)

where $\varPhi _{i}(i=1,\ldots ,3)$ are given in (8), $\varOmega =U\otimes I_{n}$, and U is defined in Theorem 1.

Proof

The proof can be directly derived from Theorem 1, so it is omitted here. $\square$

Remark 4

According to the statement in Remark 1, networks (1) and (2) are of generality and can be transformed into other forms, thus, the sufficient criteria of Theorem 1 and Theorem 2 are also effective for the inner–outer synchronization problems of different types of networks. For the case $\mathbf {T}=\mathbf {R}$, $\mu (t)\equiv 0$, $e_{\varepsilon }(t_{k+1},t_{k})=e^{\varepsilon (t_{k+1}-t_{k})}$; for the case $\mathbf {T}=h\mathbf {Z}$, $h>0$ is a constant, $\mu (t)\equiv h$, $e_{\varepsilon }(t_{k+1},t_{k}) =(1+h\varepsilon )^{\frac{t_{k+1}-t_{k}}{h}}$.

Remark 5

It is noted that the configuration matrices C and D need not be symmetric, diffusive, or irreducible, which means that networks (1) and (2) can be undirected or directed, and may also contain isolated nodes or clusters.

The results in Theorem 1 and Theorem 2 are concerned about the situation that the two dynamical networks (1) and (2) can achieve inner/outer synchronization simultaneously, for the cases that inner synchronization of network (1) and outer synchronization between networks (1) and (2), we have the following two corollaries.

Corollary 3

Network (1) can achieve inner by the controller (3), if there exist two positive constants $\gamma$, $\varepsilon$, two sets of positive constants $\{\eta _{k}\}$ and $\{b_{k}\}$, $k\in \mathbf {N}$, such that the following inequalities hold:

$$\begin{aligned}&(\varPhi ^{T}_{1}\varOmega )^{*}+\mu \varPhi ^{T}_{1} \varOmega \varPhi _{1}-\varepsilon \varOmega \le 0, \end{aligned}$$

(23)

$$\begin{aligned}&(q_{1,k}\varPhi _{3}+I_{Nn})^{T}\varOmega (q_{1,k}\varPhi _{3} +I_{Nn})-\eta _{k}\varOmega \le 0, \end{aligned}$$

(24)

$$\begin{aligned}&\displaystyle {\frac{b_{k}}{b_{k+1}}}\eta _{k} e_{\varepsilon }(t_{k+1},t_{k})exp(\gamma (t_{k+1}-t_{k}))\le 1, \end{aligned}$$

(25)

where $\varPhi _{1}$ and $\varPhi _{3}$ are given in (8), $\varOmega =U\otimes I_{n}$, and U is defined in Theorem 1.

Proof

Construct the Lyapunov function candidate $V(t)=x^{T}(t)\varOmega x(t)$. When $t\ne t_{k}$, by calculating the $\varDelta -$derivative of V(t) along the trajectories of systems (7), we have

$$\begin{aligned} V^{\varDelta }(t)= & {} x^{T}(t)\varOmega x^{\varDelta }(t)+(x^{T}(t))^{\varDelta }\varOmega x(t)\\&+\,\mu (t)(x^{\varDelta }(t))^{T}\varOmega x^{\varDelta }(t) \\= & {} x^{T}(t)\varOmega \varPhi _{1}x(t)+x^{T}(t)\varPhi ^{T}_{1}\varOmega x(t) \\&+\,\mu (t)x^{T}(t)\varPhi ^{T}_{1}\varOmega \varPhi _{1}x(t). \end{aligned}$$

By (23), we can get

$$\begin{aligned} V^{\varDelta }(t)\le \varepsilon V(t). \end{aligned}$$

From (7), (8), and (24) we can get

$$\begin{aligned} V(t^{+}_{k})= & {} x^{T}(t^{+}_{k})\varOmega x(t^{+}_{k}) \\= & {} x^{T}(t_{k})(q_{1,k}\varPhi _{3}+I_{Nn})^{T}\varOmega (q_{1,k}\varPhi _{3}+I_{Nn})x(t_{k}) \\\le & {} \eta _{k}V(t_{k}). \end{aligned}$$

The rest proof is similar to that of Theorem 1, so it is omitted here. $\square$

Corollary 4

Networks (1) and (2) can achieve outer synchronization by the controller (4) with $q_{1,k}=0$ for any k, if there exist three positive constants $\theta$, $\gamma$, $\varepsilon$, two sets of positive constants $\{\eta _{k}\}$ and $\{b_{k}\}$, $k\in \mathbf {N}$, such that the following inequalities hold:

$$\begin{aligned}&\frac{1+\mu +\mu \theta }{\theta } (\varPhi _{2}-\varPhi _{1})^{\star }-\varepsilon \varOmega \le 0, \end{aligned}$$

(26)

$$\begin{aligned}&\varPhi _{2}^{*}+\mu (1+\theta )\varPhi _{2}^{\star } +(\theta -\varepsilon )I_{Nn}\le 0, \end{aligned}$$

(27)

$$\begin{aligned}&(q_{2,k}\vartheta +I_{Nn})^{\star }-\eta _{k}I_{Nn}\le 0, \end{aligned}$$

(28)

$$\begin{aligned}&\displaystyle {\frac{b_{k}}{b_{k+1}}}\eta _{k}e_{\varepsilon } (t_{k+1},t_{k})exp(\gamma (t_{k+1}-t_{k}))\le 1, \end{aligned}$$

(29)

where $\varPhi _{1}$ and $\varPhi _{2}$ are given in (8), $\varOmega =U\otimes I_{n}$, and U is defined in Theorem 1. $\square$

Proof

Construct the Lyapunov function candidate $V(t)=e^{T}(t)e(t)$. When $t\ne t_{k}$, by calculating the $\varDelta -$derivative of V(t) along the trajectories of systems (8), we have

$$\begin{aligned} V^{\varDelta }(t)= & {} e^{T}(t)e^{\varDelta }(t)+(e^{T}(t))^{\varDelta }e(t) +\mu (t)(e^{\varDelta }(t))^{T}e^{\varDelta }(t) \\= & {} e^{T}(t)\big [\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t)\big ] \\&+\,\big [\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t)\big ]^{T}e(t) +\mu (t)\big [\varPhi _{2}e(t) \\&+\,(\varPhi _{2}-\varPhi _{1})x(t)\big ]^{T}\big [\varPhi _{2}e(t)+(\varPhi _{2}-\varPhi _{1})x(t)\big ] \\= & {} e^{T}(t)(\varPhi _{2}+\varPhi ^{T}_{2})e(t)+2e^{T}(t)(\varPhi _{2}-\varPhi _{1})x(t) \\&+\,\mu (t)\big [e^{T}(t)\varPhi ^{T}_{2}\varPhi _{2}e(t) +2e^{T}(t)\varPhi ^{T}_{2}(\varPhi _{2}-\varPhi _{1})x(t) \\&+\,x^{T}(t)(\varPhi _{2}-\varPhi _{1})^{T}(\varPhi _{2}-\varPhi _{1})x(t)\big ]. \end{aligned}$$

According to the fact that $x^{T}y+y^{T}x\le \theta x^{T}x+\frac{1}{\theta }y^{T}y$, where $\theta >0$, and by (26) and (27), we can get

$$\begin{aligned} V^{\varDelta }(t)\le \varepsilon V(t). \end{aligned}$$

From (7), (8), and (28) we can get

$$\begin{aligned} V(t^{+}_{k})= & {} e^{T}(t^{+}_{k})e(t^{+}_{k}) \\= & {} e^{T}(t_{k})(q_{2,k}\vartheta +I_{Nn})^{T}(q_{2,k}\vartheta +I_{Nn})e(t_{k}) \\\le & {} \eta _{k}V(t_{k}). \end{aligned}$$

The rest proof is similar to that of Theorem 1, so it is omitted here. $\square$

5 An Example

In this section, we give a simulation example to illustrate the effectiveness of the theoretical results.

Consider dynamical networks (1) and (2) with $n=2$, $N=5$, $\alpha =\beta =0.1$,

$$\begin{aligned}&A=B=\left( \begin{array}{cc} -4.8 &{} -0.65 \\ -0.25 &{} -5 \\ \end{array} \right) ,~{\varGamma =\left( \begin{array}{cc} 1 &{}~ 0 \\ 0 &{}~ 1 \\ \end{array}\right) },\\&C=\left( \begin{array}{ccccc} -0.9 &{} 0 &{} 0 &{} 0.3 &{} 0.6 \\ 0.2 &{} -0.8 &{} 0 &{} 0.4 &{} 0.2 \\ 0 &{} 0.3 &{} -0.7 &{} 0.4 &{} 0 \\ 0.3 &{} 0 &{} 0.2 &{} -0.6 &{} 0.1 \\ 0.1 &{} 0 &{} 0 &{} 0.4 &{} -0.5 \\ \end{array} \right) ,~D=\left( \begin{array}{ccccc} -0.5 &{} 0.3 &{} 0.1 &{} 0 &{} 0.1 \\ 0.2 &{} -0.6 &{} 0.2 &{} 0.2 &{} 0 \\ 0.4 &{} 0 &{} -0.7 &{} 0.3 &{} 0 \\ 0 &{} 0.5 &{} 0.1 &{} -0.8 &{} 0.2 \\ 0.6 &{} 0.3 &{} 0 &{} 0 &{} -0.9 \\ \end{array}\right) , \end{aligned}$$

the time scale is given as $\mathbf {T} =\displaystyle {\bigcup _{j\in \mathbf {Z}}[0.5j-0.1,0.5j+0.1]}$, then, the graininess function $\mu (t)$ is given as follows:

$$\begin{aligned} \begin{array}{rcl} \mu (t)=\left\{ \begin{array}{ll} 0,&{}t\in \displaystyle {\bigcup _{j\in \mathbf {Z}}}[0.5j-0.1,0.5j+0.1),\\ 0.3,&{}t=0.5j+0.1,~j\in \mathbf {Z}. \end{array}\right. \end{array} \end{aligned}$$

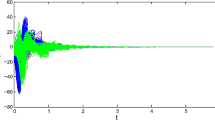
Given initial values $x_{1}(0)=(0.1,0.2)^{T}$, $x_{2}(0)=-x_{5}(0)=(-0.1,-0.1)^{T}$, $x_{3}(0)=x_{4}(0)=(0.1,-0.1)^{T}$, $y_{1}(0)=y_{3}(0)=y_{5}(0)=(0.1,-0.1)^{T}$, $y_{2}(0)=-y_{4}(0)=(-0.1,-0.1)^{T}$. Figures 1 and 2 show the states trajectories of networks (1) and (2) without any control, from which we can see that inner synchronization of network (1) and outer synchronization between networks (1) and (2) are not achieved.

To ensure networks (1) and (2) can achieve inner–outer synchronization, we design the distributed pinning impulsive controllers (3) and (4) with the control gains $q_{1,2k}=-0.005$, $q_{1,2k+1}=-0.45$ and $q_{2,2k}=-0.1$, $q_{2,2k+1}=-0.25$, and according to the form in [30], the impulsive sequence is chosen as $t_{k}=0.5k~(k\in \mathbf {N})$. Let $l_{2k}=3$, $l_{2k+1}=5$, which means that 3 nodes are controlled at impulsive instants $t_{2k}$, and 5 nodes are controlled at impulsive instants $t_{2k+1}$. In the designed control scheme, the nodes $x_{i}$ and $y_{i}~(i=1,3,5)$ are chosen to be controlled at $t_{2k}$, and the nodes $x_{i}$, $y_{i}~(i=1,\ldots ,5)$ are selected to be controlled at $t_{2k+1}$.

By using the Matlab LMI Toolbox to solve the inequalities in Theorem 1, we can get $\theta =0.05$, $\gamma =0.01$, $\varepsilon =0.1$, $\eta _{2k}=3$, $\eta _{2k+1}=0.25$, accordingly, $b_{2k}=3$, $b_{2k+1}=10~(k\in \mathbf {N})$. Therefore, networks (1) and (2) can achieve inner–outer synchronization under the designed distributed pinning impulsive controllers, see Figs. 3and 4 for illustration.

Fig. 1

Trajectories $\parallel x_{i}(t)-x_{j}(t)\parallel ~(i,j=1,\ldots ,5)$ of network (1) without control

Fig. 2

Trajectories $\parallel e_{i}(t)\parallel ~(i=1,\ldots ,5)$ between networks (1) and (2) without control

Fig. 3

Trajectories $\parallel x_{i}(t)-x_{j}(t)\parallel ~(i,j=1,\ldots ,5)$ of closed-loop network (5)

Fig. 4

Trajectories $\parallel e_{i}(t)\parallel ~(i=1,\ldots ,5)$ of closed-loop network (6)

6 Conclusion

In this paper, we have proposed a kind of network synchronization, called inner–outer synchronization. Two dynamical networks achieving inner–outer synchronization means that each of them can achieve inner synchronization, and outer synchronization between them can be also achieved. By designing suitable distributed pinning impulsive controllers, we have studied the inner–outer synchronization problems of two dynamical networks with identical and non-identical topologies on time scales. According to the theory of time scales, by using the Lyapunov function method and the mathematical induction approach, we have established two sufficient conditions for inner–outer synchronization of two networks on time scales. It has been shown that the results in this paper are applicable to not only discrete/continuous dynamical networks, but also the cases on hybrid time domains. To illustrate the effectiveness of our results, a simulation example has been given. In the future works, we will consider the effect of time delay on the synchronization results.