1 Introduction

Recently, it’s reported that discontinuous neural networks (DNNs) are successfully used to engineering tasks including dry friction, power circuits, switching in electronic circuits and so on [1,2,3]. In addition, when dealing with neural networks (NNs) with high-slope nonlinear elements, it’s often advantageous to model them with discontinuous neuron activation functions, rather than to study the case where the slope is high but of finite value [4]. Moreover, DNNs are ideal models for solving linear or nonlinear programming problems and constrained optimization problems [5,6,7,8]. So, it’s worth studying DNNs and its dynamical behaviors.

Synchronization of NNs has received considerable attention in recent years due to its potential applications [9,10,11,12,13,14,15,16,17,18]. Especially, there exist many interesting works concerning synchronization of DNNs [13,14,15,16,17,18]. To our knowledge, the Filippov solution is an effective tool for investigating synchronization of DNNs. For example, under the framework of Filippov solution, authors in [13, 15] studied the quasi-synchronization issue for the delayed DNNs. By designing a discontinuous controller which includes sign function, complete synchronization of DNNs was analyzed in [16]. The main difficulty in studying complete synchronization of DNNs is how to deal with the effects of nonidentical uncertainties of Filippov solutions. Actually, the sign function in controller plays an extremely pivotal role when complete synchronization problem for DNNs is studied. For instance, two kinds of controllers with sign function were designed to achieve exponential synchronization of DNNs with time-varying mixed delays in [17]. But, it’s well known that sign function always introduce chattering phenomenon to the system state and controlled signals which causes the bad influence or even damages equipments. Therefore, it is urgent to design new controller without sign function to overcome the effect of uncertain Filippov solutions.

It is worth highlighting that most of previous studies only focused on NNs with first-order differential states [3,4,5, 13,14,15,16,17,18]. However, since the term of inertial possesses strong background of biological application, it’s significant and necessary to introduce it into NNs [19]. This kind of NNs are called as INNs, which are modeled by second-order differential equations. Compared with traditional first-order NNs [3,4,5, 13,14,15,16,17,18], INNs exhibits more complex behaviors including chaos and bifurcation [20]. Recently, in [21,22,23,24], asymptotic synchronization of INNs has been investigated. Meanwhile, considering the better property of finite-time control such as disturbance rejection and fast convergence rate [25,26,27,28,29,30,31,32], some results on finite-time synchronization of INNs [33,34,35] have been reported. Authors in [33] designed two different continuous delayed controllers to guarantee that memristive INNs realize finite-time synchronization. In [34], several finite-time synchronization criteria of memristive INNs with time-delays were gained by considering a hybrid controller. By designing continuous and discontinuous state-feedback controllers, the problem of finite-time synchronization for INNs without delay was addressed in [35]. It is not difficult to discover that both continuous and discontinuous controllers in [33,34,35] include sign function, and the activation functions of INNs mentioned above are all continuous. Actually, the sign function seems to be indispensable for finite-time control [29, 30], and few authors consider finite-time synchronization of coupled systems with some controllers without the sign function. Meanwhile, considering the advantages of fixed-time control [36, 36,37,38,39,40,41,42], the sign function also plays a crucial role. Moreover, to the best of our knowledge, few published papers consider finite-time and fixed-time synchronization of discontinuous INNs (DINNs). This motivates us to consider finite-time and fixed-time synchronization of DINNs via non-chattering control technique.

In the literature, the effect of time delay on finite-time synchronization is very difficult to be overcome. Recently, based on 1-norm analysis, the authors in [29,30,31,32] establish an effective method in studying finite-time synchronization of time-delay systems. Especially, by designing discontinuous controllers with the sign function, finite-time synchronization of NNs with infinite-time distributed delays was considered in [32]. Moreover, it’s discovered that, though the NNs with infinite-time distributed delays can be controlled to synchronization, the settling time cannot be estimated. Obviously, it is not convenient in practice if the settling time is not available. Recently, another kind of delay called proportional delay has attracted lots of attention [43], which exists in many practical systems, such as, Web quality of service routing decision system [44] and wireless networks [45]. Moreover, synchronization of NNs with proportional delays has attracted increasing interests in recent years [46,47,48,49]. For example, finite-time synchronization of fuzzy cellular NNs with time-varying coefficients and proportional delays were derived by designing continuous controller with sign function in [49]. However, the controllers in [49] are complex because they have to design some special terms to overcome the effects of the proportional delays. That is, the terms with proportional delay are removed by the controllers. From practical point of view, the designed controller should be simple. This motivates us consider finite-time synchronization of INNs with proportional delay by designing simple controller without sign function. Note that both the infinite-time distributed delay and the proportional delay are unbounded and time-varying. However, there are some conditions on the infinite-time distributed delay such as \(\int ^{+\infty }_{0}K_{ij}(u)\mathrm {d}u=k_{ij}\) for positive constants \(k_{ij}\), while there is no special condition on the proportional delay. Since proportional delay \((1-q)t\rightarrow +\infty \) as \(t\rightarrow +\infty \), it is more difficult to synchronize systems with the proportional delay in finite time than that of systems with infinite-time distributed delay by using simple controllers without the sign function. This problem is also considered in this paper, and the settling time will be explicitly estimated.

Motivated by the above discussion, this paper investigates finite-time synchronization of DINNs with proportional delay via non-chattering controllers. Moreover, fixed-time synchronization of the DINNs with proportional delay is also considered. The main contributions are as follows:

  1. (1)

    Different from existing controllers where the sign function is indispensable to overcome the uncertainties of Filippov solutions, the designed non-chattering controllers are just state feedback, which are very simple. Moreover, the controller can overcome the effects of uncertain Filippov solutions and the unbounded and time-varying proportional delay at the same time while without inducing any chattering phenomenon;

  2. (2)

    By designing new Lyapunov functionals and utilizing 1-norm methods, novel analytical techniques are established to obtain several sufficient conditions for the DINNs to achieve drive-response synchronization in finite time and even in a fixed time. Moreover, the settling time is estimated for the two types of synchronization;

  3. (3)

    It’s discovered that the settling time of the finite-time synchronization is dependent on both the initial values and the proportional delay factor while the settling time of the fixed-time synchronization is independent of the initial values and the proportional delay factor.

The paper is organized as follows. In Sect. 2, the model of the DINNs with proportional delay is presented, and some definitions and lemmas are also given. Section 3 provides some criteria for finite-time and fixed-time synchronization of the DINNs with proportional delay by strict mathematical proofs. Then two simulation examples are presented to illuminate the effectiveness of the theoretical results in Sect. 4. Finally, conclusions are given in Sect. 5.

Notations :  \({{\mathbb {R}}}\) is the set of real number, \({\mathbb {R}}^{n}\) denotes the set of \(n\times 1\) real vectors, and \({\mathbb {R}}^{n\times m}\) denotes the set of \(n\times m\) matrices; \(\Vert \cdot \Vert _{1}\) is 1-norm of a vector or a matrix, respectively. |B| is a vector derived by taking absolute values of all elements of a vector B; \({\overline{co}}[E]\) is the closure of the convex hull of the set \(E\subset {\mathbb {R}}^{n}\).

2 Model Description and Preliminaries

Consider a DINN with proportional delay as follows:

$$\begin{aligned} \frac{\mathrm {d}^{2}x_{i}(t)}{\mathrm {d}t^{2}}=-d_{i}\frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}-c_{i} x_{i}(t)+\sum ^{n}_{j=1}a_{ij} f_{j}(x_{j}(t)) +\sum ^{n}_{j=1}b_{ij} f_{j}(x_{j}(qt))+J_{i}, \end{aligned}$$
(1)

where \(t\ge 1\), \(i,j=1,2,\dots ,n\), \(x_{i}(t)\) is the state of ith neuron, the second derivative \(\frac{\mathrm {d}^{2}x_{i}(t)}{\mathrm {d}t^{2}}\) is inertial term, \(d_{i}>0\) and \(c_{i}>0\) are constants, \(f_{j}(\cdot )\) stands for the neuron activation function, \(a_{ij}\) and \(b_{ij}\) are connection weights related to ith and jth neurons without and with delay, respectively, \(J_{i}\) represents the external input of the ith neuron, \(0<q<1\) is the factor of the proportional delay \((1-q)t\). The initial value of the DINN (1) is \(x_{i}(s)=\phi _{i}(s),\frac{\mathrm {d}x_{i}(s)}{\mathrm {d}s}=\psi _{i}(s)\), for all \(s\in [q,1]\).

Remark 1

The proportional delay exists in many practical systems, such as Web quality of service routing decision system [44] and wireless networks [45]. Note that \((1-q)t\rightarrow +\infty \) as \(t\rightarrow \infty \), which is unbounded and time-varying. Hence, it is difficult to utilize the finite-time analytical methods proposed in [29,30,31,32] in studying finite-time and fixed-time synchronization of the DINN (1).

Suppose that the activation functions \(f_{j}(\cdot )\), \(j=1,2,\dots ,n\) are discontinuous on \({\mathbb {R}}\). Hence, system (1) is a differential equation with discontinuous state on the right-hand side. In this sense, the uniqueness of the solution of system (1) may not exist. Hence, the dynamics of system (1) can be investigated in the framework of Filippov solution [50], which is given below.

Definition 1

(Filippov regularization) [50]. The Filippov set-valued map of f(x) at \(x\in {\mathbb {R}}^{n}\) is defined by

$$\begin{aligned} F(x)=\bigcap _{\delta >0}\bigcap _{\mu (\Omega )=0}{\overline{co}}[f(B(x,\delta )\backslash \Omega )], \end{aligned}$$

where \(B(x,\delta )=\{y:\Vert y-x\Vert \le \delta \}\), and \(\mu (\Omega )\) is the Lebesgue measure of set \(\Omega \), \({\overline{co}}[C]\) is the closure of the convex hull of the set C.

Throughout this paper, the following assumptions are needed.

Assumption 1

For \(i=1,2,\dots ,n\), \(f_{i}(\cdot ):{\mathbb {R}}\rightarrow {\mathbb {R}}\) is continuous except on a countable set of isolated points \(\{{\hat{\rho }}^{i}_{k}\}\), where both the right and left limits \(f_{i}^{+}({\hat{\rho }}^{i}_{k})\) and \(f_{i}^{-}({\hat{\rho }}^{i}_{k})\) exist. Moreover, \(f_{i}(\cdot )\) has at most a finite number of jump discontinuous in every bounded compact interval \({\mathbb {R}}\).

Assumption 2

For \(i=1,2,\dots ,n\), \(0\in F_{i}(0)\), and there exist nonnegative constants \(l_{i}\) and \(\varrho _{i}\) such that \(|\gamma _{i}-\delta _{i}|\le l_{i}|x-y|\)+\(\varrho _{i}\) holds for \(\forall x,y\in {\mathbb {R}}\), where \(\gamma _{i}\in F_{i}(x)\), \(\delta _{i}\in F_{i}(y)\) with \(F_{i}(x)=[\min \{f^{-}_{i}(x),f^{+}_{i}(x)\},\max \{f^{-}_{i}(x),f^{+}_{i}(x)\}].\)

Assumption 3

The activation functions \(f_{i}(\cdot )\), \(i=1,2,\dots ,n\) are bounded, i.e., there exist constants \(M_{i}>0\), \(i=1,2,\dots ,n\) such that \(|f_{i}(x)|\le M_{i}\) for \(\forall x\in {\mathbb {R}}\).

The following result states the existence of Fillipov solution of system (1).

Lemma 1

Suppose that Assumptions 1 and 2 are satisfied. Then, any initial value for (1) has at least one solution [\(x_{i}(t),\gamma _{i}(t)\)] defined on \([q,+\infty )\), where \(\gamma _{i}(t)\in F_{i}(x)\).

Proof

Let \(\nu _{i}(t)=x_{i}(e^{t})\), then DINN (1) is equivalently transformed into the following DINN with constant delay and time-varying coefficients

$$\begin{aligned} \frac{\mathrm {d}^{2}\nu _{i}(t)}{\mathrm {d}t^{2}}&=(1-d_{i}e^{t})\frac{\mathrm {d}\nu _{i}(t)}{\mathrm {d}t} +e^{t}\left( -c_{i} \nu _{i}(t) +\sum ^{n}_{j=1}a_{ij} f_{j}(\nu _{j}(t))\right. \nonumber \\&\quad \left. +\sum ^{n}_{j=1}b_{ij} f_{j}(\nu _{j}(t-\tau ))+J_{i}\right) , \end{aligned}$$

for \(t\ge 0\), \(i=1,2,\dots ,n\), where \(\tau =-\ln q>0\). Then, one can obtain the conclusion by using similar analysis methods as those in [16, 29]. The proof is completed. \(\square \)

In view of [20], let \(y_{i}(t)=\frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}\), \(i=1,2,\dots ,n\). Then system (1) can be transformed into the following equivalent system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}=y_{i}(t),\\ \frac{\mathrm {d}y_{i}(t)}{\mathrm {d}t}=-d_{i}y_{i}(t)-c_{i}x_{i}(t)+\sum ^{n}_{j=1}a_{ij} f_{j}(x_{j}(t))+\sum ^{n}_{j=1}b_{ij} f_{j}(x_{j}(qt))+J_{i}. \end{array}\right. } \end{aligned}$$
(2)

According to Definition 1 and Lemma 1, there exist \(\gamma _{j}(t)\in F_{j}(x)\), \(j=1,2,\dots ,n\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}=y_{i}(t),\\ \frac{\mathrm {d}y_{i}(t)}{\mathrm {d}t}=-d_{i}y_{i}(t)-c_{i}x_{i}(t)+\sum ^{n}_{j=1}a_{ij} \gamma _{j}(t) +\sum ^{n}_{j=1}b_{ij} \gamma _{j}(qt)+J_{i}. \end{array}\right. } \end{aligned}$$
(3)

Consider system (2) as the master system, the corresponding controlled slave system is designed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}=w_{i}(t)+u_{1i}(t),\\ \frac{\mathrm {d}w_{i}(t)}{\mathrm {d}t}=-d_{i}w_{i}(t)-c_{i}v_{i}(t)\sum ^{n}_{j=1}a_{ij} f_{j}(v_{j}(t))+\sum ^{n}_{j=1}b_{ij} f_{j}(v_{j}(qt)) +J_{i}+u_{2i}(t), \end{array}\right. } \end{aligned}$$
(4)

where \(t\ge 1\), \(i,j=1,2,\dots ,n\), \(v_{i}(t)\) is the state of the response system, \(\frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}\) is inertial term of the response system, \(u_{1i}(t)\) and \(u_{2i}(t)\) are control inputs to be designed. The initial values are: \(v_{i}(s)={\hat{\phi }}_{i}(s)\), \(\frac{\mathrm {d}v_{i}(s)}{\mathrm {d}s}={\hat{\psi }}_{i}(s)\), \(s\in [q,1]\).

Similar to (3), the Filippov solution of (4) satisfies the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}=w_{i}(t)+u_{1i}(t),\\ \frac{\mathrm {d}w_{i}(t)}{\mathrm {d}t}=-d_{i}w_{i}(t)-c_{i}v_{i}(t)+\sum ^{n}_{j=1}a_{ij} \delta _{j}((t)) +\sum ^{n}_{j=1}b_{ij} \delta _{j}(qt)+J_{i}+u_{2i}(t), \end{array}\right. } \end{aligned}$$
(5)

where \(\delta _{j}(t)\in F_{j}(v).\) Two kinds of synchronization considered in this paper are given below.

Definition 2

The master–slave systems (2) and (4) are said to achieve finite-time synchronization if, for suitable designed controllers, there exists a constant T which is dependent on the initial values of systems (2) and (4) such that \(\lim _{t\rightarrow T}\sum ^{n}_{i=1}(|v_{i}(t)-x_{i}(t)|+|w_{i}(t)-y_{i}(t)|)=0\) and \(\sum ^{n}_{i=1}(|v_{i}(t)-x_{i}(t)|+|w_{i}(t)-y_{i}(t)|)\equiv 0\) for \(t>T\). Here, T is called settling time of finite-time synchronization.

Definition 3

The master–slave systems (2) and (4) are said to achieve fixed-time synchronization if, for suitable designed controllers, there exists a constant \(T _{\max }\) which is independent of the initial values of systems (2) and (4) such that \(\lim _{t\rightarrow T _{\max }}\sum ^{n}_{i=1}(|v_{i}(t)-x_{i}(t)|+|w_{i}(t)-y_{i}(t)|)=0\) and \(\sum ^{n}_{i=1}(|v_{i}(t)-x_{i}(t)|+|w_{i}(t)-y_{i}(t)|)\equiv 0\) for \(t>T _{\max }\), and \(T _{\max }\) is called the settling time of the fixed-time synchronization.

The following definition and lemmas are useful.

Definition 4

Function \(V(x):{\mathbb {R}}^{n}\longrightarrow {\mathbb {R}}\) is called C-regular if V(x) is:

  1. 1.

    regular in \({\mathbb {R}}^{n}\);

  2. 2.

    positive definite. i.e. \(V(x)>0\) for \(x\ne 0\) and \(V(0)=0\);

  3. 3.

    radially unbounded. i.e. \(V(x)\longrightarrow \infty \) as \(\Vert x\Vert \longrightarrow \infty \).

Lemma 2

(Chain rule) [51] If \(V(x):{\mathbb {R}}^{n}\longrightarrow {\mathbb {R}}\) is C–regular, and x(t) is absolutely continuous on any compact subinterval of \([0,+\infty ]\). Then, x(t) and \(V(x(t)):[0,+\infty ]\longrightarrow {\mathbb {R}}\) are differentiable for a.a. (almost all) \(t\in [0,+\infty ]\) and

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V(x(t))=\gamma (t){\dot{x}}(t), \forall \gamma (t)\in \partial V(x(t)), \end{aligned}$$

where \(\partial V(x(t))\) is the Clarke generalized gradient of V at x(t).

Lemma 3

[36] If there exists a continuous radially unbounded function \(V:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}_{+}\cup \{0\}\) such that

  1. (1)

    \(V(z)=0\Leftrightarrow z=0\);

  2. (2)

    for some \(\alpha \), \(\beta >0\), \(0<p<1\), \(\hbar >1\), any solution z(t) satisfies the following inequality

    $$\begin{aligned} {\dot{V}}(z(t))\le -\alpha V^{p}(z(t))-\beta V^{\hbar }(z(t)), \end{aligned}$$

    then, the origin of system is globally fixed-time stable equilibrium and the fixed settling time satisfies \(T _{\max }=\frac{1}{\alpha (1-q)}+\frac{1}{\beta (\hbar -1)}\).

Lemma 4

[52] Let \(a_1, a_2, \dots , a_N\ge 0\) and \(0<\ell \le 1\), \(\wp >1\). Then the following two inequalities hold:

$$\begin{aligned} \sum ^N_{i=1}{a^\ell _i}\ge \left( \sum ^N_{i=1}{a_i}\right) ^\ell ,\quad \sum ^N_{i=1}{a^{\wp }_{i}}\ge N^{1-\wp }\left( \sum ^N_{i=1}{a_i}\right) ^{\wp }. \end{aligned}$$

3 Main Results

In this section, two kinds of non-chattering controllers are designed. By utilizing 1-norm analysis techniques, sufficient conditions for the finite-time and fixed-time synchronization between (2) and (4) are given through strict mathematical proofs. Moreover, settling time for the two kinds of synchronization are estimated. It should be noticed that, different from existing results, the controllers do not use the sign function to avoid chattering.

Denote \(r_{i}(t)=v_{i}(t)-x_{i}(t)\), \(z_{i}(t)=w_{i}(t)-y_{i}(t)\), \(i=1,2,\dots ,n\). It can be seen that synchronizing (2) and (4) is equivalent to synchronizing between (3) and (5). So, subtracting (3) from (5) derives the error system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}r_{i}(t)}{\mathrm {d}t}=z_{i}(t)+u_{1i}(t),\\ \frac{\mathrm {d}z_{i}(t)}{\mathrm {d}t}=-d_{i}z_{i}(t)-c_{i}r_{i}(t)+\sum ^{n}_{j=1}a_{ij} \zeta _{j}(t) +\sum ^{n}_{j=1}b_{ij} \zeta _{j}(qt)+u_{2i}(t), \end{array}\right. } \end{aligned}$$
(6)

with initial values \(r_{i}(s)={\hat{\phi }}_{i}(s)-\phi _{i}(s)\), \(z_{i}(s)={\hat{\psi }}_{i}(s)-\psi _{i}(s)\), \(s\in [q,1]\), where \(\zeta _{j}(t)=\delta _{j}(t)-\gamma _{j}(t)\), \(\zeta _{j}(qt)=\delta _{j}(qt)-\gamma _{j}(qt)\), \(i,j=1,2,\dots ,n\).

3.1 Finite-Time Synchronization

Design the following controllers:

$$\begin{aligned} \left\{ \begin{aligned}&u_{1i}(t)=\left\{ \begin{aligned}&-\varepsilon _{i} r_{i}(t)-\kappa \frac{r_{i}(t)}{\Vert r(t)\Vert _{1}},&\Vert r(t)\Vert _{1}\ne 0,\\&0,&\Vert r(t)\Vert _{1}=0,\\ \end{aligned} \right. \\&u_{2i}(t)= \left\{ \begin{aligned}&-\xi _{i} z_{i}(t)-\eta \frac{z_{i}(t)}{\Vert z(t)\Vert _{1}},&\Vert z(t)\Vert _{1}\ne 0,\\&0,&\Vert z(t)\Vert _{1}=0,\\ \end{aligned} \right. \\ \end{aligned} \right. \end{aligned}$$
(7)

where \(\varepsilon _{i}>0\) and \(\xi _{i}>0\), \(i=1,2,\dots ,n\) are constants to be determined, \(\eta >0\) and \(\kappa >0\) are tunable constants, and \(r(t)=(r_{1}(t), r_{2}(t),\dots r_{n}(t))^{T}\), \(z(t)=(z_{1}(t), z_{2}(t),\dots z_{n}(t))^{T}\). Note that \(\varepsilon _{i}, \xi _{i}>0\), \(\eta >0\) and \(\kappa >0\) mean that the controller (7) can access the full states of \(r_{i}(t)\) and \(e_{i}(t)\).

Remark 2

Note that, if \(\Vert r(t)\Vert _{1}=0\) and \(\Vert z(t)\Vert _{1}=0\) for some finite time t, then the synchronization is achieved and the controller is not needed, which is equivalent to \(u_{1i}(t)=u_{2i}(t)=0\). Therefore, the controllers in (7) are reasonable. The controllers (7) are very simple and do not need any information of the delay. Actually, the sign function is very important for finite-time control. Hence, the control scheme (7) essentially improve the corresponding one in [29,30,31,32,33,34,35]. Recently, finite-time synchronization of a class of NNs with continuous activation functions and proportional delays was studied in [49]. To overcome the difficulty of the effect of proportional delay, complicated controllers with the proportional delays was designed to delete the corresponding terms directly. Furthermore, the controllers in [49] have to utilize the sign function to drive the coupled systems synchronize in finite time. Compared with the controllers in [49], the controllers in (7) are very simple and do not induce chattering.

Theorem 1

Suppose that Assumptions 1 and 2 are satisfied. Consider the controller (7), if the controller gains \(\eta >0\), and \(\kappa \), \(\varepsilon _{i}\), \(\xi _{i}\) satisfy the conditions

$$\begin{aligned} \varepsilon _{i}\ge&{\bar{c}}+\sum ^{n}_{j=1}l_{i}|a_{ji}|+\sum ^{n}_{j=1}\frac{l_{i}|b_{ji}|}{q}, \end{aligned}$$
(8)
$$\begin{aligned} \xi _{i}\ge&\max \{-d_{i}+1,0\}, \end{aligned}$$
(9)
$$\begin{aligned} \kappa =&\sum ^{n}_{i=1}\sum ^{n}_{j=1}(|a_{ij}|+|b_{ij}|)\varrho _{j}+\sigma , \end{aligned}$$
(10)

then the DINN (4) can be synchronized with DINN (2) in a finite time, where \(i=1,2,\dots ,n\), \({\bar{c}}=\max \{c_{l}:l=1,2,\dots ,n\}\), \(\sigma \) is a positive constant. Moreover, the settling time is estimated as

$$\begin{aligned} T\le \frac{q}{\varpi }\left\{ \sum ^{n}_{i=1}|r_{i}(1)|+\sum ^{n}_{i=1}|z_{i}(1)| +\sum ^{n}_{i=1}\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}\int ^{1}_{q}|r_{j}(s)|ds\right\} +q, \end{aligned}$$

\(\varpi =\min \{\eta ,\sigma \}\), \(r_{j}(s)={\hat{\phi }}_{j}(s)-\phi _{j}(s)\).

Proof

Define the following Lyapunov function:

$$\begin{aligned} V(t)=\sum ^{n}_{i=1}|r_{i}(t)|+\sum ^{n}_{i=1}|z_{i}(t)|+\sum ^{n}_{i=1}\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}\int ^{t}_{qt}|r_{j}(s)|ds. \end{aligned}$$
(11)

When \(\Vert r(t)\Vert _{1}\ne 0\) and \(\Vert z(t)\Vert _{1}\ne 0\), by Lemma 2, taking the time derivative of V(t) along the trajectory of (6) and considering the controller (7), one can obtain that

$$\begin{aligned} {\dot{V}}(t)&=\sum ^{n}_{i=1}\left[ \mathrm {sign}(z_{i}(t))\left( -d_{i}z_{i}(t)-c_{i}r_{i}(t)+\sum ^{n}_{j=1}a_{ij}\zeta _{j}(t)\right. \right. \nonumber \\&\quad \left. +\sum ^{n}_{j=1}b_{ij}\zeta _{j}(qt)-\xi _{i} z_{i}(t)-\eta \frac{z_{i}(t)}{\Vert z(t)\Vert _{1}}\right) \nonumber \\&\quad +\mathrm {sign}(r_{i}(t))\left( z_{i}(t)-\varepsilon _{i} r_{i}(t)-\kappa \frac{r_{i}(t)}{\Vert r(t)\Vert _{1}}\right) \nonumber \\&\quad \left. +\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}|r_{j}(t)|-\sum ^{n}_{j=1}l_{j}|b_{ij}||r_{j}(qt)|\right] . \end{aligned}$$
(12)

From Assumption 2, one has

$$\begin{aligned} \mathrm {sign}(z_{i}(t))\sum ^{n}_{j=1}a_{ij}\zeta _{j}(t)&\le \sum ^{n}_{j=1}l_{j}|a_{ij}||r_{j}(t)|+\sum ^{n}_{j=1}|a_{ij}|\varrho _{j}, \end{aligned}$$
(13)
$$\begin{aligned} \mathrm {sign}(z_{i}(t))\sum ^{n}_{j=1}b_{ij}\zeta _{j}(qt)&\le \sum ^{n}_{j=1}l_{j}|b_{ij}||r_{j}(qt)|+\sum ^{n}_{j=1}|b_{ij}|\varrho _{j}. \end{aligned}$$
(14)

Substituting (13) and (14) into (12) yields

$$\begin{aligned} {\dot{V}}(t)&\le \sum ^{n}_{i=1}\left\{ \left[ (-d_{i}-\xi _{i})|z_{i}(t)|+{\bar{c}}|r_{i}(t)|+\sum ^{n}_{j=1}l_{j}|a_{ij}||r_{j}(t)|\right. \right. \nonumber \\&\qquad \left. +\sum ^{n}_{j=1}(|a_{ij}|+|b_{ij}|)\varrho _{j}-\eta \frac{|z_{i}(t)|}{\Vert z(t)\Vert _{1}}\right] \nonumber \\&\qquad \left. +\left[ |z_{i}(t)|-\varepsilon _{i}|r_{i}(t)|-\kappa \frac{|r_{i}(t)|}{\Vert r(t)\Vert _{1}}\right] +\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}|r_{j}(t)|\right\} \nonumber \\&\quad =\sum ^{n}_{i=1}\left( {\bar{c}}+\sum ^{n}_{j=1}l_{i}|a_{ji}|+\sum ^{n}_{j=1}\frac{l_{i}|b_{ji}|}{q}-\varepsilon _{i}\right) |r_{i}(t)| +\sum ^{n}_{i=1}\left( -d_{i}+1-\xi _{i}\right) |z_{i}(t)|\nonumber \\&\qquad +\sum ^{n}_{i=1}\left( \sum ^{n}_{j=1}(|a_{ij}|+|b_{ij}|)\varrho _{j} -\kappa \frac{|r_{i}(t)|}{\Vert r(t)\Vert _{1}}\right) -\eta \sum ^{n}_{i=1}\frac{|z_{i}(t)|}{\Vert z(t)\Vert _{1}}. \end{aligned}$$
(15)

Note that

$$\begin{aligned} \kappa \sum ^{n}_{i=1}\frac{|r_{i}(t)|}{\Vert r(t)\Vert _{1}}=\kappa \frac{\sum ^{n}_{i=1}|r_{i}(t)|}{\Vert r(t)\Vert _{1}}=\kappa \quad \mathrm {and}\quad \eta \sum ^{n}_{i=1}\frac{|z_{i}(t)|}{\Vert z(t)\Vert _{1}}=\eta . \end{aligned}$$
(16)

It is obtained from (8)–(10), (15), and (16) that

$$\begin{aligned} {\dot{V}}(t)<-(\eta +\sigma )<-\varpi <0, \end{aligned}$$
(17)

where \(\sigma =\kappa -\sum ^{n}_{i=1}\sum ^{n}_{j=1}(|a_{ij}|+|b_{ij}|)\varrho _{j}\), \(\varpi =\min \{\eta , \sigma \}\).

From (11) and (17), one knows that V(t) is positive definite and non-increasing. Hence, there exists nonnegative constant \(V^{*}\) such that

$$\begin{aligned} \lim _{t\rightarrow +\infty }V(t)=V^{*} \ \mathrm {and} \ V(t)\ge V^{*}, \ \mathrm {for}\ t\ge 1. \end{aligned}$$
(18)

Integrating both side of the inequality (17) from 1 to t, it’s easy to gain that

$$\begin{aligned} V(t)-V(1)\le -\varpi (t-1). \end{aligned}$$
(19)

Now, let’s prove that there exists \(t_{1}\in (1,+\infty )\) such that

$$\begin{aligned} \lim _{t\rightarrow t_{1}}V(t)=V^{*} \ \mathrm {and} \ V(t)\equiv V^{*}, \ \mathrm {for}\ t\ge t_{1}. \end{aligned}$$
(20)

On the contrary, suppose \(\sum ^{n}_{i=1}(|r_{i}(t)|+|z_{i}(t)|)>0\) for all \(t\in (1,+\infty )\), then there exists \(i_{e}\in \{1,2,\dots ,n\}\) or \(i_{*e}\in \{1,2,\dots ,n\}\) such that \(|r_{i_{e}}(t)|>0\) or \(|z_{i_{*e}}(t)|>0\). It is obtained from (17) that \({\dot{V}}(t)\le -\varpi <0\) for all \(t\in (1,+\infty )\). In this case, the inequality (19) means that \(\lim _{t\rightarrow +\infty }V(t)=-\infty \). This contradicts (18), and hence the inequality (19) is not true for \(t\rightarrow \infty \). Hence, there exists \(t_{1}\in (1,+\infty )\) such that 20 is true, that is, \(\lim _{t\rightarrow t_{1}}V(t)=V^{*} \ \mathrm {and} \ V(t)\equiv V^{*}, \ \mathrm {for}\ t\ge t_{1}.\)

Next, prove \(V^{*}=0\). By contradiction, suppose \(V^{*}>0\), then there are three cases: \(\sum ^{n}_{i=1}|r_{i}(t_{1})|>0\) or \(\sum ^{n}_{i=1}|z_{i}(t_{1})|>0\) or \(\sum ^{n}_{i=1}\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}\int ^{t_{1}}_{qt_{1}}|r_{j}(s)|ds>0\).

Case 1:\(\sum ^{n}_{i=1}|r_{i}(t_{1})|>0\). There exists at least one \(i_{2}\in \{1,2,\dots ,n\}\) such that \(|r_{i_{2}}(t_{1})|>0\). By (17), it is found that \({\dot{V}}(t_{1})\le -\varpi <0\). On the other hand, from the continuous of \(|r_{i_{2}}(t_{1})|\) one has that there exists a instant \(t_{2}\in (t_{1},t_{1}+\epsilon ]\), where constant \(\epsilon >0\), such that \(|r_{i_{2}}(t_{2})|>0\) and \({\dot{V}}(t_{2})\le -\varpi <0\), which contradicts to \( V(t)\equiv V^{*}\) for \(t\ge t_{1}\). Hence, \(\sum ^{n}_{i=1}|r_{i}(t_{1})|=0\).

Case 2:\(\sum ^{n}_{i=1}|z_{i}(t_{1})|>0\). It can be derived from (17) that \({\dot{V}}(t_{1})\le -\varpi <0\). Similar to the discussions in Case 1, one has \({\dot{V}}(t_{3})\le -\varpi <0\), which contradicts to \( V(t)\equiv V^{*}\) for \(t\ge t_{1}\), where \(t_{3}\in (t_{1},t_{1}+{\hat{\epsilon }}]\), \({\hat{\epsilon }}>0\). Hence, \(\sum ^{n}_{i=1}|z_{i}(t_{1})|=0\).

Case 3:\(\sum ^{n}_{i=1}\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}\int ^{t_{1}}_{qt_{1}}|r_{j}(s)|ds>0\). There exist \(i_{3}\in \{1,2,\dots ,n\}\), \(t_{4}\in [qt_{1}, t_{1}]\), and a small constant \({\bar{\epsilon }}>0\) such that \(|r_{i_{3}}(t)|>0\) for all \(t\in [t_{4}-{\bar{\epsilon }},t_{4}+{\bar{\epsilon }}]\subset [qt_{1}, t_{1}]\). Hence, \({\dot{V}}(t)\le -\varpi <0\) on \([t_{4},t_{4}+{\bar{\epsilon }}]\), i.e. V(t) is monotonously decreasing on \([t_{4},t_{4}+{\bar{\epsilon }}]\), which is also contradicts with (20).

Considering the discussions for Cases 1, 2, and 3, it is obtained that \(V^{*}=0\), and so \(\sum ^{n}_{i=1}|r_{i}(qt_{1})|=0\) and \(\sum ^{n}_{i=1}|z_{i}(t_{1})|=0\). Moreover, by the above similar analysis, it can be found that

$$\begin{aligned} r_{i}(qt)\equiv 0 \ \mathrm {and} \ z_{i}(t)\equiv 0 \quad \mathrm {for} \ t\ge t_{1}, i=1,2,\dots ,n. \end{aligned}$$
(21)

Next, it is needed to prove

$$\begin{aligned} z_{i}(qt)\equiv 0 \quad \mathrm {for} \ t\ge t_{1}, i=1,2,\dots ,n. \end{aligned}$$
(22)

Since \(r_{i}(qt_{1})=0\) and \(r_{i}(t)\equiv 0\) for \(t>qt_{1}\) and \(i=1,2,\dots ,n\), one has \(\frac{\mathrm {d}r_{i}(qt_{1})}{\mathrm {d}t}=0\). Keeping this in mind and considering \(u_{1i}(qt_{1})=0\) in (7), it is found from (6) that \(z_{i}(qt_{1})=0\), \(i=1,2,\dots ,n\). It is not difficult to find that \(z_{i}(t)\equiv 0\) for \(t\in [qt_{1},t_{1}]\) is true. On the contrary, there exist \(t_{5}>qt_{1}\) such that \(\sum ^{n}_{i=1}|z_{i}(t_{5})|>0\). Let \(t_{p}=\sup \{t\in [qt_{1},t_{5}]:\sum ^{n}_{i=1}z_{i}(t)=0\}\). It can be derived that \(t_{p}<t_{5}\), \(\sum ^{n}_{i=1}|z_{i}(t_{p})|=0\) and \(\sum ^{n}_{i=1}z_{i}(t)>0\) for all \(t\in [t_{p},t_{5}]\). Therefore, there exists \(t_{6}\in [t_{p},t_{5}]\) such that \(\sum ^{n}_{i=1}z_{i}(t)\) is monotonously increasing on the \([t_{p},t_{6}]\), which contradicts \(\ V(t)\equiv V^{*}, \ \mathrm {for}\ t\ge t_{1}\). Hence, \(z_{i}(qt)=0\) and \(z_{i}(t)\equiv 0\) for \(t>qt_{1}\), \(i=1,2,\dots ,n\).

Therefore, \(V(qt_{1})=0\) and \(V(t)\equiv 0\) for \(\forall \ t\ge qt_{1}\). Let \(V(t_{1})=0\) in (19), one has \(t_{1}\le \frac{V(1)}{\varpi }+1\). Considering the discussions above, the settling time is estimated as \(T=\frac{qV(1)}{\varpi }+q\). Based on the above discussion and Definition 2, the DINN (4) can be synchronized with DINN (2) in finite time under the controller (7). The proof is completed. \(\square \)

Remark 3

Theorem 1 is derived on the basis of 1-norm, and the key step is to obtain the inequality (17). If the 2-norm based Lyapunov functions as those in [27, 33,34,35, 49] are used, the inequality (17) can not be derived. The analytical techniques are different from those used in [27, 33,34,35, 49] because their results are based on the inequality \({\dot{V}}(t)\le -\alpha V^{\eta }(t)\) in [25], where \(\alpha >0\) and \(0<\eta <1\) are constants.

Remark 4

It should be noted that, in spite of the effect of proportional delay, which is unbounded and time varying, the finite-time synchronization between the DINNs (2) and (4) can still be achieved. Moreover, the settling time is estimated. Theorem 1 is different from the results in [32]. It is reported in [32] that NNs with infinite-time distributed delay can achieve synchronization in finite time but the settling time cannot be estimated. The main reason for the estimation of the settling time for DINNs with proportional delay is that \(qt\rightarrow +\infty \) when \(t\rightarrow +\infty \). Therefore, \(\sum ^{n}_{i=1}\sum ^{n}_{j=1}\frac{l_{j}|b_{ij}|}{q}\int ^{t}_{qt}|e_{j}(s)|ds=0\) when the synchronization has been realized.

3.2 Fixed-Time Synchronization

The settling time T in Theorem 1 is heavily dependent on the initial conditions of the error system (6). Such initial-condition-dependent settling time is not convenient in practice: (a)the settling time increases as the increasing of the initial conditions of the error system (6); (b) when the the initial conditions of (6) is not available, the settling time cannot be known. To overcome these drawbacks, novel fixed-time controllers will be considered.

Design fixed time controllers as follows:

$$\begin{aligned} \left\{ \begin{aligned}&u_{1i}(t)= \left\{ \begin{aligned}&-{\hat{\varepsilon }}_{i} r_{i}(t)-\alpha \frac{r_{i}(t)|r_{i}(t)|^{h}}{\Vert r(t)\Vert _{1}}-\beta \frac{r_{i}(t)|r_{i}(t)|^{l}}{\Vert r(t)\Vert _{1}},&\Vert r(t)\Vert _{1}\ne 0,\\&0,&\Vert r(t)\Vert _{1}=0,\\ \end{aligned} \right. \\&u_{2i}(t)= \left\{ \begin{aligned}&-{\hat{\xi }}_{i} z_{i}(t)-{\hat{\kappa }}\frac{z_{i}(t)}{\Vert z(t)\Vert _{1}}-\alpha \frac{z_{i}(t)|z_{i}(t)|^{h}}{\Vert z(t)\Vert _{1}} -\beta \frac{z_{i}(t)|z_{i}(t)|^{l}}{\Vert z(t)\Vert _{1}},&\Vert z(t)\Vert _{1}\ne 0,\\&0,&\Vert z(t)\Vert _{1}=0,\\ \end{aligned} \right. \\ \end{aligned} \right. \end{aligned}$$
(23)

where \(i=1,2,\dots ,n\), \(0<h<1\) and \(l>1\), \(\alpha >0\) and \(\beta >0\) are tunable constants, \({\hat{\varepsilon }}_{i}>0\), \({\hat{\kappa }}>0\) and \({\hat{\xi }}_{i}>0\) are to be determined later.

Remark 5

Note that, different from most of existing results for fixed-time control techniques [33, 39,40,41,42], the controllers in (23) do not use the sign function, which induces the chattering phenomenon. When the synchronization has been realized, the controllers are not needed, and hence \(\Vert z(t)\Vert _{1}=\Vert r(t)\Vert _{1}=0\). Moreover, the parameters \(0<h<1\) and \(l>1\) make the controllers easier to be tuned in practice than that in [37, 38], where the controllers require the powers of error signals to be the quotient of two odd integers. Therefore, the designed controllers in (23) improve most of existing ones for fixed-time control techniques.

Theorem 2

Suppose that Assumptions 1–3 are satisfied. If the controller gains \(\eta >0\), and \({\hat{\kappa }}\), \({\hat{\varepsilon }}_{i}\), \({\hat{\xi }}_{i}\) satisfy the conditions

$$\begin{aligned}&{\hat{\varepsilon }}_{i}\ge {\bar{c}}+\sum ^{n}_{j=1}|a_{ji}|l_{i}, \end{aligned}$$
(24)
$$\begin{aligned}&{\hat{\xi }}_{i}\ge \max \{-d_{i}+1,0\}, \end{aligned}$$
(25)
$$\begin{aligned}&{\hat{\kappa }}=\sum ^{n}_{i=1}\sum ^{n}_{j=1}|b_{ij}|M_{j}+\sum ^{n}_{i=1}\sum ^{n}_{j=1}|a_{ij}|\varrho _{j}, \end{aligned}$$
(26)

then the DINN (4) with the controllers (23) can be synchronized with DINN (2) in a fixed time: \(T _{\max }=\frac{n^{h}}{\alpha (1-h)}+\frac{2^{l-1}n^{l}}{\beta (l-1)}.\)

Proof

Consider the following Lyapunov candidate function

$$\begin{aligned} {\hat{V}}(t)=\sum ^{n}_{i=1}|r_{i}(t)|+\sum ^{n}_{i=1}|z_{i}(t)|=\Vert r(t)\Vert _{1}+\Vert z(t)\Vert _{1}. \end{aligned}$$
(27)

When \(\Vert r(t)\Vert _{1}\ne 0\) and \(\Vert z(t)\Vert _{1}\ne 0\), by Lemma 2, evaluating the time derivative of \({\hat{V}}(t)\) along the trajectory of the error system (6) and considering controllers (23), it follows that

$$\begin{aligned} \dot{{\hat{V}}}(t)&=\sum ^{n}_{i=1}\mathrm {sign}(z_{i}(t))\bigg (-d_{i}z_{i}(t)-c_{i}r_{i}(t)+\sum ^{n}_{j=1}a_{ij}\zeta _{j}(t)\nonumber \\&\quad +\sum ^{n}_{j=1}b_{ij}\zeta _{j}(qt)-{\hat{\xi }}_{i}z_{i}(t)-{\hat{\kappa }}\frac{z_{i}(t)}{\Vert z(t)\Vert _{1}}-\alpha \frac{z_{i}(t)|z_{i}(t)|^{h}}{\Vert z(t)\Vert _{1}} \nonumber \\&\quad \left. -\beta \frac{z_{i}(t)|z_{i}(t)|^{l}}{\Vert z(t)\Vert _{1}}\right) +\sum ^{n}_{i=1}\mathrm {sign}(r_{i}(t))\left( z_{i}(t)-{\hat{\varepsilon }}_{i} {r_{i}}(t)\right. \nonumber \\&\quad \left. -\alpha \frac{r_{i}(t)|r_{i}(t)|^{h}}{\Vert r(t)\Vert _{1}}-\beta \frac{r_{i}(t)|r_{i}(t)|^{l}}{\Vert r(t)\Vert _{1}}\right) . \end{aligned}$$
(28)

It can be derived from Assumption 3 that

$$\begin{aligned} \mathrm {sign}(z_{i}(t))\sum ^{n}_{j=1}b_{ij}\zeta _{j}(qt)\le \sum ^{n}_{j=1}|b_{ij}|M_{j}. \end{aligned}$$
(29)

Combing (28) with (13) and (29) yields that

$$\begin{aligned} \dot{{\hat{V}}}(t)&\le \sum ^{n}_{i=1}(-d_{i}+1-{\hat{\xi }}_{i})|z_{i}(t)|+\sum ^{n}_{i=1}\left( {\bar{c}}+\sum ^{n}_{j=1}|a_{ji}|l_{i} -{\hat{\varepsilon }}_{i}\right) |r_{i}(t)|\nonumber \\&\quad +\sum ^{n}_{i=1}\left( \sum ^{n}_{j=1}|b_{ij}|M_{j}+\sum ^{n}_{j=1}|a_{ij}|\varrho _{j}-{\hat{\kappa }}\frac{z_{i}(t)}{\Vert z(t)\Vert _{1}}\right) \nonumber \\&\quad -\alpha \sum ^{n}_{i=1}\left( \frac{|r_{i}(t)|^{h+1}}{\Vert r(t)\Vert _{1}} +\frac{|z_{i}(t)|^{h+1}}{\Vert z(t)\Vert _{1}}\right) \nonumber \\&\quad -\beta \sum ^{n}_{i=1}\left( \frac{|z_{i}(t)|^{l+1}}{\Vert z(t)\Vert _{1}}+\frac{|r_{i}(t)|^{l+1}}{\Vert r(t)\Vert _{1}}\right) . \end{aligned}$$
(30)

It can be obtained from the second inequality in Lemma 4, for \(h+1>1\) and \(l+1>1\), that

$$\begin{aligned}&-\frac{\sum ^{n}_{i=1}|r_{i}(t)|^{h+1}}{\Vert r(t)\Vert _{1}}\le -\frac{(\sum ^{n}_{i=1}|r_{i}(t)|)^{h+1}}{n^{h}\Vert r(t)\Vert _{1}}= -\frac{\Vert r(t)\Vert _{1}^{h}}{n^{h}}, \quad \mathrm {and}\nonumber \\&-\frac{\sum ^{n}_{i=1}|r_{i}(t)|^{l+1}}{\Vert r(t)\Vert _{1}}\le -\frac{\Vert r(t)\Vert _{1}^{l}}{n^{l}}. \end{aligned}$$
(31)

Similar to (31), it follows that

$$\begin{aligned} -\frac{\sum ^{n}_{i=1}|z_{i}(t)|^{h+1}}{\Vert z(t)\Vert _{1}}\le -\frac{\Vert z(t)\Vert _{1}^{h}}{n^{h}} \quad \mathrm {and}\quad -\frac{\sum ^{n}_{i=1}|z_{i}(t)|^{l+1}}{\Vert z(t)\Vert _{1}}\le -\frac{\Vert z(t)\Vert _{1}^{l}}{n^{l}}. \end{aligned}$$
(32)

Substituting (31) and (32) into (30) yields that

$$\begin{aligned} \dot{{\hat{V}}}(t)&\le \sum ^{n}_{i=1}\left( -d_{i}+1-{\hat{\xi }}_{i}\right) |z_{i}(t)|+\sum ^{n}_{i=1}\left( {\bar{c}}+\sum ^{n}_{j=1}|a_{ji}|l_{i} -{\hat{\varepsilon }}_{i}\right) |r_{j}(t)|\nonumber \\&\quad +\sum ^{n}_{i=1}\left( \sum ^{n}_{j=1}|b_{ij}|M_{j} +\sum ^{n}_{j=1}|a_{ij}|\varrho _{j}-{\hat{\kappa }}\frac{z_{i}(t)}{\Vert z(t)\Vert _{1}}\right) \nonumber \\&\quad -\frac{\alpha }{n^{h}}\left( \Vert r(t)\Vert ^{h}_{1}+\Vert z(t)\Vert ^{h}_{1}\right) -\frac{\beta }{n^{l}}\left( \Vert z(t)\Vert ^{l}_{1}+\Vert r(t)\Vert ^{l}_{1}\right) . \end{aligned}$$
(33)

Combing (33) with conditions (24)–(26) derives that

$$\begin{aligned} \dot{{\hat{V}}}(t)\le&-\frac{\alpha }{n^{h}}\left( \Vert r(t)\Vert ^{h}_{1}+\Vert z(t)\Vert ^{h}_{1}\right) -\frac{\beta }{n^{l}}\left( \Vert z(t)\Vert ^{l}_{1}+\Vert r(t)\Vert ^{l}_{1}\right) . \end{aligned}$$
(34)

Using Lemma 4 again, it is not hard to check that

$$\begin{aligned} \dot{{\hat{V}}}(t)&\le -\frac{\alpha }{n^{h}}\left( \Vert r(t)\Vert _{1}+\Vert z(t)\Vert _{1}\right) ^{h} -\frac{2^{1-l}\beta }{n^{l}}\left( \Vert z(t)\Vert _{1} +\Vert r(t)\Vert _{1}\right) ^{l}\nonumber \\&=x-\frac{\alpha }{n^{h}}V^{h}(t) -\frac{\beta }{2^{(l-1)}n^{l}}V^{l}(t). \end{aligned}$$
(35)

In view of Lemma 3, \({\hat{V}}(t)\) converges to zero in fixed time, and the settling time is estimated by \(T _{\max }=\frac{n^{h}}{\alpha (1-h)}+\frac{2^{l-1}n^{l}}{\beta (l-1)}\). Consequently, the DINN (4) is synchronized with DINN (2) in fixed time under the controller (23). The proof is completed. \(\square \)

4 Numerical Examples

In this section, two numerical examples are given to illustrate the effectiveness of the main results. Specifically, Example 1 is to verify the Theorem 1, and Example 2 aims to illustrate the Theorem 2. In simulations, the time step size is taken as 0.001.

Fig. 1
figure 1

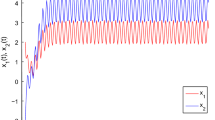
Trajectory of inertial DINN (36) with initial condition \(\phi (t)=(-0.3,1.8)^{T}, \psi (t)=(1.5, -0.7)^{T}\), \(t\in [0.75,1]\)

Full size image

Consider the following 2-dimension DINN with proportional delay:

$$\begin{aligned} \frac{\mathrm {d}^{2}x_{i}(t)}{\mathrm {d}t^{2}}&=-d_{i}\frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}-c_{i} x_{i}(t)+\sum ^{2}_{j=1}a_{ij}f_{j}(x_{j}(t))\nonumber \\&\quad \,\, +\sum ^{2}_{j=1}b_{ij}f_{j}(x_{j}(qt))+J_{i}(t),\quad i=1,2, \end{aligned}$$
(36)

where \(q= 0.75\)\(J_{1}(t)=\cos (t)\), \(J_{2}(t)=\sin (t)\), \(d_{1}=1.15\), \(d_{2}=1.2\), \(c_{1}=c_{2}=1\), \(a_{11}=-0.5\), \(a_{12}=1.2\), \(a_{21}=-1\), \(a_{22}=0.8\), \(b_{11}=-1.4\), \(b_{12}=0.6\), \(b_{21}=0.7\), \(b_{22}=-1.1\),

$$\begin{aligned} f_{j}(x_{j}(t))= {\left\{ \begin{array}{ll} \tanh (x_{j}(t))+0.01, \quad \mathrm {if} \ \ x_{j}(t)\le 0,\ \ j=1,2,\\ \tanh (x_{j}(t))-0.05, \quad \mathrm {if}\ \ x_{j}(t)>0,\ \ j=1,2. \end{array}\right. } \end{aligned}$$

When the initial conditions are chosen as \(\phi (t)=(\phi _{1}(t),\phi _{2}(t))^{T}=(-0.3,1.8)^{T}, \psi (t)=(\psi _{1}(t),\psi _{2}(t))^{T}=(1.5,-0.7)^{T}\), the trajectory of (36) is shown in Fig. 1. It is easy to check that the discontinuous activation functions \(f_{j}(\cdot )\), \(j=1,2\) satisfy Assumption 1. Moreover, by simple computation, one can get \(l_{1}=l_{2}=1\), \(\varrho _{1}=\varrho _{2}=0.06\) and \(M_{1}=M_{2}=1\). Hence, Assumptions 1–3 are all satisfied.

Example 1

Now, let’s verify Theorem 1. In this example, taking DINN (36) as the drive system, the initial values are the same as those in Fig. 1. Choose the initial values of slave system as \({\hat{\phi }}(t)=(1.5,0.85)^{T}\) and \({\hat{\psi }}(t)=(-0.2,2.1)^{T}\) for \(t\in [0.75,1]\). By simple computation, it is easy to obtain that \(\varepsilon _{1}\ge 5.3\), \(\varepsilon _{2}\ge 5.2667\), \(\xi _{1}\ge 0.15\), \(\xi _{2}\ge 0.2\), and \(\sum ^{n}_{i=1}\sum ^{n}_{j=1}(|a_{ij}|+|b_{ij}|)\varrho _{j}=0.438\). According to Theorem 1, the DINNs can realize finite-time synchronization under the controller (7) with \(\varepsilon _{1}=5.3\), \(\varepsilon _{1}=5.2667\), \(\xi _{1}=0.15\), \(\xi _{2}=0.2\), \(\eta \) and \(\kappa =0.438+\sigma \) for \(\eta \) and \(\sigma \) are positive constants. Moveover, the settling time can be explicitly obtained.

Fig. 2
figure 2

Time response of synchronization error under the controller (7) with \(\eta \) and \(\kappa \): a\(\eta =0.5\) and \(\kappa =0.938\); b\(\eta =2\), and \(\kappa =2.438\)

Full size image
Fig. 3
figure 3

Time response of synchronization error under the controller (23) with different initial values of slave system: a\({\hat{\phi }}(t)=(1.9664,-0.3135)^{T}\), \({\hat{\psi }}(t)=(-0.2181,1.0954)^{T}\); b\({\hat{\phi }}(t)=(208.4485,-165.1298)^{T}\), \({\hat{\psi }}(t)=(185.0666,210.3338)^{T}\)

Full size image

Taking \(\eta =\sigma =0.5\), one gets \(t_{1}\le 14.3225\). When \(\eta =\sigma =2\), one can obtain \(t_{1}\le 4.1431\). Figure 2 presents the time evolution of \(r_{i}(t)=v_{i}(t)-x_{i}(t)\) and \(e_{i}(t)=\frac{\mathrm {d}v_{i}(t)}{\mathrm {d}t}-\frac{\mathrm {d}x_{i}(t)}{\mathrm {d}t}\), \(i=1,2\) with different values \(\eta \) and \(\sigma \). From Fig. 2, one can see that the synchronization is achieved in a finite time. Moreover, one can also see from Fig. 2 that the synchronization time decreases as the increasing of control gains \(\eta \) and \(\sigma \), this means that the control gains \(\eta \) and \(\sigma \) are used to tune the synchronization time.

Example 2

This example is given to verify the effectiveness of Theorem 2. Taking DINN (36) as the drive system, the initial values are the same as those in Fig. 1. The initial values of slave system are randomly chosen from \([-3,3]\) and \([-300,300]\) for \(t\in [0.75,1]\). By simple computation, it is easy to obtain that \({\hat{\varepsilon }}_{1}\ge 2.5\), \({\hat{\varepsilon }}_{2}\ge 3\), \({\hat{\xi }}_{1}\ge 0.15\), \({\hat{\xi }}_{2}\ge 0.2\), and \({\hat{\kappa }}=4.01\). According to Theorem 2, the DINNs can realize fixed-time synchronization under the controller (23). Moveover, the settling time can be explicitly obtained, which is independent of the initial conditions.

Take \({\hat{\varepsilon }}_{1}=2.5\), \({\hat{\varepsilon }}_{1}=3\), \({\hat{\xi }}_{1}=0.15\), \({\hat{\xi }}_{2}=0.2\), \({\hat{\kappa }}=4.01\), \(l=1.7\), \(h=0.8\), \(\alpha =\beta =5\). According to Theorem 2, the settling time can be explicitly estimated \(T _{\max }=3.2491\). Figure 3 shows the synchronization is realized in the fixed time under the controller (23) with different initial values of salve system: (a) \({\hat{\phi }}(t)=(1.9664,-0.3135)^{T}\), \({\hat{\psi }}(t)=(-0.2181,1.0954)^{T}\); (b) \({\hat{\phi }}(t)=(208.4485,-165.1298)^{T}\), \({\hat{\psi }}(t)=(185.0666,210.3338)^{T}\).

5 Conclusions

Both finite-time and fixed-time synchronization of INNs with discontinuous activation functions and proportional delay have been studied. By constructing new Lyapunov functionals and utilizing several effective analytical methods, sufficient synchronization criteria have been derived. Moreover, the settling times are explicitly estimated. Without utilizing the sign function, the designed controllers can overcome the effects of both uncertain Filippov solutions and proportional delays and further achieve finite-time and fixed-time synchronization. Numerical simulations illustrated the effectiveness of theoretical results.

Note that the controllers (7) and (23) designed in this paper need to use the full state of each neuron, both of which are centralized controllers. Considering many advantages of distributed control, such as low communication performance requirements, good fault tolerance, strong adaptability to the environment and strong scalability, our next research topic is to design distributed non-chattering finite-time and fixed-time controllers for INNs with discontinuous activation functions and proportional delay, which is interesting and challenging.