On Impulsive Synchronization Control for Coupled Inertial Neural Networks with Pinning Control

Abstract

The impulsive control for the synchronization problem of coupled inertial neural networks involved distributed-delay coupling is investigated in the present paper. A novel impulsive pinning control method is introduced to obtain the complete synchronization of the coupled inertial neural networks with three different coupling structures. At each impulsive control instant, the pinning-controlled nodes can be selected according to our selection strategy which is dependent on the lower bound of the pinning control ratio. Our criteria can be utilized to declare the synchronization of the coupled neural networks with asymmetric and reducible coupling structures. The effectiveness of our control strategy is exhibited by typical numerical examples.

1 Introduction

Since 1980’s, several neural network systems were studied, including delayed neural networks [1,2,3,4], memristive neural networks [5, 6], stochastic neural networks [7,8,9], etc. Particularly, the inertial neural networks (INNs) were first introduced by Babcock and Westervelt, and the bifurcation and chaos problems were investigated in [10]. Since then, several interesting works were reported on the dynamic problems of the INNs, including bifurcation and stability problem [11,12,13,14,15], dissipativity analysis [16,17,18] and synchronization problems [19,20,21,22,23]. In addition, several techniques, including matrix measurement, differential inequalities and linear matrix inequalities also were used to derive the novel and interesting stability criteria for variety of INNs [12,13,14,15].

The synchronization problem was widely studied for various dynamical systems [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. A nonlinear control law [20] was designed to gain the synchronization of the drive-response INNs. A novel sampled data control method based on pinning control [19] was adopted to obtain the synchronization of INNs with reaction-diffusion term. The Lyapunov function and the differential inclusion theory were utilized to study the synchronization issue of coupled neural network with markovian jump [21] and supremums [22], respectively. In order to decrease the control cost, the pinning control [19, 35,36,37,38] was widely used in the synchronization investigation of complex dynamical networks. For instance, the pinning control was used to study the synchronization and the outputs robustness of the coupled Lure networks [35] and Boolean control networks [36, 37], respectively. Similarly, the synchronization problem of the dynamical system with nonlinear coupling was studied by using the impulsive pinning control [38], which be used in the present paper to obtain our main results. Additionally, the synchronization applications of the coupled INNs also were reported, such as image encryption [21] and secure communication [32]. Recently, the finite-time synchronization was investigated for the drive-response coupled INNs. In [33, 34], both the sampled data control and Filippov discontinuous theory were employed to obtain the finite-time and fixed-time synchronization criteria for the coupled INNs, in term of algebraic inequalities. However, few works have been involved to study the synchronization issue of the coupled INNs with hybrid couplings, by using the pinning control and impulsive control.

Based on the above-mentioned discussion, the synchronization problem is investigated for the coupled INNs with hybrid couplings here. The object is to construct the impulsive control and pinning control laws to obtain the completely synchronization of the coupled INNs. The contributions in this paper are outlined as: (1) different from the synchronization problem studied in [19,20,21,22,23, 32,33,34], the hybrid couplings are involved in the complete synchronization issue of the INNs, (2) different from the control schemes in [19,20,21,22,23, 32,33,34], a novel impulsive control and pinning control are given here to realize the synchronization for the coupled INNs with hybrid couplings, (3) a novel selection strategy of the pinning-controlled nodes at each impulsive instant is proposed for the coupled INNs, according to our pinning control criteria in terms of algebraic inequalities. The rest of this paper is organized as follows. Several preliminaries are outlined in Sect. 2. The synchronization control design based on impulsive control and pinning control are studied in Sect. 3. The numerical example part and the conclusion part are given in Sects. 4 and  5, respectively.

2 Problem Formulation

Let ${\mathbb {R}}^n$ represent the n-dimensional real space and $\otimes$ mean the Kronecker product. ${\mathfrak {Z}}^T$ represents the transpose of matrix ${\mathfrak {Z}}$ and ${\mathfrak {Z}}<0$ indicates that ${\mathfrak {Z}}$ is a negative definite matrix. $\lambda _{\mathrm{min}}({\mathfrak {Z}})$ ($\lambda _{\mathrm{max}}({\mathfrak {Z}})$) denotes the minimal (maximal) eigenvalue of the symmetrical matrix ${\mathfrak {Z}}$. I means the unit matrix of appropriate dimension. The notation $\star$ denotes the symmetric block in a symmetric matrix.

The ith node dynamic equation of the coupled INNs here is described as

$$\begin{aligned} \ddot{{\mathfrak {u}}}_i(t)=-{\mathfrak {A}}\dot{{\mathfrak {u}}}_i(t)- {\mathfrak {Bu}}_i(t) +{\mathfrak {C}}f({\mathfrak {u}}_i(t)) +{\mathfrak {D}}f({\mathfrak {u}}_i(t-\tau (t)))+{\mathfrak {J}}, \ i=1,\ldots ,N, \end{aligned}$$

(1)

where ${\mathfrak {u}}_i(t)\in {\mathbb {R}}^n$ is the state vector. ${\mathfrak {A}}=\mathrm{diag}\{a_{1},\ldots ,a_{n}\}$ and ${\mathfrak {B}}=\mathrm{diag}\{b_{1},\ldots ,b_{n}\}$ are real matrices with $a_i,b_i>0$, $i=1,\ldots ,n$. $f({\mathfrak {u}}_i(t))$ is the activation function. $\tau (t)$ is the time delay function with $0\le \tau (t)\le \tau _0$. ${\mathfrak {C}}=(c_{sj})_{n\times n}$ and ${\mathfrak {D}}=(d_{sj})_{n\times n}$ are connection weight matrices. ${\mathfrak {J}}=({\mathfrak {J}}_{1},\ldots ,{\mathfrak {J}}_{n})^T$ is the external input.

Consider the coupled INNs with hybrid couplings as follows

(2)

where $h_0$ and $\kappa _0$ represent the distributed-delay and transmittal-delay, respectively. ${\mathfrak {c}}_1$, ${\mathfrak {c}}_2$ and ${\mathfrak {c}}_3$ are the constant coupling strengths. , and are the inner coupling matrices with , $i=1,2,3$, $j=1,\ldots ,n$. ${\mathfrak {L}}^{(i)}=\left( l_{sj}^{(i)}\right) _{N\times N}$ are the coupling matrices in which $l_{sj}^{(i)}>0$ if there exists an edge from node j to node s, otherwise $l_{sj}=0$. ${\mathfrak {L}}^{(i)}$, $i=1,2,3$ also satisfy $l_{ss}^{(i)}=-\sum _{j=1,\ j\ne s}^Nl_{sj}^{(i)}$ for $s=1,\ldots ,N$. Note that the matrices ${\mathfrak {L}}^{(1)}$, ${\mathfrak {L}}^{(2)}$ and ${\mathfrak {L}}^{(3)}$ here are not assumed to be symmetric or irreducible, our impulsive control thus can be employed to synchronize the coupled INNs with those coupling structures.

The synchronization control object is given as

$$\begin{aligned} \ddot{{\mathfrak {s}}}(t)=-\,{\mathfrak {A}}\dot{{\mathfrak {s}}}(t)-{{\mathfrak {B}}}{{\mathfrak {s}}}(t) +{\mathfrak {C}}f({\mathfrak {s}}(t))+{\mathfrak {D}}f({\mathfrak {s}}(t-\tau (t)))+{\mathfrak {J}}, \end{aligned}$$

(3)

where ${\mathfrak {s}}(t)\in {\mathbb {R}}^n$. Take ${\mathfrak {e}}_i(t)={\mathfrak {u}}_i(t)-{\mathfrak {s}}(t)$, . Similarly, and , then we have the following synchronization error system

(4)

where $f({\mathfrak {e}}_i(t))=f({\mathfrak {u}}_i(t))-f({\mathfrak {s}}(t))$, $i=1,\ldots ,N$.

Set ${\mathfrak {y}}_i(t)={\mathfrak {e}}_i(t)+\dot{{\mathfrak {e}}}_i(t)$, $i=1,\ldots ,N$, the synchronization error system with impulsive control is

(5)

where ${\mathfrak {K}}_1$ and ${\mathfrak {K}}_2$ are real constants. The impulsive instants $t_k$ satisfy $0=t_0<t_1<\cdots<t_k<\ldots$ and $\lim \limits _{k\rightarrow \infty }t_k=\infty$. Let ${\mathfrak {e}}(t)=({\mathfrak {e}}_1^T(t),\ldots ,{\mathfrak {e}}_n^T(t))^T$, ${\mathfrak {y}}(t)=({\mathfrak {y}}_1^T(t),\ldots ,{\mathfrak {y}}_n^T(t))^T$ and ${F(e(t))=(f^T({\mathfrak {e}}_1(t)),\ldots ,f^T({\mathfrak {e}}_n(t)))^T}$, the system (5) can be rewritten as

(6)

Remark 1

If the constants ${\mathfrak {c}}_2$ and ${\mathfrak {c}}_3$ in the system (2) equal to zero, the coupling structures of the coupled INNs in our paper degenerate to the coupling structures discussed in [19,20,21,22,23, 32,33,34]. Thus, the impulsive control developed here can be used to study the synchronization problems in those works.

Assumption 1

[39] For $f({\mathfrak {z}})=(f_{1}({\mathfrak {z}}),\ldots ,f_{n}({\mathfrak {z}}))^{T}$ in the system (1), there exist nonnegative constants $\beta _{sj}$, for ${\mathfrak {z}}_1=({\mathfrak {z}}_{11},\ldots ,{\mathfrak {z}}_{1n})^T$ and ${\mathfrak {z}}_2=({\mathfrak {z}}_{21},\ldots ,{\mathfrak {z}}_{2n})^T\in {\mathbb {R}}^n$ such that

$$\begin{aligned} |f_s({\mathfrak {z}}_{11},\ldots ,{\mathfrak {z}}_{1n})-f_s({\mathfrak {z}}_{21}, \ldots ,{\mathfrak {z}}_{2n})| \le \sum \limits _{j=1}^n{\beta _{sj}}|{\mathfrak {z}}_{1j}-{\mathfrak {z}}_{2j}|, \ s=1,\ldots ,n. \end{aligned}$$

Definition 1

The coupled INNs (4) can realize exponential synchronization if there exist positive constants $\iota _0$ and $\nu _0$ such that the synchronization error system (6) satisfies

$$\begin{aligned} \Vert {\mathfrak {e}}_i(t)\Vert ^2+\Vert {\mathfrak {y}}_i(t)\Vert ^2 \le \iota _0{e}^{-\nu _0t} \end{aligned}$$

for any $t\ge 0$, where $i=1,\ldots ,N$ and $\Vert \cdot \Vert$ represents the Euclidean norm.

Definition 2

[40] The positive scalar ${\mathfrak {T}}_{a}$ is said be the average impulsive interval of impulsive sequence $\iota =\left\{ t_1,t_2,\ldots \right\}$ if there exist positive integer ${\mathfrak {N}}_0$ such that $\displaystyle \frac{T-t}{{\mathfrak {T}}_{a}}-{\mathfrak {N}}_0\le {\mathfrak {N}}_{\iota }(T,t)\le \displaystyle \frac{T-t}{{\mathfrak {T}}_{a}}+{\mathfrak {N}}_0$, $0\le t\le T$, where ${\mathfrak {N}}_{\iota }(T,t)$ represents the impulsive time numbers of $\iota =\left\{ t_1,t_2,\ldots \right\}$ in the time interval (t, T).

Lemma 1

[41] Let $\tau _i(t)$, $i=1,2,3$ be time delay functions with $0\le \tau _i(t)\le \iota$ and a real scalar function $F(t,u,{\bar{u}}_1,{\bar{u}}_2)$ defined on ${\mathbb {R}}^+\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}$ be nondecreasing in ${\bar{u}}_1$, ${\bar{u}}_2$ for fixed (t, u). Suppose $I_k(u): \, {\mathbb {R}}\rightarrow {\mathbb {R}}$ be nondecreasing in u. If the following inequalities hold

$$\begin{aligned}&\left\{ \begin{array}{l} D^+w(t)\le F(t,w(t),w(t-\tau _1(t)),w(t-\tau _2(t))) +\vartheta \displaystyle \int _{t-\tau _3(t)}^tw(s)\mathrm {d}s, \ t\ne t_k,\\ w(t_k)\le I_k(w(t_k^-)), \ k=1,2,\ldots , \end{array}\right. \end{aligned}$$

(7)

$$\begin{aligned}&\left\{ \begin{array}{l} D^+z(t)>F(t,z(t),z(t-\tau _1(t)),z(t-\tau _2(t))) +\vartheta \displaystyle \int _{t-\tau _3(t)}^tv(s)\mathrm {d}s, \ t\ne t_k,\\ z(t_k)\ge I_k(z(t_k^-)), \ k=1,2,\ldots {,} \end{array}\right. \end{aligned}$$

(8)

where $\vartheta >0$. Then $w(t)\le z(t)$ for $-\iota \le t\le 0$ means that $w(t)\le z(t)$ for all $t>0$, where $D^+w(t)$ represents the right upper Dini derivative of w(t).

3 Synchronization Control Design

For the real constants ${\mathfrak {K}}_1$ and ${\mathfrak {K}}_2$, take ${\tilde{\beta }}=\max \{(1+{\mathfrak {K}}_1)^2,(1+{\mathfrak {K}}_2)^2\}$ in the subsequent discussion.

3.1 Impulsive Control Design

Theorem 1

Assume that $0<{\tilde{\beta }}<1$ and the impulsive instants satisfy the Definition 2. If there are matrices ${\mathfrak {P}}_1>0$, ${\mathfrak {P}}_2>0$, diagonal matrices ${{{\varSigma }}}_j>0$, $j=1,2,3,4$ and positive constants $\theta _i>0$, $i=1,2,3$, $\alpha >0$ such that

$$\begin{aligned} {\varPi }{{\varSigma }}_2{\varPi }<\theta _1{\mathfrak {P}}_1, \ {\mathfrak {c}}_2{{\varSigma }}_3<\theta _2{\mathfrak {P}}_2, \ {\mathfrak {c}}_3{{\varSigma }}_4<\theta _3{\mathfrak {P}}_2, \end{aligned}$$

(9)

(10)

$$\begin{aligned} \alpha +\displaystyle \frac{\ln {\tilde{\beta }}}{{\mathfrak {T}}_a} +\frac{\theta _1+\theta _2+\theta _3h_0}{\beta ^{{\mathfrak {N}}_0}}<0 \end{aligned}$$

(11)

hold, where ${\varTheta }_1=-(I_N\otimes {\mathfrak {P}}_2){\mathfrak {H}}_1-{\mathfrak {H}}_1^T(I_N\otimes {\mathfrak {P}}_2)-\alpha I_N\otimes {\mathfrak {P}}_2$, ${\varTheta }_2=I_N\otimes ({\mathfrak {P}}_1+{\mathfrak {P}}_2({\mathfrak {A}}-{\mathfrak {B}}-I_n))$, , ${\varPhi }=-I_N\otimes ((2+\alpha ){\mathfrak {P}}_1-{\varPi }^T{{\varSigma }}_1{\varPi })$ and ${\varPi }=(\beta _{sj})_{n\times n}$. Then the synchronization error system (6) is exponentially stable, and the coupled INNs (2) can realize exponential synchronization.

Proof

Construct Lyapunov function as

$$\begin{aligned} V(t)={\mathfrak {e}}^T(t)(I_N\otimes {\mathfrak {P}}_1){\mathfrak {e}}(t)+ {\mathfrak {y}}^T(t)(I_N\otimes {\mathfrak {P}}_2){\mathfrak {y}}(t), \end{aligned}$$

(12)

where ${\mathfrak {P}}_1$, ${\mathfrak {P}}_2$ are positive definite matrices. Then,

(13)

where and ${\mathfrak {H}}_2=I_N\otimes ({\mathfrak {B}}-({\mathfrak {A}}-I_n))$.

For the diagonal matrices ${{{\varSigma }}_1,{{\varSigma }}_2}>0$, we obtain from Assumption 1 that

$$\begin{aligned} 2{\mathfrak {y}}_i^T(t){\mathfrak {P}}_2{\mathfrak {C}}f({\mathfrak {e}}_i(t))\le & {} {\mathfrak {y}}_i^T(t){\mathfrak {P}}_2{\mathfrak {C}}{{\varSigma }}_1^{-1}{\mathfrak {C}}^T {\mathfrak {P}}_2{\mathfrak {y}}_i(t) +f^T({\mathfrak {e}}_i(t)){{\varSigma }}_1f({\mathfrak {e}}_i(t)) \nonumber \\\le & {} {\mathfrak {y}}_i^T(t){\mathfrak {P}}_2{\mathfrak {C}}{{\varSigma }}_1^{-1} {\mathfrak {C}}^T{\mathfrak {P}}_2{\mathfrak {y}}_i(t) +{\mathfrak {e}}_i^T(t){\varPi }^T{{\varSigma }}_1{\varPi }{\mathfrak {e}}_i(t), \end{aligned}$$

(14)

$$\begin{aligned} 2{\mathfrak {y}}_i^T(t){\mathfrak {P}}_2{\mathfrak {D}}f({\mathfrak {e}}_i(t-\tau (t)))\le & {} {\mathfrak {y}}_i^T(t){\mathfrak {P}}_2{\mathfrak {D}}{{\varSigma }}_2^{-1} {\mathfrak {D}}^T{\mathfrak {P}}_2{\mathfrak {y}}_i(t) \nonumber \\&+f^T({\mathfrak {e}}_i(t-\tau (t))){{\varSigma }}_2f({\mathfrak {e}}_i(t-\tau (t)))\nonumber \\\le & {} {\mathfrak {y}}_i^T(t){\mathfrak {P}}_2 {\mathfrak {C}}{{\varSigma }}_2^{-1}{\mathfrak {C}}^T{\mathfrak {P}}_2{\mathfrak {y}}_i(t) \nonumber \\&+{\mathfrak {e}}_i^T(t-\tau (t)){\varPi }^T{{\varSigma }}_2{\varPi }{\mathfrak {e}}_i(t-\tau (t)). \end{aligned}$$

(15)

Thus,

$$\begin{aligned} 2{\mathfrak {y}}^T(t)I_N\otimes ({\mathfrak {P}}_2{\mathfrak {C}}) {F}({\mathfrak {e}}(t))\le & {} {\mathfrak {y}}^T(t)I_N\otimes ({\mathfrak {P}}_2{\mathfrak {C}} {{\varSigma }}_1^{-1}{\mathfrak {C}}^T{\mathfrak {P}}_2){\mathfrak {y}}(t) \nonumber \\&+{\mathfrak {e}}^T(t)I_N\otimes ({\varPi }^T{{\varSigma }}_1{\varPi }){\mathfrak {e}}(t), \end{aligned}$$

(16)

$$\begin{aligned} 2{\mathfrak {y}}^T(t)I_N\otimes ({\mathfrak {P}}_2{\mathfrak {D}}) {F}({\mathfrak {e}}(t-\tau (t)))\le & {} {\mathfrak {y}}^T(t)I_N\otimes ({\mathfrak {P}}_2{\mathfrak {D}} {{{\varSigma }}}_2^{-1}{\mathfrak {D}}^T{\mathfrak {P}}_2){\mathfrak {y}}(t) \nonumber \\&+{\mathfrak {e}}^T(t-\tau (t))I_N\otimes ({\varPi }^T{{{\varSigma }}}_2{\varPi }) {\mathfrak {e}}(t-\tau (t)).\qquad \end{aligned}$$

(17)

Similarly,

(18)

(19)

hold for the diagonal matrices ${{{\varSigma }}_3,{{\varSigma }}_4>0}$. Using the Eqs. (9)–(10) and the Schur complementary theorem,

$$\begin{aligned} \begin{aligned} V(t)\le&\,\alpha V(t)+\theta _1{\mathfrak {e}}^T(t-\tau (t))I_N \otimes {\mathfrak {P}}_1{\mathfrak {e}}^T(t-\tau (t))\\&+\theta _2{\mathfrak {y}}^T(t-\kappa _0)I_N\otimes {\mathfrak {P}}_2 {\mathfrak {y}}^T(t-\kappa _0) +\theta _3\displaystyle \int _{t-h_0}^t {\mathfrak {y}}^T(s)I_N\otimes {\mathfrak {P}}_2{\mathfrak {y}}(s)\mathrm {d}s\\ \le&\,\alpha V(t)+\theta _1V(t-\tau (t))+\theta _2V(t-\kappa _0) +\theta _3\displaystyle \int _{t-h_0}^tV(s)\mathrm {d}s \end{aligned} \end{aligned}$$

(20)

holds for $t\ne t_k$ and

$$\begin{aligned} \begin{aligned} V(t_k)=&\,{\mathfrak {e}}^T(t_k)I_N\otimes {\mathfrak {P}}_1{\mathfrak {e}}(t_k) +{\mathfrak {y}}^T(t_k)I_N\otimes {\mathfrak {P}}_2{\mathfrak {y}}(t_k)\\ \le&\,{(1+{\mathfrak {K}}_1)^2{\mathfrak {e}}(t_k^-)I\otimes {\mathfrak {P}}_1{\mathfrak {e}}(t_k^-) +(1+{\mathfrak {K}}_2)^2{\mathfrak {y}}(t_k^-)I\otimes {\mathfrak {P}}_2{\mathfrak {y}}(t_k^-)}\\ \le&\,{\tilde{\beta }}V(t_k^-). \end{aligned} \end{aligned}$$

(21)

According to the Eqs. (20)–(21), consider the following comparison system,

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}(t)=\alpha x(t)+\theta _1x(t-\tau (t))+\theta _2x(t-\kappa _0) +\theta _3\displaystyle \int _{t-h_0}^tx(s)\mathrm {d}s+\nu _0, \ t\ne t_k,\\ x(t_k)={\tilde{\beta }}x(t_k^-),\\ x(s)=\lambda _{\max }({\mathfrak {P}}_1)\Vert {\mathfrak {e}}(s)\Vert ^2 +\lambda _{\max }({\mathfrak {P}}_2)\Vert {\mathfrak {y}}(s)\Vert ^2+\nu _0, -\max \{\tau _0,\kappa _0,h_0\}\le s\le 0, \end{array}\right. \end{aligned}$$

(22)

where x(t) is the unique solution for any $\nu _0>0$. Using the Lemma 1 and the analysis method in the proof of the theorem 2 in the [11], the origin of the error system (6) is exponentially stable. $\square$

Corollary 1

Assume that $0<{\tilde{\beta }}<1$ and the impulsive instants satisfy the Definition 2, and the matrix ${\mathfrak {L}}^{(1)}$ is irreducible with zero-row-sum. If there are positive definite matrix ${\mathfrak {P}}_{2}>0$, diagonal matrices ${\mathfrak {P}}_{1}>0$, ${{{\varSigma }}}_{j}>0$, $j=1,2,3,4$ and positive constants $\theta _1,\theta _2,\theta _3>0$, $\alpha >0$ such that the Eq. (9), the Eq. (11) and

(23)

hold, where ${\varPsi }_1=-{\mathfrak {P}}_2({\mathfrak {A}}-I_n)-({\mathfrak {A}}-I_n)^T{\mathfrak {P}}_2-\alpha {\mathfrak {P}}_2$, ${\varPsi }_2={\mathfrak {P}}_1+{\mathfrak {P}}_2({\mathfrak {A}}-{\mathfrak {B}}-I_n)$, ${\varPhi }_1=-(2+\alpha ){\mathfrak {P}}_1+{\varPi }^T{{\varSigma }}_1{\varPi }$ and ${\varPi }$ is defined in the Theorem 1. Then the coupled INNs (2) can realize exponential synchronization.

Proof

On the one hand, ${\mathfrak {L}}^{(1)}+{\mathfrak {L}}^{(1)T}\le 0$ because ${\mathfrak {L}}^{(1)}$ is irreducible with zero-row-sum. Therefore, the following one is valid for any diagonal matrix ${\mathfrak {P}}_{1}>0$,

(24)

On the other hand,

(25)

(26)

By adopting the proceeds of the former proof in the Theorem 1, the Corollary 1 holds. $\square$

3.2 Pinning Impulsive Control Design

Let ${\mathbb {I}}(t_k)=\left\{ j_1,j_2,\ldots ,j_{m_k}\right\} \subset \left\{ 1,2,\ldots ,N\right\}$ represent the set of pinning-controlled nodes at each impulsive instant $t=t_k$. Simultaneously, readjust the node error states ${\mathfrak {e}}_i(t)$ such that

$$\begin{aligned} \begin{aligned} {\mathfrak {Z}}_{j_1}(t_k)&=\left\| {\mathfrak {e}}_{j_1}(t_k)\right\| + \left\| {\mathfrak {y}}_{j_1}(t_k)\right\| \ge \cdots \ge {\mathfrak {Z}}_{j_m}(t_k)=\left\| {\mathfrak {e}}_{j_{m}}(t_k)\right\| +\left\| {\mathfrak {y}}_{j_{m}}(t_k)\right\| \\&\ge {\mathfrak {Z}}_{j_{m+1}}(t_k)=\left\| {\mathfrak {e}}_{j_{m+1}}(t_k) \right\| +\left\| {\mathfrak {y}}_{j_{m+1}}(t_k)\right\| \\&\ge \cdots \ge {\mathfrak {Z}}_{j_N}(t_k)=\left\| {\mathfrak {e}}_{j_N}(t_k)\right\| +\left\| {\mathfrak {y}}_{j_N}(t_k)\right\| , \end{aligned} \end{aligned}$$

(27)

where $j_m,m\in \left\{ 1,2,\ldots ,N\right\}$ and $j_s\ne j_r$ if $s\ne r$. Moreover, if $\left\| {\mathfrak {e}}_{j_{m}}(t_k)\right\| + \left\| {\mathfrak {y}}_{j_{m}}(t_k)\right\| =\left\| {\mathfrak {e}}_{j_{m+1}}(t_k)\right\| +\left\| {\mathfrak {y}}_{j_{m+1}}(t_k)\right\|$, then take $j_{m}<j_{m+1}$. Consider the coupled INNs with pinning impulsive control as

(28)

where ${\mathfrak {K}}_1$ and ${\mathfrak {K}}_2$ are defined in the Eq. (5). ${\mathbb {I}}(t_k)$ is the index set of the pinning-controlled nodes at $t_k$ and $\sharp {\mathbb {I}}(t_k)=l_k$ is the number of the pinning-controlled nodes at $t=t_k$.

Definition 3

The pinning impulsive control ratio $\eta _k$ at $t=t_k$ is defined as

$$\begin{aligned} \eta _k=\displaystyle \frac{\sum \limits _{i\in {\mathbb {I}}(t_k)} {\mathfrak {e}}_i^T(t_k^-){\mathfrak {e}}_i(t_k^-)+ {\mathfrak {y}}_i^T(t_k^-){\mathfrak {y}}_i(t_k^-)}{\sum \limits _{i=1}^N{\mathfrak {e}}_i^T(t_k^-){\mathfrak {e}}_i(t_k^-) +{\mathfrak {y}}_i^T(t_k^-){\mathfrak {y}}_i(t_k^-)}= \displaystyle \frac{\sum \limits _{i\in {\mathbb {I}}(t_k)} {\mathfrak {Z}}_i(t_k^-)}{\sum \limits _{i=1}^N{\mathfrak {Z}}_i(t_k^-)}. \end{aligned}$$

Theorem 2

Assume that $0<{\tilde{\beta }}<1$ and the impulsive instants satisfy the Definition 2. If there are matrices ${\mathfrak {P}}_1>0$, ${\mathfrak {P}}_2>0$, diagonal matrices ${{{\varSigma }}}_j>0$, $j=1,2,3,4$, positive constants $\theta _j$, $j=1,2,3$, $\alpha >0$, $d\in (0,1)$ and the pinning impulsive control ratio $\eta _k\in (0,1)$ such that the Eqs. (9)–(10) and

$$\begin{aligned}&({\tilde{\beta }}-1){\underline{\lambda }}\eta _k+{\bar{\lambda }}\le d{\underline{\lambda }}, \end{aligned}$$

(29)

$$\begin{aligned}&{\alpha }+\displaystyle \frac{\ln d}{{\mathfrak {T}}_a} +\frac{\theta _1+\theta _2+\theta _3h_0}{d^{{\mathfrak {N}}_0}}<0 \end{aligned}$$

(30)

hold, where ${\bar{\lambda }}=\max \{\lambda _{\max }({\mathfrak {P}}_1), \lambda _{\max }({\mathfrak {P}}_2)\}$ and ${\underline{\lambda }}=\min \{\lambda _{\min }({\mathfrak {P}}_1), \lambda _{\min }({\mathfrak {P}}_2)\}$. The origin of the system (6) is exponentially stable and the coupled INNs (2) can realize exponential synchronization.

Proof

Clearly,

$$\begin{aligned} \begin{aligned} V(t_k)=&\displaystyle \sum \limits _{i\in {\mathbb {I}}(t_k)}{\mathfrak {e}}_i^T(t_k) {\mathfrak {P}}_1 {\mathfrak {e}}_i(t_k)+{\mathfrak {y}}_i^T(t_k){\mathfrak {P}}_2{\mathfrak {y}}_i(t_k)\\&+\displaystyle \sum \limits _{i\notin {\mathbb {I}}(t_k)} {\mathfrak {e}}_i^T(t_k){\mathfrak {P}}_2e_i(t_k)+{\mathfrak {y}}_i^T(t_k){\mathfrak {P}}_2 {\mathfrak {y}}_i(t_k)\\ =&\displaystyle \sum \limits _{i\in {\mathbb {I}}(t_k)}{\mathfrak {e}}_i^T(t_k^-) (I_n+{\mathfrak {K}}_1)^T {\mathfrak {P}}_1(I_n+{\mathfrak {K}}_1){\mathfrak {e}}_i(t_k^-)\\&+{\mathfrak {y}}_i^T(t_k^-)(I_n+{\mathfrak {K}}_2)^T{\mathfrak {P}}_2 (I_n+{\mathfrak {K}}_2) {\mathfrak {y}}_i(t_k^-)\\&+\displaystyle \sum \limits _{i\notin {\mathbb {I}}(t_k)} {\mathfrak {e}}_i^T(t_k^-){\mathfrak {P}}_1{\mathfrak {e}}_i(t_k^-) +{\mathfrak {y}}_i^T(t_k^-){\mathfrak {P}}_2{\mathfrak {y}}_i(t_k^-)\\ \le&\,{\tilde{\beta }}\displaystyle \sum \limits _{i\in {\mathbb {I}}(t_k)} {\mathfrak {e}}_i^T(t_k^-){\mathfrak {P}}_1{\mathfrak {e}}_i(t_k^-)\\&+{\mathfrak {y}}_i^T(t_k^-){\mathfrak {P}}_2{\mathfrak {y}}_i(t_k^-) +\displaystyle \sum \limits _{i\notin {\mathbb {I}}(t_k)} {\mathfrak {e}}_i^T(t_k^-){\mathfrak {P}}_1{\mathfrak {e}}_i(t_k^-) +{\mathfrak {y}}_i^T(t_k^-){\mathfrak {P}}_2{\mathfrak {y}}_i(t_k^-)\\ \le&\displaystyle \frac{({\tilde{\beta }}-1){\underline{\lambda }} \eta _k+{\bar{\lambda }}}{{\underline{\lambda }}}V(t_k^-)\le dV(t_k^-). \end{aligned} \end{aligned}$$

(31)

holds for $t=t_k$. By adopting the similar proceeds in the proof of Theorem 1, the desired result holds. $\square$

Take ${\mathfrak {P}}_1={\mathfrak {P}}_2=I_n$, ${{{\varSigma }}}_i=\delta _iI_n$, $i=0,1,2,3,4$, then the following criterion holds for pinning control.

Theorem 3

Assume that $0<{\tilde{\beta }}<1$ and the impulsive instants satisfy the Definition 2. If there are real scalars $\delta _i>0$, $i=0,1,2,3,4$, $d\in ({\tilde{\beta }},1)$ such that

$$\begin{aligned}&\displaystyle \frac{1-d}{1-{\tilde{\beta }}}\le \eta _k<1, \end{aligned}$$

(32)

$$\begin{aligned}&\alpha +\displaystyle \frac{\ln d}{{\mathfrak {T}}_a} +\frac{\delta _2\lambda _{\mathrm{max}}({\varPi }^T{\varPi })+{\mathfrak {c}}_2 \delta _3+{\mathfrak {c}}_3\delta _4h_0}{d^{{\mathfrak {N}}_0}}<0 \end{aligned}$$

(33)

hold, where $\eta _k$ is the pinning impulsive control ratio, $\alpha =\max \{-2+\delta _0+\delta _1\lambda _{\mathrm{max}}({\varPi }^T{\varPi }), \alpha _1\}$, $\alpha _1=\delta _0^{-1}\lambda _{\mathrm{max}}(({\mathfrak {A}}-{\mathfrak {B}})^T({\mathfrak {A}}-{\mathfrak {B}}))+ \delta _1^{-1}\lambda _{\mathrm{max}}({{\mathfrak {C}}}{{\mathfrak {C}}}^T)+\delta _2^{-1}\lambda _{\mathrm{max}}({{\mathfrak {D}}}{{\mathfrak {D}}}^T) +\delta _3^{-1}c_2\lambda _{\mathrm{max}}({\mathfrak {L}}^{(2)}{\mathfrak {L}}^{(2)T})$, and ${\varPi }$ is defined in the Theorem 1. The coupled INNs (2) can realize exponential synchronization.

Proof

For $\delta _i>0$, $i=0,1,2,3,4$, we have

(34)

According to the Eq. (31), this criterion holds. $\square$

Remark 2

Let $\eta ^0=\displaystyle \frac{1-d}{1-{\tilde{\beta }}}$ and N be the size of the coupled INNs. It is clear that $\eta ^0\left( 1+\sum \nolimits _{i=2}^N\frac{{\mathfrak {Z}}_{j_i}(t_k^-)}{{\mathfrak {Z}}_{j_1}(t_k^-)}\right) \le 1$ if $\eta ^0N\le 1$. Thus, $\eta ^0N\le 1$ implies that $\eta _k(t_k)= \displaystyle \frac{{\mathfrak {Z}}_{j_1}(t_k^-)}{\sum \nolimits _{i=1}^N{\mathfrak {Z}}_{j_i}(t_k^-)}=\displaystyle \frac{1}{1+\sum \nolimits _{i=2}^N \frac{{\mathfrak {Z}}_{j_i}(t_k^-)}{{\mathfrak {Z}}_{j_1}(t_k^-)}}\in [\eta ^0,1)$, in which the pinning impulsive control ratio $\eta _k$ satisfies the the Eq. (32). Therefore, the coupled INNs (2) can do realize synchronization by exerting the impulsive control on one node at each impulsive time $t_k$ if the lower bound $\eta ^0$ of the pinning control ratio $\eta _k$ satisfies $N\eta ^0<1$. Although the pinning impulsive control with one controlled node can reduce the complexity of the controller design, it will lead small ${\mathfrak {T}}_a$ which can increase the control cost. As a consequence, there is a tradeoff between the control cost and simple controller design in real practice.

Remark 3

The ratio $\eta _k$ in Definition 3 is dependent on both the impulsive instant $t_k$ and the states ${\mathfrak {e}}_i(\cdot )$ and ${\mathfrak {y}}_i(\cdot )$. Thus, at each impulsive instant $t_k$, the pinning control ratio $\eta _k$ cannot be employed to determine the controlled nodes in the the Eq. (27) directly. However, the lower bound $\eta ^0$ of the control ratio $\eta _k$ can help us to determine the number of the pinning controlled nodes. If $\eta ^0N\le 1$, the pinning controlled node is the first one in the Eq. (27). If $\eta ^0N>1$, assume that the first $s_0$ ($s_0\le N$) nodes should be pinning controlled in the Eq. (27), then we next show that $s_0\sum \nolimits _{i=1}^N{\mathfrak {Z}}_{j_i}(t_k^-)\le N\sum \nolimits _{i=1}^{s_0}{\mathfrak {Z}}_{j_i}(t_k^-)$ if the Eq. (27) holds. Clearly, the Eq. (27) implies that

$$\begin{aligned} \begin{aligned} N\sum \limits _{i=1}^{s_0}{\mathfrak {Z}}_{j_i}(t_k^-) -s_0\sum \limits _{i=1}^N{\mathfrak {Z}}_{j_i}(t_k^-)&= (N-s_0)\sum \limits _{i=1}^{s_0}{\mathfrak {Z}}_{j_i}(t_k^-)-s_0 \sum \limits _{i=s_0+1}^{N}{\mathfrak {Z}}_{j_i}(t_k^-)\\&\ge (N-s_0)s_0{\mathfrak {Z}}_{j_{s_0}}(t_k^-)-s_0(N-s_0) {\mathfrak {Z}}_{j_{s_0+1}}(t_k^-)\\&\ge 0. \end{aligned} \end{aligned}$$

(35)

Therefore, take

$$\begin{aligned} \eta _k=\displaystyle \frac{\sum \nolimits _{i=1}^{s_0}{\mathfrak {Z}}_{j_i}(t_k^-)}{\sum \nolimits _{i=1}^N{\mathfrak {Z}}_{j_i}(t_k^-)}\ge \frac{s_0}{N}\ge \eta ^0, \end{aligned}$$

(36)

which implies that $s_0>N\eta ^0$. Thus, the minimal value of the integer $\eta ^0$ is $[N\eta ^0]+1$, where $[\cdot ]$ is the integral function and N represents the size of the coupled networks.

Remark 4

According to the Eq. (32) and the Eq. (33), there are three steps to design the pinning impulsive control. 1). Choose the positive constants $\delta _i$, $i=0,1,\ldots ,4$ such that the parameter $\alpha$ is a positive constant in the Eq. (33), 2). for any given pinning control ratio $0<\eta _k<1$, determine the constant d in the Eq. (32) satisfied $0<d<1$, 3). for given ${\mathfrak {N}}_0$, determine the average impulsive interval ${\mathfrak {T}}_a$ according to the Eq. (33).

Remark 5

Note that the synchronization criteria here are not dependent on ${\dot{\tau }}(t)$, i. e. the derivative of time delay function. Thus, our results do not require that the transmission $\tau (t)$ is a derivable function [19,20,21], which shows that our developed method is more applicable in designing the synchronization controller for the coupled INNs with various transmission delays.

4 Numerical Examples

The identical node of the considered coupled INNs is described as

$$\begin{aligned} \ddot{{\mathfrak {u}}}_i(t)=-{\mathfrak {A}}\dot{{\mathfrak {u}}}_i(t)- {\mathfrak {Bu}}_i(t) +{\mathfrak {C}}f({\mathfrak {u}}_i(t))+{\mathfrak {D}}f({\mathfrak {u}}_i(t-\tau _0)), \end{aligned}$$

(37)

where ${\mathfrak {u}}_i(t)\in {\mathbb {R}}^2$, $i=1,2$, $f({\mathfrak {u}}_i) =\left[ \tanh ({\mathfrak {u}}_{i1}),\tanh ({\mathfrak {u}}_{i2})\right] ^T$, ${\mathfrak {A}}=\mathrm{diag}\{0.88,1.2\}$, ${\mathfrak {B}}=I_2$, $\tau _0=1$ and

$$\begin{aligned} {\mathfrak {C}}=\left( \begin{array}{cc} 2.1&{}-0.15\\ -5&{}3.1 \end{array}\right) , \quad {\mathfrak {D}}=\left( \begin{array}{cc} -1.5&{}-0.1\\ -0.2&{}-2.5 \end{array}\right) . \end{aligned}$$

The phase plot of the above-mentioned system is given in the Fig. 1.

Fig. 1

The phase plot of the system (37)

Fig. 2

a The delay-free case, b the transmittal delay case, c the distributed-delay case in Example 1

Fig. 3

Time histories of the variables (a). $x_{i1}$ and (b). $x_{i2}$ of the coupled INNs in Example 1

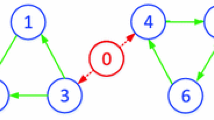
Example 1

The considered structures of the coupled INNs are illustrated in the Fig. 2. Noting that ${\mathfrak {L}}^{(1)}$ is irreducible with zero-row-sum, the Corollary 1 can be utilize to design the pinning impulsive controller for the coupled INNs. Suppose that , ${\mathfrak {c}}_1={\mathfrak {c}}_3=0.2$, ${\mathfrak {c}}_2=0.1$. Take $\alpha =7$, $\theta _1=\theta _2=\theta _3=0.5$ and solve the Eq. (9) and the Eq. (23) in MATLAB environment yields

$$\begin{aligned} {\mathfrak {P}}_1= & {} \left[ \begin{array}{cc} 1732.5&{}4.7\\ 4.7&{}691.1\end{array}\right] , \ {\mathfrak {P}}_2=\left[ \begin{array}{cc} 322.5455&{}0.4637\\ 0.4637&{}62.8682\end{array}\right] , \\ {{\varSigma }}_1= & {} \mathrm{diag}\{9809.8,1593.4\}, \ \ \ {{\varSigma }}_2=\mathrm{diag}\{741.5999,334.6486\}, \\ {{\varSigma }}_3= & {} \mathrm{diag}\{1261.4,298.1\}, \ \ \ {{\varSigma }}_4=\mathrm{diag}\{762.7841,155.3765\}. \end{aligned}$$

The time histories of the coupled INNs without impulsive control are given in the Fig. 3. Obviously, the coupled INNs cannot realize the synchronization without control input. Set ${\tilde{\beta }}=0.36$ and ${\mathfrak {N}}_0=2$, we can obtain that ${\mathfrak {T}}_a<0.055$ according to the Eq. (11). Take $t_k=0.1k$, $k=1,2,\ldots$, the time histories of the state variables are shown in the Fig. 4 and the time histories of the synchronization error are illustrated in the Fig. 5. Clearly, the coupled INNs with identical nodes (37) can achieve the synchronization under impulsive control.

Example 2

Different from the symmetrical coupling matrices in Example 1, the coupled INNs with asymmetric coupling matrices are considered in this example. The effectiveness of the Theorem 3 is verified by designing the pinning impulsive control. The considered coupling structures are illustrated in the Fig. 6.

Suppose that the coupling strength ${\mathfrak {c}}_1=1.2$, ${\mathfrak {c}}_2=1$, ${\mathfrak {c}}_3=0.5$, and the inner coupling matrices , , . Take $\delta _0=0.1$, $\delta _1=15$, $\delta _2=4$, $\delta _3=1$, $\delta _4=3$, ${\mathfrak {K}}_1={\mathfrak {K}}_2=-0.65I_2$ and $d=0.86$, the lower bound of the pinning impulsive control ratio $\eta _k$ is $\eta ^0=0.1595$ for $k=1,2,\ldots$, we have $\alpha =13.1$ which implies that ${\mathfrak {T}}_a<0.0054$ holds for ${\mathfrak {N}}_0=4$. Note that $\eta ^0=0.1595$ means that $6\eta ^0=0.9<1$. Therefore, the impulsive control can expended on only 1 node at each impulsive instant $t_k$, in order to obtain the synchronization of the coupled INNs.

For numerical simulation, set the impulsive instant $t_k=0.02k$, $k=1,2,\cdots$, the evolutions of all nodes and the synchronization error system are given in the Figs. 7 and 8, individually. Under the pinning control exerted on 1 node at each impulsive time, it is clear that the coupled INNs can achieve synchronization.

Fig. 4

Time histories of the variable (a). $x_{i1}$ and (b). $x_{i2}$ of the coupled INNs with impulsive control in Example 1

Fig. 5

Time histories of the synchronization error variables (a). $e_{i1}$ and (b). $e_{i2}$ with impulsive control in Example 1

Fig. 6

a The delay-free case, b the transmittal delay case, c the distributed-delay case in Example 2

Fig. 7

Time histories of the variables (a). $x_{i1}$ and (b). $x_{i2}$ of the coupled INNs with impulsive control in Example 2

Fig. 8

Time histories of the synchronization error variables (a). $e_{i1}$ and (b). $e_{i2}$ of the coupled INNs with impulsive control in Example 2

5 Conclusion

The synchronization controller design issue for coupled INNs with hybrid coupling has been investigated here. The distributed-delay-dependent synchronization criteria have been given based on impulsive control and pinning control. Several easy-checked algebraic criteria has been introduced to reduce the calculated amount of the criteria based on linear matrix inequalities. The selection strategy of the pinning controlled nodes is given by using the lower bound $\eta ^0$ of the pinning control ration $\eta _k$ at each impulsive control instant. Specifically, if $N\eta ^0\le 1$, the controlled node is the first one in the Eq. (27), else the pinning impulsive controlled nodes are the first $[N\eta ^0]+1$ nodes in the Eq. (27), where $[\cdot ]$ is the integral function and N represents the size of the coupled networks. Finally, two numerical examples are outlined to exhibit the capability of our control strategy. In the future work, as discussed in the works [42,43,44,45], the finite-time stability and synchronization problems of the coupled complex/octonion neural networks are investigated by using the impulsive control and pinning control strategy proposed in the present paper.