1 Introduction

In a complex network, each node represents a basic element with certain dynamical characteristics and information systems, while edges represent the relationship or connection of these basic elements [1]. From a system-theoretic point of view, a complex dynamical network can be considered as a large-scale system with special interconnections among its dynamical nodes [2, 3]. Complex networks are ubiquitous, and have been considered as a fundamental tool to understand dynamical behavior and the response of real systems such as food webs, social networks, power grids, cellular networks, World Wide Web, metabolic systems, disease transmission networks, and many others (see [4,5,6,7] and references there in). These systems exhibit complicated dynamics which are represented by a set of interconnected nodes, edges and coupling strength [9, 10]. Nowadays, extensive research work is focused on complex dynamical networks (CDNs) due to its wider applications in computer networks, biological networks, communication networks, etc.

In real complex network systems, such as in the progress of brain nervous activity, time delay occurs during the information transmission between nerve cells because of the limited speed of signal transmission as well as in the network traffic congestion systems. Thus, presence of time delays (coupling delays) in CDNs is unavoidable [11,12,13]. It leads often as a source of instability and poor performance of system behaviors, for instance, see [14,15,16]. In recent decades, considerable attention has been devoted to the time-varying delay systems due to their extensive applications in practical systems including circuit theory, chemical processing, bio engineering, complex dynamical networks, automatic control and so on. In the implementation of complex dynamical networks, time-varying delay is unavoidably encountered due to the finite speed of signal transmission over the link and the network traffic congestions [18,19,20,21].

Switched systems are a class of hybrid systems which consist of a family of subsystems and which are controlled by switching laws. There are many practical switched systems in which switching signals depend on time [22,23,24,25]. For example, in [26], the stability problem has been investigated for a class of switched-capacitor power converter, in which the network mode switched from one to another according to time. There are numerous applications for such systems, including water quality control, electric power systems, productive manufacturing systems, and cold steel rolling mills [27]. Clearly, the switching signal in the complex networks depending on time can be implemented easier than the switching signal depending on the state since it does not need to check the system states [28,29,30].

When modeling real nervous systems with interconnected nodes, stochastic effects and parameters uncertainties are probably two main resources of the performance degradations of the implemented complex networks [31]. Because in many system, synaptic transmission is a noisy process brought on by random fluctuation from the release of neurotransmitters, and the connection weights of the neuron depend on certain resistance and capacitance values that include uncertainties (see [32,33,34,35] and references there in). Hence, the stability analysis problem for stochastic time delayed complex networks with or without parameter uncertainties becomes increasingly significant, and some results related to this problem have recently been published [36,37,38,39,40]. Moreover, there exist some uncertainties due to the existence of external disturbance and modeling errors, which might lead to undesirable dynamic behaviors such as instability [42]. Thus, it is important to study the robust stability of the stochastic switched complex dynamical network against these uncertainties.

Furthermore, apart from the packet dropouts, inaccuracies or uncertainties usually occur in the implementation of the filters. The uncertainties could give rise to instability to the filtering system. To circumvent this obstacle, many researchers commit themselves to designing a resilient filter which can be insensitive with respect to filter gain uncertainties [43, 44]. The problem of filtering has been widely applied in the fields of signal processing, image processing and control applications (see [45] and references there in). However, in many practical applications, the statistical assumptions on the external noise signals cannot be known exactly. To overcome this limitation, \(H_\infty \) filtering technique has been introduced to deal with unavoidable parameter shifts and external disturbances [46]. The main objective is to design a filter such that the mapping from the external input to the filtering error is minimized or is less than a prescribed level according to the \(H_\infty \) norm see e.g. [47,48,49]. Especially, the problems of performance analysis and filter design for continuous-time and discrete-time CDNs were addressed in [50, 51], respectively. Motivated by the above discussions, in this paper, we study the \(H_\infty \) filtering problem of stochastic switched CDNs with time-varying delays.

The main contributions of this paper lie in the following aspects:

  • Suitable full-order H8 filters are designed for each node for continuous-time CDNs with time-varying delays is proposed for the first time.

  • Lyapunov–Krasovskii function is provided, and reciprocal convex combination and Jensen’s inequality approach are adopted.

  • The properties of Kronecker product is employed to derive the stability conditions in a more compact form.

  • Delay-dependent results for robust \(H_{\infty }\) is derived by using Lyapunov–Krasovskii functional approach.

  • Reciprocal convex combination approach is adopted to cope with reducing the conservatism of the established delay-dependent conditions.

  • Sufficient conditions are proposed in terms of LMIs, which can be solved by using standard numerical packages.

Notation\({\mathbb {R}}^m\) denotes the m dimensional Euclidean space and \({\mathbb {R}}^{m \times n}\) is the set of all \(m\times n\) real matrices. \(\parallel .\parallel \) denotes the Euclidean norm in \({\mathbb {R}}^n\). The superscript “\(T \)” denotes transpose of the matrix and the notation \(\breve{\mathbf {A}} \ge \breve{\mathbf {B}}\) (respectively, \(\breve{\mathbf {A}}<\breve{\mathbf {B}}\)) where \(\breve{\mathbf {A}}\) and \(\breve{\mathbf {B}}\) are symmetric matrices, means that \(\breve{\mathbf {A}}-\breve{\mathbf {B}}\) is positive semidefinite (respectively, positive definite). The notation \({\mathbb {E}}\) stands for the mathematical expectation operator. While {\(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_{t}\}_{t\ge 0},{\mathcal {P}}\)} is a probability space , where \(\Omega \) is the sample space, \({\mathcal {F}}\) is the algebra of events and \({\mathcal {P}}\) is the probability measure defined on \({\mathcal {F}}\). The shorthand \(diag\{\cdot \}\) stands for a diagonal or block diagonal matrix.

2 Problem Formulation and Preliminaries

We consider the following uncertain stochastic switched complex dynamical networks with mixed time-varying delays consisting of N identical nodes, in which each node is an n-dimensional dynamical models:

$$\begin{aligned} dx_l(t)&=[(\breve{\mathbf {E}}_{\rho _k}+\triangle \breve{\mathbf {E}}_{\rho _k}(t))x_l(t) +(\breve{\mathbf {E}}_{1\rho _k}+\triangle \breve{\mathbf {E}}_{1\rho _k}(t))f_{\rho _k}(x_l(t)) \nonumber \\&\quad +(\breve{\mathbf {E}}_{2\rho _k}+\triangle \breve{\mathbf {E}}_{2\rho _k}(t)) f_{\rho _k}(x_l(t-\delta (t)))\nonumber \\&\quad +\sum _{j=1}^Nw_{\rho _klj}\Upsilon _{1\rho _k} x_j(t) +\sum _{j=1}^Ng_{\rho _klj}\Upsilon _{2\rho _k} x_j(t-\delta (t)) \nonumber \\&\quad +(\breve{\mathbf {E}}_{x\rho _k}+ \triangle \breve{\mathbf {E}}_{x\rho _k}(t))\nu _l(t)]dt+[(\breve{\mathbf {H}}_{\rho _k} \nonumber \\&\quad +\triangle \breve{\mathbf {H}}_{\rho _k}(t))x_l(t) +(\breve{\mathbf {H}}_{1\rho _k}+\triangle \breve{\mathbf {H}}_{1\rho _k}(t))f_{\rho _k}(x_l(t)) \nonumber \\&\quad +(\breve{\mathbf {H}}_{2\rho _k}+\triangle \breve{\mathbf {H}}_{2\rho _k}(t)) f_{\rho _k}(x_l(t-\delta (t)))]dB_l(t), \nonumber \\ dy_l(t)&=[(\breve{\mathbf {E}}_{3\rho _k}+\triangle \breve{\mathbf {E}}_{3\rho _k}(t))x_l(t) +(\breve{\mathbf {E}}_{4\rho _k}+\triangle \breve{\mathbf {E}}_{4\rho _k}(t))f_{\rho _k}(x_l(t)) \nonumber \\&\quad +(\breve{\mathbf {E}}_{5\rho _k}+\triangle \breve{\mathbf {E}}_{5\rho _k}(t)) f_{\rho _k}(x_l(t-\delta (t)))\nonumber \\&\quad +(\breve{\mathbf {E}}_{y\rho _k}+\triangle \breve{\mathbf {E}}_{y\rho _k}(t))\nu _l(t)]dt+[(\breve{\mathbf {H}}_{3\rho _k} +\triangle \breve{\mathbf {H}}_{3\rho _k}(t)) x_l(t) \nonumber \\&\quad +(\breve{\mathbf {H}}_{4\rho _k}+\triangle \breve{\mathbf {H}}_{4\rho _k}(t))f_{\rho _k}(x_l(t)) \nonumber \\&\quad +(\breve{\mathbf {H}}_{5\rho _k}+\triangle \breve{\mathbf {H}}_{5\rho _k}(t)) f_{\rho _k}(x_l(t-\delta (t)))]dB_l(t), \nonumber \\ x_l(t)&=\varphi _l(t), \, \forall \ t \in [-\delta ,0],\,l= 1,2,\ldots .,N, \end{aligned}$$
(1)

where \(x_l(t)\in {\mathbb {R}}^n\) represents the state of the lth node of the system. \(\nu _l(t)\) is the exogenous disturbance inputs which belong to \(L_2[0, \infty )\); \(B_l(t)\) is zero-mean one-dimensional Wiener processes on \((\Omega , {\mathcal {F}}, {\mathcal {P}})\) satisfying \({\mathbb {E}}\{B_l(t)\} = 0\) and \({\mathbb {E}}\{B^2_l(t)\} = t\); \(y_l(t) \in R^m\) is the measured output of the lth node; \(\varphi _l(t)\) is a compatible vector-valued initial function defined on \([-\delta , 0]\); \(\breve{\mathbf {E}}_{\rho _k},\ \breve{\mathbf {E}}_{1\rho _k},\ \breve{\mathbf {E}}_{2\rho _k},\ \breve{\mathbf {E}}_{3\rho _k},\ \breve{\mathbf {E}}_{4\rho _k},\ \breve{\mathbf {E}}_{5\rho _k},\ \breve{\mathbf {H}}_{\rho _k}, \breve{\mathbf {H}}_{1\rho _k},\ \breve{\mathbf {H}}_{2\rho _k},\ \breve{\mathbf {H}}_{3\rho _k},\ \breve{\mathbf {H}}_{4\rho _k}\) and \( \breve{\mathbf {H}}_{5\rho _k}\) are known constant matrices with appropriate dimensions; \(\breve{\mathbf {E}}_{x\rho _k} \in {\mathbb {R}}^{m\times n}\) and \(\breve{\mathbf {E}}_{y\rho _k} \in {\mathbb {R}}^{m\times n}\) are some constant matrices. \(\rho _k : [0, \infty ) \rightarrow {\mathfrak {M}} = {1, 2,\ldots , m}\) is the switching signal, which is a piecewise constant function continuous from the right. \( f_{\rho _k} : {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n \) are continuously nonlinear vector functions.

\({\breve{\mathbf {W}}}_{\rho _k}= (w_{\rho _klj})_{N\times N}\) and \({\breve{\mathbf {G}}}_{\rho _k}= (g_{\rho _klj})_{N\times N}\) are the non-delayed and delayed outer-coupling matrices representing respectively the coupling strength and the topological structure of complex networks, in which \(w_{\rho _klj}\) and \(g_{\rho _klj}\) are defined as follows: if there is a connection between node l and node \(j\,(l\ne j)\), then \(w_{\rho _klj}=w_{\rho _kjl}=1\) and \(g_{\rho _klj}=g_{\rho _kjl}=1\); otherwise, \(w_{\rho _klj}=w_{\rho _kjl}=0\) and \(w_{\rho _klj}=w_{\rho _kjl}=0 \,(l\ne j)\). The row sums of \({\breve{\mathbf {W}}}_{\rho _k}\) and \({\breve{\mathbf {G}}}_{\rho _k}\) are zero, i.e., \(\sum _{j=1}^Nw_{\rho _klj} = -w_{\rho _kll}\) and \(\sum _{j=1}^Ng_{\rho _klj} = -g_{\rho _kll},\, l= 1,2,\ldots .,N.\)\(\Upsilon _{1\rho _k}= diag\{b_{a1\rho _k}, b_{a2\rho _k},\ldots .,b_{an\rho _k}\}\) and \(\Upsilon _{2\rho _k}= diag\{b_{a1\rho _k}, b_{a2\rho _k},\ldots .,b_{an\rho _k}\}\) are matrices describing the inner-coupling between the subsystems at time t and \(t-\delta (t)\) respectively; \(\delta (t)\) is the time-varying delay satisfies the following inequality

$$\begin{aligned} 0\le \delta _1\le \delta (t)\le \delta _2,\ {\dot{\delta }}(t) \le \delta _d < \infty , \end{aligned}$$

where \(\delta _1, \delta _2\) and \(\delta _d\) are known scalars.

Remark 1

In [26, 27, 30, 33], the author studied the robust analysis of switched complex networks with time delay. Since then, a lot of attempts on synchronization of stochastic complex dynamical networks have been made in [31, 36, 37]. In [50, 51], the \(H_\infty \) filtering problem of CDNs with time-varying delays has been studied. To the best of authors knowledge, \(H_\infty \) filtering analysis for stochastic switched CDNs with norm-bounded parameter uncertainties and time-varying delay by using reciprocal convex approach has not been studied still now. In this paper, we first offer an extended uncertain stochastic CDNs model containing most actual characteristics such as It’o-type stochastic disturbance, norm-bounded parameter uncertainties, and time-varying delays. Research in this area still remains challenging, which motivates this paper.

Assumption (A) The nonlinear function \({\mathbf {f}}_{\rho _k}(\cdot ) : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is assumed to be continuous and satisfies \({\mathbf {f}}(0) = 0\). Further the following sector-bounded condition holds

$$\begin{aligned}{}[{\mathbf {f}}_{\rho _k}(x) - {\mathbf {f}}_{\rho _k}(y) - {\mathbf {F}}_{\rho _k1}(x - y)]T [{\mathbf {f}}_{\rho _k}(x) - {\mathbf {f}}_{\rho _k}(y) - {\mathbf {F}}_{\rho _k2}(x - y)] \le 0 \end{aligned}$$
(2)

where \({\mathbf {F}}_{\rho _k1}\) and \({\mathbf {F}}_{\rho _k2}\) are known real constant matrices with appropriate dimensions

Assumption (B) The norm-bounded uncertainties \( \triangle \breve{\mathbf {E}}_{\rho _k}(t),\ \triangle \breve{\mathbf {H}}_{\rho _k}(t),\ \triangle \breve{\mathbf {E}}_{x\rho _k}(t),\ \triangle \breve{\mathbf {E}}_{y\rho _k}(t), \triangle \breve{\mathbf {E}}_{i\rho _k}(t)\) and \(\triangle \breve{\mathbf {H}}_{i\rho _k}(t) (i=1,\ldots ,5)\) are real-valued unknown matrices representing time-varying parameter uncertainties, and are assumed to be of the form:

$$\begin{aligned} \left[ \begin{array}{cc} \triangle \breve{\mathbf {E}}_{\rho _k}(t) &{} \triangle \breve{\mathbf {H}}_{\rho _k}(t) \\ \triangle \breve{\mathbf {E}}_{1\rho _k}(t) &{} \triangle \breve{\mathbf {H}}_{1\rho _k}(t)\\ \triangle \breve{\mathbf {E}}_{2\rho _k}(t)&{} \triangle \breve{\mathbf {H}}_{2\rho _k}(t)\\ \triangle \breve{\mathbf {E}}_{3\rho _k}(t)&{} \triangle \breve{\mathbf {H}}_{3\rho _k}(t)\\ \triangle \breve{\mathbf {E}}_{4\rho _k}(t)&{} \triangle \breve{\mathbf {H}}_{4\rho _k}(t)\\ \triangle \breve{\mathbf {E}}_{5\rho _k}(t)&{} \triangle \breve{\mathbf {H}}_{5\rho _k}(t) \end{array} \right]&=\left[ \begin{array}{c} \breve{\mathbf {M}}_{0\rho _k} \\ \breve{\mathbf {M}}_{1\rho _k} \\ \breve{\mathbf {M}}_{2\rho _k} \\ \breve{\mathbf {M}}_{3\rho _k} \\ \breve{\mathbf {M}}_{4\rho _k} \\ \breve{\mathbf {M}}_{5\rho _k} \end{array} \right] \breve{\mathbf {F}}(t)\left[ \begin{array}{cc} \breve{\mathbf {N}}_{e\rho _k}&\breve{\mathbf {N}}_{h\rho _k} \end{array} \right] , \end{aligned}$$
(3)
$$\begin{aligned} \left[ \begin{array}{c} \triangle \breve{\mathbf {E}}_{x\rho _k}(t) \\ \triangle \breve{\mathbf {E}}_{y\rho _k}(t) \end{array} \right]&=\left[ \begin{array}{c} \breve{\mathbf {M}}_{x\rho _k} \\ \breve{\mathbf {M}}_{y\rho _k} \end{array} \right] \breve{\mathbf {F}}(t) \breve{\mathbf {N}}_{a\rho _k}, \end{aligned}$$
(4)

where \(\breve{\mathbf {N}}_{e\rho _k},\ \breve{\mathbf {N}}_{h\rho _k},\ \breve{\mathbf {M}}_{x\rho _k},\ \breve{\mathbf {M}}_{y\rho _k},\ \breve{\mathbf {N}}_{a\rho _k}\) and \( \breve{\mathbf {M}}_{i\rho _k}(i=0,\ldots ,5) \) are known real constant matrices, \(\breve{\mathbf {F}}(t)\) is real time-varying matrix satisfying \(\breve{\mathbf {F}}^T(t)\breve{\mathbf {F}}(t) \le {\mathbf {I}},\) where \({\mathbf {I}}\) is an identity matrix with appropriate dimensions.

Remark 2

Our model is more popular and general than the complex dynamical networks model in [1], we introduce a new model of complex delayed dynamical networks, which includes the time-varying coupling strength, unknown time-varying diffusive coupling delay and stochastic perturbations. It is easy to check that the class of systems in the form of equations includes almost all the well-known chaotic systems with delays or without delays such as the Lorenz system, Rossler system, Chen system, Chua’s circuit as well as the delayed Mackey–Glass system or delayed Ikeda equation and so on (see references [17, 36, 41]). To illustrate the applicability of the proposed results, Barabasi–Albert (BA) scale-free network model is considered

Definition 1

The filtering error system (8) with \(\nu (t) = 0\) is said to be mean-square robustly asymptotically stable if for any \(\epsilon > 0\), there exists a \(\sigma (\epsilon ) > 0\) such that \({\mathbb {E}}\{\parallel {\tilde{x}}(t)\parallel ^2\} < \epsilon \) for any \(t\ge 0\) and all admissible uncertainties satisfying (3) and (4) when \(\sup _{t\in [-\delta ,0]}{\mathbb {E}}\{\parallel {\tilde{\varphi }}(t)\parallel ^2\} < \sigma (\epsilon )\). Moreover, if \(\lim _{t\rightarrow \infty }{\mathbb {E}}\{\parallel {\tilde{x}}(t)\parallel ^2\}=0,\) then system (8) with \(\nu (t) = 0\) is said to be globally mean-square robustly asymptotically stable.

Definition 2

For a given positive constant \(\gamma \), the filtering error system (8) is said to be mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \), if system (8)is said to be mean-square robustly asymptotically stable, and under the zero initial condition the following inequality

$$\begin{aligned} {\mathbb {E}}\Big \{\int _0^\infty (\parallel x(t)-{\hat{x}}(t)\parallel ^2)dt\Big \}\le \gamma ^2\int _0^\infty \parallel \nu (t)\parallel ^2dt \end{aligned}$$

holds for any nonzero \(\nu (t)\in L_2[0,+\infty ).\)

Remark 3

The lack of research analysis is probably due to difficulty in designing suitable filter parameters. In this situation, suitable full-order filter is designed for continuous-time CDNs with time-varying delays. In this paper, we utilized the reciprocal convex combination approach [53] to derive the sufficient conditions.

In this paper, we will design the following full-order filter to estimate the state and output in (1).

$$\begin{aligned} d{\hat{x}}_l(t)&={\mathbf {E}}_{fl\rho _k}{\hat{x}}_l(t)dt +{\mathbf {H}}_{fl\rho _k}dy_l(t), \end{aligned}$$
(5)

where \({\hat{x}}_l(t)\) is the filter state vector, \(y_l(t)\) is the output of the node. \({\mathbf {E}}_{f\rho _k}\) and \({\mathbf {H}}_{f\rho _k}\) are appropriately dimensioned filter matrices to be designed.

Define \({\tilde{x}}_l(t)=\left[ \begin{array}{cc} x^T_l(t)&{\hat{x}}^T_l(t) \end{array} \right] ^T\) and \({\tilde{\varphi }}_l(t)=\left[ \begin{array}{cc} \varphi ^T_l(t)&0^T \end{array} \right] ^T\), the filtering error system is as follows:

$$\begin{aligned} d{\tilde{x}}_l(t)&=[({\tilde{\mathbf {E}}}_{\rho _k}+ \triangle {\tilde{\mathbf {E}}}_{\rho _k}(t)){\tilde{x}}_l(t) +({\tilde{\mathbf {E}}}_{1\rho _k}+\triangle {\tilde{\mathbf {E}}}_{1\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}_l(t)) +({\tilde{\mathbf {E}}}_{2\rho _k}+\triangle {\tilde{\mathbf {E}}}_{2\rho _k}(t)) {\mathbf {K}}\nonumber \\&\quad \times f_{\rho _k}({\tilde{x}}_l(t-\delta (t)))+ {\tilde{\mathbf {G}}}_{\rho _k}{\mathbf {K}} {\tilde{x}}_l(t-\delta (t))\nonumber \\&\quad +({\tilde{\mathbf {E}}}_{3\rho _k}+\triangle { \tilde{\mathbf {E}}}_{3\rho _k}(t))\nu _l(t)]dt+[({\tilde{\mathbf {H}}}_{\rho _k} +\triangle {\tilde{\mathbf {H}}}_{\rho _k}(t)){\tilde{x}}_l(t) \nonumber \\&\quad +({\tilde{\mathbf {H}}}_{1\rho _k}+\triangle {\tilde{\mathbf {H}}}_{1\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}_l(t)) +({\tilde{\mathbf {H}}}_{2\rho _k}+\triangle {\tilde{\mathbf {H}}}_{2\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}_l(t-\delta (t)))]dB_l(t), \nonumber \\ {\tilde{x}}_l(t )&={\tilde{\varphi }}_l(t), \, \forall \ t \in [-\delta ,0],\,l= 1,2,\ldots .,N, \end{aligned}$$
(6)

With the matrix Kronecker product, the systems (5) and (6) can be rewritten in the following compact form:

$$\begin{aligned} d{\hat{x}}(t)&={\mathbf {E}}_{f\rho _k}{\hat{x}}(t)dt+{\mathbf {H}}_{f\rho _k}dy(t), \end{aligned}$$
(7)

and

$$\begin{aligned} d{\tilde{x}}(t)&=[({\tilde{\mathbf {E}}}_{\rho _k}+\triangle { \tilde{\mathbf {E}}}_{\rho _k}(t)){\tilde{x}}(t) +({\tilde{\mathbf {E}}}_{1\rho _k}+\triangle {\tilde{\mathbf {E}}}_{1\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}(t)) \nonumber \\&\quad +({\tilde{\mathbf {E}}}_{2\rho _k}+\triangle {\tilde{\mathbf {E}}}_{2\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}(t-\delta (t)))\nonumber \\&\quad + {\tilde{\mathbf {G}}}_{\rho _k}{\mathbf {K}} {\tilde{x}}(t-\delta (t))+({\tilde{\mathbf {E}}}_{3\rho _k}+\triangle { \tilde{\mathbf {E}}}_{3\rho _k}(t))\nu (t)]dt \nonumber \\&\quad +[({\tilde{\mathbf {H}}}_{\rho _k} +\triangle {\tilde{\mathbf {H}}}_{\rho _k}(t)){\tilde{x}}(t) +({\tilde{\mathbf {H}}}_{1\rho _k}+\triangle {\tilde{\mathbf {H}}}_{1\rho _k}(t))\nonumber \\&\quad \times {\mathbf {K}}f_{\rho _k}({\tilde{x}}(t)) +({\tilde{\mathbf {H}}}_{2\rho _k}+\triangle {\tilde{\mathbf {H}}}_{2\rho _k}(t)) {\mathbf {K}}f_{\rho _k}({\tilde{x}}(t-\delta (t)))]dB(t), \end{aligned}$$
(8)

where

$$\begin{aligned} {\tilde{\mathbf {E}}}_{\rho _k}&=\left[ \begin{array}{cc} \breve{\mathbf {E}}_{\rho _k}+(\breve{\mathbf {W}}_{\rho _k}\otimes \Upsilon _{1\rho _k}) &{} 0\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {E}}_{3\rho _k} &{} {\mathbf {E}}_{f\rho _k} \end{array} \right] ,\ \ {\tilde{\mathbf {E}}}_{1\rho _k}=\left[ \begin{array}{c} \breve{\mathbf {E}}_{1\rho _k}\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {E}}_{4\rho _k} \end{array} \right] ,\ \ {\tilde{\mathbf {E}}}_{2\rho _k}=\left[ \begin{array}{c} \breve{\mathbf {E}}_{2\rho _k}\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {E}}_{5\rho _k} \end{array} \right] ,\\ {\tilde{\mathbf {E}}}_{3\rho _k}&=\left[ \begin{array}{c} \breve{\mathbf {E}}_{x\rho _k}\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {E}}_{y\rho _k} \end{array} \right] ,\ \triangle {\tilde{\mathbf {E}}}_{\rho _k}(t)=\left[ \begin{array}{cc} \triangle \breve{\mathbf {E}}_{\rho _k}(t) &{} 0\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {E}}_{3\rho _k}(t) &{} 0 \end{array} \right] ,\ \triangle {\tilde{\mathbf {E}}}_{1\rho _k}(t)=\left[ \begin{array}{c} \triangle \breve{\mathbf {E}}_{1\rho _k}(t)\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {E}}_{4\rho _k}(t) \end{array} \right] ,\\ \triangle {\tilde{\mathbf {E}}}_{2\rho _k}(t)&=\left[ \begin{array}{c} \triangle \breve{\mathbf {E}}_{2\rho _k}(t)\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {E}}_{5\rho _k}(t) \end{array} \right] ,\ \triangle {\tilde{\mathbf {E}}}_{3\rho _k}(t)=\left[ \begin{array}{c} \triangle \breve{\mathbf {E}}_{x\rho _k}(t)\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {E}}_{y\rho _k}(t) \end{array} \right] ,\ {\tilde{\mathbf {H}}}_{\rho _k}=\left[ \begin{array}{cc} \breve{\mathbf {H}}_{\rho _k} &{} 0\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {H}}_{3\rho _k} &{}0 \end{array} \right] ,\\ {\tilde{\mathbf {H}}}_{1\rho _k}&=\left[ \begin{array}{c} \breve{\mathbf {H}}_{1\rho _k}\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {H}}_{4\rho _k} \end{array} \right] ,\ \ {\tilde{\mathbf {H}}}_{2\rho _k}=\left[ \begin{array}{c} \breve{\mathbf {H}}_{2\rho _k}\\ {\mathbf {H}}_{f\rho _k}\breve{\mathbf {H}}_{5\rho _k} \end{array} \right] ,\ \ \triangle {\tilde{\mathbf {H}}}_{\rho _k}(t)=\left[ \begin{array}{cc} \triangle \breve{\mathbf {H}}_{\rho _k}(t) &{} 0\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {H}}_{3\rho _k}(t) &{}0 \end{array} \right] ,\\ \triangle {\tilde{\mathbf {H}}}_{1\rho _k}(t)&=\left[ \begin{array}{c} \triangle \breve{\mathbf {H}}_{1\rho _k}(t)\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {H}}_{4\rho _k}(t) \end{array} \right] ,\ \triangle {\tilde{\mathbf {H}}}_{2\rho _k}(t)=\left[ \begin{array}{c} \triangle \breve{\mathbf {H}}_{2\rho _k}(t)\\ {\mathbf {H}}_{f\rho _k}\triangle \breve{\mathbf {H}}_{5\rho _k}(t) \end{array} \right] ,\ {\tilde{\mathbf {G}}}_{\rho _k} =\left[ \begin{array}{c} \breve{\mathbf {G}}_{\rho _k}\otimes \Upsilon _{2\rho _k}\\ 0 \end{array} \right] ,\\ {\mathbf {K}}&=\left[ \begin{array}{cc} \breve{\mathbf {I}}&0 \end{array} \right] ,\ f_{\rho _k}({\tilde{x}}(t))=\left[ \begin{array}{c} f_{\rho _k}(x(t))\\ f_{\rho _k}( {\hat{x}}(t)) \end{array} \right] . \end{aligned}$$

For the sake of convenience, let

$$\begin{aligned} \mathrm {E}_{\rho _k}&=\left[ \begin{array}{ccccccccc} {\tilde{\mathbf {E}}}_{\rho _k}&0_{2n\times 2n}&{\tilde{\mathbf {G}}}_{\rho _k}&0_{2n\times n}&{\tilde{\mathbf {E}}}_{1\rho _k}&{\tilde{\mathbf {E}}}_{2\rho _k}&0_{2n\times n}&0_{2n\times n}&{\tilde{\mathbf {E}}}_{3\rho _k}\end{array} \right] ,\\ \mathrm {H}_{\rho _k}&=\left[ \begin{array}{ccccccccc} {\tilde{\mathbf {H}}}_{\rho _k}&0_{2n\times 2n}&0_{2n\times n}&0_{2n\times n}&{\tilde{\mathbf {H}}}_{1\rho _k}&{\tilde{\mathbf {H}}}_{2\rho _k}&0_{2n\times n}&0_{2n\times n}&0_{2n\times n}\end{array} \right] ,\\ \triangle \mathrm {E}_{\rho _k}(t)&=\left[ \begin{array}{ccccccccc} \triangle {\tilde{\mathbf {E}}}_{\rho _k}(t)&0_{2n\times 2n}&0_{2n\times n}&0_{2n\times n}&\triangle {\tilde{\mathbf {E}}}_{1\rho _k}(t)&\triangle {\tilde{\mathbf {E}}}_{2\rho _k}(t)&0_{2n\times n}&0_{2n\times n}&\triangle {\tilde{\mathbf {E}}}_{3\rho _k}(t)\end{array} \right] ,\\ \triangle \mathrm {H}_{\rho _k}(t)&=\left[ \begin{array}{ccccccccc} \triangle {\tilde{\mathbf {H}}}_{\rho _k}(t)&0_{2n\times 2n}&0_{2n\times n}&0_{2n\times n}&\triangle {\tilde{\mathbf {H}}}_{1\rho _k}(t)&\triangle {\tilde{\mathbf {H}}}_{2\rho _k}(t)&0_{2n\times n}&0_{2n\times n}&0_{2n\times n}\end{array} \right] . \end{aligned}$$

Then system (8) becomes

$$\begin{aligned} d{\tilde{x}}(t)=A_1(t)dt+A_2(t)dB(t) \end{aligned}$$
(9)

with

$$\begin{aligned} A_1(t)&=(\mathrm {E}_{\rho _k}+\triangle \mathrm {E}_{\rho _k}(t))\xi (t),\nonumber \\ A_2(t)&=(\mathrm {H}_{\rho _k}+\triangle \mathrm {H}_{\rho _k}(t))\xi (t), \end{aligned}$$
(10)

where

$$\begin{aligned} \xi (t)&=[ x^T(t) \ \ {\hat{x}}^T(t) \ \ {\tilde{x}}^T(t-\delta _1){\mathbf {K}}^T \ \ {\tilde{x}}^T(t-\delta (t)){\mathbf {K}}^T \ \ {\tilde{x}}^T(t-\delta _2){\mathbf {K}}^T \ \ \\&\quad f_{\rho _k}^T({\tilde{x}}(t)){\mathbf {K}}^T \ \ f_{\rho _k}^T{\tilde{x}}^T(t-\delta (t)){\mathbf {K}}^T \\&\quad A_1^T(t){\mathbf {K}}^T \ \ A_2^T(t){\mathbf {K}}^T \ \ \nu ^T(t)]^T. \end{aligned}$$

Set \({\mathfrak {M}}\) contains m models of system (1) and in throughout this study, for each possible \(\rho _k=i \in {\mathfrak {M}},\) the system matrices of the ith mode are denoted by \(\breve{\mathbf {E}}_{i},\ \breve{\mathbf {E}}_{1i},\) etc., which are considered to be real known with appropriate dimensions.

Remark 4

In this paper, we consider a stochastic switched complex dynamical network with time-varying delay. However, it is difficult to deal with the problem, to facilitate, we need the above assumptions. Assumption (A) gives some requirements for the dynamics of network. Therefore, the resulting activation function could be non-monotonic, and are more general than the usual sigmoid functions and commonly used sector-like bounded conditions [8] in complex dynamical networks. These kind of functions will be useful in many real time systems, for example, in electronic circuits where the input–output functions of amplifiers may be neither monotonically increasing nor continuously differentiable. In addition, a more generalized sector-like condition is assumed to well describe the nonlinear functions in the network.

3 Main Results

To establish the main results of the paper, the following lemmas are needed.

Lemma 1

[52] (Jensen’s Inequality) For any constant positive-definite matrix \({\mathbf {W}} \,\in \,{\mathbb {R}}^{m\times m},\, {\mathbf {W}} = {\mathbf {W}}^T\, > 0\) and \(\alpha _1\le \alpha _2\), the following inequalities hold:

$$\begin{aligned} \,\,-(\alpha _1-\alpha _2) \int _{\alpha _2}^{\alpha _1} \phi ^T (s) {\mathbf {W}} \phi (s)ds&\le -\left( \int _{\alpha _2}^{\alpha _1} \phi (s)ds \right) ^T{\mathbf {W}} \left( \int _{\alpha _2}^{\alpha _1} \ \phi (s)ds \right) . \end{aligned}$$
(11)

Lemma 2

(Schur complement) [52] Let \({\mathbf {S}}, {\mathbf {Q}}, {\mathbf {N}}\) be given matrices such that \(\breve{\mathbf {N}}>0\), then

$$\begin{aligned} \left[ \begin{array} {cc} {\mathbf {Q}} &{} {\mathbf {S}}^T\\ {\mathbf {S}} &{} -{\mathbf {N}} \end{array} \right] \quad< 0 \quad \Leftrightarrow {\mathbf {Q}} + {\mathbf {S}}^T{\mathbf {N}}^{-1}{\mathbf {S}} < 0 . \end{aligned}$$

Lemma 3

[42] Let \({\mathbf {U}}, {\mathbf {W}}\), and \({\mathbf {X}}^T={\mathbf {X}}\) be a real matrices of appropriate dimensions. Set \({\mathbf {S}}=\{{\mathbf {V}}:{\mathbf {V}}^T{\mathbf {V}}\le {\mathbf {I}}\}\). Then

$$\begin{aligned} {\mathbf {X}}+{\mathbf {U}}{\mathbf {V}}{\mathbf {W}}+{\mathbf {W}}^T{\mathbf {V}}^T{ \mathbf {U}}^T<0,\ \ \forall \ {\mathbf {V}}\in {\mathbf {S}} \end{aligned}$$

if and only if there exist a scalar \(\epsilon >0\) such that

$$\begin{aligned} {\mathbf {X}}+\epsilon ^{-1}{\mathbf {U}}{\mathbf {U}}^T+ \epsilon {\mathbf {W}}^T{\mathbf {W}}<0. \end{aligned}$$

Lemma 4

(Lower bounds theorem) [53] Let \(h_1,h_2,\ldots .,h_N:{\mathbf {R}}^m\longmapsto {\mathbf {R}}\) have positive values in an open subset \({\mathbf {D}}\) of \({\mathbf {R}}^m\). Then, the reciprocally convex combination of \(h_i\) over \({\mathbf {D}}\) satisfies

$$\begin{aligned} \{\alpha _i\mid \alpha _i>0, \sum _i^{min}\alpha _i=1\}\sum _i \frac{1}{\alpha _i}h_i(t)=\sum _ih_i(t)+\max _{g_{i,j}(t)}\sum _{i\ne j}g_{i,j}(t) \end{aligned}$$

subject to

$$\begin{aligned} \Big \{g_{i,j}:{\mathbf {R}}^m\longmapsto {\mathbf {R}}, g_{j,i}(t) = g_{i,j}(t),\left[ \begin{array}{cc} h_i(t) &{} g_{i,j}(t) \\ g_{i,j}(t) &{} h_j(t) \end{array} \right] \ge 0\Big \}.\\ \end{aligned}$$

Lemma 5

[54] For given matrices \({\mathbf {Q}}\) and \({\tilde{\mathbf {Q}}}\) satisfying \(\left[ \begin{array}{cc} {\mathbf {Q}} &{}{\tilde{\mathbf {Q}}} \\ * &{} {\mathbf {Q}} \end{array} \right] \ge 0\), scalars \(\delta _1\) and \(\delta _2\) subject to \(\delta _{12} := \delta _2 -\delta _1 > 0\), a function \(\delta : {\mathbb {R}} \rightarrow [\delta _1, \delta _2]\), and a vector-function \(f: {\mathbb {R}} \rightarrow {\mathbb {R}}^n\) such that the integrations concerned are well defined, the following inequality holds:

$$\begin{aligned} {\mathbb {E}}\Big \{{\mathcal {L}}\int _{-\delta _2}^{-\delta _1} \int _{t+\theta }^tf^T(s){\mathbf {Q}}f(s)dsd\theta \Big \}\le \delta _{12}f^T(t){\mathbf {Q}}f(t)-\frac{1}{\delta _{12}} \eta ^T(t)\left[ \begin{array}{cc} {\mathbf {Q}} &{}{\tilde{\mathbf {Q}}} \\ * &{} {\mathbf {Q}} \end{array} \right] \eta (t),\ \forall \ t \in {\mathbb {R}}, \end{aligned}$$

where

$$\begin{aligned} \eta (t)=\left[ \begin{array}{cc} x(t-\delta _1)- x(t-\delta (t))\\ x(t-\delta (t))-x(t-\delta _2) \end{array} \right] . \end{aligned}$$

Remark 5

It has come to be widely recognized that the mode-dependent filter (5) is a powerful tool to cope with the state estimation for CDNs with fully available modes information. However, in practice, the modes information can be transmitted to the filter especially in communication network medium. Lemmas 4 and 5 are applied to the corresponding terms in the Lyapunov–Krasovskii functional V(t) in (13) to achieve less conservative results with fewer decision variables.

The following theorem presents a mean-square robust asymptotical stability with disturbance attenuation level \(\gamma \) for the filtering error system (8) in this section.

Theorem 3.1

For given scalars \(\gamma >0,\ \delta _1,\ \delta _2,\ \delta _d,\) and positive scalars \(\mu _1,\ \mu _2,\) the filtering error system (8) is mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \) if there exist matrices \({\mathbf {P}}_{i1}^T={\mathbf {P}}_{i1}>0,\ {\mathbf {Q}}_{iq}^T={\mathbf {Q}}_{iq}>0\ (q=1,2,3,4),\ {\mathbf {R}}_{iq}^T={\mathbf {R}}_{iq}>0\ (q=1,2),\ {\tilde{\mathbf {R}}}_{i2},\ {\mathbf {L}}_{i}\) and \({\mathbf {S}}_{i},\) and scalars \(\varepsilon _{im}\ (m=1,2)\) such that

$$\begin{aligned} \left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \ge 0, \left[ \begin{array} {ccc} {\tilde{\Psi }}+\varepsilon _{i1}\Gamma _e^T\Gamma _e+\varepsilon _{i2}\Gamma _h^T\Gamma _h &{} \Gamma _1 &{} \Gamma _2\\ *&{} -\varepsilon _{i1}{\mathbf {I}} &{}0\\ *&{} 0 &{}-\varepsilon _{i2}{\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(12)

where

$$\begin{aligned} {\tilde{\Psi }}&=\left[ \begin{array} {cc} \Psi &{} \mathrm {H}_i^T{\mathbf {P}}_{i1}\\ *&{} -{\mathbf {P}}_{i1} \end{array} \right] ,\ \Gamma _1=\left[ \begin{array} {c} [{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]{\mathbf {P}}_{i1}{\tilde{\Gamma }}_1+ {\mathbf {r}}_8^T{\mathbf {L}}_i\Theta _1\\ 0 \end{array} \right] ,\ \Gamma _2=\left[ \begin{array} {c} {\mathbf {r}}_9^T{\mathbf {S}}_i\Theta _2\\ {\mathbf {P}}_{i1}{\tilde{\Gamma }}_2 \end{array} \right] ,\\ \Gamma _m&=\left[ \begin{array} {cc} {\tilde{\Gamma }}_m &{} 0\\ \end{array} \right] ,\ m=e,h,\ \ \Psi =\Psi _1+\Psi _2+\Psi _3,\ \ \Psi _1=({\mathbf {r}}_1-{\mathbf {r}}_2)^T({\mathbf {r}}_1-{\mathbf {r}}_2)- \gamma ^2{\mathbf {r}}_{10}^T{\mathbf {r}}_{10},\\ \Psi _2&=[{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]{\mathbf {P}}_{i1}\mathrm {E}_{i}+\mathrm {E}_{i}^T {\mathbf {P}}_{i1}[{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]^T,\ \ \\ \Psi _3&={\mathbf {r}}_1^T({\mathbf {Q}}_{i1}+{\mathbf {Q}}_{i3}-\mu _1{\mathbf {F}}_{i1}) {\mathbf {r}}_1+{\mathbf {r}}_3^T({\mathbf {Q}}_{i2}-{\mathbf {Q}}_{i1}){\mathbf {r}}_3\\&\quad -{\mathbf {r}}_5^T{\mathbf {Q}}_{i2}{\mathbf {r}}_5+{\mathbf {r}}_4^T(-(1-\delta _d) {\mathbf {Q}}_{i3}-\mu _2{\mathbf {F}}_{i1}){\mathbf {r}}_4 \\&\quad +{\mathbf {r}}_6^T( {\mathbf {Q}}_{i4}-2\mu _1){\mathbf {r}}_6+{\mathbf {r}}_7^T(-(1-\delta _d) {\mathbf {Q}}_{i4}-2\mu _2){\mathbf {r}}_7\\&\quad +{\mathbf {r}}_8^T (\delta _1{\mathbf {R}}_{i1}+\delta _{12}{\mathbf {R}}_{i2}){\mathbf {r}}_8 -\delta _1^{-1}({\mathbf {r}}_1-{\mathbf {r}}_3)^T{\mathbf {R}}_{i1}({\mathbf {r}}_1- {\mathbf {r}}_3) \\&\quad +{\mathbf {r}}_1^T(\mu _1{\mathbf {F}}_{i2}){\mathbf {r}}_6 +{\mathbf {r}}_6^T(\mu _1{\mathbf {F}}_{i2}){\mathbf {r}}_1\\ {}&\quad +{\mathbf {r}}_4^T(\mu _2{\mathbf {F}}_{i2}){\mathbf {r}}_7+{\mathbf {r}}_7^T (\mu _2{\mathbf {F}}_{i2}){\mathbf {r}}_4 +({\mathbf {K}}\mathrm {E}_{i}- {\mathbf {r}}_8)^T{\mathbf {L}}_i^T{\mathbf {r}}_8 \\&\quad +{\mathbf {r}}_8^T{\mathbf {L}}_i( {\mathbf {K}}\mathrm {E}_{i}-{\mathbf {r}}_8) +({\mathbf {K}}\mathrm {H}_{i} -{\mathbf {r}}_9)^T{\mathbf {S}}_i^T{\mathbf {r}}_9\\ {}&\quad +{\mathbf {r}}_9^T {\mathbf {S}}_i({\mathbf {K}}\mathrm {H}_{i}-{\mathbf {r}}_9) -\delta _{12}^{-1} \left[ \begin{array} {c} {\mathbf {r}}_3-{\mathbf {r}}_4\\ {\mathbf {r}}_4-{\mathbf {r}}_5 \end{array} \right] ^T\left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{} {\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \left[ \begin{array} {c} {\mathbf {r}}_3-{\mathbf {r}}_4\\ {\mathbf {r}}_4-{\mathbf {r}}_5 \end{array} \right] ,\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad {\tilde{\Gamma }}_s=\left\{ \begin{array} {c} diag(\varvec{\Xi }_s,\breve{\mathbf {N}}_{ai}),\ if \ \ s=e, \\ diag(\varvec{\Xi }_s,0),\ \ \ if \ \ s=h, \end{array}\right. \\&\qquad \qquad \qquad \qquad \qquad \varvec{\Xi }_s=\Big \{ diag\{\breve{\mathbf {N}}_{si},\ 0,\ 0,\ 0,\ 0,\ \breve{\mathbf {N}}_{si},\ \breve{\mathbf {N}}_{si},\ 0,\ 0\},\ if \ \ s=e,h,\\ {\tilde{\Gamma }}_1&=\left[ \begin{array} {cc} \varvec{\Xi }_1 &{} \left[ \begin{array} {c} \breve{\mathbf {M}}_{xi}\\ {\mathbf {H}}_{fi} \breve{\mathbf {M}}_{yi} \end{array} \right] \end{array}\right] ,\ \ {\tilde{\Gamma }}_2=\left[ \begin{array} {cc} \varvec{\Xi }_1&0 \end{array}\right] ,\ \Theta _1= \left[ \begin{array} {cc} {\mathbf {K}}\varvec{\Xi }_1&\breve{\mathbf {M}}_{xi} \end{array}\right] , \Theta _2= \left[ \begin{array} {cc} {\mathbf {K}}\varvec{\Xi }_1&0 \end{array}\right] ,\\ \varvec{\Xi }_1&=\left[ \begin{array} {ccccc} \left[ \begin{array} {cc} \breve{\mathbf {M}}_{0i} &{} 0\\ {\mathbf {H}}_{fi} \breve{\mathbf {M}}_{3i}&{}0 \end{array}\right] &{} 0_{2n\times 3n}&{} \left[ \begin{array} {c} \breve{\mathbf {M}}_{1i}\\ {\mathbf {H}}_{fi} \breve{\mathbf {M}}_{4i} \end{array}\right] &{} \left[ \begin{array} {c} \breve{\mathbf {M}}_{2i}\\ {\mathbf {H}}_{fi} \breve{\mathbf {M}}_{5i} \end{array}\right]&0_{2n\times 2n} \end{array}\right] ,\\ {\mathbf {r}}_a&=\Big [\underbrace{0,\ldots ,0}_{a-1}\ {\mathbf {I}} \ \underbrace{ 0,\ldots ,0}_{10-a}\Big ]\ \ \ \ a=1,\ldots .,10. \end{aligned}$$

Proof

By the Schur complement lemma and Lemma 2, inequality (12) is equivalent to

$$\begin{aligned} {\tilde{\Psi }}+\Gamma _1{\tilde{\mathbf {F}}}(t)\Gamma _e+ \Gamma _e^T{\tilde{\mathbf {F}}}^T(t)\Gamma _1^T+\Gamma _2{\tilde{\mathbf {F}}}(t)\Gamma _h +\Gamma _h^T{\tilde{\mathbf {F}}}^T(t)\Gamma _2^T<0 \end{aligned}$$

with

$$\begin{aligned} {\tilde{\mathbf {F}}}(t)=diag(\underbrace{\breve{\mathbf {F}}(t),\ldots .,\breve{\mathbf {F}}(t)}_{10}). \end{aligned}$$

\(\square \)

This implies that

$$\begin{aligned} \Psi +\triangle \Psi (t)+(\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(t))^T{\mathbf {P}}_{i1}(\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(t))<0 \end{aligned}$$

with

$$\begin{aligned} \triangle \Psi (t)&=[{\mathbf {r}}_1^T \ \ {\mathbf {r}}_2^T]{\mathbf {P}}_{i1} \triangle \mathrm {E}_i(t)+ \triangle \mathrm {E}_i^T(t){\mathbf {P}}_{i1} [{\mathbf {r}}_1^T \ \ {\mathbf {r}}_2^T]^T+{\mathbf {r}}_8^T{\mathbf {L}}_i {\mathbf {K}}\triangle \mathrm {E}_{i}(t)+\triangle \mathrm {E}_{i}^T(t) {\mathbf {K}}^T{\mathbf {L}}_i^T{\mathbf {r}}_8\\ {}&\quad +{\mathbf {r}}_9^T{\mathbf {S}}_i{\mathbf {K}}\triangle \mathrm {H}_{i}(t)+ \triangle \mathrm {H}_{i}^T(t){\mathbf {K}}^T{\mathbf {S}}_i^T{\mathbf {r}}_9. \end{aligned}$$

We construct the following Lyapunov–Krasovskii functional candidate for the filtering error system (8) as

$$\begin{aligned} V(t) = \sum _{a=1}^3V_{a}(t), \end{aligned}$$
(13)

where

$$\begin{aligned} V_{1}(t)&= {\tilde{x}}^T(t){\mathbf {P}}_{i1}{\tilde{x}}(t),\\ V_{2}(t)&= \int _{t-\delta _1 }^t {\tilde{x}}^T(s){\mathbf {K}}^T{\mathbf {Q}}_{i1}{\mathbf {K}}{\tilde{x}}(s) ds +\int _{t-\delta _2 }^{t-\delta _1} {\tilde{x}}^T(s){\mathbf {K}}^T{\mathbf {Q}}_{i2}{\mathbf {K}}{\tilde{x}}(s) ds\\&\quad + \int _{t-\delta (t)}^t {\tilde{x}}^T(s){\mathbf {K}}^T{\mathbf {Q}}_{i3}{\mathbf {K}}{\tilde{x}}(s) ds+ \int _{t-\delta (t)}^t f_i^T({\tilde{x}}(s)){\mathbf {K}}^T{\mathbf {Q}}_{i4}{\mathbf {K}}f_i({\tilde{x}}(s)) ds,\\ V_{3}(t)&= \int _{-\delta _1}^0\int _{t+\beta }^tA_1^T(s) {\mathbf {K}}^T{\mathbf {R}}_{i1}{\mathbf {K}}A_1(s) dsd\beta +\int _{-\delta _2}^{-\delta _1}\int _{t +\beta }^tA_1^T(s){\mathbf {K}}^T{\mathbf {R}}_{i2}{\mathbf {K}}A_1(s) dsd\beta . \end{aligned}$$

By Ito’s differential formula, we get the following stochastic derivative along the trajectory of dynamical networks (8) from Lemmas 1 and 4 that

$$\begin{aligned} {\mathbb {E}}\{{\mathcal {L}}V_{1}(t)\}&=\xi ^T(t)\Big [2[{\mathbf {r}}_1^T \ \ {\mathbf {r}}_2^T]{\mathbf {P}}_{i1}(\mathrm {E}_i+\triangle \mathrm {E}_i(t))+ (\mathrm {H}_i+\triangle \mathrm {H}_i(t))^T{ \mathbf {P}}_{i1}(\mathrm {H}_i+\triangle \mathrm {H}_i(t))\Big ]\xi (t) \end{aligned}$$
(14)
$$\begin{aligned} {\mathbb {E}}\{{\mathcal {L}}V_{2}(t)\}&=\xi ^T(t)\Big [{\mathbf {r}}_1^T {\mathbf {Q}}_{i1}{\mathbf {r}}_1 -{\mathbf {r}}_3^T({\mathbf {Q}}_{i1}-{ \mathbf {Q}}_{i2}){\mathbf {r}}_3-{\mathbf {r}}_5^T{\mathbf {Q}}_{i2}{ \mathbf {r}}_5+{\mathbf {r}}_1^T{\mathbf {Q}}_{i3}{\mathbf {r}}_1 \nonumber \\&\quad -\,(1-\delta _d){\mathbf {r}}_4^T{\mathbf {Q}}_{i3}{\mathbf {r}}_4 +{\mathbf {r}}_6^T{\mathbf {Q}}_{i4}{\mathbf {r}}_6-(1-\delta _d) {\mathbf {r}}_7^T{\mathbf {Q}}_{i4}{\mathbf {r}}_7\Big ]\xi (t) \end{aligned}$$
(15)
$$\begin{aligned} {\mathbb {E}}\{{\mathcal {L}}V_{3}(t)\}&\le \xi ^T(t)\Bigg [{\mathbf {r}}_8^T (\delta _1{\mathbf {R}}_{i1}+\delta _{12}{\mathbf {R}}_{i2}){\mathbf {r}}_8 -\delta _1^{-1}({\mathbf {r}}_1-{\mathbf {r}}_3)^T{\mathbf {R}}_{i1}( {\mathbf {r}}_1-{\mathbf {r}}_3) \nonumber \\&\quad -\delta _{12}^{-1} \left[ \begin{array} {c} {\mathbf {r}}_3-{\mathbf {r}}_4\\ {\mathbf {r}}_4-{\mathbf {r}}_5 \end{array} \right] ^T\left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \left[ \begin{array} {c} {\mathbf {r}}_3-{\mathbf {r}}_4\\ {\mathbf {r}}_4-{\mathbf {r}}_5 \end{array} \right] \Bigg ]\xi (t) \end{aligned}$$
(16)

On the other hand, the following equations are true for any matrices \({\mathbf {L}}_i\) and \({\mathbf {S}}_i\) of appropriate dimensions according to (10).

$$\begin{aligned} 2\xi ^T(t){\mathbf {r}}_8^T{\mathbf {L}}_i[{\mathbf {K}}(\mathrm {E}_{i}+ \triangle \mathrm {E}_{i}(t))-{\mathbf {r}}_8]\xi (t)&=0, \end{aligned}$$
(17)
$$\begin{aligned} 2\xi ^T(t){\mathbf {r}}_9^T{\mathbf {S}}_i[{\mathbf {K}}(\mathrm {H}_{i}+ \triangle \mathrm {H}_{i}(t))-{\mathbf {r}}_9]\xi (t)&=0. \end{aligned}$$
(18)

From Assumption (A), for any positive scalars \(\mu _1,\ \mu _2\) the following inequalities hold,

$$\begin{aligned} -\mu _1 \left[ \begin{array}{c} {\mathbf {K}}{\tilde{x}}(t) \\ {\mathbf {K}}f_i({\tilde{x}}(t)) \end{array} \right] ^T\left[ \begin{array}{cc} {\mathbf {F}}_{i1} &{} -{\mathbf {F}}_{i2} \\ * &{} 2{\mathbf {I}} \end{array} \right] \left[ \begin{array}{c} {\mathbf {K}}{\tilde{x}}(t) \\ {\mathbf {K}}f_i({\tilde{x}}(t)) \end{array} \right] \ge 0, \end{aligned}$$
(19)
$$\begin{aligned} -\mu _2 \left[ \begin{array}{c} {\mathbf {K}}{\tilde{x}}(t-\delta (t)) \\ {\mathbf {K}}f_i({\tilde{x}}(t-\delta (t))) \end{array} \right] ^T\left[ \begin{array}{cc} {\mathbf {F}}_{i1} &{} -{\mathbf {F}}_{i2} \\ * &{} 2{\mathbf {I}} \end{array} \right] \left[ \begin{array}{c} {\mathbf {K}}{\tilde{x}}(t-\delta (t)) \\ {\mathbf {K}}f_i({\tilde{x}}(t-\delta (t))) \end{array} \right] \ge 0. \end{aligned}$$
(20)

From (19) and (20), we obtain the following

$$\begin{aligned} \xi ^T(t)\Big [{\mathbf {r}}_1^T(-\mu _1{\mathbf {F}}_{i1}){\mathbf {r}}_1 +{\mathbf {r}}_1^T(\mu _1{\mathbf {F}}_{i2}){\mathbf {r}}_6+{\mathbf {r}}_6^T( \mu _1{\mathbf {F}}_{i2}){\mathbf {r}}_1+{\mathbf {r}}_6^T(-2\mu _1) {\mathbf {r}}_6\Big ]\xi (t)\ge 0, \end{aligned}$$
(21)
$$\begin{aligned} \xi ^T(t)\Big [{\mathbf {r}}_4^T(-\mu _2{\mathbf {F}}_{i1}){\mathbf {r}}_4 +{\mathbf {r}}_4^T(\mu _2{\mathbf {F}}_{i2}){\mathbf {r}}_7+ {\mathbf {r}}_7^T(\mu _2{\mathbf {F}}_{i2}){\mathbf {r}}_4+ {\mathbf {r}}_7^T(-2\mu _2){\mathbf {r}}_7\Big ]\xi (t)\ge 0. \end{aligned}$$
(22)

The combination of (13)–(18), (21) and (22) gives that

$$\begin{aligned} {\mathbb {E}}\{{\mathcal {L}}V(t)\}\le \xi ^T(t)\Big [\Psi _2+\Psi _3+ \triangle \Psi (t)+(\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(t))^T{\mathbf {P}}_{i1} (\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(t))\Big ]\xi (t). \end{aligned}$$
(23)

Now, we present that the filtering error system (8) with \(\nu (t) = 0\) is mean-square robustly asymptotically stable. In fact, when \(\nu (t) = 0,\) we have \({\mathbb {E}}\{{\mathcal {L}}V(t)\} < 0\) from (12) and (22), since \({\mathbb {E}}\{V(t)\} > 0\) implies that

$$\begin{aligned} \beta _1{\mathbb {E}}\{\Vert {\tilde{x}}(t)\Vert ^2\}\le {\mathbb {E}}\{ V(t)\}\le {\mathbb {E}}\{ V(0)\}\le \beta _2\Big (\sup _{t\in [-\delta ,0]}{\mathbb {E}}\{\Vert {\tilde{\varphi }}(t)\Vert ^2\}\Big ), \end{aligned}$$
(24)

where \(\beta _1\) and \(\beta _2\) are positive constants. Also, we can derive \({\mathbb {E}}\{{\mathcal {L}}V(t)\}\le -\beta _3{\mathbb {E}}\{ \Vert {\tilde{x}}(t)\Vert ^2\}\) for some positive constant \(\beta _3,\) which implies that

$$\begin{aligned} {\mathbb {E}}\Big \{\int _0^t(\Vert {\tilde{x}}(s)\Vert ^2)ds\Big \} \le -\beta _3^{-1}{\mathbb {E}}\{ V(t)- V(0)\}\le \beta _3^{-1}{\mathbb {E}}\{ V(0)\}\le \beta _2\beta _3^{-1}\Big (\sup _{t\in [-\delta ,0]}{\mathbb {E}}\{\Vert {\tilde{\varphi }}(t)\Vert ^2\}\Big ). \end{aligned}$$

Thus, it is easy to see that the filtering error system (8) with \(\nu (t) = 0\) is mean-square robustly asymptotically stable.

In this end, for any nonzero \(\nu (t)\), under the zero initial condition we introduce the following index

$$\begin{aligned} T(t)= {\mathbb {E}}\Big \{\int _0^t(\Vert x(s)-{\hat{x}}(s)\Vert ^2-\gamma ^2 \nu ^T(s)\nu (s))ds\Big \}. \end{aligned}$$

Clearly,

$$\begin{aligned} T(t)&\le {\mathbb {E}}\Big \{\int _0^t(\Vert x(s)-{\hat{x}}(s)\Vert ^2- \gamma ^2\nu ^T(s)\nu (s)+{\mathcal {L}}V(s))ds\Big \}\\&\le {\mathbb {E}}\Big \{\int _0^t\xi ^T(s)\Big [\Psi +\triangle \Psi (s)+(\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(s))^T{\mathbf {P}}_{i1} (\mathrm {H}_{i}+\triangle \mathrm {H}_{i}(s))\Big ]\xi (s)ds\Big \} \,\,\, \forall \ t>0. \end{aligned}$$

Hence, if (12) holds, then \(T(t)<0\) for any \(t>0.\) Therefore, the filtering error system (8) is mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \). This completes the proof.

Now, the following theorem provides to design a filter in terms of LMIs for the filtering error system (8) by using Theorem 3.1.

Theorem 3.2

For given scalars \(\gamma >0,\ \delta _1,\ \delta _2,\ \delta _d,\) and positive scalars \(\mu _1,\ \mu _2,\) the filtering error system (8) is mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \) if there exist matrices \({\mathbf {P}}_{i1}^T={\mathbf {P}}_{i1}:=\left[ \begin{array} {cc} {\mathbf {P}}_{i11}&{}{\mathbf {P}}_{i12}\\ {\mathbf {P}}_{i12}&{} {\mathbf {P}}_{i12} \end{array} \right]>0,\ {\mathbf {Q}}_{iq}^T={\mathbf {Q}}_{iq}>0\ (q=1,2,3,4),\ {\mathbf {R}}_{iq}^T={\mathbf {R}}_{iq}>0\ (q=1,2),\ {\mathbf {E}}_{fi},\ {\mathbf {H}}_{fi},\ {\tilde{\mathbf {R}}}_{i2}, \ {\mathbf {L}}_{i}\) and \({\mathbf {S}}_{i},\) and scalars \(\varepsilon _{im}\ (m=1,2)\) such that

$$\begin{aligned} \left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \ge 0, \left[ \begin{array} {ccc} \breve{\Psi }+\varepsilon _{i1}\Gamma _e^T\Gamma _e+\varepsilon _{i2}\Gamma _h^T\Gamma _h &{} \breve{\Gamma }_1 &{} \breve{\Gamma }_2\\ *&{} -\varepsilon _{i1}{\mathbf {I}} &{}0\\ *&{} 0 &{}-\varepsilon _{i2}{\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(25)

where

$$\begin{aligned} \breve{\Psi }&=\left[ \begin{array} {cc} {\bar{\Psi }}&{} {\hat{\mathrm {H}}}_i^T\\ *&{} -{\mathbf {P}}_{i1} \end{array} \right] ,\ \breve{\Gamma }_1=\left[ \begin{array} {c} [{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]{\bar{\Gamma }}_1+{\mathbf {r}}_8^T{\mathbf {L}}_i\Theta _1\\ 0 \end{array} \right] ,\ \breve{\Gamma }_2=\left[ \begin{array} {c} {\mathbf {r}}_9^T{\mathbf {S}}_i\Theta _2\\ {\bar{\Gamma }}_2 \end{array} \right] ,\ \nonumber \\&\quad {\bar{\Psi }}=\Psi _1+{\bar{\Psi }}_2+\Psi _3,\\ {\bar{\Psi }}_2&=[{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]{\hat{\mathrm {E}}}_{i}+{\hat{\mathrm {E}}}_{i}^T[{\mathbf {r}}_1^T \ {\mathbf {r}}_2^T]^T,\ \ {\bar{\Gamma }}_1=\left[ \begin{array} {cc} \breve{\varvec{\Xi }}_1 &{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{xi}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{yi}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{xi}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{yi} \end{array} \right] \end{array}\right] ,\ \ {\bar{\Gamma }}_2=\left[ \begin{array} {cc} \breve{\varvec{\Xi }}_1&0 \end{array}\right] ,\\ \breve{\varvec{\Xi }}_1&=\left[ \begin{array} {ccccc} \left[ \begin{array} {cc} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{0i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{3i}&{}0\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{0i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{3i}&{}0 \end{array}\right] &{} 0_{2n\times 3n}&{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{1i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{4i}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{1i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{4i} \end{array}\right] &{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{2i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{5i}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{2i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{5i} \end{array}\right] \\ 0_{2n\times 2n} \end{array}\right] ,\\ {\hat{\mathrm {E}}}_{i}&=\left[ \begin{array}{ccccccccc} {\hat{\mathbf {E}}}_{i}&0_{2n\times 2n}&{\hat{\mathbf {G}}}_{i}&0_{2n\times n}&{\hat{\mathbf {E}}}_{1i}&{\hat{\mathbf {E}}}_{2i}&0_{2n\times n}&0_{2n\times n}&{\hat{\mathbf {E}}}_{3i}\end{array} \right] ,\\ {\hat{\mathrm {H}}}_{i}&=\left[ \begin{array}{ccccccccc} {\hat{\mathbf {H}}}_{i}&0_{2n\times 2n}&0_{2n\times n}&0_{2n\times n}&{\hat{\mathbf {H}}}_{1i}&{\hat{\mathbf {H}}}_{2i}&0_{2n\times n}&0_{2n\times n}&0_{2n\times n}\end{array} \right] ,\\ {\hat{\mathbf {E}}}_{i}&=\left[ \begin{array}{cc} {\mathbf {P}}_{i11}(\breve{\mathbf {E}}_{i}+(\breve{\mathbf {W}}_{i} \otimes \Upsilon _{1i}))+{\hat{\mathbf {H}}}_{fi}\breve{\mathbf {E}}_{3i} &{} {\hat{\mathbf {E}}}_{fi}\\ {\mathbf {P}}_{i12}(\breve{\mathbf {E}}_{i} +(\breve{\mathbf {W}}_{i}\otimes \Upsilon _{1i}))+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {E}}_{3i} &{} {\hat{\mathbf {E}}}_{fi} \end{array} \right] ,\ \ {\hat{\mathbf {E}}}_{1i}=\left[ \begin{array}{c} {\mathbf {P}}_{i11}\breve{\mathbf {E}}_{1i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {E}}_{4i} \\ {\mathbf {P}}_{i12}\breve{\mathbf {E}}_{1i}+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {E}}_{4i} \end{array} \right] ,\\ {\hat{\mathbf {E}}}_{2i}&=\left[ \begin{array}{c} {\mathbf {P}}_{i11} \breve{\mathbf {E}}_{2i}+{\hat{\mathbf {H}}}_{fi}\breve{\mathbf {E}}_{5i} \\ {\mathbf {P}}_{i12}\breve{\mathbf {E}}_{2i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {E}}_{5i} \end{array} \right] ,\ \ {\hat{\mathbf {E}}}_{3i}=\left[ \begin{array}{c} {\mathbf {P}}_{i11}\breve{\mathbf {E}}_{xi}+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {E}}_{yi} \\ {\mathbf {P}}_{i12}\breve{\mathbf {E}}_{xi}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {E}}_{yi} \end{array} \right] ,\ {\hat{\mathbf {H}}}_{i}=\left[ \begin{array}{cc} {\mathbf {P}}_{i11}\breve{\mathbf {H}}_{i}+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {H}}_{3i} &{} 0\\ {\mathbf {P}}_{i12}\breve{\mathbf {H}}_{i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {H}}_{3i}&{}0 \end{array} \right] ,\\ {\hat{\mathbf {H}}}_{1i}&=\left[ \begin{array}{c} {\mathbf {P}}_{i11}\breve{\mathbf {H}}_{1i}+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {H}}_{4i} \\ {\mathbf {P}}_{i12}\breve{\mathbf {H}}_{1i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {H}}_{4i} \end{array} \right] ,\ \ {\hat{\mathbf {H}}}_{2i}=\left[ \begin{array}{c} {\mathbf {P}}_{i11}\breve{\mathbf {H}}_{2i}+ {\hat{\mathbf {H}}}_{fi}\breve{\mathbf {H}}_{5i} \\ {\mathbf {P}}_{i12}\breve{\mathbf {H}}_{2i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {H}}_{5i} \end{array} \right] ,\ {\hat{\mathbf {G}}}_{i}=\left[ \begin{array}{cc} {\mathbf {P}}_{i11}(\breve{\mathbf {G}}_{i}\otimes \Upsilon _{2i})\\ {\mathbf {P}}_{i12}(\breve{\mathbf {G}}_{i}\otimes \Upsilon _{2i}) \end{array} \right] , \end{aligned}$$

and \(\Theta _m(m=1,2),\ \Gamma _s(s=e,h),\ {\mathbf {r}}_a(a=1,\ldots ,10),\ \Psi _1\) and \(\Psi _3\) are defined as in Theorem 3.1.

In this case, the parameters of the desired filter can be given by

$$\begin{aligned} {\mathbf {E}}_{fi}={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {E}}}_{fi},\ {\mathbf {H}}_{fi}={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {H}}}_{fi}. \end{aligned}$$

Proof

The proof is similar to that in Theorem 3.1. Thus, we omit its proof. \(\square \)

Case 1 If there is no stochastic disturbance, then system (8) is simplified as follows:

$$\begin{aligned} {\dot{x}}(t)&=({\mathbf {E}}_{\rho _k}+\triangle {\mathbf {E}}_{\rho _k}(t))x(t) +({\mathbf {E}}_{1\rho _k}+\triangle {\mathbf {E}}_{1\rho _k}(t)) {\mathbf {K}}f_{\rho _k}(x(t)) \nonumber \\&\quad +({\mathbf {E}}_{2\rho _k} + \triangle {\mathbf {E}}_{2\rho _k}(t)) {\mathbf {K}}f_{\rho _k}(x(t-\delta (t))) \nonumber \\&\quad + {\mathbf {G}}_{\rho _k}{\mathbf {K}} {\tilde{x}}(t-\delta (t))+({\mathbf {E}}_{3\rho _k}+\triangle { \mathbf {E}}_{3\rho _k}(t))\nu (t), \,t \ne t_\kappa \nonumber \\ x(t_\kappa )&={{\mathbf {J}}_\kappa }x(t^-_{ \kappa }), \,\, t=t_\kappa . \end{aligned}$$
(26)

Corollary 3.3

For given scalars \(\gamma >0,\ \delta _1,\ \delta _2,\ \delta _d,\) and positive scalars \(\mu _1,\ \mu _2,\) the filtering error system of system (24) based on filter (7) is mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \) if there exist matrices \({\mathbf {P}}_{i1}^T={\mathbf {P}}_{i1}:=\left[ \begin{array} {cc} {\mathbf {P}}_{i11}&{}{\mathbf {P}}_{i12}\\ {\mathbf {P}}_{i12}&{} {\mathbf {P}}_{i12} \end{array} \right]>0,\ {\mathbf {Q}}_{iq}^T= {\mathbf {Q}}_{iq}>0\ (q=1,2,3,4),\ {\mathbf {R}}_{iq}^T= {\mathbf {R}}_{iq}>0\ (q=1,2),\ {\mathbf {E}}_{fi},\ {\mathbf {H}}_{fi},\ {\tilde{\mathbf {R}}}_{i2}\) and \({\mathbf {L}}_{i},\) and scalars \(\varepsilon _{i1}\) such that

$$\begin{aligned} \left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \ge 0, \left[ \begin{array} {cc} {\hat{\Psi }}+\varepsilon _{i1}\acute{\Gamma }_e^T\acute{\Gamma }_e &{} {\hat{\Gamma }}_1 \\ *&{} -\varepsilon _{i1}{\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(27)

where

$$\begin{aligned} {\hat{\Psi }}&= \acute{\Psi }_1+\acute{\Psi }_2+\acute{\Psi }_3,\ \ \acute{\Psi }_1=(\acute{\mathbf {r}}_1-\acute{\mathbf {r}}_2)^T( \acute{\mathbf {r}}_1-\acute{\mathbf {r}}_2)-\gamma ^2\acute{\mathbf {r}}_{9}^T \acute{\mathbf {r}}_{9},\ \acute{\Psi }_2=[\acute{\mathbf {r}}_1^T \ \acute{\mathbf {r}}_2^T]\acute{\mathrm {E}}_{i}+\acute{\mathrm {E}}_{i}^T[ \acute{\mathbf {r}}_1^T \ \acute{\mathbf {r}}_2^T]^T,\\ \acute{\Psi }_3&=\acute{\mathbf {r}}_1^T({\mathbf {Q}}_{i1}+{\mathbf {Q}}_{i3} -\mu _1{\mathbf {F}}_{i1})\acute{\mathbf {r}}_1+\acute{\mathbf {r}}_3^T({\mathbf {Q}}_{i2}- {\mathbf {Q}}_{i1})\acute{\mathbf {r}}_3 \\&\quad -\acute{\mathbf {r}}_5^T{\mathbf {Q}}_{i2} \acute{\mathbf {r}}_5+\acute{\mathbf {r}}_4^T(-(1-\delta _d){\mathbf {Q}}_{i3}- \mu _2{\mathbf {F}}_{i1})\acute{\mathbf {r}}_4 \\&\quad +\acute{\mathbf {r}}_6^T( {\mathbf {Q}}_{i4}-2\mu _1)\acute{\mathbf {r}}_6+\acute{\mathbf {r}}_7^T(-(1-\delta _d) {\mathbf {Q}}_{i4}-2\mu _2)\acute{\mathbf {r}}_7 \\&\quad +\acute{\mathbf {r}}_8^T (\delta _1{\mathbf {R}}_{i1}+\delta _{12}{\mathbf {R}}_{i2})\acute{\mathbf {r}}_8 -\delta _1^{-1}(\acute{\mathbf {r}}_1-\acute{\mathbf {r}}_3)^T{\mathbf {R}}_{i1}\\&\quad \times (\acute{\mathbf {r}}_1-\acute{\mathbf {r}}_3)+\acute{\mathbf {r}}_1^T (\mu _1{\mathbf {F}}_{i2})\acute{\mathbf {r}}_6 +\acute{\mathbf {r}}_6^T (\mu _1{\mathbf {F}}_{i2})\acute{\mathbf {r}}_1 \\&\quad +\acute{\mathbf {r}}_4^T( \mu _2{\mathbf {F}}_{i2})\acute{\mathbf {r}}_7+\acute{\mathbf {r}}_7^T( \mu _2{\mathbf {F}}_{i2})\acute{\mathbf {r}}_4 +({\mathbf {K}}\mathrm {E}_{i}-{ \mathbf {r}}_8)^T{\mathbf {L}}_i^T\acute{\mathbf {r}}_8\\ {}&\quad +\acute{\mathbf {r}}_8^T {\mathbf {L}}_i({\mathbf {K}}\mathrm {E}_{i}-\acute{\mathbf {r}}_8) -\delta _{12}^{-1}\left[ \begin{array} {c} \acute{\mathbf {r}}_3-\acute{\mathbf {r}}_4\\ \acute{\mathbf {r}}_4-\acute{\mathbf {r}}_5 \end{array} \right] ^T\left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{ \tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \left[ \begin{array} {c} \acute{\mathbf {r}}_3-\acute{\mathbf {r}}_4\\ \acute{\mathbf {r}}_4-\acute{\mathbf {r}}_5 \end{array} \right] ,\\ {\hat{\Gamma }}_1&=\left[ \begin{array} {c} [\acute{\mathbf {r}}_1^T \ \acute{\mathbf {r}}_2^T]\acute{\Gamma }_1+\acute{\mathbf {r}}_8^T{\mathbf {L}}_i \acute{\Theta }_1\\ 0 \end{array} \right] , \acute{\Gamma }_1=\left[ \begin{array} {cc} \acute{\varvec{\Xi }}_1 &{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{xi}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{yi}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{xi}+ {\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{yi} \end{array} \right] \end{array}\right] ,\\ \acute{\varvec{\Xi }}_1&=\left[ \begin{array} {ccccc} \left[ \begin{array} {cc} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{0i}+ {\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{3i}&{}0\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{0i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{3i}&{}0 \end{array}\right] &{} 0_{2n\times 3n}&{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{1i}+ {\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{4i}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{1i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{4i} \end{array}\right] &{} \left[ \begin{array} {c} {\mathbf {P}}_{i11}\breve{\mathbf {M}}_{2i}+{\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{5i}\\ {\mathbf {P}}_{i12}\breve{\mathbf {M}}_{2i}+ {\hat{\mathbf {H}}}_{fi} \breve{\mathbf {M}}_{5i} \end{array}\right] \\ 0_{2n\times n} \end{array}\right] ,\\ \acute{\mathrm {E}}_{i}&=\left[ \begin{array}{cccccccc} {\hat{\mathbf {E}}}_{i}&0_{2n\times 2n}&{\hat{\mathbf {G}}}_{i}&0_{2n\times n}&{\hat{\mathbf {E}}}_{1i}&{\hat{\mathbf {E}}}_{2i}&0_{2n\times n}&{\hat{\mathbf {E}}}_{3i}\end{array} \right] ,\\&\qquad \qquad \qquad \qquad \qquad \acute{\Gamma }_s=\Big \{ diag(\acute{\varvec{\Xi }}_s,\breve{\mathbf {N}}_{ai}),\ if \ \ s=e, \\&\qquad \qquad \qquad \qquad \qquad \acute{\varvec{\Xi }}_s=\Big \{ diag\{\breve{\mathbf {N}}_{si},\ 0,\ 0,\ 0,\ 0,\ \breve{\mathbf {N}}_{si},\ \breve{\mathbf {N}}_{si},\ 0 \},\ if \ \ s=e,\\ \acute{\Theta }_1&= \left[ \begin{array} {cc} {\mathbf {K}}\acute{\varvec{\Xi }}_1&\breve{\mathbf {M}}_{xi} \end{array}\right] , \acute{\Theta }_2= \left[ \begin{array} {cc} {\mathbf {K}}\acute{\varvec{\Xi }}_1&0 \end{array}\right] ,\\ \acute{\mathbf {r}}_a&=\Big [\underbrace{0,\ldots ,0}_{a-1}\ {\mathbf {I}} \ \underbrace{ 0,\ldots ,0}_{9-a}\Big ]\ \ \ \ a=1,\ldots .,9, \end{aligned}$$

and \({\hat{\mathbf {E}}}_{i} ,\ {\hat{\mathbf {G}}}_{i},\ {\hat{\mathbf {E}}}_{1i},\ {\hat{\mathbf {E}}}_{2i}\) and \( {\hat{\mathbf {E}}}_{3i}\) are defined as in Theorem 3.2. In this case, the parameters of the desired filter can be given by

$$\begin{aligned} {\mathbf {E}}_{fi}&={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {E}}}_{fi},\ {\mathbf {H}}_{fi}={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {H}}}_{fi}. \end{aligned}$$

Proof

The proof and calculation are similar to that in Theorems 3.1 and 3.2 by choosing \({\tilde{\mathbf {H}}}_{i} =\triangle {\tilde{\mathbf {H}}}_{i}(t))={\tilde{\mathbf {H}}}_{1i}=\triangle {\tilde{\mathbf {H}}}_{1i}(t))={\tilde{\mathbf {H}}}_{2i}=\triangle {\tilde{\mathbf {H}}}_{2i}(t)) =0\). Thus, the proof is omitted. \(\square \)

Case 2 If there are no stochastic disturbance and coupling delay, then system (8) is simplified as follows:

$$\begin{aligned} {\dot{x}}(t)&=[({\mathbf {E}}_{\rho _k}+\triangle {\mathbf {E}}_{\rho _k}(t))x(t) +({\mathbf {E}}_{1\rho _k}+\triangle {\mathbf {E}}_{1\rho _k}(t)) {\mathbf {K}}f_{\rho _k}(x(t)) \nonumber \\&\quad +({\mathbf {E}}_{2\rho _k}+\triangle {\mathbf {E}}_{2\rho _k}(t)) {\mathbf {K}}f_{\rho _k}(x(t-\delta (t)))\nonumber \\&\quad +\triangle {\mathbf {E}}_{3\rho _k}(t))\nu (t), \,t\ne t_\kappa \nonumber \\ x(t_\kappa )&={{\mathbf {J}}_\kappa }x(t^-_{\kappa }), \,\, t=t_\kappa . \end{aligned}$$
(28)

Corollary 3.4

For given scalars \(\gamma >0,\ \delta _1,\ \delta _2,\ \delta _d,\) and positive scalars \(\mu _1,\ \mu _2,\) the filtering error system of system (27) based on filter (7) is mean-square robustly asymptotically stable with disturbance attenuation level \(\gamma \) if there exist matrices \({\mathbf {P}}_{i1}^T={\mathbf {P}}_{i1}:=\left[ \begin{array} {cc} {\mathbf {P}}_{i11}&{}{\mathbf {P}}_{i12} \\ {\mathbf {P}}_{i12}&{} {\mathbf {P}}_{i12} \end{array} \right]>0,\ {\mathbf {Q}}_{iq}^T={\mathbf {Q}}_{iq}>0\ (q=1,2,3,4), \ {\mathbf {R}}_{iq}^T={\mathbf {R}}_{iq}>0\ (q=1,2),\ {\mathbf {E}}_{fi},\ {\mathbf {H}}_{fi},\ {\tilde{\mathbf {R}}}_{i2}\) and \( {\mathbf {L}}_{i},\) and scalars \(\varepsilon _{i1}\) such that

$$\begin{aligned} \left[ \begin{array} {cc} {\mathbf {R}}_{i2}&{}{\tilde{\mathbf {R}}}_{i2}\\ *&{} {\mathbf {R}}_{i2} \end{array} \right] \ge 0, \left[ \begin{array} {cc} \acute{{\hat{\Psi }}}+\varepsilon _{i1}\acute{\Gamma }_e^T\acute{\Gamma }_e &{} {\hat{\Gamma }}_1 \\ *&{} -\varepsilon _{i1}{\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(29)

where

$$\begin{aligned} \acute{{\hat{\Psi }}}&= \acute{\Psi }_1+\acute{{\hat{\Psi }}}_2+\acute{\Psi }_3,\ \ \acute{{\hat{\Psi }}}_2=[\acute{\mathbf {r}}_1^T \ \acute{\mathbf {r}}_2^T]\acute{{\hat{\mathrm {E}}}}_{i}+ \acute{{\hat{\mathrm {E}}}}_{i}^T[\acute{\mathbf {r}}_1^T \ \acute{\mathbf {r}}_2^T]^T,\\ \acute{{\hat{\mathrm {E}}}}_{i}&=\left[ \begin{array}{cccccc} {\hat{\mathbf {E}}}_{i}&0_{2n\times 4n}&{\hat{\mathbf {E}}}_{1i}&{\hat{\mathbf {E}}}_{2i}&0_{2n\times n}&{\hat{\mathbf {E}}}_{3i}\end{array} \right] , \end{aligned}$$

and \(\acute{\Gamma }_e,\ {\hat{\Gamma }}_1,\ \acute{\Psi }_1,\ \acute{\Psi }_3,\ {\hat{\mathbf {E}}}_{i} ,\ {\hat{\mathbf {E}}}_{1i},\ {\hat{\mathbf {E}}}_{2i}\) and \( {\hat{\mathbf {E}}}_{3i}\) are defined as in Theorem 3.2. In this case, the parameters of the desired filter can be given by

$$\begin{aligned} {\mathbf {E}}_{fi}&={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {E}}}_{fi},\ {\mathbf {H}}_{fi}={\mathbf {P}}_{i12}^{-1}{\hat{\mathbf {H}}}_{fi}. \end{aligned}$$

Proof

The proof and calculation are similar to that in Theorems 3.1 and 3.2 by choosing \({\tilde{\mathbf {H}}}_{i} =\triangle {\tilde{\mathbf {H}}}_{i}(t))={\tilde{\mathbf {H}}}_{1i}= \triangle {\tilde{\mathbf {H}}}_{1i}(t))={\tilde{\mathbf {H}}}_{2i}= \triangle {\tilde{\mathbf {H}}}_{2i}(t)) ={\tilde{\mathbf {G}}}_{i}=0\). Thus, the proof is omitted. \(\square \)

4 Numerical Examples

In this section, a numerical example is presented to demonstrate the effectiveness of the results derived above.

Example For simplicity, we consider a uncertain stochastic switched complex dynamical networks with three nodes and the state vector of each node being two dimensional, that is \(N=3,\ l=2\) and \(\rho _k=2\) other related parameters are given as follows:

$$\begin{aligned} \breve{\mathbf {E}}_{1}&= diag\{-3,-3\},\ \breve{\mathbf {E}}_{2}=diag\{-1.2,-1.2\},\ \, \\ \breve{\mathbf {E}}_{11}&= \left[ \begin{array}{cc} -0.1 &{}-1.2\\ -0.02 &{}-0.1 \end{array}\right] , \ \,\,\breve{\mathbf {E}}_{21}= \left[ \begin{array}{cc} -0.5&{} 0.1\\ 0.1 &{}-0.5 \end{array}\right] , \ \,\, \breve{\mathbf {E}}_{31}=\left[ \begin{array}{cc} -0.12&{} 0\\ -0.4 &{}0.1 \end{array}\right] , \\ \breve{\mathbf {E}}_{41}&= \left[ \begin{array}{cc} -0.1 &{}0.2\\ -0.12 &{}-0.1 \end{array}\right] ,\ \,\, \breve{\mathbf {E}}_{51}=\left[ \begin{array}{cc} 0.1 &{}0\\ -0.5 &{}0.1 \end{array}\right] , \ \breve{\mathbf {H}}_{1} = \left[ \begin{array}{cc} 0.13&{} 0\\ 0 &{}0.41 \end{array}\right] , \\ \breve{\mathbf {H}}_{11}&= \left[ \begin{array}{cc} 0.1&{} -0.2\\ -0.02 &{}0 \end{array}\right] , \,\, \breve{\mathbf {H}}_{21}= \left[ \begin{array}{cc} 0.5&{} -0.12\\ -0.02 &{}0 \end{array}\right] , \ \breve{\mathbf {H}}_{31}= \left[ \begin{array}{cc} -0.3 &{}0\\ 0 &{}0.1 \end{array}\right] ,\\ \breve{\mathbf {H}}_{41}&=\left[ \begin{array}{cc} 0 &{}-0.2\\ 0.1&{} -0.6 \end{array}\right] , \breve{\mathbf {H}}_{51}= \left[ \begin{array}{cc} -0.1&{} 0\\ 0 &{}-0.2 \end{array}\right] ,\ \,\, \breve{\mathbf {E}}_{x1}= \left[ \begin{array}{cc} -0.19&{} 0\\ 0 &{}-0.6 \end{array}\right] ,\\ \breve{\mathbf {E}}_{y1}&=\left[ \begin{array}{cc} -0.3&{} 0\\ 0 &{}-0.16 \end{array}\right] ,\ \,\,\, \breve{\mathbf {E}}_{12}= \left[ \begin{array}{cc} -0.15 &{}-1.21\\ 0.02&{} -0.11 \end{array}\right] , \ \,\breve{\mathbf {E}}_{22}= \left[ \begin{array}{cc} -0.1&{} 0\\ 0.1&{} 0.15 \end{array}\right] ,\\ \breve{\mathbf {E}}_{32}&=\left[ \begin{array}{cc} -0.2&{} 0.2\\ -0.14&{} 0.51 \end{array}\right] , \,\, \breve{\mathbf {E}}_{42}= \left[ \begin{array}{cc} -0.21 &{}0.25\\ 0.12&{} -0.16 \end{array}\right] ,\ \, \breve{\mathbf {E}}_{52}=\left[ \begin{array}{cc} 0.16&{} 0\\ -0.15 &{}0.61 \end{array}\right] , \\ \breve{\mathbf {H}}_{2}&= \left[ \begin{array}{cc} -0.3 &{}0\\ -0.2&{} 0.41 \end{array}\right] , \ \breve{\mathbf {H}}_{12}= \left[ \begin{array}{cc} -0.5 &{}-0.2\\ 0 &{}0.2 \end{array}\right] , \breve{\mathbf {H}}_{22}= \left[ \begin{array}{cc} 0.15 &{}-0.12\\ 0&{} 0.1 \end{array}\right] , \\ \breve{\mathbf {H}}_{32}&= \left[ \begin{array}{cc} -0.3 &{}0.4\\ 0 &{}0.16 \end{array}\right] ,\ \,\, \breve{\mathbf {H}}_{42}=\left[ \begin{array}{cc} 0.3 &{}-0.2\\ 0.21 &{}-0.6 \end{array}\right] ,\ \breve{\mathbf {H}}_{52}= \left[ \begin{array}{cc} -0.1 &{}0.5\\ 0&{} -0.2 \end{array}\right] , \\ \breve{\mathbf {E}}_{x2}&= \left[ \begin{array}{cc} -0.19 &{}0\\ 0.2&{} -0.6 \end{array}\right] ,\ \,\,\, \breve{\mathbf {E}}_{y2}=\left[ \begin{array}{cc} -0.13 &{}0.3\\ 0&{} -0.16 \end{array}\right] \\ \Upsilon _{11}&=\Upsilon _{12}=\left[ \begin{array}{cc} 0.8 &{} 0\\ 0 &{} 0.8 \end{array}\right] ,\ \,\,\, \Upsilon _{21} =\Upsilon _{22}=\left[ \begin{array}{cc} 0.1 &{} 0\\ 0 &{} 0.1 \end{array}\right] ,\ \,\,\, \breve{\mathbf {N}}_{a1}=\breve{\mathbf {N}}_{a2}=\left[ \begin{array} {cc} 0.14 &{}0.16\\ 0.13 &{} 0.15 \end{array} \right] , \\ \breve{\mathbf {M}}_{01}&=\breve{\mathbf {M}}_{02}=diag\{0.5,0.5\},\, \breve{\mathbf {M}}_{11}=\breve{\mathbf {M}}_{21}=diag\{0.2,0.2\},\, \breve{\mathbf {M}}_{21}=\breve{\mathbf {M}}_{22}=diag\{0.2,0.2\},\\ \breve{\mathbf {M}}_{31}&=\breve{\mathbf {M}}_{32}=diag\{0.2,0.2\},\, \breve{\mathbf {M}}_{41}=\breve{\mathbf {M}}_{42}=diag\{0.2,0.2\},\, \breve{\mathbf {M}}_{51}=\breve{\mathbf {M}}_{52}=diag\{0.2,0.2\},\\ \breve{\mathbf {M}}_{x1}&=\breve{\mathbf {M}}_{x2}=diag\{0.2,0.2\},\, \breve{\mathbf {M}}_{y1}=\breve{\mathbf {M}}_{y2}=diag\{0.2,0.2\},\, \breve{\mathbf {N}}_{e1}=\breve{\mathbf {N}}_{e2}=diag\{0.1,0.1\},\\ \breve{\mathbf {N}}_{h1}&=\breve{\mathbf {N}}_{h2}=diag\{0.1,0.1\}. \end{aligned}$$

The coupling matrices are

$$\begin{aligned} \breve{\mathbf {W}}_{1}=\breve{\mathbf {W}}_{2}=\left[ \begin{array}{ccc} -2 &{}2 &{}0\\ 0 &{}-2 &{}2\\ 2 &{}0 &{}-2 \end{array} \right] ,\ \,\, \breve{\mathbf {G}}_{1}=\breve{\mathbf {G}}_{2}=\left[ \begin{array}{ccc} -2 &{} 1 &{} 1 \\ 1 &{} -2 &{} 1 \\ 1 &{} 1 &{} -2 \\ \end{array} \right] . \end{aligned}$$

According to (2), the relevant parameter matrices can be chosen as

$$\begin{aligned} {\mathbf {F}}_{11}={\mathbf {F}}_{21}=\left[ \begin{array} {cc} 0.05&{} 0.05\\ 0.05&{} 0.05 \end{array} \right] ,\ {\mathbf {F}}_{12}={\mathbf {F}}_{22}=\left[ \begin{array} {cc} -0.05&{} 0.05\\ -0.15 &{}-0.25 \end{array} \right] . \end{aligned}$$

For given \(\delta _1=0.05,\ \delta _2=0.08,\ \delta _d=0.5,\) by using the LMI toolbox of MATLAB to solve LMI (23), we obtain that the minimal disturbance attenuation level \(\gamma =0.557\) and the corresponding filter matrices are given by

$$\begin{aligned} {\mathbf {E}}_{f1}&= \left[ \begin{array} {cc} -5.5921 &{} 0.2530\\ 0.2283 &{} -6.2849 \end{array} \right] , \ \, {\mathbf {E}}_{f2}= \left[ \begin{array} {cc} -3.4408 &{} -0.0094\\ -0.0065 &{} -3.7484 \end{array} \right] ,\,\,\, {\mathbf {H}}_{f1}= \left[ \begin{array} {cc} -1.0417 &{} -0.5962\\ -0.5532 &{} -0.0138 \end{array} \right] , \\ {\mathbf {H}}_{f2}&= \left[ \begin{array} {cc} 0.1090 &{} -0.1278\\ -0.0948 &{} 0.7122 \end{array} \right] ,\ \ {\mathbf {P}}_{111}= \left[ \begin{array} {cc} 25.1805 &{} -0.0637\\ -0.0637 &{} 29.3758 \end{array} \right] , \ {\mathbf {P}}_{112}= \left[ \begin{array} {cc} 5.0722 &{} 0.1299\\ 0.1299 &{} 5.2250 \end{array} \right] ,\\ {\mathbf {P}}_{211}&= \left[ \begin{array} {cc} 30.0088 &{} -1.1133\\ -1.1133 &{} 43.7198 \end{array} \right] , \ {\mathbf {P}}_{212}= \left[ \begin{array} {cc} 5.7630 &{} -0.0097\\ -0.0097 &{} 7.8273 \end{array} \right] ,\ \, {\mathbf {Q}}_{11}= \left[ \begin{array} {cc} 45.7613 &{} -1.9552\\ -1.9552 &{} 54.5097 \end{array} \right] , \\ {\mathbf {Q}}_{12}&= \left[ \begin{array} {cc} 42.6713 &{} -0.4371\\ -0.4371 &{} 44.8974 \end{array} \right] ,\ \, {\mathbf {Q}}_{13}= \left[ \begin{array} {cc} 36.5842 &{} -1.9315\\ -1.9315 &{} 45.7353 \end{array} \right] , \ \, {\mathbf {Q}}_{14}= \left[ \begin{array} {cc} 17.0840 &{} -0.2281\\ -0.2281 &{} 12.9942 \end{array} \right] ,\\ {\mathbf {Q}}_{21}&= \left[ \begin{array} {cc} 32.9495 &{} -0.8270\\ -0.8270 &{} 52.1107 \end{array} \right] , \,\,\, {\mathbf {Q}}_{22}= \left[ \begin{array} {cc} 35.6719 &{} -0.4289\\ -0.4289 &{} 43.1975 \end{array} \right] ,\ \, {\mathbf {Q}}_{23}= \left[ \begin{array} {cc} 23.7386 &{} -0.9602\\ -0.9602 &{} 43.4919 \end{array} \right] , \\ {\mathbf {Q}}_{24}&= \left[ \begin{array} {cc} 11.0020 &{} -2.0292\\ -2.0292 &{} 9.2163 \end{array} \right] ,\ \, {\mathbf {R}}_{11}= \left[ \begin{array} {cc} 1.1448 &{} 0.0608\\ 0.0608 &{} 0.8824 \end{array} \right] , \ {\mathbf {R}}_{12}= \left[ \begin{array} {cc} 1.6318 &{} 0.0108\\ 0.0108 &{} 1.5230 \end{array}\right] ,\\ {\mathbf {R}}_{122}&= \left[ \begin{array} {cc} 1.3768 &{} 0.0005\\ 0.0005 &{} 1.3136 \end{array}\right] , {\mathbf {R}}_{21}= \left[ \begin{array} {cc} 1.5988 &{} 0.0170\\ 0.0170 &{} 1.1447 \end{array} \right] , \ {\mathbf {R}}_{22}= \left[ \begin{array} {cc} 1.3181 &{} 0.0059\\ 0.0059 &{} 1.0539 \end{array} \right] , \\ {\mathbf {R}}_{222}&= \left[ \begin{array} {cc} 1.0159 &{} -0.0032\\ -0.0032 &{} 0.8432 \end{array} \right] ,\ \,\, {\mathbf {L}}_1= \left[ \begin{array} {cc} 1.8882 &{} 0\\ 0 &{} 1.8882 \end{array} \right] ,\ {\mathbf {L}}_2= \left[ \begin{array} {cc} 3.9052 &{} 0\\ 0 &{} 3.9052 \end{array} \right] ,\\ {\mathbf {S}}_1&= \left[ \begin{array} {cc} 13.4054 &{} 0\\ 0 &{} 13.4054 \end{array} \right] , \ {\mathbf {S}}_2= \left[ \begin{array} {cc} 14.0987 &{} 0\\ 0 &{} 14.0987 \end{array} \right] . \end{aligned}$$

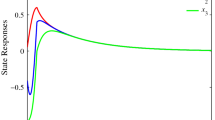
By choosing the initial conditions \(x_1(t) = [-0.5 0.1]^T,\ {\hat{x}}_1(t) = [0.5 -0.5]^T,\ x_2(t) = [-0.2 0.5]^T,\ {\hat{x}}_2(0) = [0.8 - 0.2]^T\) and the disturbance inputs as \(\nu _i(t) = sin(t)e^{-2t}\), the simulation results for Example are shown in Figs. 1 and 2. Figure 1 shows the state trajectories \(x_1(t)\), its estimates \({\hat{x}}_1(t)\) of mode \(\rho _k=1\) and Fig. 2 shows the state trajectories \(x_2(t)\), its estimates \({\hat{x}}_2(t)\) of mode \(\rho _k=2\). According to Theorem 3.2, the uncertain stochastic switched complex dynamical networks (12) with the above mentioned parameters is robustly asymptotically stable in the sense of Definition 2.

Fig. 1
figure 1

The state trajectories \(x_1(t)\) and its estimates \({\hat{x}}_1(t)\) with mode \(\rho _k=1\)

Full size image
Fig. 2
figure 2

The state trajectories \(x_2(t)\) and its estimates \({\hat{x}}_2(t)\) with mode \(\rho _k=2\)

Full size image

Remark 6

In this Table 1, more design parameters and comparisons with some existing results from computational aspects are given. In the table, \({\mathbf {S}}\) gives storage requirements, \({\mathbf {N}}\) denotes the number of LMIs, and \({\mathbf {Z}}\) is the size of the main LMI. It is noted that the method in Theorem 3.2 employed free-weighting matrices, however, it deals with the time-delay pattern and utilizes more decision variables. To avoid numerical computation complexity, LKFs with additive time-varying delays are constructed using a smaller number of decision variables (NDV) compared with the methods in [3,4,5,6]. The NDV in this paper is \(\frac{8n(n+1)}{2}+5n^{2}\). Thus, our presented results are significantly less conservative than those of the existing approaches in [3,4,5,6].

Table 1 A comparison of computational load
Full size table

5 Conclusion

The robust stability of the proposed network model have been taken into consideration in this paper, and some sufficient conditions have been established. By Lyapunov–Krasovskii functional method, an \(H_{\infty }\) filter has been designed via the solution of a set of LMIs such that the resulting augmented system is asymptotically stable with the filter error satisfying a prescribed \(H_{\infty }\) disturbance attenuation level. Then, some advanced techniques such as the free-matrix-based integral inequality and reciprocally convex combination method are used to estimate the derivative of the LKF. Finally, the feasibility and effectiveness of the developed methods has been shown by numerical example. A robust observer-based sensor fault–tolerant control for PMSM in electric vehicles; Fault detection for linear discrete time-varying systems subject to random sensor delay are investigated by the authors [55,56,57]. The idea and approach developed in those paper will be further utilized to deal with some other problems on pinning control and synchronization for general complex dynamical networks.