Bayesian Inference via Variational Approximation for Collaborative Filtering

Abstract

Variational approximation method finds wide applicability in approximating difficult-to-compute probability distributions, a problem that is especially important in Bayesian inference to estimate posterior distributions. Latent factor model is a classical model-based collaborative filtering approach that explains the user-item association by characterizing both items and users on latent factors inferred from rating patterns. Due to the sparsity of the rating matrix, the latent factor model usually encounters the overfitting problem in practice. In order to avoid overfitting, it is necessary to use additional techniques such as regularizing the model parameters or adding Bayesian priors on parameters. In this paper, two generative processes of ratings are formulated by probabilistic graphical models with corresponding latent factors, respectively. The full Bayesian frameworks of such graphical models are proposed as well as the variational inference approaches for the parameter estimation. The experimental results show the superior performance of the proposed Bayesian approaches compared with the classical regularized matrix factorization methods.

1 Introduction

Recommender systems have become increasingly popular in big data era, and are utilized in a variety of areas including e-commerce, movies, music, video, news, books, research articles, search queries, social tags, etc. [1, 2]. Recommender systems typically produce a list of recommendations through content-based filtering and collaborative filtering [3, 4]. Collaborative filtering is a method of making automatic predictions about the interests of a user by collecting references information from many other users, which is a technique widely used by recommender systems [5]. Therefore, the goal of collaborative filtering is to generalize those existing ratings in a way that predicts the unknown ratings. This is the task of filling in the missing entries into a partially observed matrix, which is also known as matrix completion [6]. In addition to collaborative filtering, the matrix completion is also applied to system identification and global positioning [7].

Collaborative filtering is first applied for user mail filtering and document filtering that the recommendation lists are produced based on the similarity of users or items in the rating matrix, which is also known as neighborhood methods [8, 9]. The sparsity of the rating matrix leads to the poor recommendation performance since the distance between different items or, alternatively, between users are almost zero when rating matrix is sparse in practice [10, 11]. An alternative approach, latent factor model (LFM), is introduced that explains the relationship between items and users by characterizing both items and users on latent factors inferred from rating patterns. LFM is highly related to the matrix factorization technique, singular value decomposition (SVD), which has many useful applications in signal processing, statistics and information retrieval [12].

SVD is a well-known matrix factorization technique, which is a generalization of the eigenvalue decomposition of symmetric matrix to arbitrary matrices. By ignoring the smaller singular values, the factorized matrix can be approximated by a lower rank matrix, which is called low-rank approximation. In mathematics, low-rank approximation is a minimization problem, in which the cost function measures the fit between a given matrix (the data) and an approximating matrix (the optimization variable), subject to a constraint that the approximating matrix has reduced rank. This approximation process can be formulated as a latent factor model, in which the dimension of the latent factor is the reduced rank [13].

Some of the successful realizations for LFM decompose the rating matrix into a user preference matrix and an item preference matrix by using SVD [10, 14]. The rating scores in the rating matrix can be interpreted as the relationship between the user and the item, which explains the user-item association by characterizing both items and users on latent factors inferred from rating patterns. Compared with the SVD method, the LFM can describe the more complex relationship between the users and the items [15]. More features for both users and items can be formulated as the latent variable in the models [15, 16].

Due to the sparsity of rating matrix, the latent factor model usually encounters the overfitting problem in practice. In order to avoid overfitting, it is necessary to use additional techniques such as regularizing the model parameters or adding Bayesian priors on parameters. It can be proven that the different regularization methods of parameters are equivalent to the different priors selection. Compared with the regularization methods, Bayesian method is more flexible and has uniform framework to solve in many applications [17, 18]. The Bayesian frameworks of LFM are based on the probabilistic graphical representation of the generative processes of rating scores in the rating matrix [19]. By introducing the latent factors, the rating scores are generated by the interaction between the attributes of the user and the item [20]. In the Bayesian framework, LFM not only can avoid overfitting, but also makes the model more explanatory through generative process of the probabilistic graphical model. The model parameters of LFM are inferred from the posterior distribution of the probabilistic graphical model. Since the posterior distribution is difficult to calculate in most applications, the variational inference is proposed for the estimation of model’s parameters [21, 22]. Variational Inference (VI) approximates the posterior distributions through optimization. The idea behind VI is to find a distribution, which is close to the target, form the candidate distributions. The closeness is measured by Kullback–Leibler.

In this paper, two latent factor models, partial latent factor model (PLFM) and biased latent factor model (BLFM), are considered. In the PLFM, the personalized information can be added into the model, which is advantageous over LFM without content-specific information and user-specific information as well [16]. In the BLFM, biases of users or items are added to reduce the impacts of subjective factors on ratings [15]. Two different generative processes of ratings are proposed for the previous LFMs by probabilistic graphical model theory with corresponding latent factors. The full Bayesian frameworks of such graphical models are proposed as well as the VI approaches for the parameter estimation. The performance of the traditional matrix decomposition methods and the Bayesian methods are investigated on the benchmark datasets, MovieLens 100k and MovieLens 1M. The experimental results show that the Bayesian method is better than the matrix decomposition method on these two models.

The rest of this paper is organized as follows. In Sect. 2, two latent factor models for collaborative filtering in the recommended system are investigated. In Sect. 3, the VI for the investigated latent factor models are proposed. Experiment results are presented in Sect. 4 to show the performance of our method. Concluding remarks are made in Sect. 5.

2 Latent Factor Models for Collaborative Filtering

Given an observation rating matrix $R=(r_{ij})_{M\times N}$ with ijth element $r_{ij}$ which measures the ith user’s preference on the jth item. R is only partially observed over subset $\varOmega$ of indices, which is composed of observed entries (i, j). We are interested in the problem of finding an approximation $\hat{r}_{ij}$ of rating $r_{ij}$.

Latent factor model is an alternative approach that approximates the rating $r_{ij}$ by the user i and item j interaction which is modeled as inner product, leading to the estimation:

$$\begin{aligned} \hat{r}_{ij} =a_i^Tb_j, \end{aligned}$$

(1)

where $a_i=(a_{i1},\ldots ,a_{iK})^T$ and $b_j=(b_{j1},\ldots ,b_{jK})^T$ are K-dimensional unobserved latent vectors, respectively governing user i’s preference over items and item j’s preference by users.

2.1 Partial Latent Factor Model

The personalized recommender system adds feature vectors of the users and the items to latent factor model [16]. Assuming that each $r_{ij}$ associates the ith user’s feature vector $x_i=(x_{i1},x_{i2},\ldots ,x_{iM_{0}})$ and the jth item’s feature vector $y_j=(y_{j1},y_{j2},\ldots ,y_{jN_{0}})$,we obtain PLFM,

$$\begin{aligned} \hat{r}_{ij}={x_i}^T\alpha +{\beta }^Ty_j+a_i^Tb_j \end{aligned}$$

(2)

where $\alpha =(\alpha _1,\ldots ,\alpha _{M_0})^T,\beta =(\beta _1,\ldots ,{\beta }_{N_0})^T$ are vectors of regression parameters, respectively for $x_i$ and $y_j$. $M_0$ and $N_0$ are dimensions of user’s feature vector and item’s feature vector, respectively. $a_i$ and $b_j$ represent K-dimensional user-specific and item-specific latent feature vectors respectively. To prevent overfitting, we regularize PLFM through L2-norm:

$$\begin{aligned} \min _{a^*,b^*,\alpha ,\beta }\sum _{(i,j)\in \varOmega }\left( r_{ij}-\left( {x_i}^T\alpha +{\beta }^Ty_j+a_i^Tb_j\right) \right) ^2+\lambda \left( \parallel a_i \parallel ^2+\parallel b_j\parallel ^2\right) . \end{aligned}$$

(3)

This minimization problem is solved by block-coordinate descent method, which is denoted as P-SVD [16].

Fig. 1

The left panel shows the probabilistic graphical model for PLFM. The right panel shows the the probabilistic graphical model for BLFM

2.2 Biased Latent Factor Models

Biased Latent Factor Models (BLFM) try to explain rating value by adding biases of users and items, denoted as $q_i$ and $p_j$ respectively [15],

$$\begin{aligned} \hat{r}_{ij} =a_i^Tb_j+\mu +q_i+p_j. \end{aligned}$$

(4)

The observed rating is divided into four components: global average $\mu$, item bias $q_i$, user bias $p_j$ and user-item interaction $a_i^Tb_j$. $q=(q_1,\ldots ,q_M),p=(p_1,\ldots ,p_N)$ represent user bias vector and item bias vector. Similarly, it is necessary to minimize regularized square error:

$$\begin{aligned} \min _{a^*,b^*,q^*,p^*}\sum _{(i,j)\in \varOmega }\left( r_{ij}-\left( a_i^Tb_j+\mu +q_i+p_j\right) \right) ^2+\lambda \left( \parallel a_i \parallel ^2+\parallel b_j\parallel ^2+q_i^2+p_j^2\right) . \end{aligned}$$

(5)

This minimization problem is solved by stochastic gradient descent, which is denoted as B-SVD [15].

3 Variation Inference for Latent Factor Models

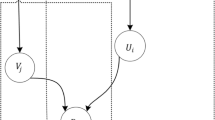
The generative processes of ratings are proposed by probabilistic graphical models with corresponding latent factors of LFM in this section. The probabilistic graphical models for both PLFM and BLFM are shown in Fig. 1. The full Bayesian frameworks of such graphical models are proposed. In the Bayesian anlaysis, three types of information are particularly important, which are the sample information, the loss function and the prior information. The prior information is non-sample information and derived from historical experience about unknown parameters in the similar situation, which cannot be ignored [23]. Given the priors and likelihood of the unknown parameters, the posterior distribution is obtained by the Bayes rule [24]. However, since the posterior distribution is difficult to calculate, we usually use approximate inference or Markov chain Monte Carlo to estimate the posterior distribution [19]. In this paper, we propose the variational inference method for estimating the unknown parameters for both investigated latent factor models.

3.1 Bayesian Inference for LFM with Additive Linear Term

In the PLFM and BLFM, we have $\hat{r}_{ij}=a_i^Tb_j+x_i^T\alpha +y_j^T\beta$ and $\hat{r}_{ij}=a_i^Tb_j+q_i+p_j+\mu$. Both models contain the interaction between useri and itemj and the additive linear combination with unknown parameters. Without loss of generality, we denote the l(w) as the linear combination $x_i^T\alpha +y_j^T\beta$ and $q_i+p_j+\mu$, where $l(\cdot )$ is a linear function about unknown parameter vector w. We get:

$$\begin{aligned} \hat{r}_{ij}=a_i^Tb_j+l(w), \end{aligned}$$

(6)

where the unknown parameters vector w represents the regression vectors $\alpha$, $\beta$ and bias vectors p, q in PLFM and BLFM, respectively. Assuming that the length of the unknown parameter vector w is $L_{w}$. Denote the user feature matrix and item feature matrix as $A=(a_1,a_2,\ldots ,a_M)$ and $B=(b_1,b_2,\ldots ,b_N)$, respectively.

In variation inference, each Q(A, B, w) is a candidate distribution for approximating the posterior p(A, B, w|R). Assuming that $\{A,B,w\}$ are independent, i.e., $Q(A,B,w)=Q(A)Q(B)Q(w)$. We need to maximize the evidence lower bound which is defined as [21]:

$$\begin{aligned} ELBO(Q)=E_{Q(A,B,w)}[\log p(R,A,B,w)-\log Q(A,B,w)] \end{aligned}$$

Lemma 1

Assuming that the unknown parameters $\{a_i,b_j,w\}$ are independent random variables. The likelihood of the observed ratings R and priors distribution over $\{A,B,w\}$ are given by:

$$\begin{aligned} p(R|A,B,w)&=\prod _{i=1}^M\prod _{j=1}^N [{\mathcal {N}}(r_{ij}|{a_i}^Tb_j+l(w),\tau ^2)]^{I_{ij}}, \end{aligned}$$

(7)

$$\begin{aligned} p(A|\sigma )&=\prod _{i=1}^M\prod _{k=1}^K{\mathcal {N}}(a_{ik}|0,{\sigma _k}^2), \end{aligned}$$

(8)

$$\begin{aligned} p(B|\rho )&=\prod _{j=1}^N\prod _{k=1}^K{\mathcal {N}}(b_{jk}|0,{\rho _k}^2), \end{aligned}$$

(9)

$$\begin{aligned} p(w)&=\prod _{l=1}^{L_w}{\mathcal {N}}(w_l|0,1), \end{aligned}$$

(10)

where $I_{ij}$ is the indicator variable that is equal to 1 if $r_{ij}$ is observed. Therefore, the factorized form of the optimal approximated distribution of posterior, i.e., $Q(A,B,w)=Q(A)Q(B)Q(w)$, can be obtained by coordinate ascent variational inference (CAVI).

The proof of Lemma 1 is shown in the “Appendix”. Lemma 1 shows the local optimal approximation of posterior distribution p(A, B, w|R) and the rating matrix R can be estimated by the approximated posterior distribution.

3.2 Variation Inference for PLFM

We apply Bayesian framework to the PLFM. Assuming that $a_{ik}$, $b_{jk}$ and $\alpha$, $\beta$ are independent random variables. The likelihood and priors distribution over $A,B,\alpha ,\beta$ can be given by (7)–(9) and:

$$\begin{aligned} p(\alpha )=\prod _{m=1}^{M_0}{\mathcal {N}}({\alpha }_m|0,1) ,p(\beta )=\prod _{n=1}^{N_0}{\mathcal {N}}({\beta }_n|0,1) \end{aligned}$$

(11)

So, the joint distribution is given by:

$$\begin{aligned} P(A,B,\alpha ,\beta ,R)=p(R|A,B,\alpha ,\beta )p(A)p(B)p(\alpha )p(\beta ) \end{aligned}$$

(12)

This completes the model which can be presented by the probabilistic graphical model for PLFM as shown in Fig. 1 (left panel). In addition, we need to calculate the posterior distribution,

$$\begin{aligned} p(A,B,\alpha ,\beta |R)=\frac{p(R|A,B,\alpha ,\beta )p(A)p(B)p(\alpha )p(\beta )}{p(R)} \end{aligned}$$

(13)

It is always impossible to achieve the optimum which can be achieved at $Q(A,B,\alpha ,\beta ) =p(A,B,\alpha ,\beta |R)$ due to the difficulty in calculating the joint distribution. According to Lemma 1, Q(A), Q(B), $Q(\alpha )$ and $Q(\beta )$ can be obtained as follows.

$$\begin{aligned} Q\left( A\right)&\propto \prod _{j=1}^M \exp \left( -\frac{1}{2}\left( a_i-{\bar{a}}_i\right) ^T\varPhi _i^{-1}\left( a_i-{\bar{a}}_i \right) \right) \end{aligned}$$

(14)

$$\begin{aligned} \varLambda _1&=\begin{pmatrix} \frac{1}{\sigma _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\sigma _K^2} \end{pmatrix},\quad \varPhi _i=\left( \varLambda _1+\sum _{j\in N\left( i\right) } \frac{\varPsi _j+{\bar{b}}_j{\bar{b}}_j^T}{\tau ^2}\right) ^{-1}, \end{aligned}$$

(15)

$$\begin{aligned} {\bar{a}}_i&=\varPhi _i\sum _{j\in N\left( i\right) }\frac{{\bar{b}}_j\left( r_{ij}-x_i^T{\bar{\alpha }}-y_j^T{\bar{\beta }}\right) }{\tau ^2}, \end{aligned}$$

(16)

where N(i) is the set of j’s such that $r_{ij}$ is observed. $\varPhi _i$ and ${{\bar{a}}_i}$ are the covariance the mean of $a_i$ respectively. $\varPsi _j$ and ${\bar{b}_j}$ are the covariance and the mean of $b_j$respectively. ${\bar{\alpha }}$ and ${\bar{\beta }}$ are the mean of $\alpha$ and $\beta$ respectively.

$$\begin{aligned} Q\left( B\right)&\propto \prod _{j=1}^N\exp \left( -\frac{1}{2}\left( b_i-{\bar{b}}_j\right) ^T\varPsi _i^{-1}\left( b_j-{\bar{b}}_j\right) \right) \end{aligned}$$

(17)

$$\begin{aligned} \varLambda _2&=\begin{pmatrix} \frac{1}{\rho _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\rho _K^2} \end{pmatrix},\quad \varPsi _j=\left( \varLambda _2+\sum _{i\in N\left( j\right) } \frac{\varPhi _i+{\bar{a}}_i{\bar{a}}_i^T}{\tau ^2}\right) ^{-1}, \end{aligned}$$

(18)

$$\begin{aligned} {\bar{b}}_j&=\varPsi _j\sum _{i\in N\left( j\right) }\frac{{\bar{a}}_i \left( r_{ij}-x_i^T{\bar{\alpha }}-y_j^T{\bar{\beta }}\right) }{\tau ^2} \end{aligned}$$

(19)

$$\begin{aligned} Q\left( \alpha \right)&\propto \exp \left( \frac{1}{2} \left( \alpha -{\bar{\alpha }}\right) ^T\varDelta _1^{-1}\left( \alpha -{\bar{\alpha }}\right) \right) \end{aligned}$$

(20)

$$\begin{aligned} \varDelta _1&=\left( I+\sum _{\left( i,j\right) \in \varOmega }\frac{x_ix_i^T}{\tau ^2}\right) ^{-1},\quad {\bar{\alpha }}=\varDelta _1\sum _{\left( i,j\right) \in \varOmega }\frac{x_i\left( r_{ij}-{\bar{a}}_i^T{\bar{b}}_j-y_j^T{\bar{\beta }}\right) }{\tau ^2} \end{aligned}$$

(21)

$$\begin{aligned} Q\left( \beta \right)&\propto \exp \left( \frac{1}{2} \left( \beta -{\bar{\beta }}\right) ^T\varDelta _2^{-1}\left( \beta -{\bar{\beta }}\right) \right) \end{aligned}$$

(22)

$$\begin{aligned} \varDelta _2&=\left( I+\sum _{\left( i,j\right) \in \varOmega }\frac{y_jy_j^T}{\tau ^2}\right) ^{-1},\quad {\bar{\beta }}=\varDelta _2\sum _{\left( i,j\right) \in \varOmega }\frac{y_j\left( r_{ij}-{\bar{a}}_i^T{\bar{b}}_j -x_i^T{\bar{\alpha }}\right) }{\tau ^2} \end{aligned}$$

(23)

This completes the algorithm presented as Algorithm 1. We iterates the variational factors Q(A),Q(B),$Q(\alpha )$ and $Q(\beta )$, updating them using (11), (14), (17) and (19) until convergence. Finally, we predict a unobserved rating by:

$$\begin{aligned} \hat{r}_{ij}={\bar{a}}_i^T{\bar{b}}_j+x_i^T{\bar{\alpha }}+y_j^T{\bar{\beta }} \end{aligned}$$

(24)

3.3 Variation Inference for BLFM

The Bayesian framework also can be applied to BLFM. Assuming that $a_{ik}$,$b_{jk}$ and $p_i$, $q_j$ are independent random variables. Supposing that the likelihood and priors over A, B, p, q can be given by (7), (8), (9),$q_i \sim N(0,1)$ and $p_j \sim N(0,1)$. Similarly, the posterior is give by:

$$\begin{aligned} p(A,B,q,p|R)=\frac{p(R|A,B,q,p)p(A)p(B)p(p)p(q)}{p(R)} \end{aligned}$$

The probabilistic graphical model for BLFM is shown in Fig. 1 (right panel). Assuming that the factorized form of VI approximation of the posterior is $Q(A,B,q,p)=Q(A)Q(B)Q(p)Q(q)$. According to Lemma 1, Q(A), Q(B), Q(p) and Q(q) can be obtained as follows

$$\begin{aligned} Q\left( A\right)&\propto \prod _{i=1}^M \exp \left( -\frac{1}{2}\left( a_i-{\bar{a}}_i \right) ^T\varPhi _i^{-1}\left( a_i-{\bar{a}}_i\right) \right) \end{aligned}$$

(25)

$$\begin{aligned} \varLambda _1&=\begin{pmatrix} \frac{1}{\sigma _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\sigma _K^2} \end{pmatrix},\quad \varPhi _i=\left( \varLambda _1+\sum _{j\in N\left( i\right) } \frac{\varPsi _j+{\bar{b}}_j {\bar{b}}_j^T}{\tau ^2}\right) ^{-1}, \end{aligned}$$

(26)

$$\begin{aligned} {\bar{a}}_i&=\varPhi _i\sum _{j\in N\left( i\right) }\frac{{\bar{b}}_j\left( r_{ij}-\mu -{\bar{q}}_i-{\bar{p}}_j\right) }{\tau ^2}, \end{aligned}$$

(27)

where $\varPhi _i$ and $\bar{a_i}$ are the covariance and the mean of $a_i$, respectively. $\varPsi _j$and $\bar{b_j}$ are the covariance and the mean of $b_j$, respectively. ${\bar{q}}_i$ and ${\bar{p}}_j$ are mean of $q_i$ and $p_j$.

$$\begin{aligned} Q\left( B\right)&\propto \prod _{j=1}^N\exp \left( -\frac{1}{2}\left( b_j-{\bar{b}}_j\right) ^T\varPsi _i^{-1}\left( b_j-{\bar{b}}_j\right) \right) \end{aligned}$$

(28)

$$\begin{aligned} \varLambda _2&=\begin{pmatrix} \frac{1}{\rho _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\rho _K^2} \end{pmatrix},\quad \varPsi _j=\left( \varLambda _2+\sum _{i\in N\left( j\right) } \frac{\varPhi _i+{\bar{a}}_i{\bar{a}}_i^T}{\tau ^2}\right) ^{-1}, \end{aligned}$$

(29)

$$\begin{aligned} {\bar{b}}_j&=\varPsi _j\sum _{i\in N\left( j\right) }\frac{{\bar{a}}_i \left( r_{ij}-\mu -{\bar{q}}_i-{\bar{p}}_j\right) }{\tau ^2} \end{aligned}$$

(30)

$$\begin{aligned} Q\left( q\right)&\propto \exp (\frac{1}{2} \left( q-\bar{q}\right) ^T\varDelta _1^{-1}\left( q-\bar{q}\right) \end{aligned}$$

(31)

$$\begin{aligned} \varDelta _1&=\left( 1+\sum _{\left( i,j\right) \in \varOmega } \frac{1}{\tau ^2}\right) ^{-1}I,\quad \bar{q}=\varDelta _1\sum _{\left( i,j\right) \in \varOmega }\frac{e\left( r_{ij}-\mu -{\bar{a}}_i^T{\bar{b}}_j-{\bar{p}}_j\right) }{\tau ^2} \end{aligned}$$

(32)

$$\begin{aligned} Q\left( p\right)&\propto \exp \left( \frac{1}{2} \left( p-\bar{p}\right) ^T\varDelta _2^{-1}\left( p-\bar{p}\right) \right) \end{aligned}$$

(33)

$$\begin{aligned} \varDelta _2&=\left( 1+\sum _{\left( i,j\right) \in \varOmega }\frac{1}{\tau ^2}\right) ^{-1}I,\quad \bar{p}=\varDelta _2\sum _{\left( i,j\right) \in \varOmega }\frac{e\left( r_{ij}-\mu -{\bar{a}}_i^T{\bar{b}}_j-{\bar{q}}_i\right) }{\tau ^2} \end{aligned}$$

(34)

where $e=(1,1,\ldots ,1)$.

Finally, we obtain an algorithm that CAVI applies to BLFM by updating $Q(A),Q(B),Q(q)$ and Q(p), as shown Algorithm 2. We can predict observed matrix R by:

$$\begin{aligned} \hat{r}_{ij}=\mu +{\bar{q}}_i+{\bar{p}}_j+{\bar{a}}_i^T{\bar{b}}_j \end{aligned}$$

(35)

4 Experiments

Several experiments are implemented for the proposed methods through real data in this section. We use movie score data sets—MovieLens 100K and MovieLens 1M as benchmark. MovieLens 100K data contains 100,000 ratings on a five-star scale from 943 users on 1082 movies and features of users and movies, whereas the MovieLens 1M data consist of 1,000,209 ratings from 6040 users on 3900 movies. For prediction, We divided the data into training set and test set, 80% of the Movielens data for training and the remaining 20% for testing. Root mean square error (RMSE) [16] is the most widely used criterion, which is given by

$$\begin{aligned} RMSE=\sqrt{\frac{1}{\mid \varOmega \mid }\sum \nolimits _{(i,j)\in \varOmega }\left( r_{ij}-\hat{r}_{ij}\right) ^2}, \end{aligned}$$

where $r_{ij}$ and $\hat{r}_{ij}$ are the observed and predicted ratings over user i and movie j.

According to those algorithms, we compare Bayesian methods with the classical regularized matrix factorization methods for different models and test the results of L2 norm-regularized SVD(L2-SVD), B-SVD, PSVD, Bayes for LFM, Bayes for PLFM and Bayes for BLFM, respectively. As Bayes for BLFM and Bayes for PLFM are based on VI to approximate posteriors, we keep the variance $\rho ^2_k$ of $b_{jk}$ fixed with values $\rho ^2_k=\frac{1}{K}$ while the variance $\sigma ^2_k$ of $a_{ik}$ fixed with values $\sigma ^2_k=1$, where K is the reduced rank in matrix decomposition and $\tau ^2$ is initialized to 1. The regression parameters $\alpha$ and $\beta$ are initialized to the solution of P-SVD while bias vectors p and q are initialized to the solution of B-SVD. For regularized matrix factorization methods, we use cross-validation to select the tuning parameters $\lambda$.

4.1 Results of MovieLens 100K

For MovieLens 100K data, we compared the performance of Bayesian methods for BLFM for rank 3, 5 and 8 matrix decompositions as shown in Fig. 2 (left panel). We can see that RMSE is minimum at rank 5 in BLFM. Figure 2 (right panel) shows RMSE is decreasing monotonically on both the training and the testing data at rank 5. For PLFM, the number of iterations is set to 190 times because this algorithm converges relatively slowly compared to BLFM. Similarly, we compared the performance of Bayes methods for PLFM for rank 3, 5 and 8 matrix decompositions as shown in Fig. 3 (left panel), which demonstrated that RMSE is minimum at rank 5 in PLFM. Fig. 3 (right panel) shows RMSE is decreasing while it increases a little in the middle of the iterates because the algorithm guarantees that the ELBO rises monotonously.

Fig. 2

The left panel shows the comparison between rank 3, 5 and 8 on training data when using VB for BLFM. The right panel shows RMSE on training and testing data when using VB for BLFM on rank 5 matrix decomposition. The X-axis shows the number of iterations, and the Y-axis shows the RMSE

Fig. 3

The left panel shows the comparison between rank 3, 5 and 8 on training data when using VB for PLFM. The right panel shows RMSE on training and testing data when using VB for PLFM on rank 5 matrix decomposition

Table 1 Comparisons of prediction performance for Bayesian method and the classical regularized matrix factorization method for MovieLens 100K

Table 1 shows the results for various algorithms at convergence on rank 5 for 100k data. We see that the Bayesian method for LFM outperforms its L2 regularized SVD by over 3.7% for BLFM. The VB for PLFM achieves an test-RMSE of 0.9251, compared to an test-RMSE of 0.9696 on regularized matrix factorization method, with an improvement 4.5%. VB for BLFM is also better than B-SVD in spite of an improvement 1.3%.

4.2 Results of MovieLens 1M

For MovieLens 1M data, the number of iterations is set to 40 times. We compared the performance of Bayesian methods for BLFM and Bayesian methods for PLFM for rank 10, 20 and 30 matrix decompositions as shown in Figs. 4 (left panel) and 5 (left panel). We can see that RMSE is minimum at rank 30 in both BLFM and PLFM. Figures 4 (right panel) and 5 (right panel) show that RMSE is decreasing rapidly on both BLFM and PLFM at rank 30, although the data size becomes bigger.

Fig. 4

The left panel shows the comparison between rank 10, 20 and 30 on training data when using VB for BLFM. The right panel shows RMSE on training and testing data when using VB for BLFM on rank 30 matrix decomposition

Fig. 5

The left panel shows the comparison between rank 10, 20 and 30 on training data when using VB for PLFM. The right panel shows RMSE on training and testing data when using VB for PLFM on rank 30 matrix decomposition

Table 2 Comparisons of prediction performance for Bayesian method and the classical regularized matrix factorization method on MovieLens 1M

Table 2 shows results for various algorithms at convergence on rank 30 for 1M data. The variational Bayesian method outperforms the classical regularized matrix factorization method, with the amount of improvement 12.3, 25.9, 27.5% for LFM, BLFM and PLFM. Overall, for those considered models, the results show the superior performance of the Bayesian approaches compared with the classical regularized matrix factorization methods.

5 Conclusions

In this paper, two popular latent factor models for collaborative filtering have been considered. The generative processes of ratings have been proposed by probabilistic graphical model theory with corresponding latent factors. The full Bayesian frameworks of such graphical models have been proposed as well the variational inference approaches for the parameter estimation. Comparisons of the prediction performance of traditional matrix decomposition methods and the Bayesian methods on the MovieLens-100k and the MovieLens-1M have been investigated. The experimental results show the superior performance of the proposed Bayesian approaches compared with the classical regularized matrix factorization methods. In particular, the best VB improvement is 27.8% over regularized matrix factorization method for BLFM on 1M data.

Appendix

Proof of Lemma 1

Noting that the ELBO can be written as:

$$\begin{aligned} ELBO\left( Q\right)&=E_{Q\left( A\right) ,Q\left( B\right) ,w}[\log P\left( A,B,w,R\right) ]-E_{Q\left( A\right) ,Q\left( B\right) ,w}[\log Q\left( A,B,w\right) ]\\&=E_{Q\left( A,B,w\right) }\left[ -\frac{1}{2}\sum _{i=1}^M\sum _{k=1}^K \left( \log \left( 2\pi {\sigma _k}^2\right) +\frac{a_{ik}^2}{{\sigma _k}^2}\right) -\frac{1}{2}\sum _{j=1}^N\sum _{k=1}^K \left( \log \left( 2\pi {\rho _k}^2\right) +\frac{b_{jk}^2}{{\rho _k}^2}\right) \right. \\&\quad -\left. \frac{1}{2}\sum _{l=1}^{L_w}\left( \log 2\pi +w_l^2\right) -\frac{1}{2}\sum _{\left( i,j\right) \in \varOmega }\left( \log \left( 2\pi \tau ^2\right) + \frac{\left( r_{ij}-\hat{r}_{ij}\right) ^2}{\tau ^2}\right) \right]&\\&\quad -E_{Q\left( A\right) }\left( \log Q\left( A\right) \right) -E_{Q\left( B\right) }\left( \log Q\left( B\right) \right) -E_{Q\left( w\right) }\left( \log Q\left( w\right) \right) \\&=-\frac{M}{2}\sum _{k=1}^K\log \left( 2\pi {\sigma _k}^2\right) -\frac{N}{2}\sum _{k=1}^K\log \left( 2\pi {\rho _k}^2\right) -\frac{{L_w}\log \left( 2\pi \right) }{2} -\frac{|\varOmega |}{2}\log \left( 2\pi \tau ^2\right) \\&\quad -\frac{1}{2}\sum _{k=1}^K\left( \frac{\sum _{i=1}^ME_{Q\left( A\right) }\left( a_{ik}^2\right) }{{\sigma _k}^2} +\frac{\sum _{j=1}^NE_{Q\left( B\right) }\left( b_{jk}^2\right) }{{\rho _k}^2}\right) -\frac{1}{2}\sum _l^{L_w}E_{Q\left( w\right) }\left( w_l^2\right) \\&\quad -\frac{1}{2}\sum _{\left( i,j\right) \in \varOmega }\frac{E_{Q\left( A\right) Q\left( B\right) Q\left( w\right) }\left( r_{ij}-\hat{r}_{ij}\right) ^2}{\tau ^2}\\&\quad -E_{Q\left( A\right) }\left( \log Q\left( A\right) \right) -E_{Q\left( B\right) }\left( \log Q\left( B\right) \right) -E_{Q\left( w\right) }\left( \log Q\left( w\right) \right) ) \end{aligned}$$

To achieve the optimal Q(A), we can maximize ELBO by fixing $Q(B),Q(\alpha )$ and $Q(\beta )$. This gives,

$$\begin{aligned} logQ\left( A\right)&=E_{Q\left( B\right) Q\left( w\right) }[\log p\left( R,A,B,w\right) ] \propto E_{Q\left( B\right) Q\left( w\right) }[\log p\left( R|A,B,w\right) +logp\left( A\right) ]\\&=-\frac{1}{2}\sum _{k=1}^K\sum _{i=1}^M\frac{a_{ik}^2}{{\sigma _k}^2} - \frac{1}{2}\sum _{\left( i,j\right) \in \varOmega } \frac{E_{Q\left( B\right) Q\left( w\right) }\left( r_{ij}-a_i^Tb_j-l\left( w\right) \right) ^2}{\tau ^2}\\&\quad \propto -\frac{1}{2}\sum _{i=1}^M a_i^T\varLambda _1 a_i+ \sum _{j\in N\left( i\right) } \frac{-2a_i^TE_{Q\left( B\right) }\left( b_j\right) E_{Q\left( w\right) } \left( r_{ij}-l\left( w\right) \right) +a_i^TE\left( b_jb_j^T\right) a_i}{\tau ^2}\\&\quad \propto -\frac{1}{2}\sum _{i=1}^Ma_i^T\varLambda _1 a_i+\sum _{j\in N\left( i\right) }a_i^T\left( \varPsi _j+{\bar{b}}_j {\bar{b}}_j^T\right) a_i\\&\qquad -2a_i^T\sum _{j\in N\left( i\right) } \frac{{\bar{b}}_j(r_{ij}-l\left( \bar{w}\right) }{\tau ^2} =-\frac{1}{2}\sum _{i=1}^M \left( a_i-{\bar{a}}_i\right) ^T\varPhi _i^{-1}\left( a_i-{\bar{a}}_i\right) \end{aligned}$$

Thus, Q(A) is given :

$$\begin{aligned}&Q\left( A\right) \propto \prod _{j=1}^M \exp \left( -\frac{1}{2}\left( a_i-{\bar{a}}_i\right) ^T\varPhi _i^{-1}\left( a_i-{\bar{a}}_i \right) \right) \\&\varLambda _1=\begin{pmatrix} \frac{1}{\sigma _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\sigma _K^2} \end{pmatrix}, \varPhi _i=\left( \varLambda _1+\sum _{j\in N\left( i\right) } \frac{\varPsi _j+{\bar{b}}_j{\bar{b}}_j^T}{\tau ^2}\right) ^{-1}, \\&{\bar{a}}_i =\varPhi _i\sum _{j\in N\left( i\right) }\frac{{\bar{b}}_j(r_{ij}-l\left( \bar{w}\right) )}{\tau ^2}, \end{aligned}$$

where N(i) is the set of j’s such that $r_{ij}$ is observed. $\varPhi _i$ and $\bar{a_i}$ are the covariance and the mean of $a_i$ respectively. $\varPsi _j$ and $\bar{b_j}$ are the covariance and the mean of $b_j$respectively. $\bar{w}$ is the mean of w. Similarly, the optimal Q(B) is gained by the same method.

$$\begin{aligned} logQ(B)&=E_{Q(A)Q(w)}[\log p(R,A,B,w)] \\&\quad \propto -\frac{1}{2}\sum _{k=1}^K\sum _{j=1}^N\frac{b_{jk}^2}{{\rho _k}^2} - \frac{1}{2}\sum _{(i,j)\in \varOmega } \frac{E_{Q(A)Q(w)}(r_{ij}-a_i^Tb_j-l(w))^2}{\tau ^2}\\&\quad \propto -\frac{1}{2}\sum _{j=1}^Nb_j^T\varLambda _2 b_j+\sum _{i\in N(j)}b_j^T(\varPhi _i+{\bar{a}}_i {\bar{a}}_i^T)b_j-2b_j^T\sum _{i\in N(j)} \frac{{\bar{a}}_i(r_{ij}-l(\bar{w}) }{\tau ^2} \\&=-\frac{1}{2}\sum _{j=1}^N (b_j-{\bar{b}}_j)^T\varPsi _j^{-1}(b_j-{\bar{b}}_j) \end{aligned}$$

Thus, Q(B) is gained:

$$\begin{aligned}&Q\left( B\right) \propto \prod _{j=1}^N\exp \left( -\frac{1}{2}\left( b_j-{\bar{b}}_j\right) ^T\varPsi ^{-1}\left( b_j-{\bar{b}}_j\right) \right) \\&\varLambda _2=\begin{pmatrix} \frac{1}{\rho _1^2}&{} &{}0\\ &{} \ddots &{}\\ 0&{}&{}\frac{1}{\rho _K^2} \end{pmatrix}, \varPsi _j=\left( \varLambda _2+\sum _{i\in N\left( j\right) } \frac{\varPhi _i+{\bar{a}}_i{\bar{a}}_i^T}{\tau ^2}\right) ^{-1},\\&{\bar{b}}_j =\varPsi _j\sum _{i\in N\left( j\right) }\frac{{\bar{a}}_j (r_{ij}-l\left( w\right) }{\tau ^2} \end{aligned}$$

Assume the linear function $l(w)=x^Tw$, where x represents the known sample.

$$\begin{aligned} \log Q\left( w\right)&=E_{Q\left( A\right) Q\left( B\right) }[\log p\left( R,A,B,w\right) ] \propto E_{Q\left( A\right) Q\left( B\right) }[\log p\left( R|A,B,w\right) +\log p\left( w\right) ]\\&=E_{Q\left( A\right) Q\left( B\right) }[-\frac{1}{2}\sum _{\left( i,j\right) \in \varOmega }\frac{\left( r_{ij}-a_i^Tb_j-x^Tw\right) ^2}{\tau ^2}-\frac{1}{2}\sum _{l=1}^{L_w}w_l^2]\\&\quad \propto -\frac{1}{2}\sum _{\left( i,j\right) \in \varOmega }E_{Q\left( A\right) ,Q\left( B\right) }\frac{2x^Tw\left( r_{ij}-a_ib_j\right) +w^Txx^Tw}{\tau ^2}-\frac{1}{2}w^Tw\\&=-\frac{1}{2}w^T\varDelta w-\frac{1}{2}\sum _{\left( i,j\right) \in \varOmega }\frac{2x^Tw\left( r_{ij}-{\bar{a}}_i{\bar{b}}_j\right) +w^Txx^Tw}{\tau ^2}\\&=-\frac{1}{2}\sum _{l=1}^{L_w} \left( w_l-\bar{w}_l\right) ^T\varDelta ^{-1}\left( w_l-\bar{w}_l\right) Q\left( w\right) \propto \exp -\left( -\frac{1}{2} \left( w -\bar{w}\right) ^T\varDelta ^{-1}\left( w-\bar{w}\right) \right) \\&\varDelta =\left( I+\sum _{\left( i,j\right) \in \varOmega }\frac{xx^T}{\tau ^2}\right) ^{-1}, \bar{w}=\varDelta \sum _{\left( i,j\right) \in \varOmega }\frac{x^T\left( r_{ij}-{\bar{a}}_i^T{\bar{b}}_j\right) }{\tau ^2} \end{aligned}$$

Therefore, the local optimal $Q(A,B,w)=Q(A)Q(B)Q(w)$ is given. $\square$