Fast and Robust Active Contours Model for Image Segmentation

Abstract

Image segmentation using local region-based active contour models can segment images with intensity inhomogeneity effectively, but their segmentation results are sensitive to the initialization and easy to get incorrect results when dealing with texture images. This paper presents a novel active contour model (ACM) for image segmentation. The proposed method adopts local kernel mapping to enhance the discriminative ability to delineate nonlinear decision boundaries between classes. In addition, we introduce a modified convex model and propose a fast evolving scheme accordingly to deal with the minimization of the model energy function. The proposed approach is validated by a comparative study over a large number of experiments on synthetic and real images. The experiments demonstrate that our method is more efficient and robust for segmenting different kinds of images compared with the state-of-the-art image segmentation methods.

1 Introduction

Image segmentation is a basic requirement in computer vision and image processing. The purpose of image segmentation is to partition an image area into some meaningful regions. However, it is still a challenging task as images are usually affected by various noise and intensity inhomogeneity. In the past decades, a lot of methods have been proposed to improve the image segmentation quality. Among them, the level set method as a member of active contour family, which was first proposed by Osher and Sethian [1] has been widely used. The advantage of this method is that it treats image segmentation as an energy minimization problem and can get accurate boundary detection with sub-pixel precision. Moreover, the method is convenient to the introduction of constraints on the solution for different tasks [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

Compared with the parametric active contour models (ACMS), level set methods represent the active contour as the zero level set of a higher dimensional function, the advantage is to realize freedom of topological transformation. Existing level set methods can be classified into three classes: edge-based methods [8,9,10], region-based methods [7, 11,12,13,14,15], and combined approaches [6, 16,17,18,19,20,21,22]. Edge-based models depend on gradient information of the image to guide curve evolution. However, they are very sensitive to noise and weak boundary. Therefore, some researchers proposed region-based models to overcome the problems, using the global region statistical information inside and outside of curve to attract contour evolution. One of the most popular region-based models is Chan–Vese (CV) model, Chan and Vese [23] applied the level set method to solve the simplified variants of Mumford–Shah model, which also called Piecewise Constant model. It does not depend on the edge information of the image, but using statistical information of regions inside and outside evolving curves to stop curves on the desired boundary. It gets satisfactory performance on images with weak boundaries. However, it usually fails to segment images with intensity inhomogeneity since the model assumes the image domain is composed of some homogenous regions. To overcome this problem, the piecewise smooth (PS) segmentation model [24] is put forward to segment images with gray uneven characteristics. Unfortunately, it’s very complex to calculate and also sensitive to the initial position of the active contour. Then, Li et al. [25] presented a local binary fitting (LBF) method to segment images with intensity inhomogeneity, using localized image information to segment images with intensity inhomogeneity. In addition, they proposed a regularize level set function by penalizing its deviation from a signed distance function. As a result, the costly re-initialization procedure has been eliminated. Next, Wang et al. [26] described local image intensities by Gaussian distribution with local means and variances as variables, it can be used to segment some simply texture images. Combining region and edge information of the image characteristics, an active contour model integrated boundary-based and region-based information was proposed by Paragios [27] to achieve more robust and better performance in segmentation.

In recent years, some researchers introduced some classical classification methods to segment images [3, 4, 6, 12, 14, 19, 21, 22]. Their methods are robust against noise to some extent and have better segmentation performance compared with some famous level set approaches [9, 23, 25]. For example, Wang et al. [6] proposed a level set method for image segmentation by incorporating local approximating the non-homogeneity-free image in a statistical analysis way which the local energy term and the Bhattacharyya coefficient is used to measure the similarity between probability distribution functions for intensities of inside and outside of the evolving contour. In general, the superiority of this method over the local region-based methods has been shown through the comparisons with representative LBF model, LIC model and LCV model [6]. However, the limitations of these models are the complex mathematical description and high computation cost.

Therefore, more efficient methods are expected to be presented for image segmentation. In this paper, we proposed a novel ACM model which is constructed by two groups—local data energy term and constraint term. The local energy term is described in a local kernelized way that could deal with image segmentation problem flexibly by kernel mapping the original image data in each local regions. However, similar to most other local active contour models [6, 7, 12, 15, 25, 33, 34], it is still sensitive to initialization of the contours. Then, we further modified the aforementioned model and proposed the convex formulation of this model to solve the initialization problem. Meanwhile, the alternating direction method of multipliers (ADMM) iteration approach [35, 36] was utilized to quickly solve the numerical minimization for the active contour propagation toward the boundaries of the images. Figure 1 shows the overall flowchart of the proposed model. To validate the efficiency and robustness of our methods, some experiments on medical images, images with intensity inhomogeneity and noise, texture images are conducted. In addition, we also make a comparative study with some state-of-the-art models to show the superiority of our methods.

Fig. 1

Overall flowchart of the proposed model

The remainder of this paper is organized as follows. Section 2 reviews several major region-based active contour models. Then the proposed models are presented in Sect. 3. In Sect. 4, some experimental results are described and analyzed using a set of synthetic and real images. Finally, this paper is summarized in Sect. 5.

2 Background

2.1 Chan–Vese Model

Mumford and Shah proposed a classic Mumford-Shah model, the model totally depends on the data term of the image to drive the evolution of contour. Then, Chan and Vese [23] presented an active contour model implemented via level set function to solve a simplified Mumford–Shah model. They proposed to minimize the following energy functional:

$$ \begin{aligned} E^{CV} (C,c_{0} ,c_{b} ) & = \lambda_{1} \int_{outside(C)} {(I - c_{b} )}^{2} dx \\ &\quad + \lambda_{2} \int_{inside(C)} {(I - c_{0} )^{2} dx} + \nu \left| C \right| \\ \end{aligned} $$

(1)

To minimize the energy function (1), the level set method is used. The curve C is represented by the zero level set. Then, the formulation of (1) can be reformulated as follows

$$ \begin{aligned} E^{CV} (u,c_{0} ,c_{b} ) & = \lambda_{1} \int {(I - c_{0} )^{2} H(\phi (x))dx} \\ &\quad + \lambda_{2} \int {(I - c_{b} )^{2} (1 - H(\phi (x))dx} \\ &\quad + \nu \int {\left| {\nabla H(\phi (x))} \right|} dx \\ \end{aligned} $$

(2)

where $\lambda_{1}$, $\lambda_{2}$, and $\mu$ are positive constants. $\phi$ is the level set function. $c_{0}$ and $c_{b}$ represent the intensity averages of the image I inside and outside $\phi$, respectively. The average intensities $c_{0}$ and $c_{b}$ can be calculated by

$$ c_{0} = \frac{{\int\limits_{\Omega } {I(x)H(\phi (x))dx} }}{{\int\limits_{\Omega } {H(\phi (x))dx} }},\quad c_{b} = \frac{{\int\limits_{\Omega } {I(x)(1 - H(\phi (x)))dx} }}{{\int\limits_{\Omega } {(1 - H(\phi (x)))dx} }} $$

(3)

where H is the Heaviside function. In practice, H is approximated by a smooth function $H_{\varepsilon }$ which defined as

$$ H_{\varepsilon } (z) = \frac{1}{2}\left| {1 + \frac{2}{\pi }\arctan \left| {\frac{z}{\varepsilon }} \right|} \right| $$

(4)

The derivative of $H_{\varepsilon }$ is written by the following function

$$ \delta_{\varepsilon } = H^{\prime}_{\varepsilon } = \frac{1}{\pi } \cdot \frac{\varepsilon }{{\varepsilon^{2} + z^{2} }} $$

(5)

Keeping $c_{0}$ and $c_{b}$ fixed, and minimizing the energy functional (2) with respect $\phi$, we derive the following gradient descent flow

$$ \begin{aligned} \frac{\partial \phi }{\partial t} & = \delta_{\varepsilon } (\phi )\left[ { - \lambda_{1} \int {\left| {I(y) - f_{1} (x)} \right|^{2} } dy} \right.\left. { + \lambda_{2} \int {\left| {I(y) - f_{2} (x)} \right|^{2} } dy} \right] \\ &\quad + \nu \delta_{\varepsilon } (\phi )div\left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) \\ \end{aligned} $$

(6)

From the energy functional (2), we know that when the values $c_{0}$ and $c_{b}$ are known, this function is non-convex, it has a good segmentation performance on the image with weak boundaries. However, the CV model assumes that the intensities in each area are constant it might fail to segment images with heavy intensity difference in the same area.

2.2 The LBF Model

Through analysis of the local image information, Li et al. [9] proposed the local binary fitting (LBF) model to segment images with intensity inhomogeneity. The energy function of LBF model can be written as follows:

$$ \begin{aligned} E^{{\it LBF}} & = \lambda_{1} \int {\left[ {\int {K_{\sigma } (x - y)\left| {I(y) - f_{1} (x)} \right|^{2} H(\phi (y))dy} } \right]} dx \\ &\quad + \lambda_{2} \int {\left[ {\int {K_{\sigma } (x - y)\left| {I(y) - f_{2} (x)} \right|^{2} (1 - H(\phi (y)))dy} } \right]} dx \\ &\quad + \mu P(\phi (x)) + \nu L(\phi (x)) \\ \end{aligned} $$

(7)

where $\lambda_{1}$, $\lambda_{2}$, $\mu$ and $\nu$ are positive constants. $K_{\sigma }$ is a Gaussian kernel function with a localization property that $K_{\sigma } (\omega )$ decreases and approaches zero as $\left| \omega \right|$ increase, and $\sigma$ is a standard deviation that controls the size of the local region, it can be expressed as.

$$ K_{\sigma } (\omega ) = \left\{ {\begin{array}{*{20}l} {\frac{1}{a}\exp \left( { - \frac{{\left| \omega \right|^{2} }}{{2\sigma^{2} }}} \right)} \hfill & {\omega \le \rho } \hfill \\ 0 \hfill & {\omega > \rho } \hfill \\ \end{array} } \right. $$

(8)

where a is a constant such that $\int {K_{\sigma } (\omega )} = 1$.

$f_{1} (x)$, $f_{2} (x)$ are two numbers that fit the image intensities near the point of x, they can be obtained by

$$ f_{1} (x) = \frac{{K_{\sigma } (x) * [I(x)H(\phi (x))]}}{{K_{\sigma } (x) * H(\phi (x))}},\quad f_{2} (x) = \frac{{K_{\sigma } (x) * [I(x)(1 - H(\phi (x)))]}}{{K_{\sigma } (x) * (1 - H(\phi (x)))}} $$

(9)

$P(\phi )$ is the distance regularizing term to penalize the deviation of the level set function from a signed distance function.

$$ P(\phi ) = \int_{\Omega } {\frac{1}{2}\left| {\nabla \phi - 1} \right|^{2} dx} $$

(10)

$L(\phi )$ is the length of the contour.

$$ L(\phi ) = \int_{\Omega } {\delta \left( \phi \right)} \left| {\nabla \phi } \right|dx $$

(11)

Due to the utilization of the local image information, this model has the capability to segment images with slight intensity inhomogeneity. However, the LBF model is sensitive to the location of initial contour and has difficulty in coping with the image with heavy noise and intensity inhomogeneity.

2.3 The LGDF Model

To effectively exploit information on local intensities, Wang et al. [7] proposed to utilize the Gaussian distribution with different means and variances to describe the local image intensities. In LGDF model, the local intensity means and variances are spatially varying functions. Actually, it is a local statistic model, compared with the LBF model, the capability in handling intensity inhomogeneity is more robust. The energy function of LGDF model embedded level set function can be written as follows:

$$ \begin{aligned} E^{LGDF} & = - \int \left[\int {K_{\sigma } (x - y)log} p_{1,x} (I(y))H(\phi (y))dy \right]dx \\ &\quad - \int \left[\int {K_{\sigma } (x - y)log} p_{2,x} (I(y))(1 - H(\phi (y)))dy \right]dx \\ &\quad + \mu P(\phi (x)) + \nu L(\phi (x)) \\ \end{aligned} $$

(12)

For each pixel x, the local intensities within its neighborhood are assumed to follow a Gaussian distribution

$$ p_{i,x} ((I(y))) = \frac{1}{{\sqrt {2\pi } \sigma_{i} (x)}}\exp \left( { - \frac{{(u_{i} (x) - I(y))^{2} }}{{2\sigma_{i} (x)^{2} }}} \right) $$

(13)

where $u_{i} (x)$ and $\sigma_{i} (x)$ are local intensity means and stand deviations, respectively. By using both the first-order and second-order statistics of local intensities, the LGDF model can not only handle noise and intensity inhomogeneity but also different regions with similar intensity means but different intensity variances. However, from [22] we know that the spatially varying variance may be unstable due to its local property.

2.4 The Kernelized Method

Mohamed et al. [4] proposed an effective level set image segmentation method by kernel mapping the image data. A kernel function maps implicitly the original data onto a higher dimension so that the piecewise constant model becomes applicable. It can express the complex modeling of the image data in a flexible way. Let $\Phi$ be a nonlinear mapping from the observation space M to a higher dimensional feature space N. Let C: $[0,1] \to \Omega$ be a closed curve. The C divides the image area into two regions: the interior of given C by $\Omega_{1} = \Omega_{C}$, the exterior $\Omega_{2} = \Omega_{C}^{c}$. The functional which measures a kernel-induced non-Euclidean distance between the observations I(x) and the regions parameters $f_{1}$, $f_{2}$ as follows:

$$ \begin{aligned} E(\Omega_{1} ,\Omega_{2} ,f_{1} ,f_{2} ) & = \int_{{\Omega_{1} }} {\left\| {\Phi (I(x)) - \Phi (f_{1} )} \right\|}^{2} dx \\ &\quad + \int_{{\Omega_{2} }} {\left\| {\Phi (I(x)) - \Phi (f_{2} )} \right\|}^{2} dx + \lambda \oint_{D} {ds} \\ \end{aligned} $$

(14)

The Mercer’s theorem [37] shows that any finitely positive semi-definite kernel represents the inner product in some higher-dimensional Hilbert space. Therefore, we do not have to know the mapping $\Phi$ exactly. We can use a kernel function $K(x_{i} ,x_{j} )$ expressed

$$ K(x_{i} ,x_{j} ) = \Phi (x_{i} )^{T} \cdot \Phi (x_{j} ),\forall (x_{i} ,x_{j} ) \in M^{2} $$

(15)

The kernel functions in the data term can be represented by the non-Euclidean distance measure in original data space:

$$ \begin{aligned} E_{K} & = \left\| {\Phi (I(x)) - \Phi (f_{i} )} \right\|^{2} \\ & = \Phi (I(x))^{T} \cdot \Phi (I(x)) - 2\Phi (f_{i} )^{T} \cdot \Phi (I(x)) + \Phi (f_{i} )^{T} \cdot \Phi (f_{i} ) \\ & = K(I(x),I(x)) + K(f_{i} ,f_{i} ) - 2K(I(x),f_{i} ) \\ \end{aligned} $$

(16)

They adopt an iterative two-step algorithm to solve the $E_{K}$ function. Firstly, fixing the curve and optimizing the regions parameters. Secondly, evolving the curve by the zero level set function with the region parameters fixed (more details can be referred to [4]). This model can obtain quantitative and comparative performance on synthetic complex images, but it would generate poor results when segmenting images with intensity inhomogeneity.

2.5 Summary

It should be noted that the CV and LBF models both use the mean intensity value to characterize either the global or local image region. Obviously, it will fail to segment the image region with heavy noise and serious inhomogeneity due to the limited characterization ability of the image region. In order to deal with this problem, some models, such as LGDF, employ the mean and variance to represent the image in the local region. However, when the data distribution dissatisfies the Gaussian distribution, it can hardly get the accurate segmentation results.

3 Proposed Method

3.1 Data Energy Term

Intensity inhomogeneity of images is caused by various factors, such as imaging devices, human factors, strength of the natural light on objects. In particular, these adverse factors usually happen in medical images, such as X-ray radiography and magnetic (MR) images. To overcome above problems, a local region-based energy term [7, 14, 15, 19, 25, 26, 28,29,30] has been proposed by many researchers. Although these methods have shown the efficiency in segmenting non-uniform intensity regions, they have difficulties in coping with heavy noise and weak boundary regions in images. From [4], we know that a kernel function can map the image data into a higher dimension which leads to a flexible and effective alternative to the complex modeling of the image data.

Inspired by the kernel mapping function and local region-based energy term, we proposed to combine the local image statistics and kernel mapping strategies, and defined the data energy term as follows:

$$ \begin{aligned} E^{D} (f_{1} ,f_{2} ) & = \lambda_{1} \int {\left[ {\int {K_{\sigma } \left| {(\Phi (I(y)) - \Phi (f_{1} (x)))} \right|^{2} dy} } \right]} dx \\ &\quad + \lambda_{2} \int {\left[ {\int {K_{\sigma } \left| {(\Phi (I(y)) - \Phi (f_{2} (x)))} \right|^{2} dy} } \right]} dx{\kern 1pt} \\ \end{aligned} $$

(17)

where $\lambda_{1}$, $\lambda_{2}$, are fixed parameters, $f_{1} (x)$ and $f_{2} (x)$ are the regions parameters. Table 1 lists some familiar kernel functions $\Phi$, and we used the radial basis function [38, 39] (RBF) kernel in our experiments.

Table 1 Examples of prevalent kernel functions

We use the level set to implement the curve evolution in (17), it can be rewritten as:

$$ \begin{aligned} E^{D} & = \lambda_{1} \int {\left[ {\int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{1} (x))} \right|^{2} H(\phi )} dy} \right]} dx \\ &\quad + \lambda_{2} \int {\left[ {\int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{2} (x))} \right|^{2} } (1 - H(\phi ))dy} \right]} dx \\ \end{aligned} $$

(18)

The constraint term can be written as follows:

$$ E^{C} = \mu P(\phi ) + \nu L(\phi ) $$

(19)

where $\mu$ and $\nu$ are positive constants which control the penalization effect, respectively.

3.2 Level Set Implementation

Now, the total energy functional is given by

$$ \begin{aligned} E^{\textit{LKF}} & = E^{D} + E^{C} \\ & = \lambda_{1} \int {\left[ {\int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{1} (x))} \right|^{2} H(\phi )} dy} \right]} dx \\ &\quad + \lambda_{2} \int {\left[ {\int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{2} (x))} \right|^{2} (1 - H(\phi ))} dy} \right]} dx \\ &\quad + \mu \int_{\Omega } {\frac{1}{2}\left| {\nabla \phi - 1} \right|^{2} dx} + \nu \int_{\Omega } {\delta \left( \phi \right)} \left| {\nabla \phi } \right|dx \\ \end{aligned} $$

(20)

It’s a novel ACM, which is called LKF model.

3.3 Gradient Descent Flow

To minimize the function $E^{\textit{LKF}}$, standard gradient descent is used. The solving process can be divided into two steps: the first step is fixing the level set function $\phi$ to solve $f_{1}$ and $f_{2}$, the second step is to update the level set function $\phi$ with the region parameters $f_{1}$, $f_{2}$ fixed. Next, we will introduce the specific procedures.

• (a) For a fixed level set function $\phi$, the derivatives of $E^{\textit{LKF}}$ with respect to $f_{i}$, $i \in \left\{ {1,2} \right\}$ produce the following equations:

  $$ \frac{{\partial E^{\textit{LKF}} }}{{\partial f_{i} }} = \lambda_{i} \iint {K_{\sigma } }\frac{{\partial (K(I,I) + K(f_{i} ,f_{i} ) - 2K(I,f_{i} ))}}{{\partial f_{i} }} $$

  (21)

  For RBF kernel, we know that $K(I,I) = K(f_{i} ,f_{i} ) = 1$, the minimum of $E^{\textit{LKF}}$ with respect to $f_{1}$, $f_{2}$ is

  $$ \begin{aligned} f_{1} & = \frac{{\int {K_{\sigma } I(x)K(I(x),f_{1} )H(\phi )dx} }}{{\int {K_{\sigma } K(I(x),f_{1} )H(\phi )dx} }}, \\ f_{2} & = \frac{{\int {K_{\sigma } I(x)K(I(x),f_{2} )(1 - H(\phi ))dx} }}{{\int {K_{\sigma } K(I(x),f_{2} )(1 - H(\phi ))dx} }}. \\ \end{aligned} $$

  (22)

• (b) With the $f_{1}$, $f_{2}$ fixed, the $E^{\textit{LKF}}$ is minimized with $\phi$ and obtained the following gradient flow equation:

  $$ \begin{aligned} \frac{\partial \phi }{\partial t} & = \delta_{\varepsilon } (\phi )\left[ { - \lambda_{1} \int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{1} (x))} \right|^{2} } dy} \right. \\ & \left. { + \lambda_{2} \int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{2} (x))} \right|^{2} } dy} \right] \\ &\quad + \mu \left( {\nabla^{2} \phi - div\left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right)} \right) + \nu \delta_{\varepsilon } (\phi )div\left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) \\ \end{aligned} $$

  (23)

  where $\nabla$ is the gradient operator, ${\text{div}}( \cdot )$ is the divergence operator. We use finite difference scheme to implement the level set evolution in this paper. The spatial partial derivatives can be approximated by using the central difference and the temporal partial derivatives were approximated by the forward difference. Furthermore, the computational cost of the level set method can be greatly reduced by only consider an inner and outer band, both sides of the curve, that is, a narrow-band [40] around the zero level set, instead of dealing with the entire domain. The procedures of the proposed algorithm are summarized in Algorithm 1.

Algorithm 1 Image segmentation with the proposed LKF model

Input: Place the initial contour $C_{0}$ and initialize the level set function $\phi$.

Repeat

Fixed level set function $\phi$, and compute $f_{1}$, $f_{2}$ by solving Eq. (22). Update $f_{1}$ and $f_{2}$.

Fixed $f_{1}$, $f_{2}$, and compute the level set function $\phi$ according to the gradient flow (23). Update $\phi$.

Until the level set evolution terminates at time t or reaches the largest number of iterations N.

Out: Extract the zero level set function from the level set function.

Similar to other local active contour models [33, 34], which are known to be sensitive to initialization, the segmentation results of our model also depend on the initialization of the contours. Actually, most of the global active contour models have the same problem, though they are less sensitive than the local models. To obtain a steady solution of the LKF model, convex formulation of it could be a reasonable direction. Next, we will talk about it.

3.4 Convex Formulation of the LKF Model

Since $\delta_{\varepsilon } (\phi ) \ge 0$ in (23), we can remove this function from the gradient descent flow equation of the LKF model, and the following one has the same stationary solution:

$$ \frac{\partial \phi }{\partial t} = ( - \lambda_{1} e_{1} (x) + \lambda_{2} e_{2} (x)) + \eta div(\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}) $$

(24)

where $e_{1}$ and $e_{2}$ are defined as follows:

$$ e_{i} (x) = \int {K_{\sigma } \left| {\Phi (I(y) - \Phi (f_{i} (x))} \right|^{2} } dy $$

(25)

Thus, the previous gradient descent flow equation is associated with the following energy:

$$ E(\phi ,e_{1} ,e_{2} ) = \int h \cdot \phi (x)dx + \eta \int {\left| {\nabla \phi (x)} \right|} dx $$

(26)

The above energy function is homogeneous of degree 1 in $\phi$, and $h = \lambda_{1} e_{1} (x) - \lambda_{2} e_{2} (x)$. As a result, it does not have a minimizer in general (do not have unique level set representations), From [35, 36], we know that a global minimizer for the function of (26) can be found with the constrained $\phi \in [0,1]$. Inspired by this, the GLKF model can be given as follows [we change the notation $\phi$ into u to avoid any confusion with the level set method in (23) and (24)]:

$$ \mathop {\hbox{min} }\limits_{0 \le u \le 1} {E^{GLKF} = \int h \cdot u(x)dx + \eta \int {\left| {\nabla u(x)} \right|} dx} $$

(27)

3.5 Numerical Minimization of the GLKF Based on ADMM

One of the most simple common schemes is the Euler–Lagrange equation techniques and explicit gradient-descent methods to cope with the computation problem of active contour evolution. Unfortunately, the regularization of the TV norm limits the speed of the numerical minimization. In a recent study, a fast and accurate numerical scheme, i.e., ADMM iteration approach, is introduced to solve the energy minimization problem of (27). The ADMM method is a technique for solving general L1-regularized problems of the form

$$ \arg \mathop {\hbox{min} }\limits_{u} \left| {\Phi u} \right|_{1} + \left\| {Au - f} \right\|^{2} $$

(28)

where $\Phi$ and A are linear operators. The ADMM method does not require regularization, continuation, or enforcement of inequality constraints and has been demonstrated to be an extremely efficient solver for L1 regularized problems.

In order to use the ADMM method to solve Eq. (27), firstly, we introduce the auxiliary variable d, $d = \nabla u$. The Eq. (27) becomes

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{0 \le u \le 1} {E^{GLKF} = \int h \cdot u(x)dx + \eta \int {\left| d \right|} dx} \\ & s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} d = \nabla u. \\ \end{aligned} $$

(29)

Then, we add a quadratic penalty function to weakly enforce the resulting equality constraint.

$$ \mathop {\hbox{min} }\limits_{0 \le u \le 1} \left\{ {\int h \cdot u(x)dx + \eta \int {\left| d \right|} dx + \frac{\lambda }{2}\left\| {d - \nabla u} \right\|^{2} } \right\} $$

(30)

To strictly enforce the constraint $d = \nabla u$, we apply ADMM iteration to the equation. The optimization problem becomes

$$ (u^{k + 1} ,d^{k + 1} ) = \arg \mathop {\hbox{min} }\limits_{0 \le u \le 1,d} \int h \cdot u(x)dx + \eta \int {\left| d \right|} dx + \frac{\lambda }{2}\left\| {d - \nabla u - b^{k} } \right\|^{2} $$

(31)

$$ b^{k + 1} = b^{k} + \nabla u^{k} - d^{k} $$

(32)

where $\lambda \ge 0,k \ge 0$, the optimal solution of u must satisfy the following equation:

$$ \Delta u = \frac{1}{\lambda }h + div(b^{k} - d^{k} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} \le u \le 1 $$

(33)

A fast approximate solution can be obtained by using a Gauss–Seidel method since this equation is strictly diagonally dominant (see [35] for more details), and $u^{k + 1}$ can be updated.

Then, the optimal solution $d^{k + 1}$ is updated using the following shrink operator:

$$ d^{k + 1} = \frac{{b^{k} + \nabla u^{k + 1} }}{{\left| {b^{k} + \nabla u^{k + 1} } \right|}}\hbox{max} \left( {\left| {b^{k} + \nabla u^{k + 1} } \right| - \frac{1}{\lambda },0} \right) $$

(34)

When the ADMM solver scheme is placed into algorithm 1, we get the following algorithm scheme for segmentation.

Algorithm 2 ADMM method for the proposed GLKF model

Initialization: Set the initial condition of the iteration approach as $u^{0} = d^{0} = b^{0} = 0,$ and $k = 0,$$i_{G} = 0.$ The maxima of k and $i_{G}$ are represented $N_{0}$ and $N_{1}$, respectively.

Repeat until $\left\| {u^{k + 1} - u^{k} } \right\| \le \varepsilon_{1}$ or $k \ge N_{0}$

Let$u_{\text{old}} = u_{\text{new}} = u^{k} .$

Repeat until $\left\| {u_{\text{old}} - u_{\text{new}} } \right\| \le \varepsilon_{2}$ or $i_{G} \ge N_{1}$

Update$u_{\text{new}}$ with the Gauss–Seidel method

Set$i_{G} = i_{G} + 1.$

End

Update$u^{k + 1}$ with $u^{k + 1} = u_{\text{new}} .$

Update$d^{k + 1}$ according to (34).

Update$b^{k + 1}$ according to (32).

Set$k = k + 1.$

End

4 Experimental Results and Discussions

The performance of our proposed models was evaluated on synthetic and real images. Our models were implemented in Matlab R2014a on a computer with Intel Core i7-4770 3.4 GHz, 8 GB RAM, and Windows 7 operating system. Unless otherwise specified, we use the following parameters setting in LKF model: $\lambda_{1} = \lambda_{2} = 1.0$, $\sigma = 3.0$, $\Delta t = 0.1$, $\in = 1$, $\mu = 1.0$, $\nu = 0.001 \times 255 \times 255$, and $\lambda = 1000$, $\eta = 0.2$, $\varepsilon_{1} = 10^{ - 5}$, $\varepsilon_{2} = 10^{ - 2}$ in GLKF model.

4.1 Segmentation of Medical Images

Firstly, we evaluated LKF model on a set of medical images from different modalities. In the first column of Fig. 2, from top to bottom, a magnetic resonance (MR) image of a left ventricle, a heart computed tomography (CT) image, an ultrasound image, a brain MR image with a tumor and an X-ray image of three fingers. Those images are all corrupted with at least one degenerative factors, including the additive noise, low contrast, low signal-to-noise ratio (SNR), weak boundaries and intensity inhomogeneity. Initial contours were overlaid on each test image with yellow circles, the evolution of those contours was illustrated in the second, third and fourth columns, and the final segmentation results were displayed in the fifth column. It is clearly seen that the LKF model drives the contours to accurately converge to the boundaries of all targeted objectives.

Fig. 2

Segmentation of five medical images using the LKF model: (1st column) test images with initial contours, (2nd–4th columns) evolution of the contours, and (5th column) final segmentation results

4.2 Segmentation of Inhomogeneity Images

Then, we tested LKF model on synthetic and real images with inhomogeneity, the segmentation results were displayed in Fig. 3. In the first row of Fig. 3, from left to right, a synthetic image with severe intensity inhomogeneity, a synthetic image with noise and intensity inhomogeneity, and three real images with intensity inhomogeneity and blurred interferents [41], the initial contours were yellow circles overlaid on each test image. The final segmentation results are presented in the second row. It shows that the LKF model can segment objectives successfully in both synthetic images and real images with severe intensity inhomogeneity or heavy noise by driving the contours accurately to the boundaries.

Fig. 3

Segmentation of images with intensity inhomogeneity by using the LKF model. The first row: the images with initial contours. The second row: final segmentation results

4.3 Comparative Evaluation

In the experiments, we gave the comparison of the LKF model with six famous methods to demonstrate the performance improvement of our model, including the CV model [23], KM model [4], LBF model [25], LIF model [33], LGDF model [7], LSACM model [34]. In Fig. 4, the same initial contours were used by all the models, and overlay on each text images with yellow circles in the first row. From the second to the eighth rows were the results of the seven methods tested on six images. In the first column, from left to right, the first image is a real blood vessel with some blurred interferents around it. The second image is a neonatal rat smooth muscle cell image with heavy interferents and weak boundaries. The last four images were selected from the Berkeley segmentation dataset 500 (BSDS500), the difficulty to segment these images was that the intensity probability distribution functions of these images present multimodality. In each model, we set $\lambda_{1} = \lambda_{2} = 1.0$, $\Delta t = 0.1$, $\nu = 0.001 \times 255 \times 255$ in CV model, set $\Delta t = 0.0001$ in KM model, set $\lambda_{1} = \lambda_{2} = 1.0$, $\sigma = 3.0$, $\Delta t = 0.1$, $\mu = 1.0$, $\nu = 0.001 \times 255 \times 255$ in LBF model, set $\Delta t = 0.1$ in LIF model, set $\lambda_{1} = 1.0$, $\lambda_{2} = 1.05$, $\sigma = 3.0$, $\Delta t = 0.1$, $\mu = 1.0$, $\nu = 0.002 \times 255 \times 255$ in LGDF model, and set $\Delta t = 0.1$ in the LSACM model. The final segmentation results of the CV, KM, LBF, LIF, LGDF, LSACM and LKF were displayed from the second to the eighth rows of the Fig. 4, it shows that our model obtains the most satisfactory segmentation results among these models. Because of only using intensity means in the global region or local region, the CV, LBF and LIF model can hardly distinguish complex texture structures, these models can’t detect the real boundaries of the objects. For the KM model, it almost fails to detect boundaries of the objects when dealing with these intensity inhomogeneity images, it’s hard to accurately represent the category information of the global region of the images. Both the LGDF and LSACM model own better distinguishability to tackle the information of the image compared with the CV, LBF and LIF models, while they still fail to segment the boundaries with abundant textures. By contrast, the LKF model can successfully extract more true boundaries in all these images.

Fig. 4

Comparisons of CV model, KM model, LBF model, LIF model, LGDF model, LSACM model, and our method for segmenting texture images. The first row: original images with initial contours. The second to the eighth rows: final segmentation results of the CV model, KM model, LBF model, LIF model, LGD model, LSACM model, and LKF model

In order to quantitative analysis of the segmentation results, we used the Berkeley segmentation dataset 500 (BSDS500) and Microsoft GrabCut database [42] to evaluate the segmentation experiments. We first focus on the Berkeley data set and randomly selected 50 images from the BSDS500 which consists of a set of natural images and their ground truth segmentation maps generated by multiple individuals [43]. The segmentation results can be assessed quantitatively and objectively by using the Probabilistic Rand Index (PRI). When K ground truths $S_{g} = \left\{ {S_{1} ,S_{2} , \ldots ,S_{K} } \right\}$ are available, the PRI of a segmentation result $S_{s}$ which is calculated as follows [44]:

$$ {\textit{PRI}}(S_{s} ,S_{g} ) = \frac{2}{N(N - 1)}\sum\limits_{\begin{subarray}{l} i,j \\ i < j \end{subarray} } {\left[ {c_{ij} p_{ij} + (1 - c_{ij} )(1 - p_{ij} )} \right]} $$

(35)

where $c_{ij} = 1$ if pixels i and j belong to the same cluster and otherwise $c_{ij} = 0$, and $p_{ij}$ is the ground truth probability of pixels i and j belonging to the same cluster. The coefficient $p_{ij}$ can be computed as the mean pixel pair relationship among all the ground truth images, which implies a binary value true indicating whether the pixel pair belonging to the same cluster or not [45]. The PRI takes a value between 0 and 1, with a higher value representing a more accurate segmentation result. In our experiments, we compared the LKF model with the CV, KM, LBF, LIF, LGDF, LSACM. The segmentation results of all the models obtained on a set of real-world images were compared quantitatively by the PRI shown in Fig. 5. It can be clearly seen that the proposed model achieves the highest PRI values in most images and substantially outperforms other models on average.

Fig. 5

PRI values of segmentation results in 50 Berkeley color images

Moreover, the obtained segmentation results were also quantitatively assessed by using the well-known F-measure [46] which is mainly used in the boundary-based segmentation evaluation. Specifically, a precision-recall framework is introduced for computing the F-measure as follows:

$$ F = \frac{PR}{\gamma R + (1 - \gamma )P} $$

(36)

Precision P is the fraction of detections that are true positives rather than false positives, while recall R is the fraction of true positives that are detected rather than missed [47] and $\gamma$ is a relative cost between P and R, and was set to 0.5 in our experiments. The value of the F-measure ranges from 0 to 1, with a higher value representing a more accurate segmentation result. The F-measures of the segmentation results obtained by applying seven algorithms to segment 50 Berkeley color images were depicted in Fig. 6. It also demonstrates that the LKF outperforms the other models in most of the test images.

Fig. 6

F-measure values of segmentation results on 50 Berkeley color images

Then, we tested these models on the Microsoft GrabCut database to evaluate segmentation quality. The error rate is used as an accurate measurement of the segmentation results, which is defined as the ratio of the number of wrongly labeled pixels to the total number of unlabeled pixels [42]. Figure 7 illustrates the error rates of various methods for all the images in the Microsoft GrabCut database. Comparing the proposed method with other methods, we can see that our method obtains the lowest error rate in most cases. Figure 8 shows some segmentation examples of various methods in the Microsoft GrabCut database. Our method effectively improves the segmentation quality and outperforms the other methods.

Fig. 7

The error rates for all the images in the Microsoft GrabCut database

Fig. 8

Segmentation examples of CV model, KM model, LBF model, LIF model, LGDF model, LSACM model, and our method in the Microsoft GrabCut database. The first row: original images with initial contours. The second to the eighth rows: final segmentation results of the CV model, KM model, LBF model, LIF model, LGD model, LSACM model, and LKF model

4.4 Initialization Sensitivity of the LKF Model

The LKF model has a greater sensitivity to initialization than global region-based methods because the LKF model calculates local intensity inside and outside the active contour like other local active contours. Figure 9 shows segmentation results in a larger array of initial contours on a test image. The results (a)–(d) in Fig. 9 demonstrated that a quality segmentation when you can start the contour in almost the right place, including the number of pixels belonging to the object region is larger than that of the background region. Three initializations, shown in (e)-(g), resulted in an incorrect segmentation boundary of the foreground since the initial contours were far away from the object region. The remaining five initializations, shown in (h)-(l), resulted in an inaccurate segmentation since the initial contours contain very little information about the object. In conclusion, the initial contour needs to be placed on a region that is relatively close to the foreground, containing enough information about the foreground to generate satisfying results.

Fig. 9

Initialization sensitivity analysis of LKF model. a–l Initialization contours on the left side and final segmentation results on the right side, respectively

4.5 Parameter Setting

The proposed LKF model has five parameters to be set manually, including the standard deviation of Gaussian kernel $\sigma$, the time step $\Delta t$, the constant $\in$ to approximate the Heaviside function, and two weighting constants $\mu$ and $\nu$ for the signed distance function $P(\phi )$ and the length of level set function $L(\phi )$, respectively.

In general, using larger time step can speed up the level set evolution, but may cause a border demarcation error if the time step is too large. Therefore, it is a tradeoff between a larger time step and boundary accuracy. Unfortunately, as far as we know, the choice of time step for the level set evolution is still mainly based on the experimental results. So, as an improved LBF model, we used the same time step $\Delta t = 0.1$ for all the experiments in our model. As in CV and LBF model, the constant $\in = 1$ has been widely used for good approximate of Heaviside function. We also fixed $\in = 1$ in our experiments.

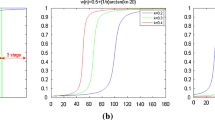
To evaluate the impact of parameter settings for $\sigma$, $\mu$ and $\nu$, the performances with different parameters are evaluated on the Microsoft Grabcut database. The scale size of $\sigma$ effects the range of exploiting image information. Figure 10a shows the quantitative evaluation of the average error rates (%) for $\sigma \in [1,20]$, we fixed $\mu = 1$, $\nu = 0.001 \times 255 \times 255$ in our experiments. It can be seen that the average error rate of the proposed method decreases with the increase of $\sigma$ when $\sigma \le 4$ and gradually increases when $\sigma > 4$.

Fig. 10

The average error rates over all 50 images on the MSRC data set with different values of a$\sigma$, b$\mu$ and c$\nu$, respectively

To eliminate the need of the re-initialization and maintain the signed distance in traditional level set methods, an internal energy term $\int_{\Omega } {\frac{1}{2}\left| {\nabla \phi - 1} \right|^{2} dx}$ has been introduced to penalize the deviation of the level set function from a signed distance function. To quantitatively evaluate the impact of $\mu$, we fixed $\sigma = 3$, $\nu = 0.001 \times 255 \times 255$. Figure 10b indicates the average error rate of different $\mu$ for $\mu \in [0,2]$. It illustrates that the average error rate of the proposed model slightly decreases with the increase of $\mu$ when $\mu \le 1$ and gradually increases when $\mu > 1$, in particular, the average error rate dramatically increases when $\mu \ge 1.6$. Therefore, $\mu = 1$ is widely used in variational level set methods.

The parameter $\nu$ in the internal $\int_{\Omega } {\delta \left( \phi \right)} \left| {\nabla \phi } \right|dx$ term controls the smoothness of the zero level set curve. To quantitatively evaluate the impact of $\nu$, we fixed $\sigma = 3$, $\mu = 1$. Figure 10c shows the average error rate of different $\nu$ for $\nu \in [0,100]$. It shows that the values of average error rate have been slightly affected by the parameter $\nu$, the minimum average error rate is about 5.5%, and the maximum value is about 6.25%. The larger the $\nu$ is, the smoother the segmentation boundaries are. In contrast, if we choose $\nu$ too small, the segmentation boundaries may not be smooth enough and the corresponding segmentation results may not be robust against noise. In terms of our experiments, a quality segmentation result may obtain if we choose a value of $\nu$ from a range [40, 70].

4.6 The Evolution Contours of the GLKF Model

Since the nonconvex property of the LKF model, it inevitably needs the initialization contour relatively close to the segmentation object. To address this problem, we proposed a modified LKF model called GLKF model was proposed. In order to get a better understanding, the same test image (the image in Fig. 9) is used. Figure 11 shows the segmentation results of the GLKF model, the first row displays the evolution of the contours and the second row shows the corresponding results of u in the formulation (27). From Fig. 11, we can see that the GLKF model can overcome contour initialization problem beautifully.

Fig. 11

Segmentation results of the GLKF model. The first row shows the evolution of the contours. The second row displays the results of u in algorithm 2

4.7 Computational Complexity Analysis

Theoretically, the proposed LKF model has computational complexity $O(M_{0} M_{1} )$, where $M_{0}$ and $M_{1}$ are the size of the image and kernel, respectively. In algorithm 2, the main numerical computation is the iteration of k and $i_{G}$, so the GLKF model has the time complexity $O(N_{0} N_{1} )$, where $N_{0}$ and $N_{1}$ are the maxima of k and $i_{G}$, respectively. In fact, $N_{0}$ and $N_{1}$ are usually much smaller than the size of the image $M_{0}$. As a result, the GLKF model is much faster than the LKF model. Table 2 shows the run-time performance on test images presented in Fig. 2. It is worth mentioning that we can further reduce the complexity of our method by using the generalized power method of sparse principal component analysis (GP-SPCA) [48]. be mainly focused on it in the future work, which would be one of our focuses in the future.

Table 2 CPU time for the LKF model and the GLKF model to the images shown in Fig. 1 in the same order

5 Conclusions

In this paper, we proposed a novel active contour model which is called LKF model. The experiments on several real and synthetic images have demonstrated the efficiency of our method on medical images, images with intensity inhomogeneity, nature images. In addition, the superiority of it over the traditional region and local region-based methods has been shown through the comparisons with the representative CV model, KM model, LBF model, LIF model, LGDF model and LSACM model.

However, the LKF model is sensitive to the initialization of contours. To overcome this problem, we further modified the LKF model and proposed the GLKF model. It is a convex formulation, so it can avoid the initialization problem, meanwhile, a fast algorithm ADMM is used to solve this model. In the future, we will focus on a new active contour model for image segmentation and introducing GP-SPCA or other parallel optimization methods to further accelerate the computation.