Robust Subspace Segmentation by Self-Representation Constrained Low-Rank Representation

Abstract

Low-rank representation (LRR) and its variants have been proved to be powerful tools for handling subspace segmentation problems. In this paper, we propose a new LRR-related algorithm, termed self-representation constrained low-rank presentation (SRLRR). SRLRR contains a self-representation constraint which is used to compel the obtained coefficient matrices can be reconstructed by themselves. An optimization algorithm for solving SRLRR problem is also proposed. Moreover, we present an alternative formulation of SRLRR so that SRLRR can be regarded as a kind of Laplacian regularized LRR. Consequently, the relationships and comparisons between SRLRR and some existing Laplacian regularized LRR-related algorithms have been discussed. Finally, subspace segmentation experiments conducted on both synthetic and real databases show that SRLRR dominates the related algorithms.

1 Introduction

Subspace segmentation algorithms aim to partition a group of high-dimensional data samples into several linear subspaces where they are assumed to be drawn from [1,2,3,4,5,6]. Due to the prominent achievements in many real-world applications such as motion segmentation [1, 2, 7], face clustering [8, 9] and so on, graph-based subspace segmentation methods [1,2,3,4, 7,8,9] have attracted a lot of researchers’ attentions.

Sparse subspace clustering (SSC) [1, 2] and low-rank representation (LRR) [3, 4] may be the two most representative graph-based algorithms. They both want to seek a reconstruction coefficient matrix ${\mathbf {Z}}$ for a data set ${\mathbf {X}}$ which satisfies ${\mathbf {X}}=\mathbf {XZ}+{\mathbf {E}}$, where ${\mathbf {E}}$ represents the reconstruction residual. Then an affinity graph ${\mathbf {G}}$ could be obtained with $[{\mathbf {G}}]_{ij}=(|[{\mathbf {Z}}]_{ij}|+|[{\mathbf {Z}}]_{ji}|)/2,[{\mathbf {G}}]_{ij}$ denotes the (i, j)-th element of matrix ${\mathbf {G}}$. Finally, the well-known spectral clustering algorithm, normalize cut (Ncut) [10], could be used to get the final subspace segmentation results.

The main difference between SSC and LRR is that they impose different constraints on the reconstruction coefficient matrix ${\mathbf {Z}}$. SSC excepts ${\mathbf {Z}}$ to be a sparse matrix, while LRR hopes ${\mathbf {Z}}$ to have minimal rank. As it is known to all, in graph-based subspace segmentation methods, it is critical to construct an affinity graph which can reveal the intrinsic structure for a data set. Compared to SSC, LRR is proven to be more powerful to discover the global intrinsic structures of data sets and less sensitive to corrupted data [3, 4]. Hence, LRR usually achieves better results than those of SSC in subspace segmentation applications. Consequently, many LRR-related research works have been developed. For example, Zhuang et al. proposed a kind of non-negative low-rank and sparse representation (NNLRSR) [11] which compels the coefficient matrices obtained by LRR to be sparse and non-negative. Zheng et al. introduced a locality constraint into LRR and proposed a so called low-rank representation with locality constraint (LRRLC) algorithm [12]. Tang et al. designed a structure-constrained LRR (SCLRR) algorithm which was much similar to LRRLC and claimed that NNLRSR was actually a special case of SCLRR [13]. Wei et al. analyzed the subspace segmentation procedures of LRR-based algorithms and developed a spectral clustering steered low-rank representation method (SCSLRR) [9]. SCSLRR could be regarded as an extension of SCLRR. Recently, Zhuang et al. proposed a new locality-preserving low-rank representation ($L^2R^2$) [14] by only picking the K neighbors of each data point to reconstruct itself. Lu et al. added a graph regularizer of coefficient matrices into LRR and proposed a graph-regularized low-rank representation (GLRR) [15]. Yin et al. used a similar strategy and provided a non-negative Laplacian regularized low-rank representation (NSLLRR) [16] based on NNLRSR. Then GLRR could be considered as a special case of NSLLRR. Zhang et al. extended classical LRR to handle subspace segmentation problems for data with multiview features and invented a low-rank tensor constrained multiview subspace clustering algorithm [17].

In addition, we also note that some algorithms which used different constraints on reconstruction coefficient matrices also achieved promising results in subspace segmentation tasks. For instance, Lu et al. presented a least square regression method (LSR) which tried to minimize the Frobenius norms of coefficient matrices [18]. By following the methodology of SCSLRR, Wu et al. suggested to combine Ncut and LSR together [19]. Hu et al. hoped the coefficient matrices to maintain the locality structures of original data sets, so they designed a kind of smooth representation clustering (SMR) [20] algorithm. Zhao et al. claimed that a group sparse coefficient matrix could also discover the intrinsic structure of a data set [21]. For the sake of alleviating the sensitivity of the obtained coefficient matrices to noise, Dong et al. designed a joint nuclear norm and group sparse constraint minimization method for subspace segmentation [22].

Based on the studies on LRR and its various extensions, we know that the obtained low-rank coefficient matrices are actually the affinity matrices of data sets. A coefficient matrix, in which the similarities between homogeneous data samples are enhanced and the similarities between heterogeneous data samples are decreased, would produce good subspace segmentation results. In order to seek this kind of coefficient matrices, in this paper, we firstly proposed a new LRR-related subspace segmentation algorithm, termed self-representation constrained low-rank representation (SRLRR). In SRLRR, a new self-representation constraint on coefficient matrices was devised, which was used to force the coefficient matrices could be linearly reconstructed by themselves. We deeply analyzed the obtained coefficient matrices of SRLRR and explained the advantages of SRLRR for subspace segmentation tasks. Secondly, we presented an alternative form of SRLRR which could be regarded as a kind of Laplacian-regularized LRR. Then we stated the relationships between the SRLRR and some existing Laplacian-regularized LRR-based algorithms including GLRR, SMR and NSLLRR. We believe that the comparisons would be helpful for understanding our proposed algorithm. Thirdly, extensive subspace segmentation experiments conducted on both synthetic and real data sets would show SRLRR outperforms the related algorithms.

The rest of this paper is organized as follows: Sect. 2 beiefly reviews LRR algorithm. Section 3 introduces the motivation of self-representation constrained low-rank representation (SRLRR) method and presents the optimization algorithm. The further discussions on SRLRR and the relationships between SRLRR and some existing LRR-based algorithms are presented in Sect. 4. In Sect. 5, subspace segmentation experiments on both synthetic and real world databases are performed to show the effectiveness of SRLRR. Finally Sect. 6 gives the conclusions.

2 Preliminaries

2.1 Notations

We first provide some important notations adopted in the following sections of this paper in Table 1.

Table 1 Some important notations used in this paper

2.2 Low-Rank Representation (LRR)

Suppose a group of data samples ${\mathbf {X}}= [{\mathbf {x}}_1,{\mathbf {x}}_2,\cdots ,{\mathbf {x}}_n]\in R^{D\times n}$, and each data can be represented by the linear combination of the data set itself ${\mathbf {X}}$. Namely,

$$\begin{aligned} {\mathbf {X}} = \mathbf {XZ}, \end{aligned}$$

(1)

where ${\mathbf {Z}} = [{\mathbf {z}}_1,{\mathbf {z}}_2,\cdots ,{\mathbf {z}}_n]\in R^{n\times n}$ is the coefficient matrix with each ${\mathbf {z}}_i$ being the representation of ${\mathbf {x}}_i$. Low-rank representation (LRR) aims to find a proper ${\mathbf {Z}}$ with minimal rank which satisfies Eq. (1). However, in real applications, data points are usually corrupted with some noise and outliers. Hence, the objective function of LRR can be expressed as follows:

$$\begin{aligned}&{\min }_{\mathbf {Z,E}}\, \Vert {\mathbf {Z}}\Vert _*+\lambda \Vert {\mathbf {E}}\Vert _{2,1}, \nonumber \\&s.t.\quad {\mathbf {X}} = \mathbf {XZ}+{\mathbf {E}}, \end{aligned}$$

(2)

where $\Vert {\mathbf {Z}}\Vert _*$ is the nuclear norm of ${\mathbf {Z}}$ ( i.e., the sum of the singular values of the matrix) [23] which is a convex substitute of $rank({\mathbf {Z}})$.) $\lambda >0$ is used to balance the effects of the two terms. $\Vert {\mathbf {E}}\Vert _{2,1}=\sum _{j=1}^n\sqrt{\sum _{i=1}^n([{\mathbf {E}}]_{i,j})^2}$ is an error term which can characterize the sample-specific outliers [24]. Actually, alternative matrix norms could also be adopted. For example, the $l_{1}$-norm of ${\mathbf {E}}$, namely $\Vert {\mathbf {E}}\Vert _{1} = \sum _{i=1}^n\sum _{j=1}^n|[{\mathbf {E}}]_{ij}|$ can be used to model noise satisfies Laplacian distribution. And the Frobenius norm, $\Vert {\mathbf {E}}\Vert _F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n[{\mathbf {E}}]_{ij}^2}$, is able to fit Gaussian noise.

In fact, the noise in real world data usually is very complex. Many works attempted to model different kinds of noise in real word data. For instance, under the Baysian framework, Zhao et al. argued to use a mixture of Gaussian to fit a wide range of noises such as Laplacian, Gaussian, sparse noises and any combinations of them [25]. Wang et al. claimed that the alternative coefficients of noise in frequency domain are constant w.r.t. their variance, so they proposed a new method based on discrete cosine transform (DCT) to handle complex noise [26]. They also designed a DCT-based regularizer which is efficient in visual recovery for data with large percentage of corruption [27].

Finally, as we mentioned in Sect. 1, once ${\mathbf {Z}}$ is obtained by LRR, an affinity graph ${\mathbf {G}}$ can be defined. Then Ncut is used to produce the subspace segmentation results.

3 Self-Representation Constrained Low-Rank Representation (SRLRR)

3.1 Motivation

According to the descriptions in the previous section, ${\mathbf {Z}}$ is the linear reconstruction coefficient matrix of ${\mathbf {X}}$. Consider the noise-free model of LRR, we have ${\mathbf {X}}=\mathbf {XZ}$. Furthermore, according to LRR, the reconstruction coefficient matrix ${\mathbf {Z}}$ can also be regraded as the representation of ${\mathbf {X}}$. As proved by some manifold learning algorithms such as locally linear embedding (LLE) [28] and sparsity preserving projection (SPP) [29], an appropriate representation of a original data set should follow the reconstruction relationship of the original data set. Hence, replace ${\mathbf {X}}$ by ${\mathbf {Z}}$ in Eq. (1), we have

$$\begin{aligned} {\mathbf {Z}} = \mathbf {ZZ}={\mathbf {Z}}^2. \end{aligned}$$

(3)

The above equation is called self-representation constraint on ${\mathbf {Z}}$ which means the coefficient matrix should be able to reconstructed by itself. We add Eq. (3) into the objective function of LRR and explicitly enforce each column of ${\mathbf {Z}}$ to sum to one¹ [30]. Then the self-representation constrained LRR (SRLRR) problem can be defined as follows:

$$\begin{aligned} \begin{array}{cc} {\min }_{\mathbf {Z,E}} &{} \Vert {\mathbf {Z}}\Vert _*+\beta \Vert {\mathbf {Z}}-{\mathbf {Z}}^2\Vert _F^2+\lambda \Vert {\mathbf {E}}\Vert _{2,1}, \\ s.t. &{} {\mathbf {X}} = \mathbf {XZ}+{\mathbf {E}}, {\mathbf {1}}_n{\mathbf {Z}}={\mathbf {1}}_n,\\ \end{array} \end{aligned}$$

(4)

where $\beta$ is a positive real number, ${\mathbf {1}}_n=[1,1,\cdots ,1]\in R^{1\times n}$.

3.2 Explanation

Some researchers may argue that the coefficient matrix ${\mathbf {Z}}$ which satisfies the self-representation constraint, e.g. ${\mathbf {Z}} = \mathbf {ZZ}={\mathbf {Z}}^2$ can only be ${\mathbf {Z}}={\mathbf {0}}$ or ${\mathbf {Z}}={\mathbf {I}}$. Hence, they regard the self-representation constraint is erroneous. In fact, any idempotent matrix could satisfies the self-representation constraint. An idempotent matrix could have many formulations including two simplest ones, namely ${\mathbf {0}},{\mathbf {I}}$. It is known that the rank of an idempotent matrix equals its trace. Because the lowest-rank constraint in Eq. (4), ${\mathbf {I}}$ would not be a solution to SRLRR. Moreover, the constraint ${\mathbf {1}}_n{\mathbf {Z}}={\mathbf {1}}_n$ will prevent SRLRR to get the solution ${\mathbf {Z}}={\mathbf {0}}$.

We now discuss the possible formulation of the solution to SRLRR. Suppose a group of data samples generated from C clusters, namely ${\mathbf {X}}=[{\mathbf {X}}_1,{\mathbf {X}}_2,\cdots ,{\mathbf {X}}_C]$. Here ${\mathbf {X}}_i\in R^{D\times n_i},n_i$ is the number of samples in the i-th cluster. We know that the optimal solution to the classical LRR problem is block-diagonal, namely

$$\begin{aligned} {\mathbf {Z}}=\left( \begin{array}{cccc} {\mathbf {Z}}_1 &{} 0 &{} 0 &{} 0\\ 0 &{} {\mathbf {Z}}_2 &{} 0 &{} 0\\ 0 &{} 0 &{} \ddots &{} 0\\ 0 &{} 0 &{} 0 &{} {\mathbf {Z}}_C\\ \end{array} \right) , \end{aligned}$$

where ${\mathbf {Z}}_i$ is an $n_i\times n_i$ matrix [3, 4]. Because SRLRR is designed based on LRR, the coefficient matrix obtained by SRLRR should also be block-diagonal. In addition, in SRLRR, ${\mathbf {Z}} = \mathbf {ZZ}$ and ${\mathbf {1}}_n{\mathbf {Z}}={\mathbf {1}}_n$, hence ${\mathbf {Z}}_i = {\mathbf {Z}}_i{\mathbf {Z}}_i$ and ${\mathbf {1}}_{n_i}{\mathbf {Z}}_i = {\mathbf {1}}_{n_i}$. Moreover, ${\mathbf {Z}}_i$ should also be low rank (but can not be ${\mathbf {0}}$ because of ${\mathbf {1}}_{n_i}{\mathbf {Z}}_i = {\mathbf {Z}}_i$). Then an idempotent matrix with low-rank constraint which also satisfies the sum of each column be 1 (namely, ${\mathbf {1}}_{n_i}{\mathbf {Z}}_i = {\mathbf {1}}_{n_i}$), so we have

$$\begin{aligned} {\mathbf {Z}}_{i}=\left( \begin{array}{ccc} \frac{1}{n_i} &{} \cdots &{} \frac{1}{n_i}\\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{n_i} &{} \cdots &{} \frac{1}{n_i}\\ \end{array} \right) . \end{aligned}$$

This property of the coefficient matrix obtained by SRLRR will enhance the similarities of data samples in the same subspace, so the coefficient matrix ${\mathbf {Z}}$ will be more suitable for reveal the subspace relationship of data samples than that of LRR. In the subsequent sections, we will present an alternative formulation of SRLRR and discuss its superiorities to the related algorithms.

3.3 Optimization

In this subsection, we will show how to solve the proposed SRLRR problem [namely, Eq. (4)]. The well-known alternating direction method (ADM) [31] is adopted. Firstly, Eq. (4) can be converted to the following equivalent problem:

$$\begin{aligned} \begin{array}{cc} {\min }_{\mathbf {Z,J,T,E}} &{} \Vert \mathbf {J}\Vert _*+\beta \Vert \mathbf {Z}-\mathbf {ZT}\Vert _F^2+\lambda \Vert \mathbf {E}\Vert _{2,1}, \\ s.t. &{} \mathbf {X} = \mathbf {XZ}+\mathbf {E},\mathbf {Z}=\mathbf {J},\mathbf {Z} = \mathbf {T},\mathbf {1}_n\mathbf {Z}=\mathbf {1}_n.\\ \end{array} \end{aligned}$$

(5)

Here $\mathbf {J,T}$ are two auxiliary variables. Then the we can define the augmented Lagrangian function of Eq. (5) as follows:

$$\begin{aligned}&{\min }_{\mathbf {Z,J,T,E}} \Vert \mathbf {J}\Vert _*+\beta \Vert \mathbf {Z}-\mathbf {ZT}\Vert _F^2+\lambda \Vert \mathbf {E}\Vert _{2,1},\nonumber \\&\quad +\,\langle \mathbf {Y}_1,\mathbf {X-XZ-E}\rangle +\langle \mathbf {Y}_2, \mathbf {Z} - \mathbf {J}\rangle +\langle \mathbf {Y}_3,\mathbf {Z}-\mathbf {T}\rangle +\langle \mathbf {Y}_4,\mathbf {1}_n\mathbf {Z}-\mathbf {1}_n\rangle \nonumber \\&\quad +\, \mu /2\big (\Vert \mathbf {X-XZ-E}\Vert _F^2+\Vert \mathbf {Z}-\mathbf {J}\Vert _F^2+\Vert \mathbf {Z}-\mathbf {T}\Vert _F^2+\Vert \mathbf {1}_n\mathbf {Z}-\mathbf {1}_n\Vert _F^2\big ), \end{aligned}$$

(6)

where ${\mathbf {Y}}_1,{\mathbf {Y}}_2,{\mathbf {Y}}_3$ and ${\mathbf {Y}}_4$ are four Lagrangian multipliers, $\mu$ is a positive parameter. Then the variables in the above problem can be optimized alternately.

• 1. Update ${\mathbf {J}}$ with fixed other variables Suppose in the kth iteration, ${\mathbf {Z}}^k, {\mathbf {T}}^k, {\mathbf {E}}^k$ are computed. We drop the irrelevant terms of ${\mathbf {J}}$ in Eq. (6), then we have:

  $$\begin{aligned}&{\min }_{\mathbf {J}^k} \Vert \mathbf {J}^k\Vert _*+\langle \mathbf {Y}^k_2,\mathbf {Z}^k-\mathbf {J}^k\rangle +\Vert \mathbf {Z}^k-\mathbf {J}^k\Vert _F^2\nonumber \\&\quad ={\min }_{\mathbf {J}^k} \Vert \mathbf {J}^k\Vert _*+\mu ^k/2\Vert \mathbf {Z}^k-\mathbf {J}^k+\mathbf {Y}^k_2/\mu ^k\Vert _F^2. \end{aligned}$$

  (7)

  The optimal solution ${\mathbf {J}}^{k+1}$ to the above problem satisfies ${\mathbf {J}}^{k+1} = {\mathbf {U}}^k\mathbf {\Theta }_{1/\mu ^k}({\mathbf {S}}^k)({\mathbf {V}}^k)^T$, where ${\mathbf {U}}^k{\mathbf {S}}^k({\mathbf {V}}^k)^T$ is the SVD of matrix ${\mathbf {Z}}^k+{\mathbf {Y}}_2^k/\mu ^k,\mathbf {\Theta }$ is the singular value thresholding operator [23].

• 2. Update ${\mathbf {T}}$ with fixed other variables Similar to the above processing, we neglect the irrelevant terms of ${\mathbf {T}}$ in Eq. (6), then in kth iteration, Eq. (6) becomes

  $$\begin{aligned}&{\min }_{\mathbf {T}^k} \beta \Vert \mathbf {Z}^k-\mathbf {Z}^k\mathbf {T}^k\Vert _F^2+\langle \mathbf {Y}^k_3, \mathbf {Z}^k - \mathbf {T}^k\rangle +\mu ^k/2\Vert \mathbf {Z}^k-\mathbf {T}^k\Vert _F^2\nonumber \\&\quad ={\min }_{\mathbf {T}^k} \beta \Vert \mathbf {Z}^k-\mathbf {Z}^k\mathbf {T}^k\Vert _F^2+\mu ^k/2\Vert \mathbf {Z}^k -\mathbf {T}^k+\mathbf {Y}^k_3/\mu ^k\Vert _F^2, \end{aligned}$$

  (8)

  hence ${\mathbf {T}}^{k+1}=\big (2\beta ({\mathbf {Z}}^T)^k{\mathbf {Z}}^k+\mu ^k\big )^{-1}\big (2\beta ({\mathbf {Z}}^k)^T{\mathbf {Z}}^k+\mu ^k({\mathbf {Z}}^k+{\mathbf {Y}}^k_3/\mu ^k)\big )$.

• 3. Update ${\mathbf {Z}}$ with fixed other variables We also collect the relevant terms w.r.t ${\mathbf {Z}}$ in Eq. (6), then we have

  $$\begin{aligned}&{\min }_{\mathbf {Z}^k} \beta \Vert \mathbf {Z}^k-\mathbf {Z}^k\mathbf {T}^k\Vert _F^2+\langle \mathbf {Y}^k_1,\mathbf {X-X}\mathbf {Z}^k-\mathbf {E}^k\rangle +\langle \mathbf {Y}^k_2, \mathbf {Z}^k - \mathbf {J}^k\rangle \nonumber \\&\qquad +\,\langle \mathbf {Y}^k_3, \mathbf {Z}^k - \mathbf {T}^k\rangle +\langle \mathbf {Y}^k_4,\mathbf {1}_n\mathbf {Z}^k-\mathbf {1}_n\rangle +\mu ^k/2\big (\Vert \mathbf {X-X}\mathbf {Z}^k-\mathbf {E}^k\Vert _F^2\nonumber \\&\qquad +\,\Vert \mathbf {Z}^k-\mathbf {J}^k\Vert _F^2+\Vert \mathbf {Z}^k-\mathbf {T}^k\Vert _F^2+\Vert \mathbf {1}_n\mathbf {Z}^k-\mathbf {1}_n\Vert _F^2\big )\nonumber \\&\quad ={\min }_{\mathbf {Z}^k} \beta \Vert \mathbf {Z}^k(\mathbf {I}-\mathbf {T}^k)\Vert _F^2+\mu /2\big (\Vert \mathbf {X-X}\mathbf {Z}^k-\mathbf {E}^k+\mathbf {Y}^k_1/\mu ^k\Vert _F^2\nonumber \\&\qquad +\,\Vert \mathbf {Z}^k-\mathbf {J}^k+\mathbf {Y}^k_2/\mu ^k\Vert _F^2+\Vert \mathbf {Z}^k-\mathbf {T}^k+\mathbf {Y}^k_3/\mu ^k\Vert _F^2+\Vert \mathbf {1}_n\mathbf {Z}-\mathbf {1}_n+\mathbf {Y}^k_4/\mu ^k\Vert _F^2\big ),\nonumber \\ \end{aligned}$$

  (9)

  where ${\mathbf {I}}\in R^{n\times n}$ is a identity matrix. By taking the derivation of Eq. (9) with respect to ${\mathbf {Z}}^k$ and set it to be zero, the following equation holds:

  $$\begin{aligned}&\mu ^k\big (\mathbf {X}^T\mathbf {X}+2\mathbf {I}+\mathbf {1}_n\mathbf {1}_n^T\big )\mathbf {Z}^k+2\beta \mathbf {Z}^k(\mathbf {I}-\mathbf {T}^k)(\mathbf {I}-\mathbf {T}^k)^T-\mu ^k\Big (\mathbf {X}^T(\mathbf {X-E}^k+\mathbf {Y}^k_1/\mu ^k)\nonumber \\&\quad +\,\mathbf {J}^k-\mathbf {Y}_2^k/\mu ^k+\mathbf {T}^k-\mathbf {Y}_3^k/\mu ^k+\mathbf {1}_n^T(\mathbf {1}_n-\mathbf {Y}^k_4/\mu ^k)\Big )=0. \end{aligned}$$

  (10)

  It can be found that Eq. (10) is a Sylvester equation [32] w.r.t. ${\mathbf {Z}}^k$. Hence it could be solved by using the Matlab function lyap().

• 4. Update ${\mathbf {E}}$ with fixed other variables Drop the irrelevant terms w.r.t. ${\mathbf {E}}$ in Eq. (6), then in the kth iteration, we have:

  $$\begin{aligned}&{\min }_{\mathbf {E}^k} \lambda \Vert \mathbf {E}^k\Vert _{2,1}+\langle \mathbf {Y}_1^k,\mathbf {X-XZ}^k-\mathbf {E}^k\rangle +\mu ^k/2\Vert \mathbf {X-XZ}^k-\mathbf {E}^k\Vert _F^2\nonumber \\&\quad = {\min }_{\mathbf {E}^k} \lambda \Vert \mathbf {E}^k\Vert _{2,1}+\mu ^k/2\Vert \mathbf {X-XZ}^k-\mathbf {E}^k+\mathbf {Y}_1^k/\mu ^k\Vert _F^2 \end{aligned}$$

  (11)

  The above problem could be solved by following the Lemma presented in [3, 4].

Lemma 1

Let ${\mathbf {Q}}=[{\mathbf {q}}_1,{\mathbf {q}}_2,\cdots ,{\mathbf {q}}_i,\cdots ]$ be a given matrix. If the optimal solution to

$$\begin{aligned} {\min }_{\mathbf {P}}\nu \Vert \mathbf {P}\Vert _{2,1} + \frac{1}{2}\Vert \mathbf {P}-\mathbf {Q}\Vert _F^2 \end{aligned}$$

(12)

is ${\mathbf {P}}^*$, then the i-th column of ${\mathbf {P}}^*$ is

$$\begin{aligned} \mathbf {P}^*(:,i)=\left\{ \begin{array}{ll} \frac{\Vert \mathbf {q}_i\Vert _2-\nu }{\Vert \mathbf {q}_i\Vert _2}\mathbf {q}_i, &{} \hbox {if }\nu <\Vert \mathbf {q}_i\Vert _2; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

(13)

5. Update parameters with fixed other variables The precise updating schemes for parameters existed in Eq. (6) are summarized as follows:

$$\begin{aligned} {\mathbf {Y}}_1^{k+1}= & {} {\mathbf {Y}}_1^{k} + \mu ^k({\mathbf {X}}-\mathbf {XZ}^{k}-{\mathbf {E}}^{k}),\nonumber \\ {\mathbf {Y}}_2^{k+1}= & {} {\mathbf {Y}}_2^{k} + \mu ^k({\mathbf {Z}}^{k}-{\mathbf {J}}^k),\nonumber \\ {\mathbf {Y}}_3^{k+1}= & {} {\mathbf {Y}}_3^{k} + \mu ^k({\mathbf {Z}}^{k}-{\mathbf {T}}^{k}),\nonumber \\ {\mathbf {Y}}_4^{k+1}= & {} {\mathbf {Y}}_4^k + \mu ^k({\mathbf {1}}_n{\mathbf {Z}}^k-{\mathbf {1}}_n),\nonumber \\ \mu ^{k+1}= & {} \min (\mu _{max},\rho \mu ^k), \end{aligned}$$

(14)

where $\mu _{max}$ and $\rho$ are two given positive parameters.

3.4 Algorithm

The algorithmic procedure of SRLRR is summarized in Algorithm 1.

4 Further Discussions

In this section, we will firstly analysis SRLRR algorithm from another perspective, then explain the relationships between SRLRR and some existing LRR-related algorithms.

4.1 Laplacian Regularized View of SRLRR

We rewrite the objective function of SRLRR [Eq. (4)] in the following form:

$$\begin{aligned}&{\min }_{\mathbf {Z,E}} \Vert {\mathbf {Z}}\Vert _*+\beta \Vert {\mathbf {Z}}-{\mathbf {Z}}^2\Vert _F^2+\lambda \Vert {\mathbf {E}}\Vert _{2,1}\nonumber \\&\quad = {\min }_{\mathbf {Z,E}}\Vert {\mathbf {Z}}\Vert _*+\beta tr\big ({\mathbf {Z}}({\mathbf {I}}-{\mathbf {Z}})({\mathbf {I}}-{\mathbf {Z}})^T{\mathbf {Z}}^T\big )+\lambda \Vert {\mathbf {E}}\Vert _{2,1}\nonumber \\&\quad = {\min }_{\mathbf {Z,E}}\Vert {\mathbf {Z}}\Vert _*+\beta tr\big ({\mathbf {Z}}{\mathbf {L}}{\mathbf {Z}}^T\big )+\lambda \Vert {\mathbf {E}}\Vert _{2,1}, \end{aligned}$$

(15)

where ${\mathbf {L}}=({\mathbf {I}}-{\mathbf {Z}})({\mathbf {I}}-{\mathbf {Z}})^T$. The second row of Eq. (15) holds because of $\Vert {\mathbf {Z}}-{\mathbf {Z}}^2\Vert _F^2 =\Vert {\mathbf {Z}}({\mathbf {I}}-{\mathbf {Z}})\Vert _F^2 =tr\big (({\mathbf {I}}-{\mathbf {Z}})^T{\mathbf {Z}}^T{\mathbf {Z}}({\mathbf {I}}-{\mathbf {Z}})\big ) =tr\big ({\mathbf {Z}}({\mathbf {I}}-{\mathbf {Z}})({\mathbf {I}}-{\mathbf {Z}})^T{\mathbf {Z}}^T\big )$. Based on these deductions, it can be seen that the self-representation constraint is transformed to a kind of Laplacian regularizer [15, 16, 33,34,35,36,37,38].

The usage of a Laplacian regularizer is to characterize the manifold structure of a data set. And a well-designed Laplacian regularizer will be great helpful to improve the performances of different algorithms [15, 16, 33,34,35,36,37,38]. Besides the classical Laplacian regularizer [15, 16, 33,34,35,36], from the purpose of revealing the manifold structures of data sets, Laplacian regularizers could be devised in many different ways. For example, Wang et al. used a locality linear reconstruction method to construct a kind of Laplacian regularizer and stated its rationality [39]. Yu et al. adopted a multimodal hypergraph Laplacian regularizer to build a group of manifolds [37]. Yu et al. also used the patch alignment skill to devise a kind of Laplacian regularizer [38].

From this viewpoint, we discuss the connections between SRLRR and some existing Laplacian-regularized LRR-related methods and explain the superiorities of SRLRR to them.

4.2 Relationship with Some Existing Laplacian-Regularized LRR-Related Methods

4.2.1 Relationship with Graph-Regularized Low-Rank Representation (GLRR)

Equation (15) is much similar to the objective function of GLRR [15] listed as the following equation:

$$\begin{aligned} \begin{array}{cc} {\min }_{\mathbf {Z,E}}&{}\Vert \mathbf {Z}\Vert _*+\beta tr\big (\mathbf {Z}\mathbf {L_K}\mathbf {Z}^T\big )+\lambda \Vert \mathbf {E}\Vert _{2,1}\\ s.t.&{} \mathbf {X} = \mathbf {XZ}+\mathbf {E}. \end{array} \end{aligned}$$

(16)

In GLRR, the Laplacian matrix $\mathbf {L_K}$ is devised based on KNN (K-nearest-neighbor) method² [40] and the similarities between pairwise data samples are manually set. However, the neighborhood size K in KNN method is usually difficult to choose. An improper value of K will have terrible impacts on the performance of a graph-based method [41]. And it is also difficult to manually determine a suitable value for the similarity of a pair of data samples. Consequently, the Laplacian matrix $\mathbf {L_K}$ in GLRR may not be able to faithfully reveal the manifold structure of a data set.

As we mentioned above, Wang et al. pointed out that the reconstruction coefficient matrix ${\mathbf {Z}}$ of a data set is also capable for designing a suitable Laplacian matrix (namely ${\mathbf {L}}=({\mathbf {I}}-{\mathbf {Z}})({\mathbf {I}}-{\mathbf {Z}})^T$)³ [39]. Hence the defined Laplacian matrix ${\mathbf {L}}$ in SRLRR is reasonable. In addition, different from the method in [39], the coefficient matrix ${\mathbf {Z}}$ obtained by SRLRR could be able to reveal the global structures of data sets with the help of the low-rank constraint. Moreover, ${\mathbf {Z}}$ is updated in each iteration and would recovery the truth reconstruction relationship for a data set more precisely. Therefore, the Laplacian regularizer defined in SRLRR is more appropriate for recovery the manifold structures of different kinds of data sets.

4.2.2 Relationship with Smooth Representation Clustering (SMR)

Smooth representation clustering (SMR) [20] is a simple and efficient subspace segmentation algorithm whose objective function can be expressed as follows:

$$\begin{aligned} \begin{array}{cc} {\min }_{\mathbf {Z}} &{} tr(\mathbf {ZL_KZ}^T)+\lambda \Vert \mathbf {E}\Vert _F^2,\\ s.t. &{} \mathbf {X}=\mathbf {XZ}+\mathbf {E}, \end{array} \end{aligned}$$

(17)

where $\mathbf {L}_{\mathbf{K}}$ is also defined based on KNN, $\Vert {\mathbf {E}}\Vert _F^2$ represents the Frobenius norm of matrix ${\mathbf {E}}$. Compared with Eq. (16), it could be found that SMR is actually a special case of GLRR without the low-rank constraint. Hence, SMR inherits the drawbacks of GLRR. The formulation of SMR inspires us to think whether the low-rank constraint can be abandoned in SRLRR either? In our experiments, we found that if the low-rank constraint on ${\mathbf {Z}}$ in SRLRR is dropped, the performance of SRLRR would degenerate sharply. This may be the low-rank constraint can guarantee the coefficient matrix to be block diagonal which is important to SRLRR as we stated in Sect. 3.2.

4.2.3 Relationship with Non-negative Laplacian Regularized Low-Rank Representation (NSLLRR)

NSLLRR [16] could be regard as an extension of GLRR whose objection function can be expressed as follows:

$$\begin{aligned} \begin{array}{cc} {\min }_{\mathbf {Z,E}}&{}\Vert \mathbf {Z}\Vert _*+\alpha \Vert \mathbf {Z}\Vert _1+\beta tr\big (\mathbf {Z}\mathbf {L_K}\mathbf {Z}^T\big )+\lambda \Vert \mathbf {E}\Vert _{2,1}\\ s.t.&{} \mathbf {X} = \mathbf {XZ}+\mathbf {E}, \mathbf {Z}\ge \mathbf {0} \end{array} \end{aligned}$$

(18)

where ${\mathbf {0}}\in R^{n\times n}$ is a matrix with each element equals zero. In NSLLRR, the Laplacian matrix is constructed in the similar way as used in GLRR and SMR. Hence, the drawback of GLRR remains in NSLLRR. Moreover, there are four parameters $\alpha , \beta , \lambda$ and the neighborhood size K needed to be adjusted in NSLLRR, which will make NSLLRR more difficult to achieve satisfactory results.

Finally, we present the following Table 2 to summarize the differences between SRLRR and the close related algorithms such as LRR, GLRR, SMR and NSLLRR.

Table 2 The differences between SRLRR and some LRR-related algorithms

4.3 Computational Complexity Analysis

In this subsection, we will analyze the computational complexity of SRLRR, namely Algorithm 1. Suppose the data matrix ${\mathbf {X}}\in {R}^{D\times n}$, then ${\mathbf {Z}} \in {R}^{n\times n}$. The time consumed for running Algorithm 1 is mainly composed of updating $\mathbf {J,T,Z,E}$.

We then discuss the updating method for $\mathbf {J,T,Z,E}$ respectively. Firstly, updating ${\mathbf {J}}$ requires to computing the singular value decomposition (SVD) of an $n\times n$ matrix. The time complexity of performing SVD is $O(n^3)$. Secondly, the computation burden of seeking the pseudo-inverse of an $n\times n$ matrix is $O(n^3)$. Hence, the time complexity of updating ${\mathbf {T}}$ is $O(n^3)$. Thirdly, updating ${\mathbf {Z}}$ needs to solve a Sylvester equation which will also takes $O(n^3)$. Fourthly, the time complexity is O(n) when Lemma 1 is used to update ${\mathbf {E}}$. Therefore, we can see that the time complexity of each iteration of Algorithm 1 is $O(n^3)$. Suppose the number of iteration is N, the total complexity of Algorithm 1 is $N\times O(n^3)$. Hence, the complexity of SRLRR is the same order as LRR algorithm [4].

5 Experiments

In this section, extensive subspace segmentation experiments will be conducted to verify the effectiveness of SRLRR. Some representative and related algorithms such as SSC [1], LRR [3, 4], SCLRR [5], NSLLRR [16],⁴ LSR [18] will also be evaluated for comparisons. Four types databases including a synthetic data set, Hopkins 155 motion segmentation database [42], face image databases (such as ORL database [43], the extended Yale B database [44], AR database [45]) and other two image databases including MNIST (http://yann.lecun.com/exdb/mnist/) and COIL-20 [27] will be adopted.

5.1 Experiments on the Synthetic Data

The synthetic data is generated by strictly following the methodology used in [3]. It is draw from 5 independent subspaces $\{{\mathcal {C}}_i\}_{i=1}^5$, whose basis $\{{\mathbf {B}}_i\}_{i=1}^5$ are computed by ${\mathbf {B}}_{i+1}={\mathbf {R}}{\mathbf {B}}_i,1\le i\le 4$, where ${\mathbf {R}}$ is a random rotation and ${\mathbf {B}}_i$ is a orthogonal matrix of dimension $100\times 4$. Then we construct a $100\times 100$ data matrix ${\mathbf {X}}=[{\mathbf {X}}_1,{\mathbf {X}}_2,{\mathbf {X}}_3,{\mathbf {X}}_4,{\mathbf {X}}_5]$ by sampling 20 data points from each subspace ${\mathbf {X}}_i={\mathbf {B}}_i{\mathbf {Q}}_i,1\le i\le 5$ with ${\mathbf {Q}}_i$ be a $4\times 20$ matrix satisfies uniform distribution. Moreover, some data is randomly selected to add Gaussian noise with zero mean and variance $0.3\Vert {\mathbf {x}}\Vert _2$. Finally, the above mentioned algorithms are used to segment the data into 5 clusters and the segmentation accuracy⁵ of each method is recorded. The segmentation accuracy (averaged from 20 random trials) of each algorithm varies with the variation of corruption is shown in Fig. 1 (The corresponding parameters of different algorithms are set to their best values which are also reported in Fig. 1).

Fig. 1

The segmentation accuracy versus variation the range of corruption for each method. Notice: the neighborhood size K in NSLLRR is set to be 10. We test the performance of NSLLRR with different neighborhood sizes and chose the best one

From Fig. 1, we can get several interesting observations: (1) Laplacian-regularized LRR methods (SRLRR and NSLLRR) outperform LRR and SCLRR; (2) SRLRR constantly achieves the best results and dominates NSLLRR. It can be concluded that the self-represent constraint defined in SRLRR is more helpful for revealing the intrinsic structures of data sets than the classical Laplacian constraint used in NSLLRR; (3) SSC and LSR are inferior to LRR-based algorithms.

Moreover, we also illustrate the affinity graphs obtained by all the evaluated algorithms in Fig. 2. Here a generated synthetic data set with $40\%$ corruption is adopted. The segmentation accuracies obtained based on the affinity graphs are also presented in the captions of each sub-figure. From Fig. 2, we can find that (1) the block structures of the affinity graph learned by LRR-related algorithms are better to reveal the intrinsic structures of the synthetic data set than those obtained by SSC and LSR; (2) compared to other LRR-related algorithms, SRLRR is better to discovery the structure of the fourth subspace denoted by the read pointers in Fig. 2.

Fig. 2

The affinity graphs computed by a SSC, b LSR, c LRR, d SCLRR, e NSLLRR and f SRLRR

Finally, we test the performances of SRLRR with different matrix norms for modelling noise and outliers. Here, three frequently used matrix norms, such as $l_{2,1}$-norm, $l_1$-norm and Frobenius norm are used. And the segmentation accuracy curves of SRLRR with the three different norms of error matrix ${\mathbf {E}}$ are plotted in Fig. 3. From Fig. 3, we can see that (1) SRLRR with $l_{2,1}$-norm error term achieves the best values; (2) if we use $l_1$-norm to model the noise, the performances of SRLRR become very poor when the percentage of corruption is large than $10\%$. Hence, in the following experiments, we will use $l_{2,1}$-norm to characterize the noise existed in data sets.

Fig. 3

The performances of SRLRR with different matrix norms imposed on the error terms

5.2 Experiments on Hopkins 155 Database

Hopkins 155 database is a well-known motion segmentation database. It consists of 120 sequences motions of two motions and 35 sequences of three motions.⁶ The features are extracted and tracked along with the motion in all frames, and errors were manually removed for each sequence. Then each sequence could be viewed as a single clustering problem, hence there are 155 clustering tasks in total. Fig. 4 presents two sample images of Hopkins 155 database.

Fig. 4

Sample Images of Hopkins 155 motion segmentation database. a 1R2RC, b arm

Fig. 5

The performance of SRLRR versus the variation of parameters $\lambda ,\beta$. The vertical axis denotes the segmentation errors, the left horizontal axis and right horizontal axis represent the variations of $\lambda$ and $\beta$ respectively

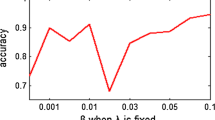
For computational efficiency, we perform a preprocessing step to project the data to be 12-dimensional⁷ by principal component analysis (PCA) [40]. We first test the sensitivity of SRLRR to its parameters $\beta$ and $\lambda$. $\beta$ and $\lambda$ are chosen to vary in the intervals [0.001, 7] and [0.01, 10] respectively. And the segmentation errors⁸ achieved by SRLRR with corresponding values are illustrated in Fig. 5. Clearly, it can be found that the performance of SRLRR is much stable when $\beta$ and $\lambda$ vary in relative large ranges. Furthermore, we also recorded the detailed statistics of the segmentation errors of the evaluated algorithms including Mean, standard deviation (Std.) and maximal error(Max.) in Table 3. We set the two parameters in SRLRR as $\beta =5,\lambda =10$ according to the above sensitivity testing experiments. The parameters in other evaluated algorithms are tuned to their best values by following the disciplines described in the corresponding related references (also reported in Table 3).

Table 3 The segmentation errors ($\%$) of different algorithms on Hopkins 155 database

From Table 3, we can see that (1) the mean of segmentation errors on the data sets with 2 motions and all data sets obtained by SRLRR are all slightly better than those of other algorithms; (2) the standard deviation on all data sets obtained by SRLRR is also superior to those of other algorithms; (3) all the best values are achieved SRLRR and NSLLRR.

5.3 Experiments on Face Image Databases

Three well-known face image databases including ORL [43], the extend Yale B [44] and AR face database [45] will be used in the experiments performed in this subsection. The brief information of the three databases are introduced as follows:

ORL database contains 400 face images (without noise) of 40 persons. Each person has 10 different images. These images were taken at different times, varying the lighting, facial expressions (open/closed eyes, smiling/not smiling) and facial details (glasses/no glasses).

The extended Yale B face database contains 38 human faces and around 64 near frontal images under different illuminations per individual. Some images in this database were corrupted by shadow. We just selected images from first 10 classes of the extended Yale B database to form a heavily corrupted subset. In our experiments, all the images from ORL and the extended Yale B database are resized to $32\times 32$ pixels.

AR database consists of over 4000 face images of 126 persons. For each individual, 26 pictures were taken in two sessions (separated by two weeks) and each section contains 13 images. These images include front view of faces with different expressions, illuminations and occlusions. In our experiments, the pictures from the first 20 persons (520 images) of AR will be taken. And each image is resized into $50\times 40$ pixels. Some sample images from the three databases are shown in Fig. 6a–c respectively.

Fig. 6

Sample images from a ORL, b the extend Yale B and c AR databases

We still first test the performance of SRLRR on the three databases when the parameters varies. In the following experiments, for computational efficiency, we project the data into its corresponding PCA subspace whose dimension equals $n-1$. n is the number of data sample in each database. Then we let the two parameters $\beta ,\lambda$ change in interval [0.001, 10] and record the segmentation accuracies obtained by SRLRR. The experiments results are reported in Fig. 7a–c.

Fig. 7

The segmentation accuracies obtained by SRLRR with different values of parameters on three face image databases. a ORL, b Yale B, c AR

From Fig. 7, we can find that SRLRR is insensitive to the two parameters $\beta ,\lambda$ when these databases are used. Moreover, the best experimental results of SRLRR on the three databases are recorded in Table 4. For comparison, the segmentation accuracies achieved by the other evaluated algorithms are also reported. Form Table 4, it can be seen that (1) the best experiments results on the three databases are all achieved by SRLRR; (2) especially, on the extend Yale B database, the result of SRLRR is much better than those of other algorithms.

For further comparisons, we also performed subspace segmentation experiments on some sub-databases constructed from the above used three image databases. Each sub-database contains the images from q persons (q changes from a relative small number to the total number of class). Then the six evaluated algorithms are performed to obtain the subspace segmentation accuracies. In these experiments, all the corresponding parameters in each evaluated algorithm are varied from 0.001 to 10, and the best values corresponding to the highest accuracy of each evaluated algorithm are chosen. Finally, the segmentation accuracy curve of each algorithm againsts the number of class q are plotted in Fig. 8.

Clearly, form Fig. 8, we can find that (1) in all the experiments, the best results are almost achieved by SRLRR; (2) the results of SRLRR are much better than those of other algorithms on the AR database.

5.4 Experiments on Other Image Databases

We hope to further verify the effectiveness of SRLRR on different kinds of databases. Therefore, two frequently used image databases, MNIST (http://yann.lecun.com/exdb/mnist/) and COIL-20 [46] are adopted in this section. The brief information of the two databases are summarized as follows:

MNIST database has images from 10 handwritten digits, namely 0-9. In the following experiments, we construct a subset which consists of the first 50 samples of each digits training data set. Then each image is resize to $28\times 28$ pixels.

COIL-20 database contains total 1440 images of size $32\times 32$ from 20 different subjects and each object has 72 images. We take first 36 images of each object to form a subset. The sample images of the two databases are illustrated in the following Fig. 9.

Table 4 The segmentation accuracies ($\%$) of different algorithms on the three image databases

Fig. 8

The segmentation accuracies obtained by the evaluated algorithms versus the variations of number of class on different databases. a ORL, b the extend Yale B, c AR

Fig. 9

Sample images from a MNIST, b COIL-20 databases

Based on the previous experiments, we can conclude that SRLRR is insensitive to its parameters. Hence, we just present the subspace segmentation results obtained by SRLRR and other algorithms on the two databases. The similar strategies used in the experiments conducted on the face image databases will be also adopted in the following experiments. Hence, the subspace segmentation accuracies of different evaluated algorithms on the sub-databases with q-subjects (extracted from the two databases) will be recorded. Fig. 10 plots the segmentation accuracy curves of the six algorithms change with the number of subject (class). Obviously, these experimental results also present the conclusion that SRLRR is superior to the related algorithms.

Fig. 10

The segmentation accuracies obtained by the evaluated algorithms versus the variations of number of class on different databases. a MNIST, b COIL-20

Moreover, one may doubt on the segmentation accuracy curves obtained by the evaluated algorithms in Figs. 8 and 10. It seems that some of them increase and the others decrease. We know that each curve in Figs. 8 and 10 recorded the best results of an evaluated algorithm with corresponding parameters and different numbers of class (person or subject). In most cases, with the number of class increases, it will be more difficult for subspace segmentation algorithms to correctly segment data samples to their true subspace. Hence, the segmentation accuracy curves will decrease constantly in most cases.⁹ However, in some situations, the distribution of data and the search strategies adopted for determining the best parameters of different algorithms may prevent the evaluated algorithms to obtain the best results. Hence, the segmentation accuracy curves will increase sometimes.

All the above experiments show that SRLRR is superior to the related algorithms. Here we summarize the reasons for explaining the successes of SRLRR: On one hand, as we explained in Sect. 3.2, the self-representation constraint defined in SRLRR would make the similarity between each pair-wise homogenous data points (in a same subspace) strictly larger than 0. However, other related algorithms may not satisfy this property. Hence, the coefficient matrices obtained by SRLRR would be more powerful to characterize the subspace structures of data sets. On the other hand, SRLRR could be regarded as a kind of Laplacian regularized LRR method. However, different from the existing Laplacian regularized LRR methods, SRLRR uses the obtained low-rank coefficient matrix to define a Laplacian matrix. Because the low-rank coefficient matrix could reveal the intrinsic structure of an original data set in a certain extent, the defined Laplacian matrix is more suitable to recovery the manifold structure of the original data set. The two reasons guarantee the effectiveness of SRLRR and help SRLRR to achieve satisfactory results in the above subspace segmentation experiments.

6 Conclusion

In this paper, we proposed a new LRR-related algorithm, termed self-representation low-rank representation (SRLRR). In SRLRR, we devised a new self-representation constraint based on the analysis on coefficient matrices obtained by LRR method. The self-representation constraint makes the coefficient matrices should be able to reconstruct themselves. And we proved that it could also be transferred to be a kind of Laplacian regularizer. We described the rationality of the proposed self-representation constraint and stated the relationships between SRLRR and some existing related algorithms. Finally, subspace segmentation experiments performed on both synthetic and real databases showed the effectiveness of SRLRR.