Abstract
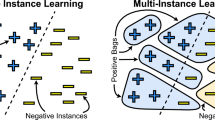
Multiple instance learning attempts to learn from a training set consists of labeled bags each containing many unlabeled instances. In previous works, most existing algorithms mainly pay attention to the ‘most positive’ instance in each positive bag, but ignore the other instances. For utilizing these unlabeled instances in positive bags, we present a new multiple instance learning algorithm via semi-supervised laplacian twin support vector machines (called Miss-LTSVM). In Miss-LTSVM, all instances in positive bags are used in the manifold regularization terms for improving the performance of classifier. For verifying the effectiveness of the presented method, a series of comparative experiments are performed on seven multiple instance data sets. Experimental results show that the proposed method has better classification accuracy than other methods in most cases.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Multiple instance learning (MIL) has received intense attention recently in the field of machine learning. MIL was introduced in [1] when Dietterich et al. were investigating the problem of binding ability of a drug activity prediction. In MIL framework, the training set is consisted of labeled bags, and each bag contains many unlabeled instances. A positive training bag contains at least one positive instance, whereas a negative bag is consisted of negative instances. Following the seminal work of Dietterich et al., a number of MIL methods were proposed, such as Diverse Density (DD) [2], EM-DD [3], mi-SVM [4], MI-SVM [4], Citation-kNN [5], RELIC [6], ID3-MI [7], RIPPER-MI [7], DD-SVM [8], MI-Ensemble [9], MI-Boosting [10], MI-LR [11], MI-NN [12], MICA [13], SVM-CC [14], MI-NPSVM [15], MI-NSVM [16] and MBSTAR [17]. MIL can be used in many applications, such as image retrieval [2, 12, 18], image categorization [19], text categorization [4, 20], natural scene classification [2] and web mining [21].
Semi-supervised learning (SSL) is another branch of machine learning. In SSL, there are a small number of labeled training examples and abundant unlabeled instances, and the goal of SSL is to exploit these unlabeled instances to help improving the performance of supervised learning. Semi-supervised support vector machines have been studied by many researchers, such as \(S^3VM\) [22], \(V^3SVM\) [23] and \(CV^3SVM\) [23]. Semi-supervised support vector machines attempt to maximize the margin on both labeled and unlabeled data, by assigning unlabeled data to appropriate classes such that the resulting margin is the maximum. LapSVM [24] is a general framework for semi-supervised learning, which can classify data that become available after the training process, without having to retrain the classifier or resort to various heuristics. Following the seminal work of LapSVM, many SSL methods were proposed, such as Lap-TSVM [25], LTPMSVM [26] and Lap-STSVM [27].
In previous works, most existing MIL algorithms mainly pay attention to the ‘most positive’ instance in each positive bag, but ignore the other instances. However, these data repository is available when the classifier is being built, so a SSL framework can be considered. Using SSL framework to deal with MIL problems is an interesting idea, for now there are only few papers in this filed, such as MissSVM [28] and MISSL [29]. Recently, the research of nonparallel classifiers have been a new hot spot [30], and inspired by the success of Lap-TSVM, LTPMSVM and Lap-STSVM, in this paper we propose a new multiple instance classifier named as Multiple Instance Semi-supervised Laplacian Twin Support Vector Machines (Miss-LTSVM). The basic steps of the Miss-LTSVM algorithm are illustrated in Fig. 1. It is known that a positive bag may contain positive as well as negative instances, hence, we divide each positive bag into two parts: the ‘most positive’ instance and the ‘label unknown’ instances. In Miss-LTSVM, we regard all the instances in negative bags as labeled negative instances, regard all the ‘most positive’ instances as labeled positive instances, regard all the ‘label unknown’ instances as unlabeled instances. In our method, the unlabeled instances are used in the manifold regularization terms \(||f_1||_{\mathscr {M}}^2\) and \(||f_2||_{\mathscr {M}}^2\) for improving the performance of classifier.
The rest of the paper is organized as follows. Section 2 gives a brief review on the Lap-TSVM. Section 3 proposes the Miss-LTSVM algorithm. Experiments and results analysis are performed in Sect. 4. Conclusions are given in Sect. 5.
2 Lap-TSVM
Lap-TSVM can exploit the geometry information of the marginal distribution embedded in unlabeled data to construct a more reasonable classifier.
Given a set of labeled data (1) and a set of unlabeled data (2)
where \(x_i \in R^n, i=1,\ldots ,l+u\), \(y_i \in \{ 1,-1 \}, i=1,\ldots ,l\). Lap-TSVM seeks a pair of nonparallel hyperplanes
by solving two primal problems:
and
where A is consisted of all positive data, B is consisted of all negative data, \(e_1\), \(e_2\) and e are vectors of one, \(\xi \) and \(\eta \) are slack vectors, \(M \in R^{(l+u)\times n}\) includes all of labeled data and unlabeled data, \(L=D-W\), D is a diagonal matrix with its i-th diagonal \(D_{ii}=\Sigma _{j=1}^{l+u} W_{ij}\). W is weight matrix defined by k nearest neighbors or graph kernels:
By using the Lagrangian multiplier method, the Wolfe dual forms of (3) and (4) can be written as follows:
where \(H=[A,e_1]\), \(J=[M,e]\), \(G=[B,e_2]\), and the augmented vectors \(v_1=[w_1^\mathrm{T},b_1]^\mathrm{T}\) and \(v_2=[w_2^\mathrm{T},b_2]^\mathrm{T}\) are given by
Once vectors \(v_1\) and \(v_2\) are obtained from (8) and (9), the separating planes
are known. A new data point \(x \in R^n\) is assigned to the positive class or negative class, depending on which of the two hyperplanes it lies closest to, i.e.
3 Miss-LTSVM
Given a training set
where \(B_i=\{ x_{i1},\ldots ,x_{in_i} \}\), \(x_{ij}\in R^n\), \(j=1,\ldots ,n_i\), \(i=1,\ldots ,p+q\); \(B_i\), \(i=1,\ldots ,p\) are positive bags, i.e. \(Y_i=1\), \(i=1,\ldots ,p\); \(B_{p+i}\), \(i=1,\ldots ,q\) are negative bags, i.e. \(Y_{p+i}=-1\), \(i=1,\ldots ,q\); \(n_i\) is the instance number of the bag \(B_i\), \(i=1,\ldots ,p+q\). Let \(m_1 = n_1+n_2+\ldots +n_p\) be the number of all instances in positive bags, \(m_2 = n_{p+1}+n_{p+2}+\ldots +n_{p+q}\) be the number of all instances in negative bags, \(m=m_1+m_2\). The subscripts set of \(B_i\) is expressed as:
3.1 Linear Miss-LTSVM
The goal of Miss-LTSVM is to construct two nonparallel hyperplanes
and
such that, the hyperplane (12) is close to the ‘positive’ instances in positive bags and is far from all the instances in negative bags, the hyperplane (13) is close to all instances in negative bags and is far from the ‘positive’ instances in positive bags.
For the MIL algorithms based on TSVM, the ‘most positive’ instance of each positive bag is the instance that closest to the hyperplane (12) and farthest from the hyperplane (13), so the two primal problems of Miss-LTSVM are constructed as follows:
and
where \(c_{1}, c_{2}, c_{3}\) are the pre-specified penalty parameters, \({\hat{B}} \in R^{m_{2} \times n}\) is consisted of all the instances belonging to the negative bags, \(M \in R^{m \times n}\) includes all of the instances belonging to the positive and negative bags, L is the graph Laplacian and the definition of L can be found in Sect. 2, \(e_1, e_2\) and e are the vectors of ones of appropriate dimensions, \(\xi =[\xi _1,\xi _2,\ldots ,\xi _{m_2}]^\mathrm{T}\) and \(\eta =[\eta _1,\eta _2,\ldots ,\eta _p]^\mathrm{T}\) are slack variables for the errors on the instances of negative bags and positive bags, respectively.
For the ‘most positive’ instance of each positive bag, Mangasarian and Wild [30] show that there exist convex combination coefficients set \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\), such that the ‘most positive’ instances can be represented as
where \(\lambda _j^i \ge 0\) and \(\sum \limits _{j \in {\mathfrak {J}}(i)} \lambda _j^i = 1\). Then the optimization problems (14) and (15) can be rewritten as
and
Obviously, problems (17) and (18) are not convex quadratic programming problems (QPPs), an iterative method which includes two strategies of updating can be used to obtain their approximate solutions.
(I) Fixing \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\), update \(w_1, b_1\) and \(w_2, b_2\). For fixed \(\lambda _j^i\), we can obtain
where \(\hat{x}_i\) represents the ‘most positive’ instance of the bag \(B_i\). Let \({\hat{A}}= [\hat{x}_1, \hat{x}_2, \ldots , \hat{x}_p]^\mathrm{T}\), the optimization problems (17) and (18) turn to
and
Compare the problems (20)–(21) with the problems (3)–(4), we know that the problems (20) and (21) amount to a standard Lap-TSVM problem when the ‘most positive’ instances are known.
In summary, when \({\hat{A}}\) is obtained, \(w_1, b_1, w_2, b_2\) can be computed by solving the problems (20) and (21). In addition, the unlabeled instances in positive bags are used in the manifold regularization terms \(||f_1||_{{\mathscr {M}} }^2=(w_1^\mathrm{T} M^\mathrm{T} + e^\mathrm{T} b_1)L(Mw_1 + eb_1)\) and \(||f_2||_{{\mathscr {M}} }^2=(w_2^\mathrm{T} M^\mathrm{T} + e^\mathrm{T} b_2)L(Mw_2 + eb_2)\) for improving the performance of classifier.
(II) Fixing \(w_1,b_1,w_2,b_2\), update \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\). For fixed \(w_1,b_2\) and \(w_2,b_2\), the optimization problems (17) and (18) can be reduced to
and
Here (22) is a standard QPP, (23) is a linear programming problem (LPP), and problem (23) can be reformulated as
where \(\hat{e}_1^\mathrm{T} = [1,\ldots ,1,0,\ldots ,0] \in R^{(p+m_1)}\), and
where \(\hat{x}_w^i = [(w_2 \cdot x_{i1}), \ldots , (w_2 \cdot x_{i n_i})]^\mathrm{T}, \ i=1,\ldots ,p\).
From above, we know that \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\) can be obtained by solving the problem (22) or (24). For simplicity, we only use the optimization problem (24) to update \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\). In problem (24), only \(w_2, b_2\) are used, hence, our algorithm can be divided into two steps. The first step is to obtain the optimum solution \(w_2, b_2, \lambda _j^i\) by iteratively solving the problems (21) and (24). The second step is to get the optimum solution \(w_1, b_1\) by solving the problem (20) with the obtained optimum solution \(\{ \lambda _j^i| j \in {\mathfrak {J}}(i), i=1,\ldots ,p \}\). The specific process of our method is described as follows.

3.2 Nonlinear Miss-LTSVM
Similar to the linear case, the goal of nonlinear Miss-LTSVM is to construct two nonparallel hyperplanes
where \( \varphi (\cdot ): {\mathbb {X}} \rightarrow {\mathbb {H}} \) is a feature mapping from feature space to reproducing kernel hilbert space (RKHS). We consider \(w_1,w_2\) in the subspace \(span \{ \varphi (x_1), \varphi (x_2), \ldots , \varphi (x_m) \}\) of \(\mathbb {H}\), then \(w_1=\varphi ^\mathrm{T}(M) u_1\), \(w_2=\varphi ^\mathrm{T}(M)u_2\), where \(u_1^\mathrm{T} = [u_{11},u_{12}, \ldots , u_{1m}]\), \(u_2^\mathrm{T}= [u_{21},u_{22}, \ldots , u_{2m}]\), \(\varphi (M)=[\varphi (x_1),\ldots ,\varphi (x_m)]^\mathrm{T}\), the nonparallel hyperplanes (25) turn to
where \(K(x,M)=[k(x,x_1),\ldots ,k(x,x_m)]^\mathrm{T}\).
Similar to problems (17) and (18), the two nonparallel hyperplanes in (26) are constructed by solving the following two optimization problems
and
where
Like the linear case, we also use the iteration strategy to solve the two nonconvex QPPs.
(I) For the fixed \(\lambda _j^i\), substitute (19) into (27) and (28), respectively.
and
where
The Wolfe dual forms of (29) and (30) are:
where \(P=[K({\hat{A}},M),e_1]\), \(Q=[K({\hat{B}},M),e_2]\), \(F=[K_M,e]\), \(U = \left[ {\begin{array}{*{20}{c}} K_M &{} 0 \\ 0 &{} 1 \end{array}} \right] \), then we get
(II) Using the fixed \(u_2,b_2\), the optimization problem (28) can be reduce to
where
\(\tilde{x}_w^i = [u_2^\mathrm{T} K(x_{i1},M), \ldots , u_2^\mathrm{T} K(x_{i n_i},M)]^\mathrm{T}, \ i=1,\ldots ,p\), and the definitions of \(\hat{e}_1^\mathrm{T}, \gamma , \hat{E}\) are the same as the linear case.
In summary, the nonlinear Miss-LTSVM is an extension of linear case by using the kernel function, such as the RBF kernel \(k(x_1,x_2)=exp(-||x_1-x_2||^2/ \sigma ^2)\) where \(\sigma \) is a real parameter. Through the above discussion, we can obtain \(u_{1}, b_{1} , u_{2}, b_{2}, \lambda \) by iteratively solving the problems (33), (34) and (35), respectively. The detail algorithm of nonlinear Miss-LTSVM is roughly the same as the linear case.
4 Experiments
In this section, in order to demonstrate the capability of our algorithms, we perform some comparison experiments with MICA [13], mi-SVM [4], MI-SVM [4], MI-NPSVM [15], MI-NSVM and MI-TSVM [16]. We use the same datasets and roughly the same test method as the ones in [31]. All the experiments are implemented in MATLAB (R2012b) running on a PC with system configuration Intel (R) Core (TM) i3 (2.53 GHz) with 2 GB of RAM. The ‘quadprog’ and ‘linprog’ functions in Matlab are used to solve the related optimization problems in this paper, \(10\%\) samples of the data are randomly taken from our datasets as testing samples and the rest are used as training samples. All the experiments running 10 times. The regularization parameters \(c_1, c_2, c_3\), RBF kernel parameter \(\sigma \) and weight matrix parameter \(\sigma _1\) are all selected from the set \(\{ 2^i| i=-5,\ldots ,5 \}\), the K-nearest neighbor parameter k is selected from 1 to 11, all the parameters are selected by tenfold cross validation on the tuning set comprising of random \(20\%\) of the training data. For simplicity, set \(c_2 = c_3\), we firstly fixed \(k=2, \sigma _1=2\), search the optimal parameter \(c_1\), \(c_2\) and \(\sigma \) (only for nonlinear case), then fixed the selected parameter \(c_1\), \(c_2\) and \(\sigma \) search k and \(\sigma _1\), repeat this until convergence. Figure 2 shows an example of the iterative steps, from it we can see that the proposed algorithm converges very quickly. Set \(\epsilon = 10^{-3}\), the maximum number of iterations is 100.
Seven datasets are used in this paper, two of them come from the UCI machine learning repository [32], and five from [4, 33]. The UCI datasets ‘Musk1’ and ‘Musk2’ involve bags of molecules and their activity levels, which are commonly used in multi-instance classification. ‘Elephant’, ‘Fox’ and ‘Tiger’ datasets come from an image annotation task whose goal is to determine whether or not a given animal is present in an image. ‘TST1’ and ‘TST2’ data sets come from the OHSUMED data and the task is to learn binary concepts associated with the Medical Subject Headings of MEDLINE documents. The detailed information about these data sets can be seen from Table 1.
Table 2 shows the classification accuracies of all methods on the linear and nonlinear case, respectively, where the best results are boldfaced and the results for MICA, MI-TSVM and MI-NSVM on all datasets are taken from [16], the results for mi-SVM and MI-SVM are taken from [4], and the results for MI-NPSVM on all datasets are taken from [15]. In terms of classification accuracy, linear Miss-LTSVM has the best correctness on the data sets of ‘Elephant’, ‘Fox’, ‘Tiger’ and ‘TST2’, nonlinear Miss-LTSVM gets the best correctness on ‘TST1’ data set. Hence, our methods have the best recognition rate on most cases, and the results on data sets ‘Musk1’ and ‘Musk2’ are comparable with the best correctness of other methods. We also find that the five twin based methods perform better than mi-SVM and MI-SVM, this means that twin based methods are more suitable for multiple instance classification. For the results on ‘Musk1’ and ‘Musk2’ data sets, our classification accuracies are lower than MI-TSVM, MI-NPSVM and MI-NSVM, this may be because our optimal parameters found by iteration method are locally optimal solution.
Figure 3 shows the positive and negative classification accuracy of our method on the first five data sets. The positive classification accuracy is higher than negative accuracy on the data sets of ‘Musk1’, ‘Fox’ and ‘Tiger’, this means that more instances in negative bags are misclassified. On ‘Musk2’ and ‘Elephant’ data sets, it has little difference between positive accuracy and negative accuracy.
From the results on ‘Musk1’ and ‘Musk2’ data sets, we find that our methods couldn’t outperform other methods. We concluded that this is because our optimal parameters found by iterative method are local optimal solution. In order to verify this deduction and increase the classification accuracy, a new Laplacian matrix constructor [34] is introduced:
where \(e_{ij} = || x_i - x_j ||_2^2\) is the distance between instances \(x_i\) and \(x_j\). For Eq. (36), only one parameter is involved: the number of neighbors k. The experimental results on ’Musk1’ and ‘Musk2’ data sets are shown in Table 3, where the best results are boldfaced.
From Table 3, we find that using the new method both two algorithms we proposed have achieved better classification accuracies. This means that our deduction is right.
5 Conclusions
In this paper, we proposed a new multiple instance learning algorithm via semi-supervised laplacian twin support vector machines (called Miss-LTSVM). In this method, all instances of positive bags are used in the manifold regularization terms to improve the performance of classifier. In order to verify the effectiveness of Miss-LTSVM, some comparative experiments with MICA, mi-SVM, MI-SVM, MI-NPSVM, MI-NSVM and MI-TSVM on ‘Musk1’, ‘Musk2’, ‘Elephant’, ‘Fox’ , ‘Tiger’, ‘TST1’ and ‘TST2’ seven data sets are performed. Experiment results show that Miss-LTSVM has better classification accuracies than other methods in most cases. In this issue, there are lots of works to do, such as, generalization of modeling, improvement of algorithms and so on.
References
Dietterich TG, Lathrop RH (1997) Solving the multiple-instance problem with axis-parallel rectangles. Artif Intell 89:31–71
Maron O, Ratan AL (1998) Multiple-instance learning for natural scene classification. In: 15th international conference on machine learning. Morgan Kaufmann Publishers Inc., San Francisco, pp 341–349
Zhang Q, Goldman S (2002) Em-dd: an improved multiple instance learning technique. Adv Neural Inf Process Syst 14:1073–1080
Andrews S, Tsochantaridis I, Hofmann T (2003) Support vector machines for maultiple-instance learning, In: Advances in neural information processing systems 15, MIT Press, pp 561–568
Wang J, Zucker JD (2000) Solving the multi-instance problem: a lazy learning approach, ICML00, San Francisco, pp 1119–1125
Ruffo G (2000) Learning single and multiple instance decision trees for computer security applications, Doctoral dissertation, Department of Computer Science, University of Turin, Torino
Chevaleyre Y, Zucker JD (2001) A framework for learning rules from multiple instance data, ECML01. Freiburg, pp 49–60
Chen Y, Wang JZ (2004) Image categorization by learning and reasoning with regions. J Mach Learn Res 5:913–939
Zhou ZH, Zhang ML (2003) Ensembles of multi-instance learners, ECML03. Croatia, Cavtat- Dubrovnik, pp 492–502
Xu X, Frank E (2004) Logistic regression and boosting for labeled bags of instances, PAKDD04. Sydney, pp 272–281
Ray S, Craven M (2005) Supervised versus multiple instance learning: an empirical comparison, ICML05. Bonn, pp 697–704
Ramon J, Raedt LD (2000) Multi-instance neural networks. In: Proceedings of the ICML-2000 workshop on attribute-value and relational learning. Morgan Kaufmann Publishers, San Francisco, pp 53–60
Mangasarian OL, Wild EW (2008) Multiple instance classification via successive linear programming. J Optim Theory Appl 137(1):555–568
Yang ZX, Deng NY (2009) Multi-instance support vector machine based on convex combination, In: The 8th international symposium on operations research and its applications (ISORA09), pp 481–487
Zhang Q, Tian Y, Liu D (2013) Nonparallel support vector machines for multiple-instance learning. Procedia Comput Sci 17:1063–1072
Qi Z, Tian YJ, Yu XD, Shi Y (2014) A multi-instance learning algorithm based on nonparallel classifier. Appl Math Comput 241:233–241
Bandyopadhyay S, Ghosh D, Mitra R (2015) MBSTAR: multiple instance learning for predicting specific functional binding sites in microRNA targets. Sci Rep 5:8004–8004
Hong R, Wang M, Gao Y et al (2014) Image annotation by multiple-instance learning with discriminative feature mapping and selection. IEEE Trans Cybern 44(5):669–680
Bi J, Chen Y, Wang JZ (2005) A sparse support vector machine approach to region-based image categorization. Cvpr 1:1121–1128
Kundakcioglu OE, Seref O, Pardalos PM (2010) Multiple instance learning via margin maximization. Appl Numer Math 60(4):358–369
Zhou ZH, Jiang K, Li M (2005) Multi-instance learning based web mining. Appl Intell 22(2):135–147
Bennett KP, Demiriz A (1999) Semi-supervised support vector machines. Proc Neural Inf Process Syst 11:368–374
Fung G, Mangasarian OL (2000) Semi-supervised support vector machines for unlabeled data classification. Optim Methods Softw 15(1):29–44
Belkin M, Niyogi P, Sindhwani V (2006) Manifold regularization: a geometric framework for learning from labeled and unlabeled examples. J Mach Learn Res 7:2399–2434
Qi Z, Tian Y, Yong S (2012) Laplacian twin support vector machine for semi-supervised classification. Neural Netw 35(11):46–53
Yang Z, Xu Y (2015) Laplacian twin parametric-margin support vector machine for semi-supervised classification. Neurocomputing 171(C):325–334
Chen WJ, Shao YH, Hong N (2014) Laplacian smooth twin support vector machine for semi-supervised classification. Int J Mach Learn Cybern 5(3):459–468
Zhou ZH, Xu JM (2007) On the relation between multi-instance learning and semi-supervised learning, ICML’07. In: Proceedings of the 24th international conference on machine learning, pp 1167–1174
Rahmani R, Goldman SA (2006) MISSL: multiple-instance semi-supervised learning. In: Proceedings of the international conference on machine learning (ICML). pp 705–712
Gao XZ, Fan LY, Xu HT (2016) A novel method for classification of matrix data using twin multiple rank SMMs. Appl Soft Comput 48:546–562
Mangasarian OL, Wild EW (2008) Multiple instance classification via successive linear programming. J Optim Theory Appl 137(1):555–568
Murphy PM, Aha DW Uci machine learning repository, www.ics.uci.edu/mlearn/mlrepository.html
Nie FP, Wang XQ et al. (2016) The Constrained Laplacian Rank Algorithm for graph-based clustering. In: Proceedings of the 13th AAAI conference on artificial intelligence (AAAI-16)
Acknowledgements
This work is supported by the National Science Foundation of China under Grant Nos. 61273251 and 61673220.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gao, X., Sun, Q. & Xu, H. Multiple Instance Learning via Semi-supervised Laplacian TSVM. Neural Process Lett 46, 219–232 (2017). https://doi.org/10.1007/s11063-017-9579-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-017-9579-5