1 Introduction

Model-based clustering has been the topic of extensive research in the past [3]. It is very essential and critical to many computer vision, image processing, data mining and pattern recognition applications [12, 15, 36, 45]. In these applications finite Gaussian mixture models have been widely used as a formal approach to clustering [23, 30, 38, 47]. Unfortunately, the inadequacy of the Gaussian model has been apparent in various applications. Recently, several contributions have occurred to propose other finite mixture models, in order to overcome the limitations related to the Gaussian assumption, and a number of authors began to pay attention to indications of non-Gaussian behaviour in real data [1, 6, 31, 58]. For instance, the authors in [9, 10, 20] have proposed the consideration of the finite Dirichlet mixture which offers high flexibility and ease of use. This mixture has been successfully applied recently to a variety of challenging problems (see, for instance, [19, 52, 53]). However, it has some drawbacks, such as its restrictive negative covariance structure, as discussed in [6, 7] where the author has proposed the finite Beta-Liouville mixture as an efficient alternative and has discussed central issues related to the adoption of this mixture namely parameters estimation and model selection. The finite Beta-Liouville mixture has been shown to be an efficient alternative to the Gaussian and the Dirichlet especially when dealing with proportional data (e.g. normalized histograms). It has met with significant success in numerous real-world applications such as dynamic textures categorization, human activities modeling and recognition, and facial expressions recognition [17, 18].

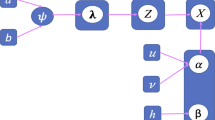
One of the most challenging problems regarding finite mixture modeling is to determine the appropriate number of mixture components. This difficulty can be tackled by assuming that there is an infinite number of components through Dirichlet process [21, 26] as done in [8]. One useful extension of the conventional Dirichlet process framework is to place a Bayesian hierarchy on it, resulting in the so-called hierarchical Dirichlet process, where the base distribution of the Dirichlet process is itself distributed according to another Dirichlet process. Recently, the hierarchical Dirichlet process framework has shown promising results dealing with problems of modeling grouped data where observations are organized into groups and these groups are statistically linked by sharing mixture components [54, 55]. Thus, the first contribution of this paper is to go a step further by extending our previous works about the Beta-Liouville mixture via the consideration of a nonparametric Bayesian approach based on hierarchical Dirichlet process [54, 55]. The resulting model is learned via a variational Bayes framework that we have developed by considering batch settings. A major goal of machine learning techniques is to provide systems that can improve their performance as they observe new data or information [13, 22]. In practice, since data often arrive sequentially in time, one is interested in performing learning on-line. Therefore, our second contribution is to extend the proposed batch algorithm to online settings. We validate both algorithms using a challenging application namely visual scenes categorization.

The rest of this paper is organized as follows. Section 2 describes the hierarchical Dirichlet process mixture model of Beta-Liouville distributions. Both the batch and online variational approaches to learn the proposed model are developed in Section 3. Section 4 is devoted to the experimental results. Finally, concluding remarks are given in Section 5.

2 Model Specification

In this section, first, we present an overview of the finite Beta-Liouville distribution; then, we introduce the framework of hierarchical Dirichlet process mixture model; finally, we propose the hierarchical infinite Beta-Liouville mixture model.

2.1 Finite Beta-Liouville Mixture Model

If a D-dimensional random vector \(\mathbf {X} = (X_1,\ldots ,X_D)\) is distributed according to a Beta-Liouville distribution, then its probability density function (pdf) is defined by [7]:

$$\begin{aligned} \small \mathrm {BL}(\mathbf {X}|\varvec{\theta }) = \frac{\varGamma \left( \sum _{l=1}^D\alpha _l\right) \varGamma (\alpha +\beta )}{\varGamma (\alpha ) \varGamma (\beta )}\prod _{l=1}^D\frac{X_l^{\alpha _l-1}}{\varGamma (\alpha _l)} \bigg (\sum _{l=1}^DX_l\bigg )^{\alpha -\sum _{l=1}^D\alpha _l} \bigg (1-\sum _{l=1}^DX_l\bigg )^{\beta -1} \end{aligned}$$
(1)

where \(\varvec{\theta }= (\alpha _1,\ldots ,\alpha _D,\alpha ,\beta )\) is the vector of parameters of the Beta-Liouville distribution. For a random vector \(\mathbf {X}\) which is generated from a finite Beta-Liouville mixture model with M components, we have

$$\begin{aligned} p(\mathbf {X}|\varvec{\pi },\varvec{\theta })=\sum _{k=1}^K \pi _k\mathrm {BL}(\mathbf {X}|\varvec{\theta }_k) \end{aligned}$$
(2)

where \(\varvec{\theta }_k = (\alpha _{k1},\ldots ,\alpha _{kD},\alpha _k,\beta _k)\) is the vector of parameters of the Beta-Liouville distribution \(\mathrm {BL}(\cdot )\) corresponding to component k. The vector of mixing coefficients \(\varvec{\pi } = (\pi _1,\ldots ,\pi _K)\) is subject to the constraints: \(0\le \pi _k\le 1\) and \(\sum _{k=1}^K\pi _k=1\).

2.2 Hierarchical Dirichlet Process Mixture Model

A two-level hierarchical Dirichlet process is defined as the following: Given a grouped data set with M groups where each group is associated with a Dirichlet process \(G_j\), and the indexed set of Dirichlet processes \(\{G_j\}\) shares a base distribution \(G_0\) which is itself distributed according to a Dirichlet process with the concentration parameter \(\gamma \) and base distribution H:

$$\begin{aligned} G_0\sim & {} \mathrm {DP}(\gamma ,H)\nonumber \\ G_j\sim & {} \mathrm {DP}(\lambda ,G_0) \qquad \text {for each } j,\, j \in \{1, \ldots , M\} \end{aligned}$$
(3)

where j is the index for each group of data. Please notice that the above hierarchy can be readily extended to have more than two levels.

In our work, we construct the hierarchical Dirichlet process using the stick-breaking construction [24, 51]. In the global-level, the global measure \(G_0\) is distributed according to the Dirichlet process \(\mathrm {DP}(\gamma ,H)\) as

$$\begin{aligned} G_0= & {} \sum _{k=1}^\infty \psi _k\delta _{\varOmega _k} \qquad \psi _k = \psi '_k\prod _{s=1}^{k-1}(1-\psi '_s)\nonumber \\&\psi '_k \sim \mathrm {Beta}(1,\gamma ) \qquad \varOmega _k \sim H \end{aligned}$$
(4)

where \(\delta _{\varOmega _k}\) is an atom at \(\varOmega _k\), and \(\{\varOmega _k\}\) is a set of independent random variables drawn from H. \(\psi _k\) is the stick-breaking variable and satisfies \(\sum _{k=1}^\infty \psi _k=1\). Since \(G_0\) is the base distribution of the Dirichlet processes \(G_j\), then the atoms \(\varOmega _k\) are shared among all \(\{G_j\}\) and are only differ in weights based on the property of Dirichlet process [55].

For each group-level Dirichlet process \(G_j\), we also apply the conventional stick-breaking representation according to [57] as

$$\begin{aligned} G_j= & {} \sum _{t=1}^\infty \pi _{jt}\delta _{\varpi _{jt}} \qquad \pi _{jt} = \pi '_{jt}\prod _{s=1}^{t-1}(1-\pi '_{js}) \nonumber \\&\pi '_{jt} \sim \mathrm {Beta}(1,\lambda ) \qquad \varpi _{jt} \sim G_0 \end{aligned}$$
(5)

where \(\delta _{\varpi _{jt}}\) are group-level atoms at \(\varpi _{jt}\), \(\{\pi _{jt}\}\) is a set of stick-breaking weights which satisfies \(\sum _{t=1}^\infty \pi _{jt}=1\). Since \(\varpi _{jt}\) is distributed according to the base distribution \(G_0\), it takes on the value \(\varOmega _k\) with probability \(\psi _k\).

Next, we introduce a binary latent variable \(W_{jtk} \in \{0,1\}\) as an indicator variable: \(W_{jtk} = 1\) if \(\varpi _{jt}\) maps to the global-level atom \(\varOmega _k\); otherwise, \(W_{jtk} = 0\). Thus, we have \(\varpi _{jt}=\varOmega _k^{W_{jtk}}\). As a result, group-level atoms \(\varpi _{jt}\) do not need to be explicitly represented. Since \(\varvec{\psi }\) is a function of \(\varvec{\psi }'\) according to the stick-breaking construction of the Dirichlet process as shown in Eq. (4), the indicator variable \(\mathbf {W}= (W_{jt1}, W_{jt2}, \ldots )\) is distributed as

$$\begin{aligned} p(\mathbf {W}|\varvec{\psi }')=\prod _{j=1}^M\prod _{t=1}^\infty \prod _{k=1}^\infty \big [\psi _k'\prod _{s=1}^{k-1}(1-\psi _s')\big ]^{W_{jtk}} \end{aligned}$$
(6)

According to Eq. (4), the prior distribution of \(\varvec{\psi }'\) is a specific Beta distribution as

$$\begin{aligned} p(\varvec{\psi }')= \prod _{k=1}^\infty \mathrm {Beta}(1,\gamma _k)= \prod _{k=1}^\infty \gamma _k(1-\psi _k')^{\gamma _k-1} \end{aligned}$$
(7)

For the grouped data set \(\mathcal {X}=(X_{j1},\ldots X_{jN})\), let i index the observations within each group j. We assume that each variable \(\zeta _{ji}\) is a factor corresponding to an observation \(X_{ji}\), and the factors \(\varvec{\theta }_j=(\zeta _{j1},\zeta _{j2},\ldots )\) are distributed according to the Dirichlet process \(G_j\), one for each j. Thus, we can write the likelihood function in the form

$$\begin{aligned}&\zeta _{ji}\, |\, G_j \sim G_j\nonumber \\&X_{ji} \,|\, \zeta _{ji} \sim F(\zeta _{ji}) \end{aligned}$$
(8)

where \(F(\zeta _{ji})\) denotes the distribution of the observation \(X_{ji}\) given \(\zeta _{ji}\), and the base distribution H of \(G_0\) provides the prior distribution for the factors \(\zeta _{ji}\). This framework is known as the hierarchical Dirichlet process mixture model, in which each group is associated with an infinite mixture model, and the mixture components are shared among these mixture models due to the sharing of atoms \(\varOmega _k\) among all \(\{G_j\}\).

Since each factor \(\zeta _{ji}\) is distributed according to \(G_j\) based on Eq. (8), it takes the value \(\varpi _{jt}\) with probability \(\pi _{jt}\). It is convenient to place a binary indicator variable \(Z_{jit} \in \{0,1\}\) for \(\zeta _{ji}\). That is, \(Z_{jit} = 1\) if \(\zeta _{ji}\) is associated with component t and maps to the group-level atom \(\varpi _{jt}\); otherwise, \(Z_{jit} = 0\). Therefore, we have \(\zeta _{ji} = \varpi _{jt}^{Z_{jit}}\). Because \(\varpi _{jt}\) also maps to the global-level atom \(\varOmega _k\) as we mentioned previously, we then have \(\zeta _{ji} = \varpi _{jt}^{Z_{jit}}=\varOmega _k^{W_{jtk}Z_{jit}}\). Since \(\varvec{\pi }\) is a function of \(\varvec{\pi }'\) according to the stick-breaking construction as shown in Eq. (5), the indicator variable \(\mathbf {Z}= (Z_{ji1}, Z_{ji2}, \ldots )\) is distributed as

$$\begin{aligned} p(\mathbf {Z}|\varvec{\pi }')=\prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^\infty [\pi _{jt}'\prod _{s=1}^{t-1}(1-\pi _{js}')]^{Z_{jit}} \end{aligned}$$
(9)

The prior distribution of \(\varvec{\pi }'\) is a specific Beta distribution in the form

$$\begin{aligned} p(\varvec{\pi }')= \prod _{j=1}^M\prod _{t=1}^\infty \mathrm {Beta}(1,\lambda _{jt})= \prod _{j=1}^M\prod _{t=1}^\infty \lambda _{jt}(1-\pi _{jt}')^{\lambda _{jt}-1} \end{aligned}$$
(10)

2.3 Hierarchical Infinite Beta-Lioouville Mixture Model

In this subsection, we propose the hierarchical Dirichlet process mixture model of Beta-Liouville distributions, which may also be referred to as the hierarchical infinite Beta-Liouville mixture model. Given a grouped data set \(\mathcal {X}\) with M groups, it is assumed that each D-dimensional data vector \(\mathbf {X}_{ji} = (X_{ji1},\ldots ,X_{jiD})\) is drawn from a hierarchical infinite Beta-Liouville mixture model where j is the index for each group of the data. Then the likelihood function of the proposed hierarchical infinite Beta-Liouville mixture model with latent variables can be written as

$$\begin{aligned} p(\mathcal {X})= \prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^\infty \prod _{k=1}^\infty \big [\mathrm {BL}(\mathbf {X}_{ji}|\varvec{\theta }_k)\big ]^{Z_{jit}W_{jtk}} \end{aligned}$$
(11)

where \(\varvec{\theta }_k = (\alpha _{k1},\ldots ,\alpha _{kD},\alpha _k,\beta _k)\) is the vector of parameters of the Beta-Liouville distribution.

Next, we need to place conjugate priors over parameters \(\alpha _l\), \(\alpha \) and \(\beta \). Since \(\alpha _l\), \(\alpha \) and \(\beta \) are positive, Gamma distributions \(\mathcal {G}(\cdot )\) are adopted to approximate conjugate priors for these parameters. Then, we have the following prior distributions for \(\alpha _l\), \(\alpha \) and \(\beta \), respectively:

$$\begin{aligned} p(\alpha _l|u_l,v_l)= & {} \mathcal {G}(\alpha _l|u_l,v_l)=\frac{v_l^{u_l}}{\varGamma (u_l)}\alpha _l^{u_l-1}e^{-v_l\alpha _l} \end{aligned}$$
(12)
$$\begin{aligned} p(\alpha |g,h)= & {} \mathcal {G}(\alpha |g,h)=\frac{h^g}{\varGamma (g)}\alpha ^{g-1}e^{-h\alpha } \end{aligned}$$
(13)
$$\begin{aligned} p(\beta |g',h')= & {} \mathcal {G}(\beta |g',h')=\frac{h'^{g'}}{\varGamma (g')} \beta ^{g'-1}e^{-h'\beta } \end{aligned}$$
(14)

where \(\mathcal {G}(\cdot )\) is the Gamma distribution with positive parameters.

3 Model Learning Via Variational Bayes

3.1 Batch Variational Inference for Hierarchical Infinite Beta-Liouville Mixture Model

In this subsection, we develop a batch variational Bayes framework [2, 4] for learning the hierarchical infinite Beta-Liouville mixture model. To simplify notations, we define \(\varTheta = \{\mathbf {Z},\mathbf {W},\varvec{\psi }',\varvec{\pi }',\varvec{\theta }\}\) as the set of latent variables and unknown random variables. The main idea of variational learning is to calculate an approximation \(q(\varTheta )\) for the true posterior distribution \(p(\varTheta |\mathcal {X})\) by maximizing the lower bound of the logarithm of the marginal likelihood \(p(\mathcal {X})\), which is given by

$$\begin{aligned} \mathcal {L}(q) = \int q(\varTheta )\ln [ p(\mathcal {X},\varTheta )/q(\varTheta )] d\varTheta \end{aligned}$$
(15)

In this work, we adopt the factorial approximation [4] (or mean fields approximation), which has been successfully applied in the past to complex models involving incomplete data, to factorize \(q(\varTheta )\) into disjoint tractable factors. We also apply the truncation technique as described in [5] to truncate the variational approximations of global- and group-level Dirichlet processes at levels K and T as

$$\begin{aligned} \psi _K'= & {} 1, \quad \sum _{k=1}^K\psi _k = 1, \quad \psi _k = 0 \;\;\text {when}\;\; k>K \end{aligned}$$
(16)
$$\begin{aligned} \pi _{jT}'= & {} 1, \quad \sum _{t=1}^T\pi _{jt} = 1, \quad \pi _{jt} = 0 \;\;\text {when}\;\; t>T \end{aligned}$$
(17)

where the truncation levels K and T are variational parameters which can be freely initialized and will be optimized automatically during the learning process.

In variational Bayes learning, the general expression for the optimal solution to a specific variational factor \(q_s(\varTheta _s)\) is given by [4]:

$$\begin{aligned} q_s(\varTheta _s) = \frac{\exp \bigl \langle \ln p(\mathcal {X},\varTheta )\bigr \rangle _{i\ne s}}{\int \exp \bigl \langle \ln p(\mathcal {X},\varTheta )\bigr \rangle _{i\ne s}d\varTheta } \end{aligned}$$
(18)

where \(\langle \cdot \rangle _{i\ne s}\) is the expectation with respect to all the distributions of \(q_i(\varTheta _i)\) except for \(i = s\). Therefore, we can obtain the variational solution for each factor as

$$\begin{aligned} q(\mathbf {Z})= & {} \prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^T\rho _{jit}^{Z_{jit}} \end{aligned}$$
(19)
$$\begin{aligned} q(\mathbf {W})= & {} \prod _{j=1}^M\prod _{t=1}^T\prod _{k=1}^K\vartheta _{jtk}^{W_{jtk}} \end{aligned}$$
(20)
$$\begin{aligned} q(\varvec{\alpha }_l)= & {} \prod _{k=1}^K \prod _{l=1}^D \mathcal {G}(\alpha _{kl}|\tilde{u}_{kl},\tilde{v}_{kl}) \end{aligned}$$
(21)
$$\begin{aligned} q(\varvec{\alpha })= & {} \prod _{k=1}^K \mathcal {G}(\alpha _k|\tilde{g}_k,\tilde{h}_k) \end{aligned}$$
(22)
$$\begin{aligned} q(\varvec{\beta })= & {} \prod _{k=1}^K\mathcal {G}(\beta _k|\tilde{g}_k',\tilde{h}_k') \end{aligned}$$
(23)
$$\begin{aligned} q(\varvec{\pi }')= & {} \prod _{j=1}^M\prod _{t=1}^T \mathrm {Beta}(\pi _{jt}'|a_{jt},b_{jt}) \end{aligned}$$
(24)
$$\begin{aligned} q(\varvec{\psi }')= & {} \prod _{k=1}^K \mathrm {Beta}(\psi _k'|c_k,d_k) \end{aligned}$$
(25)

where the corresponding hyperparameters in the above equations can be calculated by

$$\begin{aligned} \rho _{jit}= & {} \frac{\exp (\widetilde{\rho }_{jit})}{\sum _{s=1}^T\exp (\widetilde{\rho }_{jis})} \end{aligned}$$
(26)
$$\begin{aligned} \widetilde{\rho }_{jit}= & {} \sum _{k=1}^K\langle W_{jtk}\rangle \left[ \mathcal {\widetilde{I}}_k+\mathcal {\widetilde{H}}_k+ \left( \bar{\alpha }_k-\sum _{l=1}^D\bar{\alpha }_{kl}\right) \ln \left( \sum _{l=1}^DX_{jil}\right) +\sum _{l=1}^D(\bar{\alpha }_{kl}-1)\ln X_{jil}\right. \nonumber \\&\left. +\,(\bar{\beta }_k-1)\ln \left( 1-\sum _{l=1}^DX_{jil}\right) \right] +\langle \ln \pi _{jt}'\rangle + \sum _{s=1}^{t-1}\langle \ln (1-\pi _{js}')\rangle \end{aligned}$$
(27)
$$\begin{aligned} \vartheta _{jtk}= & {} \frac{\exp (\widetilde{\vartheta }_{jtk} )}{\sum _{s=1}^K\exp (\widetilde{\vartheta }_{jts})} \end{aligned}$$
(28)
$$\begin{aligned} \widetilde{\vartheta }_{jtk}= & {} \sum _{i=1}^N\langle Z_{jit}\rangle \left[ \mathcal {\widetilde{I}}_k+\mathcal {\widetilde{H}}_k+ \left( \bar{\alpha }_k -\sum _{l=1}^D\bar{\alpha }_{kl}\right) \ln \left( \sum _{l=1}^DX_{jil}\right) +\sum _{l=1}^D(\bar{\alpha }_{kl}-1)\ln X_{jil}\right. \nonumber \\&\left. +\,(\bar{\beta }_k-1)\ln \left( 1-\sum _{l=1}^DX_{jil}\right) \right] +\langle \ln \psi _k'\rangle + \sum _{s=1}^{k-1}\langle \ln (1-\psi _s')\rangle \end{aligned}$$
(29)
$$\begin{aligned} a_{jt}= & {} 1+\sum _{i=1}^N\langle Z_{jit}\rangle , \qquad b_{jt} = \lambda _{jt} + \sum _{i=1}^N\sum _{s=t+1}^T\langle Z_{jis}\rangle \end{aligned}$$
(30)
$$\begin{aligned} c_k= & {} 1+\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle , \quad d_k = \gamma _k +\sum _{j=1}^M\sum _{t=1}^T\sum _{s=k+1}^K\langle W_{jts}\rangle \end{aligned}$$
(31)
$$\begin{aligned} \tilde{u}_{kl}= & {} u_{kl} + \sum _{j=1}^M\sum _{t=1}^T \langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \bar{\alpha }_{kl}\bigg [\varPsi \left( \sum _{l=1}^D\bar{\alpha }_{kl}\right) -\varPsi (\bar{\alpha }_{kl}) \nonumber \\&+\, \varPsi ' \left( \sum _{l=1}^D\bar{\alpha }_{kl}\right) \sum _{s\ne l}^D(\langle \ln \alpha _{ks}\rangle -\ln \bar{\alpha }_{ks})\bar{\alpha }_{ks}\bigg ] \end{aligned}$$
(32)
$$\begin{aligned} \tilde{v}_{kl}= & {} v_{kl}-\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \left[ \ln X_{jil}-\ln \left( \sum _{l=1}^DX_{jil}\right) \right] \end{aligned}$$
(33)
$$\begin{aligned} \tilde{g}_k= & {} g_k + \sum _{j=1}^M\sum _{t=1}^T \langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \bar{\alpha }_k\bigl [\varPsi (\bar{\alpha }_k+\bar{\beta }_k) \nonumber \\&-\, \varPsi (\bar{\alpha }_k)+ \bar{\beta }_k \varPsi '(\bar{\alpha }_k+\bar{\beta }_k)(\langle \ln \beta _k\rangle -\ln \bar{\beta }_k) \bigr ] \end{aligned}$$
(34)
$$\begin{aligned} \tilde{h}_k= & {} h_k-\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \ln \left( \sum _{l=1}^DX_{jil}\right) \end{aligned}$$
(35)
$$\begin{aligned} \tilde{g}_k'= & {} g_k' + \sum _{j=1}^M\sum _{t=1}^T \langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \bar{\beta }_k\bigl [\varPsi (\bar{\alpha }_k+\bar{\beta }_k) \nonumber \\&-\, \varPsi (\bar{\beta }_k)+ \bar{\alpha }_k \varPsi '(\bar{\alpha }_k+\bar{\beta }_k)(\langle \ln \alpha _k\rangle -\ln \bar{\alpha }_k) \bigr ] \end{aligned}$$
(36)
$$\begin{aligned} \tilde{h}_k'= & {} h_k'-\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \ln \left( 1-\sum _{l=1}^DX_{jil}\right) \end{aligned}$$
(37)

where \(\varPsi (\cdot )\) is the digamma function. \(\mathcal {\widetilde{I}}_k\) and \(\mathcal {\widetilde{H}}_k\) in Eqs. (27) and (29) are the lower bounds of \(\mathcal {I}_{k} = \bigg \langle \ln \frac{\varGamma (\sum _{l=1}^D\alpha _{kl})}{\prod _{l=1}^D\varGamma (\alpha _{kl})} \bigg \rangle \) and \(\mathcal {H}_k = \bigg \langle \ln \frac{\varGamma (\alpha _k+\beta _k)}{\varGamma (\alpha _k)\varGamma (\beta _k)}\bigg \rangle \), respectively. Since these expectations are computationally intractable, we apply the second-order Taylor series expansion to calculate their lower bounds. The expected values in the above formulas are defined as

$$\begin{aligned} \bar{\alpha }_{kl}= & {} \frac{\tilde{u}_{kl}}{\tilde{v}_{kl}}, \quad \bar{\alpha }_k = \frac{\tilde{g}_k}{\tilde{h}_k}, \quad \bar{\beta }_k = \frac{\tilde{g}_k'}{\tilde{h}_k'} \end{aligned}$$
(38)
$$\begin{aligned} \langle Z_{jit}\rangle= & {} \rho _{jit}, \quad \langle W_{jtk}\rangle =\vartheta _{jtk}, \quad \bigl \langle \ln \alpha _{kl}\bigr \rangle = \varPsi (\tilde{u}_{kl}) - \ln \tilde{v}_{kl} \end{aligned}$$
(39)
$$\begin{aligned} \bigl \langle \ln \alpha _k\bigr \rangle= & {} \varPsi (\tilde{g}_k) - \ln \tilde{h}_k \quad \bigl \langle \ln \beta _k\bigr \rangle = \varPsi (\tilde{g}_k') - \ln \tilde{h}_k' \end{aligned}$$
(40)
$$\begin{aligned} \bigl \langle \ln \pi _{jt}'\bigr \rangle= & {} \varPsi (a_{jt})-\varPsi (a_{jt}+b_{jt}) \end{aligned}$$
(41)
$$\begin{aligned} \bigl \langle \ln (1-\pi _{jt}')\bigr \rangle= & {} \varPsi (b_{jt})-\varPsi (a_{jt}+b_{jt}) \end{aligned}$$
(42)
$$\begin{aligned} \bigl \langle \ln \psi _k'\bigr \rangle= & {} \varPsi (c_k)-\varPsi (c_k+d_k) \end{aligned}$$
(43)
$$\begin{aligned} \bigl \langle \ln (1-\psi _k')\bigr \rangle= & {} \varPsi (d_k)-\varPsi (c_k+d_k) \end{aligned}$$
(44)

Since the update equations for the variational factors are coupled together through the expected values of other factors, the optimization process can be solved in a way analogous to the EM algorithm and the complete algorithm is summarized in Algorithm 1. The convergence of the variational learning algorithm is guaranteed and can be inspected through evaluation of the variational lower bound [4].

figure a

3.2 Online Variational Inference for Hierarchical Infinite Beta-Liouville Mixture Model

Compared with batch learning algorithms, online algorithms are more efficient when handling large-scale or sequentially arriving data. In this section, we extend the batch variational framework for learning hierarchical infinite Beta-Liouville mixture model to an online version by adopting the algorithm proposed in [48]. Assume that we have already obtained a data set \(\mathcal {X}\) with N data points. In addition, data points are continuously observed in an online manner. Therefore, we have to estimate the variational lower bound corresponding to a fixed amount of data. The expected value of the logarithm of the model evidence \(p(\mathcal {X})\) for this finite size of data can be calculated as

$$\begin{aligned} \langle \ln p(\mathcal {X})\rangle _\phi = \int \phi (\mathcal {X})\ln \biggl (\int p(X|\varTheta )p(\varTheta )\mathrm {d}\varTheta \biggr )\mathrm {d}\mathcal {X} \end{aligned}$$
(45)

where \(\varTheta = \{\mathbf {Z},\mathbf {W},\varvec{\psi }',\varvec{\pi }',\varvec{\theta }\}\). \(\phi (\mathcal {X})\) represents an unknown probability distribution for observed data. Then, the corresponding expected variational lower bound can be calculated as

$$\begin{aligned} \langle \mathcal {L}(q)\rangle _\phi= & {} \bigl \langle \sum _{\mathbf {Z}}\int q(\varLambda )q(\mathbf {Z})\ln \bigg [\frac{p(\mathcal {X},\mathbf {Z}|\varLambda ) p(\varLambda )}{q(\varLambda )q(\mathbf {Z})}\biggr ]\mathrm {d}\varLambda \bigr \rangle _\phi \nonumber \\= & {} N\int q(\varLambda )\mathrm {d}\varLambda \bigl \langle \sum _{\mathbf {Z}}q(\mathbf {Z}) \ln \biggl [\frac{p(\mathbf {X},\mathbf {Z}|\varLambda )}{q(\mathbf {Z})}\biggr ]\bigr \rangle _\phi + \int q(\varLambda )\ln \biggl [\frac{p(\varLambda )}{q(\varLambda )}\biggr ]\mathrm {d}\varLambda \nonumber \\ \end{aligned}$$
(46)

Now consider r as the actual amount of data that we have observed. The corresponding current lower bound for the observed data can be calculated by

$$\begin{aligned} \mathcal {L}^{(r)}(q) = \frac{N}{r}\sum _{i=1}^r\int q(\varLambda )\mathrm {d}\varLambda \sum _{\mathbf {Z}_i}Q(\mathbf {Z}_i) \ln \biggl [\frac{p(\mathbf {X}_i,\mathbf {Z}_i|\varLambda )}{q(\mathbf {Z}_i)}\biggr ]+ \int q(\varLambda )\ln \biggl [\frac{p(\varLambda )}{q(\varLambda )}\biggr ]\mathrm {d}\varLambda \end{aligned}$$
(47)

where \(\varLambda = \{\mathbf {W}, \varvec{\psi }',\varvec{\pi }',\varvec{\alpha }_l, \varvec{\alpha },\varvec{\beta }\}\). Please notice that in our case r increases over time while N is fixed. According to [48], the objective function of our online algorithm is the expected log evidence for a fixed amount of data as shown in Eq. (45). Thus, our online learning algorithm calculates the same quantity even if the amount of the observed data increases. As a matter of fact, we use the observed data to improve the estimation quality of the expected variational lower bound Eq. (46) which approximates the expected log evidence Eq. (45).

In order to apply the online variational learning algorithm, we need to successively maximize the current variational lower bound \(\mathcal {L}^{(r)}(q)\) with respect to each variational factor. Assume that we have already observed a data set \(\{X_1, \ldots X_{(r-1)}\}\). After obtaining a new observation \(X_r\), we can maximize the current lower bound \(\mathcal {L}^{(r)}(q)\) with respect to \(q(\mathbf {Z}_r)\) while other variational factors remain fixed to their \((r-1)\)th values: \(q^{(r-1)}(\mathbf {W})\), \(q^{(r-1)}(\varvec{\alpha }_l)\), \(q^{(r-1)}(\varvec{\alpha })\), \(q^{(r-1)}(\varvec{\beta })\), \(q^{(r-1)}(\varvec{\pi }')\) and \(q^{(r-1)}(\varvec{\psi }')\). Thus, the variational solution to \(q(\mathbf {Z}_r)\) can be updated as

$$\begin{aligned} q(\mathbf {Z}_r) = \prod _{j=1}^M\prod _{t=1}^T\rho _{jtr}^{Z_{jtr}} \end{aligned}$$
(48)

where

$$\begin{aligned} \rho _{jtr} = \frac{\exp (\widetilde{\rho }_{jtr} )}{\sum _{f=1}^T\exp (\widetilde{\rho }_{jtr})} \end{aligned}$$
(49)

and

$$\begin{aligned} \widetilde{\rho }_{jtr}= & {} \sum _{k=1}^K\langle W_{jtk}^{(r-1)}\rangle \Bigg [\mathcal {\widetilde{I}}_k^{(r-1)}+\left( \bar{\alpha }_k^{(r-1)} -\sum _{l=1}^D\bar{\alpha }_{kl}^{(r-1)}\right) \ln \left( \sum _{l=1}^DX_{jrl}\right) \nonumber \\&+\,\sum _{l=1}^D\left( \bar{\alpha }_{kl}^{(r-1)}-1\right) \ln X_{jrl} +\left( \bar{\beta }_k^{(r-1)}-1\right) \ln \left( 1-\sum _{l=1}^DX_{jrl}\right) \nonumber \\&+\,\mathcal {\widetilde{H}}_k^{(r-1)}\Bigg ]+\langle \ln \pi _{jt}'^{(r-1)}\rangle + \sum _{s=1}^{t-1}\langle \ln (1-\pi _{js}'^{(r-1)})\rangle \end{aligned}$$
(50)

Next, the current lower bound \(\mathcal {L}^{(r)}(q)\) is maximized with respect to to \(q^{(r)}(\mathbf {W})\), while \(q(\mathbf {Z}_r)\) is fixed and other variational factors remain at their \((r-1)\)th values. Thus, the variational factor to \(q^{(r)}(\mathbf {W})\) can be updated as

$$\begin{aligned} q^{(r)}(\mathbf {W}) = \prod _{j=1}^M\prod _{t=1}^T\prod _{k=1}^K\left( \vartheta _{jtk}^{(r)}\right) ^{W_{jtk}^{(r)}} \end{aligned}$$
(51)

where the hyperparameter \(\vartheta _{jtk}^{(r)}\) is given by

$$\begin{aligned} \vartheta _{jtk}^{(r)} = \vartheta _{jtk}^{(r-1)}+ \xi _r\Delta \vartheta _{jtk}^{(r)} \end{aligned}$$
(52)

where \(\xi _r\) is the learning rate which is used to reduce the earlier inaccurate estimation effects that contributed to the lower bound and accelerate the convergence of the learning process. In this work, we adopt a learning rate function introduced in [57], such that \(\xi _r = (\eta _0 + r)^{-\varsigma }\), subject to the constraints \(\varsigma \in (0.5,1]\) and \(\eta _0\ge 0\). In Eq. (52), \(\Delta \vartheta _{jtk}^{(r)}\) is the natural gradient of the hyperparameter \(\vartheta _{jtk}^{(r)}\). The natural gradient of a hyperparameter is obtained by multiplying the gradient by the inverse of Riemannian metric, which cancels the coefficient matrix for the posterior parameter distribution. Thus, these natural gradients can be calculated as

$$\begin{aligned} \Delta \vartheta _{jtk}^{(r)} = \vartheta _{jtk}^{(r)}-\vartheta _{jtk}^{(r-1)} = \frac{\exp \left( \widetilde{\vartheta }_{jtk}^{(r)} \right) }{\sum _{f=1}^K\exp \left( \widetilde{\vartheta }_{jtf}^{(r)}\right) }-\vartheta _{jtk}^{(r-1)} \end{aligned}$$
(53)

where

$$\begin{aligned} \widetilde{\vartheta }_{jtk}^{(r)}= & {} N\rho _{jtr} \Bigg [\mathcal {\widetilde{I}}_k^{(r-1)}+ \left( \bar{\alpha }_k^{(r-1)} -\sum _{l=1}^D\bar{\alpha }_{kl}^{(r-1)}\right) \ln \left( \sum _{l=1}^DX_{jrl}\right) \nonumber \\&+\,\sum _{l=1}^D \left( \bar{\alpha }_{kl}^{(r-1)}-1\right) \ln X_{jrl} +\left( \bar{\beta }_k^{(r-1)}-1\right) \ln \left( 1-\sum _{l=1}^DX_{jrl}\right) \nonumber \\&+\,\mathcal {\widetilde{H}}_k^{(r-1)}\Bigg ]+\langle \ln \psi _k'^{(r-1)}\rangle +\, \sum _{s=1}^{k-1}\langle \ln (1-\psi _s'^{(r-1)})\rangle \end{aligned}$$
(54)

In the following step, the current lower bound \(\mathcal {L}^{(r)}(q)\) is maximized with respect to \(q^{(r)}(\varvec{\pi }')\), \(q^{(r)}(\varvec{\psi }')\), \(q^{(r)}(\varvec{\alpha }_l)\), \(q^{(r)}(\varvec{\alpha })\) and \(q^{(r)}(\varvec{\beta })\) as

$$\begin{aligned} q^{(r)}(\varvec{\pi }')= & {} \prod _{j=1}^M\prod _{t=1}^T \mathrm {Beta}\left( \pi _{jt}'^{(r)}|a_{jt}^{(r)},b_{jt}^{(r)}\right) \end{aligned}$$
(55)
$$\begin{aligned} q^{(r)}(\varvec{\psi }')= & {} \prod _{k=1}^K \mathrm {Beta}\left( \psi _k'^{(r)}|c_k^{(r)},d_k^{(r)}\right) \end{aligned}$$
(56)
$$\begin{aligned} q^{(r)}(\varvec{\alpha }_l)= & {} \prod _{k=1}^K \prod _{l=1}^D \mathcal {G}\left( \alpha _{kl}^{(r)}|\tilde{u}_{kl}^{(r)},\tilde{v}_{kl}^{(r)}\right) \end{aligned}$$
(57)
$$\begin{aligned} q^{(r)}(\varvec{\alpha })= & {} \prod _{k=1}^K \mathcal {G}\left( \alpha _k^{(r)}|\tilde{g}_k^{(r)},\tilde{h}_k^{(r)}\right) \end{aligned}$$
(58)
$$\begin{aligned} q^{(r)}(\varvec{\beta })= & {} \prod _{k=1}^K \mathcal {G}\left( \beta _k^{(r)}|\tilde{g}_k'^{(r)},\tilde{h}_k'^{(r}\right) \end{aligned}$$
(59)

where the hyperparameters are given by

$$\begin{aligned} a_{jt}^{(r)}= & {} a_{jt}^{(r-1)}+ \xi _r\Delta a_{jt}^{(r)}, \quad b_{jt}^{(r)} = b_{jt}^{(r-1)}+ \xi _r\Delta b_{jt}^{(r)} \end{aligned}$$
(60)
$$\begin{aligned} c_k^{(r)}= & {} c_k^{(r-1)}+ \xi _r\Delta c_k^{(r)}, \quad d_k^{(r)} = d_k^{(r-1)}+ \xi _r\Delta d_k^{(r)} \end{aligned}$$
(61)
$$\begin{aligned} \tilde{u}_{kl}^{(r)}= & {} \tilde{u}_{kl}^{(r-1)} + \xi _r\Delta \tilde{u}_{kl}^{(r)}, \quad \tilde{v}_{kl}^{(r)} = \tilde{v}_{kl}^{(r-1)} + \xi _r\Delta \tilde{v}_{kl}^{(r)} \end{aligned}$$
(62)
$$\begin{aligned} \tilde{g}_k^{(r)}= & {} \tilde{g}_k^{(r-1)} + \xi _r\Delta \tilde{g}_k^{(r)}, \quad \tilde{h}_k^{(r)} = \tilde{h}_k^{(r-1)} + \xi _r\Delta \tilde{h}_k^{(r)} \end{aligned}$$
(63)
$$\begin{aligned} \tilde{g}_k'^{(r)}= & {} \tilde{g}_k'^{(r-1)} + \xi _r\Delta \tilde{g}_k'^{(r)}, \quad \tilde{h}_k'^{(r)} = \tilde{h}_k'^{(r-1)} + \xi _r\Delta \tilde{h}_k'^{(r)} \end{aligned}$$
(64)

The corresponding natural gradients in the above equations can be calculated as

$$\begin{aligned} \Delta a_{jt}^{(r)}= & {} 1+N\rho _{jrt}- a_{jt}^{(r-1)} \end{aligned}$$
(65)
$$\begin{aligned} \Delta b_{jt}^{(r)}= & {} \lambda _{jt} + N\sum _{s=t+1}^T\rho _{jsr} - b_{jt}^{(r-1)} \end{aligned}$$
(66)
$$\begin{aligned} \Delta c_k^{(r)}= & {} 1+\sum _{j=1}^M\sum _{t=1}^T\vartheta _{jtk}^{(r)}- c_k^{(r-1)} \end{aligned}$$
(67)
$$\begin{aligned} \Delta d_k^{(r)}= & {} \gamma _k +\sum _{j=1}^M\sum _{t=1}^T\sum _{s=k+1}^K\vartheta _{jts}^{(r)}- d_k^{(r-1)} \end{aligned}$$
(68)
$$\begin{aligned} \Delta \tilde{u}_{kl}^{(r)}= & {} u_{kl} + N\sum _{j=1}^M\sum _{t=1}^T \vartheta _{jtk}^{(r)} \rho _{jrt} \bigg [\varPsi \left( \sum _{l=1}^D\bar{\alpha }_{kl}^{(r-1)}\right) -\varPsi \left( \bar{\alpha }_{kl}^{(r-1)}\right) \nonumber \\&+\, \varPsi ' \left( \sum _{l=1}^D\bar{\alpha }_{kl}^{(r-1)}\right) \sum _{s\ne l}^D \left( \langle \ln \alpha _{ks}^{(r-1)}\rangle -\ln \bar{\alpha }_{ks}^{(r-1)}\right) \bar{\alpha }_{ks}^{(r-1)}\bigg ]\bar{\alpha }_{kl}^{(r-1)}-\tilde{u}_{kl}^{(r-1)}\nonumber \\ \end{aligned}$$
(69)
$$\begin{aligned} \Delta \tilde{v}_{kl}^{(r)}= & {} v_{kl}-N\sum _{j=1}^M\sum _{t=1}^T\vartheta _{jtk}^{(r)} \rho _{jrt}\left[ \ln X_{jrl}-\ln \left( \sum _{l=1}^DX_{jrl}\right) \right] -\tilde{v}_{kl}^{(r-1)} \end{aligned}$$
(70)
$$\begin{aligned} \Delta \tilde{g}_k^{(r)}= & {} g_k + N\sum _{j=1}^M\sum _{t=1}^T \vartheta _{jtk}^{(r)} \rho _{jrt} \bar{\alpha }_k^{(r-1)}\bigg [\varPsi \left( \bar{\alpha }_k^{(r-1)}+\bar{\beta }_k^{(r-1)}\right) - \varPsi (\bar{\alpha }_k^{(r-1)})\nonumber \\&+\, \bar{\beta }_k^{(r-1)} \varPsi ' \left( \bar{\alpha }_k^{(r-1)}+\bar{\beta }_k^{(r-1)}\right) \left( \langle \ln \beta _k^{(r-1)} \rangle -\ln \bar{\beta }_k^{(r-1)}\right) \bigg ]-\tilde{g}_k^{(r-1)} \end{aligned}$$
(71)
$$\begin{aligned} \Delta \tilde{h}_k^{(r)}= & {} h_k-N\sum _{j=1}^M\sum _{t=1}^T\vartheta _{jtk}^{(r)} \rho _{jrt}\ln (X_{jrl})-\tilde{h}_k^{(r-1)} \end{aligned}$$
(72)
$$\begin{aligned} \Delta \tilde{g}_k'^{(r)}= & {} g_k' + N\sum _{j=1}^M\sum _{t=1}^T \vartheta _{jtk}^{(r)} \rho _{jrt} \bar{\beta }_k^{(r-1)}\Bigg [\varPsi \left( \bar{\alpha }_k^{(r-1)}+\bar{\beta }_k^{(r-1)}\right) - \varPsi \left( \bar{\beta }_k^{(r-1)}\right) \nonumber \\&+\, \bar{\alpha }_k^{(r-1)} \varPsi ' \left( \bar{\alpha }_k^{(r-1)}+\bar{\beta }_k^{(r-1)}\right) \left( \langle \ln \alpha _k^{(r-1)}\rangle -\ln \bar{\alpha }_k^{(r-1)}\right) \Bigg ]-\tilde{g}_k'^{(r-1)} \end{aligned}$$
(73)
$$\begin{aligned} \Delta \tilde{h}_k'^{(r)}= & {} h_k'-N\sum _{j=1}^M\sum _{t=1}^T\vartheta _{jtk}^{(r)} \rho _{jrt}\ln (1-X_{jrl})-\tilde{h}_k'^{(r-1)} \end{aligned}$$
(74)

Since the hyperparameters of \(q^{(r)}(\varvec{\pi }')\), \(q^{(r)}(\varvec{\psi }')\), \(q^{(r)}(\varvec{\alpha })\) \(q^{(r)}(\varvec{\beta })\) and \(q^{(r)}(\varvec{\alpha }_l)\) are independent from each other, they can be updated in parallel. We repeat this online variational inference procedure until all the variational factors are updated with respect to the current arrived observation. It is worth mentioning that the online variational algorithm can be defined as a stochastic approximation method [27] for estimating the expected lower bound and the convergence is guaranteed if the learning rate satisfies the following conditions [48]:

$$\begin{aligned} \sum _{r=1}^{\infty }\xi _r = \infty \;, \qquad \sum _{r=1}^\infty \xi _r^2<\infty \end{aligned}$$
(75)

The online variational inference for hierarchical infinite Beta-Liouville mixture model is summarized in Algorithm 2. The computational complexity for the proposed online variational hierarchical infinite Beta-Liouville mixture model is \(\mathcal {O}(MTKD)\) in each iteration. In contrast, its batch learning counterpart requires \(\mathcal {O}(NMTKD)\) in each iteration, where N in this case represents the size of the data set that is observed. This is due to the fact that the batch algorithm updates the variational factors using the whole data set in each iteration, and thus its estimation quality is improved much more slowly than in the case of the online one. Please also notice that the total computational time depends on the number of iterations that is required to converge.

figure b

3.3 Discussion

Regarding the learning of mixture models, other popular approximation schemes may also be applied. Indeed, two classes of approximation techniques can be broadly defined, depend on whether they rely on stochastic or deterministic approximations. Stochastic techniques, such as Markov chain Monte Carlo (MCMC) [46], are based on numerical sampling and can provide exact results in theory if given infinite computational resource. Nevertheless, in practice, the use of sampling method is limited to small-scale problems due to the high computational cost. Moreover, it is often difficult to analysis the convergence. By contrast, the deterministic approximation schemes such as expectation prorogation [39, 40] and variational Bayes are based on analytical approximations to the posterior distribution. Expectation prorogation, which is based on the assumed-density filtering [37], is a recursive approximation scheme based on the minimization of a Kullback-Leibler divergence between the true model’s posterior and an approximation. Compared with variational Bayes, expectation prorogation can provide comparable learning results if the data set is relatively small, whereas its performance would be degraded for large-scale data set [35]. In our work, we adopt variational Bayes as the approximation method for model learning. The variational approach is based on analytical approximations to the posterior distribution, which has received a lot of attention and has provided good generalization performance as well as computational tractability in various applications. Additionally, variational Bayes has also increased the power and flexibility of mixture models by allowing full inference about all the involved parameters and then simultaneous model selection and parameters estimation.

4 Experimental Results

We validate the proposed online hierarchical infinite Beta-Liouville mixture model (referred to as OnHInBL) through a real-world application namely scene recognition. Indeed, the availability of relatively cheap digital communication and the popularity of the WWW has made image databases largely available. A lot of research works have been devoted to the development of efficient image representation and classification approaches [11, 29, 34, 43, 44, 49, 50]. This task is challenging and has a lot of potential applications. Examples of applications include multimedia retrieval, annotation, summarizing and browsing [14, 16, 33, 41, 42]. An important step is the extraction of the images content descriptors [28, 56]. According to [59], “scene” represents a place where a human can act within or navigate. The goal of scene recognition is to classify a set of natural images into a number of semantic categories. In our work, we perform the scene recognition using our OnHInBL model with a bag-of-visual words representation. In this experiment, our specific choice for initializing the hyperparameters is the following: \((\lambda _{jt}, \gamma _k, u_{kl}, v_{kl}, g_k, h_k, g_k', h_k')= (0.1,0.1,1,0.1,1,0.1,1,0.1)\). Parameters \(\varsigma \) and \(\eta _0\) of the learning rate are set to 0.65 and 64, respectively. Furthermore, the global truncation level K is set to 750 and the group truncation level T is set to 80. It is worth mentioning that these specific choices were found convenient in our experiment.

4.1 Experimental Design

The procedure for performing scene recognition using the proposed OnHInBL model and bag-of-visual words representation is described as the following: First, we extract and normalize PCA-SIFT descriptorsFootnote 1 (36-dimensional) [25] from original images using the Difference-of-Gaussian (DoG) detector [32]. Next, our OnHInBL is used to model these obtained PCA-SIFT feature vectors. More specifically, each image \(\mathcal {I}_j\) is treated as a “group” in our hierarchical model and is associated with an infinite mixture model \(G_j\). Thus, each PCA-SIFT feature vector \(X_{ji}\) of the image \(\mathcal {I}_j\) is considered to be drawn from \(G_j\) and the mixture components of \(G_j\) are treated as “visual words”. Then, a global vocabulary is constructed and is shared among all groups (images) through the common global infinite mixture model \(G_0\) within our hierarchical model. It is noteworthy that this setting matches the desired design of a hierarchical Dirichlet process mixture model where observations are organized into groups and these groups are statistically linked by sharing mixture components. Indeed, an important step in bag-of-visual words representation is the construction of visual vocabulary. As we may notice, most of previously proposed approaches have to apply a separate vector quantization method (such as K-means) to build the visual vocabulary, where the size of the vocabulary is normally chosen manually. This problem can be tackled elegantly in our approach since the construction of the visual vocabulary is part of our hierarchical Dirichlet process mixture framework. As a result, the size of the vocabulary (i.e. the number of mixture components in the global-level mixture model) can be inferred automatically from the data thanks to the property of nonparametric Bayesian model. Then, the “bag-of-words” paradigm is employed and a histogram of “visual words” for each image is computed. Since the goal of our experiment is to determine which scene category that a testing image \(\mathcal {I}_j\) belongs to, we need to introduce an indicator variable \(B_{jm}\) associated with each image (or group) in our hierarchical Dirichlet process mixture framework. \(B_{jm}\) denotes image \(\mathcal {I}_j\) comes from category m and is drawn from another infinite mixture model which is truncated at level J. This means that we need to add a new level of hierarchy to our hierarchical infinite mixture model with a sharing vocabulary among all scene categories. In our experiment, we truncate J to 50 and initialize the hyperparameter of the mixing probability of \(B_{jm}\) to 0.1. Finally, we assign a testing image into the category which results the highest posterior probability according to Bayes’ decision rule.

Fig. 1
figure 1

Sample scene images from the SUN database

Full size image

4.2 Data set and Results

We conducted our test on a challenging scene data set namely Scene UNderstanding (SUN) database which contains 899 scene categories and 130,519 images.Footnote 2 Images within each category were obtained using WordNet terminology from various search engines on the internet [59]. In our case, we randomly chose 16 of the 899 categories (e.g. “abbey”, “aqueduct”, “lighthouse”, and “beach”) in the SUN database to evaluate the performance of our approach. Furthermore, we have to ensure that each selected category must have at least 100 images. Thus, each of these categories contains 100 scene images and therefore we have 1600 images in total. We randomly divided this data set into two halves: one for training (to learn the model and build the visual vocabulary), the other one for testing. Sample images from each scene tested category can be viewed in Fig. 1.

Table 1 The average scene recognition rate (%) and the corresponding the runtime (s) using different methods for the SUN database. The numbers in parenthesis are the standard deviation of the corresponding quantities
Full size table
Fig. 2
figure 2

Confusion matrix obtained by OnHInBL for the SUN database

Full size image

The proposed approach was evaluated by running it 30 times. We compared our OnHInBL approach with several other mixture-modeling approaches for scene recognition, in order to demonstrate its advantages. Our goal for the comparison can be summarized in three-fold: to compare the online learning algorithm with the batch one; to compare the hierarchical Dirichlet process framework with the conventional Dirichlet process one; to compare Beta-Liouville mixture models with Gaussian ones on modeling proportional data. Thus, the proposed OnHInBL model was compared with: the batch hierarchical infinite Beta-Liouville mixture model (BaHInBL), the online infinite Beta-Liouville mixture (OnInBL) model and the online hierarchical infinite Gaussian mixture model (OnHInGau). All of these models were learned using variational inference. For the experiment of using OnInBL model, its visual vocabulary was built using the K-means algorithm and the size of its visual vocabulary was manually set to 600. The testing data in our experiments is supposed to arrive sequentially in an online manner except for the approach using BaHInBL model. Table 1 shows the average results of our OnHInBL model and the three other tested model for scene recognition on the SUN database. As illustrated in this table, both the proposed online approach (OnHInGDFs) and its batch counterpart (BaHInBL) can obtain the highest recognition rates among all tested approaches. Figures 2 and 3 present the confusion matrices obtained by OnHInBL and BaHInBL, respectively for the tested database. Each entry (i, j) of the confusion matrix denotes the number of images in category i that are assigned into category j. As shown in these two figures, we observed that the overall average recognition accuracy was 70.81 % (error rate of 29.19 %) using OnHInBL, and 71.27 % (error rate of 28.73 %) using BaHInBL. Although BaHInBL provided slightly higher recognition rate (71.27 %) than the one obtained by OnHInBL (70.81 %), their difference is not statistically significant according to Student’s t-test (i.e., we have calculated p-values between 0.1351 and 0.2512 for different runs). Therefore, OnHInBL is more favorable since it was significantly faster than BaHInBL as shown in Table 1, because of its online learning property. This can be explained by the fact that the batch algorithm updates the variational factors by using the whole data set in each iteration, and thus its estimation quality is improved more slowly than in the case of the online one. Moreover, OnHInBL outperformed OnInBL (70.81 vs. 66.34 %) as shown Table 1, which demonstrates the merits of using hierarchical Dirichlet process framework over the conventional Dirichlet process one. According to Table 1, better performance obtained by OnHInBL than the one acquired by OnHInGau verifies that the Beta-Liouville mixture model has a better modeling capability for proportional data than Gaussian mixture model.

Fig. 3
figure 3

Confusion matrix obtained by BaHInBL for the SUN database

Full size image

5 Conclusion

In this paper, we have proposed a statistical clustering framework based on Beta-Liouville distribution. This statistical framework is developed from a nonparametric Bayesian perspective via a hierarchical Dirichlet process. For the learning of the model’s parameters both variational approaches are proposed. The first one works on batch settings and the second one is incremental. The experimental results that have concerned image databases categorization have shown that our method is promising and has interesting advantages. It is noteworthy that in the proposed model, all data features are used for model learning. However, in practice, not all the features are important and some may be irrelevant. These irrelevant features may not contribute to the learning process or even degrade clustering results. Thus, one possible future work can be devoted to the inclusion of a feature selection scheme within the proposed framework in order to chooses the “best” feature subset for improving clustering performance.