Introduction

In the first paper of this series [1], we have presented computational experiments with cerebellar model and compared the features of the computational data with properties of biological climbing fiber cell (ClFC) firing patterns. The results obtained in that paper led us to the hypothesis that climbing fiber cells impulses are signals of the inner mechanics of the cerebelloolivary loop and are not causally connected with the organism’s behaviour errors.

The goal of this article is to make the computational model in [1] more realistic. In particular, we analyze in detail behaviour of the model with three (periodic, non-periodic, concatenated(2 ClFCs)) different modes of activation of granule cells (while [1] used only simple periodic granule cell environment). We use two types (periodic and non-periodic) of the extracerebellar input to the model and we also explore simple cases of simultaneous work of two ClFC modules (while [1] used only periodic extracerebellar input and only one ClFC module).

The results obtained here might serve as an additional argument in favour of the hypothesis proposed in [1] and also enables formulation of problems for further analysis.

Results of computational experiments

Properties of the model

Following [1, 2], we use the system of Mauk equations. These equations describe changes of synaptic weights from granule cells (GrCs) to Purkinje cells (PCs) depending on the activity of granule cells and on the moments of climbing fiber cell activation. The processes of synaptic weight changes depend on eligibility function for each granule cell to Purkinje cell synapse [3, 4]. The eligibility function is determined by granule cells activity. The system dynamics depends also on the function \(\chi (t)=\chi (t-t^*(t))\), where \(t^*(t)\) is the moment of the last ClFC excitation before the moment t.

$$\begin{aligned} \chi (\tau )= {\left\{ \begin{array}{ll} -A, &{} \text {if}\ \tau < \Delta \\ a, &{} \text {if}\ \tau >= \Delta \end{array}\right. } \end{aligned}$$

where \(A>0, a>0.\)

We use A which is significantly larger than a.

Following [1] we introduce equilibrium ClFC interval \(T_{equ} = \Delta (1 + A/a)\) and suppose that \(T_{equ}\) is equal to 1 second to establish correspondence between the average ClFC interspike interval duration in model and in live cerebellum.

The cerebellum model was embedded in periodic environment (as in [1]) or non-periodic environment (described in detail below) and we observed the process of equalization of the total input to the climbing fiber cell provided with plasticity of granule cells to Purkinje cell synapses.

Granule cell activity patterns

In computational experiments we used three basic types of GrCs activation patterns:

  1. (1)

    periodic activation patterns (Fig. 1abc)

  2. (2)

    non-periodic activation pattern (Fig. 1d)

  3. (3)

    "double periodic" activation pattern (Fig. 1e).

For periodic patterns, each granule cell was active with k=1 or k=2 bursts of activity over the period. Each burst lasts for L ms and bursts are separated from each other by periods of silence. The number of simultaneously active granule cells m was kept constant in each computational experiment session.

Figure 1a shows the case with one granule cell burst per period (k=1). GrCs are activated one by one equidistantly in time domain forming periodic input to the Purkinje cell. The case k=1 is trivial in a sense that all possible variations of GrC activity can be reduced to the described Fig. 1a by proper permutation of GrC indices.

For the case k=2 we considered two substantially different activation patterns (Fig. 1bc). Figure 1b was designed "by hand" as a simple example satisfying the mentioned above constraints on variables k, L, m.

Construction of pattern at Fig. 1c was based on partly restricted random selection. Besides the stated above restrictions on k, L, m variables (in this case k=2), there was chosen refractory period \(T_r\) such that the same granule cell can not generate two bursts with the interval less than \(T_r\) between the bursts starting points.

Fig. 1
figure 1

Granule cells activity patterns. Point with abscissa t and ordinate i is black if granule cell number i is active at time t. Time in ms

Full size image

We refer to Fig. 1b as low-entropy GrC activity pattern and to Fig. 1c as high-entropy GrC activity pattern because the former is highly ordered (simply described in few words) activity pattern while generation of the latter includes k*N random steps (where N is the number of granule cells) and the existence of every such step adds a value of about 1.0 bits to the pattern entropy.

For the non-periodic activity patterns (Fig. 1d) we used the random integer number of periods of granule cell activation (as in Fig. 1c) which were interrupted with random duration stops at the fixed phase of granule cell activity dynamics.

In "double-periodic" activity pattern (Fig. 1e) the granule cells activation pattern for i=1-300 over the period t=1-3600 ms presents nine successive copies of Fig. 1c. Granule cells activation pattern for i=301-600 over the period t=1-3600 ms presents four successive and properly scaled copies of Fig. 1c. The patterns of Fig. 1c,e were used for modelling of two ClFCs and two Purkinje cells working on the same set of granule cells.

Computational experiments with one burst of granule cell activation over the cycle (k=1)

Experiments presented in Figs. 2(a-c) and 2(d-f) differ only in the way of granule cells weights initialization. In the first case, the weights were randomly evenly distributed over the interval [360; 400]. In the second case, all the initial weights were set to the same single value of 360.

Comparison of cases (top and middle rows at Fig. 2) shows that the way of GrC weight initialization has practically no effect on statistics of interspike intervals as can be seen on Poincare plots in Fig. 2bc. However there is a substantial difference in the time course of equalization which is discussed in Section 2.6.

Figure 2a shows the fragments of the external input to ClFC, input to the ClFC from PC and the sum of both. The fragments are taken at the time 12000 seconds when convergence has been completed. It should be emphasized that we use no kind of noise in our simulations. However, the Poincare plot (Fig. 2b) shows that pairs of sequential intervals seemingly randomly fill the positive quadrant of the coordinates plane. As it has been noted in previous paper, the white strips at Poincare plot are simply explained by the fact that both the external signal to the system and excitation pattern of granule cells are strictly periodic[1].

Fig. 2
figure 2

Computational experiments with k=1. In all figures (here and in Figs.3, 4) with the amplitudes of signals the units of signal values are arbitrary chosen to properly represent the variable components of the signals

Full size image

Figure 2(g-i) shows behaviour of the system when the external signal to the ClFC is non-periodic as described above. It should be noted again that the total input to the ClFC (i.e. the sum of external signal to ClFC and signal from the Purkinje cell) becomes practically constant. However, in this case the Poincare plot is much more homogeneous than in cases of Figs. 2(b) and 2(e) as is expected because the signal which comes to the system over granule cells is non-periodic. It should be noted again that Poincare plot looks random despite there was no noise in the system. The convergence time was 6500 seconds.

Figure 2(b,e,h) present Poincare plots of successive interspike intervals of ClFC impulse sequences corresponding to Fig. 2(a,d,g). Figure 2(c,f,i) present the distribution function of weight values in the steady state.

Fig. 3
figure 3

Computational experiments with k=2

Full size image

The presented data demonstrate that the simple activation of granule cells (k-th granule cell is active at time intervals [i*T+k : i*T+k+L] in milliseconds, where i=0,1,2...; T is period in ms; L is burst duration) is appropriate for the task of equalizing the total input to the ClFCs. Equalization plots at Fig. 2a,d are similar. Poincare plots at Fig. 2b,e look identical (though they do not coincide in fine details). In the case k=1, each synapse in fact corresponds to a fixed phase of external signal and existence of two peaks in the final weight distribution can be explained by existence of two corresponding peaks in distribution of values of external (sine) function.

The results at Fig. 2 demonstrate that initial distribution of weights has a substantial influence on the dynamics of the external signal equalization. It should be noted that the pattern of ClFC activity looks like random[1]. Poincare plots from Fig. 2(b,e,h) demonstrate the presence of dynamic chaos in the cerebellar module [5, 6].

In the experiments corresponding to Fig. 2(a-f) the number of simultaneously active granule cells was m=10. In experiment corresponding to Fig. 2(g-i) m=5. In other experiments we varied m from 3 to 20 without substantially affecting the qualitative features of system dynamics.

Adding noise to Purkinje cell does not qualitatively change the dynamics of the system (not shown).

Computational experiments with k=2

In case k=1 there was only one possible sequence of granule cells activation up to granule cells numeration order. There are much more possible sequences for k=2 than for k=1. The convergence of the system to the equalized state of the total input to the ClFC substantially depends on the properties of these sequences.

Figure 3(a,b) presents the results of the experiment where the sequence of granule cell activation is given by the plot of Fig. 2b. The description of this sequence has low entropy. Experiments presented at Fig. 2(d-i) were performed with the sequence of granule cells activation presented at Fig. 1c (later will be referred to as random granule cell activation sequence)[1]. The sequence was generated randomly while satisfying the following conditions: at each time moment exactly m=15 granule cells are active; each granule cell has two bursts of activation of L=10ms each during the period of the external signal; the distance between two bursts of the same granule cell always exceeds R=40 milliseconds. For random sequence (Fig. 1b) the minimum error was 0.003 of extracerebellar signal sine amplitude value. It was achieved at  40min. This equalization time was minimal of the computational experiments described in this paper.

Poincare plots for all three experiments presented at Fig. 3 represent more or less random distribution of data points over the coordinate space with clear white bands (discussed in detail earlier) for Fig. 3b,e and with much less expressed patternization for the non-periodic external signal. Weight distribution of granule cells in the final state for the experiment presented at Fig. 3gh is shown at Fig. 3i. Weight distribution for the experiment of the Figs. 3de and 3gh do not substantially differ from Fig. 3i.

Fig. 4
figure 4

Computational experiments with two ClFCs

Full size image

Experiments with 2 Purkinje cells each having their own ClFC

Figure 4 demonstrates two series of experiments: (a-c) and (d-f). In each of them we had two ClFC loops each having one ClFC and one PC. Both series of experiments shared the common set of granule cells (the number of granule cells n=300). In experiment that is demonstrated at Fig. 4a-c, the external signal to the ClFCs had the same frequency. The activity of all granule cells was periodic high-entropy with k=2 as shown at Fig.1c (i.e. the same as was used at Fig. 3d-f). At Fig. 4a, external signals to ClFCs were shifted in phase of \(\pi /2\) relatively to each other. Figure 4a shows that for both ClFCs the external signal is successfully equalized. Poincare plots for both ClFCs look practically indistinguishable for human observer and one of them is presented at Fig. 4b. Figure 4c shows that ClFCs impulse sequences crosscorrelation function has small amplitude oscillations. These oscillations have a period equal to \(T_{equ}\). Figure 4d-f also shows the experiment with two Purkinje cells and two ClFCs sharing the same set of granule cells (the number of granule cells n=600). However in this case a half of granule cells was cyclic with period \(T_1\)=400ms and the other half of granule cells was cyclic with period \(T_2\)=900ms as shown at Fig.1e. Both sequences of granule cell activity were random with k=2. Figure 4d demonstrates fairly good equalization of the external signal of both ClFCs like in Fig. 4a. The Poincare plots for impulse sequences of both ClFCs look very similar to each other so only one of them is shown at Fig. 4e. There is a substantial difference between Figs. 4b and 4e as the first has the same white strips as in previously described experiments while Fig. 4e shows interference of those strips for two periods of external signal which were used in these experiments. The crosscorrelation function for impulse activities between the two ClFCs (Fig. 4f) shows practically absent correlation between two ClFCs impulse sequences. As average interspike interval of both sequences in our experiments is equal to \(T_{equ}\)=1s, the mean value of crosscorrelation function is equal to 0.001 (per one millisecond interval).

Time course of equalization of the total input to the ClFC

We have demonstrated above that the total input to the ClFC gradually becomes equalized in time domain. As a measure of equalization quality, we use the quantitative dimensionless parameter defined as the average value of the modulus of deflection of the total input to the ClFC from the average input to the ClFC in the interval divided by the amplitude of extracerebellar signal to the ClFC. In other terms, equalization measure, EQ(t), at time t after beginning of the computational experiment is defined as:

$$\begin{aligned} EQ(t) = \frac{1}{t_{avg}*A_{ext}}\sum _{t-t_{avg}<\tau \le t}|(Y(\tau ) - \overline{Y}(t)|\end{aligned}$$

where:

\(Y(t) = PC(t) + EI(t)\) is the total input to the ClFC;

PC(t) is PC output;

EI(t) is external extracerebellar input;

\(t_{avg}\) = 10 000 milliseconds is the period over which the averaging is applied;

\(A_{ext}\) is the amplitude of extracerebellar signal;

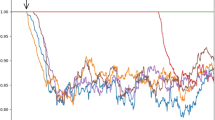
$$\begin{aligned} \overline{Y}(t) = \frac{1}{t_{avg}}\sum _{t-t_{avg}<\tau \le t}Y(\tau ) \end{aligned}$$

In Fig. 5 time course of equalization is presented for all the computational experiments described above. The figure needs following comments:

  1. 1)

    The abscissa is the same for all subplots of Fig. 5 and includes time from t=0 to t=7e4 seconds;

  2. 2)

    The ordinate scale is identical for most of subplots except the scale for Fig. 5a is 10 times finer and the scale for Fig. 5b is 1000 times finer than for Fig. 5a.

For granule cell sequential activation (k=1, Fig. 5abc) the final EQ is the lowest for all tested settings. It is notable that with the fixed initial values of synaptic weights (Fig. 5b) the accuracy level to which equalization converges is much better than for random initialization (Fig. 5a). Accuracy for non-periodic signal (Fig. 5c) is about 3 times less than for periodic signal (Fig. 5a); in both cases initial synaptic weights were not fixed to the same value but were randomly evenly distributed within an interval. Accuracy for non-periodic signals for k=2 (Fig. 5f) is just about 1.3 times worse than for periodic signal (Fig. 5e). Note that for k=2 the difference between these cases is substantially less than for k=1.

Fig. 5
figure 5

The average value of deviation of signal from average value in sequencing test intervals. Averaging is performed over sequential test intervals (test interval duration is 10 000 milliseconds). Pay attention to the ordinate scale

Full size image

Figure 5g shows convergence for two ClFCs for extracerebellar signals with the same frequency but different phases. The final accuracies for these two signals are different probably reflecting random variation in suitability of a concrete pattern to concrete phases of signal. The last two plots (Fig. 5hi) show that equalization of two independent embedding signals yields approximately same time course of equalization.

Discussion

As a result of computational experiments we have found the following:

  1. 1)

    With one burst of GrC firing over the period of the embedding signal, simple one-by-one sequence of granule cell excitation yields perfect equalization of the total input to the ClFC. The final equalization measure is about 400 times better in the case of fixed initial synaptic weights from granule cells to PCs than in the case of random initialization. Also equalization of the total input to ClFC can be achieved in case of non-periodic embedding of the cerebellar module. It is essential to underline that equalization happens in total absence of noise in the system. Practically in all computational sessions the ClFC firing pattern looks random as can be seen on Poincare plots of successive intervals of ClFC firing.

  2. 2)

    Single pattern of GrC activation can provide simultaneous equalization of signals with two different phases of the extracerebellar input to two ClFCs. Also it can provide equalization of two independent embeddings. It is important that the crosscorrelation function between firing sequences of two ClFCs which are involved in simultaneous equalization of different extracerebellar signals shows practically no correlation.

  3. 3)

    The rate and final quality of convergence of the signal equalization to the stationary state in different conditions demonstrates substantial diversity described in detail in Section 2.6.

The experiments in Fig. 2 demonstrate the convergence of the dynamical system which provides equalization of the total input to the ClFC to the random looking process. Its final equalization quality in the case of GrC sequential activation (k=1) substantially depends on details of the initial state. It might be achieved for periodical as well as non-periodical embedding environments. The random looking pattern of ClFC activation in these cases ought to be attributed to the dynamic chaos which emerges in the explored system under the described conditions.

On the basis of obtained results we can proceed to the following conclusions. The experiments demonstrate that total input equalization to the ClFC might be observed with periodic GrC activity patterns. Besides, there are at least some classes of non-periodic signals which yield the same equalization properties as periodic embeddings. Computational experiments with two bursts of activity of granule cells over the period (k=2) show importance of properties of granule cells activity pattern. In fact, in k=2 case the final equalization quality in our experiments was highest for the high-entropy GrC activity patterns.

The reason for that phenomenon might be connected with the general role of complexity in functioning of information systems[7,8,9]. Sequences with high entropy give implementation of more complex information conversion algorithms than sequences with low entropy. In information processing problems (in particular, in coding problems) that is known to be of great importance. Random codes, being high entropy, have high efficiency, while low entropy codes have low information efficiency[10].

The third series of experiments shows that even in case when two ClFCs are dealing with the same periodic signal but the phase of the signal differs for the two ClFCs the patterns of firing of two ClFCs look statistically independent. The same is true when different ClFCs equalize signals of two different frequencies on the same flow of GrC impulses.

As one of the results of our computational experiments we can conclude that the patterns of activity of ClFCs are looking random and independent of each other regardless of whether the signals equalized by different ClFCs are similar or not.

As the observed phenomenae are found in case when no noise is present in the system there is a need to appeal to dynamic chaos to explain the cerebellum module behaviour in our computational experiments as already has been stated in [1]. Chaotic phenomenae explored in our works are different from the phenomenae studied in [11, 12]. In the latter case the chaos emerges as a collective behaviour of many ClFCs tightly connected with electrical synapses (gap junctions) while in our work each individual ClFC module provides the source of its own chaotic dynamics. So results of our experiments demonstrate that the pattern of activity of ClFCs can be explained by the involvement of the ClFC in equalization of the total input to these cells provided with the help of plasticity of GrC to PC synapses controlled by the ClFC excitation. Thus the immediate problems for further studies of the work of cerebellar module should include understanding of the mechanisms of dynamic chaos in this system and also searches for the possible role of gap junction connections between ClFCs as the previous interpretation of their involvement in generation of chaos [11] is doubtful as pointed above.