Introduction

Blasting has been a widely used rock-breaking technique in various fields, particularly in open-pit and underground mining (Monjezi et al., 2013; Wang et al., 2018a, b; Li et al., 2022a; Chen and Zhou, 2023; Hosseini et al., 2023). However, studies revealed that a significant portion of the energy (over 70%) produced by blasting is wasted, while the remaining energy is utilized to break and displace hard rocks (Khandelwal and Singh, 2005; Singh and Singh, 2005; Hosseini et al., 2022a, b). Moreover, blasting also raises environmental concerns, particularly in surface mining (Fig. 1). Among various environmental issues, flyrock stands out as the most hazardous and destructive (Bakhtavar et al., 2017; Hasanipanah et al., 2017; Mahdiyar et al., 2017; Koopialipoor et al., 2019; Nguyen et al., 2019; Murlidhar et al., 2021). Bajpayee et al. (2004) reported that flyrock was the direct cause of at least 40% of fatal accidents and 20% of serious accidents in blasting accidents. Accordingly, it is extremely important to calculate the flyrock distance (FD) to prevent deaths, damage to equipment, and other serious accidents.

Figure 1
figure 1

Negative impacts of blasting in open-pit mines

Full size image

In previous studies (Lundborg et al., 1975; Roth, 1979; Gupta, 1980; Olofsson, 1990; Richards and Moore, 2004; McKenzie, 2009), a variety of empirical formulas were proposed to predict and control FD. Bagchi and Gupta (1990) established an empirical formula between stemming (ST), burden (B) and FD. Little (2007) developed an empirical formula based on the drill hole angle, B, ST, and explosive charge per meter (CPM) to predict FD. Trivedi et al. (2014) also used the ratio of ST to B to establish an empirical equation for estimating FD. Nevertheless, the prediction performance of the empirical formula is not ideal. The most obvious reason is the absence of valid parameters and the simple consideration of the linear and nonlinear relationship between the parameters and the predicted target (Zhou et al., 2020a, b). In addition to empirical formulas, various researchers have attempted to estimate FD using statistical analyses, such as Monte Carlo simulation methods, and simple and multiple regression equations (Rezaei et al., 2011; Ghasemi et al., 2012; Raina et al., 2014; Armaghani et al., 2016; Faradonbeh et al., 2016; Ye et al., 2021). However, the regression and simulation models have obvious shortcomings, namely (a) new data other than the original data can reduce the reliability of the regression model (Marto et al., 2014); and (b) a historical database cannot be used to control/determine input distribution of a simulation model (Little and Blair, 2010). Generally, there are two types of parameters that contribute to estimating FD: controllable and uncontrollable. Controllable parameters, commonly referred to as blast design parameters, include hole diameter (H), B, ST, CPM, powder factor (PF), spacing (S), total charge, hole depth (HD), and delay timing (Rezaei et al., 2011; Trivedi et al., 2015; Rad et al., 2018; Han et al., 2020; Zhou et al., 2020a). These parameters can be adjusted manually and have a direct impact on the generation of flyrock. Figure 2 illustrates several potential conditions and corresponding mechanisms that induce face bursting. Furthermore, if the ratio of ST to H is small and the stemming quality is poor, it may lead to cratering and rifling (Lundborg and Persson, 1975; Ghasemi et al., 2012; Saghatforoush et al., 2016; Hasanipanah et al., 2018a). In contrast, uncontrollable parameters refer to characteristic indices related to the physical properties of a rock mass, such as rock density (RD), blastability index (BI), and block size (BS) (Monjezi et al., 2010, 2012; Hudaverdi & Akyildiz, 2019), geological properties of a rock mass including geological strength index (GSI), rock mass rating (RMR), rock quality designation (RQD), and uniaxial compressive strength (UCS) (Trivedi et al., 2015; Asl et al., 2018), as well as environmental factors like weathering index (WI) (Murlidhar et al., 2021).

Figure 2
figure 2

Three important flyrock generation mechanisms

Full size image

Over the past few years, a broad spectrum of artificial intelligence (AI) algorithms represented by machine learning (ML) models has been developed and employed to forecast FD based on both controllable and uncontrollable parameters (Table 1). In general, a single ML method was usually employed to predict FD, e.g., artificial neural network (ANN) (Monjezi et al., 2010, 2011; Hosseini et al., 2022a, b, c; Wang et al., 2023), least squares–support vector machine (LS–SVM) (Rad et al., 2018), extreme learning machine (ELM) (Lu et al., 2020), support vector regression (SVR) (Armaghani et al., 2020; Guo et al., 2021b), back-propagation neural network (BPNN) (Yari et al., 2016), adaptive neuro-fuzzy inference system (ANFIS) (Armaghani et al., 2016), random forest (RF) (Han et al., 2020; Ye et al., 2021), and deep neural network (DNN) (Guo et al., 2021a). Nonetheless, most single ML models, particularly ANN, SVR, RF, and ANFIS, have low learning rates and easily fall into local optimum (Wang et al., 2004; Moayedi and Armaghani, 2018; Wang et al., 2021b; Li et al., 2022a, b). However, it is extremely time-consuming and difficult to select hyperparameter parameters of a single ML model by manual methods for solving complex problems (Li et al., 2022d). In other words, the hyperparameter selection problem can also be considered as an optimization problem. Recently, the use of metaheuristic algorithms is effective for solving optimization problems (Monjezi et al., 2012; Armaghani et al., 2014; Kumar et al., 2018). Besides, metaheuristic algorithms have been noticed and used to improve the predictive ability of traditional ML models in solving engineering problems, including evolution-based (Majdi and Beiki, 2010; Yagiz et al., 2018; Zhang et al., 2022a), physics-based (Khatibinia and Khosravi, 2014; Liu et al., 2020; Momeni et al., 2021), and swarm-based (Zhou et al., 2021c; Li et al., 2022a, b, 2023; Adnan et al., 2023a, b; Ikram et al., 2023a; Zhou et al., 2023a, b, c, d) methods. Swarm-based optimization methods, such as the grey wolf optimization algorithm (GWO), sparrow search algorithm (SSA), and Harris hawks optimization (HHO), offer the advantage of requiring only a few parameters, namely population and iteration, to be adjusted in order to enhance the optimized performance (Kardani et al., 2021; Li et al., 2021d; Zhou et al., 2021b, c, 2022b, c, 2023c, d). To improve the accuracy of single ML model for predicting FD, researchers have applied various metaheuristic algorithms-based swarm to the hyperparameter optimization of ML models (Hasanipanah et al., 2016, 2018b; Kalaivaani et al., 2020; Murlidhar et al., 2020, 2021; Guo et al., 2021b; Nguyen et al., 2021; Fattahi and Hasanipanah, 2022). However, the performance of metaheuristic algorithms-based swarm is limited by the lack of initial population diversity (Zhou et al., 2021d, 2022d). Meanwhile, the low precision convergence and convergence time of metaheuristic algorithms in the optimization of multi-dimensional complex problems have already become traditional weaknesses (Li et al., 2021c).

Table 1 Reviewed ML models for predicting FD
Full size table

Therefore, the objective of this study was to develop a novel and comprehensive optimization model, which combines multi-strategies (MS) and HHO algorithm to optimize SVR model for predicting FD. The proposed model is named the MSHHO–SVR model. A database was created based on the monitoring of 262 blasting operations from various open-pit mines, where a series of influence parameters related to FD were collected. Three other ML models and an empirical equation were also developed to predict FD and were compared with the HHO–SVR and MSHHO–SVR models. The prediction performance of all models was evaluated using root mean square error (RMSE), mean absolute error (MAE), determination coefficient (R2), and variance accounted for (VAF) in both training and testing phases. Additionally, the Shapley additive explanations (SHAP) method, an emerging additive explanatory method, was employed to calculate the influence of input parameters on FD in the sensitivity analysis.

Methodologies

Support Vector Regression

SVR is a specialized algorithm within the family of support vector machines (SVM) developed by Vapnik (1995) for resolving regression problems. For the SVR algorithm, the structural risk minimization (SRM) is the core of the optimizer algorithm used to obtain the minimum training error (Li et al., 2021b; Zhou et al., 2021c; Zhang et al., 2022b). In other words, the nonlinear regression prediction is also a function fitting problem by using SVR model, which can be described as:

$$f(z) = w\Psi (z) + b$$
(1)

where w represents a weight vector, \(\Psi (z)\) describes a nonlinear mapping between input space and high-dimensional space, b represents a model error also called threshold value. Then, the minimization of w and b can be calculated according to the SRM as:

$$\begin{gathered} {\text{Minimize}}:C\left( {\nu \vartheta + \frac{1}{M}\sum\nolimits_{i = 1}^{M} {(\zeta_{i} ,\zeta_{i}^{*} )} } \right) + \left\| W \right\|^{2} /2 \hfill \\ {\text{Subject to}}\left\{ \begin{gathered} (w\Psi (z_{i} ) + b_{i} ) - s_{i} \le \vartheta + \zeta_{i} ,i = 1,2, \ldots ,M \hfill \\ s_{i} - (w\Psi (z_{i} ) + b_{i} ) \le \vartheta + \zeta ,i = 1,2, \ldots ,M \hfill \\ \zeta_{i}^{*} \ge 0,\vartheta \ge 0,i = 1,2, \ldots ,M \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(2)

Finally, Eq. 1 is rewritten as:

$$f(z) = \sum\nolimits_{j = 1}^{M} {\left( {\delta_{i} - \delta_{i}^{*} } \right)} \kappa \left( {z_{i} ,z_{j} } \right) + b$$
(3)

where C represents a penalty factor for balancing the model smoothness, \(\zeta_{i}\) and \(\zeta_{i}^{*}\) represent the slack parameters, M denotes number of pattern records, \(\left\| W \right\|^{2} /2\) represents the smoothness, \(\vartheta\) is set to default value of 0.1, and \(\kappa \left( {z_{i} ,z_{j} } \right) = \Psi (z_{i} )\Psi (z_{j} )\) indicates the kernel function. In this study, the radial basis function (RBF) was employed as a widely used kernel function to solve the prediction problem. Therefore, C and the kernel parameter (\(\gamma\)) were the main hyperparameters of SVR model in this study.

Harris Hawks Optimization

The HHO algorithm, developed by Heidari et al. (2019), is an emerging metaheuristic optimization algorithm, which is inspired by the unique cooperative hunting activities of Harris’s hawk in nature called “surprise pounce.” For solving the optimization problems, each Harris’s hawk can be considered as a candidate solution, and the best solution is faulty when considered as the prey. The standard HHO is split into two parts named the exploration and the exploitation, as well as different perching and attacking strategies (Fig. 3a).

Figure 3
figure 3

A standard HHO algorithm: (a) all phases; (b) soft besiege with progressive rapid dives; (c) hard besiege with progressive rapid dives

Full size image

Exploration is the beginning of a successful foraging campaign. Harris’s hawks use their dominant eyes to search for and track prey. Especially when prey is highly alert, they wait, observe, and monitor for about 2 h. There are two different perching strategies that can be executed with the same probability or chance, which are expressed mathematically as (Zhou et al., 2021b):

$$X\left( {n + 1} \right) = \left\{ {\begin{array}{*{20}l} {X_{{{\text{rand}}}} (n) - r_{1} \left| {X_{{{\text{rand}}}} (n) - 2r_{2} X\left( n \right)} \right| \,\, q \ge 0.5} \\ {(X_{{{\text{prey}}}} (n) - X_{m} \left( n \right)) - r_{3} (L_{B} + r_{4} (U_{B} - L_{B} )) \,\, q < 0.5} \\ \end{array} } \right.$$
(4)

where \(X\left( n \right)\) and \(X\left( {n + 1} \right)\) denote the positions of hawks in the nth and n + 1th iterations, respectively; \(X_{{{\text{rand}}}} (n)\) and \(X_{{{\text{prey}}}} (n)\) illustrate the positions of the randomly selected hawk and prey in nth iteration, respectively. The parameters q, r1, r2, r3, and r4 represent random numbers varying from 0 to 1 in each iteration. LB and UB delegate the lower and upper boundaries of the internal parameters, respectively. Notably, the mean position of the hawks (\(X_{{\text{m}}} \left( n \right)\)) is expressed as:

$$X_{{\text{m}}} \left( n \right) = \frac{1}{I}\sum\nolimits_{i = 1}^{I} {X_{i} (n)}$$
(5)

where I is the number of Harris’s hawks and \(X_{i} (n)\) illustrates the position of the ith individual hawk in the nth iteration.

After identifying the prey and its location, the hawks can select from a range of attacking strategies based on the available energy. The energy consumption during the attack is mathematically expressed as:

$$E = 2E_{0} \left( {1 - \frac{n}{T}} \right)$$
(6)

where E and E0 represent the escaping energy and initial energy of the prey, respectively; n indicates the current iteration, and the maximum number of iterations is illustrated by T in the HHO algorithm. When E is less than 1, hawks continue to stay in exploration phase to obtain a better prey. In contrast, hawks start to execute different attack strategies to hunt prey in exploitation phase.

In the exploitation phase, hawks can choose the appropriate attacking strategy according to the different escape behaviors and energy surplus of prey. Assuming the prey has an escape chance of prey is Ec, then the chances of successful escape and capture are expressed as \(E_{{\text{c}}} \ge 0.5\) or \(E_{{\text{c}}} < 0.5\). Combining the escaping energy of prey, there are four possible attacking strategies selected by hawks to hunt prey, as written in Eqs. 7, 8, 9, and 10.

No. 1. Soft besiege: this attack strategy is triggered once the prey (e.g., rabbit) has enough escape energy (\(\left| E \right| \ge 0.5\)) but still did not escape out of hawk’s territory (\(E_{c} \ge 0.5\)).

$$\begin{gathered} X\left( {n + 1} \right) = \Delta X(n) - E\left| {JX_{{{\text{prey}}}} (n) - X\left( n \right)} \right| \hfill \\ \Delta X(n) = X_{{{\text{prey}}}} (n) - X\left( n \right) \hfill \\ \end{gathered}$$
(7)

No. 2. Hard besiege: once the escape energy of prey is exhausted (\(\left| E \right| < 0.5\)) but it still does not escape the hawk’s territory (\(E_{{\text{c}}} \ge 0.5\)), hawks initiate the hard besiege strategy to capture the prey.

$$X\left( {n + 1} \right) = X_{{{\text{prey}}}} (n) - E\left| {\Delta X\left( n \right)} \right|$$
(8)

No. 3. Soft besiege with progressive rapid dives (see Fig. 3b): When the prey has enough escape energy (\(\left| E \right| \ge 0.5\)) and can use different deceptive behaviors to escape the hawk’s territory (\(E_{{\text{c}}} < 0.5\)).

$$\begin{gathered} Y = X_{{{\text{prey}}}} (n) - E\left| {JX_{{{\text{prey}}}} (t) - X\left( n \right)} \right| \hfill \\ Z = Y + S \times {\text{LF}}(D) \hfill \\ X\left( {n + 1} \right) = \left\{ {\begin{array}{*{20}c} {Y\;{\text{if}}\;{\text{Fitness}}\left( Y \right) < {\text{Fitness}}\left( {X\left( n \right)} \right)} \\ {Z\;{\text{if}}\;{\text{Fitness}}\left( Z \right) < {\text{Fitness}}\left( {X\left( n \right)} \right)} \\ \end{array} } \right. \hfill \\ \end{gathered}$$
(9)

No. 4. Hard besiege with progressive rapid dives (see Fig. 3c): if the prey has less escape energy (\(\left| E \right| < 0.5\)) while can take different deceptive behaviors to escape the hawk's territory (\(E_{{\text{c}}} < 0.5\)), hawks try to save more moving distance for hunting the prey. This trigger condition of No. 4 strategy is similar to No. 3.

$$\begin{gathered} Y^{*} = X_{{{\text{prey}}}} (n) - E\left| {JX_{{{\text{prey}}}} (t) - X_{{\text{m}}} \left( n \right)} \right| \hfill \\ Z^{*} = Y^{*} + S \times {\text{LF}}(D) \hfill \\ X\left( {n + 1} \right) = \left\{ {\begin{array}{*{20}c} {Y^{*} \;{\text{if}}\;{\text{Fitness}}\left( {Y^{*} } \right) < {\text{Fitness}}\left( {X\left( n \right)} \right)} \\ {Z^{*} \;{\text{if}}\;{\text{Fitness}}\left( {Z^{*} } \right) < {\text{Fitness}}\left( {X\left( n \right)} \right)} \\ \end{array} } \right. \hfill \\ \end{gathered}$$
(10)

where \(\Delta X(n)\) represents the difference of position between prey and hawk in the nth iteration, J represents the intensity of escape movement, which is changed randomly between 0 and 2; D and S express the dimension of searching space and a random vector, respectively; Fitness () represents the fitness evaluation function in iteration; and LF describes the levy flight function, which can be written as:

$${\text{LF}}(x) = 0.01 \times \frac{\mu \times \sigma }{{\left| \upsilon \right|^{{\frac{1}{\beta }}} }},\;\sigma = \left( {\frac{{\Gamma (1 + \beta ) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{\frac{1}{\beta }}}$$
(11)

where \(\mu\) and \(\upsilon\) represent random values in the range of [0, 1], and \(\beta\) represents a constant, which is set to 0.5 by default in the HHO algorithm.

Harris Hawks Optimization with Multi-Strategies

Despite the extensive use of the HHO algorithm in solving various engineering problems by many researchers (Moayedi et al., 2020; Murlidhar et al., 2021; Zhang et al., 2021; Zhou et al., 2021d; Kaveh et al., 2022), it still faces the challenge of low convergence accuracy and premature convergence while dealing with high-dimensional and complex optimization problems. To address these issues, several methods have been proposed to enhance the performance of the HHO algorithm, including chaotic local search (Elgamal et al., 2020), self-adaptive technique (Wang et al., 2021a; Zou and Wang, 2022), hybridizing supplementary algorithms (Fan et al., 2020; Hussain et al., 2021). In any case, the goal of improving HHO is to optimize the initial HHO algorithm’s exploration and exploitation. In this study, three strategies named chaotic mapping, Cauchy mutation, and adaptive weight were used to enhance the performance of the initial HHO algorithm.

Chaotic Mapping

Several studies have shown that chaotic mapping can be used to create a more diverse population by using chaotic sequences (Kohli and Arora, 2018). Among the chaotic mapping functions, logistic mapping is used widely to enrich the diversity of population for improving the performance of metaheuristic algorithms (Hussien and Amin, 2022). Therefore, the initial population of the HHO was generated by using a logistic mapping written as:

$${\text{Log}}^{s + 1} = \kappa {\text{Log}}^{s} (1 - {\text{Log}}^{s} ) \, 0 \le \kappa \le 4$$
(12)

and the novel candidate solution generated can be obtained as:

$$Cs = {\text{TP}} \times (1 - \varepsilon ) + \varepsilon C_{i}^{\prime } , \, i = 1,2, \ldots ,s$$
(13)

where \({\text{Log}}^{s + 1}\) and \({\text{Log}}^{s}\) represent the s + 1 and s order chaotic sequence, respectively; \(\kappa\) represents a constant between 0 and 4; Cs delegates the candidate solution; TP illustrates the target position; \(C^{\prime}\) represents the maps; and \(\varepsilon\) represents a factor related to the iteration, which is calculated as:

$$\varepsilon = \frac{{{\text{Max}}_{{{\text{iteration}}}} - {\text{Cur}}_{{{\text{iteration}}}} + 1}}{{{\text{Max}}_{{{\text{iteration}}}} }}$$
(14)

where \({\text{Max}}_{{{\text{iteration}}}}\) represents the maximum number of iterations, and \({\text{Cur}}_{{{\text{iteration}}}}\) indicates the current iteration.

Cauchy Mutation

The Cauchy distribution function is a simple yet effective method for addressing the problem of metaheuristic algorithms being susceptible to local optima (Yang et al., 2018). The Cauchy variation can augment the diversity of a population in the search space of hawks, thereby improving the global search capability of the original HHO algorithm. The mathematical representation of Cauchy mutation is written as:

$$f\left( x \right) = \frac{1}{{\uppi }}\left( {\frac{1}{{x^{2} + 1}}} \right)$$
(15)

After applying the Cauchy mutation, the search algorithm can explore more global optima, thus:

$$X_{{{\text{best}}}}^{*} = X_{{{\text{best}}}} + X_{{{\text{best}}}} \times {\text{Cauchy}}(0,1)$$
(16)

Adaptive Weight

An adaptive weight method was employed in this study to update the position of prey during the exploitation phase in the HHO algorithm. The adaptive weight factor (wf) has different functions in improving the performance of local optimization, such as a smaller wf can increase the exploitation time and result in a better solution. This process is represented as:

$$w_{{\text{f}}} = \sin \left( {\frac{{{\uppi } \times {\text{Cur}}_{{{\text{iteration}}}} }}{{2{\text{Max}}_{{{\text{iteration}}}} }} + {\uppi }} \right) + 1$$
(17)
$$X_{{{\text{prey}}}}^{*} (t) = w_{{\text{f}}} \times X_{{{\text{prey}}}} (t)$$
(18)

The framework of using the MSHHO-based SVR model to predict FD is shown in Figure 4. Besides, four comparison models were established to compare the predictive performance with the HHO- and MSHHO-based SVR models, including ELM, KELM, BPNN, and empirical models. The principles of these models above were described in detail in literature (Roth, 1979; Huang et al., 2006; McKenzie, 2009; Chen et al., 2016; Yari et al., 2016; Zhang and Goh, 2016; Wang et al., 2017; Elkatatny et al., 2018; Luo et al., 2019; Shariati et al., 2020; Jamei et al., 2021). To learn relationships between the input parameters and FD accurately, the database was divided into two subsets, i.e., training set and test set (70% and 30% of the total data, respectively). Note that all data should be normalized into the range of 0 to 1 or − 1 to 1. The latter was considered in this study. Furthermore, the fitness function built by RMSE was set as the only criterion for evaluating the performance of each hybrid model. The better model with the suitable hyperparameters has lower value of fitness than other models. Finally, all developed models should be evaluated using performance indices or other evaluation approaches like as regression analysis and Taylor diagrams (Zhou et al., 2021c, 2023a, b).

Figure 4
figure 4

Framework of FD prediction

Full size image

Study Site and Dataset

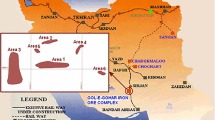
In order to forecast the flyrock phenomenon, six open-pit mines (i.e., Taman Bestari, Putri Wangsa, Trans Crete, Ulu Tiram, Masai, and Ulu Choh) were investigated in Malaysia. Their locations are shown in Figure 5. A big data survey showed that the total amount of blasting in these mines reached 240,000 tons a year, with average of 15 large-scale blasting operations carried out every month (Han et al., 2020). The blasting operation with high charge and high frequency is bound to cause a serious flyrock phenomenon (see Fig. 5). According to Table 1, different controllable and uncontrollable parameters were used as predictors in previous flyrock studies. In this study, we monitored 262 blasts and recorded six individual influence parameters, namely H, HD, BTS, ST, MC, and PF, as input parameters to predict FD. Although uncontrollable parameters of RQD and Rn were also measured, only the range values were recorded and could not be adopted in this study. Figure 6 shows the distribution of the input parameters.

Figure 5
figure 5

Locations of six open-pit mines in Malaysia used for predicting FD

Full size image
Figure 6
figure 6

Distribution pattern of input parameters

Full size image

Figure 7 displays the correlation coefficients and data distributions of the input parameters and output parameters. The purpose of the correlation analysis was to select the appropriate parameters to build the prediction model. Two parameters that are highly correlated with each other are a burden in building a model because their contributions to the target prediction are approximate. However, if the direct correlation coefficient (R) between an input parameter and the predicted target is large, it indicates that the input parameter has a key influence on whether the target can be accurately predicted. As shown in this picture, the values of R between input parameters are low, and each input parameter has a good linear relationship with FD. Therefore, the six parameters selected can be used to build the prediction model.

Figure 7
figure 7

Correlations between input and output parameters

Full size image

Model Evaluation

To evaluate the reliability and accuracy of the proposed model, as well as three other ML models and an empirical formula for predicting FD, it was necessary to apply statistical indices to quantify their predictive performance. RMSE, R2, MAE, and VAF are widely utilized as performance indices in model evaluation, as reported in several published studies (Hasanipanah et al., 2015; Armaghani et al., 2021; Jamei et al. 2021; Murlidhar et al. 2021; Zhou et al. 2021a; Dai et al., 2022; Du et al., 2022; Ikram et al., 2022a, b; Li et al. 2022c; Mikaeil et al. 2022; Chen et al., 2023; Ikram et al., 2023b; Zhou et al. 2023d). These aforementioned indices are defined as follows.

$${\text{RMSE}} = \sqrt {\frac{1}{U}\sum\limits_{u = 1}^{U} {\left( {{\text{FD}}_{o,u} - {\text{FD}}_{p,u} } \right)^{2} } }$$
(19)
$$R^{{2}} = 1 - \frac{{\left[ {\sum\nolimits_{u = 1}^{U} {({\text{FD}}_{o,u} - {\text{FD}}_{p,u} )} } \right]^{2} }}{{\left[ {\sum\nolimits_{u = 1}^{U} {(FD_{o,u} - \overline{{FD_{o} }} )} } \right]^{2} }}$$
(20)
$${\text{MAE}} = \frac{1}{U}\sum\limits_{u = 1}^{U} {\left| {{\text{FD}}_{o,u} - {\text{FD}}_{p,u} } \right|}$$
(21)
$${\text{VAF}} = \left[ {1 - \frac{{{\text{var}} ({\text{FD}}_{o,u} - {\text{FD}}_{p,u} )}}{{{\text{var}} ({\text{FD}}_{o,u} )}}} \right] \times 100\%$$
(22)

where U represents the number of used samples in the training or testing phase; \({\text{FD}}_{o,u}\) and \(\overline{{{\text{FD}}_{o} }}\) indicate observed FD value of the uth sample and mean of observed FD values, respectively; and \({\text{FD}}_{p,u}\) indicates the predicted FD value of the uth sample.

Developing the Models for Predicting FD

In this study, an enhanced HHO algorithm with multi-strategies was employed to select the hyperparameters of SVR model for predicting FD. The other five different models, i.e., HHO–SVR, ELM, KELM, BPNN, and empirical formula, were also considered for comparison with the predictive performance of the proposed MSHHO–SVR model. The procedures for model development and assessment are described in the following sections.

Evaluation Performance of MSHHO Model

As previously mentioned, the logistic mapping of chaotic sequences was used to initialize the population of HHO for increasing swarm diversity, the Cauchy mutation was utilized to expand the search space and improve the global search capability (i.e., exploration) of HHO, and the local optimization capability (i.e., exploitation) was improved by assigning the adaptive weight strategy. Three MSHHO algorithms were generated by using the aforementioned strategies, namely HHO–Logistic mapping (HHO–Log), HHO–Cauchy mutation and adaptive weight (MHHO), and MHHO–Log. To compare the performance of MSHHO algorithms with the initial HHO, six benchmark functions consisting of three unimodal functions and three multimodal functions (Zhou et al., 2022a) were used to obtain the objective function values as shown in Table 2. The performance of different algorithms can be demonstrated by the average (Aver.) and standard deviation (S.D.) values of their objective functions. To balance out the interference of other conditions, the dimension and iteration time were set as 30 and 200 in each algorithm. Besides, the initial population was given three values (25, 50 and 75) to increase the complexity and reliability of the verification. The results of performance evaluation for all algorithms are shown in Table 3. As can be seen in this table, all enhanced HHO algorithms obtained better performance than the unchanged HHO algorithm by resulting in lower values of Aver. and S.D. of objective functions, especially for the MHHO–Log algorithm. It can be noted that each algorithm had the best performance with a population of 50 in different functions. Figures 8 and 9 reflect the dynamic convergence performance of all algorithms based on the unimodal and multimodal benchmark functions during 200 iterations. It is obvious that the MHHO–Log had the lowest values of objective function in F6 when the population was 50. Furthermore, the performance of all MSHHO algorithms was improved to be superior to HHO by adjusting the population, the capability of global search and local optimization.

Table 2 Benchmark functions adopted in this study
Full size table
Table 3 Results of six testing bench functions with different HHO algorithms
Full size table
Figure 8
figure 8

Comparisons between HHO and MSHHO by using the unimodal benchmark functions

Full size image
Figure 9
figure 9

Comparisons between HHO and MSHHO by using the multimodal benchmark functions

Full size image

Development of MSHHO–SVR Model

After verifying the performance of all MSHHO algorithms, a series of hybrid models that combine MSHHO algorithms and SVR was developed to search the optimized hyperparameters for predicting FD. To confirm the optimization performance of MSHHO, the populations were also set equal to 25, 50 and 75 in 200 iterations. Figure 10 displays the iteration curves of all hybrid models with different populations. The lowest fitness value of each hybrid SVR model was obtained in the population of 50. In particular, the MHHO–Log–SVR model with 50 populations had the best performance by means of the lowest value of fitness among all models. The rest of the results of the minimum values of fitness are given in Table 4. Therefore, the MHHO–Log–SVR model was considered the optimal MSHHO model for forecasting FD, namely the MSHHO–SVR model.

Figure 10
figure 10

Development results of HHO–SVR and MSHHO–SVR models

Full size image
Table 4 Statistical analysis of fitness of all hybrid models with different populations
Full size table

Development of ELM Model

The ELM model's development solely depends on the number of neurons present in a single hidden layer (Li et al. 2022a, b). In order to obtain the most accurate ELM model for estimating FD, seven models were constructed using different number of neurons ranging from 20 to 200. The R2 was utilized to evaluate the predictive ability of these models. The results of the seven models during both the training and testing phases are reported in Table 5. The results indicate that increasing the number of neurons in the training phase results in an increased value of R2. However, the third ELM model achieved the highest R2 value (0.8173) using the test data with 80 neurons in a hidden layer. Accordingly, the final ELM model with 80 neurons in a hidden layer was employed to predict FD in this study.

Table 5 Performance evaluation of ELM models with different number of neurons
Full size table

Development of KELM Model

The KELM model eliminates the need for selecting and determining the number of neurons in the hidden layer, instead it relies on kernel function (such as the RBF) parameters to optimize the performance of the ELM model (Huang et al., 2011). Similar to the SVR model, the range of regularization coefficient (K) and \(\gamma\) of KELM model must be defined manually. Zhu et al. (2018) used a range of 2−20–220 for K and \(\gamma\). Baliarsingh et al. (2019) considered the K and \(\gamma\) in the range of 2−8–28 to solve their problem. Therefore, the variation range of hyperparameters of KELM model was considered as 2-2, 2-1, …, 27, 28 to predict FD. The development results of KELM models in the training and testing phases are shown in Figure 11. As can be shown in Figure 11a, K had a positive relationship with any value of \(\gamma\). However, if K was smaller than 21, the R2 increases first and then decreases as \(\gamma\) increases, and the turning point was when \(\gamma\) = 21. However, the highest value of R2 was obtained in the testing phase when K was 24 and \(\gamma\) was 2−1. As can be realized, the best hyperparameters of KELM model were 24 (K) and 2−1 (\(\gamma\)) for predicting FD.

Figure 11
figure 11

Development of KELM model: (a) training phase; (b) testing phase

Full size image

Development of BPNN Model

The BPNN model was devised with the purpose of minimizing predictive errors through the application of back-propagation to regulate the weights and biases of the neural network. This technique has gained widespread usage in addressing a range of engineering problems (Li et al., 2021a). The BPNN is also a typical multilayer neural network with input, hidden, and output layers. To develop a BPNN model, the numbers of hidden and neurons are the major concerns. Although a better performing BPNN model has more hidden layers and neurons, it may result in overfitting and it may increase unnecessary computation time (Yari et al., 2016). Several formulas can be used to calculate the neurons of hidden layers (Han et al., 2018). The values of R2 were used here to describe the BPNN performance in the training and testing phases (Fig. 12). Ultimately, the neural network model with a configuration of 6–5–4–1 (i.e., 6 neurons in the input layer, 5 neurons in the first hidden layer, 4 neurons in the second hidden layer, and 1 neuron in the output layer) achieved the highest R2 value in the testing phase. This model was determined to be the most optimal BPNN model for predicting FD in this study.

Figure 12
figure 12

Performance of the BPNN model: (a) training phase; (b) testing phase

Full size image

Development of Empirical Equation

There are many empirical formulas for predicting FD by using blast design parameters (Lundborg et al., 1975; Roth, 1979; Gupta, 1980; Olofsson, 1990). Nevertheless, the accuracy of empirical models is extremely dependent on input parameters (Richards and Moore, 2004; Little, 2007; Ghasemi et al., 2012; Trivedi et al., 2014; Zhou et al., 2021c). Therefore, a multiple linear regression formula was established, which describes the relationship between the considered six controllable parameters and FD; thus,

$${\text{D}}_{{{\text{flyrock}}}} = 0.39 \times {\text{H}} + 0.44 \times {\text{HD}} + 46.4 \times {\text{BTS}} - 0.27 \times {\text{ST}} + 0.21 \times {\text{MC}} + 121.65 \times {\text{PF}} - 31.6$$
(23)

where Dflyrock represents FD.

Results and Discussion

After obtaining the ideal hyperparameters for all models, each model was run based on the same database and their prediction performances were evaluated using RMSE, R2, MAE, and VAF. Table 6 presents the results of performance comparison of the proposed model and other five models in the training phase. It can be seen intuitively that the performance indices of SVR models optimized by HHO and MSHHO were significantly superior to other models. The best and worst models were the MSHHO–SVR and ELM models, respectively, with RMSEs of 12.2822 and 28.3539, R2 values of 0.9662 and 0.8197, MAEs of 8.5034 and 21.6415, and VAF values of 96.6161 % and 81.965 %, respectively. Following the MSHHO–SVR model, other models, including the HHO–SVR model, KELM model, BPNN model, and empirical equation, exhibited favorable performance based on the aforementioned evaluation metrics for predicting FD.

Table 6 Comparison of the performance of models (in the training phase)
Full size table

The regression diagrams were used to evaluate the performance of the six models in the training phase as shown in Figure 13. The horizontal axis represents the observed FD values, while the predicted values are listed on the vertical axis. Each diagram includes a line at 45°, which is colored differently per model. The points along these lines indicate that the error between the predicted and the observed values is zero. A greater number of points on or close to the 45° line indicate that a model has better predictive accuracy. Meanwhile, the dotted lines with the equation of y = 1.1x and y = 0.9x were set as the prediction boundaries, and those points outside these boundaries indicate poor performance. As can be seen in this picture, the predicted values by MSHHO–SVR model were more concentrated on the 45° line, followed by HHO–SVR model, KELM model, BPNN model, empirical and ELM model. Meanwhile, the MSHHO–SVR model had better performance indices compared to the other models.

Figure 13
figure 13

Regression diagrams of all models using the training set: (a) HHO–SVR; (b) MSHHO–SVR; (c) ELM; (d) KELM; (e) BPNN; (f) Empirical

Full size image

It is worth noting that a model that performed well in the training phase cannot be directly applied to predict FD. In order to verify their efficacy, the proposed model, along with five others, should undergo validation using the test set. It is important to note that the models may not necessarily reproduced the same luminous results in the testing phase. Table 7 displays the results of the four performance indices generated by all the models. The MSHHO–SVR model emerged as the most effective among them, yielding the highest R2 (0.9691) and VAF (96.9178%), as well as the lowest RMSE (9.6685) and MAE (7.4618). Conversely, the empirical model displayed poor prediction accuracy with RMSE of 26.4389, R2 of 0.7689, MAE of 20.4681, and VAF of 76.9583%. Furthermore, the empirical equation also generated predictive values that deviated significantly from the 45° line. Conversely, the MSHHO–SVR model's prediction performance was the most superior (Fig. 14), whereby all its predicted values fell within the prediction boundary and were positioned closer to the 45° line. The HHO–SVR model, followed by the BPNN model and the KELM model, performed less effectively than the MSHHO–SVR model in FD prediction.

Table 7 Comparison of the performance of models (in the testing phase)
Full size table
Figure 14
figure 14

Regression diagrams of all models using the test set: (a) HHO–SVR; (b) MSHHO–SVR; (c) ELM; (d) KELM; (e) BPNN; (f) Empirical

Full size image

Figure 15 presents graphical Taylor diagrams that comprehensively compare the predictive performances of all models in both the training and testing phases. In the Taylor diagrams, the RMSE and R of observed value were set by default to 0 and 1, respectively. Then, the positions of all models can be determined according to the values of S.D., RMSE, and R of the respective prediction results. Accordingly, the best model has less deviations from the observed values compared to the other models. As can be seen in these diagrams, the MSHHO–SVR model was certainly closer to the observed values in both the training and testing phases, indicating that it is the best model for predicting FD.

Figure 15
figure 15

Graphical Taylor diagrams for comparison of all models. The horizontal and vertical axes represent S.D. of predicted values per model, which are drawn by blue circular lines. The green circles represent the RMSEs of different models, and the black lines from the origin (0, 0) to the outermost circle shows the R in the range of 0 to 1

Full size image

Figure 16 illustrates the curves of observed and predicted FDs using the test set, enabling a detailed assessment of the predictive performance of each of the six models. Overall, there is little difference between the predicted and observed curves for all models. However, local observation shows that the values predicted by the empirical models had large errors from the observed values of samples Nos. 33–35, and the errors obtained by ELM, KELM, and BPNN models were almost the same but significantly larger than that obtained by the HHO–SVR model. Compared to the HHO–SVR model, there was little error between the predicted and observed values of samples Nos. 20–30 based on the MSHHO–SVR model, which means that the MSHHO–SVR model was more suitable for predicting FD than of the other models based on prediction accuracy.

Figure 16
figure 16

Curves for predicting FD in the testing phase by all models

Full size image

In order to further compare prediction performance between the HHO–SVR and MSHHO–SVR models, the relative deviation was defined to measure the difference in prediction performance of the proposed models in the training and testing phases. If the relative deviation is greater than 10% or less than − 10%, the prediction is considered wrong. According to the obtained results (Fig. 17), the relative deviation of the MSHHO–SVR model was more concentrated in the range [− 10%, 10%] compared to that of the HHO–SVR model in both of the training and testing phases. This is strong evidence that MSHHO can help SVR do a much better job of predicting FD.

Figure 17
figure 17

Variation in relative deviation for evaluating the performance of HHO–SVR and MSHHO–SVR mode

Full size image

Although six controllable parameters related to the blasting design were considered as input parameters in this study, the importance of each of them still needs to be checked in the MSHHO–SVR model. The SHAP method inspired by cooperative game theories is used widely to calculate parameter importance (Lundberg and Lee, 2017; Chelgani et al., 2021; Zhou et al., 2022b; Qiu & Zhou, 2023). The result of the importance scores obtained using SHAP values is shown in Figure 18. As can be seen in this figure, the order of parameter importance is H > PF > MC > HD > ST > BTS with mean SHAP values of 40.25, 19.98, 10, 3.81, 3.76, and 2.81, respectively. The biggest advantage of the SHAP method is that the influence of features can be reflected per sample, which also shows the positive and negative influence of a parameter. Figure 19 displays the influence of each parameter on FD prediction. In this figure, the overlap points depict the SHAP value distribution per parameter. The higher the positive or negative SHAP values, the greater the impact on FD prediction. The results illustrate that FD significantly increases with H and PF. Meanwhile, all input parameters are positively correlated with FD.

Figure 18
figure 18

Importance scores of input parameters

Full size image
Figure 19
figure 19

Influence results of each parameter on FD prediction

Full size image

In this study, the MSHHO–SVR model has confirmed as the effective model to predict FD with an excellent performance, which is similar with most of published hybrid models for the years 2012–2022 as shown in Table 8. The best model was HHO–MLP proposed by Murlidhar et al. (2021) by means of the highest value of R2 (0.998). However, the difference in the used number of samples in database and considered input parameters is the root cause of the difference in model performance. Based on the same data set considered in this study, Ye et al. (2021) developed genetic programming (GP) and RF models to predict FD with good prediction accuracy of R2 are 0.908 and 0.9046, respectively; Armaghani et al. (2020) proposed a SVR model to estimate FD with high accuracy (R2 = 0.9373); Murlidhar et al. (2020) used biogeography-based optimization (BBO) to optimize the ELM model for predicting FD, with R2 = 0.94. The current study has yielded superior results for predicting FD, as determined by the use of the most effective model, the MSHHO–SVR, which yielded higher R2 values (0.9662 for the training set and 0.9691 for the test set). Therefore, the authors are confident that the proposed MSHHO–SVR model exhibits superior performance compared to the existing models on the same dataset.

Table 8 Comparison of the proposed model with other hybrid models in FD prediction
Full size table

Conclusion

Flyrock has long been a significant safety concern in open-pit mines. This study examined a rich database from six open-pit mines in Malaysia, comprising 262 blasting operations. A novel optimization model that combines HHO and MS was developed to fine-tune the SVR model, named the MSHHO–SVR model. This model was compared for predictive performance with other models, including the HHO–SVR, ELM, KELM, BPNN, and empirical models for predicting FD. The main conclusions of this study are listed as follows.

  1. (1)

    The evaluation results indicated that the MSHHO–SVR model had the highest predictive accuracy among all models, as reflected by its RMSEs of 12.2822 and 9.6685, R2 values of 0.9662 and 0.9691, MAEs of 8.5034 and 7.4618, and VAF values of 96.6161% and 96.9178% in the training and testing phases, respectively.

  2. (2)

    It was verified that multi-strategies can significantly improve the performance of the HHO algorithm for tunning the hyperparameters of the SVR model. In addition, the combination of MSHHO and SVR model had superior prediction accuracy compared to the other models using the same FD database.

  3. (3)

    The result of sensitivity analysis showed that H was the most sensitive parameter and BTS was the least sensitive parameter to FD. The importance rankings of the other input parameters were PF, MC, HD, and ST. Note that all input parameters, especially H and PF, were positively correlated with FD.

Although the proposed novel hybrid model was able to predict FD with satisfactory predictive accuracy, if the range of input parameter values extends beyond those employed in this study, the findings may be subject to bias. Therefore, it is necessary to obtain more data from field investigation and inspection to enrich the database and improve the model generalization. Furthermore, some physics rules between input parameters and the model output can be included in future flyrock studies. In this regard, predicted FD by using previous empirical formulas can be considered as model inputs. This idea might be more interesting for mining and civil engineers because they can learn more about how data are prepared and how input and output parameters are related.