1 Introduction

As a practicable technique to preserve the desired signal (DS) and reject the interferences simultaneously, adaptive beamforming design garners much attention in radar, remote sensing, wireless communication, sonar, and seismology, etc. Reed et al., 1974; Lorenz & Boyed, 2005; Fabrizio et al., 2003). The Capon beamformer (Capon, 1969), as a prominent adaptive method, can hold outstanding performance when the true steering vector of the DS is employed. However, in view of the existence of the DS component in the training data, this beamformer may suffer from self-nulling effect when the steering vector of the DS mismatches its true value (Shahbazpanahi et al., 2003; Tu & Ng, 2014; Zhang et al., 2021a).

To make the Capon beamformer insensitive to steering vector mismatch, several algorithms have been promoted in past decades. For instance, the loading methods in (Li et al., (2003); Mestre & Lagunas, 2006; Du et al., 2010; Zhuang et al., 2016) are known as feasible techniques, including the diagonal loading (DL) approach in (Li et al., 2003) which adds a fixed identity matrix to the sample covariance matrix (SCM). The variable diagonal loading (VDL) approach in (Zhuang et al., 2016) loads a variable matrix that amends the loading factor in accordance with input signal-to-noise ratio (SNR). To proceed, the eigen-subspace beamformer (ESB) in (Feldman & Griffiths, 1994) and modified eigen-subspace beamformer (MESB) in (Huang et al., 2012) project the DS steering vector onto the signal-plus-interference subspace (SIS) and signal subspace (SS), respectively, to mitigate steering vector mismatch. Moreover, along with the fast development on convex optimization theory, a class of robust algorithms based on steering vector constrained optimization appears (Hassanien & Wong, 2008; Khabbazibasmenj & Hassanien, 2012; Lie et al., 2011; Stoica et al., 2003), such as the robust Capon beamformer (RCB) in (Stoica et al., 2003), of which the core concept is to estimate the DS steering vector in a given uncertainty set by maximizing array output power. In (Hassanien & Wong, 2008), the sequential quadratic programming (SQP) algorithm aims to estimate the steering vector of the DS by finding the vector that owns maximum array output power and subjects to some specific constraints. Nonetheless, in terms of that the aforementioned approaches make use of the SCM, which contains significant DS component at strong input SNR case, to finish beamforming, they cannot work well because the exact DS would be wrongly suppressed as an interference.

Recently, a large deal of interference-plus-noise covariance matrix (INCM) reconstruction approaches in (Gu & Leshem, 2012; Huang et al., 2015; Li et al., 2019; Xie et al., 2019; Yang et al., 2017; Yuan & Gan, 2017; Zhu et al., 2020) has been studied to reduce the impact of the DS component in the SCM. The INCM-quadratically constrained quadratically programming (INCM-QCQP) algorithm in (Gu & Leshem, 2012) reconstructs the INCM with the Capon spectrum in the outside region of the DS’s and establishes an QCQP problem to correct the DS steering vector. In (Yuan & Gan, 2017), a novel subspace- based-INCM (NS-INCM) estimation method suggests to pre-estimate the steering vectors of the interferences with the Capon spectrum in each interference region, then utilizes the ESB to further improve the interference steering vectors. In addition, the middle sub-array-INCM reconstruction (MSA-INCM) algorithm in (Li et al., 2019) proposes to determine a selection matrix to convert the training samples with mutual coupling into the middle sub-array training data without mutual coupling, then combines the similar idea in the INCM-QCQP to estimate the INCM. Unfortunately, since the aforesaid INCM reconstruction algorithms always need to act Capon spectrum integral or interference steering vectors optimization with the help of prior information about the interference regions or directions, they are not only computationally inefficient in the situation of multiple interferences but also significantly vulnerable to the imprecise information of the interferences.

Lately, a steering vector of the DS and INCM alternative and iterative estimation robust beamformer (AIERB) is derived in (Yang et al., 2020), of which the steering vector of the DS and INCM are estimated by optimizing the vector nearing the SS as much as possible and separating the DS component from the training data, respectively. Although this algorithm makes great progress in maintaining undistorted response on the DS without reducing anti-interference capability, it cannot be applied at low input SNR case in terms of the subspace swap effect. Additionally, this beamformer needs a lot of iterative processes to guarantee that the estimated DS steering vector and INCM can converge optimal values.

In this paper, a DS steering vector optimization problem with subspace-based constrains is provided to tackle steering vector mismatch. The basic principle of the proposed optimization problem is to maximize the array output power as well as force the revised steering vector not approaching the noise subspace (NS) and interference subspace (IS) simultaneously. The NS can be easily acquired by eigen-decomposing the SCM but the IS is tough to be estimated because the training samples involve the DS in general. In such cases, two original INCM reconstruction means, i.e. direct DS matrix removal and indirect DS blocking and matrix transition, are thus developed to get a faithful IS. Up to now, through settling the optimization problem with the NS and IS, the steering vector of the DS is estimated indeed, which follows the beamforming weight vector extractions by means of orthogonal projection (OP) criterion (Subbaram & Abend, 1993). Unlike the AIERB, the devised approaches are free of iterative procedures, and able to provide satisfactory output SINR at low DS power level case.

This paper contributes to the adaptive beamforming field in the following aspects.

  1. (1)

    A novel steering vector of the DS optimization problem using subspace-based constraints is proposed to mitigate steering vector mismatch, whose core idea is to estimate the DS steering vector by maximizing array output power and compelling the steering vector after correction getting away from the NS and IS. The derived steering vector optimization problem with such constraints is capable of overcoming the steering vector of the DS mismatch at both weak and strong DS scenarios.

  2. (2)

    Two efficient INCM reconstruction ways, which are based upon direct DS matrix removal and indirect DS blocking and matrix transition, respectively, are developed to estimate the IS needed in the DS steering vector optimization. The presented INCM reconstruction means can operate well in the case of direction error and array imperfections without performing Capon spectrum integral or interference steering vectors estimation.

  3. (3)

    Two OP criterion-based weight vector extraction schemes are investigated to improve the robustness of the promoted robust adaptive beamformers. Thus, the designed methods can be used in limited number of snapshots scenario due to the fast convergence of the OP criterion.

  4. (4)

    The computational complexity of the offered algorithms are analyzed, and some important factors on completing the derived beamformers are discussed in detail. Moreover, the output SINR of the proposed and state-of-the-art methods are simulated to validate the effectiveness of ours through typical experiments.

The rest of this paper is organized as follows. The signal model is given in Sect. 2. Conventional optimization algorithms are presented in Sect. 3. In Sect. 4, the proposed algorithms are introduced in detail. Section 5 contains several simulations. Conclusion is drawn in Sect. 6.

2 Signal model

Consider a linear array with M elements, receiving far-field narrowband signals including one DS from \(\theta_{0}\) and J interferences from \(\theta_{i} ,i = 1,2, \cdots ,J\). The training data at the kth snapshot is modeled as:

$$ {\mathbf{x}}(k) = {\mathbf{a}}(\theta_{0} )s_{0} (k) + \sum\limits_{i = 1}^{J} {{\mathbf{a}}(\theta_{i} )s_{i} (k)} + {\mathbf{n}}(k) $$
(1)

where \({\mathbf{a}}(\theta_{i} ),i = 0,1, \cdots ,J\) and \(s_{i} (k),i = 0,1, \cdots ,J\) represent the signal steering vectors and waveforms, respectively, \({\mathbf{n}}(k)\) denotes the Gaussian white noise component. Here the DS component, interference component, and noise component are constantly incoherent at each snapshot. Then, the ideal covariance matrix can be written as:

$$ {\mathbf{R}} = E\{ {\mathbf{x}}(k){\mathbf{x}}^{{\text{H}}} (k)\} = {\mathbf{R}}_{S} + {\mathbf{R}}_{IN} $$
(2)

where \(E\{ \cdot \}\) and \(( \cdot )^{{\text{H}}}\) denote the statistical expectation and conjugate transpose, respectively, \({\mathbf{R}}_{S} = \sigma_{0}^{2} {\mathbf{a}}(\theta_{0} ){\mathbf{a}}^{{\text{H}}} (\theta_{0} )\) and \({\mathbf{R}}_{IN} = \sum\nolimits_{i = 1}^{J} {\sigma_{i}^{2} {\mathbf{a}}(\theta_{i} ){\mathbf{a}}^{{\text{H}}} (\theta_{i} )} + \sigma_{n}^{2} {\mathbf{I}}\) stand for the ideal DS matrix with the DS power \(\sigma_{0}^{2}\) and INCM with the interference powers \(\sigma_{i}^{2} ,i = 1,2, \cdots ,J\), respectively, \(\sigma_{n}^{2}\) and \({\mathbf{I}}\) denote the noise power and identity matrix, respectively.

Aiming at minimizing array output power with maintaining permanent response to the DS, the Capon beamformer can achieve maximum output SINR in the case of actual DS steering vector \({\mathbf{a}}(\theta_{0} )\). The Capon beamformer is always formulated as (Shahbazpanahi et al., 2003):

$$ \begin{gathered} \begin{array}{*{20}c} {\mathop {\min }\limits_{{\mathbf{w}}} } & {{\mathbf{w}}^{{\text{H}}} {\mathbf{Rw}}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {{\text{s.t.}}} & {{\mathbf{w}}^{{\text{H}}} {\mathbf{a}}(\theta_{0} ) = 1} \\ \end{array} \hfill \\ \end{gathered} $$
(3)

with the solution \({\mathbf{w}}_{Capon} = {\mathbf{R}}^{ - 1} {\mathbf{a}}(\theta_{0} )/{\mathbf{a}}^{{\text{H}}} (\theta_{0} ){\mathbf{R}}^{ - 1} {\mathbf{a}}(\theta_{0} )\).

Since the ideal covariance matrix \({\mathbf{R}}\) cannot be reached in practical engineering, it is always replaced by the SCM:

$$ {\hat{\mathbf{R}}} = \frac{1}{K}\sum\limits_{k = 1}^{K} {{\mathbf{x}}(k){\mathbf{x}}^{{\text{H}}} (k)} $$
(4)

where K denotes the number of snapshots.

3 Conventional algorithms

As mentioned earlier, if the DS steering vector is not accurate, the performance of the Capon beamformer will severely drop. To combat this issue, Li et al. have created the steering vector of the DS optimization problem as (Stoica et al., 2003):

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{{\mathbf{a}}(\theta_{0} )}} } & {{\mathbf{a}}^{{\text{H}}} (\theta_{0} ){\hat{\mathbf{R}}}^{ - 1} {\mathbf{a}}(\theta_{0} )} \\ {{\text{s.t.}}} & {||{\mathbf{a}}(\theta_{0} ) - {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} \le \varepsilon } \\ \end{array} $$
(5)

where \(\tilde{\theta }_{0}\) and \(\varepsilon\) stand for the presumed direction of the DS and uncertainty set level, respectively, \(|| \cdot ||_{2}\) is the L-2 norm operator. The main weaknesses of this method are that the uncertainty set level is hard to be optimally determined and \({\mathbf{a}}(\theta_{0} )\) may converge to the interference directions.

In view of the shortcomings in (5), Gu et al. have provided to correct the DS steering vector with the following optimization problem (Gu & Leshem, 2012):

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{{\mathbf{e}}_{ \bot } }} } & {({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )^{{\text{H}}} {\mathbf{R}}_{IN}^{ - 1} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )} \\ {{\text{s.t.}}} & {\begin{array}{*{20}c} {({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )^{{\text{H}}} {\mathbf{R}}_{IN} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } ) \le {\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} ){\mathbf{R}}_{IN} {\mathbf{a}}(\tilde{\theta }_{0} )} \\ {{\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} ){\mathbf{e}}_{ \bot } = 0} \\ \end{array} } \\ \end{array} $$
(6)

where \({\mathbf{e}}_{ \bot }\) stands for the mismatch vector orthogonal to \({\mathbf{a}}(\tilde{\theta }_{0} )\). Even though the inequality constraint in (6) can keep the steering vector away from the interference directions, the objective function in (6) is incapable of guaranteeing \({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot }\) converging to the actual DS direction.

On account of the persistent drawbacks in the aforementioned optimization models, Yang et al. have made the DS steering vector estimation model as (Yang et al., 2020):

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{{\mathbf{e}}_{ \bot } }} } & {||{\mathbf{U}}_{N}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} } \\ {{\text{s.t.}}} & {\begin{array}{*{20}c} {||{\mathbf{U}}_{I}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} \le ||{\mathbf{U}}_{I}^{{\text{H}}} {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} } \\ {{\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} ){\mathbf{e}}_{ \bot } = 0} \\ \end{array} } \\ \end{array} $$
(7)

where \({\mathbf{U}}_{N}\) and \({\mathbf{U}}_{I}\) represent the NS and IS, respectively. Apparently, if the DS power level is low, the actual steering vector of the DS cannot be comprised in the orthogonal subspace of \({\mathbf{U}}_{N}\), and thus solving problem (7) will lead to steering vector mismatch growing larger.

4 Proposed algorithm

In this section, a novel steering vector of the DS optimization problem using the NS based and IS based constraints is established firstly. Afterwards, in order to solve the derived optimization problem, two efficient INCM estimation means are introduced in detail. Finally, the weight vectors based upon OP criterion are further studied to improve the robustness.

4.1 Steering vector of the DS optimization

Considering the disadvantages of the listed optimization models (5)-(7), we intend to optimize the steering vector of the DS by seeking the compensated steering vector which has maximum array output power and does not locate in the NS and IS all together.

As we all know, the signal direction can be found in the aid of the following searching function, which is generally termed as the Capon spectrum:

$$ P(\theta ) = \frac{1}{{{\mathbf{a}}^{{\text{H}}} (\theta ){\hat{\mathbf{R}}}^{ - 1} {\mathbf{a}}(\theta )}} $$
(8)

Enlightened by the direction finding schemes based on the Capon spectrum, we can optimize the DS steering vector as below through assuming \({\mathbf{a}}(\theta_{0} ) = {\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot }\):

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{{\mathbf{e}}_{ \bot } }} } & {({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )^{{\text{H}}} {\hat{\mathbf{R}}}^{ - 1} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )} \\ {{\text{s.t.}}} & {{\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} ){\mathbf{e}}_{ \bot } = 0} \\ \end{array} $$
(9)

Clearly, in light of that the SCM also collects the interference-plus-noise components, solving optimization problem (9) may result in the corrected steering vector of the DS converging to the NS or IS, which will significantly reduce the output performance.

In such a situation, the following two constraints should be imposed to make sure that the corrected DS steering vector can get away from the NS and IS simultaneously:

$$ \begin{array}{*{20}c} {||{\mathbf{U}}_{N}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} \le ||{\mathbf{U}}_{N}^{{\text{H}}} {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} } \\ {||{\mathbf{U}}_{I}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} \le ||{\mathbf{U}}_{I}^{{\text{H}}} {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} } \\ \end{array} $$
(10)

Then, through combining (9) and (10), the steering vector of the DS optimization problem can be reformulated as:

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{{\mathbf{e}}_{ \bot } }} } & {({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )^{{\text{H}}} {\hat{\mathbf{R}}}^{ - 1} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )} \\ {{\text{s.t.}}} & {\begin{array}{*{20}c} {||{\mathbf{U}}_{N}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} \le ||{\mathbf{U}}_{N}^{{\text{H}}} {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} } \\ {||{\mathbf{U}}_{I}^{{\text{H}}} ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )||_{2}^{2} \le ||{\mathbf{U}}_{I}^{{\text{H}}} {\mathbf{a}}(\tilde{\theta }_{0} )||_{2}^{2} } \\ {{\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} ){\mathbf{e}}_{ \bot } = 0} \\ \end{array} } \\ \end{array} $$
(11)

The first constraint in (11) is used to force \({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot }\) not approaching the NS, the second constraint in (11) is added to avoid \({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot }\) getting close to the IS, and the third constraint in (11) is imposed to ensure the orthogonality between \({\mathbf{e}}_{ \bot }\) and \({\mathbf{a}}(\tilde{\theta }_{0} )\). Therefore, if we look for \({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot }\) by minimizing the inverse of array output power, i.e. maximizing the array output power, the maximum output power of the DS will be reached indeed, which can result in the accurate estimation on the DS steering vector. It should be remarked that \({\hat{\mathbf{R}}}^{ - 1}\), \({\mathbf{U}}_{N} {\mathbf{U}}_{N}^{{\text{H}}}\), and \({\mathbf{U}}_{I} {\mathbf{U}}_{I}^{{\text{H}}}\) are positive definite, and therefore (11) is a convex QCQP problem (Gu & Leshem, 2012), whose feasible solution can be easily obtained by employing the open CVX tool box (Grant et al., 2014).

Comparing the proposed steering vector of the DS optimization problem to the aforesaid ones (5)-(7), we note that the main differences between them are as follows. (i) The objective function in (11) is possible to find the steering vectors lying on the complete signal region while after solving the objective function in (6), we can only get the steering vectors locating in the interference region. Also, resolving the objective function in (7) will result in the corrected steering vector moving towards non-DS direction at low DS power level, whereas this consequence cannot happen after solving the objective function in (11). (ii) The IS based constraint in (11) can guarantee the revised steering vector getting away from each steering vector of the interference but the constraint in (5) fails to attain this result. (iii) Using the IS related constraint in (11) rather than the INCM-based constraint in (6) is more effective to avoid the steering vector after compensation nearing the interference directions, which is due to the resolution advantage of the subspace-based direction finding approaches (Yang et al., 2020).

In order to tackle the problem (11), both the NS and IS need to be estimated in advance. As is said in the multiple signal classification (MUSIC) method (Schmidt, 1986), if the SCM inaccuracy from the finite number of snapshots is disregarded, a reliable estimation on the NS can be given as:

$$ {\hat{\mathbf{U}}}_{N} = [{{\varvec{\upeta}}}_{J + 2} ,{{\varvec{\upeta}}}_{J + 3} , \cdots ,{{\varvec{\upeta}}}_{M} ] $$
(12)

where \({{\varvec{\upeta}}}_{i} ,i = J + 2,J + 3, \cdots ,M\) represent the non-principal eigen-vectors of the SCM. It is noteworthy that the signal number J + 1 in this paper is always assumed to be a prior, thus the dimension of the NS or IS is easily to be confirmed.

To continue, the IS is still unknown because the INCM is generally unavailable. In the next two subsections, two INCM reconstruction ways will be presented to resolve the IS.

4.2 INCM Reconstruction

4.2.1 Direct DS matrix removal way

On the basis of the possible DS region \(\Theta\), we can estimate the direction extension-based DS matrix as follows according to its definition:

$$ {\tilde{\mathbf{R}}}_{S} = \sum\limits_{i = - l}^{l} {\tilde{\sigma }_{i}^{{2}} {\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ){\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} + i\Delta )} $$
(13)

where \(\tilde{\sigma }_{i}^{{2}} = 1/{\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ){\hat{\mathbf{R}}}^{ - 1} {\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} + i\Delta ),i = - l, - l + 1, \cdots ,l\) denote the corresponding Capon powers of the steering vectors \({\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ),i = - l, - l + 1, \cdots ,l\), \(l\) and \(\Delta\) denote the direction extension number and extension interval, respectively. Presently, we can directly remove the DS matrix from the SCM to reconstruct the INCM as:

$$ {\tilde{\mathbf{R}}}_{IN} = {\hat{\mathbf{R}}} - {\tilde{\mathbf{R}}}_{S} $$
(14)

The direction extension-based DS matrix \({\tilde{\mathbf{R}}}_{S}\) is apparently an overestimated one (i.e. \({\tilde{\mathbf{R}}}_{S}\) will contain more DS component than \({\mathbf{R}}_{S}\) due to the direction extension processing), so the reconstructed \({\tilde{\mathbf{R}}}_{IN}\) might suffer from rank deficiency. As a result, we need to revise \({\tilde{\mathbf{R}}}_{IN}\) as:

$$ {\tilde{\mathbf{R}}}_{IN,1} = {\tilde{\mathbf{R}}}_{IN} + \psi {\mathbf{I}} $$
(15)

where \(\psi\) denotes a small loading factor. Then, we can realize the estimate of the IS as:

$$ {\tilde{\mathbf{U}}}_{I} = [{\mathbf{u}}_{1} ,{\mathbf{u}}_{2} , \cdots ,{\mathbf{u}}_{J} ] $$
(16)

where \({\mathbf{u}}_{i} ,i = 1,2, \cdots ,J\) denote the principal eigen-vectors corresponding to \({\tilde{\mathbf{R}}}_{IN,1}\).

It is worth emphasizing that the reconstructed INCM in (15) can be viewed as an improved version of that in (Ruan & Lamare, 2014), which cannot completely remove the DS matrix from the SCM when the steering vector mismatch exists. Although the INCM reconstruction way based on direct DS matrix removal is robust to arbitrary-type mismatches, it cannot obtain the accurate INCM because of the remaining cross-term between the DS component and interference component or noise component (Zheng et al., 2019). Even worse, in the situation of strong input SNR, a minor steering vector mismatch may leads to a major INCM imprecision. That is to say, using the direct DS matrix removal way to get the INCM is not a wise choice to offer the IS. To settle these issues, another INCM estimation scheme via indirect DS blocking and matrix transition is devised in the next subsection.

4.2.2 Indirect DS blocking and matrix transition way

The blocking matrix is firstly specified as \({\tilde{\mathbf{R}}}_{SN}^{ - 1}\), where \({\tilde{\mathbf{R}}}_{SN}^{{}}\) represents the direction extension-based DS-plus-noise covariance matrix (DSNCM) and has an expression as:

$$ {\tilde{\mathbf{R}}}_{SN} = \sum\limits_{i = - l}^{l} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{i}^{{2}} {\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ){\mathbf{a}}^{{\text{H}}} (\tilde{\theta }_{0} + i\Delta )} + \tilde{\sigma }_{n}^{2} {\mathbf{I}} $$
(17)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{i}^{{2}} ,i = - l, - l + 1, \cdots ,l\) and \(\tilde{\sigma }_{n}^{2}\) respectively stand for the pre-defined signal powers associated to the steering vectors \({\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ),i = - l, - l + 1, \cdots ,l\) and estimated noise power.

Notably, if both \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{i}^{{2}} \gg \tilde{\sigma }_{n}^{2} ,i = - l, - l + 1, \cdots ,l\) and \(2l + 1 < M\) can be met, \({\tilde{\mathbf{R}}}_{SN}^{ - 1}\) performs the characteristic as (for details of derivation, see Appendix 1):

$$ {\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{a}}(\tilde{\theta }_{0} + i\Delta ) \cong {\mathbf{0}},i = - l, - l + 1, \cdots ,l $$
(18)

with \({\mathbf{0}}\) being the all-zero column vector.

Utilizing \({\tilde{\mathbf{R}}}_{SN}^{ - 1}\) herein to process the training data in (1), we can obtain:

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k) = {\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{a}}(\theta_{0} )s_{0} (k) + \sum\limits_{i = 1}^{J} {{\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{a}}(\theta_{i} )s_{i} (k)} + {\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{n}}(k) $$
(19)

It should be stated that the DS component has been greatly reduced due to (18), then the term \({\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{a}}(\theta_{0} )s_{0} (k)\) can be dropped, which leads to the approximate expression of (19) as:

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k) \cong \sum\limits_{i = 1}^{J} {{\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{a}}(\theta_{i} )s_{i} (k)} + {\tilde{\mathbf{R}}}_{SN}^{ - 1} {\mathbf{n}}(k) $$
(20)

Accordingly, the covariance matrix termed as the quasi INCM, can be calculated as:

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN} = \frac{1}{K}\sum\limits_{k = 1}^{K} {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}(k){\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}^{{\text{H}}} (k)} $$
(21)

The noise component in (20) has been changed, thus the quasi INCM \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN}\) should be revised as:

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN,2} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN} - \tilde{\sigma }_{n}^{2} {\tilde{\mathbf{R}}}_{SN}^{ - 1} ({\tilde{\mathbf{R}}}_{SN}^{ - 1} )^{{\text{H}}} + \tilde{\sigma }_{n}^{2} {\mathbf{I}} $$
(22)

Subsequently, the quasi INCM after revision \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN,2}\) can be eigen-decomposed as:

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN,2} = \sum\limits_{i = 1}^{M} {\lambda_{i} {\mathbf{v}}_{i} {\mathbf{v}}_{i}^{{\text{H}}} } = \sum\limits_{i = 1}^{J} {{\mathbf{v}}_{i} (\lambda_{i} - \tilde{\sigma }_{n}^{2} ){\mathbf{v}}_{i}^{{\text{H}}} } + \tilde{\sigma }_{n}^{2} {\mathbf{I}} $$
(23)

where \(\lambda_{i} ,i = 1,2, \cdots ,M\) stand for the descending eigen-value, and \({\mathbf{v}}_{i} ,i = 1,2, \cdots ,M\) denote the related eigen-vectors. Hence, we can implement the matrix transition to realize the INCM reconstruction as (for details of derivation, see Appendix 2):

$$ {\hat{\mathbf{R}}}_{IN} = \sum\limits_{i = 1}^{J} {{\tilde{\mathbf{R}}}_{SN} {\mathbf{v}}_{i} (\lambda_{i} - \tilde{\sigma }_{n}^{2} ){\mathbf{v}}_{i}^{{\text{H}}} {\tilde{\mathbf{R}}}_{SN}^{{\text{H}}} } + \tilde{\sigma }_{n}^{2} {\mathbf{I}} $$
(24)

After that, we can obtain the estimated IS as:

$$ {\hat{\mathbf{U}}}_{I} = [{\mathbf{q}}_{1} ,{\mathbf{q}}_{2} , \cdots ,{\mathbf{q}}_{J} ] $$
(25)

where \({\mathbf{q}}_{i} ,i = 1,2, \cdots ,J\) denote the primary eigen-vectors corresponding to \({\hat{\mathbf{R}}}_{IN}\).

It is worth noticing that the indirect DS blocking and matrix transition way does better than that in (Yang et al., 2020) in blocking the DS component from the training data, and this is because that the blocking matrix in (Yang et al., 2020) only removes the signal associated to the estimated DS steering vector whereas ours can reduce the signals related to the presumed steering vector of the DS and its proximal ones. Furthermore, the indirect way also differs from the direct way in the following aspects. (i) The estimated steering vector powers in (13) are variable but the pre-defined ones in (17) stay fixed. (ii) The accuracy on the DS matrix in (13) depends on both steering vectors and their related powers while the accuracy on the DSNCM in (17) only relies on the steering vectors. iii) The direct way is just able to eliminate signals from some particular directions \(\{ \theta |\theta = \tilde{\theta }_{i} + i\Delta ,i = - l, - l + 1, \cdots ,l\}\) whereas the indirect way can block signals from the entire region \(\{ \theta |\theta \in [\tilde{\theta }_{0} - l\Delta ,\tilde{\theta }_{0} + l\Delta ]\}\) if the parameters \(l\) and \(\Delta\) are soundly selected.

4.3 Weight vector computation

Substituting the estimated NS \({\hat{\mathbf{U}}}_{N}\) in (9) and IS \({\tilde{\mathbf{U}}}_{I}\) in (16) or \({\hat{\mathbf{U}}}_{I}\) in (25) back into the devised optimization problem (11), the compensated DS steering vector is easily resolved as below:

$$ {\tilde{\mathbf{a}}}(\tilde{\theta }_{0} ) = \frac{{\sqrt M ({\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } )}}{{||{\mathbf{a}}(\tilde{\theta }_{0} ) + {\mathbf{e}}_{ \bot } ||_{2} }} $$
(26)

Currently, the estimations on the DS steering vector and IS are finished, then we can adopt the OP criterion (Subbaram & Abend, 1993) to respectively compute the weight vectors of the proposed beamformers as:

$$ {\mathbf{w}}_{SVO - DDMR} = {\tilde{\mathbf{P}}}_{I}^{ \bot } {\tilde{\mathbf{a}}}(\tilde{\theta }_{0} ) $$
(27)

and

$$ {\mathbf{w}}_{SVO - IDBMT} = {\hat{\mathbf{P}}}_{I}^{ \bot } {\tilde{\mathbf{a}}}(\tilde{\theta }_{0} ) $$
(28)

where \({\tilde{\mathbf{P}}}_{I}^{ \bot } = ({\mathbf{I}} - {\tilde{\mathbf{U}}}_{I} {\tilde{\mathbf{U}}}_{I}^{{\text{H}}} )\) and \({\hat{\mathbf{P}}}_{I}^{ \bot } = ({\mathbf{I}} - {\hat{\mathbf{U}}}_{I} {\hat{\mathbf{U}}}_{I}^{{\text{H}}} )\) are the orthogonal complement projection matrices of \({\tilde{\mathbf{U}}}_{I}\) and \({\hat{\mathbf{U}}}_{I}\), respectively. It should be noted that the normalization factors are ignored in (27) and (28) because they have no effect on increasing the output SINR.

For convenience, the proposed steering vector optimization beamformers using direct DS matrix removal way and indirect DS blocking and matrix transition way are respectively abbreviated as SVO-DDMR and SVO-IDBMT. The overall steps of the SVO-DDMR and SVO-IDBMT are summarized in Algorithm 1 and Algorithm 2, respectively.

Algorithm 1: Steps of the SVO-DDMR

 

1: Calculate the SCM \({\hat{\mathbf{R}}}\) with (4);

 

2: Estimate the NS \({\hat{\mathbf{U}}}_{N}\) with (12);

 

3: Reconstruct the INCM \({\tilde{\mathbf{R}}}_{IN,1}\) with (13)-(15);

 

4: Estimate the IS \({\tilde{\mathbf{U}}}_{I}\) with (16);

 

5: Solve the mismatch vector \({\mathbf{e}}_{ \bot }\) with (11);

 

6: Compensate the DS steering vector \({\tilde{\mathbf{a}}}(\tilde{\theta }_{0} )\) with (26);

 

7: Obtain the weight vector \({\mathbf{w}}_{SVO - DDMR}\) with (27)

 

Algorithm 2: Steps of the SVO-IDBMT

 

1: Calculate the SCM \({\hat{\mathbf{R}}}\) with (4);

 

2: Estimate the NS \({\hat{\mathbf{U}}}_{N}\) with (12);

 

3: Obtain the quasi INCM \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R} }}_{IN,2}\) with (17), (19), (21), and (22);

 

4: Reconstruct the INCM \({\hat{\mathbf{R}}}_{IN}\) with (23) and (24);

 

5: Estimate the IS \({\hat{\mathbf{U}}}_{I}\) with (25);

 

6: Solve the mismatch vector \({\mathbf{e}}_{ \bot }\) with (11);

 

7: Compensate the DS steering vector \({\tilde{\mathbf{a}}}(\tilde{\theta }_{0} )\) with (26);

 

8: Obtain the weight vector \({\mathbf{w}}_{SVO - IBDMT}\) with (28)

 

4.4 Complexity analysis

In this part, we detailed analyze the complexity of the proposed beamforming approaches. The computational complexity of the SVO-DDMR is dependent on calculating the SCM with O(KM2), estimating the NS with O(M3), reconstructing the INCM and estimating the IS with O((2 l + 1)M2) + O(M3), solving the mismatch vector and compensating the DS steering vector with O((M-J-1)M2) + O(JM2) + O(M3) + O(M3.5), and obtaining the weight vector with O(M2). As a result, the overall computational complexity of the SVO-DDMR is O(M3.5) + O(4M3) + O((K + 2 l + 1)M2). The computational complexity of the SVO-IDBMT depends on calculating the SCM with O(KM2), estimating the NS with O(M3), obtaining the quasi INCM, reconstructing the INCM, and estimating the IS with O((2 K + 2 l + 2)M2) + O(3M3), solving the mismatch vector and compensating the DS steering vector with O((M-J-1)M2) + O(JM2) + O(M3) + O(M3.5), and obtaining the weight vector with O(M2). Consequently, the complete computational complexity of the SVO-IDBMT is O(M3.5) + O(6M3) + O((3 K + 2 l + 2-J)M2).

Following the results shown in (Ruan & Lamare, 2014; Yang et al., 2020), and (Zhang et al., 2021b), we have listed the complexity of different algorithms in Table 1, where I1 denotes the number of iterations in the SQP, S1 denotes the number of grids in the DS region, S2 denotes the number of grids in the interference region, N1 represents the dimension of the SS in the DS matrix, N2 represents the the dimension of the IS in the interference matrix, S3 stands for the number of grids in the whole signal region, and I2 stands for the number of iterations in the AIERB.

Table 1 Complexity Of Different Algorithms
Full size table

4.5 Discussion

In the provided SVO-DDMR and SVO-IDBMT, there are four vital factors, i.e. direction extension number \(l\) and extension interval \(\Delta\) in (13) and (17), loading factor \(\psi\) in (15), and signal powers \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{i}^{{2}} ,i = - l, - l + 1, \cdots ,l\) in (17), that will influence the performance. As for the signal powers \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{i}^{{2}} ,i = - l, - l + 1, \cdots ,l\) in (17), they can be directly fixed to \(10^{2} trace({\hat{\mathbf{R}}})\) (Yang et al., 2020). In addition, the direction extension number \(l\) and extension interval \(\Delta\) in (13) should be selected so that any signal involved in the possible DS region \(\Theta\) can be reduced as much as possible, which means that the direction extension interval \(\Delta\) should be small. Likewise, the direction extension number \(l\) and extension interval \(\Delta\) in (17) should be set to meet \([\tilde{\theta }_{0} - l\Delta ,\tilde{\theta }_{0} + l\Delta ] \cong \Theta\) with the premise \(2l + 1 < M\). As regards the loading factor \(\psi\) in (15), it can be set as the mean of tiny eigen-value of the SCM to avoid rank deficiency.

5 Simulation

A uniform linear array (ULA) with M = 8 omnidirectional elements spaced half a wavelength apart is considered, where the wavelength is set to be 0.05 m. One DS from 10° and two interferences from −25° and 45°, respectively impinge on the ULA. The INR of two interferences are equally fixed to 30 dB.

To accomplish the proposed beamformers, the DS region \(\Theta\) is set as \([\tilde{\theta }_{0} - 5^\circ ,\tilde{\theta }_{0} + 5^\circ ]\), and thus the direction extension number \(l\) and extension interval \(\Delta\) in the SVO-DDMR and SVO-IDBMT are fixed to 10 and 1° and 3 and 2°, respectively, to fully cover this region. The noise power and loading factor are both fixed to the mean of the SCM’s minor eigen-values.

The compared approaches include the ESB (Feldman & Griffiths, 1994), RCB (Stoica et al., 2003), SQP (Hassanien & Wong, 2008), INCM-QCQP (Gu & Leshem, 2012), NS-INCM (Yuan & Gan, 2017), and AIERB (Yang et al., 2020), and their simulation parameters are as follows. (i) The dimension of the SIS in the ESB is always given as 3. (ii) The uncertainty set level in the RCB is taken as 0.3 M. (iii) The DS region \(\Theta\) in the SQP is set the same as that in the proposed methods, of which the number of grids S1 is fixed to 100, the interference region is chosen as \([ - 90^\circ ,\tilde{\theta }_{0} - 5^\circ ) \cup (\tilde{\theta }_{0} + 5^\circ ,90^\circ ]\), of which the number of grids S2 is fixed to 500, the dimensions of the SS N1 and IS N2 are 4 and 6, respectively. (iv) The interference region in the INCM-QCQP is same as that in the SQP. (v) The signal region in the NS-INCM is set as \([\tilde{\theta }_{0} - 5^\circ ,\tilde{\theta }_{0} + 5^\circ ] \cup [\tilde{\theta }_{1} - 5^\circ ,\tilde{\theta }_{1} + 5^\circ ] \cup [\tilde{\theta }_{2} - 5^\circ ,\tilde{\theta }_{2} + 5^\circ ]\) with \(\tilde{\theta }_{1}\) and \(\tilde{\theta }_{2}\) being the presumed directions of the interferences, of which the number of grids S3 is fixed to 300. (vi) The DS region \(\Theta\) and pre-defined signal powers in the AIERB are set the same as that in the proposed methods, and the iterative termination tolerance is selected as 0.00001. (vii) The optimal beamformer (OPT) is realized as:

$$ {\mathbf{w}}_{OPT} = \frac{{{\mathbf{R}}_{IN}^{ - 1} {\mathbf{a}}(\theta_{0} )}}{{{\mathbf{a}}^{{\text{H}}} (\theta_{0} ){\mathbf{R}}_{IN}^{ - 1} {\mathbf{a}}(\theta_{0} )}} $$
(29)

In this section, every result is an average of 400 Monte-Carlo runs.

5.1 Steering vector mismatch due to direction error

The first example is performed in the scenario of steering vector mismatch due to direction error, where the direction error is set to obey uniform distribution of \([ - e_{d} ,e_{d} ]\) with \(e_{d}\) being the direction error upper bound.

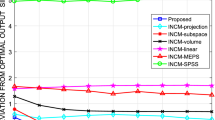
Figure 1 displays the output SINR versus direction error of different algorithms, where the input SNR and number of snapshots are respectively fixed to 20 dB and 50. From Fig. 1, it can be readily found that the SVO-DDMR, SVO-IDBMT, INCM-QCQP, NS-INCM, and AIERB operator better than other methods when the direction error upper bound is large, which can be owning to the effective INCM reconstructions.

Fig. 1
figure 1

Output SINR versus direction error upper bound in the scenario of direction error

Full size image

Further, Fig. 2 shows the output SINR versus input SNR of different algorithms, where the number of snapshots is fixed to 50 and the direction error is subject to uniform distribution of \([ - 3^\circ ,3^\circ ]\). As we can view that due to the subspace swap effect, the output SINR of the AIERB will significantly drop in the case of low DS power level. Other SCM-based methods cannot work well at high input SNR case because of the signal self-nulling effect presence. In contrast, the proposed and other INCM estimation approaches can reach desired output SINR at strong DS case. Although the SVO-DDMR is unable to preserve good performance at input SNR > 25 case, it at least works better than the SCM-based ones.

Fig. 2
figure 2

Output SINR versus input SNR in the scenario of direction error

Full size image

To proceed, Fig. 3 presents the output SINR versus number of snapshots of different algorithms, where the input SNR is fixed to 0 dB and the direction error is subject to uniform distribution of \([ - 3^\circ ,3^\circ ]\). No matter in small or large number of snapshots, the output SINR of the devised and other INCM reconstruction algorithms are relatively close, which indicates that the SVO-DDMR and SVO-IDBMT can be used in limited number of snapshots scenario.

Fig. 3
figure 3

Output SINR versus number of snapshots in the scenario of direction error

Full size image

5.2 Steering vector mismatch due to direction and element position errors

The second example is carried out in the scenario of steering vector mismatch due to direction and element position errors, where the direction error is subject to uniform distribution of \([ - 3^\circ ,3^\circ ]\) and the position error of each element is set to be away from its theoretical one, to obey uniform distribution of \([ - e_{p} ,e_{p} ]\) with \(e_{p}\) being the position error upper bound.

Figure 4 exhibits the output SINR versus position error of different algorithms, where the input SNR and number of snapshots are respectively fixed to 20 dB and 50. From this figure, we can notice that the AIERB and proposed SVO-DDMR and SVO-IDBMT keep high output SINR in the whole range of position error upper bound, whereas other methods are incapable of offering good output SINR because of the steering vector of the DS and INCM estimation error. Further, since the AIERB costs high complexity in iterative estimation, its robustness is undoubtedly superior than that of the the SVO-IDBMT and SVO-DDMR.

Fig. 4
figure 4

Output SINR versus element position error upper bound in the scenario of direction and element position errors

Full size image

Figure 5 also demonstrates the output SINR versus input SNR of different algorithms, where the number of snapshots is fixed to 50 and the position error is subject to uniform distribution of \([ - 0.005,0.005]\). Clearly, in light of the element position error existence, the output SINR of the SCM-based algorithms will rapidly decline once the signal self-nulling effect appears. For the INCM-QCQP and NS-INCM, which employ ideal array manifold information to yield the INCM, cannot adequately suppress the interferences, and thus their performance degrades severally. Instead, since the steering vector of the DS and INCM estimation in the presented methods are training data-based and the training data can reflect the exact array structure, the SVO-DDMR and SVO-IDBMT behave better than other beamformers but the AIERB in the scenario of high DS power level. Even the AIERB outperforms the proposed approaches at input SNR > 20 dB case, it cannot be applied in weak DS situation. Moreover, the output SINR of the SVO-IDBMT is higher than that of the SVO-DDMR when input SNR > 20 dB, and this can be owing to our advanced design of using indirect DS blocking and matrix transition way to estimate the INCM.

Fig. 5
figure 5

Output SINR versus input SNR in the scenario of direction and element position errors

Full size image

To continue, Fig. 6 assesses the output SINR versus number of snapshots of different algorithms, where the input SNR is fixed to 20 dB and the position error is subject to uniform distribution of \([ - 0.005,0.005]\). It can be concluded from Fig. 6 that the output SINR of the proposed beamformers converge faster than that of the ESB, RCB, and SQP and can reach the peaks when the number of snapshots equals to 40. Apparently, the promoted two approaches enjoy enough robustness in the event of finite training samples.

Fig. 6
figure 6

Output SINR versus number of snapshots in the scenario of direction and element position errors

Full size image

5.2.1 Steering vector mismatch due to direction and element gain and phase errors

The third example is executed in the scenario of steering vector mismatch due to direction and element gain and phase errors, where the direction error is subject to uniform distribution of \([ - 3^\circ ,3^\circ ]\) and the gain error and phase error of each element are set to obey uniform distributions of \([ - e_{g} ,e_{g} ]\) and \([ - e_{ph} ,e_{ph} ]\) with \(e_{g}\) and \(e_{ph}\) respectively being the gain error upper bound and phase error upper bound.

Figure 7 tests the output SINR versus gain and phase errors of different algorithms, where the input SNR and number of snapshots are respectively fixed to 20 dB and 50. As we can observe from Fig. 7, following the increases of gain error upper bound and phase error upper bound, the provided SVO-DDMR and SVO-IDBMT constantly outperform other approaches except the AIERB, and this can be owning our accurate DS steering vector and INCM estimation. Although the robustness of our methods would drop a little when the gain and phase errors are large, they are still close to the optimal value.

Fig. 7
figure 7

Output SINR versus gain and phase errors upper bound in the scenario of direction and gain and phase errors

Full size image

Likewise, Fig. 8 verifies the output SINR versus input SNR of different algorithms, where the number of snapshots is fixed to 50 and the gain and phase errors are subject to uniform distributions of \([ - 0.3{\text{dB}},0.3{\text{dB}}]\) and \([ - 3^\circ ,3^\circ ]\). In terms of the existence of gain and phase errors, the output SINR of the INCM-QCQP and NS-INCM are far away from that of the OPT, and this can be ascribed to their poor interference rejection capabilities. As for the ESB, RCB, and SQP, even they can sufficiently suppress the interferences, the self-nulling effect occurred at strong input SNR case restrains their applications. On the contrary, the output SINR of the SVO-DDMR and SVO-IDBMT always remain outstanding levels across the whole range of input SNR. Moreover, there is no doubt that the AIERB is superior to the proposed methods at input SNR > 20 dB, but its high computational load cannot be ignored.

Fig. 8
figure 8

Output SINR versus input SNR in the scenario of direction and gain and phase errors

Full size image

Also, Fig. 9 simulates the output SINR versus number of snapshots of different algorithms, where the input SNR is fixed to 20 dB and the gain and phase errors are subject to uniform distributions of \([ - 0.3{\text{dB}},0.3{\text{dB}}]\) and \([ - 3^\circ ,3^\circ ]\). It is straightforward to find that the derived algorithms and other INCM reconstruction methods have better convergence than the SCM- based methods. Therefore, the SVO-DDMR and SVO-IDBMT can suit for small training size scenario.

Fig. 9
figure 9

Output SINR versus number of snapshots in the scenario of direction and gain and phase errors

Full size image

6 Conclusion

A new DS steering vector optimization problem using subspace-based constraints has been introduced in this paper, whose main purpose is to alleviate steering vector mismatch. In particular, the NS based and IS based constraints are employed to realize DS steering vector optimization via maximizing array output power. To solve the formed optimization problem, two efficient INCM reconstruction schemes are then put forward to estimate the IS with high accuracy. After getting the IS, the steering vector of the DS is precisely estimated, in what follows the OP criterion-based weight vector computations. Representative experiments have demonstrated that the proposed algorithms with high efficiency are robust to steering vector mismatch arisen from direction error and array imperfections at both weak and strong input SNR cases.