1 Introduction

In array signal processing direction-of-arrival (DOA) estimation is an important issue for a number of applications such as radar, sonar and wireless communications (Krim and Viberg 1996). Several methods are proposed for the estimation of unknown source locations and one of the most popular method in this context is the MUSIC (MUltiple SIgnal Classification) algorithm (Schmidt 1986). The effectiveness of the MUSIC algorithm is attributed to the orthogonality of signal and noise spaces. The performance limit of the MUSIC algorithm is to estimate up to \(K\le M-1\) source directions for an M-element sensor array.

While uniform array structures such as uniform linear and circular arrays (Friedlander and Weiss 1991) are mostly used in the literature, nonuniform arrays gain much interest in recent studies. A general form for nonuniform array is random array structures which are considered in Lo (1964), Elbir and Tuncer (2016) and Elbir (2017). While random arrays provide flexibility to deploy the sensor elements, the number of resolvable sources is limited with the same order as for the uniform arrays. Recently, sparse array structures are introduced as a promising structure since they enjoy the increased degrees of freedom (DOF) for the estimation of more sources than sensors, namely \(K > M\) (Pillai et al. 1985; Pal and Vaidyanathan 2010; Abramovich et al. 1998, 1999; Pal and Vaidyanathan 2011). Sparse array structures are mainly useful in radar tracking applications where there are more targets than the number of physical antennas in the environment (Vaidyanathan and Pal 2010). Furthermore, sparse array geometries provide the effective use of antenna elements where the same estimation performance is achieved with less number of antennas. One of the nonuniform array structures is the minimum redundancy arrays (MRAs) which are discussed in Pillai et al. (1985). While MRA provides higher DOF than usual uniform linear arrays (ULAs), there is no closed for expression for the sensor positions of an MRA for a certain number of sensors M (Pal and Vaidyanathan 2010). In Abramovich et al. (1998, 1999), the augmentation of covariance matrices for enhancing DOF is proposed where the resulting covariance matrix is not positive semidefinite for a finite number of snapshots. In Pal and Vaidyanathan (2010), nested array structures are proposed for estimating \(O(M^2)\) sources with O(M) sensors. Since nested arrays have more closely spaced sensors which eventually cause relatively higher mutual coupling, coprime array structures are introduced in Pal and Vaidyanathan (2011), Wang et al. (2017) and Liu and Vaidyanathan (2017) where the array is composed of less number of element pairs that are closely spaced and hence less coupling occurs. Using a coprime array, up to \(K \le MN\) sources can be identified with only \(2M + N -1 \) sensor elements. To increase the DOF of the sparse array, NA with increased DOF is proposed in Huang et al. (2018) where the proposed approach can provide \((P^2-1)/2+P\) DOF where P is the number of antennas in the array. Virtual array interpolation (VAI) technique is proposed in Zhou et al. (2018) to map the array data to fill the holes in the virtual array. While this approach provides the same DOF, the DOA estimation performance is improved due to array interpolation. Note that above array structures are 1-dimensional (1-D) and they cannot be employed for 2-D (azimuth and elevation) DOA estimation.

Apart from 1-D DOA estimation with sparse arrays, 2-D DOA estimation techniques are also proposed with the use of sparse array geometries (Wu et al. 2016; Zheng et al. 2017; Liu et al. 2015). However these works do not explicitly use the sparsity structure of the array to increase the DOF. For instance, the authors in Wu et al. (2016) propose a coprime planar array (CPA) structure where the proposed approach fails to resolve more sources than sensors (See Table 2). In particular, CPA consists of \(P_1\times P_1\) and \(P_2\times P_2\) subarrays where \(P_1\) and \(P_2\) are coprime integers. It is reported that this method can resolve \(K \le \text {min} \{P_1^2,P_2^2\} -1\) sources with \(M_{\text {CPA}}= P_1^2 + P_2^2\) sensor elements. The method in Zheng et al. (2017) generalizes the construction of coprime planar arrays (GCPA) and Zheng et al. (2017) uses \(N_1\times M_1\) and \(N_2 \times M_2\) two subarrays where \(N_1,N_2\) and \(M_1,M_2\) are coprime integer sets. Hence GCPA can resolve \(K \le \text {min}\{N_1M_1,N_2M_2\}-1\) which provides higher DOF than CPA using \(M_{\text {GCPA}} = N_1M_1 + N_2M_2\) sensors. While GCPA provides more DOF, it uses large number of elements. In order avoid the use of large number of antennas, L-shaped array geometries are also used in Liu et al. (2015) where a sparse recovery method is employed. However, the estimated azimuth and elevation angles are not paired, i.e., ambiguous 2-D DOA angles are obtained.

Instead of planar arrays, L-shaped arrays provide much simpler structure and it is widely used for 2-D DOA estimation (Yang et al. 2016; Dong et al. 2016a; Tayem et al. 2016; Dong et al. 2016b, 2017). In Yang et al. (2016), steering matrix estimation is done for the estimation of azimuth and elevation angles separately. In Dong et al. (2016a), L-shaped nested arrays are considered for the same problem. In Tayem et al. (2016), Dong et al. (2016b, 2017), augmented data matrices are constructed for aperture and snapshot extension to utilize the structure of L-shaped arrays. While L-shaped array provides less complexity since it requires 1-D search algorithm, it usually suffers from the angle pairing problem in 2-D DOA estimation scenario. In above studies, this issue is solved with various techniques which are mainly based on the use of cross-covariance matrix.

Above sparse array structures provide limited number of DOF where the theoretical maximum DOF of an M-element array is \( M(M - 1) + 1\) (Pal and Vaidyanathan 2010). Hence there is a need to enhance the DOF that can be achieved from the antenna array through signal processing. The motivation of this study is to reduce the complexity of the parameter estimation and obtain sufficient estimation accuracy with the given array structure. Hence, an L-shaped coprime array (LCA) structure is proposed in this paper for 2-D DOA estimation. The proposed array structure consists of two portions, namely y- and z-axis portions. Each portion is composed of \(2M + N -1\) sensors where M and N are coprime integers. Since the sensor at the origin is commonly placed the total number of sensors is \(M_{\text {LCA}}= 4M + 2N - 3\). The proposed method can resolve \(K \le MN \) sources and it provides much less sensor elements as compared to other 2-D nonuniform arrays such as CPA (Wu et al. 2016) and GCPA (Zheng et al. 2017). In order to estimate the 2-D DOA angles the coprime structure of each portion is utilized and a longer virtual ULA is constructed by vectorization of the covariance matrix of data from each portion. Since the obtained data model is in Vandermonde form, spatial smoothing is employed then the rank-enhanced covariance matrix is obtained (Pal and Vaidyanathan 2011; Liu and Vaidyanathan 2015). The covariance matrices of each portions, y- and z-axis, are used for azimuth and elevation angles estimation respectively. In order to obtain paired 2-D DOA angles, the cross-covariance matrix between the data of each portion is used and automatically paired 2-D DOA estimation is achieved. The main contributions of this paper are as follows

  1. 1.

    A new array geometry, namely L-shaped coprime array, is proposed where LCA requires much less sensor elements as compared to the other planar coprime arrays for 2-D parameter estimation.

  2. 2.

    The proposed method is advantageous in terms of computational complexity where it does not require 2-D search method which is a computational prohibitive task and it can simply be performed using 1-D search algorithms such as the MUSIC algorithm for azimuth and elevation separately.

  3. 3.

    Since the virtual array data of each portion enjoys the Vandermonde structure, root-MUSIC method can also be employed which further accelerates the computation time.

  4. 4.

    The statistical performance of the proposed method is evaluated through several experiments and it is shown that LCA provides less root-mean-square error (RMSE) as compared to the other array geometries.

Fig. 1
figure 1

L-shaped coprime array structure for \(M = 2\), \(N = 5\) and \(d = \lambda /2\). a The real sensor positions. b Co-array of each portion of LCA. c The contagious part of each co-array

Full size image

2 Array signal model

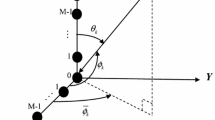
Consider an L-shaped array composed of two portions placed in y- and z-axis as seen in Fig. 1a. Let each portion consists of two subarrays with 2M- and N-element subarrays where \(M < N\) and \(M,N \in {\mathbb {N}}^{+}\) are coprime numbers (Pal and Vaidyanathan 2011). The locations of the 2M sensors are in the set \({\mathbb {S}}_{2M} = \{Nmd: 0\le m \le 2M-1 \}\) and the locations of the N sensors are in the set \({\mathbb {S}}_{N}=\{Mnd : 0\le n \le N-1 \}\) respectively where d is the fundamental element spacing in the array and \(d=\lambda /2\) for narrowband source signals to avoid spatial aliasing (Stoica and Moses 2005). This property yields \(2M+N -1\) sensors in each portion. Hence the total number of sensors in the array is \(M_{\text {LCA}} = 4M + 2N - 3\) where the sensor at the origin is the common element in all subarrays. Assume that there are K source signals impinging on the array from directions \(\{\theta _k,\phi _k\}_{k=1}^K\) where \(\theta _k\) and \(\phi _k\) are being the elevation and the azimuth angle of the kth source respectively. Then the outputs of each portion are given by

$$\begin{aligned} \ \mathbf{y }(t_i)&= \sum _{k=1}^{K} \mathbf a _{\text {Y}}(\phi _k) {{s}}_k(t_i) + \ \mathbf{n _{\text {Y}}}(t_i) \end{aligned}$$
(1)
$$\begin{aligned} \ \mathbf{z }(t_i)&= \sum _{k=1}^{K} \mathbf{a _{\text {Z}}}(\theta _k) {{s}}_k(t_i) + \ \mathbf{n _{\text {Z}}}(t_i) \end{aligned}$$
(2)

where \(i = 1,\ldots ,T\) and T is the number of snapshots and \(\ \mathbf{n _{\text {Y}}}(t_i),\mathbf{n _{\text {Z}}}(t_i) \in {\mathbb {C}}^{(2M+N-1)}\) are temporarily and spatially white noise vectors. \(\{{s}_k(t_i)\}_{k=1,i=1}^{K,T}\) is the set of uncorrelated source signals and \(\mathbf{a _{\text {Y}}}(\phi _k),\mathbf{a _{\text {Z}}}(\theta _k)\) denote the steering vectors corresponding to the kth source and their ith elements are given by

$$\begin{aligned} \left[ \mathbf{a _{\text {Y}}}(\phi _k)\right] _i&= {\text {exp}} \left\{ j\frac{2\pi }{\lambda } y_i \sin (\phi _k) \right\} \end{aligned}$$
(3)
$$\begin{aligned} \left[ \mathbf{a _{\text {Z}}}(\theta _k)\right] _i&= {\text {exp}} \left\{ j\frac{2\pi }{\lambda } z_i \sin (\theta _k)\right\} \end{aligned}$$
(4)

where \([\cdot ]_i\) denotes ith element of the vector quantity. Note that the azimuth and elevation angles are defined different than the conventional definition as in Dong et al. (2016b, 2016a) and a unique transformation between each other can always be performed without loss of generality. \(\lambda \) is the wavelength and \(y_i,z_i \in {\mathbb {S}}\) where \({\mathbb {S}}\) which is defined as

$$\begin{aligned} {\mathbb {S}} = \left\{ {Mnd} : 0\le n \le N-1 \right\} \cup \left\{ {Nmd} : 0\le m \le 2M-1 \right\} \end{aligned}$$

The aim in this work is to estimate DOAs \(\{\theta _k,\phi _k\}_{1\le k \le K} \) of \(K \le MN\) sources by using only \(M_{\text {LCA}} = 4M + 2N-3\) sensors when the sensor positions \(\{y_i,z_i \}_{1\le i \le 2M+N-1}\) are known.

Remark 1

Due to the computation of the noise subspace in the MUSIC algorithm, the proposed method requires the knowledge of the number of sources K. While the estimation process of K is an important issue in many fields of array signal processing (Wax and Kailath 1985; Yang and Xie 2015), in this paper it is assumed that K is known a priori.

3 DOA estimation with coprime arrays

Using the array model in (1) and (2), the covariance matrices for each portion are defined as

$$\begin{aligned} \mathbf{R }_{\text {Y}}&= E \{\mathbf{y }(t) \ \mathbf{y }^H(t)\} = \mathbf{A }_{\text {Y}} \mathbf{R }_{\text {S}} \mathbf{A }_{\text {Y}}^H + \sigma _n^2 \mathbf{I } \end{aligned}$$
(5)
$$\begin{aligned} \mathbf{R }_{\text {Z}}&= E \{\mathbf{z }(t) \ \mathbf{z }^H(t)\} = \mathbf{A }_{\text {Z}} \mathbf{R }_{\text {S}} \mathbf{A }_{\text {Z}}^H + \sigma _n^2 \mathbf{I } \end{aligned}$$
(6)

where \(\mathbf A _{\text {Y}}\) and \(\mathbf A _{\text {Z}}\) are \((2M+N-1) \times K\) steering matrices whose kth columns are \(\mathbf a _{\text {Y}}(\phi _k)\) and \(\mathbf a _{\text {Z}}(\theta _k)\) respectively. \(\mathbf R _{\text {S}} = \text {diag}\{\sigma _1^2,\ldots ,\sigma _K^2\}\) is \(K \times K\) signal correlation matrix, \(\mathbf I \) is the identity matrix and \(\sigma _n^2\) is the noise variance.

Due to the structure of coprime arrays, a longer virtual array can be constructed by taking advantage of the second order statistics \(\mathbf R _{\text {Y}}\) and \(\mathbf R _{\text {Z}}\). While the real array includes the lags given in the set \({\mathbb {S}}\), the elements of \(\mathbf R _{\text {Y}}\) and \(\mathbf R _{\text {Z}}\) can provide a larger positions set whose elements constitute the difference co-array \({\mathbb {S}}_{\text {diff}}\) which is defined as the unique terms in the set

$$\begin{aligned} {\mathbb {S}}^2 = \left\{ (Mn -Nm)d : 0\le n \le N-1, 0\le m \le 2M-1 \right\} . \end{aligned}$$

In Fig. 1b, the difference co-array of each portion of the LCA is presented. In order to exploit the co-array structure inherit in the covariance matrices, vectorization is applied to \(\mathbf R _{\text {Y}}\) and \(\mathbf R _{\text {Z}}\) and we get

$$\begin{aligned} \mathbf{{y} }_{{\mathbb {S}}^2}&= \text {vec} \{ \mathbf {R} _{\text {Y}} \} = \mathbf{{A} }_{{\text {Y}}_{{{\mathbb {S}}^2}}} \mathbf {p} + \mathbf{{n} }_{\text {Y}_{{{\mathbb {S}}^2}}} \end{aligned}$$
(7)
$$\begin{aligned} \mathbf{{z} }_{{\mathbb {S}}^2}&= \text {vec} \{ \mathbf {R} _{\text {Z}} \} = \mathbf{{A} }_{{\text {Z}}_{{{\mathbb {S}}^2}}} \mathbf {p} + \mathbf{{n} }_{{\text {Z}}_{{{\mathbb {S}}^2}}} \end{aligned}$$
(8)

where \(\mathbf{{A} }_{{\text {Y}}_{{\mathbb {S}^2}}} = \mathbf{{A} }_{\text {Y}} \circledcirc \mathbf{{A} }_{\text {Y}}\), \(\mathbf{{A} }_{{\text {Z}}_{{\mathbb {S}^2}}} = \mathbf{{A} }_{\text {Z}} \circledcirc \mathbf{{A} }_{\text {Z}}\) and \(\circledcirc \) denotes the Khatri–Rao product (Khatri and Rao 1968; Pal and Vaidyanathan 2011). \(\mathbf {p} = [\sigma _1^2,\ldots , \sigma _K^2]^T\) represents the signal powers and \(\mathbf{{n} }_{\text {Y}_{{\mathbb {S}^2}}} = \mathbf{n }_{\text {Z}_{{\mathbb {S}^2}}} = \text {vec}\{ \sigma _n^2 \mathbf {I} \}\). Now observe that \(\mathbf{{y} }_{{{\mathbb {S}^2}}}\) can be viewed as the output of a virtual array with sensor positions \(\mathbb {S}_{\text {diff}}\) which includes \(2MN+1\) contiguous terms from \(-MN\) to MN as seen in Fig. 1c. Hence a longer virtual ULA can be constructed from the row elements of \(\mathbf{y }_{{{\mathbb {S}^2}}}\), say \(\mathbf{y }_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\), where the virtual array position set for contagious part \({\mathbb {S}_{\text {diff}}^{\text {ULA}}}\) is defined as

$$\begin{aligned} {\mathbb {S}_{\text {diff}}^{\text {ULA}}} = \left\{ nd: -MN\le n \le MN \right\} \end{aligned}$$
(9)

which the set of sensor positions of \((2MN+1)\)-element virtual ULA. Therefore the rows of \(\mathbf{{y} }_{\mathbb {S}^2}\) and \(\mathbf{{z} }_{\mathbb {S}^2}\) corresponding to \({\mathbb {S}_{\text {diff}}^{\text {ULA}}}\) are collected and the following model is obtained, i.e.

$$\begin{aligned} \mathbf{y }_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}= & {} \mathbf{A }_{{\text {Y}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}} \mathbf p + \mathbf{n }_{{\text {Y}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}} \end{aligned}$$
(10)
$$\begin{aligned} \mathbf{z }_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}= & {} \mathbf{A }_{{\text {Z}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}} \mathbf p + \mathbf{n }_{{\text {Z}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}} \end{aligned}$$
(11)

where \( \mathbf{A }_{{\text {Y}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}}, \mathbf{A }_{{\text {Z}}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}} \in \mathbb {C}^{(2MN+1) \times K}\) are the array manifold matrices corresponding to the sensor elements with positions \(y_i,z_i \in {\mathbb {S}_{\text {diff}}^{\text {ULA}}}\). In order to estimate the DOA angles, the MUSIC algorithm can be applied to the covariance matrices of \(\mathbf{y }_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\) and \(\mathbf{z }_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\). Since the resultant covariances will be rank 1, spatial smoothing is required to estimate the DOA angles. In order to obtain a spatially smoothed covariance matrix a rank-enhanced Toeplitz positive semidefinite matrix is constructed (Liu and Vaidyanathan 2015) where the smoothed covariance matrix is obtained from the observations \(\mathbf{y }(t_i)\) and \(\mathbf{z }(t_i)\) directly. Then the smoothed covariance matrix \(\mathbf R _{\text {Y-SS}}\) is obtained as

$$\begin{aligned} \mathbf R _{\text {Y-SS}} = \left( \begin{array}{llll} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _L &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{L-1} &{} \ldots &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{1} \\ \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{L+1} &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{1} &{} \ldots &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{2} \\ \begin{array}{r} \vdots \end{array}&\begin{array}{r} \vdots \end{array}&\ddots&\begin{array}{r} \vdots \end{array}\\ \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{2L-1} &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{2L-2} &{} \ldots &{} \left[ \tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}\right] _{L} \end{array}\right) \end{aligned}$$

where \(L = (|\mathbb {S}_{\text {diff}}^{\text {ULA}}| +1)/2 = MN+1\) and

$$\begin{aligned}{}[\tilde{\mathbf{y }}_{\mathbb {S}_{\text {diff}}^{\text {ULA}}}]_l = \frac{1}{\mathbb {L}(l)} \sum _{n_1,n_2 \in \mathbb {L}(l)}^{} [\tilde{\mathbf{R }}_{\text {Y}}]_{n_1,n_2} \end{aligned}$$
(12)

where \(\tilde{\mathbf{R }}_{\text {Y}} = \frac{1}{T}\sum _{i = 1}^{T} \mathbf y (t_i) \mathbf y ^H(t_i)\) is the sample covariance matrix and \(\mathbb {L}(l)\) is defined as

$$\begin{aligned} \mathbb {L}(l)= \{(n_1,n_2) \in \mathbb {S}^2: n_1 - n_2 = l, l \in \mathbb {S}_{\text {diff}}^{\text {ULA}} \} \end{aligned}$$
(13)

In other words, \(\mathbb {L}(l)\) is set of the pairs \((n_1,n_2)\) that has contribution to the co-array index l. Note that \(\mathbf R _{\text {Y-SS}} \in \mathbb {C}^{(MN+1)\times (MN+1)}\) provides the same DOA estimation performance as compared to the conventional smoothed covariance matrix computed in Pal and Vaidyanathan (2011) for finite snapshot case (Liu and Vaidyanathan 2015). Once \(\mathbf R _{\text {Y-SS}}\) and \(\mathbf R _{\text {Z-SS}}\) are computed they are inserted into the MUSIC algorithm to obtain the MUSIC pseudo-spectra as

$$\begin{aligned} P_{\text {Y}}(\phi )&= \frac{1}{\mathbf{a}_{\text {Y}}^H(\phi ) \mathbf{U}_{{\text {Y}}_n} \mathbf{U}_{{\text {Y}}_n}^H \mathbf{a}_{\text {Y}}(\phi ) } \end{aligned}$$
(14)
$$\begin{aligned} P_{{\text {Z}}}(\theta )&= \frac{1}{\mathbf{a}_{\text {Z}}^H(\theta ) \mathbf{U}_{{\text {Z}}_n} \mathbf{U}_{{\text {Z}}_n}^H \mathbf{a}_{\text {Z}}(\theta ) } \end{aligned}$$
(15)

where \(\mathbf a _{\text {Y}}(\phi )\) and \(\mathbf a _{\text {Z}}(\theta )\) are the steering vectors constructed by using the position sets \(y_i, z_i \in \mathbb {S}_{\text {diff}}^{\text {ULA-SS}}\) where \(\mathbb {S}_{\text {diff}}^{\text {ULA-SS}} = \{nd: 0\le n \le MN \}\). \(\mathbf U _{{\text {Y}}_n}\) and \(\mathbf U _{{\text {Z}}_n}\) are the noise subspace eigenvector matrices of \(\mathbf R _{\text {Y-SS}}\) and \(\mathbf R _{\text {Z-SS}}\) respectively.

Fig. 2
figure 2

The azimuth and elevation estimation performance of LCA with \(M = 4\), \(N=5\), \(M_{\text {LCA}} = 23\). The number of sensors in each portion is \(2M + N-1 = 12\) and number of sources is \(K = 20\), \(\mathrm{SNR} = 0\) dB and the number of snapshots is \(T = 500\). The true locations of the sources are denoted with vertical lines and \({\bar{\phi }} = \sin (\phi )\) and \({\bar{\theta }} = \sin (\theta )\)

Full size image

In Fig. 2, the line spectra for azimuth \(P_{\text {Y}}(\phi )\) and elevation \(P_{{\text {Z}}}(\theta )\) is presented by using \(\mathbf R _{\text {Y-SS}}\) and \(\mathbf R _{\text {Z-SS}}\) in the MUSIC algorithm. While \(P_{\text {Y}}(\phi )\) and \(P_{{\text {Z}}}(\theta )\) provide peaks at true source locations, the estimated azimuth and elevation angles are not paired due to 1-D searches. In order to obtain a paired estimation results, the cross-covariance matrix of two portions of LCA is utilized in the following section for accurate 2-D DOA estimation.

4 2-D paired DOA estimation With LCA

In order to obtain the paired DOA estimates, the cross-covariance of \(\mathbf y (t_i)\) and \(\mathbf z (t_i)\) is computed. In the following we first discuss the estimation of the azimuth angles by using only \(\mathbf y (t_i)\). Then the elevation angles are estimated which are automatically paired with the estimated azimuth angles.

4.1 Azimuth angle estimation

The MUSIC pseudo-spectrum given in (14) is used and the azimuth angle estimates can be obtained from the K highest peaks of \(P_{\text {Y}}(\phi )\). Once the azimuth angles are estimated the estimated array steering matrix \(\hat{\mathbf{A }}_{\text {Y}} \in \mathbb {C}^{(2M+N -1) \times K}\) can be constructed as

$$\begin{aligned} \hat{\mathbf{A }}_{\text {Y}} = [ \mathbf a _{\text {Y}}({\hat{\phi }}_1),\ldots , \mathbf a _{\text {Y}} ({\hat{\phi }}_K)] \end{aligned}$$
(16)

where \(\{{\hat{\phi }}_k\}_{k=1}^K\) is the set of estimated azimuth angles. In the sequel, \(\hat{\mathbf{A }}_{\text {Y}}\) will be used for elevation angle estimation.

4.2 Elevation angle estimation

In order to estimate the elevation angles the cross-covariance matrix is computed as

$$\begin{aligned} \mathbf{R}_{\text {YZ}} = E \{\mathbf{y}(t) \mathbf{z}^H(t) \} = \mathbf{A}_{\text {Y}} \mathbf{R}_{\text {S}} \mathbf{A}_{\text {Z}}^H \end{aligned}$$
(17)

where the noise terms are vanished due to assumption that the noise is spatially white. Note that in practice, sample cross-covariance matrix \(\hat{\mathbf{R }}_{{\text {YZ}}}= \frac{1}{T}\sum _{i=1}^{T} \mathbf y (t_i)\mathbf z ^H(t_i)\) is available and the noise terms are very small. Now our aim is to estimate the steering matrix \(\mathbf A _{\text {Z}}\) whose columns correspond to the elevation angles which are paired with the columns of the estimated steering matrix \(\hat{\mathbf{A }}_{\text {Y}}\).

Remark 2

Since the columns of \(\mathbf{A }_{\text {Y}}\) and \(\mathbf A _{\text {Z}}\) have the same order, this process will yield an automatically paired azimuth and elevation angle estimates.

Hence we solve the following least squares problem, i.e.

$$\begin{aligned} \hat{\mathbf{A }}_{\text {Z}} = \arg \min _\mathbf{A _{\text {Z}}} || \mathbf R _{{\text {YZ}}} - \hat{\mathbf{A }}_{\text {Y}} \mathbf{R }_{\text {S}} \mathbf A _{\text {Z}}^H ||_F^2 \end{aligned}$$
(18)

where the knowledge of \(\mathbf{R }_{\text {S}}\) is required for the computation of \(\mathbf A _{\text {Z}}\). In order to estimate \(\mathbf R _{\text {S}}\) we consider the eigendecomposition of the covariance matrix \(\mathbf R _{{\text {Y}}}\) in (5) as

$$\begin{aligned} \mathbf{R }_{{\text {Y}}} = \mathbf U _{\text {Y}} \varvec{\Lambda } \mathbf U _{\text {Y}}^H \end{aligned}$$
(19)

where \(\mathbf U _{\text {Y}} = [\mathbf U _{{\text {Y}}_s}\text { } \mathbf U _{{\text {Y}}_n} ]\) and \(\mathbf U _{{\text {Y}}_s}\), \(\mathbf U _{{\text {Y}}_n}\) are the signal and noise subspace eigenvector matrices respectively. \(\varvec{\Lambda }\) is a diagonal matrix composed of the eigenvalues of \(\mathbf R _{{\text {Y}}}\). (19) can also be written as

$$\begin{aligned} \mathbf R _{{\text {Y}}} = \mathbf U _{{\text {Y}}_s}\varvec{\Lambda }_s \mathbf U _{{\text {Y}}_s}^H + \mathbf U _{{\text {Y}}_n} \varvec{\Lambda }_n \mathbf U _{{\text {Y}}_n}^H \end{aligned}$$
(20)

where \(\varvec{\Lambda }_s\in \mathbb {C}^{K\times K}\) and \(\varvec{\Lambda }_n\in \mathbb {C}^{(2M+N-1-K)\times ( 2M + N- 1-K)}\) are diagonal matrices composed of the eigenvalues of \(\mathbf R _{{\text {Y}}}\) with respect to signal and noise subspaces respectively. Using (5), (20) and the fact that the columns of \(\mathbf{A }_{{\text {Y}}}\) and \(\mathbf U _{\text {Y}_s}\) span the same space, \(\mathbf R _{\text {S}}\) can be estimated from

$$\begin{aligned} \hat{\mathbf{R }}_{\text {S}} = \hat{\mathbf{A }}_{{\text {Y}}}^{\dagger } \mathbf U _{{\text {Y}}_s} \varvec{\Lambda }_s \mathbf U _{{\text {Y}}_s}^H \left( \hat{\mathbf{A }}_{{\text {Y}}}^H\right) ^{\dagger } \end{aligned}$$
(21)

where \( (\cdot )^{\dagger }\) denotes the Moore-Penrose pseudo-inverse operation. Then the steering matrix \(\mathbf A _{\text {Z}}\) is estimated from (18) by using the following closed form expression, i.e.

$$\begin{aligned} \hat{\mathbf{A }}_{\text {Z}} = \left( \hat{\mathbf{R }}_{\text {S}}^{-1}\left( \hat{\mathbf{A }}_{{\text {Y}}}\right) ^{\dagger }{} \mathbf R _{{\text {YZ}}} \right) ^H. \end{aligned}$$
(22)

Using (21), (22) can be written explicitly as

$$\begin{aligned} \hat{\mathbf{A }}_{\text {Z}} = \left( \left( \hat{\mathbf{A }}_{{\text {Y}}}^{\dagger } \mathbf U _{{\text {Y}}_s} \varvec{\Lambda }_s \mathbf U _{{\text {Y}}_s}^H (\hat{\mathbf{A }}_Y^H)^{\dagger }\right) ^{-1} \hat{\mathbf{A }}_{{\text {Y}}} ^{\dagger }{} \mathbf R _{{\text {YZ}}} \right) ^H. \end{aligned}$$
(23)

Note that the size of the estimated steering matrix \(\hat{\mathbf{A }}_{\text {Z}}\) is \({(2M+N-1)\times K}\) and in underdetermined case we have \((2M+N-1) < K\). While in this case the covariance matrix of \(\hat{\mathbf{A }}_{\text {Z}}\) does not lead to accurate results due to rank-deficiency, we instead use the columns of \(\hat{\mathbf{A }}_{\text {Z}}\) to estimate the elevation angles one by one so that each elevation angle is paired with the corresponding azimuth angle. Hence the elevation angles can be estimated by the MUSIC algorithm using the covariance matrix \(\hat{\mathbf{R }}_{{\text {Z}}_k}\) which is given as

$$\begin{aligned} \hat{\mathbf{R }}_{{\text {Z}}_k}= [\hat{\mathbf{A }}_{\text {Z}}]_{:,k} [\hat{\mathbf{A }}_{\text {Z}}]_{:,k}^H. \end{aligned}$$
(24)

In other words, \(\hat{\mathbf{R }}_{{\text {Z}}_k}\) can be obtained for the kth column of \(\hat{\mathbf{A }}_{\text {Z}}\). Since \(\text {rank}\{ \hat{\mathbf{R }}_{{\text {Z}}_k}\} =1 \), 1-D MUSIC algorithm is used to estimate \(\theta _k\). In particular, \(\theta _k\) is estimated from

$$\begin{aligned} {\hat{\theta }}_k = \arg \max _{\theta } \frac{1}{\mathbf{a}_{\text {Z}}^H(\theta )\mathbf{G}_k\mathbf{G}_k^H \mathbf{a}_{\text {Z}}(\theta )} \end{aligned}$$
(25)

for \(k = 1\ldots ,K\) where \(\mathbf a _{\text {Z}}(\theta ) \in \mathbb {C}^{(2M+N -1)}\) is the steering vector corresponding to the position set \(z_i \in \mathbb {S}\). \(\mathbf G _k\in \mathbb {C}^{(2M+N -1) \times (2M+N -2)}\) is the noise subspace eigenvector matrix of \(\hat{\mathbf{R }}_{{\text {Z}}_k}\).

Remark 3

When there are sources with the same azimuth (elevation) but different elevation (azimuth) angles. The proposed 2-D DOA estimation technique can be applied by first estimating the elevation (azimuth) then pairing them with azimuth (elevation) angles to achieve unambiguous 2-D DOA estimation.

5 Computational complexity

In this section, the complexity of the proposed method is discussed. In order to estimate the azimuth angles 1-D spectral search is required together with the computation of the singular value decomposition (SVD) of \(\mathbf R _{{\text {Y-SS}}}\) to obtain the noise subspace. Hence \(O\left( \left( MN+1\right) ^3 + N_{\phi }\left( MN+1\right) \left( MN+1-K\right) \right) \) is the complexity of azimuth angle estimation where \((MN+1)^3\) is the complexity of SVD and \(N_{\phi }\) is the number of search angles in the grid. In order to estimate the elevation angles, the SVD of \(\hat{\mathbf{R }}_{\text {Z}_k}\) is computed for \(k=1,\ldots ,K\). Hence the complexity order of elevation angle estimation is \(O\left( K\left( MN+1\right) ^3 + KN_{\theta }\left( MN+1\right) MN\right) \) where \(N_{\theta }\) is the number of search angles in the elevation grid. Since the spectral search is much heavier burden than the other operations, it suffices to state the complexity of the proposed method as \(O \left( \left( MN+1\right) \left( N_{\phi }\left( MN+1-K \right) + KN_{\theta }MN\right) \right) \) where we ignore the other terms. In order compare the complexity of the proposed method with GCPA and CPA we note the following. GCPA and CPA uses \(M_1\times N_1\), \(M_2\times N_2\) and \(P_1\times P_1\), \(P_2\times P_2\) arrays respectively which require much higher number of sensors than LCA. Another disadvantage of GCPA and CPA is to use 2-D search algorithms which require \(N_{\phi }N_{\theta }\) grid points to compute the MUSIC pseudo-spectrum. The complexity of the algorithm in Zheng et al. (2017) using GCPA is \(O\left( N_{\phi }N_{\theta }\left( M_1N_1(M_1N_1-K) + M_2N_2(M_2N_2-K) \right) \right) \) which is much higher than the complexity of the proposed method due to 2-D search has complexity of \(N_{\phi }N_{\theta }\) and MN is usually lower than \(M_1N_1+M_2N_2\). The complexity of the method in Wu et al. (2016) for CPA is \(O\left( N_{\phi }N_{\theta }\frac{P_1^4}{P_2^2} + N_{\phi }N_{\theta }\frac{P_2^4}{P_1^2} \right) \) which is also much higher than the complexity of the proposed method. In Table 1, the complexities of the arrays are summarized.

Table 1 Computational complexity comparison
Full size table

6 Numerical simulations

In this section, the performance of the proposed method is evaluated with numerical simulations. We compare the performance of the proposed array geometry in terms of the maximum number of resolvable sources with the same number of antennas. Then we show the DOA estimation performance of competing sparse arrays to demonstrate the superior performance of our LCA geometry. In Table 2, the number of sensors required to resolve K sources is presented where the number of sensor elements are kept minimum for different K values. The performance limits of LCA, CPA and GCPA are \(K \le MN\), \(K \le \text {min} \{P_1^2,P_2^2\} -1\,K \le \text {min}\{N_1M_1,N_2M_2\}-1\) respectively. As it is seen from the table, LCA requires the lowest number of sensors to resolve K sources in all the scenarios considered. Furthermore, as K increases, the efficiency of LCA becomes much significant in terms of the required number of sensors. Since CPA and GCPA has planar structures they require two uniform rectangular arrays, hence they have relatively larger number of sensors as compared to LCA.

In Fig. 3, the line spectrums for azimuth (a) and elevation (b)–(c) are presented for \(K = 12\), SNR=0dB and \(T=500\). As it is seen the proposed method can handle resolving \(K = 12\) sources with using 9 sensor in each portion and \(M_{\text {LCA}} = 4M+2N-3= 17\) for \(M = 3\) and \(N = 4\). Moreover the azimuth and elevation angle estimates are paired after the cross-covariance matrix is used. Note that the other 2-D sensor arrays based on coprime property such as GCPA or CPA cannot work in this scenario. For instance CPA requires \(M_{\text {CPA}}=40\) and GCPA requires \(M_{\text {GCPA}}=30\) sensors respectively to resolve \(K = 12\) sources.

Table 2 Number of sensors required to resolve K sources with different array configurations: LCA, CPA and GCPA. Note that the number of real sensors are given as \(M_{\text {LCA}} = 4M+2N-3\), \(M_{\text {CPA}}= P_1^2 + P_2^2-1\) and \(M_{\text {GCPA}} = N_1M_1 + N_2M_2-1\)
Full size table
Fig. 3
figure 3

Azimuth (a) and elevation (b)–(c) spectrums for LCA with \(M = 3\), \(N = 4\), \(M_{\text {LCA}} = 17\). The number of sensors in each portion is \(2M + N -1 = 9\). The source directions are located equally spaced in the following intervals \(\phi \in [-0.45,0.45]\) and \(\theta \in [-0.45,0.45]\) respectively. The true source locations are denoted with vertical dashed lines. The number of sources is \(K = 12\). \(\mathrm{SNR} =0\) dB and \(T = 500\)

Full size image

In order to explicitly demonstrate the performance of the proposed method to pair the azimuth and elevation angles, another experiment is conducted where the source locations are not selected in increasing order. In this experiment the source locations (in radians) are selected in order as

$$\begin{aligned}&\{\phi _k\}_{k = 1}^K \in \{ 0.0444, -0.2222, -0.0444, -0.4000, \nonumber \\&\quad 0.3111, -0.1333, 0.2222, 0.4000, -0.3111, 0.1333 \}\\&\{\theta _k\}_{k = 1}^K \in \{0.0333, -0.1667, -0.0333, -0.3000, \nonumber \\&\quad 0.2333, -0.1000, 0.1667, 0.3000, -0.2333, 0.1000\}. \end{aligned}$$

Hence there are \(K=10 \) sources. The number of sensors is \(M_{\text {LCA}} = 15\) for \(M = 2\), \(N = 5\). The number of sensors in each portion is \(2M + N -1 = 8\), \(\mathrm{SNR} = 0\) dB and \(T = 500\). The simulation results are presented in Fig. 4. As it is seen, azimuth and elevation angles are paired and accurately estimated. Note that the pairing performance of the proposed method is attributed to the estimation of the steering matrix \(\mathbf A _{\text {Z}}\) by using the estimated azimuth angles. Therefore the estimation accuracy of the azimuth angles constitutes an important step for elevation angle estimation. This is a general issue in all L-shaped array structures since the estimation performance of the azimuth angle affects the accuracy of the elevation angle estimation. This is due to the fact that azimuth and elevation angle estimation problems are coupled (Elbir and Tuncer 2016; Filik and Tuncer 2010).

Fig. 4
figure 4

Azimuth (a) and elevation (b)–(c) spectrums for LCA with \(M = 2\), \(N = 5\), \(M_{\text {VCA}} = 15\). The number of sensors in each portion is \(2M + N -1 = 8\). The number of sources is \(K = 10\), \(\mathrm{SNR} =0\) dB and \(T = 500\). The vertical lines denote the true source locations

Full size image

In Fig. 5, the comparison of the LCA, CPA and GCPA is done for different SNR levels. Note that the RMSE calculation is performed in terms of both azimuth and elevation as

$$\begin{aligned} \text {RMSE}_{\text {DOA}} = \left( {\frac{1}{2JK}\sum _{j = 1}^{J} \sum _{k = 1}^{K } \left( \phi _{k} - {\hat{\phi }}_{k,j} \right) ^2 + \left( \theta _{k} - {\hat{\theta }}_{k,j} \right) ^2 }\right) ^{1/2} \end{aligned}$$

where J is the number of Monte Carlo experiments and \(J=100\) is selected. For fair comparison, the number of sensors of the arrays are selected closely as \(M_{\text {LCA}} = 39\), \(M_{\text {CPA}} = 40\) and \(M_{\text {GCPA}} = 39\). Note that this selection is sufficient to demonstrate the performances. While CPA has one more sensor than GCPA, it still performs poorer due to its lack of array aperture. In this scenario there are \(K=6\) sources and \(T = 500\). As seen from Fig. 5, LCA has superior performance as compared to CPA and GCPA. Another issue that needs to be pointed out is the number of maximum resolvable sources in this scenario. Using these placements of the arrays, GCPA and CPA can resolve up to 17 ( \(\text {min}\{18,22 \}-1\)) and 15 (\(\text {min}\{16,25\}-1\)) sources respectively. However LCA in this scenario can resolve up to 55 (\(MN= 5 \cdot 11\)) sources which is much larger than the limits of other array structures.

Fig. 5
figure 5

The RMSE versus SNR graph for different array structures. The parameters of arrays are as follows: LCA with \(M = 5\), \(N =11\), \(M_{\text {LCA}} = 39\). CPA with \(P_1 =4\), \(P_2 = 5\), \(M_{\text {CPA}} = 40\). GCPA with \(M_1 = 3\), \(N_1=6\), \(M_2 = 2\), \(N_2 = 11\), \(M_{\text {GCPA}} = 39\). The number of sources is \(K = 6\) and \(T = 500\). The azimuth and elevation angles of the sources are located equally spaced in \(\phi \in [-0.3,0.3]\) and \(\theta \in [-0.4,0.4]\) respectively

Full size image

7 Conclusions

In this paper, a new method and an array geometry which is an L-shaped coprime array (LCA), is proposed for 2-D DOA estimation. The major advantage of the proposed approach is to eliminate the requirement of large number of antennas to resolve more sources than sensors. The proposed array structure can resolve up to MN sources while using only \( 2M+N-1\) sensors in each portion. LCA has totally \(4M+2N-3\) real sensor elements which is much less (especially for large values of K) than the other coprime-based array structures such as GCPA and CPA. Another advantage is that the proposed DOA estimation technique provides automatically paired 2-D DOA angles of the sources. The proposed approach has robust performance even when one of the azimuth and elevation angles of the sources are the same. The pairing of the azimuth and elevation angles is performed where the steering matrices are estimated by utilizing the cross-covariance matrix of data of each portion. Since 1-D searches are used, the proposed approach enjoys less computational time as compared to the conventional 2-D grid search techniques. In future work, we reserve to study the performance of 3-D sparse array geometries for DOA estimation problem (Elbir 2017).