Image encryption using sparse coding and compressive sensing

Abstract

An encryption algorithm based on sparse coding and compressive sensing is proposed. Sparse coding is used to find the sparse representation of images as a linear combination of atoms from an overcomplete learned dictionary. The overcomplete dictionary is learned using K-SVD, utilizing non-overlapping patches obtained from a set of images. Compressed sensing is used to sample data at a rate below the Nyquist rate. A Gaussian measurement matrix compressively samples the plain image. As these measurements are linear, chaos based permutation and substitution operations are performed to obtain the cipher image. Bit-level scrambling and block substitution is done to confuse and diffuse the measurements. Simulation results verify the performance of the proposed technique against various statistical attacks.

1 Introduction

Multimedia data communication plays a vital role in ecommerce, navigation and information systems, entertainment, education, military communication and industries. All these applications require fast and secure transmission of the data, which in turn necessitates the use of encryption as well as compression. With the incessant use of multimedia in mobility communication and the ease of accessibility, the security of data is of paramount importance. Security can be achieved by the encryption of data. Chaos has been widely used in the encryption of data because of its inherent properties. Chaotic systems are periodic and highly sensitive.

Several chaos based image encryption schemes have been proposed. Zahmoul et al. (2017) proposed a new chaotic map based on Beta function. The new map was used to generate pseudo random sequences utilized to perform permutation and substitution operations. The experimental results showed that the proposed method is highly secure compared to other chaos based encryption schemes. Xu et al. (2016) proposed a bit-level image encryption algorithm based on piecewise linear chaotic maps. Plain image is converted into two equal sized binary sequences. Then permutation is done at bit-level by interchanging the binary elements of the sequences. In Hanis and Amutha (2019) a modified logistic map based authenticated image encryption scheme is proposed. The modified logistic map is used to construct key matrices, which are then used to encrypt the images.

Encryption provides data security whereas compression of data assist in easy storage and transmission. Compression and encryption can be done separately, or they can be performed simultaneously reducing the computational overhead. Compressive Sensing (CS) (Donoho 2006) is a technique for compressively sampling sparse data. In CS, a sparse signal can be recovered from few linear measurements (Candes and Wakin 2008). Several CS based image compression-encryption schemes are available in literature.

Zhang et al. (2016) showed the relation between CS and symmetric key encryption. The random projection using sensing matrix is associated with encryption and the signal recovery to decryption. The parameters used to generate the measurement matrix acts as the shared secret key between the communicating entities. The robustness of the CS based encryption schemes against brute-force attack, noise attacks, packet loss and shear attacks are demonstrated in Cambareri et al. (2015), Huang and Sakurai (2011) and Orsdemir et al. (2008). Huang et al. (2014) employed a block cipher structure to break the linearity in the CS measurements. They also used a parallel computing environment, which greatly increased the encryption speed. In papers (Chen et al. 2016; Ponuma and Amutha 2018a, b, c; Zhou et al. 2016, 2014a) compressive sensing is employed to obtain joint image compression-encryption. Zhou et al. (2014b) proposed a novel hybrid image compression-encryption scheme using circulant measurement matrix. The seed for the circulant matrix is generated using a logistic map and the chaotic map parameters acts as the shared secret key.

In this paper, a sparse coding and compressive sensing based image encryption technique is proposed. Digital image possess some intrinsic features like bulk data capacity, redundancy of data and strong correlation among pixels, which can be exploited to achieve superior compression. Natural images can be sparsely represented using over complete dictionary (Olshausen and Field 1997). The dictionary can be a fixed dictionary or a learned dictionary. The fixed basis like DCT, wavelets, curvelets are not adaptive. A learned dictionary trained from a set of input images, provides better sparse representation of the image. The dictionary learning can be performed using algorithms like K-SVD (Aharon et al. 2006), MOD (Engan et al. 2007), RLS-DLA (Skretting and Engan 2010) etc. K-SVD is widely used for dictionary learning. In the proposed scheme, the inherent sparsity of the image is represented using a learned basis obtained using non-overlapping patches from a set of images. The sparse coefficients are then subjected to the compressive sensing process. The image recovery is done using Orthogonal Matching Pursuit (OMP) algorithm (Tropp and Gilbert 2007). The remainder of the paper is organized as follows. Section 2 reviews the concepts of CS theory and dictionary learning. The proposed framework for image encryption scheme is provided in Sect. 3. The experimental results and analysis are given in Sect. 4. Section 5 concludes the paper.

2 Methodology

2.1 Compressive sensing

Compressive sensing (Baraniuk 2007) states that a sparse signal can be reconstructed from a set of undersampled data with high probability. For a signal $x\in R^N$, the sparse representation $\alpha$ is given by

$$\begin{aligned} \alpha =\varPsi ^Tx. \end{aligned}$$

(1)

where $\varPsi$ is the basis. The basis can be an orthogonal matrix (discrete cosine transform, discrete wavelet transform etc.) or a learned dictionary. If the signal can be represented as a linear combination of few vectors from the sparsifying basis, then the signal can be recovered successfully. The signal is recovered from linear measurements obtained by using the measurement matrix $\varPhi \in R^{M \times N}$. The linear measurement y is represented as

$$\begin{aligned} y=\theta \alpha \end{aligned}$$

(2)

where $\theta =\varPhi \varPsi$ is the sensing matrix. A s-sparse signal can be reconstructed from M measurements $(M<< N)$, if the sensing matrix $\theta$ satisfies the Restricted Isometry Property (RIP) (Candes 2008). By assuming that x can be expressed in the basis $\varPsi$, $\alpha$ can be estimated by solving the following $L_1$ norm minimization problem.

$$\begin{aligned} min \Vert \alpha \Vert _1 \ \text {subject to} \ y=\theta \alpha \end{aligned}$$

(3)

Iterative greedy algorithms can be used to solve the above convex optimization problem.

2.2 Dictionary learning

For a compressively sensed data to be recovered successfully the signal should be sparse in a domain, i.e. in a dictionary. The dictionary can be a fixed dictionary or a learned dictionary. The dictionary learning algorithm aims to find a dictionary, that sparsely represents the signal. In Olshausen and Field (1997), it is shown that an overcomplete dictionary D containing K prototype signal atoms for columns $\{d_j\}, j=1, 2, \ldots , K$ can be used to represent a signal x as a sparse linear combination of these atoms. The representation of x may be either exact $x= D\alpha$ or approximate $x\approx D\alpha$, satisfying $\Vert x-D\alpha \Vert _2 \le \epsilon$. The vector $\alpha \in R^K$ contains the representation coefficients of the signal x.

In dictionary learning the goal is to find a dictionary D that yields a better sparse representation for a set of images. The K-SVD technique of dictionary learning is used in this paper. This iterative method alternates between a sparse coding stage and a dictionary update stage. The dictionary is learned using the patches $x_i$ extracted from the grayscale image set.¹ Each image of size $H\times W$ is first divided into non-overlapping blocks ($B_i$) of size $\sqrt{N} \times \sqrt{N}$. The blocks are then vectorized to form the training patches of size $N \times 1$. The Dictionary D is first initialized with K randomly extracted patches from the training set based on a threshold (thr) obtained using spatial frequency (SF) of the image blocks. The spatial frequency of the blocks (Bi) is taken as the threshold. In Huang and Jing (2007) the Spatial Frequency is defined as

$$\begin{aligned}&SF=\sqrt{{(RF)}^2+{(CF)}^2} \nonumber \\&RF=\sqrt{\frac{1}{\sqrt{N}\times \sqrt{N}}\mathop {\sum \limits _{j=1}^{\sqrt{N}}\sum \limits _{k=2}^{\sqrt{N}}}[B_i(j, k)-B_i(j, k+1)]^2} \nonumber \\&CF=\sqrt{\frac{1}{\sqrt{N}\times \sqrt{N}}\mathop {\sum \limits _{j=2}^{\sqrt{N}}\sum \limits _{k=1}^{\sqrt{N}}}[B_i(j, k)-B_i(j-1, k)]^2} \end{aligned}$$

(4)

where RF and CF are the row and column frequency respectively. The patches for the initial dictionary are selected as given in Ashwini and Amutha (2018). The patches $(p_i)$ are sorted in ascending order based on spatial frequency and divided into five sets as follows,

$$\begin{aligned} \left\{ \begin{array}{ll} SF(p_i)<\frac{thr}{4},&{}\quad p_i\in Set\ 1 \\ \frac{thr}{4}\le SF(p_i)<\frac{thr}{2},&{}\quad p_i\in Set\ 2\\ \frac{thr}{2}\le SF(p_i)<{thr},&{}\quad p_i\in Set\ 3\\ thr<SF(p_i)<2thr,&{}\quad p_i\in Set\ 4\\ SF(p_i)\ge 2thr, &{}\quad p_i\in Set\ 5 \end{array}\right. \end{aligned}$$

(5)

From the five sets, K patches are selected to initialize the dictionary. The first K/5 and last K/5 patches are selected from the first and second set respectively. From the sets 3, 4 and 5 the first K/10 and last K/10 patches are selected. Using these K selected patches as the atoms of the initial dictionary and K-SVD algorithm, the learned dictionary D is trained. The dictionary is learned using a sparsity parameter $T_1=10$ i.e. the sparsity of each atom in the dictionary is 10. The size of the resulting dictionary is $N \times K$. As both smooth and textured patches are selected uniformly the learned dictionary provides better approximation of the image.

2.3 Measurement matrix

In CS, generally a random measurement matrix provides dimensionality reduction. The measurement matrix construction must ensure the reconstruction of the sparse signal from the reduced measurements. The commonly used measurement matrices are constructed from random variables that follow Gaussian, Bernoulli distribution etc. The measurement matrix can also be structurally random like Hadamard , Circulant etc. In this paper, a measurement matrix constructed using Gaussian random variables is used to obtain compressed measurements. The Gaussian matrix is of size $M \times N$ and matrix elements are zero mean and variance 1/M Gaussian random variables. The whole matrix is used as the key and it is shared between the sender and the receiver using a secured channel. By employing the measurement matrix as the secret key, security is embedded in compressive sensing technique.

Fig. 1

Block diagram of the sparse coding and compressive sensing based encryption

3 The proposed encryption algorithm

The block diagram of the sparse coding and compressive sensing based image encryption scheme is shown in Fig. 1. The encryption is implemented using four keys. The measurement matrix acts as the first key. The other three keys are the parameters of the three logistic maps used for scrambling and substitution operations. The encryption algorithm is as follows:

• 1. The input image of size $H\times W$ is divided into b blocks of size $\sqrt{N}\times \sqrt{N}$. The blocks are non-overlapping. Each block is then vectorized to form a sequence x of size $N\times 1$.

• 2. The sparse code $(\alpha )$ of x is computed using the learned dictionary D and OMP algorithm. The sparsity is set at $\textit{T}=12$. The sparse code $(\alpha )$ of dimension $K\times 1$, sparsely represents x such that

  $$\begin{aligned} x=D\alpha \end{aligned}$$

  (6)

• 3. CS is used to compressively sample $\alpha$ using the Gaussian measurement matrix $\varPhi$. The measurements are of dimension $M\times 1$ and the number of measurements $M = \lfloor Sampling Ratio \times N\rfloor$.

  $$\begin{aligned} y_m=\varPhi \alpha \end{aligned}$$

  (7)

• 4. The measurements for all the b blocks of the image is computed and the measurement vectors are concatenated to form an encrypted image (Cimg) of size $M\times b$.

• 5. The encrypted image (Cimg) is mapped to the interval [0, 255] using the following mapping

  $$\begin{aligned} C_{map}(i, j)=\left\lfloor \frac{C_{img}(i, j)-C_{imgmin}}{C_{imgmax}-C_{imgmin}}\right\rfloor \times 255 \end{aligned}$$

  (8)

• 6. The mapped image is then encrypted using a logistic map by scrambling and substitution operations. The logistic map is generated based on the following equation,

  $$\begin{aligned} t_{l+1}=\mu t_l (1-t_l), t_l \in [0, 1] \end{aligned}$$

  (9)

  The logistic map is used to generate a sequence $(t_l)$ of length $M \times b$ which is then converted into integer sequence in the interval [0, 7].

  $$\begin{aligned} t_l=\lfloor mod(t_l \times 10^3, 8)\rfloor \end{aligned}$$

  (10)

• 7. Each pixel of $C_{map}$ is decomposed into an 8-bits binary number. The binary digits of each pixel are subjected to cyclic right shift operation by using $t_l$ and then converted to integer value. The encrypted image $C_{scr}$ is of size $M \times b$.

  $$\begin{aligned} C_{scr}(i, j)=bitshift(C_{img}(i, j), t_l(i, j)) \end{aligned}$$

  (11)

• 8. The bit scrambled encrypted image is then subjected to a substitution operation. A pseudorandom sequence $(PR_1)$ that is in the interval [0, 255] is generated using the logistic map. The chaotic sequence $(t_2)$ of size $M \times 1$ is converted into an integer sequence as follows:

  $$\begin{aligned} PR_1=mod(t_2\times 10^7, 256) \end{aligned}$$

  (12)

  The substitution operation for each column of $C_{scr}$ results in an encrypted image $\hat{C}$. The substitution operation is as follows,

  $$\begin{aligned} \hat{C}(n)={\left\{ \begin{array}{ll} C_{scr}(n)\oplus PR_1, n= 1 \\ C_{scr}(n)\oplus PR_1 \oplus \hat{C}(n-1), otherwise \end{array}\right. } \end{aligned}$$

  (13)

  where $n = 1, 2, \ldots , b$.

• 9. To further increase the security the encrypted image $\hat{C}$, it is first reshaped to form a cipher image of size $H_1\times W$. Then it is divided into four equal sized blocks, followed by another round of substitution operation as shown in (13) using another random sequence $(PR_2)$ generated using logistic map.

The decryption procedure involves the inverse of the techniques performed in the encryption stage. The ciphered image is decrypted using the parameters of the three logistic maps, $C_{imgmax}$ and $C_{imgmin}$. The original image is recovered using the OMP algorithm using the measurement matrix $\varPhi$.

4 Experimental results and analysis

The proposed scheme is verified using the test images from the USC-SIPI database. The test image cameraman of size $256\times 256$ is shown in Fig. 2a. The learned dictionary is trained as discussed in Sect. 2. The K-SVD algorithm² is used for training. The size of the learned dictionary is $64\times 100$. The measurement matrix is created as given in Sect. 2. The learned dictionary D is used to sparsely represent the test images. The test image is divided into non-overlapping blocks of size $8\times 8$. Each block is rasterized to form a sequence of length $64\times 1$. The block sparsity is set at $T=12$ and the OMP algorithm is used to sparsely represent the image. The sparse coefficients are of size $100\times 1$. The matrix $\varPhi$ then measures the sparse coefficients. The measurements are then scrambled and subjected to a pseudorandom encryption to obtain the cipher image shown in Fig. 2b. The two chaotic sequences are generated with initial conditions $\mu _{10} = 3.99$, $\mu _{20} = 3.96$, $\mu _{30} = 3.65$, $t_{10} = 0.23$ and $t_{20} = 0.18$, $t_{30} = 0.5301$. The encryption scheme was tested with several test images. The sparse coefficients were recovered using the OMP algorithm at the receiver.

Fig. 2

a Original image, b ciphered image, c recovered image

4.1 PSNR and SSIM analysis

The Peak Signal to Noise Ratio (PSNR) and Structural Similarity Index (SSIM) is used to evaluate the reconstruction performance of the proposed scheme. For an image of size $N\times N$ the PSNR is computed using the formula,

$$\begin{aligned} \text {PSNR}=10 \log \frac{255^2}{(1/N^2)\sum \limits _{i=1}^N\sum \limits _{j=1}^N [PI(i, j)-PI^\prime (i, j)]^2 } \end{aligned}$$

(14)

where PI(i, j) is the plain image and $PI^\prime (i, j)$ is the reconstructed image. The SSIM between the original and the recovered image is computed by using the mean ($\mu$), standard deviation ($\sigma$) and cross-covariance ($\sigma _{pp^\prime }$) of both images.

$$\begin{aligned} \text {SSIM}=\frac{(2\mu _p\mu _{p^\prime }+C_1)(2\sigma _{pp^\prime }+C_2)}{(\mu _p^2+\mu _{p^\prime }^2+C_1)(\sigma _p^2+\sigma _{p^\prime }^2+C_2)} \end{aligned}$$

(15)

where $C_1 = 0.01\times (2^8-1)$, $C_2 = 0.01\times (2^8-1)$. For a sampling ratio of 0.5 the PSNR and SSIM of the test images are computed. The test images are of size $256\times 256$. The metrics are compared with the schemes proposed in Hu et al. (2017) and Zhou et al. (2014a). Table 1 indicates that the proposed scheme achieves better reconstruction quality for the test images Lakes and Peppers in comparison with other schemes. A 1 dB increase in PSNR is obtained than that obtained in Hu et al. (2017). The PSNR is approximately same as that of the scheme in Zhou et al. (2014a). The average SSIM is higher than (Hu et al. 2017; Zhou et al. 2014a) by 26.83%, 56.99% respectively.

Table 1 PSNR and SSIM analysis

4.2 Histogram analysis

Image statistics can be used by an intruder to determine useful information from a transmitted image. Histogram represents the distribution of the gray levels in an image. Hence the cipher image histogram should be dissimilar from the histogram of the plain image. Also, the cipher image histogram must be uniform. Figure 3, shows the histogram of the test images and their corresponding cipher. The histogram of the ciphers is relatively uniform, which indicates that the proposed encryption algorithm has the ability to resist statistical attacks. Also, the histogram of the cipher image does not resemble the histogram of the plain image.

Fig. 3

a Cameraman, b Elaine, c house, d peppers, Histogram of e cameraman, f Elaine, g house, h peppers, i encrypted cameraman, j encrypted elaine, k encrypted house, l encrypted peppers

4.3 Correlation coefficient analysis

The adjacent pixels in digital images are redundant and have high degree of correlation. In the proposed scheme the plain image is encrypted as a noise like random image. Therefore, the adjacent pixel correlation in the cipher image must be very less. The correlation coefficient is measured by randomly selecting 2000 adjacent pixels in the horizontal, vertical and diagonal directions. The correlation coefficient is computed as follows,

$$\begin{aligned} r_{xy}=\frac{\text {cov}(p,q)}{\sqrt{S(p) S(q)}} \end{aligned}$$

(16)

where

$$\begin{aligned} \text {cov}(p, q)= & {} \frac{1}{2000}\sum \limits _{i=1}^{2000}[p_i-E(p)][q_i-E(q)]\\ S(p)= & {} \frac{1}{2000}\sum \limits _{i=1}^{2000}[p_i-E(p)]^2, E(p)=\frac{1}{2000}\sum \limits _{i=1}^{2000}p_i \end{aligned}$$

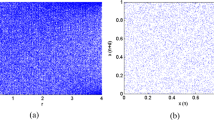
The correlation coefficients of the ciphered image are tabulated in Table 2, from which we know that the correlation between the adjacent pixels is irrelevant. In comparison to the correlation coefficient achieved by the algorithms (Hu et al. 2017; Zhou et al. 2014a) the proposed method achieves minimum correlation for the test image Boat in the horizontal and diagonal directions. The correlation coefficients of other test images are comparable to other schemes. The Fig. 4 shows the comparison of adjacent pixel correlation for the plain image cameraman and its corresponding cipher image.

Table 2 Correlation analysis

Fig. 4

Scatter plot for cameraman image. Adjacent pixels in Plain Image a Horizontal, b vertical, c diagonal direction; Adjacent pixels in Cipher Image d horizontal, e vertical, f diagonal direction

4.4 Entropy analysis

Information entropy can used to determine the randomness of the encrypted image. For a grayscale image to be random the gray levels has to be uniformly distributed. For a noise like ciphered image the information entropy must be nearer to 8. The information entropy is computed using

$$\begin{aligned} H(m)=-{\displaystyle \sum ^{255}_{i=0} Pr(m_i)\log _2 Pr(m_i)} \end{aligned}$$

(17)

where $Pr(m_i)$ is the probability of occurrence of gray level m. The information entropy is presented in Table 3. The average entropy of the proposed scheme is 7.9969 which is better than (Hu et al. 2017; Zhou et al. 2014a) and also closer to the ideal value.

Table 3 Entropy of plain image and cipher image

4.5 UACI and NPCR analysis

An image encryption algorithm must be highly sensitive. The algorithm should generate a completely different cipher image, even for a one-bit pixel change. The Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) are the measures that verify the sensitivity of the encryption algorithm.

$$\begin{aligned} \text {NPCR}= & {} \sum \limits _{i, j}\frac{D(i, j)}{M\times N}\times 100\% \end{aligned}$$

(18)

$$\begin{aligned} \text {UACI}= & {} \frac{1}{M\times N}\frac{\sum \limits _{i, j}|CI_1(i, j)-CI_2(i, j)|}{L}\times 100\% \end{aligned}$$

(19)

$CI_1(i, j)$ and $CI_2(i, j)$ are the two ciphered images and L is the number of gray levels. D(i, j) is determined based on the rule

$$\begin{aligned} D(i. j)={\left\{ \begin{array}{ll} 0, CI_1(i, j)=CI_2(i, j)\\ 1, \text {otherwise} \end{array}\right. } \end{aligned}$$

(20)

The NPCR and UACI values tabulated in Table 4 indicates that the algorithm can resist differential attacks as they are close to the theoretical values 99.61 and 33.46 respectively. As the scheme in Zhou et al. (2014a) does not employ permutation and substitution operations its NPCR and UACI values are less. The average NPCR and UACI of the proposed scheme and scheme in Zhou et al. (2014a) are closer to the theoretical value.

Table 4 NPCR and UACI analysis

4.6 Key space analysis

The Gaussian measurement matrix is used as the $Key_1$ in the encryption process. If the data precision is $10^{15}$ and the matrix size is $M\times N$, the keyspace for $Key_1$ is $(10^{15})^{M\times N}$. The $Key_2$, $Key_3$ and $Key_4$ are the parameters of the three logistic maps i.e. $\mu _1$, $\mu _2$, $\mu _3$, $t_{10}$, $t_{20}$ and $t_{30}$. The key space for $Key_2$, $Key_3$ and $Key_4$ is $(10^{15})^6$. A large keyspace ensures that the proposed scheme resists brute-force attack. The brute-force attack becomes infeasible as the effort required to decipher the key, grows exponentially with increasing key space.

$$\begin{aligned} KeySpace=(10^{15})^{M\times N}\times 10^{90} \end{aligned}$$

(21)

The key space of the proposed scheme is compared with the schemes in Hu et al. (2017) and Zhou et al. (2014a) and it is shown in Table 5. The key space achieved using the proposed scheme is larger and hence greater the security.

Table 5 Key space analysis

4.7 Deviation from uniform histogram

The histogram of the cipher must be uniform i.e. the probability of occurrence of each pixel is uniform. For a cipher image (C) of size $M\times N$ the ideal histogram is mathematically represented as

$$\begin{aligned} Ideal\_Hist(C(i, j))={\left\{ \begin{array}{ll} \frac{M\times N}{256}, 0\le C(i, j)\le 255 \\ 0, \text {otherwise} \end{array}\right. } \end{aligned}$$

(22)

The strength of the algorithm can be verified using the deviation of the cipher image histogram from the ideal histogram. A lower value of $D_H$ represents a better encryption quality. The deviation from ideal histogram is given as:

$$\begin{aligned} D_H=\frac{\sum |Ideal\_Hist(C(i, j))-Hist(C(i, j))|}{M\times N} \end{aligned}$$

(23)

Table 6 compares the deviation of the histogram of the cipher from the ideal uniform histogram. We infer that the deviation is minimal in the proposed scheme, which indicates that the cryptanalysis of the histogram for statistical information by the intruder is difficult. The average DH of the proposed scheme is better than the compared algorithms (Hu et al. 2017; Zhou et al. 2014a) by 26.14% and 27.78% respectively.

Table 6 Deviation from uniform histogram

5 Conclusion

In this paper, an encryption technique based on sparse coding and compressive sensing is proposed. The sparse coding using a learned dictionary provides a better representation of the image. Compressive sensing is used concurrently encrypt as well as compress data. The data is compressive sampled and randomly projected using the Gaussian measurement matrix. The security of the measurements is further enhanced by employing a chaos based bit scrambling and pseudorandom encryption. The experimental analysis performed shows that the proposed algorithm provides cryptographically strong cipher image.