Improved axis rotation MTD algorithm and its analysis

Abstract

In radar detection, weak targets’ range migration often happens during long time integration. To detect weak targets effectively, an improved axis rotation moving target detection (IAR-MTD) is introduced and analysed in detail. IAR-MTD can detect weak targets by compensating the linear part of range migration via the axis rotation and coherently integrating the echoes via moving target detection (MTD). Then the realization of IAR-MTD is derived. Furthermore, the coherent integration gain of IAR-MTD is analysed, which is better than that of traditional MTD, Radon–Fourier transform (RFT) and Keystone transform (KT). Subsequently, to decrease the computational complexity of IAR-MTD, some suggestions are given. Besides, unambiguous Doppler estimation, the tolerance of acceleration, and the multi-target detection of IAR-MTD are analysed respectively. Finally, some numerical experiments are provided to show the performance of IAR-MTD in different conditions and testify the advantages of IAR-MTD over MTD, RFT and KT. The result indicates that IAR-MTD may effectively detect the weak moving targets with constant radial velocity and it is compatible with MTD radar system.

1 Introduction

Moving target detection (MTD) (Skolnik 2002; Barton 2004; Richards 2005; Mahafza 2003) can detect moving targets without prior knowledge, e.g. targets’ motion speed, range, etc. At present, many low signal-to-noise ratio (SNR) moving targets appear (Bao 1999; Skolnik et al. 2001). These targets, which are difficult to be detected via traditional methods for range migration, are called weak targets throughout this paper. For high speed weak targets, range migration is inevitable for their high speed motion. For low speed weak targets, range migration also happens with integration time increasing or range resolution improving which brought by the transmitted signal’s bandwidth increasing. So MTD, which is confined by the target’s resident time in a single range cell, may be ineffective in weak target detection.

To improve the detection performance of weak targets, an available way is increasing integration time. There are two kinds of integration methods, i.e., incoherent integration and coherent integration. Some typical incoherent integration methods are adopted, e.g. Hough transform (HT) (Carlson et al. 1994a, b, c), Radon transform (RT) (Carretero-Moya et al. 2009), Dynamic programming (DP) (Qiang et al. 2002; Deng et al. 2011; Grossi et al. 2001), Particle filter (PF) (Boers and Driessen 2001, 2003, 2004) and so on. But, incoherent integration has a low integration gain for targets’ phase fluctuation not being compensated. So when the echo’s SNR is extremely low, these incoherent integration methods are invalid.

To detect weak targets, some coherent integration methods have been proposed (Wang and Liu 2010; Wang and Zhang 2000; Qi et al. 2003; Tao et al. 2010; Perry et al. 2007, 1999; Zhang and Zeng 2005; Zeng 2005; Xu et al. 2011a, b; Yu et al. 2012; Xu et al. 2015; Carretero-Moya et al. 2009). Wang and Liu (2010) have proposed an automatic range migration correction method based on the similarity of Doppler slices’ envelope. However, this method may not be used in low SNR case. Wang and Zhang (2000) have introduced a range and Doppler migration compensation method based on range stretching and joint time frequency processing. But this method has a high computational complexity. Qi et al. (2003) and Tao et al. (2010) have proposed a signal detection and parameter estimation method based on Fractional Fourier transform (FRFT). However, FRFT is also complicated and confined by target’s resident time in a range cell. Perry et al. (1999, 2007) have introduced Keystone transform (KT) for synthetic aperture radar ground moving targets imaging. Zhang and Zeng (2005a, b) have firstly introduced KT, which can compensate the echo envelopes’ linear range migration, for weak target detection. After KT, the echoes have been concentrated in a same range cell, which can be coherently integrated by MTD. KT is a useful method for eliminating linear range migration, but this method requires the repeated colossal amount interpolation operations. Xu et al. (2011a, b) and Yu et al. (2012) have proposed Radon–Fourier transform (RFT), which combines RT and Fourier transform (FT), for target detection via long time coherent integration. RFT may compensate the echoes’ envelope and phase shifting, and realize coherent integration by searching targets’ speed. However, the computational complexity of RFT is high. Xu et al. (2015) have proposed a new detector to detect range spread maneuvering target embedded in compound-Gaussian clutter, which combine the short-time coherent integration and long time similarity integration. For range spread maneuvering target, the performance of the new detector, which is better than the existing detectors, is testified by experimental results.

For the chirp pulse radar system, based on a constant radial velocity motion mode, an improved axis rotation MTD (IAR-MTD) algorithm is introduced briefly in Rao et al. (2015) and is analysed detailedly in this paper. Compared with MTD, IAR-MTD can coherently integrate the echoes of the weak target with linear range migration. Different from RFT, IAR-MTD can compensate linear range migration with low computational complexity. Compared with axis rotation MTD (AR-MTD) (Rao et al. 2014), IAR-MTD can alleviate the loss of coherent integration gain resulted from axis rotation transform error and can avoid Doppler frequency and Doppler frequency resolution varying with axis rotational angle. Subsequently, the realization of IAR-MTD is derived. Furthermore, the performance of IAR-MTD is analysed on five aspects, i.e., coherent integration gain, computational complexity, unambiguous Doppler estimation, tolerance of acceleration and multi-target detection. It is shown that IAR-MTD has a better coherent integration gain than that of MTD, RFT and KT. In comparison with RFT which need fast implementations, IAR-MTD itself is a fast implementation based on fast FT (FFT). Besides, the searching operation of RFT is a two-dimensional joint searching combined range dimension with velocity dimension, while the searching operation of IAR-MTD is two one-dimensional searching along the range dimension and the velocity dimension respectively. Therefore, the computational complexity of IAR-MTD is lower than that of RFT. Subsequently, the unambiguous Doppler estimation of IAR-MTD is introduced, which is similar to that of RFT. Moreover, the tolerance of acceleration and the multi-target detection are discussed. Finally, some numerical experiments show the performance of IAR-MTD in different backgrounds.

The remainder of this paper is organized as follows. In Sect. 2, the signal model is established. IAR-MTD is introduced in detail in Sect. 3. Performance analysis of IAR-MTD follows in Sect. 4. In Sect. 5, some numerical experiments are provided. Conclusions are given in Sect. 6.

2 Signal model

Assume that a linear frequency modulated (LFM) pulse signal $s_{T} \left( t \right)$, which transmitted by a pulse Doppler (PD) radar, may be given as

$$ s_{T} \left( t \right) = p\left( t \right)\exp \left( {j2\pi f_{c} t} \right) $$

(1)

where $p\left( t \right) = rect\left( {\frac{t}{{T_{p} }}} \right)\exp \left( {j\pi K_{r} t^{2} } \right)$, $t$ indicates the time, $T_{p}$ represents the pulse duration, $K_{r} = B/T_{p}$ is the frequency rate of LFM signal, $B$ is the transmitted signal bandwidth and $f_{c}$ is the carrier frequency.

Let $t = \hat{t} + t_{m} = \hat{t} + mT$, where $\hat{t}$ is the fast time which indicates the propagation time of electromagnetic wave, $t_{m} = mT$ is the slow time which indicates the transmitted time of radar pulse signal. $m$ is the number of pulses, $T$ is the pulse repetition interval, and the pulse repetition frequency (PRF) equals $1/T$.

Suppose that an air moving target with a constant radial velocity $v$ appears on initial range $R_{0}$ at $t_{m} = 0$. Then the target’s linear range migration may be written as

$$ R\left( {t_{m} } \right) = R_{0} + vt_{m} $$

(2)

After the coherent demodulation, the two-dimensional echoes may be given as

$$ s\left( {\hat{t},t_{m} } \right) = p\left( {\hat{t} - \frac{{2R\left( {t_{m} } \right)}}{c}} \right)\exp \left( { - j\frac{{4\pi f_{c} }}{c}R\left( {t_{m} } \right)} \right) = p\left( {\hat{t} - \frac{{2R\left( {t_{m} } \right)}}{c}} \right)\exp \left( { - j\frac{4\pi }{\lambda }R\left( {t_{m} } \right)} \right) $$

(3)

where $c$ is the speed of light and $\lambda$ is the wavelength. After pulse compression, the echoes may be represented as

$$ s\left( {\hat{t},t_{m} } \right) = A\sin c\left( {B\left( {\hat{t} - \frac{{2R\left( {t_{m} } \right)}}{c}} \right)} \right)\exp \left( { - j\frac{4\pi }{\lambda }R\left( {t_{m} } \right)} \right) $$

(4)

where $sinc\left( \cdot \right)$ is the sinc function, $A$ is the complex amplitude of the echoes after pulse compression. Here, $A$ is assumed to be a constant. Substituting (2) into (4), then

$$ s\left( {\hat{t},t_{m} } \right) = A\sin c\left( {B\left( {\hat{t} - \frac{2}{c}\left( {R_{0} + vt_{m} } \right)} \right)} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {R_{0} + vt_{m} } \right)} \right) $$

(5)

Let $\hat{t} = \frac{2r}{c}$, where $r$ is the rfange. Then (5) is rewritten as

$$ s\left( {r,t_{m} } \right) = A\sin c\left( {\frac{2B}{c}\left( {r - \left( {R_{0} + vt_{m} } \right)} \right)} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {R_{0} + vt_{m} } \right)} \right) $$

(6)

The target’s Doppler frequency is defined as

$$ f_{d} = - 2v/\lambda $$

(7)

For a PD radar, the radar receiver will sample the target’s echoes with sampling frequency $f_{s}$. So the target’s range can be described as a range cell number. Assume that $f_{s}$ equals $B$, then $n_{r} = \frac{2B}{c}r$, $n_{R0} = \frac{2B}{c}R_{0}$, where $n_{r}$ is the range cell number of $r$, $n_{R0}$ is the range cell number of $R_{0}$. Then (6) is written as

$$ s\left( {n_{r} ,m} \right) = A\sin c\left( {n_{r} - n_{R0} - \frac{2B}{c}vmT} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} + vmT} \right)} \right) $$

(8)

According to the signal model, the moving target echoes are distributed along a straight line in the coordinate system $\left( {n_{r} - m} \right)$. Figure 1 shows the variation of a target’s range with slow time when the target moves away from the radar with a positive radial velocity $v$. It is clear that linear range migration happens along the slow time dimension.

Fig. 1

Linear range migration in coordinate system $\left( {n_{r} - m} \right)$

3 IAR-MTD algorithm and realization

3.1 Improved axis rotation transform

AR-MTD is proposed in Rao et al. (2014). The axis rotational relationship is given as

$$ \left\{ \begin{array}{l} m^{\prime\prime} = round\left( {m\cos \alpha + n_{r} \sin \alpha } \right) \hfill \\ n_{r}^{''} = round\left( { - m\sin \alpha + n_{r} \cos \alpha } \right) \hfill \\ \end{array} \right.\quad \alpha \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right) $$

(9)

where the operator $round\left( \cdot \right)$ represents that rounds the value to the nearest integer, $\alpha$ is the axis rotational angle, and $v = \frac{c}{2B \times T}\tan \alpha$. The old coordinate system $\left( {n_{r} - m} \right)$ is transformed into a new coordinate system $\left( {n_{r}^{''} - m^{\prime\prime}} \right)$ via the axis rotation in Fig. 2.

Fig. 2

Axis rotation in AR-MTD algorithm

However, there are some drawbacks in AR-MTD. Firstly, the axis rotational relationship will bring transform error. Notably, the operator $round\left( \cdot \right)$ in (9) is only for simplicity. However, the transform error will be introduced by $round\left( \cdot \right)$. The error in $n_{r}^{''}$ may be acceptable because $n_{r}^{''}$ relates to the target’s position. But, the error in $m^{\prime\prime}$ could not be ignored because it relates to the phase of the target’s echoes. The phases of echoes, $- j\frac{4\pi }{\lambda }vm^{\prime\prime}T\cos \alpha$, are sensitive to the transform error which will result in a great loss of coherent integration gain.

Secondly, in some higher accuracy applications, the new Doppler frequency $f_{d}^{'} = f_{d} \cos \alpha$ (i.e., the Doppler frequency after the axis rotation transform) may appear in a wrong Doppler channel for the transform error brought by $round\left( \cdot \right)$ when $f_{d}^{'}$ is transformed back into the original Doppler frequency $f_{d}$.

Finally, the frequency resolution of Doppler filter may vary with the axis rotational angle $\alpha$. The relationship is given as

$$ \rho_{d}^{'} = \rho_{d} \cos \alpha $$

(10)

where $\rho_{d}$ is the original Doppler frequency resolution, $\rho_{d}^{'}$ is the new Doppler frequency resolution. The variation of the Doppler frequency resolution will result in some difficulties in signal processing.

To circumvent these drawbacks, an improved algorithm for AR-MTD is introduced and analysed in this paper. Figure 3 shows the transform of coordinate systems. The modified axis rotational relationship is given as

$$ \left\{ \begin{array}{l} m^{\prime} = m \hfill \\ n_{r}^{'} = round\left( { - m\sin \alpha + n_{r} \cos \alpha } \right) \hfill \\ \end{array} \right. \quad \alpha \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right) $$

(11)

where $\alpha$ is the axis rotational angle, and $v = \frac{c}{2B \times T}\tan \alpha$. That is

$$ \left\{ \begin{array}{l} m = m^{\prime} \hfill \\ n_{r} = round\left( {m^{\prime}\tan \alpha + n_{r}^{'} \frac{1}{\cos \alpha }} \right) \hfill \\ \end{array} \right.\quad \alpha \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right). $$

(12)

Fig. 3

Echoes are concentrated in a range cell via the improved axis rotation, where $\alpha$ is the rotational angle

Substituting (12) into (8), then

$$ s\left( {n_{r}^{'} ,m^{\prime}} \right) = A\sin c\left( {\frac{1}{\cos \alpha }\left( {n_{r}^{'} - n_{R0} \cos \alpha } \right)} \right)\exp \left( { - j\frac{4\pi }{\lambda } \cdot \frac{c}{2B}n_{R0} } \right)\exp \left( {j2\pi f_{d} m^{\prime}T} \right) $$

(13)

It is shown from (13) that all echoes have been concentrated in the range cell $n_{R0}^{'} = n_{R0} \cos \alpha$. The first exponential term is the initial phase of echoes in this range cell. The second exponential term is the value of carrier phase caused by Doppler effect. It should be noticed that the Doppler frequency in (13) is $f_{d}$ not $f_{d}^{'}$. Accordingly, the Doppler frequency resolution is $\rho_{d}$ not $\rho_{d}^{'}$. In a word, the drawbacks mentioned above are rectified or alleviated. Additionally, it should be noticed that the improved axis rotation transform is a special case of the axis rotation transform which is proposed in Rao et al. (2014). Actually, the Cartesian coordinate axis is transformed into a skew/slanting coordinate axis via the improved axis rotation transform, i.e., Eq. (12) or (13).

3.2 Analysis of discrete echoes

Although the echoes, which are transformed via the improved axis rotation, can be coherently integrated by Doppler filter bank, e.g. MTD, there are some differences between IAR-MTD and MTD in integration process.

Theoretically, the signal’s complex amplitude equals $A$ when $n_{r}^{'} = n_{R0} \cos \alpha$. In fact, it is smaller than $A$ because of the target’s linear range migration. The discussion is given as follow.

For convenience, we rewrite (8) here:

$$ s\left( {n_{r} ,m} \right) = A\sin c\left( {n_{r} - n_{R0} - \frac{2B}{c}vmT} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} + vmT} \right)} \right) . $$

(14)

Let $\Delta f_{d} = - \frac{B\lambda }{c}f_{d}$, where $\Delta f_{d}$ is defined as Doppler frequency offset. Then (14) may be given as

$$ s\left( {n_{r} ,m} \right) = A\sin c\left( {\left( {n_{r} - n_{R0} } \right) + \Delta f_{d} mT} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} + vmT} \right)} \right) . $$

(15)

Let $n_{r} = n_{R0}$, the echoes in the range cell $n_{R0}$ may be written as

$$ s\left( {n_{R0} ,m} \right) = A\sin c\left( {\Delta f_{d} mT} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} + vmT} \right)} \right) . $$

(16)

Let $n_{r} = n_{R0} + 1$, the echoes may be given as

$$ s\left( {n_{R0} + 1,m} \right) = A\sin c\left( {1 + \Delta f_{d} mT} \right)\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} + vmT} \right)} \right) . $$

(17)

It is interesting that the target’s echoes envelope in a range cell is the function $\sin c\left( \cdot \right)$ along the slow time dimension. And the function $\sin c\left( \cdot \right)$ will shift with the variation of range cell. For convenience, ${\text{s}}\left( {n_{R0} ,m} \right)$ is represented as ${\text{s}}\left( m \right)$

$$ s\left( m \right) = \tilde{A}\sin c\left( {\Delta f_{d} mT} \right)\exp \left( {j2\pi f_{d} mT} \right) , $$

(18)

where $\tilde{A} = A\exp \left( { - j\frac{4\pi }{\lambda }\left( {\frac{c}{2B}n_{R0} } \right)} \right)$.

The analysis of echoes is given in Fig. 4. Figure 4a shows the amplitude losses of the echoes in a single range cell for linear range migration. Figure 4b shows that the echoes are concentrated in a range cell after the improved axis rotation transform.

Fig. 4

Analysis of echoes. a Amplitude losses of the echoes in a range cell will happen for linear range migration. b Echoes are concentrated in a range cell after the improved axis rotation transform

In Fig. 4a, the slanting dashed line represents the continuous echoes $s\left( {r,t_{m} } \right)$, and the horizontal separating solid lines are the discrete echoes $s\left( {n_{r} ,m} \right)$. In a single range cell, the slanting dashed line is replaced by a horizontal solid line. Therefore, there are some losses in amplitude. For example, point $A1$ is the continuous echo and the amplitude is $\tilde{A}$, which is replaced by point $A2$ with amplitude being $\tilde{A}\sin c\left( {\Delta f_{d} mT} \right)$ in that range cell. In Fig. 4b, several horizontal separating lines in different range cells are transformed into a horizontal line in the single range cell $n_{R0}^{'} = n_{R0} \cos \alpha$, and the echoes in range cell $n_{R0}^{'}$ are $s\left( {n_{R0}^{'} ,m^{\prime}} \right)$.

Let $K = ceil\left( {\frac{v \times CPI}{{\rho_{r} }}} \right)$, $M = round\left( {\frac{PRF \times CPI}{K}} \right)$, where $CPI$ is the coherent processing interval, which equals coherent integration time in this paper. $\rho_{r}$ is the range resolution which equals $c/2B$, $K$ is the range cell number of target’s linear range migration during $CPI$ and $K \ge 2$ for linear range migration, the operator $ceil\left( \cdot \right)$ represents that rounds the value toward positive infinity, $M$ is the number of transmitted pulses during the target staying in a range cell.

Let $n_{r}^{'} = n_{R0} \cos \alpha$, then $s\left( {n_{r}^{'} ,m^{\prime}} \right) = s\left( {n_{R0} \cos \alpha ,m^{\prime}} \right)$. For simplicity, $s\left( {n_{R0} \cos \alpha ,m^{\prime}} \right)$ is represented as ${\text{s}}\left( {m^{\prime}} \right)$. Figure 4b shows $s\left( {m^{\prime}} \right)$ may be represented by $s\left( m \right)$ via time shift and combination operation. The relationship is given as

$$ s\left( {m^{\prime}} \right) = s_{1} \left( {m^{\prime}} \right)R_{KM} \left( {m^{\prime}} \right) = \left( {\mathop \sum \limits_{k = 0}^{K} s_{2} \left( {m - kM} \right)} \right)R_{KM} \left( {m^{\prime}} \right) , $$

(19)

where

$$ s_{1} (m\prime ) = \sum\nolimits_{k = 0}^{K} {s_{2} (m - kM)} , $$

(20)

$$ s_{2} \left( m \right) = s\left( m \right)R_{M} \left( {m + \frac{M}{2} - 1} \right), $$

(21)

and $R_{KM} \left( \cdot \right)$,$R_{M} \left( \cdot \right)$ are the rectangular sequences which lengths are $KM$ and $M$ respectively.

3.3 Realization of IAR-MTD

It is well known that MTD can realize moving target detection via Doppler filter bank. So, the signal may be coherently integrated via MTD after the improved axis rotation transform. However, there are some differences in performance between MTD and IAR-MTD. The discussion is given as follow.

As we know, MTD is realized by discrete Fourier transform (DFT). While the DFT of the echoes after the improved axis rotation transform is presented as follow. Without loss of generality, suppose that $CPI$ is one second. Thus the number of transmitted pulses equals PRF.

Let $L = PRF$, then the $L$-point DFT of $s\left( m \right)$ is

$$ S\left( l \right) = \frac{{\tilde{A}}}{{\left| {\Delta f_{d} } \right|}}\frac{\pi }{T}R_{{2\Delta f_{d} }} \left( {\frac{2\pi }{{\Delta f_{d} }}\left( {l - f_{d} } \right)} \right) l = 0,1,2, \ldots ,L - 1 $$

(22)

where $R_{{2\Delta f_{d} }} \left( \cdot \right)$ is a rectangular sequence which length is $2\Delta f_{d}$.The $L$-point DFT of $R_{M} \left( {m + \frac{M}{2} - 1} \right)$ is

$$ E_{L1} \left( l \right) = \exp \left( {j\frac{\pi }{L}l} \right)\frac{{\sin \frac{\pi }{K}l}}{{\sin \frac{\pi }{L}l}} l = 0,1,2, \ldots ,L - 1 $$

(23)

where $E_{L1} \left( \cdot \right)$ is a sinc function sequence which length is $L$.Accordingly, the $L$-point DFT of $s_{2} \left( m \right)$ is

$$ S_{2} \left( l \right) = S\left( l \right)*E_{L1} \left( l \right) = \frac{{\tilde{A}}}{{\left| {\Delta f_{d} } \right|}}\frac{\pi }{T}R_{{2\Delta f_{d} }} \left( {\frac{2\pi }{{\Delta f_{d} }}\left( {l - f_{d} } \right)} \right)*\exp \left( {j\frac{\pi }{L}l} \right)\frac{{\sin \frac{\pi }{K}l}}{{\sin \frac{\pi }{L}l}} l = 0,1,2, \ldots ,L - 1 $$

(24)

where the operator * is the convolution operation. Obviously, the amplitudes of $l = f_{d} \pm \Delta f_{d}$ are identical, but the phases are not identical. And the difference of phase, i.e. $j\frac{{2\pi \Delta f_{d} }}{L}$, is small when $L$ is large enough.

The $L$-point DFT of $s_{1} \left( {m^{\prime}} \right)$ is

$$ S_{1} \left( l \right) = S_{2} \left( l \right) \cdot \left( { - 1} \right)^{l} \frac{{\sin \frac{K + 1}{K}\pi l}}{{\sin \frac{1}{K}\pi l}} l = 0,1,2, \ldots ,L - 1 $$

(25)

It should be noticed that $S_{1} \left( l \right)$ equals $\left( {K + 1} \right)S_{2} \left( l \right)$ when $l$ is an integer multiple of $K$. And $S_{1} \left( l \right)$ equals $S_{2} \left( l \right)$ when $l$ is not an integer multiple of $K$.

When $l_{1} = f_{d} + \Delta f_{d} = \left( {\frac{{f_{c} - B}}{{f_{s} }}} \right)K = \left( {\frac{{f_{c} }}{{f_{s} }} - 1} \right)K$ and $l_{2} = f_{d} - \Delta f_{d} = \left( {\frac{{f_{c} + B}}{{f_{s} }}} \right)K = \left( {\frac{{f_{c} }}{{f_{s} }} + 1} \right)K$, $S_{1} \left( l \right)$ equals $\left( {K + 1} \right)S_{2} \left( l \right)$ which is the maximum of $S_{1} \left( l \right)$. Moreover, $\Delta l = \left| {l_{1} - l_{2} } \right| = 2K$. However, $S_{1} \left( l \right)$ equals $S_{2} \left( l \right)$ when $l = f_{d}$. It is known that the $S_{1} \left( l \right)$ has two spectral peaks at $l = f_{d} \pm \Delta f_{d}$, and there is no peak at $l = f_{d}$.

When $CPI = 1s$, $K \times M = PRF = L$. Thus the $L$-point DFT of $R_{KM} \left( {m^{\prime}} \right)$ is

$$ R_{L2} \left( l \right) = \exp \left( { - j\frac{L - 1}{L}\pi l} \right)\frac{{\sin \left( {\pi l} \right)}}{{\sin \left( {\frac{\pi }{L}l} \right)}}\quad l = 0,1,2, \ldots ,L - 1. $$

(26)

where $R_{L2} \left( \cdot \right)$ is a rectangular sequence which length is $L$.

And the $L$-point DFT of $s\left( {m^{\prime}} \right)$ is

$$ S_{0} \left( l \right) = S_{1} \left( l \right)*R_{L2} \left( l \right) = S_{1} \left( l \right)*\exp \left( { - j\frac{L - 1}{L}\pi l} \right)\frac{{\sin \left( {\pi l} \right)}}{{\sin \left( {\frac{\pi }{L}l} \right)}}\quad l = 0,1,2, \ldots ,L - 1 $$

(27)

Obviously, the amplitude of $S_{0} \left( {f_{d} - \Delta f_{d} } \right)$ equals that of $S_{0} \left( {f_{d} + \Delta f_{d} } \right)$ and the difference of phase is $- j\frac{L - 1}{L}2\pi \Delta f_{d}$. When $L$ is large enough, $\exp \left( { - j\frac{L - 1}{L}2\pi \Delta f_{d} } \right)$ nearly equals $1$.

Based on the above discussion, the conclusion may be drawn that the spectrum $S_{0} \left( l \right)$ of $s\left( {m^{\prime}} \right)$ has two spectral peaks at $l = f_{d} \pm \Delta f_{d}$ and the difference of phases between the two spectral peaks is small. So the value of the peaks can be coherently added and the final output of IAR-MTD is almost $2\left( {K + 1} \right)\frac{{\tilde{A}}}{{\left| {\Delta f_{d} } \right|}}\frac{\pi }{T}$.

4 Analysis of IAR-MTD algorithm

In Sect. 3, IAR-MTD is introduced to circumvent the drawbacks in AR-MTD and the realization of the IAR-MTD is described. In this section, the performance of IAR-MTD will be discussed on five aspects, i.e., coherent integration gain, computational complexity, unambiguous Doppler estimation, tolerance of acceleration and multi-target detection.

4.1 Coherent integration gain

To detect weak targets in noisy condition, the echo’s SNR should exceed some detection threshold. So it is necessary to analyse the integration gain of IAR-MTD to ensure with how low SNR the target can be detected.

Assume that the minimum detectable SNR is defined as $SNR_{min}$. Then

$$ SNR_{min} = SNR_{target,min} + G_{PC} + G_{IAR - MTD} \left( {dB} \right) $$

(28)

where $SNR_{target,min}$ is the minimum SNR of the weak target‘s raw echoes, $G_{PC}$ is the gain of pulse compression, $G_{IAR - MTD}$ is the gain of coherent integration via IAR-MTD. $G_{PC}$ may be given as

$$ G_{PC} = 10\log_{10} D \left( {dB} \right) $$

(29)

where $D = B \times T_{p}$ is the time bandwidth product of the transmitted pulse signal.

Because the final output of IAR-MTD is $2\left( {K + 1} \right)\frac{{\tilde{A}}}{{\left| {\Delta f_{d} } \right|}}\frac{\pi }{T}$, $G_{IAR - MTD}$ can be presented as

$$ G_{IAR - MTD} = 10\log_{10} \left( {2\left( {K + 1} \right)\left( {\frac{1}{{\left| {\Delta f_{d} } \right|}}\frac{\pi }{T}} \right)} \right) \approx 10\log_{10} \left( {2\pi \times CPI \times PRF} \right) \left( {dB} \right) $$

(30)

It should be noticed that $G_{IAR - MTD}$ is acquired by adding the values of the two spectral peaks. When $K \gg 1$, $\left( {K + 1} \right) \approx \left| {\Delta f_{d} } \right| \times CPI$. Accordingly, the approximation in Eq. (30) is established. Moreover, when linear range migration does not happen, IAR-MTD will degenerate into MTD and it is unnecessary to perform axis rotation operation. Accordingly, there is only a spectral peak.

4.2 Computational complexity

To detect the weak moving target with unknown velocity, the axis rotational angle $\alpha$ should be searched from $- \pi /2$ to $\pi /2$. If the angle $\alpha$ equals $arctan\left( {\frac{v \times 2B \times T}{c}} \right)$ which corresponds to the target velocity $v$, $S_{0} \left( l \right)$ will have two peaks at the location of $l = f_{d} \pm \Delta f_{d}$.

The searching for the angle $\alpha$ will increase the computational complexity. For example, if the angle searching step $\Delta \alpha$ equals $arctan\left( {\frac{1 \times 2B \times T}{c}} \right)$, which corresponds to the target’s velocity searching step $\Delta v$ equalling 1 m/s, the number of searching may be 1020 times when the radial velocity of the target is nearly 3-Mach. The searching complexity is huge and it will worsen the algorithm’s real-time performance. Fortunately, the problem may be alleviated in real applications. Firstly, the target’s velocity (i.e., rotational angle $\alpha$) is limited to some fixed region via prior knowledge (e.g. from minimum to maximum assumed target velocity). And we can choose an appropriate angle searching step according to Doppler resolution. With the searching region and the number of searching reduced, the computational complexity will decrease. Secondly, some searching strategies may be adopted, e.g. the searching procedure could be divided into two parts (i.e., first, search the axis rotational angle region with a wider searching step, and then search the exact axis rotational angle with a narrower searching step). Lastly, the searching for the correct axis rotational angle is a convex optimization problem, and some optimization methods could be adopted to reduce the computational complexity, e.g. Gradient descent method, Steepest descent method, Newton’s method and so on.

It should be noticed that the relationship between the angle searching step $\Delta \alpha$ and the velocity searching step $\Delta v$ is function $\tan \left( \cdot \right)$, which is a nonlinear function. That means same velocity searching steps will result in different angle searching steps $\Delta \alpha$ with $\alpha$ increasing. However, in most cases, since the angle searching region is near to zero, the relationship between $\Delta \alpha$ and $\Delta v$ is linear.

Table 1 gives the operation component of IAR-MTD. The main operation of IAR-MTD is the axis rotation and FFT. Therefore, the computational complexity of IAR-MTD is decided by the number of angle searching.

Table 1 Operation component of IAR-MTD

4.3 Unambiguous Doppler estimation

The ambiguous speed response is an intractable problem for the traditional Doppler filter bank, e.g. MTD. The Doppler filter responses will periodically repeat along the searching radial velocity with a certain cycle $PRF$. So for the filter bank with searching area of $\left[ { - PRF/2,PRF/2} \right]$, the responses for the targets with Doppler frequency $f_{d} + p \times PRF$ will be identical, where $p$ is an uncertain integer. That is, after the MTD filtering, the target’s true Doppler frequency $f_{d}$ cannot be ascertained and the Doppler frequency is still ambiguous (Xu et al. 2011). To solve the problem, some techniques have been adopted (Zhu et al. 2011). However, the ambiguous speed response of IAR-MTD may be avoided well, which is similar to that of RFT (Xu et al. 2011). It is known that different axis rotational angles correspond to different velocities. If the current axis rotational angle mismatches the current target velocity, in other words, when the velocity mismatch is larger than the velocity resolution, the number of pulses that can be coherently integrated is few and the output will approach zero.

Figure 5 shows the reason that ambiguous speed response could be avoided. Assume that the angle $\alpha$ corresponds to the target’s speed $v$ and the angle $\beta$ corresponds to an ambiguous speed, the output of coherent integration is near to zero when the axis rotational angle equals $\beta$.

Fig. 5

Number of pulse is few when the rotational angle corresponds to an ambiguous speed

4.4 Tolerance of acceleration

In Sect. 2, the signal model is built on the moving target with a constant radial velocity $v$. However, the moving target usually has acceleration in real application. As we know, range migration may be divided into two parts: the first part is the linear range migration brought by target’s velocity; the second part is the nonlinear range migration brought by target’s acceleration.

IAR-MTD could compensate linear range migration, but cannot compensate nonlinear range migration. If there is a target with a radial acceleration or manoeuvring motion, the coherent integration performance will decrease with integration time increasing. So it is necessary to research the tolerance of acceleration for IAR-MTD.

The coherent integration gain is decided by the number of pulses that could be coherently integrated. When a target has a radial acceleration or manoeuvring motion, not only the nonlinear range migration may exceed the width of a range cell but also the Doppler frequency of the target may shift. Hence, the number of pulses that can be coherently integrated may decrease.

The coherent integration time, which Doppler frequency is confined in a Doppler resolution cell, is given as

$$ \left| {2a_{max} CPI/\lambda } \right| < \rho_{d} = 1/CPI $$

(31)

where $a_{max}$ is the maximum of target’s acceleration. Then the maximum of $CPI$, which is constrained by Doppler resolution, is

$$ CPI_{Doppler} \le \sqrt {\lambda /\left( {2a_{max} } \right)} $$

(32)

The coherent integration time, which the nonlinear range migration is limited in a range cell, is given as

$$ a_{max} CPI^{2} /2 \le \rho_{r} $$

(33)

Then the maximum of $CPI$, which is constrained by range resolution, is

$$ CPI_{curvature} \le \sqrt {2\rho_{r} /a_{max} } $$

(34)

To coherently integrate effectively, $CPI$ should be a minimum between $CPI_{Doppler}$ and $CPI_{curvature}$. That is

$$ CPI = min\left( {CPI_{Doppler} ,CPI_{curvature} } \right) . $$

(35)

4.5 Multi-target detection performance

Similar to MTD, IAR-MTD can realize the detection of multi-target with constant radial velocity. For moving targets with constant radial velocity, they may be distinguished by range or Doppler frequency. Suppose that the echoes have been processed via the improved axis rotation transform. Then, there are three cases should be discussed. In the first case that the targets have a same constant radial velocity but locate in different range cells, the targets can be distinguished by their ranges. In the second case that the targets have different constant radial velocities and locate in a same range cell, the targets can be distinguished by their different Doppler frequencies. In the last case that the targets have a same constant radial velocity and locate in a same range cell, the targets may be differentiated by raid cluster resolution technique (Du et al. 2004) or have to be considered as a target.

In summary, the performance of multi-target detection is determined by both range resolution and Doppler resolution. Hence, with the transmitted signal bandwidth $B$ or the coherent integration time increasing, the multi-target detection performance will improve.

5 Numerical experiments

To verify the performance of IAR-MTD, some numerical experiments are presented in this section. A non-fluctuating simple point target model and an additive white Gaussian noise background are assumed. The experiment parameters are given as follows: $R_{0} = 200\;{\text{km}}$, $v = 100\;{\text{m/s}}$, $f_{c} = 150\;{\text{MHz}}$, $B = 30\;{\text{MHz}}$, $T_{p} = 2\;\mu {\text{s}}$, $G_{PC} = 10\log_{10} \left( {T_{p} \times B} \right) = 17.78\;{\text{dB}}$, $PRF = 3000\;{\text{Hz}}$, $f_{s} = 60\;{\text{MHz}}$, CPI = 1 s, false alarm probability $P_{fa} = 10^{ - 6}$, the number of Monte Carlo experiments is $10^{8}$ times.

5.1 Detection performance of IAR-MTD in different SNR backgrounds

To verify the detection performance of IAR-MTD in different SNR backgrounds, two experiments are presented as follows.

5.1.1 Integration effect of IAR-MTD

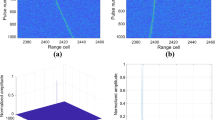
In this experiment, the input SNR is assumed to be -15 dB. Although the raw echoes are submerged by noise, the echoes after pulse compression, which are shown in Fig. 6a, may be observed for $G_{PC}$ equalling 17.78 dB. Obviously, a linear range migration happens in Fig. 6a. Figure 6b shows the coherent integration effect of IAR-MTD when the axis rotational angle $\alpha$ equals 0.0133 rad, which corresponds the radial velocity equalling 100 m/s. In Fig. 6b, there are two peaks which may be identical in amplitude and phase. The reason for the double peaks is given in Sect. 3.3.

Fig. 6

Integration effect of IAR-MTD. a Linear range migration in coordinate system $\left( {n_{r} - m} \right)$. b Normalized output of IAR-MTD ($\alpha$ = 0.0133 rad, $v$ = 100 m/s)

5.1.2 Detection performance of IAR-MTD

As we know, the higher the coherent integration gain, the better the detection performance. The coherent integration gains of MTD, RFT (Xu et al. 2011) and IAR-MTD are given as

$$ G_{MTD} = 10\log_{10} \left( {CPI_{MTD} \times PRF} \right) \left( {dB} \right) , $$

(36)

$$ G_{RFT} = 10\log_{10} \left( {CPI_{RFT} \times PRF} \right) \left( {dB} \right) $$

(37)

and

$$ G_{IAR - MTD} = 10\log_{10} \left( {2\pi \times CPI_{IAR - MTD} \times PRF} \right) \left( {dB} \right) . $$

(38)

As linear range migration happens, $CPI_{MTD}$ is the least of the three algorithms, and $G_{MTD}$ is the least accordingly. $CPI_{RFT}$ may be equal to $CPI_{IAR - MTD}$, however, $G_{IAR - MTD}$ may be greater than $G_{RFT}$ by comparing (37) with (38).

The detection performance of IAR-MTD, MTD, RFT and KT are given in this experiment. When the input SNR varies from − 55 to − 15 dB, the relationship curve between detection probability $\left( {P_{d} } \right)$ and the input SNR is shown in Fig. 7. The theoretical values of IAR-MTD and RFT are calculated via (28), (29), (30) and (37). The real values of IAR-MTD, MTD and KT are the results of the experiment. It is clear that the detection performance of IAR-MTD is the best of the four algorithms. The difference between the theoretical value and the real value of IAR-MTD results from the losses of echoes amplitude for the linear range migration, the error of the axis rotation transform, the difference of phases between the two spectral peaks, and the approximation of $G_{IAR - MTD}$.

Fig. 7

Detection probability of IAR-MTD, MTD, RFT and KT $\left( {P_{fa} = 10^{ - 6} } \right)$

5.2 Detection performance of IAR-MTD in different searching step backgrounds

Since MTD can be realized by FFT without any other computation, the computational complexity of MTD is the lowest of the four algorithms. But, that the coherent integration time of MTD is also the shortest limits the application of MTD. Compensating linear range migration via KT and realizing coherent integration via MTD can increase coherent integration time and improve coherent integration gain distinctly, but interpolation operation increases system burden. RFT requires a two-dimensional joint searching along the range dimension and the velocity dimension, which will increase the computational complexity. Moreover, RFT cannot directly use the FFT-based filter bank because the input series are different for different filters (Xu et al. 2011). So RFT need the optimality and fast implementations which are proposed in Yu et al. (2012). Also, the computational complexity of the fast algorithms of RFT is only infinitely close to that of the FFT-based algorithm, e.g. MTD. However, IAR-MTD successfully decouples the two-dimensional searching into two one-dimensional searching along the range dimension and the velocity dimension respectively. Therefore, the computational complexity of IAR-MTD is much lower than that of RFT.

To decrease the computational complexity of searching axis rotational angle $\alpha$ in IAR-MTD, some searching strategies could be adopted in real applications, e.g. adaptive searching step or two searching steps.

To compare the effect of angle errors, two experiments are given as follows.

5.2.1 Large angle error

In this experiment, the input SNR equals − 15 dB and the radial velocity of the target is assumed to be 100 m/s. The maximal velocity error may be $\pm$ 5 m/s when the searching step equals 10 m/s. In comparison with Figs. 6b and 8a shows that the locations of the peaks are incorrect. Moreover, the coherent integration gain will decrease with the axis rotational angle error increasing. The larger the error, the less the coherent integration gain. Fortunately, some searching tactics may be adopted to decrease the error, e.g. searching with an alterable step.

Fig. 8

Comparison of different angle errors. a Normalized output of IAR-MTD ($\alpha$ = 0.0140 rad, $v$ = 105 m/s). b Normalized output of IAR-MTD ($\alpha$ = 0.0136 rad, $v$ = 102 m/s). c Detection probability of different small angle errors ($\alpha$ = 0.0131 rad, $v$ = 98 m/s; $\alpha$ = 0.0132 rad, $v$ = 99 m/s; $P_{fa} = 10^{ - 6}$)

5.2.2 Small angle error

Unlike the large angle error scenario, a small angle error would not generate wrong peak locations (Fig. 8b). But the coherent integration gain will still decrease for the axis rotational angle error. The detection performance of different small angle errors is presented in this experiment. The input SNR varies from − 50 to − 30 dB. Figure 8c shows the relationship between $P_{d}$ and the input SNR. It is clear that the detection performance will decrease when angle error increases.

5.3 Detection performance of IAR-MTD in different accelerations backgrounds

The target motion model in Sect. 2 is assumed to be a constant radial velocity motion. In real applications, the target constant radial velocity motion may fluctuate during long time coherent integration. In this experiment, the detection performance of different accelerations is shown in Fig. 9. Compared with the effect of angle error which is shown in Fig. 8c, the effect of acceleration is obvious and the detection performance will decrease greatly with the acceleration increasing. It should be noticed that IAR-MTD is proposed to eliminate the linear range migration. The nonlinear range migration which caused by the acceleration could not be eliminated by IAR-MTD. So the detection performance will decrease.

Fig. 9

Detection probability of different accelerations $\left( {P_{fa} = 10^{ - 6} } \right)$

5.4 Detection performance of IAR-MTD in multi-target detection background

IAR-MTD has the capability of detecting multi-target. Suppose that there are three targets with constant radial velocity in this experiment. Target 1: $v_{1} = 10\;{\text{m/s}}$; Target 2: $v_{2} = 50\;{\text{m/s}}$; Target 3: $v_{3} = 10\;{\text{m/s}}$. The target 1 and target 2 initially locate in a same range cell. The distance between the target 1 and target 3 is ten range cells. The input SNR is assumed to be − 15 dB and the other system parameters are identical to those in Sect. 5.1.

Figure 10a shows the echoes after pulse compression. The two parallel lines are the echoes of target 1 and target 3, which have the same radial velocity and the different initial ranges. The two crossed lines are the echoes of target 1 and target 2, which have the same initial range and the different radial velocities.

Fig. 10

Detection performance of IAR-MTD in multi-target detection. a Linear range migration of multi-target echoes in coordinate system $\left( {n_{r} - m} \right)$. b Normalized output of IAR-MTD ($\alpha$ = 0.0013 rad, $v$ = 10 m/s). c Normalized output of IAR-MTD ($\alpha$ = 0.0067 rad, $v$ = 50 m/s)

Figure 10b shows two peaks which correspond to target 1 and target 3 respectively. Obviously, target 1 and target 3 can be distinguished by range. There is a small peak on the left which represents target 2. Figure 10c shows a main peak which represents target 2. And the small peak on the right represents target 3. The small peak of target 1 overlaps the peak of target 2. Obviously, the targets can be distinguished by Doppler frequency.

6 Conclusions

A novel coherent integration detection algorithm IAR-MTD for detecting weak moving targets is presented in this paper. Different from the existing algorithms, IAR-MTD could perform the procedure of linear range migration compensation and realize target’s velocity estimation.

Furthermore, the realization of IAR-MTD is derived and that the coherent integration gain of IAR-MTD is better than that of MTD, RFT and KT is testified. Then some strategies are suggested to decrease computational complexity. Subsequently, unambiguous Doppler estimation is discussed, which is similar to that of RFT. Moreover, the analysis of the acceleration’s tolerance shows that the nonlinear range migration is hardly eliminated by IAR-MTD. Subsequently, the multi-target detection ability of IAR-MTD is verified. Finally, some experiments show the detection performance of IAR-MTD in different parameter backgrounds.

On the basis of the analysis in the paper, a conclusion may be drawn that: the improved axis rotation transform is a special case of the axis rotation transform and, in fact, the Cartesian coordinate axis is transformed into a skew/slanting coordinate axis via the improved axis rotation transform. Furthermore, for the weak moving targets with constant radial velocity, IAR-MTD may increase the detecting range and the detection probability. Compared with MTD, RFT and KT, IAR-MTD has a better coherent integration performance and a lower computational complexity. And IAR-MTD, which is treated as an improved algorithm of MTD, could be applied in MTD radar system.