1 Introduction

Due to the demand for lightweight manipulators, high-speed operation, and a high payload-to-weight ratio, flexible manipulators are gaining popularity over bulky rigid manipulators in various fields such as medicine, aerospace, construction, etc. The dynamics of these manipulators are more complex than rigid manipulators due to the presence of both elastic and rigid degrees of freedom. There are various methods adopted to simulate the dynamics of these manipulators, which include the Finite Element Method (FEM), Assumed Mode Method (AMM), and Finite Segment Method (FSM) etc. An extensive literature review has been conducted, encompassing these techniques applied to flexible manipulators ranging from single-link to multi-link manipulator systems [1, 2]. The most used techniques for the dynamics of flexible manipulators are FEM and AMM. A comparison of these two techniques has been done by [3, 4]. The former approach, which involves more state space equations, requires additional simulation time. However, it is applicable to manipulators with non-uniform shapes as well [3]. On the other hand, the latter approach is more suitable for manipulators that possess a uniform shape. In terms of accuracy, the assumed mode method (AMM) generally yields more precise results for hub angle, while the finite element method (FEM) tends to provide more accurate outcomes for hub velocity and hub acceleration. These findings are in comparison to experimental results [4]. Other researchers [5–10] etc. have used FEM for dynamics. This technique offers the advantage of easy implementation on manipulators with complex shapes, in addition to uniform-shaped manipulators. It is particularly beneficial for systems that involve more than two manipulators, as it tends to yield improved results in such cases [3]. Several researchers [11–16] have used AMM for the dynamics of flexible manipulators. Dynamics studies on flexible manipulators with payload are done in [17, 18]. In this technique, the shape functions are typically determined, assuming the links are cantilever beams in the local frame. However, for manipulators with complex shapes, it becomes challenging to determine the exact shape functions, making it impractical to simulate such manipulators using the assumed mode method (AMM). Nonetheless, due to its fewer state space equations, AMM is well-suited for simulating uniform-shaped manipulators. In the current research, as the manipulators are uniform-shaped, AMM is employed for modeling their dynamics. The equations of motion are derived using the hybrid Euler-Lagrangian equation and DeNOC matrices [19], which facilitate the transformation of uncoupled system equations into coupled system equations, as demonstrated by previous work [16]. The dynamics model is validated with literature before going to the control part.

Once an accurate dynamic model is established, the subsequent task involves designing a suitable controller to attain the desired performance. This is especially crucial for flexible manipulators, as they are more susceptible to vibration-related challenges compared to rigid manipulators. Achieving effective control in such scenarios is not a straightforward process. The controller utilized in this study combines open-loop input shaping techniques [20] with feedback control to effectively suppress vibrations during trajectory tracking. However, it is important to note that open-loop input shaping techniques can be sensitive to external disturbances and errors in system properties [5]. These factors need to be carefully considered and accounted for during the controller design process to ensure robust and reliable performance. The robustness analysis of these techniques has been studied by many researchers as reviewed by [21]. Indeed, the robustness of the input shaping techniques can be enhanced by incorporating higher modes or higher derivative shapers. By considering higher-order derivatives or incorporating additional modes in the shaping process, the controller becomes more capable of mitigating disturbances, reducing errors, and achieving improved robustness in vibration suppression during trajectory tracking. Under the feedback control, various techniques like PD control [22], time-delay based control [14], adaptive control [23] and sliding mode control [24, 25] etc. have been implemented in the literature. A PD control alone is implemented on a two-link rigid-flexible manipulator for controlling the position [26] with attached payload. A significant drawback of feedback controllers is their potential to excite modes that are not precisely modeled [5]. However, a promising approach is to design a controller combining both feedback control and input shaping techniques. By combining these two approaches, the controller can leverage the benefits of each technique simultaneously. The feedback controller helps in accurately tracking the desired trajectory and compensating for model uncertainties and disturbances, while the input shaping techniques aid in suppressing vibrations and reducing unwanted oscillations during the motion. This combined approach allows for improved control performance, better trajectory tracking, and enhanced vibration suppression than using either technique in isolation. The same has been done by some researchers [25, 27, 28]. The controller has been mostly implemented on a square or circular trajectory without any payload. This paper goes beyond the current standing of the controller, where it is implemented on a trajectory combining linear and circular paths by attaching the different payloads. The paper also presents the tracking of B-Splines trajectories. Our paper’s key novelty/contributions includes:

  1. 1.

    The main novelty of this paper is to track complex B-Splines trajectories using the hybrid controller, which is not reported in the literature to the best of the authors’ knowledge.

  2. 2.

    In the literature, most researchers focused on simpler trajectories like circular or square without considering any payloads. However, in the current manuscript, a demonstration of the controller in tracking complex trajectories containing both linear and circular paths, considering different payloads, has been presented.

  3. 3.

    The current manuscript also analyzes the impact of payload and configuration for a two-link flexible manipulator on the natural frequency.

In summary, researchers have utilized feedback controllers in combination with command shaping techniques, although there remains a need to evaluate the effectiveness of such controllers for trajectory combination of linear and curved paths with payload. This paper initially presents the dynamic modeling of two-link flexible manipulators in Sect. 2.1, validated using existing literature. In Sect. 2.2, a controller is designed by integrating command shaping techniques with a proportional-derivative (PD) controller to achieve the desired performance. The dynamic model’s validation is carried out prior to the implementation of the control scheme. Finally, in Sect. 3, the performance of hybrid controllers is compared with that of PD control when used independently for cases, with and without payload. The section also shows the tracking of B-Splines trajectory and the effect of flexibility. Finally, the paper ends with conclusions and future scope.

2 Simulation methodology

The first subsection presents the dynamic model of the two-link flexible manipulator. It describes the equations and methodology used to capture the system’s dynamics, including the payload.

The second subsection focuses on the controller design. This includes utilizing command shaping techniques and a proportional-derivative (PD) controller. The objective is to achieve the desired performance in terms of trajectory tracking and vibration suppression.

2.1 Dynamics model

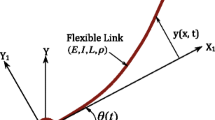
The dynamics of a two-link flexible manipulator, illustrated in Fig. 1, is established by modeling the links as Euler-Bernoulli beams. The deformation of the beams is calculated using the assumed mode method. For each link, two modes are taken into account in the transverse direction, effectively reducing the system with an infinite number of degrees of freedom to a system with only six degrees of freedom. The equations of motion are derived using a hybrid Euler-Lagrangian formulation along with DeNOC (Decoupled Natural Orthogonal Complements) matrices [19].

Fig. 1
figure 1

A two-link flexible manipulator system

Full size image

First, the mass matrix and convective inertia vector are formulated for the uncoupled links according to (1) and (2), respectively. The indices \(i=1\) and 2 represent the first and second links, respectively [16]. In these equations, \(\rho _{i}\) is mass density of links, \(\boldsymbol{{S}_{i}}\) being the shape function matrix, \(\bar{\boldsymbol{r}}_{i}\) is position vector of any point on \(i\)th link in its local frame, \(a_{i}\) is the link length, \(\bar{a}_{i}\) is variable distance along link length and \(\boldsymbol{\Omega}_{i}=\boldsymbol{\omega}_{i} \times \left [\left ( \boldsymbol{\omega}_{i} \times \overline{\boldsymbol{r}}_{{i}}\right )+ \boldsymbol{S}_{\boldsymbol{i}} \boldsymbol{\dot{d}}_{i}\right ]\), where \(\boldsymbol{\omega}_{i}\) is angular velocity vector and \(\boldsymbol{\dot{d}}_{i}\) is rate of elastic coordinates for link. The vector \(\boldsymbol{d}_{\boldsymbol{i}}\) is written as \(\left [d_{i 1} \hspace{0.2cm} d_{i 2}\right ]^{T}\).

$$ \boldsymbol{M}_{\boldsymbol{i}}=\int _{0}^{a_{i}} \rho _{i}\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{1} & -\overline{\boldsymbol{r}}_{i} \times \mathbf{1} & \boldsymbol{S}_{i} \\ & -\overline{\boldsymbol{r}}_{i} \times \left ( \overline{\boldsymbol{r}}_{i} \times \mathbf{1}\right ) & \overline{\boldsymbol{r}}_{i} \times \boldsymbol{S}_{i} \\ \operatorname{sym} & & \boldsymbol{S}_{i}^{T} \boldsymbol{S}_{ \boldsymbol{i}} \end{array}\displaystyle \right ] d \bar{a}_{i} $$
(1)
$$ \gamma _{i}=\int _{0}^{a_{i}} \rho _{i}\left [ \textstyle\begin{array}{c} \boldsymbol{\Omega}_{i} \\ \overline{\boldsymbol{r}}_{i} \times \boldsymbol{\Omega}_{i} \\ \boldsymbol{S}_{i}^{T} \boldsymbol{\Omega}_{i} \end{array}\displaystyle \right ] d \bar{a}_{i} $$
(2)

Then Newton-Euler’s form of equations can be written as shown in (3). In this equation, \(\boldsymbol{\dot{t}}\), \(\boldsymbol{\gamma}\), and \(\boldsymbol{w}^{*}\) are the rate of twist vector, Coriolis component vector, and wrench vector, respectively.

$$ M \boldsymbol{\dot{t}}+\boldsymbol{\gamma}=\boldsymbol{w}^{*} $$
(3)

Here, \(\boldsymbol{M}=\operatorname{diag}\left [\boldsymbol{M}_{1} \hspace{0.2cm} \boldsymbol{M}_{2}\right ]\) and \(\boldsymbol{\gamma}=\left [\boldsymbol{\gamma}_{1} \hspace{0.2cm} \boldsymbol{\gamma}_{2}\right ]^{T}\). Then DeNOC matrices [19] are written by satisfying the kinematics constraints. The DeNOC matrices \(\left (\boldsymbol{N}_{l}\right. \) and \(\boldsymbol{N}_{\boldsymbol{d}}\)) are shown in (4).

$$ \boldsymbol{N}_{l}=\left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol {1} & \boldsymbol {O} \\ \boldsymbol{A}_{21} & \boldsymbol {1} \end{array}\displaystyle \right ], \boldsymbol {N}_{d}=\left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol {P}_{1} & \boldsymbol{\hat{O}} \\ \boldsymbol{\hat{O}} & \boldsymbol {P}_{2} \end{array}\displaystyle \right ] $$
(4)

For \(i=1\) and 2,

$$ \boldsymbol{P}_{i}=\left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol{p}_{i} & \boldsymbol{0} \\ \mathbf{0} & \mathbf{\bar{I}}\end{array}\displaystyle \right ], \boldsymbol{p}_{i}=\left [ \textstyle\begin{array}{c} \mathbf{0} \\ \mathbf{z}_{i}\end{array}\displaystyle \right ], {\textbf{z}}_{i}=\left [ \textstyle\begin{array}{c} {0} \\ {0} \\ 1 \end{array}\displaystyle \right ] $$
$$ \boldsymbol{A}_{i, i-1}=\left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol{R}_{i, i-1} & \boldsymbol{F}_{i-1} \\ \widetilde{\boldsymbol{O}} & \overline{\boldsymbol{O}}\end{array}\displaystyle \right ] $$

Here,

$$ \boldsymbol{R}_{i, i-1}=\left [ \textstyle\begin{array}{c@{\quad}c} \boldsymbol{I} & \boldsymbol{a}_{i, i-1} \times \boldsymbol{I} \\ \boldsymbol {0} & \boldsymbol{I}\end{array}\displaystyle \right ], \boldsymbol{F}_{i}=\left [ \textstyle\begin{array}{c} \boldsymbol{S}_{i} \\ \boldsymbol {\Delta}_{i}\end{array}\displaystyle \right ] $$

.

$$ \boldsymbol{S}_{i}=\left [ \textstyle\begin{array}{c@{\quad}c} 0 & 0 \\ S_{i 1} & S_{i 2} \\ 0 & 0\end{array}\displaystyle \right ] $$

\(\boldsymbol{a}_{i, i-1}\) is the vector from \(O_{i}\) to \(O_{i-1}, \hspace{0.15cm} \boldsymbol {\Delta}_{i}\) is associated with the derivative of shape functions. \(\boldsymbol{S}_{i}\) is the shape function matrix, here \({S}_{i1}\) and \({S}_{i2}\) are the shape functions corresponding to first and second modes, respectively. The order of matrix \(\boldsymbol{M}\) and \(\boldsymbol{N}_{\boldsymbol{l}}\) is same and equal to \(16 \times 16\), while the order of matrix \(\boldsymbol{N}_{\boldsymbol{d}}\) is \(16 \times 6\), and \(\boldsymbol{p}_{i}\) is vector of order \(6 \times 1\). The unit matrices \(\boldsymbol {1}\), \(\boldsymbol{I}\), and \(\mathbf{\bar{I}}\), while zero matrices/vectors \(\mathbf{0}\), \(\boldsymbol{O} \), \(\widetilde{\mathbf{O}} \), \(\overline{\mathbf{O}}\), and \(\hat{\mathbf{O}}\) are taken as per the order compatibility of full matrix or vector.

By pre-multiplying equation (3) with the transpose of the product of DeNOC matrices, the coupled equations for the two links can be obtained [16]. This process helps eliminate the constraints and yields the final equations corresponding to the generalized coordinates. After performing the DeNOC matrices multiplication and eliminating the constraints, the system equations are reduced to a set of six equations representing the generalized coordinates. These equations capture the dynamics of the two-link flexible manipulator and provide a concise representation of the system’s behavior.

$$ \boldsymbol{N}_{d}^{T} \boldsymbol{N}_{l}^{T}(\boldsymbol{M} \dot{\boldsymbol{t}}+\boldsymbol {\gamma})=\boldsymbol{N}_{d}^{T} \boldsymbol{N}_{l}^{T} \boldsymbol {w}^{*}=\boldsymbol{\tau}= \boldsymbol{\tau}^{E}+\boldsymbol{\tau}^{g}+\boldsymbol{\tau}^{s} $$
(5)

The vector of generalized coordinate is written as \(\boldsymbol{q}=\left [\theta _{1} \hspace{0.1cm} d_{11} \hspace{0.1cm} d_{12} \hspace{0.1cm} \theta _{2} \hspace{0.1cm} d_{21} \hspace{0.1cm} d_{22}\right ]^{T}\) and twist vector and its rate in terms of DeNOC matrices are written as \(\boldsymbol {t}=\boldsymbol {N}_{l} \boldsymbol{N}_{d} \dot{\boldsymbol{q}}\) [16] and \(\dot{\boldsymbol{t}}=\boldsymbol{N}_{l} \boldsymbol{N}_{d} \ddot{\boldsymbol{q}}+\dot{\boldsymbol{N}}_{l} \boldsymbol{N}_{d} \dot{\boldsymbol{q}}+\boldsymbol{N}_{l} \dot{\boldsymbol{N}}_{d} \dot{\boldsymbol{q}}\), respectively. The final equations are written as shown in (6) after all multiplications, where \(\boldsymbol{I}=\boldsymbol{N}_{\boldsymbol{d}}^{T} \boldsymbol{N}_{l}^{T} \boldsymbol{M} \boldsymbol{N}_{\boldsymbol{l}} \boldsymbol{N}_{ \boldsymbol{d}}\) and \(\boldsymbol{h}=\) \(\boldsymbol{N}_{\boldsymbol{d}}^{T} \boldsymbol{N}_{l}^{T} \bigl( \boldsymbol{M}\bigl (\boldsymbol{N}_{l} \dot{\boldsymbol{N}}_{ \boldsymbol{d}}+\dot{\boldsymbol{N}}_{\boldsymbol{l}} \boldsymbol{N}_{ \boldsymbol{d}} \bigr) \dot{\boldsymbol{q}}+ \boldsymbol{\gamma} \bigr)\). The vectors \(\boldsymbol{\tau}^{E}, \boldsymbol{\tau}^{g}\), and \(\boldsymbol{\tau}^{s}\) are the generalized force vectors corresponding to actuator efforts, gravitational forces, and strain energy respectively. The strain energy for bending is calculated by (7); here, \(V_{s}\) is the strain energy of links due to deformation.

$$ \boldsymbol{I} \ddot{\boldsymbol{q}}+\boldsymbol{h}=\boldsymbol{\tau}^{E}+ \boldsymbol{\tau}^{g}+\boldsymbol{\tau}^{s} $$
(6)
$$ \boldsymbol{\tau}^{s}= \frac {\partial V_{s}}{\partial \boldsymbol{q}_{i}}, \hspace{0.2cm} \text{ where } \hspace{0.2cm} V_{s}=\sum _{i=1}^{n} \frac{1}{2} \int _{0}^{a_{i}} E I_{z z}\left ( \frac{\partial ^{2} \boldsymbol{S}_{i} \boldsymbol{d}_{i}}{\partial \bar{a}_{i}^{2}} \right )^{2} d \bar{a}_{i} $$
(7)

2.1.1 Paylaod related matrix and vector

In this subsection, the inertia matrix and vector of the Coriolis component related to the payload attached at the end-effector are calculated. These calculations are necessary to account for the additional mass and inertial effects caused by the payload. This allows designing control strategies and analyzing the system’s response with better accuracy, considering the influence of the payload on the manipulator’s motion. The kinetic energy of payload mass is written as (8). In this, \(m_{p}\) is the mass of the payload, and \(\dot{\boldsymbol{r}}_{p}\) is the position vector of the end-effector.

$$ {T}_{p}=\frac{1}{2} m_{p} \dot{\boldsymbol{r}}_{p}^{T} \dot{\boldsymbol{r}}_{p} $$
(8)

Here,

$$ \boldsymbol{r}_{p} = \boldsymbol{Q_{1}} \left ( \left [ \textstyle\begin{array}{c} l_{1} \\ u_{1}(l_{1},t) \\ 0 \end{array}\displaystyle \right ] + \boldsymbol{Q_{2}}\boldsymbol{Q_{\gamma}} \left [ \textstyle\begin{array}{c} l_{2} \\ u_{2}(l_{2},t) \\ 0 \end{array}\displaystyle \right ] \right ) $$
$$ \boldsymbol{Q_{r}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} cos(\theta _{r}) & -sin(\theta _{r})&0 \\ sin(\theta _{r}) & cos(\theta _{r}) & 0 \\ 0&0&1 \end{array}\displaystyle \right ] \hspace{0.3cm} $$

In this, r = 1, 2, \(\gamma \) (slope of first link tip).

Now using \(\dot{\boldsymbol{r}}_{p} = \boldsymbol{J} \dot{\textbf{q}}\), where \(J\) is Jacobian, the kinetic energy can be written as (9).

$$ {T}_{p} = \frac{1}{2} m_{p} \dot{\boldsymbol{q}}^{T} {\boldsymbol{J}}^{T} \boldsymbol{J} \dot{\boldsymbol{q}} $$
(9)

To continue the derivation using the Lagrangian equation on kinetic energy and assuming there is no potential energy due to the absence of gravity on the payload, one can derive the mass matrix and the vector of convective inertia as follows:

$$\begin{aligned} \boldsymbol{I}_{p} &= m_{p} \boldsymbol{J}^{T} \boldsymbol{J} \end{aligned}$$
(10a)
$$\begin{aligned} \boldsymbol{h}_{p} &= \dot{\boldsymbol{M}} \dot{\boldsymbol{q}} - \frac{\partial T_{p}}{\partial \boldsymbol{q}} \end{aligned}$$
(10b)

The final inertia matrix and vector of convective inertia are written as \(\boldsymbol{I}+\boldsymbol{I}_{p}\) and \(\boldsymbol{h}+\boldsymbol{h}_{p}\), respectively, in (6).

2.2 Controller design

To achieve the desired end effector path shown in Fig. 2a while minimizing vibrations, a controller is developed by combining command shaping techniques with a proportional-derivative (PD) feedback controller, as shown in Fig. 2b. This section will provide a more detailed explanation of the command shaping technique and the proportional-derivative (PD) controller, discussing each of them separately.

Fig. 2
figure 2

(a) Desired trajectory to be tracked and (b) Block diagram of complete system

Full size image

2.2.1 Command shaping techniques

The objective is to attain a vibration-free response when tracking trajectories with flexible manipulators. This is accomplished by applying of command shaping techniques [20], wherein residual vibrations are suppressed by a series of carefully timed and appropriately scaled impulses. It is well understood that the superposition of second-order systems can show any \(n\)th order system. The transfer function of such a second-order damped system can be given by (11).

$$ G(s)= \frac {\omega _{n}^{2}}{\left (s^{2}+2 \zeta \omega _{n}+\omega _{n}^{2}\right )} $$
(11)

Here, \(\omega _{n}\) and \(\zeta \) are the natural frequency and damping ratio of the system. The impulse response of the second-order system is given by (12). Here, \(A\) is the impulse magnitude at time (\(t_{0}\)).

$$ y(t)=\frac {A \omega _{n}}{\sqrt{1-\varsigma ^{2}}} e^{-\omega _{n} \varsigma \left (t-t_{0}\right )} \sin \left (\omega _{n} \sqrt{1- \varsigma ^{2}}\left (t-t_{0}\right )\right ). $$
(12)

Using the principle of superposition, the response of the sequence of \(\mathrm{N}\) impulse can be found as \(y(t)=P \sin \left (\omega _{d} t+\right. \) \(\beta )\), where

$$\begin{aligned} &\omega _{d}=\omega _{n} \sqrt{1-\varsigma ^{2}}, P=\sqrt{\left (\sum _{i=1}^{N} P_{i} \cos \left (\omega _{d} t_{i} \right )\right )^{2}+\left (\sum _{i=1}^{N} P_{i} \sin \left (\omega _{d} t_{i}\right )\right )^{2}} \quad \text{and} \\ & P_{i}= A_{i} \omega _{n} / \sqrt{1-\varsigma ^{2}} e^{-\omega _{n} \varsigma \left (t-t_{0}\right )}. \end{aligned}$$

Here, \(A_{i}\) and \(t_{i}\) are the amplitude and time instants of the \(i\)th impulse. The Magnitude of Single-mode residual vibration is obtained (13), as the outcome of the sequence of impulses. \(N\) is the number of impulses in sequence and \(t_{N}\) is the time location of last impulse.

$$ V\left (\omega _{n}, \varsigma \right )=e^{-\omega _{n} \varsigma t_{N}} \sqrt{V_{c}^{2}+V_{s}^{2}} $$
(13)
$$ V_{c}=\sum _{i=1}^{N} A_{i} e^{\zeta \omega _{n} t_{i}} \cos \left ( \omega _{d} t_{i}\right ) \quad \text{ and } \quad V_{s}=\sum _{i=1}^{N} A_{i} e^{\varsigma \omega _{n} t_{i}} \sin \left (\omega _{d} t_{i} \right ) $$

ZVDD (Zero Vibration and Double Derivative) shaper: It is possible to divide a single impulse into a sequence of impulses by imposing constraints on the magnitude of impulses and vibrations. This technique is referred to as ZV (Zero Vibration) and ZVD (Zero Vibration Derivative) shaping when an impulse is divided into two and three impulses, respectively. In order to enhance robustness, higher-order shapers are typically employed, and one such example is the ZVDD (Zero Vibration and Derivative-Derivative) shaper. The final time and amplitude variables for ZVDD shaper are shown in (15) after solving constraints (14), where \(M=e^{-\zeta \pi / \sqrt{1-\zeta ^{2}}}\).

$$ V\left (\omega _{n}, \varsigma \right )=0, \hspace{0.2cm} \frac {\partial V}{\partial \omega _{n}}=0, \hspace{0.2cm} \frac {\partial ^{2} V }{\partial \omega _{n}{ }^{2}}=0, \hspace{0.2cm} \sum _{i=1}^{4} A_{i}=1 \hspace{0.2cm} { and } \hspace{0.2cm} A_{i}>0 \hspace{0.1cm} { for \hspace{0.1cm} all } \hspace{0.1cm} i $$
(14)
$$ \left [ \textstyle\begin{array}{c} A \\ t \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac{1}{1+3 M+3 M^{2}+M^{3}} & \frac{3 M}{1+3 M+3 M^{2}+M^{3}} & \frac{3 M^{2}}{1+3 M+3 M^{2}+M^{3}} & \frac{M^{3}}{1+3 M+3 M^{2}+M^{3}} \\ 0 & \frac{\pi}{\omega _{d}} & \frac{2 \pi}{\omega _{d}} & \frac{3 \pi}{\omega _{d}} \end{array}\displaystyle \right ] $$
(15)

2.2.2 Proportional-Derivative (PD) controller

For trajectory tracking, a PD controller is utilized as a feedback system. The expression for the input torque vector in PD control is represented in (16). In this case, the feedback is solely based on the rigid coordinates, which are used to compute the necessary torque. Here \(\boldsymbol{\theta}_{\boldsymbol{d}}\) and \(\boldsymbol{\theta}_{\boldsymbol{a}}\) are the vector of desired and actual hub angles of links, while \(\boldsymbol{K}_{\boldsymbol{p}}\) and \(\boldsymbol{K}_{\boldsymbol{d}}\) are the gain for feedback. Vector \(\boldsymbol{\theta}_{\boldsymbol{d}}\) is computed through the application of inverse kinematics to the manipulator system. In order to achieve rest-to-rest motion, the tip acceleration is assumed to follow a bang-bang pattern. By integrating the tip acceleration once and twice, the tip velocity and position, respectively, are obtained. A trajectory is exactly tracked by optimizing \(\boldsymbol{K}_{\boldsymbol{p}}\) and \(\boldsymbol{K}_{\boldsymbol{d}}\) for rigid manipulators before going to a flexible system. After several iterations, considering the manipulators as rigid, the exact trajectory has been successfully tracked using \(\boldsymbol{K}_{\boldsymbol{p}}=\operatorname{diag}\left [ \begin{array}{l@{\quad}l} 200 & 200\end{array} \right ]\) and \(\boldsymbol{K}_{\boldsymbol{d}}=\) \(\operatorname{diag}\left [ \begin{array}{l@{\quad}l} 10 & 10\end{array} \right ]\). The gains are very high written as\(\boldsymbol{K}_{ \boldsymbol{p}}=\operatorname{diag}\left [ \begin{array}{l@{\quad}l} 5000 & 5000\end{array} \right ]\) and \(\boldsymbol{K}_{\boldsymbol{d}}=\) \(\operatorname{diag}\left [ \begin{array}{l@{\quad}l} 100 & 100\end{array} \right ]\) for B-splines trajectory tracking. The simulations are done in three key steps. Firstly, gains are optimized using rigid manipulators to achieve precise trajectory tracking. Next, the investigation shifts to assess the impact of flexibility while maintaining other factors the same. Finally, the study employs command shaping techniques in the third step to mitigate vibrations arising from flexibility. In essence, the consistent use of gains in the first and second steps enables an evaluation of flexibility’s effects, while applying command shaping in the third step aims to diminish vibration levels associated with the flexible manipulator.

$$ \tau =\boldsymbol{K}_{p}\left (\boldsymbol{\theta}_{d}- \boldsymbol{\theta}_{a}\right )+\boldsymbol{K}_{d}\left ( \dot{\boldsymbol{\theta}}_{d}-\dot{\boldsymbol{\theta}}_{a}\right ) $$
(16)

3 Results and discussion

3.1 Dynamics model validation

First, the dynamic model is validated, then the controller is implemented to get the vibration suppression. For the validation of the dynamic model, links length are kept as \(1 \mathrm{~m}\) while \(E I_{z z}=1000 \hspace{0.1cm} \mathrm{Nm}^{2}\), where \(E\) is Young’s modulus of elasticity, and \(I_{z z}\) is the area moment of inertia in bending. The free fall simulation is done under gravity, where initial angles are kept as −90° and 5° for the first and second link, respectively.

The hub angles for the first link and second link are shown in Fig. 3a and 3b, while tip deflections for the same are shown in Fig. 3c and 3d, respectively. The results are found to be very close to the literature [16].

Fig. 3
figure 3

Hub angle and tip deflection variation with respect to time

Full size image

3.2 Trajectory tracking

After validation of the dynamic model, a simulation is done for tracking the semicircular trajectory using a two-link flexible manipulator. The links are of length \(0.5 \hspace{0.1cm} \mathrm{~m}\), made of material with density \(7850 \hspace{0.1cm} \mathrm{Kg} / \mathrm{m}^{3}\), and modulus of elasticity equals to \(210 \hspace{0.1cm} \mathrm{GPa}\). The cross-section of links is in the form of a rectangle with thickness \(2 \mathrm{~mm}\) and width \(27 \mathrm{~mm}\). The center of the semicircular trajectory of radius \(15 \mathrm{~cm}\) is at \(75 \mathrm{~cm}\) from the fixed joint of the manipulator, as shown in Fig. 2a.

The motion initiates from an extreme point and concludes at the same point, ensuring complete trajectory tracking. MATLAB was utilized to determine the natural frequency and damping ratio as \(3.6139 \mathrm{~Hz}\) and 0.025, respectively, at the extreme point. During the tracking process, variation in the natural frequency due to changes in the configuration has been considered in calculations. The overall trajectory duration is 3 seconds, with 2 seconds allocated for the semicircular path and 1 second for the linear path. Figure 4a and 4b display the tip acceleration and position, respectively, for the semicircular path. The tip velocity can be inferred by integration of the tip acceleration plot or slope of tip position plot. It is evident that the tip velocity initially begins from zero, then increases, subsequently decreases, and eventually settles back to zero. This pattern facilitates achieving a rest-to-rest motion.

Fig. 4
figure 4

Tip acceleration and position along the semicircular path (Color figure online)

Full size image

The inverse kinematics and Jacobian calculations are employed to determine the hub angles and hub angular velocities as functions of time for both links. Figure 5a displays the shaped and unshaped hub angles for the first link, while Fig. 5b represents the shaped and shaped hub angles for the second link.

Fig. 5
figure 5

Hub angles along complete trajectory (Color figure online)

Full size image

Tip deflection obtained for the first and second links are shown in Fig. 6a and 6b, respectively. It is clear that deflections have been reduced using the command shaping, with some time delay. The maximum deflections for the first link and second link are \(6.334 \mathrm{~mm}\) and \(1.135 \mathrm{~mm}\) without shaping, while the same has been reduced to around \(4.468 \mathrm{~mm}\) and \(0.8729 \mathrm{~mm}\) with command shaping, respectively. The end effector position while tracking the trajectory is shown in Fig. 10a. The maximum errors between desired and obtained trajectory are \(6.887 \mathrm{~mm}\) and \(8.242 \mathrm{~mm}\), which has been reduced to \(5.214 \mathrm{~mm}\) and \(3.041 \mathrm{~mm}\) for the curved and linear part, respectively, of the trajectory using command shaping. The time delay for tracking the trajectory is 0.6966 sec, which is almost twice the length of the shaper, as shaping is done separately for the curved and linear parts of the path.

Fig. 6
figure 6

Tip deflections along complete trajectory (Color figure online)

Full size image

3.3 Effect of payload

This subsection analyzes the effect of the payload attached to the end-effector of a two-link manipulator on the natural frequency, tip deflections, and tracking control.

As the manipulator moves along the trajectory, the end-effector reaches different points (P1, P2, P3, and P4), shown in Fig. 2a, causing changes in the system’s configuration. These changes in configuration lead to variations in the natural frequency of the system, as depicted in Table 1. The percentage difference with respect to the natural frequency at P1 is presented in both Table 1 and Table 2, reflecting the combined influence of the system’s configuration and the attached payload.

Table 1 Effect of configuration on natural frequency [Hz]
Full size table
Table 2 Effect of payload on natural frequency (Hz)
Full size table

The effect of the attached payload on tip deflection is shown in Fig. 7a and Fig. 7b for the first and second links, respectively, when command shaping is not active. The impact is also depicted in Fig. 8a and Fig. 8b when command shaping is active. It is clear from the figures that the payload has a significant effect on tip deflection, while command shaping tends to reduce it. Tip deflection for the first link has been reduced from 6.334 mm to 4.468 mm, and the second link tip deflection has been reduced from 1.135 to 0.8729 for the case without any payload. Further, for the case with a 25-gm payload, the first link tip deflection was suppressed from 6.443 mm to 5.011 mm, and the second link tip deflection was reduced from 2.193 mm to 0.8729 mm. The tip deflection for the first link has been reduced from 9.849 mm to 7.37 mm using command shaping with a 100-gm payload. The same has been suppressed from 5.51 mm to 2.802 mm using command shaping with a 100-gm payload for the second link.

Fig. 7
figure 7

Tip deflections for the first link and second links without command shaping

Full size image
Fig. 8
figure 8

Tip deflections for the first link and second links with command shaping

Full size image

In Fig. 9a, the end-effector path, with and without the payload is shown when command shaping is not active. It visually demonstrates how the presence of the payload affects the trajectory followed by the end-effector. In Fig. 9b, the end-effector path with and without the payload is depicted when command shaping is active. This comparison helps us understand the impact of command shaping on the trajectory and how it mitigates the effects of the payload, resulting in a more controlled and desired end-effector path. In Fig. 10, the comparison of the end-effector path is presented for both shaped and unshaped input signals. The results are shown for two scenarios: without any payload and with a payload of 100 grams. The tracking error without any payload has already been discussed. The tracking error with 100 gm payload has been reduced from 12 mm and 7.099 mm to 7.41 mm and 3.188 mm for curved and linear paths, respectively, using command shaping. This comparison allows us to assess the effectiveness of the shaping technique in achieving the desired end-effector path while considering the presence of a payload. By examining the trajectories in both cases, we can observe the influence of input shaping on reducing the deviations caused by the payload and improving the tracking performance of the manipulator.

Fig. 9
figure 9

End-effector path with and without a payload

Full size image
Fig. 10
figure 10

End-effector path for shaped and unshaped commands

Full size image

3.4 B-splines tracking

This section focuses on the tracking of B-Spline curves and compares the effects of flexibility with a rigid system. Then, presenting the vibration suppression by implementing a command shaping-based controller. Two B-Splines curves, namely BS1 and BS2, as shown in Fig. 11, are generated using control points for analysis. The B-Splines curves, BS1 and BS2 are constructed using five control points, as depicted in Fig. 11. Initially, a rigid body model is employed to track these trajectories, and the gains are optimized to achieve a close match with the desired trajectory. However, it is observed that tracking such complex trajectories necessitates the utilization of higher gain values. The specific values of the gains utilized in this study are mentioned in Sect. 2.2.2.

Fig. 11
figure 11

B-Splines curves used for tracking

Full size image

Once the rigid body model successfully tracks the B-Splines curves using the optimized gains, the same gain values are then employed for trajectory tracking with the flexible body model. This approach allows for a direct comparison between the rigid and flexible body models in terms of flexibility. The B-Splines tracking is shown in Fig. 12. For BS1, the trajectory tracking error is found to be around 7-8 cm, with the maximum value being more than 10 cm at different locations. The same for BS2 has been found around 5-7 cm at different locations. It is observed that the tracking error is higher compared to the trajectory discussed in Sect. 3.2. This indicates the need for a more robust controller to achieve accurate tracking of complex B-Splines trajectories. The flexibility and non-linear characteristics of the manipulator introduce additional challenges in reducing tracking errors. To achieve that in the case of B-Splines trajectories, command shaping is implemented. Joint torques are calculated using the command-shaped feedforward plus proportional-derivative feedback control [29]. The results are shown in Fig. 13. It is worth mentioning that the tracking error has been reduced for both curves significantly, specifically when the end-effector approaches the endpoint. For BS1, the maximum tracking error has been reduced to 1.6 cm, while the same is close to a few millimeters around the most part of the trajectory. For BS2, the maximum tracking error has been reduced to approximately 2 cm, while the same is close to a few millimeters around the most part of the trajectory.

Fig. 12
figure 12

Tracking of curves by rigid and flexible systems

Full size image
Fig. 13
figure 13

Vibration suppression during tracking of curves for flexible system

Full size image

4 Conclusions

The paper demonstrates the performance of a hybrid controller in tracking a complex trajectory that combines curved and linear paths compared to trajectories available in the literature, which are either pure linear or circular by attached payload at the end-effector. Prior to the control study, the dynamics of a two-flexible manipulator system are developed considering two modes in the transverse direction. The equations of motion are derived using a hybrid Euler-Lagrangian formulation and DeNOC matrices. The dynamics model is initially validated before proceeding to the control analysis.

For control purposes, a hybrid controller is designed, combining command shaping techniques with a proportional derivative (PD) feedback controller. The feedback controller ensures accurate trajectory tracking, while the command shaping techniques aim to suppress vibrations during trajectory tracking. The effects of command shaping are clearly illustrated in the results and compared with the results obtained without command shaping.

The performance of the controller is evaluated with both with and without payload cases using a semicircular trajectory that needs to be tracked within a time frame of 3 seconds. The effect of change in configuration and different payloads on natural frequency while tracking has been calculated and presented in detail. The proposed control scheme effectively suppresses vibrations in both cases, with and without attached payload. The results include the tip deflections for both links with shaped and unshaped input commands for both cases: with and without attached payload. The degree of vibration suppression along the trajectory is quantified and presented in the results. The paper also explores the tracking of complex B-Splines trajectories, where it needs a high value of gains. The tracking error is calculated to show the effect of link flexibility. Further, vibration suppression has been achieved using command shaping. The paper shows the robustness of the controller with respect to the trajectory and payload. In the future, the controller will be implemented in the experimental setup.