Symbolic integration of multibody system dynamics with the finite element method

Abstract

With the widespread use of computer-aided engineering (CAE) to solve computational mechanics problems, engineering design has become more accurate and efficient. The integration of the finite element method (FEM) and flexible multibody dynamics (FMD) is a typical application of computational mechanics. It constitutes an important contribution to engineering development, but its potential is restrained by numerical computation. Computational time is a critical factor that influences the efficiency and cost of design and analysis. The advent of symbolic computation enables faster simulation code, but the symbolic integration of FEM and FMD is at the initial stages. A general symbolic integration procedure is presented in this paper. The performance of the symbolic model is compared with models from the literature and numerically-based commercial software.

1 Introduction

The advent of symbolic programming enables faster simulation code, via which the development of FMD has made significant achievements [20, 22, 28] that show better performance over numerically-based simulations. There are several symbolically-based FMD software packages, such as Dymola and Robotran, which have libraries of flexible beams and plates to increase the fidelity of system-level models. However, since all these flexible bodies use classical variational methods [12], their usage is limited to simple geometries.

The symbolic integration of FMD with FEM is at the initial stages, and publications in this area are scarce. Certain researchers have demonstrated simple integration examples using the Modelica symbolic language [30] in Dymola and shown dramatic reduction of computational cost compared with numerical computation [11], but the detailed process of implementation is not presented.

The method described in this paper is a general way of implementation using symbolic computation via MapleSim, which is a multi-domain physical modeling environment built on Maple’s technology that provides users with a general-purpose symbolic computation environment. The dynamic equations of a flexible beam based on the finite-element approach [24] are explicitly derived in symbolic form first, which are modified specifically to realize the implementation. Newly-defined explicit expressions regarding the geometric stiffening nonlinearity are derived based on the classic Rayleigh beam theory, which is specific for the nodal approach. In addition, the graph-theoretical (GT) method [28] is used to implement the FMD system equations in MapleSim. With this approach, highly-optimized system equations are generated.

There are two main approaches, which differ in the selection of coordinate systems, used to formulate the dynamic equations of motion of deformable bodies in FMD: the floating frame of reference (FFR) [25] and absolute nodal coordinate (ANCF) methods [26]. A large amount of research work has been done to validate the functionality of the two methods in the analysis of flexible beams [3, 5].

FFR is currently the mainstream approach adopted by most commercial FMD software packages. This method defines the configuration of the flexible body in terms of two sets of coordinates: reference coordinates and elastic coordinates. Reference coordinates define the location and orientation of a selected body-fixed frame. Elastic coordinates describe the body deformation with respect to the body-fixed frame. The potential energy defined using these local elastic coordinates yields a simple expression assuming small strains. The expressions of the kinetic energy as well as the virtual work of the forces, however, are highly nonlinear since they are written in terms of coupled reference and elastic coordinates. As a result, FFR will generate a simple and usually constant stiffness matrix while unavoidably yielding a deformation-dependent mass matrix and nonlinear inertia forces. This approach is widely used and proven efficient in modeling flexible bodies under large overall motion with small deformation [23–25].

ANCF, according to its name, uses coordinates with respect to the inertia frame directly to define the configuration of the deformable body. Its conceptual difference in the formulation makes it effective in modeling deformable bodies with large deformation since it uses no infinitesimal rotations as elastic coordinates. The difference also comes with the fact that due to the elimination of the coupling of reference and elastic coordinates, the mass matrix becomes constant, which no longer depends on the body deformation. However, using absolute coordinates will bring complexity into the formulation of continuum mechanics because the stiffness matrix turns to be nonlinear even in the case of a linear elastic body with small deformation [26].

A number of test problems have been developed to compare these two methods [6, 9, 10]. Most of the cases show a good agreement between the two approaches, but some cases indicate results diverge when the deformation of the body is large [10]. Although ANCF has been used by many researchers to analyze flexible multibody problems, the ANCF technology is not yet well developed as demonstrated by the study presented in [4].

The FEM formulation presented in this article is based on FFR for 3 key reasons:

• 1. Small deformation is often assumed for FMD problems.

• 2. Body-fixed frames cooperate well with the symbolically pre-defined joint connectors (revolute, prismatic, etc.) built in MapleSim to solve rotating beam problems.

• 3. A general approach, which has been widely accepted, is sought for the symbolic FEM-FMD development at the initial development stage.

The Bernoulli–Euler (BE) beam theory [1] is usually the first choice to formulate the flexible beam equations considering that the deformable components in multibody systems are often slender links. The Rayleigh beam has the same properties as the BE beam while it adds cross-sectional rotary inertia to the BE formulation. The key assumption under the BE theory is the plane sections of the beam initially perpendicular to the centroidal axis will remain plane and perpendicular to the axis after deformation, which implies that the shear strain and stress are zero. As pointed out in [1], this formulation can be used for load cases wherein stresses due to bending are the most significant. Another critical assumption states that accurate description of the beam deformation will only be guaranteed under small deflection with small strains. Based on empirical data, it is estimated that the maximum deflection ratio of the tip deformation over the beam length to be $10\%$, and errors will become intolerable if beyond this limit. Certain cases involving large and fast rigid-body motion of the flexible body lead to the inexact modeling of the deformation by using the conventional formulation. Theoretically, the assumption of small strains omits higher-order terms in the full strain energy expression [27]. This hypothesis decouples different types of deformation (bending, axial, and torsion), and the uncoupled bending and axial deformations result in the failure to model the dynamic stiffening effect. This effect, usually referred to as geometric elastic nonlinearity [18], is critical in FMD when the deformable components undergo large and fast rigid-body motions.

A number of mathematical modifications [2, 7, 18] based on the original BE formulation have been developed to tackle geometric elastic nonlinearity. However, these modal-based methods suffer from computational inefficiency due to the necessity to include many axial deformation modes to approximate the displacement field. An alternative formulation derived by Mayo and Dominguez [17] manually added a foreshortening term in the expression of axial displacement field. This approach distinguishes the shortening-induced and strain-induced displacements, and yields the traditionally constant stiffness matrix. The nonlinearity was moved from the elastic forces to inertia, external, and reactive forces. This approach is computationally efficient [16] and widely used in numerous examples [15, 21] to approximate the stiffening effect. The foreshortening formulation is added in the Rayleigh beam formulation in this article, and the associated terms are symbolically expressed in explicit form that we could not find in other publications.

2 Symbolic finite-element modeling of 3D flexible beams with geometrical nonlinearity

2.1 Global position vector

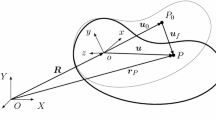
The global position vector $\mathbf{{r}}^{i}$ is used to locate an arbitrary point $P$ on the $i$th element of the flexible body shown in Fig. 1 with respect to the inertia frame $XYZ$. The velocity and acceleration vectors differentiated from the global position vector are used, respectively, to integrate the kinetic energy and virtual work, from which the mass matrix and inertia forces are extracted.

Fig. 1

Finite-element beam coordinate systems and position vectors ($P_{0}$ refers to the point $P$ before deformation)

The global position vector, using the conventional displacement fields, is defined by Shabana [24] as

$$ {\mathbf{{r}}^{i}} = \mathbf{{R}} + \mathbf{{A}} { \mathbf{{u}}^{i}} = \mathbf{{R}} + \mathbf{{A}} \bigl( \mathbf{{u}}_{0}^{i} + \mathbf{{u}}_{f}^{i} \bigr) , $$

(2.1)

where the position vector ${\mathbf{{r}}^{i}}$ is written in terms of the reference coordinates $\mathbf{{R}}$, which defines the location of the body-fixed frame $xyz$, and the local position vector ${{\mathbf{{u}}} ^{i}}$ of point $P$ is shown in Fig. 1; $\mathbf{{A}}$ is the rotation matrix of $xyz$ relative to $XYZ$; ${{\mathbf{{u}}}^{i}}$ can be seen as the summation of the local position vector in the undeformed state ${\mathbf{{u}}_{0}^{i}}$ and the local displacement vector ${\mathbf{{u}}_{f}^{i}}$ defined, respectively, as

$$\begin{aligned} \mathbf{{u}}_{0}^{i} &= {\mathbf{{N}}^{i}} { \mathbf{{q}}_{0}}, \end{aligned}$$

(2.2)

$$\begin{aligned} \mathbf{{u}}_{f}^{i} &= {\mathbf{{N}}^{i}} { \mathbf{{B}}_{2}} {\mathbf{{q}}_{f}}, \end{aligned}$$

(2.3)

where $\mathbf{B}_{2}$ is a linear transformation matrix [24] that arises from imposing the fixed-free reference condition, and to eliminate inactive deformation coordinates; $\mathbf{q}_{0}$ is the vector of original values of the nodal coordinates in the undeformed state; $\mathbf{q}_{f}$ contains the time-variant nodal deformation coordinates; the matrix $\mathbf{N} ^{i}$ is defined as

$$ {\mathbf{{N}}^{i}} = {\mathbf{{S}}^{i}} { \mathbf{{B}}}_{1}^{i}, $$

(2.4)

where $\mathbf{{S}}^{i}$ is the shape function matrix defined for beam elements, and $\mathbf{{B}}_{1}^{i}$ is the connectivity matrix used to associate the nodal coordinates for the $i$th element from ${\mathbf{{q}}_{0}}$ and ${\mathbf{{q}}_{f}}$ [24]. Substituting Eqs. (2.2) and (2.3) into Eq. (2.1), the local and global position vectors can be written in terms of the reference and nodal coordinates as

$$\begin{aligned} \mathbf{{u}}^{i} &= {\mathbf{{N}}^{i}} { \mathbf{{q}}_{n}} , \end{aligned}$$

(2.5)

$$\begin{aligned} {\mathbf{{r}}^{i}} &= \mathbf{{R}} + \mathbf{{A}} { \mathbf{{N}}^{i}} {\mathbf{{q}} _{n}} , \end{aligned}$$

(2.6)

where ${\mathbf{{q}}_{n}}$ is the vector of total nodal coordinates defined as

$$ {\mathbf{{q}}_{n}} = {\mathbf{{q}}_{0}} + { \mathbf{{B}}_{2}} {\mathbf{{q}}_{f}} . $$

(2.7)

Using the method of Mayo and Dominguez [17], the foreshortened local position vector $\mathbf{{u}}_{G}^{i}$ is derived by adding a foreshortening value in the axial displacement of the local position vector ${{\mathbf{{u}}}^{i}}$ in Eq. (2.1):

$$ \mathbf{{u}}_{G}^{i} = {{\mathbf{{u}}}^{i}} + \left \{ \textstyle\begin{array}{c} u_{s}^{i} \\ 0 \\ 0 \end{array}\displaystyle \right \}, $$

(2.8)

where the subscript $G$ refers to the geometrically nonlinear formulation, and $u_{s}^{i}$ represents a negative foreshortening value in the axial direction. The foreshortening amount of a single element can be calculated as

$$ {u_{s}^{ei}} = - \frac{1}{2} \int_{0}^{l_{i}} \bigl(u'_{fy}{}^{2} + u'_{fz} {}^{2} \bigr)\,dx , $$

(2.9)

where $l_{i}$ is the length of the element, $u_{fy}$ and $u_{fz}$ are the transverse displacements along $y$ and $z$ directions, and the prime (′) denotes the derivative with respect to $x$. To calculate the total foreshortening of a beam discretized by more than one finite element, some critical factors must be considered. When the beam has several finite elements, the foreshortening calculated in Eq. (2.9) only represents the shortened amount produced in that element by its own deflection instead of the whole amount with respect to the base frame. Even though the nodal coordinates represent the actual transverse displacements with respect to the base frame, the integration along a finite length $l_{i}$ makes $u_{s}^{ei}$ only able to represent a local shortening of the single element. Attention should be paid to the integration of $u_{s}^{ei}$, as it cannot be integrated along the entire length $L$ of the beam when using FEM. The shape function matrix of each element uses its own nodal coordinates to estimate an arbitrary point displacement within that element, so the integration must be taken within the same element. Integrating Eq. (2.9) along the entire beam length will yield incorrect results. The total shortening accumulated by the finite elements located between the base frame and the $i$th element should be calculated by the sum of the shortenings of the $i-1$ elements plus that of itself, as shown in Fig. 2. Therefore, the axial foreshortening of an arbitrary point on the $i$th element is defined as

$$ u_{s}^{i} = \sum_{i = 1}^{i - 1} {u_{s}^{ei}} + u_{s,x} ^{ei} = \mathbf{{B}}_{s}^{i}{\mathbf{{B}}_{2}} { \mathbf{{q}}_{f}}, $$

(2.10)

where the matrix $\mathbf{{B}}_{s}^{i}$ is taken as

$$ \mathbf{{B}}_{s}^{i} = - {({\mathbf{{B}}_{2}} { \mathbf{{q}}_{f}})^{T}} {\mathbf{{H}}^{i}} $$

(2.11)

where ${\mathbf{{H}}^{i}}$ is a symmetric matrix, which is a function of the spatial coordinate $x$, defined as

$$ \mathbf{{H}}^{i} = - \frac{1}{2} \Biggl[ \sum _{n = 1}^{i - 1} { \int_{0}^{l} { \bigl(\mathbf{{N}} {{_{y}^{nT}}^{\prime }} {\mathbf{{N}}} {{_{y}^{n}} ^{\prime }} + \mathbf{{N}} {{_{z}^{nT}}^{\prime }} {\mathbf{{N}}} {{_{z}^{n}} ^{\prime }} \bigr)\,dx} } + \int_{0}^{x} { \bigl(\mathbf{{N}} {{_{y}^{iT}}^{\prime }} {\mathbf{{N}}} {{_{y}^{i}}^{\prime }} + \mathbf{{N}} {{_{z}^{iT}}^{\prime }} {\mathbf{{N}}} {{_{z}^{i}}^{\prime }} \bigr)\,dx} \Biggr] , $$

(2.12)

where $\mathbf{{N}}{_{y}^{i}}$ and $\mathbf{{N}}{_{z}^{i}}$ are the rows associated with the transverse deformations of $\mathbf{{N}}{^{i}}$ defined in Eq. (2.4). Using Eqs. (2.8) and (2.10), the global position vector defined by Eqs. (2.1)–(2.7) can be rewritten as

$$ \mathbf{r}^{i} = \mathbf{R} + \mathbf{Au}_{G}^{i} = \mathbf{R} + \mathbf{A} \bigl(\mathbf{N}^{i} \mathbf{q}_{0} + \mathbf{N}_{G}^{i} \mathbf{q}_{f} \bigr), $$

(2.13)

where $\mathbf{N}_{G}^{i}$ is defined as

$$ \mathbf{N}_{G}^{i} = \bigl( \mathbf{N}^{i} + 2 \mathbf{B}_{H}^{i} \bigr) \mathbf{B}_{2} $$

(2.14)

and $\mathbf{B}_{H}^{i}$ is

$$ \mathbf{B}_{H}^{i} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{B}_{s}^{i}& \boldsymbol{0}& \boldsymbol{0} \end{array}\displaystyle \right ] ^{T}. $$

(2.15)

The modification in the shape function is associated with the deformation coordinates only, which takes the foreshortening effect into account, and does not affect the coordinates in the reference configuration. This shape function is used in the symbolic implementation to obtain the numerical results.

Fig. 2

Accumulated shortenings of the elements

The global velocity vector can be obtained by differentiating the redefined global position vector in Eq. (2.13) with respect to time

$$ \dot{\mathbf{r}}^{i} = \dot{\mathbf{R}} - \mathbf{A} \tilde{\mathbf{u}}_{G} ^{i}{\boldsymbol{\omega }} + \mathbf{{AN}}_{G}^{i}{\dot{\mathbf{{q}}}}_{f}, $$

(2.16)

where $\tilde{\mathbf{{u}}}_{G}^{i}$ is the skew-symmetric matrix of $\mathbf{{{u}}}_{G}^{i}$, and $\boldsymbol{\omega }$ is the angular velocity vector of $xyz$ resolved in the local coordinate system. The symmetry of the time-invariant matrix $\mathbf{{H}}^{i}$ defined in Eq. (2.12) is used during the differentiation of $\mathbf{{B}}_{H} ^{i}{\mathbf{{B}}_{2}}{\mathbf{{q}}_{f}}$ with respect to time.

The global acceleration vector can be derived by differentiating ${{\dot{\mathbf{{r}}}}^{i}}$ defined in Eq. (2.16) as

$$ \ddot{\mathbf{r}}^{i} = \ddot{\mathbf{R}} - \mathbf{A}\tilde{\mathbf{u}}_{G} ^{i} \dot{\boldsymbol{\omega }} + \underline{\mathbf{A}\tilde{\boldsymbol{\omega}}^{2} \mathbf{u}_{G}^{i}} + \underline{2 \mathbf{{A}} \tilde{\boldsymbol{\omega }} \mathbf{N}_{G} ^{i}{{\dot{\mathbf{{q}}}}_{f}}} + \underline{ \mathbf{A}\dot{\mathbf{B}}_{H}^{i} \mathbf{B}_{2} \dot{\mathbf{q}}_{f}} + \mathbf{AN}_{G}^{i} \ddot{\mathbf{{q}}}_{f}, $$

(2.17)

where $\tilde{\boldsymbol{\omega}}$ is the skew-symmetric matrix of the angular velocity, and ${\dot{\mathbf{B}}}_{H}^{i}$ is calculated as

$$ {\dot{\mathbf{B}}}_{H}^{i} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \dot{\mathbf{q}}_{f}^{T}\mathbf{{H}}^{i}& \boldsymbol{0}& \boldsymbol{0} \end{array}\displaystyle \right ] ^{T}. $$

(2.18)

The underlined terms are used to derive the quadratic velocity force vector in Sect. 2.3.

2.2 Mass matrix

The element mass matrix can be derived from the kinetic energy expression of the $i$th element defined as

$$ T^{i} = \frac{1}{2} \int_{V^{i}} \rho^{i} \dot{\mathbf{r}} ^{i T}\dot{\mathbf{r}}^{i} \,d V^{i} = \frac{1}{2} \int_{0} ^{l^{i}} \rho^{i} \dot{\mathbf{r}}^{iT}\dot{\mathbf{r}}^{i} A^{i}\, dx, $$

(2.19)

where $\rho^{i}$ and $V^{i}$ are the mass density and volume, and $A^{i}$ and $l^{i}$ are the cross-section area and length of the element, respectively. Substituting Eq. (2.16) into Eq. (2.19) yields

$$ {T^{i}} = \frac{1}{2}{{\dot{\mathbf{{q}}}}^{i}} {}^{T}\!\mathbf{M}^{i} {{\dot{\mathbf{{q}}}}^{i}}, $$

(2.20)

where $\dot{\mathbf{q}}$ represents the time-derivatives of the total generalized coordinates:

$$ \dot{\mathbf{{q}}} = \left[ \textstyle\begin{array}{c@{\quad}c} \dot{\mathbf{q}}_{r}^{T}& \dot{\mathbf{q}}_{f}^{T} \end{array}\displaystyle \right]^{T} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \dot{\mathbf{R}}^{T} & \boldsymbol{\omega}^{T} &\dot{\mathbf{q}}_{f}^{T} \end{array}\displaystyle \right ] , $$

(2.21)

where $\mathbf{q}_{r}$ is the vector of reference coordinates; $\mathbf{M}^{i}$ is the mass matrix for the $i$th element,

$$ \mathbf{M}^{i} = \int_{0}^{l^{i}} \rho^{i} \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} [\mathbf{I}] & [ - \mathbf{A}\tilde{\mathbf{u}}_{G}^{i}] & [ \mathbf{AN}_{G}^{i} ] \\ & [ \tilde{\mathbf{u}}_{G}^{i\,\,\,T} \tilde{\mathbf{u}}_{G} ^{i}] & [\tilde{\mathbf{u}}_{G}^{i}\mathbf{N}_{G}^{i}] \\ \operatorname{sym}& & [ \mathbf{N}_{G}^{iT} \mathbf{N}_{G}^{i}] \end{array}\displaystyle \right ] A^{i}\, dx. $$

(2.22)

Having the mass matrix of each element, one can obtain the total mass matrix of the body by summing up all the element mass matrices:

$$ \mathbf{M} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathbf{m}_{rr} &\mathbf{m}_{r\theta }&\mathbf{{m}}_{rf} \\ & \mathbf{m}_{\theta \theta }& \mathbf{m}_{\theta f} \\ \operatorname{sym}& &\mathbf{m}_{ff} \end{array}\displaystyle \right ] = \sum \limits_{i = 1}^{n} \mathbf{M}^{i}, $$

(2.23)

where $n$ is the number of elements, and $\mathbf{{M}}$ is the total mass matrix; the subscripts $r$, $\theta$, and $f$ indicate the coupling of rigid-body translation, rotation, and flexible-body deformation, respectively.

2.3 Generalized forces

Quadratic velocity force

The quadratic velocity force vector is part of the inertia force that becomes significant when rotational rigid-body motion exists, and it consists of gyroscopic and Coriolis forces. The virtual work of the inertia force of the $i$th element is defined as

$$ \delta W^{i} = \int_{V^{i}} \rho^{i} \delta \mathbf{r}^{iT} \ddot{\mathbf{r}}^{i} \,dV = \delta \mathbf{q}^{T} \mathbf{Q}_{v}, $$

(2.24)

where ${\mathbf{{r}}^{i}}$ is defined in Eq. (2.13), and its virtual change can be written as

$$ \delta \mathbf{{r}}^{i} = \delta {\mathbf{{R}}} - \mathbf{A} \tilde{\mathbf{u}}_{GN} ^{i}\delta \boldsymbol{\omega } + \mathbf{A} \mathbf{{N}}_{G}^{i} \delta \mathbf{q}_{f}, $$

(2.25)

and $\delta \mathbf{{q}}$ is the virtual change of the generalized coordinates, $[ \begin{array}{c@{\ }c@{\ }c} \delta \mathbf{{R}} & \delta {\boldsymbol{\omega }} & \delta {\mathbf{{q}}_{f}} \end{array}]$; $\mathbf{Q}_{v}$ is the quadratic velocity force vector. Only the underlined parts of ${{\ddot{\mathbf{{r}}}}^{i}}$ in Eq. (2.17) are involved in deriving the quadratic velocity force, as one can prove that the other terms are related to the kinetic energy that has been used to derive the mass matrix in Eq. (2.22). Therefore, using Eqs. (2.24)–(2.25) and the underlined terms of ${{\ddot{\mathbf{{r}}}}^{i}}$, the quadratic velocity force vector of the $i$th element can be written as

$$ \mathbf{Q}_{v} = \left [ \textstyle\begin{array}{c} \mathbf{Q}_{vr} \\ \mathbf{Q}_{v\theta } \\ \mathbf{Q}_{vf} \end{array}\displaystyle \right ] = \int_{0}^{{l^{i}}} \rho^{i} A^{i}\left [ \textstyle\begin{array}{c} \mathbf{A}\tilde{\boldsymbol{\omega }}^{2} \mathbf{u}_{G}^{i} + 2 \mathbf{A}\tilde{\boldsymbol{\omega }} \mathbf{N}_{G}^{i}\dot{\mathbf{q}}_{f} + \mathbf{A}\dot{\mathbf{B}}_{H}^{i}{\mathbf{{B}}_{2}}\dot{\mathbf{q}}_{f} \\ - \tilde{\mathbf{u}}_{G}^{iT}\tilde{\boldsymbol{\omega}}^{2} \mathbf{{u}}_{G}^{i} - 2\tilde{\mathbf{u}}_{G}^{iT}\tilde{\boldsymbol{\omega }}\mathbf{N} _{G}^{i} \dot{\mathbf{q}}_{f} - \tilde{\mathbf{u}}_{G}^{iT}\dot{\mathbf{B}} _{H}^{i}\mathbf{B}_{2}\dot{\mathbf{q}}_{f} \\ \mathbf{{N}}_{G}^{iT}(\tilde{\boldsymbol{\omega }}^{2}\mathbf{u} _{G}^{i} + 2{\tilde{\boldsymbol{\omega }}\mathbf{N}}_{G}^{i}{\dot{\mathbf{{q}}}} _{f} + \dot{\mathbf{B}}_{H}^{i}{\mathbf{{B}}_{2}}{{\dot{\mathbf{{q}}}}_{f}}) \end{array}\displaystyle \right ]\, dx. $$

(2.26)

Generalized gravitational force

The virtual work due to gravity can be expressed as

$$ \delta W_{g}^{i} = \int_{V^{i}} \rho^{i} \mathbf{g}^{T} \delta \mathbf{r}^{i}\, dV = \delta \mathbf{q}^{T} \mathbf{Q}_{g}, $$

(2.27)

where $\mathbf{g}$ is the gravity vector defined as $\mathbf{g} = [ \begin{array}{c@{\ }c@{\ }c} 0& {-}g &0 \end{array}] ^{T}$ if the gravity is determined along $-Y$ axis, and $g$ is the gravity value. Substituting $\delta \mathbf{r}_{i}$ defined in Eq. (2.25) into Eq. (2.27), the generalized gravitational force vector $\mathbf{Q}_{g}$ is obtained as

$$ \mathbf{Q}_{g} = \left [ \textstyle\begin{array}{c} \mathbf{Q}_{gr} \\ \mathbf{Q}_{g\theta } \\ \mathbf{Q}_{gf} \end{array}\displaystyle \right ] = \int_{0}^{l^{i}} \rho^{i} A^{i} \left [ \textstyle\begin{array}{c} \mathbf{g}^{T} \\ - \mathbf{g}^{T} \mathbf{A}\tilde{\mathbf{u}}_{G}^{i} \\ \mathbf{g}^{T}\mathbf{AN}_{G}^{i} \end{array}\displaystyle \right ]\, dx. $$

(2.28)

Generalized external force

The external force applied on a body can either be a point load or a distributed load. If the load is distributed, the derivation of the generalized external force vector will be similar to the generalized gravitational force vector as the gravity is a typical distributed load. The derivation of the generalized external force vector resulting from a single point load is presented here. The force vector has three components, which are defined in the global coordinate system, that is,

$$ \mathbf{F} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} F_{1}& F_{2}& F_{3} \end{array}\displaystyle \right ] ^{T}. $$

(2.29)

The virtual work of the force $\mathbf{{F}}$ is defined as

$$ \delta W_{e} = \mathbf{F}^{T}\delta \mathbf{r}_{p}, $$

(2.30)

where $\delta \mathbf{r}_{p}$ is the virtual change of the global position vector of the point $P$ to which the load is applied. Substituting $\delta \mathbf{r}_{p}$ calculated by Eq. (2.25) into Eq. (2.30), the generalized external force vector $\mathbf{Q}_{e}$ can be derived as

$$ {\mathbf{{Q}}_{e}} = \left [ \textstyle\begin{array}{c} \mathbf{{Q}}_{er} \\ \mathbf{{Q}}_{e\theta } \\ \mathbf{{Q}}_{ef} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \mathbf{{F}}^{T} \\ {-} \mathbf{{F}}^{T} \mathbf{A}\tilde{\mathbf{u}}_{G}^{p} \\ \mathbf{F}^{T}\mathbf{AN}_{G}^{p} \end{array}\displaystyle \right ]. $$

(2.31)

It is necessary to know, in advance, with which element the point $P$ is associated so that only the corresponding element equations are used to calculate $\delta \mathbf{r}_{p}$. The superscript $p$ indicates the equations for the $p$th element, assuming point $P$ is on this element. One may notice that the rotational component $\mathbf{Q}_{e\theta }$ is the generalized moment caused by the point load. If there is any additionally applied moment on the body, it can be directly applied to the corresponding node.

2.4 Stiffness matrix

The strain energy can be generalized as

$$ U = \frac{1}{2}\mathbf{q}_{f}^{T} \mathbf{K}_{f} \mathbf{q}_{f}, $$

(2.32)

where $\mathbf{K}_{f}$ is the total stiffness matrix of the flexible beam. The full expression of the stiffness matrix corresponding to the conventional Bernoulli–Euler beam theory has been well developed in [24], which is applicable to the Rayleigh beam. It is derived by considering the normal stain energy with addition of independent torsional strain energy; thus the axial, bending, and torsional stiffness are decoupled. It is proved in [17] that, after adding the foreshortening term in the axial displacement field, the normal strain energy defined for the conventional theory is unchanged. Therefore, the linear stiffness matrix defined in [24] can be used for the geometrically nonlinear formulation.

3 Symbolic integration with multibody systems

The finite-element beam model implemented in MapleSim is referred to as “MapleSim FEM.” MapleSim has its own multibody systems dynamics library from where users can select different types of multibody components (bodies, drivers, joints, etc.) and configure open- or closed-loop mechanisms. Different from traditional FMD modeling methods, MapleSim uses graph theory [28] to generate the global constraint equations and system equations of motion.

The current finite-element implementation in MapleSim adopts a nodal approach, also referred to as transient analysis in some commercial software packages, which generates the system equations in terms of all elastic nodal coordinates. The modal approach, as opposed to the nodal approach, has been used by others to reduce the problem dimensionality. However, it requires the user to pre-compute a modal analysis [8] that relies heavily on numerical modeling procedures, which need remodeling to obtain new system equations when changing geometrical or material parameters. Symbolic computation is able to recall the equations pre-defined for each body and joint from the library and combine them automatically (using graph theory) for every multibody system during modeling. There is no need to go back to remodel a flexible body if its parameters have changed, since the equations contain only the symbolic parameters that can be given any numerical value before time integration. Moreover, the modal approach often needs a large number of finite elements to obtain a set of exact mode shapes, but the nodal approach only needs a small number since it fully utilizes the shape function that describes the deformation of the material points.

For a flexible body component in multibody systems, what needs to be formulated are two sets of terminal (constitutive) equations with graph-theoretic (GT) edges associated with each. The first one is referred to as the body element that defines generalized forces and torques, and the second one is referred to as an “arm” that serves to locate any arbitrary point on the body where an imparted load (external load, joint reaction, etc.) is applied.

3.1 Body element

In practice, when defining the terminal equations for the body element of a flexible component, they are separated into two parts which are, respectively, corresponding to rigid-body and flexible-body equations since the total coordinates associated with a flexible body are divided as $\mathbf{q} = [ \begin{array}{c@{\ }c} \mathbf{{q}}_{r} & \mathbf{q}_{f} \end{array} ] ^{T}$.

Reference terminal equations (rigid-body)

The terminal equations of generalized rigid-body forces and torques are defined as

$$\begin{aligned} {\mathbf{{F}}_{rb}} &= - ({\mathbf{{m}}_{rr}} {\ddot{\mathbf{{R}}}} + {\mathbf{{m}}_{r\theta }} {\dot{\mathbf{\omega}}} + { \mathbf{{m}}_{rf}} {{\ddot{\mathbf{{q}}}} _{f}}) + { \mathbf{{Q}}_{gr}} + {\mathbf{{Q}}_{vr}} + \langle \mathbf{{Q}}_{er} \rangle , \end{aligned}$$

(3.1)

$$\begin{aligned} {\mathbf{{T}}_{rb}} &= - ({\mathbf{{m}}_{\theta r}} {\ddot{\mathbf{{R}}}} + {\mathbf{{m}}_{\theta \theta }} {\dot{\mathbf{{\omega }}}} + { \mathbf{{m}}_{ \theta f}} {{\ddot{\mathbf{{q}}}}_{f}}) + { \mathbf{{Q}}_{g\theta }} + {\mathbf{{Q}}_{v\theta }}\; + \langle \mathbf{{Q}}_{e\theta } \rangle , \end{aligned}$$

(3.2)

where the subscript $rb$ refers to rigid-body; the $\mathbf{m}$ terms are defined in Eq. (2.23); the $\textbf{Q}_{g}$ and $\mathbf{Q}_{v}$ terms are, respectively, the components of the gravitational force vector of Eq. (2.28) and the quadratic velocity force vector of Eq. (2.26). Notice that the external loads surrounded by angle brackets $\langle {} \rangle$ are omitted in GT models, since they are already represented by the built-in force drivers (applied loads) or dependent virtual work element (reactions) [28].

Elastic terminal equations (flexible-body)

The terminal equation of the generalized elastic force is written as

$$ {\mathbf{{F}}_{fb}} = - ({\mathbf{{m}}_{fr}} {\ddot{\mathbf{{R}}}} + {\mathbf{{m}}_{f\theta }} {\dot{\boldsymbol{\omega }}} + { \mathbf{{m}}_{ff}} {{\ddot{\mathbf{{q}}}}_{f}}) - { \mathbf{{K}}_{f}} {\mathbf{{q}}_{f}} + { \mathbf{{Q}}_{gf}} + {\mathbf{{Q}}_{vf}} + { \mathbf{{Q}}_{ef}} . $$

(3.3)

Notice that the force $\textbf{F}$ defined in Eq. (2.30) that was used to derive ${\mathbf{{Q}}_{ef}}$ can be either the external loads or reaction forces.

3.2 Arm element

The kinematics of any point of interest on the beam are given by:

$$\begin{aligned} {\mathbf{{r}}_{P}} &= {\mathbf{{u}}^{i}} , \end{aligned}$$

(3.4)

$$\begin{aligned} {{\dot{\mathbf{{r}}}}_{P}} &= {\boldsymbol{\omega }} \times {{ \mathbf{{u}}^{i}}} + {\mathbf{{N}}^{i}} {{\dot{\mathbf{{q}}}}_{f}} , \end{aligned}$$

(3.5)

$$\begin{aligned} {{\ddot{\mathbf{{r}}}}_{P}} &= \dot{\boldsymbol{\omega}} \times {{\mathbf{{u}}^{i}}} + {\boldsymbol{\omega }} \times {\boldsymbol{ \omega }} \times {{{{\mathbf{{u}}^{i}}}}} + 2{\boldsymbol{\omega }} \times {\mathbf{{N}}^{i}} {{\dot{\mathbf{{q}}}}_{f}} + { \mathbf{{N}}^{i}} {{\ddot{\mathbf{{q}}}} _{f}} , \end{aligned}$$

(3.6)

$$ \mathbf{{A}}_{P}\text{: rotation matrix by 1--2--3 sequence of} \ \boldsymbol{\theta}_{P} = \mathbf{N}^{i\,\prime }\mathbf{{q}}_{f} , $$

(3.7)

$$\begin{aligned} {{\boldsymbol{\omega }}_{P}} & = \dot{\boldsymbol{ \theta }} _{P}= {\mathbf{{N}}^{i}}^{\prime } \dot{\mathbf{{q}}}_{f} , \end{aligned}$$

(3.8)

$$\begin{aligned} \dot{\boldsymbol{\omega}}_{P} &= \ddot{\boldsymbol{\theta}}_{P} = \mathbf{N}^{i\,\prime } \ddot{\mathbf{q}}_{f} , \end{aligned}$$

(3.9)

where the subscript $P$ refers to a distal point $P$ shown in Fig. 1; ${\mathbf{{u}}^{i}}$ is the local position vector of the point P defined in Sect. 2.1; $\boldsymbol{\omega }$ is the angular velocity vector of $xyz$; $\mathbf{N}^{i}$ is defined by $\mathbf{N}_{G}^{i}$ in Eq. (2.14); $\mathbf{A}_{P}$ is the rotation transformation matrix of the frame of reference whose origin is at the distal point $P$ with respect to the body-fixed frame; $\boldsymbol{\omega}_{P}$ is the corresponding angular velocity of the distal point reference frame relative to the body-fixed frame. Since the deformation has been assumed small, the slopes of point $P$, estimated by $\boldsymbol{\theta} _{P}$, are used as Euler angles to evaluate the rotation matrix $\mathbf{A}_{P}$. For greater accuracy, high-fidelity approaches [29] should be used to calculate the rotation matrix; $\boldsymbol{\omega}_{P}$ is estimated here by the time derivative of $\boldsymbol{\theta}_{P}$.

3.3 System equations

The assembly of system equations is done using graph theory [20, 28] and depends on “tree” and “co-tree” selections [19]. Dependent coordinates at joints can be eliminated using appropriate tree selection unless certain reaction results are needed. The Lagrange multipliers in the kinetic equations depend on the co-tree selection. For open-loop systems, the kinetic equations can be expressed by the ordinary differential equations (ODEs)

$$ \mathbf{M}^{*} \ddot{\mathbf{{q}}}^{*} = \mathbf{{Q}}^{*} , $$

(3.10)

where all coordinates of $\mathbf{{q}^{*}}$ are independent, and the stars on symbols indicate system-level equations. In constructing Eq. (3.10), the rigid- and flexible-body loads in Sect. 3.1, as well as other pre-defined loads from joint-connected components or force drivers, are symbolically substituted to form the inertia loads $\mathbf{M}^{*}\ddot{\mathbf{{q}}}^{*}$ and generalized loads $\mathbf{Q}^{*}$.

Constraint equations, $\mathbf{C}(\mathbf{q}^{*},t) = \mathbf{0}$, are derived by using $\mathbf{r}_{P}$ in Eq. (3.4), with point $P$ representing the joint location, in the traditional vector summations around closed kinematic chains. It is shown in [28] that different reactions (Lagrange multipliers) appear in the kinetic equations in Eq. (3.10) when different trees are selected, and the system equations are represented by a set of differential algebraic equations (DAEs) comprising the kinetic and constraint equations together. Details of using the terminal equations defined in Sects. 3.1 and 3.2 to assemble system equations using graph theory are given in [14].

4 Examples

4.1 Planar spin-up flexible beam

The planar rotating flexible beam is a benchmark problem for testing dynamic analysis of flexible bodies under large overall motion [13], which is shown in Fig. 3. The beam is rigidly attached to a rotating hub which is driven with an angular displacement $\theta (t)$ about the $Y$ axis, and the gravity is assumed zero. The focus is the free-tip transverse deformation.

Fig. 3

Planar spin-up beam

The geometric and material properties taken from [13] are: length $L= 10\mbox{ m}$, cross-sectional area $A=0.0004\ \hbox{m}^{2}$, mass density $\rho = 3000\ \hbox{kg/m} ^{3}$, second moment of area $I_{y}=I_{z} = 2 \times 10^{-7}~\hbox{m}^{4}$, Young’s modulus $E = 7\times 10^{10}\ \hbox{N/m} ^{2}$, and shear modulus $G = 2.7\times 10^{10}\ \hbox{N/m}^{2}$. The prescribed motion of the hub is written as

$$ \theta (t) = \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{{{\omega_{s}}}}{{{T_{s}}}} [ {\frac{{{t^{2}}}}{2} + {{(\frac{ {{T_{s}}}}{{2\pi }})}^{2}}(\cos (\frac{{2\pi t}}{{{T_{s}}}}) - 1)} ] , & t < {T_{s}}, \\ \omega_{s}(t - \frac{{{T_{s}}}}{2}),& t \ge {T_{s},} \end{array}\displaystyle \right . $$

(4.1)

where ${\omega_{s}}$ is set to $6.0\ \mbox{rad}/\mbox{s}$, and ${T_{s}}$ to $15\ \hbox{s}$.

Five elements are used to model the beam in MapleSim FEM, and both conventional linear and geometrically nonlinear formulations are used separately to predict the deformation. MapleSim FEM can shift between the two implemented formulations. The results are validated by using the built-in analytical beam model in MapleSim, which uses the nonlinear formulation presented in Shi et al. [29]. The tip transverse deflection of the beam predicted by the three formulations is shown in Fig. 4.

Fig. 4

Tip deflection of the spin-up beam

The peak deflection magnitude of the nonlinear FEM (geometrically nonlinear formulation) is $0.573\ \hbox{m}$, and the result is very close to that predicted by the analytical beam and result in [17] with a root-mean-square error (RMSE) of 0.074%. However, the linear FEM (conventional linear formulation) fails to predict the correct deformation after about $t=4\ \hbox{s}$. The reason for this is because the linear FEM is unable to capture the dynamic stiffening effect [13] when the beam spins with a relatively high angular speed.

For structural analysis in a steady state, or dynamic analysis with small and slow overall motion, or with stiffer flexible bodies, the dynamic stiffening that is largely associated with centrifugal and Coriolis effects is negligible. In this case, the linear functions inside the conventional formulation are sufficient to model the deformation of the body. This can be shown by applying another set of properties to the beam, which makes the beam stiffer while the motion is kept the same. The stiffer properties are: length $L= 3\ \hbox{m}$, cross-sectional area $A=0.005\ \hbox{m}^{2}$, mass density $\rho = 3000\ \hbox{kg}/\mbox{m}^{3}$, second moment of area $I_{y}=I_{z} = 1.989 \times 10^{-6}\ \hbox{m}^{4}$, Young’s modulus $E = 7\times 10^{10}\ \hbox{N}/\mbox{m}^{2}$, and shear modulus $G = 2.7\times 10^{10} \ \hbox{N}/\mbox{m}^{2}$. The tip transverse deflection of the stiffer beam predicted by the three formulations is shown in Fig. 5. Although slight differences exist between the linear FEM and the other two, they agree quite well with an RMSE less than 0.001% since the dynamic stiffening effect becomes negligible for the stiffer beam.

Fig. 5

Tip deflection of the stiffer beam

The computational (CPU) times of 4000 time steps for 1 to 5 elements are also recorded for both cases. The CPU time can be divided into two categories, one being the time to generate the system equations (modeling time), and the second one is used for numerical time-integration (simulation time). The CPU time is shown in Table 1. The modeling time is the same for both cases due to the generation of the same symbolic system equations. The simulation time of the linear FEM for the first case is not shown because of its failure after $t=4~\hbox{s}$. It can be seen from the table that the computational cost associated with the nonlinear FEM increases dramatically with the number of elements while the cost for the linear FEM increases gently. If 10 minutes is set as a limit for the modeling time, which users can probably tolerate for simple mechanisms, the corresponding number of finite elements of a flexible beam in the current MapleSim FEM is about 24 with the linear formulation and 8 with the nonlinear one, respectively. Note that the modeling time is incurred only once; after the symbolic equations are generated for a system, any number of simulations can be performed.

Table 1 CPU time (sec) for 1 to 5 elements

The RMSEs from the results of using 1–5 elements are given in Table 2. The convergence for both FEM models is reached at using only 1–2 elements. Although one can use more than 2 elements to refine the results, it is efficient to use 1 or 2 elements to quickly get numerical results which are quite accurate. In addition, the small RMSE results from the 2nd case (stiffer beam) indicate that the predicted results are very accurate under small deformations, which coheres with the beam theory assumption described in Sect. 1.

Table 2 RMSEs ($\%$) for 1 to 5 elements

4.2 Planar slider–crank mechanism with flexible crankshaft and connecting rod

This slider–crank mechanism example is used to test the functionality of the finite-element flexible beam with a closed-loop mechanism and to help further demonstrate the usage of the conventionally linear and the geometrically nonlinear formulations. This mechanism is taken from [10] as shown in Fig. 6. The flexible crankshaft has a length of $0.152\ \hbox{m}$, a cross-sectional area of $7.854 \times 10^{ - 5}~\mbox{m}^{2}$, a second moment of area of $4.909 \times 10^{ - 10}~\mbox{m}^{4}$, a mass density of $2770~\mbox{kg}/\mbox{m}^{3}$, and a Yonge’s modulus of $1.0 \times 10^{9}~\mbox{N}/\mbox{m} ^{2}$. The connecting rod has a length of $0.304~\mbox{m}$, and has the same dimensions and material properties as the crankshaft with the exception of the Yonge’s modulus, which is $0.5 \times 10^{8}~\mbox{N}/\mbox{m}^{2}$. The slider is assumed massless. The crankshaft of the system is assumed to be driven by the following torque expressed in N/m:

(4.2)

The crankshaft is modeled using one element, and the connecting rod is modeled using two elements. Figure 7 shows the midpoint deformation results of the connecting rod measured with respect to its body-fixed frame obtained by using the two FEM formulations along with the result recorded in [10]. It is seen that the three sets of results agree well with each other. The nonlinear FEM generates a very small difference of the deformation because the connecting rod is quite short so that the centrifugal and Coriolis effects discussed in the preceding section are negligible. In addition, the difference between the result in [10] and the others is probably due to that the beam model in the reference adopts a modal approach. This difference will be discussed particularly in the next example problem.

Fig. 6

Slider–crank mechanism

Fig. 7

Deformation of the midpoint of the connecting rod

The position of the slider block is plotted in Fig. 8. It is shown that the influence of the slight difference of the deformation to the position of the slider block is trivial.

Fig. 8

Position of the slider block

4.3 Spatially rotating flexible beam

In this section, a spatial manipulator with a flexible link, shown in Fig. 9, is modeled by the MapleSim FEM with the nonlinear nodal formulation and validated by the built-in analytical beam model. The results are compared with an MSC. ADAMS/Nastran model which uses a numerical modal approach.

Fig. 9

Schematic of the spatial manipulator with a flexible link

The mechanism shows that the flexible beam is attached to a hub that can rotate about a vertical $Y$ axis. The beam can also rotate about its body-fixed horizontal $z_{b}$ axis. There is a tip mass attached to the beam which adds additional inertia and weight. The spatial motion of the manipulator is such that when $t< 1\ \hbox{s}$ there is no rotation so that the beam is static, which is the same as a cantilever beam under gravity; when $1\ \hbox{s}\le t<2\ \hbox{s}$ the beam is spinning only about the $Y$ axis like a planar spin-up beam; when $2\ \hbox{s}\le t<3\ \hbox{s}$ the beam has spatial motion about both the $Y$ and $z_{b}$ axis. The prescribed angular motions about both axes are defined as

$$ \dot{\theta }= \left \{ \textstyle\begin{array}{l@{\quad}l} 0, & t < 1\ \hbox{s}, \\ \omega_{\theta }, & 1~\hbox{s} \le t < 3~\hbox{s}, \end{array}\displaystyle \right . \qquad \dot{\beta }= \left \{ \textstyle\begin{array}{l@{\quad }l} 0, & t < 2\ \hbox{s}, \\ \omega_{\beta }, &2~\hbox{s} \le t < 3\ \hbox{s}, \end{array}\displaystyle \right . $$

(4.3)

where $\omega_{\theta }$ is set to $\pi~\hbox{rad/s}$, and $\omega_{\beta }$ is set to $\pi /2~\hbox{rad/s}$. The parameters of the flexible beam are: length $L= 3 \ \hbox{m}$, cross-sectional area $A=0.005~\hbox{m}^{2}$, mass density $\rho = 3000~\hbox{kg/m}^{3}$, second moment of area $I_{y}=I_{z} = 1.989 \times 10^{-6}~\hbox{m}^{4}$, Young’s modulus $E = 7.0 \times 10^{10}~\hbox{N/m}^{2}$, shear modulus $G = 2.7\times 10^{10}~\hbox{N/m}^{2}$, and gravity $g = 9.81~\hbox{m/s}^{2}$. The rigid hub has a radius of $0.5~\hbox{m}$, and the tip mass has a mass of $30~\hbox{kg}$.

The “CBEAM” formulation and nonlinear element formulation “LAGR” embedded in Nastran are selected, respectively, to construct the beam properties and element equations, and 10 elements are used to generate the mode shapes of the flexible beam before assembling the mechanism in MSC. ADAMS. On the other hand, two elements are used for the MapleSim FEM. Both results are validated by the analytical beam model in MapleSim. The tip deflection magnitudes predicted by the three models are plotted in Fig. 10. The results of all three models are in good agreement with an RMSE of 0.23%, though a small difference observed between MSC. ADAMS/Nastran and the other two after $t=2.5~\hbox{s}$.

Fig. 10

Tip deflection magnitudes

This negligible difference can be explained by the different values of axial foreshortening predicted by MSC. ADAMS/Nastran and the other two models shown in Fig. 11, as the tip transverse deflections from the three models are converged exactly shown in Fig. 12. Different approaches of nonlinear formulation between Nastran and MapleSim FEM and the fact that Nastran forces the selection of lumped mass distribution when generating the mode shapes could both result in the small divergence of the axial deformation. Since the nonlinear formulation embedded in the analytical beam model uses the same foreshortening approach as the MapleSim FEM, they generate the same foreshortening value.

Fig. 11

Tip axial deflection along the $x_{b}$ axis (Analytical and MapleSim FEM results converge)

Fig. 12

Tip transverse deflection along the local $y_{b}$ and $z_{b}$ axis (all results converge)

Although the modal approach (Nastran) and the nodal approach (MapleSim FEM) both display comparable accuracy when modeling this problem, a large difference exists between them in terms of ability to converge. For such an example where low-frequency flexible modes are dominating, only one element is sufficient for the MapleSim FEM to reach convergence with an RMSE of 0.02% as shown in Fig. 13. This is because the displacement field of an element described by the shape functions is accurate enough to directly predict the actual deformation of the flexible body in simple conditions.

Fig. 13

Tip transverse deflection for different numbers of elements (MapleSim FEM)

Unlike the nodal approach, the modal approach usually relies on a larger number of elements in order to generate accurate mode shapes. The ability to reach convergence for Nastran is shown in Fig. 14. The RMSEs from the results of using 3, 6, and 10 elements are, respectively, 1.49%, 0.26%, and 0.24%. It is obvious that using the mode shapes generated by 3 elements is insufficient to predict accurate deformation results, so at least 6 elements are usually used to obtain a good estimation. Even 10 or more elements have to be selected in order to refine the results afterwards.

Fig. 14

Tip transverse deflection for different numbers of elements (MSC. ADAMS/Nastran)

Associated with the larger number of elements and selection of mode shapes is always a higher cost. When considering the CPU time, it will take less than $10~\hbox{s}$ for MapleSim FEM to finish one round of calculation when using one element for this example, which includes both modeling and simulation time. However, it will take about 2.6 minutes for MSC. ADAMS to finish the simulation when using 6 elements for this example. Other than that, if the user wants to change the number of elements in MapleSim FEM, he or she can just type a different number before each simulation without doing anything else when using the nodal approach. The modal approach needs the user to redefine the flexible body in Nastran and generate a new set of mode shapes, which requires many manual operations. Therefore, the convenience of manipulation should not be compared solely on the CPU time.

Moreover, since the symbolic computation is able to generate the equations of motion as a pre-processor, parameters other than the number of elements, such as dimensional and material properties, can be easily changed afterwards. For this example, if using the symbolic approach, the user can modify the beam density, length, cross-sectional area, Young’s modulus and so forth very conveniently. Plus, equations do not have to be regenerated. This allows the user to have more time to analyze many different results associated with varying parameters, which will benefit control and design engineers to efficiently optimize the system.

5 Conclusions

The objective of integrating the FEM with FMD using symbolic computation has been successfully completed using the nodal formulation and GT approach. The nonlinear FEM beam formulation is based on the Rayleigh beam theory, and a foreshortening formulation is added to capture the dynamic stiffening effect. Planar spin-up and spatially rotating beam examples are used to examine the convergence of the FEM beam model in FMD, and CPU time is used as the criteria to assess its performance. It is shown that the symbolic FEM model provides good accuracy with less computational cost and more convenience of manipulation when compared with numerical approaches.

Using symbolic computation, the future extension from beam elements to those with more complex geometries seems promising. However, the total number of degrees of freedom generated by the nodal formulation is an outstanding issue to be resolved. It can be worthwhile to develop or implement specific coordinate reduction techniques, such as nodal condensation or substructuring approaches, which fully take advantage of symbolic computation.