1 Introduction

Spatial revolute joints are mechanical components used for the power transmission in many machines and mechanisms. These mechanical joints are commonly exposed to static and dynamic loading that can be applied both to centered and misaligned elements. The analysis of the behavior of non-ideal joints is an important topic of research since it allows understanding the effect of several design features that may lead to a substantial reduction of the energy consumption and increased performance of many mechanical systems. Previous studies involving the numerical modeling of such kinematic joints were performed considering a two-dimensional approach [1,2,3,4,5,6]. The results issued from those analyses are only valid for particular conditions that may not occur in most operating conditions. Indeed, when the third dimension is taken into account, further aspects may be analyzed such as the axial misalignment between the journal and the bearing, the effect of both the radial and axial clearance, as well as the outcome resulting from an asymmetric loading [7,8,9,10]. In addition, the effect of the bearing thickness on the generated reaction force, the impact velocity of the journal on the bearing surface as well as the friction phenomena associated with the contact surfaces definitely have a non-negligible influence on the system dynamics.

In fact, the problem of the dynamic modeling of mechanisms and mechanical systems with planar revolute clearance joints has been extensively investigated over the last decades [11,12,13]. However, there exist many systems mounted on spatial revolute joints, such as the engine rotor and the robot arm, which exhibit out-of-plane motion. There are also many planar systems that include misaligned joint axes, and they operate only because of the clearance joints, and hence these systems should be considered as spatial systems. For these spatial cases, the available methodologies for planar revolute joints with clearance joints are no longer valid; it is necessary to develop appropriate formulations to account for these geometric aspects [14]. Furthermore, the contact behavior developed between the journal and bearing surfaces require accurate models that must take into account not only the normal [15] and tangential forces [16] but also the rolling effect [17]. The latter aspect has been neglected in almost all published works, and constitutes the main motivation for this work. Therefore, the development of the spatial revolute clearance joint models to assess the influence of the clearance on the systems’ response is still a significant and demanding topic when modeling dynamic multibody systems.

The contact force model considered to compute the intra-joint contact forces in spatial revolute clearance joints plays a key role in the system’s behavior. Most of the works utilized the well known Lankarani and Nikravesh contact force model [18]. However, this approach has some limitations due to the nature of the contact associated with the length of the journal. In turn, most of the analytical research works performed in the past decades considered that the contacting surfaces were modeled with linear or nonlinear spring–damper elements [19,20,21]. Veluswami et al. [22] experimentally demonstrated that the dynamic response and the contact duration were of more complex nature, and dependent on the impact velocity and clearance size. Gummer and Sauer [23] also investigated the influence of the contact geometry in clearance joints on the contact stiffness and energy loss. Based on the Johnson contact model [24] and Lankarani and Nikravesh approach [18], Pereira et al. [25, 26] developed an enhanced contact force model to describe the interaction between a journal and bearing. These authors demonstrated that the enhanced contact force model has better performance than the Johnson approach, both in terms of range of application and simplicity. However, in the above-mentioned works, the effect of rolling action between the journal and bearing surfaces is simply neglected. More recently, an analysis on the influence of the joint clearances in a mechanism of a circuit breaker (i.e., a 42 degree-of-freedom mechanism made of seven links with seven revolute joints and four unilateral contacts with friction) was performed by Akhadkar et al. [27]. In this work, the spatial revolute joints were modeled with both radial and axial clearances taking into account contact with flanges. A mention should also be given to the work presented by Ambrósio and Pombo [28] in which the authors proposed a formulation for both perfect and clearance/bushing joints. It was accomplished by utilizing the same kinematic information, thus making the modeling data of these joints similar and enabling their easy permutation in the context of multibody systems modeling. Moreover, the described methodology is appropriate to deal with most of the typical mechanical joints and easily extended to many other joint types.

The main contribution of this work is a realistic 3D finite element model that has been elaborated taking into account realistic characteristics regarding the geometry of the operating parts (i.e., operative clearances), the mechanical properties of the involved materials and possible relative misalignment between the journal and bearing elements that compose a spatial revolute joint [29]. The developed tool allows for the evaluation of the intra-joint contact forces generated at the journal–bearing interfaces, as well as stress and strain cartographies in any region of the model. An extensive set of simulations is performed with the purpose of obtaining the relation between the joint reaction forces and some of the joint parameters, namely, radial and axial clearances, bearing thickness, as well as the impact velocity when contact occurs and angle of axial misalignment. Lastly, a calculation was made on the rolling action of the journal onto the bearing surface. With the purpose of facilitating the post-processing of data and establishing a connection among the FEM and MBD approaches, a set of simulations have been performed on a benchmark problem, namely the well known slider–crank mechanism.

2 Methods

2.1 Contact scenarios and detection. Contact kinematics

In planar motion the analysis of axial clearance in the joints is disregarded, since this degree of freedom is not taken into account. The value of the quoted clearances can be evaluated as follows:

$$\begin{aligned} c_{\text{r}} =& R_{i} - R_{j} , \end{aligned}$$
(1)
$$\begin{aligned} c_{\text{a}} =& \frac{L_{i}}{2} - \frac{L_{j}}{2} , \end{aligned}$$
(2)

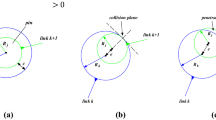
where \(c_{\text{r}}\) and \(c_{\text{a}}\) denote the radial and axial clearance, respectively, \(R_{i}\) and \(R_{j}\) are the radii, and \(L_{i}\) and \(L_{j}\) are the lengths of the bodies, as depicted in Fig. 1.

Fig. 1
figure 1

Schematics of a non-ideal spatial revolute joint [14]

Full size image

In order to properly model a spatial revolute joint with radial and axial clearances, it is crucial not to disregard any of the several possible contact scenarios that may arise in the interaction of the journal with the bearing [14]. It should be emphasized that some of the contact cases can be unlikely, since the chance of some contact scenarios is directly related to the dimensions of the journal and bearing. The geometric proportions of the bodies introduce some limitations that do not allow the joint to have some particular configurations. Once the methodology for the determination of the contact points is established according to each contact scenario, the next phase involves the characterization of the contact kinematics for each collision as a function of the contact points, for the bearing and journal, respectively. One of the utmost important steps to achieve a proper model of a spatial revolute joint is to select a suitable contact force model. Such a model should define with great level of precision the forces acting in the journal and bearing during the collisions that occur in the course of the operating conditions of the mechanical system.

2.2 FEM: development of an improved model for non-ideal spatial revolute joints

A 3D FE mesh was created in ABAQUS® [30] using 8-node linear brick and 6-node linear triangular prism elements to simulate the functional interaction between the journal and bearing. Elastic properties were attributed to both parts to mimic the elastic response (\(E = 207~\mbox{GPa}\) and \(\nu = 0.3\)), as well as the mass properties (\(7800~\mbox{kg}/\mbox{m}^{3}\)) to undergo dynamic modeling of the joint parts. Two initial conditions were imposed according to the way that the loading action has been put to vary with time: (i) quasi-statically and (ii) dynamically. In the former, both models were initially put in contact with each other, from which the journal was forced to move radially towards the bearing surface with a prescribed displacement. The latter condition considered the journal positioned coaxially relative to the bearing model in the initial step, from which the journal was launched towards the internal bearing surface with a prescribed velocity, till the former attained the equilibrium. An additional analysis was made to mimic the rolling effect of the journal onto the bearing surface, taking into account the plastic behavior of both models.

Boundary conditions (Fig. 2a) were imposed to simulate extreme operating situations in 3D spatial revolute joints that were partially constrained by outer clamping devices. Those conditions are characterized by the impediment of radial deformations of half the external area of the bearing surface, while forcing the journal movement towards the unconstrained side (as performed in [26]). This analysis allows reproducing extreme conditions that may occur in equipment such as pendulums that induce important radial deformations in bearing devices and 3D slider–crank mechanisms. In the numerical model, the set of nodes composing the external upper half of the bearing were impeded to move along the \(x\), \(y\) and \(z\) directions, while the set of nodes defining the journal axis was forced to move along the radial direction of \(\delta _{\text{max}} = 0.05~\mbox{mm}\). During this process, the resulting reaction force was continuously monitored in the nodes sited in the journal axis (being equal to the generated overall contact force). The mechanical elements were considered as two elastic bodies that interact mechanically with each other. This meant that both journal and bearing models were allowed to deform locally, with an amplitude that is governed by the elastic properties of the involved materials and the mechanical constraints. The amplitude of deformation did not correspond to any permanent bend due to plastic behavior of the involved materials caused by damage. Therefore, the indentation herein referred as pseudo-penetration was actually an elastic deformation that occurred in the contact region. Contact conditions were established at the interfaces of each body to prevent interpenetration. Therefore, the penalty method has been used to simulate the contact interaction of the journal with the bearing surface, which has constituted a stiff approximation of hard contact. As finite-sliding is prone to occur in the interface of both members (surface-to-surface contact), a hard pressure–over closure relationship turns effective when the penalty method is used. According to this formulation, the contact force is proportional to the penetration distance (linear trend), which renders some degree of penetration in the bearing possible.

Fig. 2
figure 2

Front view (a) and side (cut) view (b) of the 3D developed FE meshes for the bearing and journal members and respective geometric parameters

Full size image

The criterion employed to select the most adequate mesh size in the modeling has resulted from a trade-off between the overall computation time and the achievable degree of accuracy for the present analysis. Therefore, the model that accomplished this compromise in a better way corresponds to the one that presents an element size of \(0.3125\mbox{ mm}\) in the bearing region, presenting a maximum error for the normal contact force of \(3.12\%\), comparative to the most refined mesh with an element size of \(0.15625\mbox{ mm}\). Thus, the attained model (Fig. 2) is constituted by 281600 3D solid elements with a total of 15649613 nodes. These values elucidate the computational effort that the third dimension has introduced (total number of variables of the problem equal to 4118883). Since the contact domain in the rolling analysis is not known a priori, both meshes were uniformly and equally refined. For each of the performed analyses, the same (uniform) mesh refinement was adopted to assure mesh-independence of the outputs.

A significant number of numerical simulations were performed for the following conditions: \(R_{\text{B}} = 10.0\mbox{ mm}\), \(L_{\text{B}} = 20.0\mbox{ mm}\) and \(c_{\text{a}} = 1.0\mbox{ mm}\), which led to \(L_{\text{J}} = 18.0\mbox{ mm}\) (in Fig. 1, \(i\) denotes the bearing while \(j\) is the journal). The considered radial clearance (\(c_{ \text{r}} = 0.5\mbox{ mm}\)) was somehow an exaggerated value for a worn equipment, rendering the radius of the journal \(R_{\text{J}} = 9.5\mbox{ mm}\). Nevertheless, this choice was justified by the necessity to perform comparisons on the obtained results with those in [26]. The simulation of the damping effect (\(1 \times 10^{-3}\mbox{ kg}/\mbox{s}\)) was simply considered to allow the convergence of the numerical model in the first loading increments. However, this practice had no effect on the attained results. Regarding the simulations presented in Sects. 3.1, 3.2 and 3.3, the real material damping due to internal damping was set to 1, since the contact was purely elastic. Therefore, these simulations did not account for the energy dissipation. It should also be highlighted that Coulomb friction was assumed between the two surfaces, with the friction coefficient set equal to 0.1. When feasible, each plot is presented with its corresponding regression of the type \(F_{\text{n}} = K_{\text{pr}} \times \delta ^{n}\) in order to identify the variation on the contact stiffness \(K\). The term related with the contact stiffness allows establishing a direct relation between the contact force and the pseudo-penetration regardless of the exponent obtained in the power regressions that were calculated. Thus, although the value of \(K_{\text{pr}}\) might increase or decrease, this does not mean that the same trend is observed for the value of the contact stiffness, \(K\).

3 Results and discussion

3.1 Influence of the bearing thickness

Most of the models previously developed to study the contact interaction between journal and bearing parts assumed that the latter is merely a cylindrical surface of zero thickness. However, this simplification is not realistic because the components are solid and might be treated as such (Fig. 3).

Fig. 3
figure 3

Distribution of the normal stresses along the radial direction for the modeled bearing with thicknesses \(t_{\text{B}} = 2\), 4, 6, 8 and \(10\mbox{ mm}\)

Full size image

Figure 4a shows the plot of contact forces \(F_{\text{n}}\) for \(t_{\text{B}} = 2\), 4, 6, 8 and \(10\mbox{ mm}\) for a radial clearance of \(c_{\text{r}} = 0.5\mbox{ mm}\). The curve-fitting for this data allowed obtaining the presented laws of the type \(F_{\text{n}} = K _{\text{pr}} \times \delta ^{n}\), which rendered the contact stiffness possible. This process has been accomplished for coefficients of determination not smaller than 0.999. Figure 4b shows how the normal contact force varies with the pseudo-penetration of the journal into the bearing model, for different values of the bearing thickness. Figure 4b allows observing the increase of the contact stiffness with the bearing thickness \(t_{\text{B}}\). It should be noticed that although the value of \(K_{\text{pr}}\) decreases in the transition from \(t_{\text{B}} = 6\mbox{ mm}\) to \(t_{\text{B}} = 8\mbox{ mm}\), one should bear in mind that the exponent \(n\) is reduced from 1.0254 to 1.0205. This result is coherent, as it means that the force required to produce the same pseudo-penetration is larger in thicker bearings than in thinner ones. In the following simulations, a bearing model with \(4\mbox{ mm}\) of thickness was considered.

Fig. 4
figure 4

Influence of the pseudo-penetration \(\delta \) on the normal contact force \(F_{\text{n}}\) (a) and the carpet plotting showing the effect of the bearing thickness \(t_{\text{B}}\) (b)

Full size image

3.2 Dynamic simulations: effect of the impact velocity

The effect of the initial velocity of the journal on the contact force generated by the interaction with the bearing was investigated with the same premises as in the previous studies (e.g., mesh refinement, boundary conditions and initial position of the journal, compared to the bearing), considering the following initial velocities of the journal: \(v = 0.05\), 0.08, 0.10, 0.15 and \(0.20\mbox{ m}/\mbox{s}\). The selection of these initial velocities did not aim to mimic any particular operating scenario, since the aim was only to obtain deformation amplitudes similar to those obtained in Sects. 3.1 and 3.3. Moreover, these simulations allowed to mimic the inertial effect of the journal (since the mass was ascribed to each model: we considered \(\rho=7800~\mbox{kg}/\mbox{m}^{3}\)), namely the reacting force generated in the contact of the journal with the bearing surface. Dynamic stress and displacement responses were analyzed in this study employing general nonlinear dynamic analysis, with moderate dissipation (Hilber–Hughes–Taylor time integrator [31]). Time integration was performed using implicit operators, meaning that the operator matrix had to be inverted, while a set of simultaneous nonlinear dynamic equilibrium equations were solved at each time increment. For this purpose, Newton’s method was used to get the solution iteratively. These operators are unconditionally stable for linear systems, and do no present mathematical limit on the size of the time increment that can be used to integrate a linear system. Implicit integration schemes used in this study took due care of the influence of the time step size [31] on the prediction of the response, such as the rate of variation of the applied loading action, the nature of the nonlinear damping and stiffness properties, and period of vibration of the mechanical system. A maximum increment over the period ratio (\(\Delta t /T\)) less than \(1/10\) was used to get consistent results. In these simulations the analysis has concluded when the velocity of the journal reached zero.

Figures 5a and 5b allow observing the influence of the starting (release) velocity of the journal model on the normal contact (reacting) force generated in the contact with the bearing surface, for each monitored pseudo-penetration. It also shows the evolution of the contact force with the pseudo-penetration for each value of the considered initial velocity. Figure 5a enables us to conclude that the maximum contact force increases with the initial velocity, which is followed by an increase of the attained maximum displacement (i.e., pseudo-penetration). This result occurs when the journal velocity tends to zero. The evolution of the contact force with the attained pseudo-penetration (for the same prescribed initial velocity) is clearly nonlinear, which contrasts with the trend observed when the journal is subjected to quasi-static loading (straight line in Fig. 5a). This discrepancy increases with the mass of the journal, due to the inertia of the journal member (since the mass of both parts was modeled in this study). Therefore the above mentioned power regression of the type \(F_{\text{n}} = K_{\text{pr}} \times \delta^{n}\) was not applied in these results. Another analysis that may be performed concerns the difference between the contact load issued by the quasi-static condition (trend plotted in Fig. 5a) and those obtained for different initial velocities of the journal at the point where the maximum contact force is attained. It can be concluded that this difference tends to zero when the initial velocity of the journal decreases, which proves the soundness of the performed numerical analyses.

Fig. 5
figure 5

Influence of the pseudo-penetration \(\delta \) on the normal contact force \(F_{\text{n}}\) (a) and the carpet plot showing the effect of the impact velocity \(v\) (b)

Full size image

3.3 Influence of the journal–bearing misalignment

Real mechanisms present imperfections in their components, which imply misalignment in their joints. Such phenomenon may lead to nonuniform wear of their functional surfaces, generating operative instabilities on the mechanical system, which are at the origin of vibrations and noise release. In this work the misalignment of the cylindrical contact is defined in terms of the angle \(\theta \), formed by the longitudinal axes (Fig. 6). Hence, the following amplitudes regarding the misalignment angle were considered (Fig. 6): \(\theta = 1.0^{\circ}\), \(1.5^{\circ}\), \(2.0^{\circ}\), \(2.5^{\circ}\) and \(\theta _{\text{max}}\). Figure 6 allows perceiving that the maximum angle of misalignment is implicitly related with the radial clearance, with \(\theta _{\text{max}}\) written as follows:

$$ c_{\text{r}} + R_{\text{J}}(1-\cos \theta _{\text{max}}) - \biggl(\dfrac{L_{\text{J}}}{2} \biggr) \sin \theta _{\text{max}} = 0. $$
(3)
Fig. 6
figure 6

Schematic of the journal–bearing misalignment with representative geometrical parameters

Full size image

According to this equation, the value of \(\theta _{\text{max}}\) corresponds to the case in which the interference of the journal with the bearing (i.e., \(d=0\) in Fig. 6) is verified. Thus, for a radial clearance of \(c_{\text{r}} = 0.5\mbox{ mm}\), it is possible to obtain a misaligned configuration not higher than \(3.28^{\circ}\). For each value of \(\theta \), a single node of the journal (point \(P_{1}\) in Fig. 6) was first put in contact with the bearing surface (i.e., \(d = 0\) in Fig. 6), assuring that the journal is axially centered with the bearing. Then, a prescribed vertical displacement (\(\delta = 0.05\mbox{ mm}\)) was applied to the nodes that compose the journal axis in the radial direction to induce a pseudo-penetration into the bearing model. Figure 7 shows the normal stress distribution along the radial direction for two misalignment angles (\(\theta =1^{\circ}\) and \(\theta =2.5^{\circ}\)), considering \(c_{\text{r}} = 0.5\mbox{ mm}\).

Fig. 7
figure 7

Side (cut) view of the journal–bearing interaction showing the distribution of normal stress (in MPa) along the radial direction for the simulations regarding the effect of the misalignment angle, for \(c_{\text{r}} = 0.5\mbox{ mm}\) and \(\theta = 1.0^{\circ}\) (a) and \(\theta = 2.5^{\circ}\) (b)

Full size image

The contact (reacting) force on the interface of both bodies along with the corresponding power regression are plotted in Fig. 8a. Accordingly, Fig. 8b shows the influence of the angle of misalignment on the normal contact force developed in the interface of the bearing and the journal members, for the issued pseudo-penetrations.

Fig. 8
figure 8

Influence of the pseudo-penetration \(\delta \) on the normal contact force \(F_{\text{n}}\) (a) and the carpet plot showing the effect of the misalignment angle \(\theta \) (b)

Full size image

For the same pseudo-penetration value \(\delta \), the increase of \(\theta \) is followed by both the decrease in the contact force and contact stiffness, for the same pseudo-penetration value, \(\delta \). It should be noticed that in the transition from \(\theta = 1.5^{\circ}\) to \(2.0^{\circ}\) despite the fact that \(K_{\text{pr}}\) increases, the exponent \(n\) increases. These results are consistent with the thought that for higher misalignment the contact area between both bodies decreases, that is, there is less material to react mechanically.

3.4 Rolling effect

The last phenomenon treated in this study was the rolling between the two cylindrical contacting surfaces. In these simulations, both parts are no longer modeled as purely elastic. Hence, plastic behavior was assumed following an isotropic hardening yield curve taken from [32]. Isotropic elasticity was assumed with both journal and bearing domains, yielding a Young modulus of \(E = 207~\mbox{GPa}\) and Poisson ratio of \(\nu = 0.3\), i.e., the very same values applied in previous simulations. The strain hardening is described using 11 points on the yield stress versus plastic strain curve, with an initial yield stress of \(168.2~\mbox{MPa}\) and a maximum yield stress of \(448.45~\mbox{MPa}\). No rate dependence or temperature dependence was taken into account in this study. It must be also mentioned that Coulomb friction was assumed between the two surfaces, with a friction coefficient of 0.3. Friction plays a vital role in this process, as it is the only mechanism by which the journal outer surface assumes an angular movement (i.e., relative displacement).

An angular velocity of \(\omega _{\text{B}} = 12.56\mbox{ rad}/\mbox{s}\) was first imposed to the bearing axis. Simultaneously, a vertical displacement was prescribed to the journal until it could reach a maximum penetration depth of \(\delta _{\text{max}} = 1.00\mbox{ mm}\). The contact interaction of both members (journal and bearing) was analyzed taking into account the elastoplastic behavior of the material used to fabricate the revolute joint. The authors assumed that the material presents an isotropic hardening yield behavior. Hence, the combined effect of the imposed radial displacement (along the \(y\) direction in Fig. 2a) and the angular displacement of the journal both may lead to a stress state that induces a permanent deformation of both models in the contacting regions. As a consequence, this strategy follows neither a linear dynamics simulation nor a stationary one. The approach configures a transient nonlinear dynamics simulation.

When a point on the surface of the journal has just made contact with the bearing, the outer cylindrical surface of the journal was observed to move slower than the point on the surface of the bearing, while a relative slip between the two surfaces was registered. Also, as a region on the journal started adhering to the bearing wall, then this very model (bearing) has been seen to start moving faster. After a certain distance, the referred region (i.e., the one belonging to the journal) got stuck to it, thus acquiring the same angular velocity. Regarding the rolling phenomena, three stages may be considered: (i) an initial stage, in which the relative speed is nonnegligible and slip between the two members is observed; (ii) an intermediary stage, characterized by a considerable reduction of slip, in which the relative speed tends to zero (though a steady-state regime is not fully reached); and (iii) a final stage, for which a stabilization of the difference between the angular velocities is attained. This behavior puts into evidence that rolling without slipping is not verified in this analysis. Fig. 9 allows understanding the kinematics of two arbitrary nodes of each body that are put in contact with each other, one belonging to the bearing and other to the journal. The results ensuing and presented in advance were obtained from the performed simulations and fully corroborate what should be expected regarding the movement of the two components.

Fig. 9
figure 9

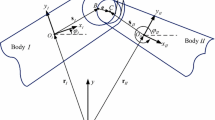
Schematics of the relative displacement of two arbitrary nodes, \(N_{\text{B}}\) and \(N_{\text{J}}\), of the bearing and journal FE mesh, respectively, during the simulations elaborated to study the effect of the rolling between the two surfaces in contact in two consecutive displacement increments

Full size image

As depicted in Fig. 9, regarding a predefined node located in the inner cylindrical surface of the bearing (lower index B), the vector \({{\mathbf{U}}^{N_{\text{B}}}}_{0i}\) denotes the displacement of node \(N_{\text{B}}\) from its starting position (upper index 0) to the position adopted in the \(i\)th iteration of the simulation. This is a consequence of the imposed angular velocity \(\omega _{\text{B}} = 12.56~\mbox{rad}/\mbox{s}\). The results obtained in the performed simulations were the Cartesian components (\(x\) and \(y\)) of the displacement vector \({{\mathbf{U}}^{N_{\text{B}}}}_{0i}\), i.e., \({{U_{1}}^{N_{\text{B}}}} _{0i}\) and \({{U_{2}}^{N_{\text{B}}}}_{0i}\) (\(i = 1, 2\) in Fig. 9). The condition of permanent contact implies that \(\|{{\mathbf{N}}_{\text{B}}}^{i}\| = R_{\text{B}} = 10\mbox{ mm}\) and \(\|{{\mathbf{N}}_{\text{J}}}^{i'}\| = R_{\text{J}} = 9.5\mbox{ mm}\). Additionally, the instantaneous centers of rotation of each body are not coincident with each other due to the consideration of a finite value for the radial clearance. The magnitude of the displacement vector can be easily computed (Eq. (4)) and, as a consequence, since the magnitude of the vector that defines the position of the node \({{\mathbf{N}}_{\text{B}}}^{i}\) is always equal to the radius of the bearing, the angle \(\phi \) is also easily obtained trough the relationship presented in Eq. (5):

$$\begin{aligned} \bigl\| {{\mathbf{U}}^{N_{\text{B}}}}_{0i}\bigr\| ^{2} =& \bigl( {{{U_{1}}^{N_{ \text{B}}}}_{0i}} \bigr)^{2} + \bigl({{{U_{2}}^{N_{\text{B}}}}_{0i}} \bigr)^{2}, \end{aligned}$$
(4)
$$\begin{aligned} \sin \biggl(\dfrac{\phi _{i}}{2} \biggr) =& \dfrac{\frac{\|{{\mathbf{U}} ^{N_{\text{B}}}}_{0i}\|}{2}}{R_{\text{B}}} . \end{aligned}$$
(5)

It is worth to refer that the same calculations cannot be applied to the nodes belonging to the journal, simply due to the fact that each node which composes the mesh of the journal presents two distinct movement patterns: (i) a rotation around the instantaneous longitudinal axis of the journal, as a direct consequence of the angular velocity imposed in the bearing, when the two devices are put in contact with each other, and (ii) a vertical displacement, as a result of the imposed penetration depth \(\delta_{\text{max}}\). Effectively, it is not possible to dissociate the two movements, so, merely an estimation of the angular velocity attained by the journal can be made:

$$\begin{aligned} \sin \biggl(\dfrac{\gamma _{i}}{2} \biggr) =& \dfrac{\frac{\|{{\mathbf{U}}^{N_{\text{J}}}}_{0i}\|}{2}}{R_{\text{J}}} , \end{aligned}$$
(6)
$$\begin{aligned} \dot{\gamma _{i}} =& \lim_{\Delta t\rightarrow 0} \dfrac{\gamma (t^{0}+ \Delta t)-\gamma (t^{0})}{\Delta t} = \dfrac{\gamma _{i}}{t^{{N_{\text{J}}}^{i}}-t^{0}} . \end{aligned}$$
(7)

Once the set of values of the angle \(\phi \) for a certain period of time depicted in Fig. 10a are obtained, and due to the fact that the time step is well defined and known, the values related with the angular velocity of the nodes that belong to the bearing wall can be easily calculated employing Eq. (8). This procedure renders it possible to conclude that the attained angular velocity matches perfectly the value imposed in the initial conditions, i.e., \(12.56\mbox{ rad}/\mbox{s}\) (a trend shown in Figs. 10a and 10b). Thus, it can be concluded that although the journal is forced to penetrate into the bearing model, it does not conflict with the prescribed angular velocity. Hence,

$$ \dot{\phi _{i}} = \lim_{\Delta t\rightarrow 0} \dfrac{\phi (t^{0}+ \Delta t)-\phi (t^{0})}{\Delta t} = \dfrac{\phi _{i}}{t^{{N_{\text{B}}} ^{i}}-t^{0}} \cong \omega _{\text{B}} = 12.56 \text{ rad/s.} $$
(8)
Fig. 10
figure 10

Evolution of \(\phi \) and \(\gamma \), the angles that allow determining the angular velocities of the bearing and journal (a), and representation of the angular velocities, \(\dot{\phi }\) and \(\dot{\gamma}\), related with the angular velocity of the bearing and journal (b), respectively

Full size image

Figure 10b illustrates the evolution of the angular velocity of both the bearing and journal as a function of time. One can observe for the initial iterations the above referred aspect regarding the sticking of the journal onto the bearing wall. In this initial period, the journal gains velocity, tending to an approximate value of the bearing angular velocity as time goes by.

The nonlinear response of the material is triggered when the stress state estimated locally leads to yielding, which may occur in a very differentiated manner along the contact area according to the generated equilibrium of forces. This nonlinear phenomenon leads to important modifications on the contact geometry, which are visible in the generated strain profiles of both the radial and tangential directions. Figure 11a shows the plot of the principal strains after 0.250 seconds, both for the bearing and journal models, when the journal attains the maximum penetration amplitude and angular displacement. In this illustration (Fig. 11a), the journal model has been hidden, being substituted by its external surface that is defined to allow for the contact interaction modeling. Figure 11b exhibits the labeling of elements in the interface showing the computed principal strains. The tangential strains induced by rolling generate the asymmetry that is visible in the strain field of the bearing model. This cartography has then been post-processed to show the wave profiles (inversions) of both the radial and tangential strains that are generated in the contacting region (Figs. 12a and 12b), revealing asymmetric amplitudes. Important inversions of normal stresses (tensile vs. compressive) in the vicinity of the contact region of the journal with the bearing are at the origin of the plotted data. The amplitude of these profiles is more important in the bearing model than in journal due to clear differences of their inertial properties.

Fig. 11
figure 11

Principal strains after 0.250 seconds, both for the bearing and journal models (a), and the labeling of elements in the interface showing the computed principal strains (b)

Full size image
Fig. 12
figure 12

Wave profiles (inversions) of both radial and tangential strains that are generated in the contacting region regarding the bearing model (a) and the journal model (b)

Full size image

4 Application example: 3D slider–crank mechanism

4.1 Mechanism description

A benchmark problem is presented through a 3D slider–crank mechanism, allowing us to acknowledge the differences that exist when the problem is analyzed through the combination of the referred MBD formulation and FEM. Thus, four rigid bodies (including ground) describe the slider–crank model under scrutiny (Fig. 13), namely the crank (body 2), the connecting rod (body 3) and a piston (body 4). The model includes four distinct kinematic joints: (i) an ideal revolute joint that connects the ground and the crank (5 constraints), (ii) an ideal revolute joint between the crank and the connecting rod (5 constraints), (iii) a non-ideal revolute joint between the connecting rod and the piston (0 constraints), and (iv) an ideal translational joint that links the ground and the piston (5 constraints). Regarding the revolute joint with clearance, it must be emphasized that the bearing is localized in the connecting rod, while the journal belongs to the piston.

Fig. 13
figure 13

3D slider–crank mechanism with one non-ideal revolute joint

Full size image

The length and the inertial properties of each body are presented in Table 1. The initial conditions, namely positions and velocities, should fulfill the constraint equations to minimize the constraints violation during the simulation. Bearing this in mind, the initial conditions for this mechanism are displayed in Tables 2 and 3.

Table 1 Dimensional and inertia properties of each body
Full size table
Table 2 Initial positions for the dynamic analysis
Full size table
Table 3 Initial velocities for the dynamic analysis
Full size table

Beyond the inertia and reaction forces, the weight of each body is the only external force considered, and it is applied in the negative direction of \(z\) axis (\(g = 9.81~\mbox{m}/\mbox{s}^{2}\)). The process of integration is solved with the implementation of the ODE45 method (a solver for ordinary differential equations based on Runge–Kutta method with a variable time step available in MATLAB®) [33, 34] with a variable time step, for a maximum time step of \(\Delta t_{\text{max}} = {10^{-5}}\mbox{ s}\). Concerning the non-ideal revolute joint, the geometrical parameters, material and inertial properties of both the bearing and journal are displayed in Table 4, with a coefficient of kinetic friction \(\mu = 0.1\). The restitution factor \(c_{\text{e}}\) has a value of 0.9, hence inelastic collisions occur and subsequently the kinetic energy is not conserved.

Table 4 Geometrical parameters, material and specific mass of the bearing and journal that constitute the analyzed non-ideal revolute joint
Full size table

4.2 Motion analyses

The dynamic response of the slider–crank mechanism can be represented by tracing the evolution of the position, velocity and acceleration of the slider, since the bodies were simulated as rigid. The figures presented in this section are relative to the movement of the slider from its starting position till the position adopted in the iteration corresponding to \(t = 0.1\mbox{ s}\). This was done merely to avoid the superposition of data due to the fact that the position achieved by the center of mass of the slider is the same at every \(t = T/2\), with \(T\) being the period of oscillation of the movement. Six simulations were performed for the same scenario and conditions, in which the only difference was the mathematical model implemented to compute the generated normal contact force developed in the interface of the colliding members of the non-ideal revolute joint. Thus, the cylindrical contact force models (used in the context of MBD) that were chosen were those presented in [35], [36] and [26]. The mathematical law deduced from the FE model was obtained on the basis of the best agreement with the initial conditions applied to the mechanism. The law implemented was that presented in Fig. 4a for the considered bearing thickness of \(t_{\text{B}} = 4\mbox{ mm}\) (i.e., \(F_{\text{n}} = 338240 \delta ^{1.0114}\)). When implementing the FE model with the term related with the energy dissipation, the expression assumes the form

$$ F_{\text{n}} = 338240 \delta ^{1.0114} \biggl[ 1+ \frac{3(1-c_{e}^{2})}{4} \frac{\dot{\delta }}{\dot{\delta }^{(-)}} \biggr]. $$

By inspecting Fig. 14a, it can be inferred that the existence of clearance in the joint influences the slider velocity by leading to a staircase-like shape for the velocity versus time response. The periods of constant velocity observed for the slider (Fig. 14b) mean that the journal can freely move inside the bearing boundaries. The sudden velocity changes are due to the impact between the journal and bearing. When a smooth change in the velocity curve of the slider is observed, we have an indication that the journal and bearing are in continuous contact.

Fig. 14
figure 14

Velocity of the center of mass of the slider within the first \(0.1\mbox{ s}\) (a) and detailed view of the velocity of the center of mass of the slider, in which we denoted the free-flight motion of the journal inside the bearing wall (b) with \(\mu = 0.1\)

Full size image

The slider acceleration is subjected to high peaks caused by impact forces that are propagated through the rigid bodies of the mechanism, as observed in Fig. 15a. In addition, and only for the FE model presented in this work, the analyses related with the acceleration of the center of mass of the slider were also performed considering the absence of friction between the journal and bearing, as shown in Fig. 15b. One should notice that the generated normal contact forces and the attained accelerations are intrinsically related with each other (i.e., higher forces are equivalent to higher accelerations, and vice versa). Concerning the FE model, it can be concluded that when taking into account the energy dissipation term, the normal contact forces are smaller and, as a consequence, the peaks observed in the acceleration of the center of mass of the slider are also less visible and present lower magnitudes. The reasons for such behavior are the following: (i) the term related with the energy dissipation \([ \frac{3(1-c_{e}^{2})}{4}\frac{\dot{\delta }}{ \dot{\delta }^{(-)}} ]\) is negative in the restitution phase of the contact (the convention adopted in this work implies that in the compression phase the penetration velocity is positive, while in the restitution phase it assumes negative values) and (ii) the normal contact forces are calculated with the values obtained for the penetration and disregarding the dissipation term leading to higher penetration depths, and confirming that the coefficient of restitution, \(c_{e}\), plays a fundamental role in the issued results.

Fig. 15
figure 15

Acceleration of the center of mass of the slider within the first \(0.1\mbox{ s}\) (a) and the effect of the static friction coefficient in the results provided by the FE model (b) with \(\mu = 0.1\)

Full size image

4.3 Phase portraits and energy loss

As previously mentioned, the value of the radial clearance considered in the scope of these simulations (\(c_{\text{r}} = 0.5\mbox{ mm}\)) is somehow an exaggerated value for worn equipment. Therefore, it is expected that a highly nonlinear motion between the journal and bearing occurs, since the motion does not repeat from cycle to cycle. This is confirmed by the respective phase portraits, depicted in Fig. 16a, where chaotic behavior can clearly be observed. This chaotic response is notably higher in the Johnson model and in the FE model (w/o dissipation) than in the remaining ones, suggesting that impacts followed by some rebounds take place. Concerning the models of Lankarani & Nikravesh, Pereira et al. and in the FE models (w/ dissipation), one can observe a quasi-periodic motion, because the orbits fill up the phase portraits in a fully predictable manner. Regarding the FE model, the respective phase portraits are in agreement with the aforementioned hypothesis that when considering the dissipative term the normal contact forces are smaller and, as a consequence, the behavior of the mechanism tends to be smoother, with less impacts taking place. Concerning the influence of the friction effect, depicted in Fig. 16b, as expected, when implementing the FE models without the dissipation term, the behavior of the mechanism tends to be much more chaotic due to the fact that the collisions between the journal and the bearing generate higher penetration values, and therefore higher normal contact forces are developed. It can also be inferred that the chaotic behavior of the mechanism relies on the level of sensitivity to the prescribed initial conditions. Though the analyses have not taken into account any other values for the radial clearance, when the magnitude of this variable is reduced, the dynamic behavior tends to be periodic or regular, which indicates that the journal follows the bearing wall.

Fig. 16
figure 16

Phase portraits for the analyzed models (a) and the effect of the coefficient of kinetic friction in the results provided by the FE model (b) with \(\mu = 0.1\)

Full size image

An important mention should now be given to the friction model implemented in the performed simulations which was the model first presented in [37]. This model states that the friction always opposes relative motion between contacting bodies and its magnitude is proportional to the normal contact force. The model depends on the direction of the relative velocity, excluding when the relative velocity is null, as the friction force is a multivalued function of the external tangential force. This model can be described as

$$ \textbf{F}_{\text{f}} = \textstyle\begin{cases} F_{\text{C}}\operatorname{sgn}(\mathbf{v}_{\text{T}}) & \mbox{if }\|\mathbf{v}_{\text{T}}\| \neq 0,\\ \min(\|\textbf{F}_{\text{e}}\|,F_{\text{C}})\operatorname{sgn}(\textbf{F}_{\text{e}})& \mbox{if }\|\mathbf{v}_{\text{T}}\| = 0, \end{cases} $$
(9)

where

$$ F_{\text{C}} = \mu \|\textbf{F}_{\text{n}}\|, $$
(10)

in which \(\textbf{F}_{\text{n}}\) is the normal force, \(F_{\text{C}}\) is the magnitude of Coulomb friction, \(\mu \) is the kinetic coefficient of friction, \(\textbf{F}_{\text{e}}\) is the external tangential force, and \(\mathbf{v}_{\text{T}}\) is the relative velocity of the contacting bodies. This model presents a dependence on the velocity by the signum function,

$$ \operatorname{sgn}(\mathbf{v}_{\text{T}}) = \textstyle\begin{cases} \frac{\mathbf{v}_{\text{T}}}{\|\mathbf{v}_{\text{T}}\|} & \mbox{if } \|\mathbf{v}_{\text{T}}\| \neq 0,\\ \mathbf{0} & \mbox{if }\|\mathbf{v}_{\text{T}}\| = 0, \end{cases} $$
(11)

where \(\mathbf{0}\) is a null vector.

When considering the dissipation term, the generated normal contact forces are smaller. Consequently, the friction forces are smaller, which means that the energy losses due to this effect are much less pronounced, implying a smaller variation in the total mechanical energy of the mechanism. Bearing this in mind, this assumption is totally corroborated by the analysis of Figs. 17a and 17b, in which the influence of the friction phenomena was exploited. When neglecting the friction effect, the energy losses that occur in the mechanism are merely due to the normal contact and, eventually, a direct outcome of the considered coefficient of restitution. Thus, in this case (\(\mu = 0\)), by implementing the FE model and without taking into account the dissipation term, i.e., \(c_{e} = 1\), the collisions are perfectly elastic and the loss of energy of the mechanism is practically zero. On the other hand, when considering the effect of the coefficient of restitution (\(c_{e} = 0.9\) for the performed analysis), inelastic collisions occur and subsequently the kinetic energy is not conserved.

Fig. 17
figure 17

Variation of the mechanical energy of the 3D slider–crank mechanism when implementing the FE model considering the effect of the static friction coefficient (a) and a more detailed view when implementing the FE model considering the effect of the static friction coefficient, within the first \(0.01\mbox{ s}\) of simulation (b)

Full size image

5 Conclusions

The results ensued by the numerical model following a quasi-static analysis enabled concluding that the contact force decreases with the bearing thickness, which was justified by the increase of the bearing compliance. It was also noticed that the impact velocity led to an increase of the (pseudo) penetration on the bearing surface, which was attributed to the effect of the inertia. The simulation of the axial misalignment allowed concluding about the diminishing of the contact force, as the contact area of both members tends to decrease during contact. A three-dimensional slider–crank mechanism was chosen to perform a MultiBody Dynamics analysis, incorporating the previously examined model of a three-dimensional non-ideal revolute joint. The analysis provided the monitoring of the velocity and acceleration of the slider, together with the reaction forces developed with the opposing ground. The results were consistent with other MBD analyses obtained for the same three-dimensional mechanism. It was concluded that the model is able to predict much higher peaks both for the acceleration-time response and reaction forces than would result if the simulated joint had been simulated as an ideal (i.e., non-realistic) revolute joint. Also, the phase portraits revealed that the analyzed system (joint included) may exhibit nonlinear and eventually chaotic behavior, in particular when the effect of radial clearance is analyzed. This observation allows concluding that the design of mechanisms with revolute joints may be a very complex task to undertake, pointing to the necessity of the incorporation of nonlinear controllers as a way to ensure the dynamical stability of the system. Thus, it is of paramount importance to develop realistic numerical-analytical tools that allow accurately previewing the dynamic response of spatial multibody mechanical systems.