Deduction method of the overall transfer equation of linear controlled multibody systems

Abstract

The transfer matrix method for multibody systems (MSTMM), which is a highly efficient and novel approach for multibody system dynamics, was proposed and perfected in the past 20 years. The deduction of the overall transfer equation of the system is one of the key techniques in MSTMM. The topology figure of the dynamics model of multibody systems is a novel pictorial expression to describe the relationship among the state vectors of connection points of different elements in MSTMM. In this paper, the block diagram in control theory is introduced and incorporated into the topology figure of the dynamics model to represent the connection relationship between different mechanical elements in the system as well as the control relations. Meanwhile, the transfer equations of the controlled element, control subsystem and the overall transfer equation of the linear controlled multibody systems are deduced. The proposed method greatly reduces the efforts to study the linear controlled multibody systems since the procedures are stylized. Two numerical examples are given to validate the proposed method.

1 Introduction

A multibody system comprises bodies (rigid or deformable) and hinges in an arbitrary fashion. Typically, bodies may undergo large translational and rotational displacements while ideal joints kinematically constrain the relative motions between two adjacent bodies. Along with the requirement by the development in engineering technology, the theory and techniques of multibody system dynamics (MSD) [1–6], such as modeling approaches, formulations of system equations of motion, integration algorithms etc., were put forward and improved creatively by many scholars and experts continually in the past 50 years. The classical transfer matrix method (TMM) is an old approach in structural dynamics [7] and rotordynamics [8]. Later the finite element transfer matrix method (FETMM) was presented by Dokanish [9] to analyze the vibration of plate structures. The Riccati TMM was put forward by Horner [10] to overcome the computational difficulties in calculating the eigenvalues. Further, Kumar et al. [11] proposed the discrete time transfer matrix method (DT-TMM) to study the dynamics response of time-variant structures.

It has been more than 20 years since the transfer matrix method for multibody systems (MSTMM) was established by Xiaoting Rui and his co-workers [12]. On the one hand, the transfer matrix method for linear multibody systems (linear MSTMM) was first introduced by Rui in 1993 and was used to analyze the natural vibration characteristics of multi-rigid-flexible-body systems [13]. The linear MSTMM was then perfected by developing new transfer matrices and orthogonal properties of linear multibody system [14] and further extended to two dimensional systems [15]. Moreover, Bestle and Abbas [16] proposed an approach to improve the computational stability and accuracy. On the other hand, by combining TMM with linearization and numerical integration procedures, the discrete time transfer matrix method of multibody systems (DT-MSTMM) was introduced and gradually developed by Rui in 1999, which could be applied to time-variant, nonlinear, large-motion, general multibody systems [17, 18]. More recently, MSTMM was enhanced by (i) proving an automatic deduction theorem of overall transfer equation of general multibody system which facilitates the programming [19, 20], (ii) by improving the computational accuracy of MSTMM, meanwhile simplifying the derivation for transfer equations of elements [21].

The goal of a control system is to adjust the input $u$ of the plant so that its output $y$ can vary as we expect. The regulator problem is to regulate $u$ so that the influence of the disturbance $d$ on $y$ can be canceled. The servo problem, on the other hand, is to adjust $u$ so that the output $y$ can track the behavior of a reference input $r$. In both cases, the error signal $e = y - r$ is expected to be controlled as small as possible. The algorithm to adjust $u$ according to the information obtained is called controller $G_{c}$ [22]. The block diagram can rightly describe the transfer relations among the signals between different components in a system, represent the cause-and-effect relation between different variables, and indicate the calculation of those variables [23, 24]. Since typically one desperately demands fast response and accurate manipulation of the dynamics of a system, the control of a multibody system has been one of the focuses in MSD [25]. For a controlled dynamics system, it’s generally necessary to establish the global dynamics equation of the system, whose dimension will go up with the increase of the system’s degrees of freedom (DOF), thus resulting in low computational speed.

Strictly speaking, various engineering mechanical systems, such as machine tools, weaponry, carrier rockets, airplane and vehicles, as well as electromechanical systems with a controller, are nonlinear and time-variant multibody systems. However, more often than not, the engineering demand in accuracy can be satisfied in many situations even using the model of a linear multibody system, such as in multi-rocket launch systems consisting of tens of bodies, beams, springs and dampers in any spatial arrangement with a tree or closed-loop topology [12–14]. The linear MSTMM shares a similar procedure with linear control theory based on Laplace transformation, which sets up a bridge between control theory and MSD [26]. Generally speaking, linear MSTMM has the following advantages: (i) no global dynamics equations of the system are required, (ii) overall transfer matrix has low order, (iii) the assembly of the overall transfer equation is highly stylized programming, (iv) and a linear multibody system composed of both discrete and continuous elements can be elegantly modeled without discretization in the whole frequency domain, resulting in exact solutions. Although linear MSTMM has so many merits, there are only a few articles reporting its combination with control. In 1976, Book [27] first mentioned that TMM could be used to model controlled dynamics system in the frequency domain. In 1983, Book and Majette [28] established the frequency model of mechanical arms and converted it into the state space in the time domain to analyze the dynamics response and design the controller. In the context of FETMM, Hung et al. [29] added the control signal into the state vector and successfully solved both collocated and non-collocated control problems of a chain system. Based on Hung’s thoughts, Yang et al. [30] put forward the modeling approach of a branched system in the frequency domain and studied the dynamics response of the controlled system in the time domain by using the orthogonality of the augmented state vector in MSTMM. In 2006, Lu et al. [31] utilized the extended transfer matrix method to study the steady state response of a controlled chain system, which can be applied to non-collocated feedback control. Another noticeable work was carried out by Ryan Krauss. He used the extended TMM to model the non-collocated feedback control of the chain system. According to the sensor and actuator position along the transfer direction, both upstream and downstream cases were studied. In his work, the state vector of the sensor element had to be expressed by that of the actuating element using the transfer equation between them, resulting in a compact form of the overall transfer matrix of the system by successive multiplication of transfer matrices [32]. Further, he proposed a method to determine the parameters of the controller based on Contour Plots [33]. More recently, the combination of the block diagram with TMM was adopted by Dieter Bestle to express the relationship between the controlled variables and the input signal intuitively [26]. Further, Hossam applied this method for the tuning of the parameters of the controller on a $1/4$ car model [34].

The above existing modeling approaches have, more or less, the following characteristics. First, the control subsystem has to be merged into the transfer matrix of the controlled element, and is considered a part of the transfer matrix of the mechanical element. Second, the transfer matrix of the controlled element may depend on other elements. These two issues break the encapsulation as well as modularity of the transfer matrix of the controlled mechanical element and do not facilitate the programming. Third, the control relations and processing cannot be reflected in the dynamics system in a straightforward way. Fourth, they are typically only suitable for a dynamics system with a simple topological structure like the chain system.

Based on linear MSTMM, this paper presents a scenario to model general linear controlled multibody systems in the frequency domain. There is no need to augment the state vector by adding “1” or the control signal. The transfer equations of the controlled (mechanical) element are derived, while the control force (or control input signal) is considered separately rather than merged into the transfer matrix of the element. Further, the transfer equation of the control subsystem is defined rather than integrated in the transfer equation of the controlled (mechanical) element. Meanwhile, by combining the topology figure of the dynamics model of multibody systems [20] with the block diagrams in the control theory [26], the proposed topology figure of controlled multibody systems is utilized to describe the connection topology of different elements as well as the control relations. The overall transfer equation of the controlled chain system and the tree system are then deduced easily. The proposed method greatly reduces the efforts to study linear controlled multibody systems since the procedure is stylized. It also lays a potential foundation to automatically deduce the overall transfer equation of linear controlled multibody systems with a computer. The approach is fit for general spatial linear multibody systems under linear control. One basic example illustrates the concepts, and another numerical example of a flexible manipulator is given to demonstrate the application of the proposed method. The results are compared with the simulation and test in [32], which validates the approach of this paper.

2 Outline of the transfer equation of multibody systems

The basic idea of MSTMM is to [12, 17]: break up a complex multibody system into several body elements and hinge elements first, then establish the transfer equations and the transfer matrices of these elements, and at last, according to the system topology, deduce the overall transfer equation and the overall transfer matrix of the system by hand and by a computer automatically.

2.1 Elements with one inboard end and one outboard end

The transfer equation of element $j$ can be denoted as

$$ \boldsymbol{Z}_{j,O} = \boldsymbol{U}_{j} \boldsymbol{Z}_{j,I} , $$

(1)

where $\boldsymbol{U}_{j}$ is the transfer matrix of element $j$, $\boldsymbol{Z}_{j,I}$ and $\boldsymbol{Z}_{j,O}$ are the state vectors of the inboard and outboard ends for element $j$, respectively.

2.2 Elements with multiple inboard ends and one outboard end

Assuming the number of inboard ends is $N$, one can write the transfer equation as [20]

$$ \boldsymbol{Z}_{j,O} = \sum_{k = 1}^{N} \boldsymbol{U}_{j,I_{k}}\boldsymbol{Z}_{j,I_{k}} , $$

(2)

where $\boldsymbol{U}_{j,I_{k}}$ is the transfer matrix corresponding to the $k$th inboard end of element $j$. $\boldsymbol{Z}_{j,I_{k}}$ and $\boldsymbol{Z}_{j,O}$ are the state vectors of the $k$th inboard end and the outboard end of element $j$, respectively.

Typically, the geometrical equation of the elements with multiple inboard ends and one outboard end takes the form [20]

$$ \boldsymbol{H}_{j,I_{1}}\boldsymbol{Z}_{j,I_{1}} = \boldsymbol{H}_{j,I_{k}}\boldsymbol{Z}_{j,I_{k}}\quad ( k = 2,3, \ldots,N ). $$

(3)

2.3 Controlled elements

2.3.1 The control device taking effect on its adjacent two bodies

As shown in Fig. 1(a), an elastic damping hinge and a plunger are connected in parallel. Inside the plunger there is gas or liquid which can offer control forces on its adjacent bodies located at both sides of the hinges. The magnetorheological or piezoelectric material, which applies additional forces on the adjacent bodies of the hinge because of magnetorheological or piezoelectric effects, may also replace the plunger.

Fig. 1

Control device and elastic damping hinge connected in parallel

As shown in Fig. 1(b), the control force, $f_{jc}$, can be regarded as an internal force acting on the connected body elements through the inboard end $I$ and outboard end $O$ of the hinge. Thus, we simply regard the actuated hinge as controlled element in this case. The positive directions of the control force and the axes of inertial coordinate system are denoted with an arrow in the figure. The positive directions of internal forces that act on the elastic damping hinge by the adjacent bodies are also drawn using an arrow in the figure according to the sign convention in [12].

Regardless of the mass of the hinge element, due to the force equilibrium, one can obtain

$$ q_{x_{O}} = q_{x_{I}}. $$

(4)

For a spring and a damper, one has

$$ q_{x_{O}} = k_{j} ( x_{I} - x_{O} ) + c_{j} ( \dot{x}_{I} - \dot{x}_{O} ) + f_{c}. $$

(5)

For the damped free vibration, the state vector $\boldsymbol{z}$ can be expressed as $\boldsymbol{z} = \boldsymbol{Z}e^{\lambda t}$, where $\boldsymbol{Z}$ is the complex amplitude and $\lambda$ is the complex eigenvalue. Thereby, the transfer equation of the controlled element can be deduced according to Eqs. (4) and (5) as

$$\begin{aligned} \boldsymbol{Z}_{j,O} : =& \left [ \textstyle\begin{array}{c} X \\ Q_{x} \end{array}\displaystyle \right ]_{O} = \left [ \textstyle\begin{array}{c@{\quad}c} 1 & - \frac{1}{k_{j} + c_{j}\lambda} \\ 0 & 1 \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} X \\ Q_{x} \end{array}\displaystyle \right ]_{I} + \left [ \textstyle\begin{array}{c} \frac{1}{k_{j} + c_{j}\lambda} \\ 0 \end{array}\displaystyle \right ]F_{jc} \\ =:&\boldsymbol{U}_{j}\boldsymbol{Z}_{j,I} + \boldsymbol{E}_{jc}F_{jc} , \end{aligned}$$

(6)

where

$$\begin{aligned} \boldsymbol{U}_{j} =& \left [ \textstyle\begin{array}{c@{\quad}c} 1 & - \frac{1}{k_{j} + c_{j}\lambda} \\ 0 & 1 \end{array}\displaystyle \right ], \end{aligned}$$

(7)

$$\begin{aligned} \boldsymbol{E}_{jc} =& \left [ \textstyle\begin{array}{c} \frac{1}{k_{j} + c_{j}\lambda} \\ 0 \end{array}\displaystyle \right ]. \end{aligned}$$

(8)

Hereby, $\boldsymbol{E}_{jc}$ is defined as the extraction matrix of control force of the controlled element $j$. $\boldsymbol{U}_{j}$ is the transfer matrix of the elastic damping hinge. $F_{jc}$ is the complex amplitude of $f_{jc}$.

2.3.2 The control device affecting only a single body

In the vehicle suspension design, there exist the concepts of a “skyhook damper” and a “skyhook spring” [35]. They are hypothetical spring and damper between the vehicle and the inertial ground. The “skyhook damper” and “skyhook spring” correspond to a virtual force acting on the vehicle and can be regarded as an external force. Meanwhile, for a pulse jet fixed on an object, the pulse thrust can also be considered as an external force acting on the object when the change of the mass distribution of the system can be neglected if the consumption of the fuel in the pulse jet is in essence trivial. Naturally, we regard the body, which is actuated by control forces, as controlled element in this case.

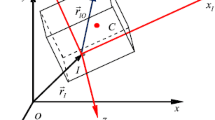
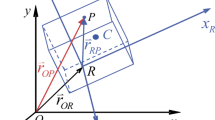
Figure 2 shows a rigid body $j$ experiencing spatial motion with $N$ inboard ends and one outboard end. The body is connected with other elements through its inboard ends $I_{L}\ ( L = 1,2, \ldots,N )$ and outboard end $O$. The control force $\boldsymbol{f}_{jc}$ generated by the control device is acting on point $P_{c}$ of the rigid body. The $oxyz$ frame is the inertial coordinate system corresponding to the equilibrium position and orientation of the rigid body. Its origin represents the equilibrium position of the first input point of the rigid body. And $O_{2}x_{2}y_{2}z_{2}$ is the body-fixed reference frame whose base point is the first input point of the rigid body. The rigid body has 6 DOFs with respect to its inboard body element. Denote the coordinate matrix of any point $P$ of the rigid body by $\boldsymbol{r}_{P} = [ x \ \ y \ \ z]_{P}^{T}$ in the $oxyz$ frame and $\boldsymbol{l}_{I_{1}P}$ in the $O_{2}x_{2}y_{2}z_{2}$ frame, respectively. Represent the mass center of the rigid body by $C$. Further, the angular displacements of the rigid body, which can be regarded as a vector due to small rotations, are expressed using three coordinates in the $oxyz$ frame and denoted as $\boldsymbol{\theta} = [\theta_{x} \ \ \theta_{y} \ \ \theta_{z} ]^{T}$. The matrix of moment of inertia about the first input point $I_{1}$ in the body-fixed frame $O_{2}x_{2}y_{2}z_{2}$ is $\boldsymbol{J}_{I_{1}}$.

Fig. 2

Rigid body with multiple inboard ends and one outboard end vibrating in space

Due to the fact that the orientation angles of a rigid body are global variables, and the orientation angles at the input point and output point should be the same,

$$ \boldsymbol{\theta}_{O} = \boldsymbol{\theta}_{I_{1}}. $$

(9)

The geometrical relationship between the first input point and output point of the rigid body can be expressed as

$$ \boldsymbol{r}_{O} = \boldsymbol{r}_{I_{1}} - \tilde{ \boldsymbol{l}}_{I_{1}O}\boldsymbol{\theta}_{I_{1}}. $$

(10)

According to the theorems of momentum for a system of particles and considering the sign convention for internal forces [12], one obtains

$$ m\ddot{\boldsymbol{r}}_{I_{1}} - m\tilde{\boldsymbol{l}}_{I_{1}C} \ddot{\boldsymbol{\theta}} = \sum_{L = 1}^{N} \boldsymbol{q}_{I_{L}} - \boldsymbol{q}_{O} + \boldsymbol{f}_{jc} , $$

(11)

where $m$ is the mass of the rigid body; $\boldsymbol{q}_{I_{L}}$, $\boldsymbol{q}_{O}$ and $\boldsymbol{f}_{jc}$ are the coordinate matrices of the internal forces and control force at the input point $I_{L}$, output point $O$ and point $P_{c}$ in the $oxyz$ inertial reference frame, respectively. Here, the positive directions of $\boldsymbol{f}_{jc}$ coincide with the positive directions of the axes of the $oxyz$ frame.

Equation (11) can be rewritten as

$$ \boldsymbol{q}_{O} = - m\ddot{\boldsymbol{r}}_{I_{1}} + m \tilde{\boldsymbol{l}}_{I_{1}C}\ddot{\boldsymbol{\theta}} + \sum _{L = 1}^{N} \boldsymbol{q}_{I_{L}} + \boldsymbol{f}_{jc}. $$

(12)

Due to the theorems of relative moment of momentum about the moving point $I_{1}$ of a rigid body,

$$ \boldsymbol{J}_{I_{1}}\ddot{\boldsymbol{\theta}}_{I} + m \tilde{\boldsymbol{l}}_{I_{1}C}\ddot{\boldsymbol{r}}_{I_{1}} = \sum _{L = 2}^{N} \tilde{\boldsymbol{l}}_{I_{1}I_{L}} \boldsymbol{q}_{I_{L}} - \tilde{\boldsymbol{l}}_{I_{1}O} \boldsymbol{q}_{O} + \tilde{\boldsymbol{l}}_{I_{1}P_{c}} \boldsymbol{f}_{jc} - \sum_{L = 1}^{N} \boldsymbol{m}_{I_{L}} + \boldsymbol{m}_{O} , $$

(13)

where $\boldsymbol{m}_{I_{L}}$ and $\boldsymbol{m}_{O}$ are the coordinates matrices of the internal moments at the input point $I_{L}$ and output point $O$ in the inertial reference frame, respectively.

Substituting Eq. (12) into Eq. (13), one obtains

$$ \boldsymbol{m}_{O} = m\tilde{\boldsymbol{l}}_{OC} \ddot{ \boldsymbol{r}}_{I_{1}} + ( \boldsymbol{J}_{I_{1}} + m \tilde{ \boldsymbol{l}}_{I_{1}O}\tilde{\boldsymbol{l}}_{I_{1}C} ) \ddot{ \boldsymbol{\theta}}_{I_{1}} + \sum_{L = 1}^{N} \boldsymbol{m}_{I_{L}} + \sum_{L = 1}^{N} \tilde{\boldsymbol{l}}_{I_{L}O}\boldsymbol{q}_{I_{L}} + \tilde{ \boldsymbol{l}}_{P_{c}O}\boldsymbol{f}_{jc}. $$

(14)

By substituting $\boldsymbol{z} = \boldsymbol{Z}e^{\lambda t}$ into Eqs. (9), (10), (12), and (14), the transfer equation of the controlled element can be acquired as

$$\begin{aligned} \boldsymbol{Z}_{j,O} : =& \left [ \textstyle\begin{array}{c} \boldsymbol{R} \\ \boldsymbol{\varTheta} \\ \boldsymbol{M} \\ \boldsymbol{Q} \end{array}\displaystyle \right ]_{O} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{I}_{3} & - \tilde{\boldsymbol{l}}_{I_{1}O} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ m\lambda^{2}\tilde{\boldsymbol{l}}_{OC} & \lambda^{2} ( \boldsymbol{J}_{I_{1}} + m\tilde{\boldsymbol{l}}_{I_{1}O}\tilde{\boldsymbol{l}}_{I_{1}C} ) & \boldsymbol{I}_{3} & \tilde{\boldsymbol{l}}_{I_{1}O} \\ - m\lambda^{2}\boldsymbol{I}_{3} & m\lambda^{2}\tilde{\boldsymbol{l}}_{I_{1}C} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{R} \\ \boldsymbol{\varTheta} \\ \boldsymbol{M} \\ \boldsymbol{Q} \end{array}\displaystyle \right ]_{I_{1}} \\ &{} + \sum_{L = 2}^{N} \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \tilde{\boldsymbol{l}}_{I_{L}O} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{Om}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{R} \\ \boldsymbol{\varTheta} \\ \boldsymbol{M} \\ \boldsymbol{Q} \end{array}\displaystyle \right ]_{I_{L}} + \left [ \textstyle\begin{array}{c} \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} \\ \tilde{\boldsymbol{l}}_{P_{c}O} \\ \boldsymbol{I}_{3} \end{array}\displaystyle \right ] \boldsymbol{F}_{jc} \\ =:&\boldsymbol{U}_{j,I_{1}} \boldsymbol{Z}_{j,I_{1}} + \sum _{L = 2}^{N} \boldsymbol{U}_{j,I_{L}} \boldsymbol{Z}_{j,I_{L}} + \boldsymbol{E}_{jc}\boldsymbol{F}_{jc} , \end{aligned}$$

(15)

where

$$\begin{aligned} \boldsymbol{U}_{j,I_{1}} =& \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{I}_{3} & - \tilde{\boldsymbol{l}}_{I_{1}O} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ m\lambda^{2}\tilde{\boldsymbol{l}}_{OC} & \lambda^{2} ( \boldsymbol{J}_{I_{1}} + m\tilde{\boldsymbol{l}}_{I_{1}O}\tilde{\boldsymbol{l}}_{I_{1}C} ) & \boldsymbol{I}_{3} & \tilde{\boldsymbol{l}}_{I_{1}O} \\ - m\lambda^{2}\boldsymbol{I}_{3} & m\lambda^{2}\tilde{\boldsymbol{l}}_{I_{1}C} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} \end{array}\displaystyle \right ], \end{aligned}$$

(16)

$$\begin{aligned} \boldsymbol{U}_{j,I_{L}} =& \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \tilde{\boldsymbol{l}}_{I_{L}O} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} \end{array}\displaystyle \right ], \end{aligned}$$

(17)

$$\begin{aligned} \boldsymbol{E}_{jc} = &\left [ \textstyle\begin{array}{c} \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} \\ \tilde{\boldsymbol{l}}_{P_{c}O} \\ \boldsymbol{I}_{3} \end{array}\displaystyle \right ]. \end{aligned}$$

(18)

Hereby, $\boldsymbol{E}_{jc}$ is the extraction matrix of the control force of controlled element $j$. $\tilde{\boldsymbol{l}}_{P_{c}O}$ is the skew-symmetric matrix of $\boldsymbol{l}_{P_{c}O}. \boldsymbol{U}_{j,I_{k}}$ is the transfer matrix of the rigid body of spatial motion with $N$ inboard ends and one outboard end. $\boldsymbol{F}_{jc}$ is the complex amplitude of $\boldsymbol{f}_{jc}$.

The geometrical relationship between the first input point and other input points of the rigid body can be expressed as

$$ \boldsymbol{r}_{I_{1}} = \boldsymbol{r}_{I_{L}} + \tilde{ \boldsymbol{l}}_{I_{L}O}\boldsymbol{\theta}_{I_{1}}\quad ( L = 2,3, \ldots,N ). $$

(19)

Obviously,

$$ \boldsymbol{\theta}_{I_{1}} = \boldsymbol{\theta}_{I_{L}}\quad ( L = 2,3, \ldots,N ). $$

(20)

By substituting $\boldsymbol{z} = \boldsymbol{Z}e^{\lambda t}$ into Eqs. (19) and (20), one acquires the geometrical equation of the controlled element as

$$\begin{aligned} \boldsymbol{H}_{j,I_{1}}\boldsymbol{Z}_{j,I_{1}} : =& \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{I}_{3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \end{array}\displaystyle \right ]_{I_{1}}\left [ \textstyle\begin{array}{c} \boldsymbol{R} \\ \boldsymbol{\varTheta} \\ \boldsymbol{M} \\ \boldsymbol{Q} \end{array}\displaystyle \right ]_{I_{1}} \\ = & \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{I}_{3} & \tilde{\boldsymbol{l}}_{I_{L}O} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \\ \boldsymbol{O}_{3 \times 3} & \boldsymbol{I}_{3} & \boldsymbol{O}_{3 \times 3} & \boldsymbol{O}_{3 \times 3} \end{array}\displaystyle \right ]_{I_{L}}\left [ \textstyle\begin{array}{c} \boldsymbol{R} \\ \boldsymbol{\varTheta} \\ \boldsymbol{M} \\ \boldsymbol{Q} \end{array}\displaystyle \right ]_{I_{L}} =:\boldsymbol{H}_{j,I_{L}} \boldsymbol{Z}_{j,I_{L}} . \end{aligned}$$

(21)

3 Topology figure of the dynamics model of multibody systems

The topology figure of a general multibody system, which contains a closed-loop subsystem, is shown in Fig. 3.

Fig. 3

Description of the topology figure for a non-tree system

In Fig. 3, a circle ∘ denotes a body element, an arrow → denotes a hinge element, the “0” denotes a boundary end. Since the transfer direction is prescribed from tips to root of a tree structure in [20], all elements can be regarded as having multiple inboard ends and one outboard end (an element with one inboard end and one outboard end is the special case of an element with multiple inboard ends and one outboard end). For a general system that consists of closed-loop subsystems, the deduction of its overall transfer equation can be treated as that of a tree system after “cutting” the closed-loop structure at the junction $P_{16,19}$ of body 16 and hinge 19 and regarding the state vectors that emerge at the “cutting point” as the tip “boundaries”. The notations are also explicitly set in [20], and are used to describe the transfer equations and the geometrical equations for each element. Moreover, [20] also provides the approach used for deducing the overall transfer equation of a general system.

4 Deduction of the overall transfer equation for linear controlled multibody systems

4.1 Single feedback control loop in a chain (sub-)system

The system shown in Fig. 4 is made up of 3 lumped masses and 3 elastic damping hinges. $m_{3}$ is affected by the periodic external disturbance force $f_{d}$, thus the system vibrates along the $x$-axis with damping. In order to reduce the vibration of lamped mass $m_{1}$, the feedback control is introduced, where the control error signal originates from $m_{1}$ and the control force acting on the two ends of elastic hinge 4 is $f_{c} = - K_{a}\ddot{x}_{1,2} - K_{v}\dot{x}_{1,2} - K_{d}x_{1,2}$ whose positive direction is shown in Fig. 4. In the following, the overall transfer equation for the controlled multibody system will be derived using MSTMM, and the eigenvalue of the system and the steady-state frequency response $H ( j\varOmega ) = X_{1,0}/F_{d}$ will be analyzed and computed.

Fig. 4

A 3-DOF forced damped vibration system with feedback control

Elements are numbered as 1 to 6 from right to left, respectively, and the boundaries are denoted as 0. The state vectors of each connection point of elements $i$ and $j$ share the same form, namely $\boldsymbol{Z}_{i,j} = [X,Q_{x}]_{i,j}^{T}$. Since the left end is fixed and the right end is free, the boundary conditions of the system are $\boldsymbol{Z}_{6,0} = [0 \ \ Q_{x}]_{6,0}^{T}$ and $\boldsymbol{Z}_{1,0} = [X \ \ 0 ]_{1,0}^{T}$. The transfer direction is from left to right. Figure 5 shows the topology figure of the dynamics model for the controlled multibody system, where the solid arrows represent hinge elements and circles represent body elements. The arrows and circles connect with each other in a sequence to describe the connection topology of elements and denote the transfer direction of the state vector in an uncontrolled system.

Fig. 5

The topology figure of the dynamics model for the controlled multibody system which is made up of the control subsystem and the topology figure of the dynamics model

In order to demonstrate the control relations in the topology figure of the dynamics model, a control subsystem that originates from the measurement device and terminates on the outboard end of the control device (or actuator) is introduced. It is drawn using dashed–dotted arrows and blocks in Fig. 5.

The control subsystem is explained as follows. The measurement of the displacement of element 1, namely $x_{1,2}$, is taken as the error signal for the control subsystem, which corresponds to

$$ X_{1,2} = \boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2} , $$

(22)

where

$$ \boldsymbol{E}_{\boldsymbol{Z}_{1,2}} = [1 \quad 0 ]. $$

(23)

Hereby, $\boldsymbol{E}_{\boldsymbol{Z}_{1,2}}$ is defined as the extraction matrix of the measurement signal from the state vector $\boldsymbol{Z}_{1,2}$.

Then the error signal $x_{1,2}$ is transmitted to the controller, and the control force can be generated by the actuator as

$$ f_{c} = g_{c}x_{1,2} , $$

(24)

where $g_{c}$ is the control law to be determined.

By substituting the transformation $f_{c} = F_{c}e^{\lambda t}$ and $x_{1,2} = X_{1,2}e^{\lambda t}$ into $f_{c} = - K_{a}\ddot{x}_{1,2} - K_{v}\dot{x}_{1,2} - K_{d}x_{1,2}$, the following equation can be obtained:

$$ F_{c} = G_{c} ( \lambda )X_{1,2} , $$

(25)

where

$$ G_{c} ( \lambda ) = - K_{a}\lambda^{2} - K_{v}\lambda - K_{a}. $$

(26)

$G_{c}$ is the expression of the control law under modal coordinates. According to Eq. (6), for the controlled element 4,

$$ \boldsymbol{Z}_{3,4} = \boldsymbol{U}_{4} \boldsymbol{Z}_{5,4} + \boldsymbol{E}_{4c}F_{c}. $$

(27)

Substituting Eqs. (22) and (25) into Eq. (27) results in

$$ \boldsymbol{Z}_{3,4} = \boldsymbol{U}_{4} \boldsymbol{Z}_{5,4} + \boldsymbol{E}_{4c}G_{c} ( \lambda )\boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2}. $$

(28)

The transfer equation of the control subsystem is defined as

$$ \boldsymbol{Z}_{4c}: = \boldsymbol{E}_{4c}G_{c} ( \lambda )\boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2} =: \boldsymbol{U}_{4c}\boldsymbol{Z}_{1,2} , $$

(29)

where

$$ \boldsymbol{U}_{jc} = \boldsymbol{E}_{jc}G_{c} ( \lambda )\boldsymbol{E}_{\boldsymbol{Z}_{1,2}} \quad ( j = 4 ) $$

(30)

is defined as the transfer matrix of the control subsystem, which readily describes the whole process of measurement, the emerging of error signal, the processing of the controller, and the generation of the control force by the actuator acting on the controlled element $j$.

After being merged into the whole system, the transfer equation of controlled element 4 is

$$ \boldsymbol{Z}_{3,4} = \boldsymbol{U}_{4} \boldsymbol{Z}_{5,4} + \boldsymbol{Z}_{4c} = \boldsymbol{U}_{4}\boldsymbol{Z}_{5,4} + \boldsymbol{U}_{4c} \boldsymbol{Z}_{1,2}. $$

(31)

The transfer equations of elements 1, 2, 3, 5 and 6 take the form of

$$ \boldsymbol{Z}_{j,O} = \boldsymbol{U}_{j} \boldsymbol{Z}_{j,I}\quad ( j = 1,2,3,5,6 ) , $$

(32)

where $\boldsymbol{U}_{j}\ ( j = 1,3,5 )$ and $\boldsymbol{U}_{j} \ ( j = 2,6 )$ are the transfer matrices of a one-dimensional lumped mass and an elastic damping hinge, respectively.

According to the topology figure, the stave vector of the measurement point can be expressed as

$$ \boldsymbol{Z}_{1,2} = \boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{Z}_{3,4}. $$

(33)

By substituting Eq. (33) into Eq. (31), one can eliminate the state vector $\boldsymbol{Z}_{1,2}$ of the measurement point and thus obtain

$$ \boldsymbol{Z}_{3,4} = \boldsymbol{U}_{4} \boldsymbol{Z}_{5,4} + \boldsymbol{U}_{4c}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{Z}_{3,4}. $$

(34)

As a consequence, the relationship between the state vectors of the inboard end and outboard end of the controlled element 4 is

$$ \boldsymbol{Z}_{3,4} = ( \boldsymbol{I} - \boldsymbol{U}_{4c} \boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1} \boldsymbol{U}_{4}\boldsymbol{Z}_{5,4}. $$

(35)

Let

$$ \boldsymbol{U}_{4}^{c} = ( \boldsymbol{I} - \boldsymbol{U}_{4c}\boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1}\boldsymbol{U}_{4}. $$

(36)

Equation (35) can then be read as

$$ \boldsymbol{Z}_{3,4} = \boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5,4}. $$

(37)

From the topology figure and Eq. (37), one acquires

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{Z}_{3,4} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5,4} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{Z}_{6,0} , \end{aligned}$$

(38)

namely

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}} = \left [ \textstyle\begin{array}{c@{\quad}c} - \boldsymbol{I} & \boldsymbol{T}_{6 - 1} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{6,0} \end{array}\displaystyle \right ] = \boldsymbol{0}, $$

(39)

where

$$ \boldsymbol{T}_{6 - 1} = \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}. $$

(40)

Knowing the above equation, one can write the overall transfer equation of the controlled chain system according to the automatic deduction theorem of the overall transfer equation of a chain system in [20], by replacing the transfer matrix $\boldsymbol{U}_{4}$ of the elastic damping hinge with $\boldsymbol{U}_{4}^{c}$. Further, $\boldsymbol{U}_{4}^{c}$ is the multiplication of $\boldsymbol{U}_{4}$ by a coefficient matrix which is the inverse matrix of the identity matrix $\boldsymbol{I}$ minus the successive premultiplication of all transfer matrices of elements in the mechanical transfer path from the outboard end of the controlled element to the measurement device, continually premultiplied by the transfer matrix of the control subsystem.

In the following, the system that vibrates with damping under the external disturbance force $f_{d}$ acting on element 3 will be analyzed. The topology figure of the dynamics model for the controlled system with forced vibration is shown in Fig. 6.

Fig. 6

Topology figure of the dynamics model for the controlled system with forced vibration

Compared to Fig. 5, element 3 is forced by a periodic external force whose transfer equation can be expressed as

$$ \boldsymbol{Z}_{3,2} = \boldsymbol{U}_{3} \boldsymbol{Z}_{3,4} + \boldsymbol{E}_{3d}F_{d} , $$

(41)

where $\boldsymbol{E}_{3d} = \bigl [ {\scriptsize\begin{matrix}{}0 \cr 1\end{matrix}} \bigr ]$.

In comparison with Eq. (32), Eq. (41) has one more term in the disturbance force. The form of the transfer equations of other elements remains the same. Consequently, one can obtain the transfer matrices of all the elements in a damped forced vibration system by simple substitution $\lambda \rightarrow j\varOmega$ in the preceding transfer matrices of all elements in the damped free vibration analysis.

It is obvious that Eq. (31) is still valid for the damped forced vibration system. From Fig. 6 and Eq. (41), the state vector of the measurement point can be expressed as

$$ \boldsymbol{Z}_{1,2} = \boldsymbol{U}_{2} \boldsymbol{Z}_{3,2} = \boldsymbol{U}_{2} ( \boldsymbol{U}_{3}\boldsymbol{Z}_{3,4} + \boldsymbol{E}_{3d}F_{d} ). $$

(42)

By substituting Eq. (42) into Eq. (31), one eliminates the state vector of the measurement point and thus obtains

$$\begin{aligned} \boldsymbol{Z}_{3,4} =& ( \boldsymbol{I} - \boldsymbol{U}_{4c} \boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1} \boldsymbol{U}_{4}\boldsymbol{Z}_{5,4} + ( \boldsymbol{I} - \boldsymbol{U}_{4c}\boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1}\boldsymbol{U}_{4c}\boldsymbol{U}_{2} \boldsymbol{E}_{3d}F_{d} \\ =:& \boldsymbol{U}_{4}^{c}\boldsymbol{Z}_{5,4} + ( \boldsymbol{I} - \boldsymbol{U}_{4c}\boldsymbol{U}_{2} \boldsymbol{U}_{3} )^{ - 1}\boldsymbol{U}_{4c} \boldsymbol{U}_{2}\boldsymbol{E}_{3d}F_{d} . \end{aligned}$$

(43)

A combination with the topology given in Fig. 6 results in

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{Z}_{3,2} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} ( \boldsymbol{U}_{3}\boldsymbol{Z}_{3,4} + \boldsymbol{E}_{3d}F_{d} ) \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5,4} + \bigl[ \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{E}_{3d} + \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3} ( \boldsymbol{I} - \boldsymbol{U}_{4c}\boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1}\boldsymbol{U}_{4c}\boldsymbol{U}_{2} \boldsymbol{E}_{3d} \bigr]F_{d} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{Z}_{6,0} + \bigl[ \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{E}_{3d} + \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3} ( \boldsymbol{I} - \boldsymbol{U}_{4c} \boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1} \boldsymbol{U}_{4c}\boldsymbol{U}_{2}\boldsymbol{E}_{3d} \bigr]F_{d} \\ =:&\boldsymbol{T}_{6 - 1}\boldsymbol{Z}_{6,0} + \boldsymbol{T}_{d - 1}F_{d}. \end{aligned}$$

(44)

The above equation is the overall transfer equation of the system, which can be written in partitioned matrix form as

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}}: = [ {-} \boldsymbol{I} \quad \boldsymbol{T}_{6 - 1} ] \left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{6,0} \end{array}\displaystyle \right ] = - \boldsymbol{T}_{d - 1}F_{d}. $$

(45)

Considering the boundary conditions $\boldsymbol{Z}_{6,0} = [ 0 \ \ Q_{x}]_{6,0}^{T}$ and $\boldsymbol{Z}_{1,0} = [X \ \ 0]_{1,0}^{T}$, Eq. (45) may be reduced to

$$ \boldsymbol{U}_{\mathit{all}}^{*}\boldsymbol{Z}_{\mathit{all}}^{*} = - \boldsymbol{T}_{d - 1}F_{d} , $$

(46)

where $\boldsymbol{Z}_{\mathit{all}}^{*} = [ X_{1,0} \ \ Q_{x_{6,0}} ]^{T}$ is composed of the unknown state variables only, and $\boldsymbol{U}_{\mathit{all}}^{*}$ is a $2 \times 2$ square matrix resulting from elimination of all columns of $\boldsymbol{U}_{\mathit{all}}$ associated with zeros in $\boldsymbol{Z}_{\mathit{all}}$ (i.e., $\boldsymbol{U}_{\mathit{all}}^{*}$ is composed of the first and fourth columns of $\boldsymbol{U}_{\mathit{all}}$ given in Eq. (45)).

Obviously,

$$ H ( j\varOmega ) = X_{1,0}/F_{d} = - [1 \quad 0] \boldsymbol{U}_{\mathit{all}}^{* - 1}\boldsymbol{T}_{d - 1}. $$

(47)

The dynamics parameters of the system are given as: $m_{1} = 0.5~\mbox{kg}$, $m_{3} = 3~\mbox{kg}$, $m_{5} = 10~\mbox{kg}$, $K_{2} = 200~\mbox{N}/\mbox{m}$, $K_{4} = 150~\mbox{N}/\mbox{m}$, $K_{6} = 300~\mbox{N}/\mbox{m}$, $C_{2} = 0.1~\mbox{N} \, \mbox{s}/\mbox{m}$, $C_{4} = 0.5~\mbox{N} \, \mbox{s}/\mbox{m}$, $C_{6} = 2.5~\mbox{N} \, \mbox{s}/\mbox{m}$, $K_{a} = 5.0~\mbox{N} \, \mbox{s}^{2}/\mbox{m}$, $K_{v} = 5.0~\mbox{N} \, \mbox{s}/\mbox{m}$, $K_{d} = 5.0~\mbox{N}/\mbox{m}$. In Fig. 7, the curves of the steady-state frequency response $H ( j\varOmega ) = X_{1,0}/F_{d}$ with $\varOmega \in [ 10^{ - 1},10^{3} ]$ are plotted according to Eq. (47) and the Newton method, respectively. As can be seen, the two methods show good agreement. A comparison of the frequency response between the uncontrolled system without feedback and the controlled system is pictured in Fig. 8.

Fig. 7

The amplitude–frequency characteristics and the phase–frequency characteristics of the displacement of lumped mass $m_{1}$ under the external excitation in the controlled system

Fig. 8

A comparison of the frequency response of $H ( j\varOmega ) = X_{1,0}/F_{d}$ between the uncontrolled system and the controlled system

By setting $F_{d} = 0$ in Eq. (46) and substituting the transformation $\varOmega \to - i\lambda$ into the transfer matrix of each element, one can rightly obtain Eq. (39) as

$$ \boldsymbol{U}_{\mathit{all}}^{*}\boldsymbol{Z}_{\mathit{all}}^{*} = \boldsymbol{0}. $$

(48)

The nonzero solution of Eq. (48) must satisfy

$$ \Delta \bigl( \lambda^{r},\lambda^{i} \bigr) = \det \boldsymbol{U}_{\mathit{all}}^{*} = 0. $$

(49)

Table 1 exhibits the eigenvalues of the controlled system with free damped vibration solved by Eq. (49) (see [13]) and the Newton method. The two approaches reach good agreement.

Table 1 The eigenvalues of the controlled system shown in Fig. 4 with free damped vibration

4.2 Multiple feedback control loops existing in a chain (sub-)system

In the preceding section, the case that a single feedback control loop exists in a chain (sub-)system has been discussed. The transfer equations (6) and (15) of controlled elements, as well as Eqs. (22) and (25) which correspond to the emerging of error signal and the generation of control force, have a general form.

As a short conclusion, the transfer equation of a controlled element takes general form

$$ \boldsymbol{Z}_{j,O} = \sum_{L = 1}^{N} \boldsymbol{U}_{j}\boldsymbol{Z}_{j,I_{L}} + \boldsymbol{E}_{jc}\boldsymbol{F}_{jc} =:\sum _{L = 1}^{N} \boldsymbol{U}_{j,I_{L}} \boldsymbol{Z}_{j,I_{L}} + \boldsymbol{Z}_{jc} , $$

(50)

where $\boldsymbol{U}_{j,I_{L}}$ is the transfer matrix corresponding to the $L$th inboard end of the uncontrolled element $j$, $\boldsymbol{E}_{jc}$ is the extraction matrix of control force of controlled element $j$. The element with single inboard end and single outboard end can be regarded as a special case of elements with more than two ends (multiple inboard ends and single outboard end) when $L = 1$.

A control subsystem consists of the following components: (i) a sensor for generating the measurement signal, (ii) a comparator computing the error signal, (iii) a controller adjusting the input signal of the controlled element according to the error signal and certain algorithms, and (iv) an actuator (or control device) generating the control force and acting on the controlled element. The transfer equation of the control subsystem can always be written as

$$ \boldsymbol{Z}_{jc} = \boldsymbol{E}_{jc} \boldsymbol{G}_{c}\boldsymbol{E}_{\boldsymbol{Z}_{m,n}}\boldsymbol{Z}_{m,n} = \boldsymbol{U}_{jc}\boldsymbol{Z}_{m,n} , $$

(51)

where $\boldsymbol{E}_{jc}$ is the extraction matrix of control force of the controlled element $j$, $\boldsymbol{G}_{c}$ is the expression of the control law in modal coordinates, $\boldsymbol{Z}_{m,n}$ is the state vector of measurement point, $\boldsymbol{E}_{\boldsymbol{Z}_{m,n}}$ is the extraction matrix of measurement signal from the state vector $\boldsymbol{Z}_{m,n}$, and

$$ \boldsymbol{U}_{jc} = \boldsymbol{E}_{jc} \boldsymbol{G}_{c}\boldsymbol{E}_{\boldsymbol{Z}_{m,n}} $$

(52)

is the transfer matrix of the control subsystem.

Hence, a general discussion about the topology figure of the dynamics model of a controlled multibody system regardless of the specific system will be conducted below.

4.2.1 Two feedback control loops intersecting each other

There are two feedback control loops intersecting each other in the chain (sub-)system as shown in Fig. 9. The feedback signal of control loop 1 originates from the inboard end of body element 1, and the control forces are internal forces which act on body 5 and body 3 connected by hinge element 4. At the same time, the feedback signal of control loop 2 comes from the outboard end of body element 3, and the control force is an external force acting on body 7.

Fig. 9

The topology figure of the dynamics model of a controlled system with two feedback control loops intersect each other

For control loop 1, the transfer equation of the control subsystem is

$$ \boldsymbol{Z}_{4c} = \boldsymbol{E}_{4c} \boldsymbol{G}_{c1}\boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2} =:\boldsymbol{U}_{4c}\boldsymbol{Z}_{1,2}. $$

(53)

From the transfer equation of controlled element 4, one has

$$ \boldsymbol{Z}_{3, 4} = \boldsymbol{U}_{4} \boldsymbol{Z}_{5, 4} + \boldsymbol{Z}_{4c} = \boldsymbol{U}_{4}\boldsymbol{Z}_{5, 4} + \boldsymbol{U}_{4c} \boldsymbol{Z}_{1,2}. $$

(54)

The state vector of the measurement point is known from the topology figure as

$$ \boldsymbol{Z}_{1,2} = \boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{Z}_{3,4}. $$

(55)

From Eqs. (53)–(55), one deduces

$$ \boldsymbol{Z}_{3, 4} = ( \boldsymbol{I} - \boldsymbol{U}_{4c} \boldsymbol{U}_{2}\boldsymbol{U}_{3} )^{ - 1} \boldsymbol{U}_{4}\boldsymbol{Z}_{5, 4} =:\boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5, 4}. $$

(56)

For control loop 2, the transfer equation of the control subsystem is

$$ \boldsymbol{Z}_{7c} = \boldsymbol{E}_{7c} \boldsymbol{G}_{c2}\boldsymbol{E}_{\boldsymbol{Z}_{3,2}}\boldsymbol{Z}_{3,2} =:\boldsymbol{U}_{7c}\boldsymbol{Z}_{3,2}. $$

(57)

From the transfer equation of controlled element 7, one gets

$$ \boldsymbol{Z}_{7, 6} = \boldsymbol{U}_{7} \boldsymbol{Z}_{7, 8} + \boldsymbol{Z}_{7c} = \boldsymbol{U}_{7}\boldsymbol{Z}_{7, 8} + \boldsymbol{U}_{7c} \boldsymbol{Z}_{3,2}. $$

(58)

The state vector of the measurement point can be obtained from the topology figure in combination with Eq. (56), namely

$$\begin{aligned} \boldsymbol{Z}_{3,2} =& \boldsymbol{U}_{3} \boldsymbol{Z}_{3,4} \\ =& \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5,4} \\ =& \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{Z}_{7,6} . \end{aligned}$$

(59)

By substituting Eq. (59) into Eq. (58) to eliminate the intermediate variable $\boldsymbol{Z}_{3,2}$, one obtains

$$ \boldsymbol{Z}_{7, 6} = \boldsymbol{U}_{7} \boldsymbol{Z}_{7, 8} + \boldsymbol{U}_{7c}\boldsymbol{U}_{3} \boldsymbol{U}_{4}^{c}\boldsymbol{U}_{5} \boldsymbol{U}_{6}\boldsymbol{Z}_{7,6}. $$

(60)

That is to say, the relationship between the state vectors of inboard end and outboard end of the controlled element 7 is

$$ \boldsymbol{Z}_{7, 6} = \bigl( \boldsymbol{I} - \boldsymbol{U}_{7c} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6} \bigr)^{ - 1} \boldsymbol{U}_{7}\boldsymbol{Z}_{7, 8}. $$

(61)

Let

$$ \boldsymbol{U}_{7}^{c} = \bigl( \boldsymbol{I} - \boldsymbol{U}_{7c}\boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6} \bigr)^{ - 1} \boldsymbol{U}_{7}, $$

(62)

then Eq. (61) can be rewritten as

$$ \boldsymbol{Z}_{7, 6} = \boldsymbol{U}_{7}^{c} \boldsymbol{Z}_{7,8}. $$

(63)

As a conclusion from Eq. (62), for a chain system which has $N$ control loops intersecting one another, if one consecutively numbers the $N$ control loops along the opposite direction of the transfer direction from the root (the end of transfer path) to the tip (the start of transfer path) as $1, 2, \dots, N$, the $\boldsymbol{U}_{e_{j}}^{c}$ of the controlled element $e_{j}$ actuated by the $j$th control loop can be calculated by the following approach:

• (a) Let $j = 1$;

• (b) $\boldsymbol{U}_{e_{j}}^{c}$ is the multiplication of $\boldsymbol{U}_{e_{j}}$ of the corresponding uncontrolled element by a coefficient matrix which is the inverse matrix of the identity matrix $\boldsymbol{I}$ minus the successive premultiplication of all transfer matrices of elements in the mechanical transfer path from the outboard end of the controlled element to the measurement device, continually premultiplied by the transfer matrix of the control subsystem.

• (c) Replace the transfer matrix $\boldsymbol{U}_{e_{j}}$ of uncontrolled element $e_{j}$ by $\boldsymbol{U}_{e_{j}}^{c}$;

• (d) $j = j + 1$;

• (e) If $j = N$ then stop, otherwise go back to step (b).

By combining the topology figure with Eqs. (56) and (63), one obtains

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{Z}_{3,4} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{Z}_{5,4} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{Z}_{7,6} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{Z}_{7,8} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{U}_{8}\boldsymbol{Z}_{8,0} , \end{aligned}$$

(64)

namely

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}} = \left [ \textstyle\begin{array}{c@{\quad}c} - \boldsymbol{I} & \boldsymbol{T}_{8 - 1} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{8,0} \end{array}\displaystyle \right ] = \boldsymbol{0}, $$

(65)

where

$$ \boldsymbol{T}_{8 - 1} = \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{U}_{8}. $$

(66)

From Eq. (66), one can write the overall transfer equation of the controlled chain system with multiply control loops intersecting each other according to the automatic deduction theorem of the overall transfer equation of a chain system in [20], by replacing the transfer matrix $\boldsymbol{U}_{4}$ and $\boldsymbol{U}_{7}$ of the uncontrolled elements with $\boldsymbol{U}_{4}^{c}$ and $\boldsymbol{U}_{7}^{c}$.

4.2.2 Outer feedback control loop enclosing inner feedback control loop

In the chain (sub-)system shown in Fig. 10, the outer feedback control loop encloses the inner feedback control loop. The feedback signal of inner-loop control subsystem comes from the outboard end of body element 3, and the control force is an external force acting on body element 7. The feedback signal of the outer-loop control subsystem originates from the input end of body element 1, and the control forces are internal forces acting on body element 7 and body element 9 through hinge element 8.

Fig. 10

The topology figure of the dynamics model of a controlled system with outer feedback control loop enclosing inner feedback control loop

For the inner-loop control subsystem, one obtains

$$ \boldsymbol{Z}_{7c} = \boldsymbol{G}_{c2} \boldsymbol{E}_{\boldsymbol{Z}_{3,2}}\boldsymbol{Z}_{3,2} = \boldsymbol{U}_{7c} \boldsymbol{Z}_{3,2}. $$

(67)

According to the transfer matrix of controlled element 7,

$$ \boldsymbol{Z}_{7, 6} = \boldsymbol{U}_{7} \boldsymbol{Z}_{7, 8} + \boldsymbol{U}_{7c}\boldsymbol{Z}_{3,2}. $$

(68)

Following the topology figure, the state vector of the measurement point can be read as

$$ \boldsymbol{Z}_{3,2} = \boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{Z}_{7,6}. $$

(69)

From Eqs. (67)–(69), one deduces

$$ \boldsymbol{Z}_{7, 6} = ( \boldsymbol{I} - \boldsymbol{U}_{7c} \boldsymbol{U}_{3}\boldsymbol{U}_{4}\boldsymbol{U}_{5} \boldsymbol{U}_{6} )^{ - 1}\boldsymbol{U}_{7} \boldsymbol{Z}_{7, 8} =:\boldsymbol{U}_{7}^{c} \boldsymbol{Z}_{7, 8}. $$

(70)

For the outer-loop control subsystem, one acquires

$$ \boldsymbol{Z}_{8c} = \boldsymbol{E}_{8c} \boldsymbol{G}_{c1}\boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2} = \boldsymbol{U}_{8c}\boldsymbol{Z}_{1,2}. $$

(71)

From the transfer equation of the controlled element 8, we have

$$ \boldsymbol{Z}_{7, 8} = \boldsymbol{U}_{8} \boldsymbol{Z}_{9, 8} + \boldsymbol{U}_{8c}\boldsymbol{Z}_{1,2}. $$

(72)

The state vector of the measurement point can be written by using the topology figure combined with Eq. (70) as

$$\begin{aligned} \boldsymbol{Z}_{1,2} =& \boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}\boldsymbol{U}_{5} \boldsymbol{U}_{6}\boldsymbol{Z}_{7,6} \\ =& \boldsymbol{U}_{2}\boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{U}_{7}^{c}\boldsymbol{Z}_{7,8} . \end{aligned}$$

(73)

Through Eqs. (72) and (73), one can eliminate the intermediate variable $\boldsymbol{Z}_{1,2}$ and obtain

$$ \boldsymbol{Z}_{7, 8} = \boldsymbol{U}_{8} \boldsymbol{Z}_{9, 8} + \boldsymbol{U}_{8\mathrm{c}}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}\boldsymbol{U}_{5} \boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{Z}_{7,8}. $$

(74)

Namely, the relationship between the state vectors of the inboard end and outboard end of controlled element 8 is

$$ \boldsymbol{Z}_{7, 8} = \bigl( \boldsymbol{I} - \boldsymbol{U}_{8\mathrm{c}} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \bigr)^{ - 1}\boldsymbol{U}_{8}\boldsymbol{Z}_{9, 8}. $$

(75)

Let

$$ \boldsymbol{U}_{8}^{c} = \bigl( \boldsymbol{I} - \boldsymbol{U}_{8\mathrm{c}}\boldsymbol{U}_{2}\boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{U}_{7}^{c} \bigr)^{ - 1} \boldsymbol{U}_{8}, $$

(76)

then Eq. (75) can be rewritten as

$$ \boldsymbol{Z}_{7, 8} = \boldsymbol{U}_{8}^{c} \boldsymbol{Z}_{9, 8}. $$

(77)

Equation (76) leads us to a short summary. For a chain system which has $N$ control loops enclosed one by one, if one consecutively numbers the $N$ control loops from inside to outside as $1, 2, \dots, N$, the $\boldsymbol{U}_{e_{j}}^{c}$ of the controlled element $e_{j}$ actuated by the $j$th control loop can also be calculated by the recursive approach mentioned in Sect. 4.2.1.

From Eqs. (70) and (77) and the topology figure, one obtains

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{Z}_{7,6} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{Z}_{7,8} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{U}_{8}^{c}\boldsymbol{Z}_{9,8} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2} \boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{U}_{7}^{c} \boldsymbol{U}_{8}^{c}\boldsymbol{U}_{9} \boldsymbol{Z}_{9,0} , \end{aligned}$$

(78)

namely

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}} = \left [ \textstyle\begin{array}{c@{\quad}c} - \boldsymbol{I} & \boldsymbol{T}_{9 - 1} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{9,0} \end{array}\displaystyle \right ] = \boldsymbol{0}, $$

(79)

where

$$ \boldsymbol{T}_{9 - 1} = \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4}^{c} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}^{c} \boldsymbol{U}_{8}^{c}\boldsymbol{U}_{9}. $$

(80)

From the equation above, one can write the overall transfer equation of the controlled chain system with outer control loop enclosing inner control loop according to the automatic deduction theorem of the overall transfer equation of a chain system in [20], by replacing the transfer matrix $\boldsymbol{U}_{7}$ and $\boldsymbol{U}_{8}$ of the uncontrolled elements with $\boldsymbol{U}_{7}^{c}$ and $\boldsymbol{U}_{8}^{c}$.

4.3 Feedback control in a tree system

The dynamics topology figure of the controlled system is shown in Fig. 11. The feedback signal of the control subsystem derives from the outboard end of body 2, and the control force acts on body 6. It can be seen that the control subsystem spans body 2 at which there exists a bifurcation in the mechanical tree system. Then the overall transfer equation of this system is deduced as follows.

Fig. 11

The topology figure of the dynamics model for the controlled multibody system where the control subsystem spans the mechanical element with multiple inboard ends and one outboard end in a tree system

For the control subsystem, one obtains

$$ \boldsymbol{Z}_{6c} = \boldsymbol{E}_{6c} \boldsymbol{G}_{c}\boldsymbol{E}_{\boldsymbol{Z}_{2,1}}\boldsymbol{Z}_{2,1} = \boldsymbol{U}_{6c}\boldsymbol{Z}_{2,1}. $$

(81)

The transfer equation of the controlled element 6 given by Eq. (50) can be read as

$$ \boldsymbol{Z}_{6,4} = \boldsymbol{U}_{6,7} \boldsymbol{Z}_{6,7} + \boldsymbol{U}_{6,8} \boldsymbol{Z}_{6,8} + \boldsymbol{Z}_{6c}. $$

(82)

It can be seen from the topology figure that the state vector of the measurement point is

$$\begin{aligned} \boldsymbol{Z}_{2,1} =& \boldsymbol{U}_{2,3} \boldsymbol{Z}_{2,3} + \boldsymbol{U}_{2,4} \boldsymbol{Z}_{2,4} \\ =& \boldsymbol{U}_{2,3}\boldsymbol{Z}_{2,3} + \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{Z}_{6,4} . \end{aligned}$$

(83)

Substituting Eqs. (81), (83) into Eq. (82) and eliminating the intermediate variables $\boldsymbol{Z}_{6c}$ and $\boldsymbol{Z}_{2,1}$, one can achieve

$$\begin{aligned} \boldsymbol{Z}_{6,4} =& ( \boldsymbol{I} - \boldsymbol{U}_{6c} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4} )^{ - 1} \boldsymbol{U}_{6,7}\boldsymbol{Z}_{6,7} + ( \boldsymbol{I} - \boldsymbol{U}_{6c}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} )^{ - 1}\boldsymbol{U}_{6,8}\boldsymbol{Z}_{6,8} \\ &{} + ( \boldsymbol{I} - \boldsymbol{U}_{6c}\boldsymbol{U}_{2,4} \boldsymbol{U}_{4} )^{ - 1}\boldsymbol{U}_{6c} \boldsymbol{U}_{2,3}\boldsymbol{Z}_{2,3} . \end{aligned}$$

(84)

In the above equation, let

$$\begin{aligned} \boldsymbol{U}_{6,7}^{c} = &( \boldsymbol{I} - \boldsymbol{U}_{6c}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} )^{ - 1}\boldsymbol{U}_{6,7}, \end{aligned}$$

(85a)

$$\begin{aligned} \boldsymbol{U}_{6,8}^{c} =& ( \boldsymbol{I} - \boldsymbol{U}_{6c}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} )^{ - 1}\boldsymbol{U}_{6,8}, \end{aligned}$$

(85b)

$$\begin{aligned} \boldsymbol{T}_{2 - 6}^{c} =& ( \boldsymbol{I} - \boldsymbol{U}_{6c}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} )^{ - 1}\boldsymbol{U}_{6c}\boldsymbol{U}_{2,3}. \end{aligned}$$

(85c)

Then Eq. (84) can be rewritten as

$$ \boldsymbol{Z}_{6,4} = \boldsymbol{U}_{6,7}^{c} \boldsymbol{Z}_{6,7} + \boldsymbol{U}_{6,8}^{c} \boldsymbol{Z}_{6,8} + \boldsymbol{T}_{2 - 6}^{c} \boldsymbol{Z}_{2,3}. $$

(86)

Since the control subsystem spans element 2 possessing more than two ends, the state vector $\boldsymbol{Z}_{6,4}$ at the outboard end of the controlled element 6 is not only associated with the state vectors $\boldsymbol{Z}_{6,7}$ and $\boldsymbol{Z}_{6,8}$ at the inboard ends of element 6 itself, but also the state vector $\boldsymbol{Z}_{2,3}$ (which does not appear in the control loop) at the inboard ends of the bifurcation element 2 related to the measurement point. It can be seen from Eqs. (85a)–(85c) that $\boldsymbol{U}_{6,7}^{c}$ and $\boldsymbol{U}_{6,8}^{c}$ are the multiplication of $\boldsymbol{U}_{6,7}$ and $\boldsymbol{U}_{6,8}$ of the corresponding uncontrolled element by a coefficient matrix, respectively. The coefficient matrix can be derived in the same manner as described in Sects. 4.1, 4.2.1, and 4.2.2. Meanwhile, $\boldsymbol{T}_{2 - 6}^{c}$ is the successive premultiplication of the transfer matrix along the mechanical transfer path from the inboard end (which does not appear in the control loop) of the bifurcation element 2 to the measurement device, premultiplied by the transfer matrix of the control subsystem, and then continually premultiplied by the preceding coefficient matrix.

Combining the topology figure with Eq. (86), one derives

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} ( \boldsymbol{U}_{2,3}\boldsymbol{Z}_{2,3} + \boldsymbol{U}_{2,4}\boldsymbol{Z}_{2,4} ) \\ = &\boldsymbol{U}_{1}\boldsymbol{U}_{2,3} \boldsymbol{Z}_{2,3} + \boldsymbol{U}_{1} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{Z}_{6,4} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2,3} \boldsymbol{Z}_{2,3} + \boldsymbol{U}_{1} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4} \bigl( \boldsymbol{U}_{6,7}^{c}\boldsymbol{Z}_{6,7} + \boldsymbol{U}_{6,8}^{c}\boldsymbol{Z}_{6,8} + \boldsymbol{T}_{2 - 6}^{c}\boldsymbol{Z}_{2,3} \bigr) \\ =& \boldsymbol{U}_{1} \bigl( \boldsymbol{U}_{2,3} + \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{T}_{2 - 6}^{c} \bigr)\boldsymbol{Z}_{2,3} + \boldsymbol{U}_{1} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{U}_{6,7}^{c} \boldsymbol{Z}_{6,7} + \boldsymbol{U}_{1} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{U}_{6,8}^{c} \boldsymbol{Z}_{6,8} \\ =& \boldsymbol{U}_{1} \bigl( \boldsymbol{U}_{2,3} + \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{T}_{2 - 6}^{c} \bigr)\boldsymbol{U}_{3}\boldsymbol{U}_{5} \boldsymbol{Z}_{5,0} + \boldsymbol{U}_{1} \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{U}_{6,7}^{c} \boldsymbol{U}_{7}\boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} \\ &{}+ \boldsymbol{U}_{1}\boldsymbol{U}_{2,4} \boldsymbol{U}_{4}\boldsymbol{U}_{6,8}^{c} \boldsymbol{U}_{8}\boldsymbol{U}_{10}\boldsymbol{Z}_{10,0} . \end{aligned}$$

(87)

Let

$$ \boldsymbol{U}_{2,3}^{c} = \boldsymbol{U}_{2,3} + \boldsymbol{U}_{2,4}\boldsymbol{U}_{4}\boldsymbol{T}_{2 - 6}^{c}, $$

(88)

then Eq. (87) can be rewritten as

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{U}_{2,3}^{c}\boldsymbol{U}_{3} \boldsymbol{U}_{5}\boldsymbol{Z}_{5,0} + \boldsymbol{U}_{1}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} \boldsymbol{U}_{6,7}^{c}\boldsymbol{U}_{7} \boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} + \boldsymbol{U}_{1}\boldsymbol{U}_{2,4}\boldsymbol{U}_{4} \boldsymbol{U}_{6,8}^{c}\boldsymbol{U}_{8} \boldsymbol{U}_{10}\boldsymbol{Z}_{10,0} \\ =:& \boldsymbol{T}_{5 - 1}\boldsymbol{Z}_{5,0} + \boldsymbol{T}_{9 - 1}\boldsymbol{Z}_{9,0} + \boldsymbol{T}_{10 - 1}\boldsymbol{Z}_{10,0} . \end{aligned}$$

(89)

The above equation is exactly the main transfer equation of the controlled system. Note that when replacing the transfer matrices $\boldsymbol{U}_{6,7}$, $\boldsymbol{U}_{6,8}$ and $\boldsymbol{U}_{2,3}$ of the uncontrolled elements by $\boldsymbol{U}_{6,7}^{c}$, $\boldsymbol{U}_{6,8}^{c}$ and $\boldsymbol{U}_{2,3}^{c}$, respectively, one can obtain the main transfer equation of the controlled tree system by means of the automatic deduction theorem of the overall transfer equation for a tree system mentioned in [20].

Considering the geometrical equation of element 6,

$$ \boldsymbol{H}_{6,7}\boldsymbol{Z}_{6,7} = \boldsymbol{H}_{6,8}\boldsymbol{Z}_{6,8}, $$

(90)

and combining the topology figure, one obtains

$$ - \boldsymbol{H}_{6,7}\boldsymbol{U}_{7} \boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} + \boldsymbol{H}_{6,8} \boldsymbol{U}_{8}\boldsymbol{U}_{10} \boldsymbol{Z}_{10,0} =:\boldsymbol{G}_{9 - 6} \boldsymbol{Z}_{9,0} + \boldsymbol{G}_{10 - 6} \boldsymbol{Z}_{10,0} = \boldsymbol{0}. $$

(91)

Considering the geometrical equation of the element 2,

$$ \boldsymbol{H}_{2,3}\boldsymbol{Z}_{2,3} = \boldsymbol{H}_{2,4}\boldsymbol{Z}_{2,4}, $$

(92)

and combining Eq. (86) and the topology figure, one acquires

$$\begin{aligned} \boldsymbol{H}_{2,3}\boldsymbol{U}_{3}\boldsymbol{U}_{5} \boldsymbol{Z}_{5,0} =& \boldsymbol{H}_{2,4} \boldsymbol{U}_{4}\boldsymbol{Z}_{6,4} \\ =& \boldsymbol{H}_{2,4}\boldsymbol{U}_{4} \bigl( \boldsymbol{U}_{6,7}^{c}\boldsymbol{Z}_{6,7} + \boldsymbol{U}_{6,8}^{c}\boldsymbol{Z}_{6,8} + \boldsymbol{T}_{2 - 6}^{c}\boldsymbol{Z}_{2,3} \bigr) \\ =& \boldsymbol{H}_{2,4}\boldsymbol{U}_{4} \bigl( \boldsymbol{U}_{6,7}^{c}\boldsymbol{U}_{7} \boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} + \boldsymbol{U}_{6,8}^{c}\boldsymbol{U}_{8} \boldsymbol{U}_{10}\boldsymbol{Z}_{10,0} + \boldsymbol{T}_{2 - 6}^{c}\boldsymbol{U}_{3} \boldsymbol{U}_{5}\boldsymbol{Z}_{5,0} \bigr) . \end{aligned}$$

(93)

After simple arrangements of Eq. (93), we have

$$ - \bigl( \boldsymbol{H}_{2,3} - \boldsymbol{H}_{2,4} \boldsymbol{U}_{4}\boldsymbol{T}_{2 - 6}^{c} \bigr) \boldsymbol{U}_{3}\boldsymbol{U}_{5}\boldsymbol{Z}_{5,0} + \boldsymbol{H}_{2,4}\boldsymbol{U}_{4} \boldsymbol{U}_{6,7}^{c}\boldsymbol{U}_{7} \boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} + \boldsymbol{H}_{2,4} \boldsymbol{U}_{4}\boldsymbol{U}_{6,8}^{c} \boldsymbol{U}_{8}\boldsymbol{U}_{10}\boldsymbol{Z}_{10,0} = \boldsymbol{0}. $$

(94)

Let

$$ \boldsymbol{H}_{2,3}^{c} = \boldsymbol{H}_{2,3} - \boldsymbol{H}_{2,4}\boldsymbol{U}_{4}\boldsymbol{T}_{2 - 6}^{c}, $$

(95)

then Eq. (94) can be rewritten as in the following form:

$$\begin{aligned} & - \boldsymbol{H}_{2,3}^{c}\boldsymbol{U}_{3} \boldsymbol{U}_{5}\boldsymbol{Z}_{5,0} + \boldsymbol{H}_{2,4}\boldsymbol{U}_{4}\boldsymbol{U}_{6,7}^{c} \boldsymbol{U}_{7}\boldsymbol{U}_{9}\boldsymbol{Z}_{9,0} + \boldsymbol{H}_{2,4}\boldsymbol{U}_{4} \boldsymbol{U}_{6,8}^{c}\boldsymbol{U}_{8} \boldsymbol{U}_{10}\boldsymbol{Z}_{10,0} \\ &\quad =:\boldsymbol{G}_{5 - 2}\boldsymbol{Z}_{5,0} + \boldsymbol{G}_{9 - 2}\boldsymbol{Z}_{9,0} + \boldsymbol{G}_{10 - 2}\boldsymbol{Z}_{10,0} = \boldsymbol{0}. \end{aligned}$$

(96)

Equations (91) and (96) are the geometrical transfer equations. Note that by replacing the matrix $\boldsymbol{H}_{2,3}$ by $\boldsymbol{H}_{2,3}^{c}$, we obtains the geometrical transfer equations of the controlled tree system according to the automatic deduction theorem of the overall transfer equation for a tree system proposed in [20].

Summarizing Eqs. (89), (91) and (96) in matrix from, the overall transfer equation of the controlled tree system is obtained as

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} - \boldsymbol{I} & \boldsymbol{T}_{5 - 1} & \boldsymbol{T}_{9 - 1} & \boldsymbol{T}_{10 - 1} \\ \boldsymbol{O} & \boldsymbol{O} & \boldsymbol{G}_{9 - 6} & \boldsymbol{G}_{10 - 6} \\ \boldsymbol{O} & \boldsymbol{G}_{5 - 2} & \boldsymbol{G}_{9 - 2} & \boldsymbol{G}_{10 - 2} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{5,0} \\ \boldsymbol{Z}_{9,0} \\ \boldsymbol{Z}_{10,0} \end{array}\displaystyle \right ] = \boldsymbol{0}. $$

(97)

5 Numerical example

A flexible robot, called small articulated manipulator II (SAMII) and reported in [32], will be addressed here as a numerical example to validate the proposed method. The dynamics model is shown in Fig. 12(a). A linear model is built considering a small rotation and vibration along $y$ axis, where all links are configured vertically in their equilibrium positions. The cantilever Euler–Bernoulli beam (EB beam) numbered 6 is mounted at its tip fixed to the ceiling. A base spring/damper numbered 7 is modeled due to the flexibility between the ceiling and the beam. A rigid body number 5 is fixed at the other side of the beam. Meanwhile, a rigid link numbered 3 is articulated by a revolute hinge numbered 4 to rigid body 5. In a similar manner, a terminal rigid link numbered 1 is connected with link 3 through a revolute hinge. Hinge 4 is considered locked, and thus modeled by a torsional spring/damper. Finally, hinge 2 is actuated by a hydraulic motor in series with a torsional spring/damper. Two boundaries are numbered 0.

Fig. 12

(a) The dynamics model of SAMII and (b) its topology figure with an open loop

For position control purpose, an optical encoder measures the relative angle $\theta$ of hinge 2 in degrees, that is,

$$ \theta = \theta_{\mathit{link}1} - \theta_{\mathit{link}3} = \theta_{1,2} - \theta_{3,2}. $$

(98)

At the same time, in order to suppress the vibration of the terminal link 1, an accelerometer is mounted on the end of beam 6 to measure the acceleration $\ddot{y}_{5,6}$.

The actuator is a hydraulic motor controlled by a servo-value, whose dynamics is modeled with the transfer function expressed as [32]:

$$ G_{\mathit{act}}: = \frac{\varTheta_{c}}{V} = \frac{K_{\mathit{act}}p}{s ( s + p )} , $$

(99)

where $v$ is the input voltage to the actuator and $\theta_{c}$ is the relative angle generated by the motor, $K_{\mathit{act}}$ and $p$ are two constants, while $s$ is the Laplace variable.

For hinge 2, considering the internal compliance, the actuator is modeled to be connected by a torsional spring/damper in series, which is shown in Fig. 13(a). Thereby, the transfer equation of hinge 2 is deduced as follows.

Fig. 13

(a) The dynamics model of the hydraulic motor and (b) its force analysis

The actuated hinge is numbered as $j$. The moments acting on its inboard end $I$ and outboard end $O$ are depicted with their positive directions in Fig. 13(a). In order to analyze the dynamics of the spring/damper and the motor, respectively, a separation is made in Fig. 13(b). For the torsional spring/damper, one has

$$\begin{aligned} &K'_{j} ( \theta_{m} - \theta_{zI} ) + C'_{j} ( \theta_{m} - \dot{ \theta}_{zI} ) = m_{m}, \end{aligned}$$

(100)

$$\begin{aligned} &m_{m} = m_{zI}. \end{aligned}$$

(101)

For the motor that can generate a relative angle $\theta_{c}$ between the output point $O$ and the internal intermediate point $M$ (not drawn in the figure), the geometry can be read as

$$ \theta_{c} = \theta_{zO} - \theta_{m}. $$

(102)

Neglecting its inertia results in

$$ m'_{m} = m_{zO}. $$

(103)

Due to Newton’s third law, one obtains

$$ m_{m} = m'_{m}. $$

(104)

By eliminating the intermediate variables $m_{m}$, $m'_{m}$, $\theta_{m}$ and carrying out the transformation $z = Ze^{\lambda t}$, one deduces the transfer equation as

$$ \left [ \textstyle\begin{array}{c} \varTheta_{z} \\ M_{z} \end{array}\displaystyle \right ]_{j,O} = \left [ \textstyle\begin{array}{c@{\quad}c} 1 & \frac{1}{K'_{j} + C'_{j}\lambda} \\ 0 & 1 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \varTheta_{z} \\ M_{z} \end{array}\displaystyle \right ]_{j,I} + \left [ \textstyle\begin{array}{c} 1 \\ 0 \end{array}\displaystyle \right ] \varTheta_{c}. $$

(105)

Finally, considering that the input point $I$ and output point $O$ are constrained by a revolute hinge, Eq. (105) can be easily extended to

$$\begin{aligned} \boldsymbol{Z}_{j,O} : =& \left [ \textstyle\begin{array}{c} Y \\ \varTheta_{z} \\ M_{z} \\ Q_{y} \end{array}\displaystyle \right ]_{j,O} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 \\ 0 & 1 & \frac{1}{K'_{j} + C'_{j}\lambda} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c} Y \\ \varTheta_{z} \\ M_{z} \\ Q_{y} \end{array}\displaystyle \right ]_{j, I} + \left [ \textstyle\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\displaystyle \right ] \varTheta_{c} \\ =:& \boldsymbol{U}_{j} \boldsymbol{Z}_{j,I} + \boldsymbol{E}_{jc} \varTheta_{c}\quad ( j = 2 ) . \end{aligned}$$

(106)

Hereby, it should be noted that Eq. (106) is slightly different from Eq. (50) as transfer equations for a controlled element. In Eq. (50), the control force $F_{jc}$ is the control input signal to the element $j$ under control, while in Eq. (106) the actuator output $\varTheta_{c}$ is selected as the control input signal to the controlled element $j$. However, this subtle difference has no influence on the form of transfer equation (50) of controlled elements in spirit due to a simple substitution $\varTheta_{c} \to F_{jc}$.

The state vector of any connecting point $P_{i,j}$ is defined as $\boldsymbol{Z}_{i,j} = [ Y \ \ \varTheta_{z} \ \ M_{z} \ \ Q_{y} ]_{i,j}^{T}$ in the system. For other uncontrolled elements in Fig. 12(a), their transfer equations are all in the form of Eq. (1). For the unactuated hinge 4 and base spring 7, their transfer matrices rightly take the form in Eq. (106). Thereby, as a short conclusion,

$$ \boldsymbol{U}_{j} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 \\ 0 & 1 & \frac{1}{K'_{j} + C'_{j}\lambda} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\displaystyle \right ]\quad ( j = 2,4,7 ),\qquad \boldsymbol{E}_{2c} = \left [ \textstyle\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\displaystyle \right ]. $$

(107)

For the longitudinally vibrating rigid body and EB beam, their transfer matrices can be found in [12] and are listed below as

$$ U_{j} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & b_{1} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ - m\lambda^{2} ( b_{1} - c_{1} ) & \lambda^{2} ( J_{zI} - mb_{1}c_{1} ) & 1 & b_{1} \\ - m\lambda^{2} & - m\lambda^{2}c_{1} & 0 & 1 \end{array}\displaystyle \right ] \quad ( j = 1,3,5 ), $$

(108)

where $m$ is the mass, $J_{zI}$ is the moment of inertial with respect to the input point $I$, $c_{1}$ is the distance from input point $I$ to mass center $C$, $b_{1}$ is the distance from input point $I$ to output point $O$, and $\lambda$ is the complex variable,

$$\begin{aligned} \begin{aligned} & \boldsymbol{U}_{6} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} S & \frac{T}{\beta} & \frac{U}{EI\beta^{2}} & \frac{V}{EI\beta^{3}} \\ \beta V & S & \frac{T}{EI\beta} & \frac{U}{EI\beta^{2}} \\ EI\beta^{2}U & EI\beta V & S & \frac{T}{\beta} \\ EI\beta^{3}T & EI\beta^{2}U & \beta V & S \end{array}\displaystyle \right ], \\ & S = \frac{\mathit{ch} + c}{2},\quad\ \ T = \frac{\mathit{sh} + s}{2},\quad\ \ U = \frac{\mathit{ch} - c}{2},\quad\ \ V = \frac{\mathit{sh} - s}{2}, \\ & \mathit{ch} = \cosh (\beta l), \quad\ \ \mathit{sh} = \sinh ( \beta l ), \quad\ \ c = \cos ( \beta l ), \quad\ \ s = \sin ( \beta l ), \quad\ \ \beta = \sqrt[4]{ - \bar{m}\lambda / ( EI )} ,\end{aligned} \end{aligned}$$

(109)

where $EI$ is the bending stiffness, $l$ is the length of the beam, and $\bar{m}$ is the mass per length.

5.1 Open-loop modeling

The topology figure of the uncontrolled system is depicted in Fig. 12(b) where two boundaries are numbered 0 and the transfer direction is from up to down. The open-loop system has one input, the voltage $v$ driving the hydraulic actuator, and two outputs, the measurements on relative angle $\theta$ and acceleration $\ddot{y}_{5,6}$. In the following paragraph, the two transfer functions $\frac{\varTheta}{V}$ and $\frac{\ddot{Y}_{5,6}}{V}$ will be deduced.

According to the transfer equation of element 2, the dynamics of the actuator and the topology figure in Fig. 12(b), one obtains

$$ \boldsymbol{Z}_{1,2} = \boldsymbol{U}_{2} \boldsymbol{Z}_{3,2} + \boldsymbol{E}_{2c} \varTheta_{c} = \boldsymbol{U}_{2}\boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{U}_{7}\boldsymbol{Z}_{7,0} + \boldsymbol{E}_{2c}G_{\mathit{act}}V. $$

(110)

Further,

$$ \boldsymbol{Z}_{1,0} = \boldsymbol{U}_{1} \boldsymbol{Z}_{1,2} = \boldsymbol{T}_{7 - 1} \boldsymbol{Z}_{7,0} + \boldsymbol{T}_{d}V , $$

(111)

where

$$\begin{aligned} &\boldsymbol{T}_{7 - 1} = \boldsymbol{U}_{1} \boldsymbol{U}_{2}\boldsymbol{U}_{3}\boldsymbol{U}_{4} \boldsymbol{U}_{5}\boldsymbol{U}_{6}\boldsymbol{U}_{7}, \end{aligned}$$

(112a)

$$\begin{aligned} &\boldsymbol{T}_{d} = \boldsymbol{U}_{1} \boldsymbol{E}_{2c}G_{\mathit{act}}. \end{aligned}$$

(112b)

Then, Eq. (111) can be written in a compact form resulting in the overall transfer equation

$$ \boldsymbol{U}_{\mathit{all}}\boldsymbol{Z}_{\mathit{all}}: = [ \boldsymbol{I}_{4} \quad {-} \boldsymbol{T}_{7 - 1} ]\left [ \textstyle\begin{array}{c} \boldsymbol{Z}_{1,0} \\ \boldsymbol{Z}_{7,0} \end{array}\displaystyle \right ] = \boldsymbol{T}_{d}V. $$

(113)

Due to the boundary conditions

$$ \boldsymbol{Z}_{1,0} = [ Y \quad \varTheta_{z} \quad 0 \quad 0 ]_{1,0}^{T}, \qquad \boldsymbol{Z}_{7,0} = [ 0 \quad 0 \quad M_{z} \quad Q_{y} ]_{7,0}^{T}, $$

(114)

one can eliminate the zeroes in $\boldsymbol{Z}_{\mathit{all}}$ and the corresponding columns in $\boldsymbol{U}_{\mathit{all}}$, that is,

$$ \boldsymbol{U}_{\mathit{all}}^{*}\boldsymbol{Z}_{\mathit{all}}^{*} = \boldsymbol{T}_{d}V. $$

(115)

Thereby, the unknown variables in the boundary state vector can be expressed in terms of the system input $V$ as

$$ \boldsymbol{Z}_{\mathit{all}}^{*} = \boldsymbol{U}_{\mathit{all}}^{*\ \ {-} 1} \boldsymbol{T}_{d}V =:\left [ \textstyle\begin{array}{c} \mathop{\boldsymbol{u}_{1}}\limits_{2 \times 1}\\ \ldots \\ \mathop{\boldsymbol{u}_{2}}\limits_{2 \times 1} \end{array}\displaystyle \right ]V. $$

(116)

Further,

$$\begin{aligned} \varTheta =& \varTheta_{1,2} - \varTheta_{3,2} = [ 0 \quad 1 \quad 0 \quad 0 ] ( \boldsymbol{Z}_{1,2} - \boldsymbol{Z}_{3,2}) = [0 \quad 1 \quad 0 \quad 0 ] \bigl( \boldsymbol{U}_{1}^{ - 1} \boldsymbol{Z}_{1,0} - \boldsymbol{T}_{7 - 3} \boldsymbol{Z}_{7,0} \bigr) \\ =& [ 0 \quad 1\quad 0 \quad 0 ]\left ( \boldsymbol{U}_{1}^{ - 1} \left [ \textstyle\begin{array}{c} \boldsymbol{u}_{1} \\ 0 \\ 0 \end{array}\displaystyle \right ] - \boldsymbol{T}_{7 - 3}\left [ \textstyle\begin{array}{c} 0 \\ 0 \\ \boldsymbol{u}_{2} \end{array}\displaystyle \right ] \right )V , \end{aligned}$$

(117a)

$$\begin{aligned} Y_{5,6} =& [1 \quad 0 \quad 0 \quad 0 ]\boldsymbol{Z}_{5,6} = [ 1 \quad 0 \quad 0 \quad 0 ]\boldsymbol{T}_{7 - 6} \boldsymbol{Z}_{7,0} \\ =& [ 1 \quad0 \quad 0 \quad 0 ]\boldsymbol{T}_{7 - 6}\left [ \textstyle\begin{array}{c} 0 \\ 0 \\ \boldsymbol{u}_{2} \end{array}\displaystyle \right ]V , \end{aligned}$$

(117b)

where

$$ \boldsymbol{T}_{7 - 3} = \boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5}\boldsymbol{U}_{6} \boldsymbol{U}_{7},\qquad \boldsymbol{T}_{7 - 6} = \boldsymbol{U}_{6}\boldsymbol{U}_{7}. $$

(117c)

Eventually, the two transfer functions can be obtained as

$$\begin{aligned} \frac{\varTheta}{V} =& [ 0 \quad 1 \quad 0 \quad 0 ]\left ( \boldsymbol{U}_{1}^{ - 1}\left [ \textstyle\begin{array}{c} \boldsymbol{u}_{1} \\ 0 \\ 0 \end{array}\displaystyle \right ] - \boldsymbol{T}_{7 - 3}\left [ \textstyle\begin{array}{c} 0 \\ 0 \\ \boldsymbol{u}_{2} \end{array}\displaystyle \right ] \right ), \end{aligned}$$

(118a)

$$\begin{aligned} \frac{\ddot{Y}_{5,6}}{V} =& s^{2} [1 \quad 0 \quad 0 \quad 0 ] \boldsymbol{T}_{7 - 6}\left [ \textstyle\begin{array}{c} 0 \\ 0 \\ \boldsymbol{u}_{2} \end{array}\displaystyle \right ] , \end{aligned}$$

(118b)

where $s$ is the Laplace variable.

5.2 Closed-loop modeling

The control subsystem in [32] consists of two control loops, namely, inner feedback loop for position control and outer feedback loop for vibration suppression. The position control loop utilizes the measurement of relative hinge angle $\theta$ as feedback to track the desired angular displacement $\theta_{d}$ so that

$$ v = G_{\theta} ( \theta_{d} - \theta ) , $$

(119)

where $G_{\theta} = 1$ is the gain to amplify the error signal in this case.

Combining Fig. 12(b) and Eqs. (98), (99), (119), it is natural to obtain the topology figure for a system with position control subsystem in Fig. 14(a), from which one can easily infer that

$$ \boldsymbol{E}_{\boldsymbol{Z}_{3,2}} = \boldsymbol{E}_{\boldsymbol{Z}_{1,2}}: = [ 0 \quad 1 \quad 0 \quad 0 ]. $$

(120)

Fig. 14

The topology figure of the dynamics model with (a) $\theta$ feedback, and (b) both $\theta$ and $\ddot{y}_{5,6}$ feedback

In order to further reduce the vibration, an inertial damping control scheme [36] is taken to move hinge 2 out of phase with the vibration so that the resulting inertial forces and moments counteracting the vibration. The acceleration $\ddot{y}_{5,6}$ is taken as the feedback signal and added to the desired hinge motion $\hat{\theta}_{d}$ according to

$$ \varTheta_{d} = \hat{\varTheta}_{d} - G_{a}s^{2}Y_{5,6} , $$

(121)

where $s$ is the Laplace variable and $G_{a}$ is a low-pass filter that takes the form

$$ G_{a} = \frac{K_{a}\omega_{c}^{2}}{s^{2} + 2\zeta \omega_{c}s + \omega_{c}^{2}} , $$

(122)

where $K_{a} = 18$, $\zeta = 0.707$, $\omega_{c} = 12.566$ (rad/s) in this case.

By combining the topology figure of Fig. 14(a) and Eqs. (121), (122), Fig. 14(b) can be finally obtained as the topology figure for a system with both position control and vibration suppression. In Fig. 14(b), one can easily infer that

$$ \boldsymbol{E}_{\boldsymbol{Z}_{5,6}} = [ 1 \quad 0 \quad0 \quad 0 ]. $$

(123)

Based on Fig. 14(b), the overall transfer equation of the system with two control loops will be deduced as follows.

For controlled element 2, one gets

$$\begin{aligned} \boldsymbol{Z}_{1,2} =& \boldsymbol{U}_{2} \boldsymbol{Z}_{3,2} + \boldsymbol{E}_{2c} \varTheta_{c} \\ =& \boldsymbol{U}_{2}\boldsymbol{Z}_{3,2} + \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \bigl( \hat{ \varTheta}_{d} - G_{a}s^{2}Y_{5,6} - \varTheta \bigr) \\ =& \boldsymbol{U}_{2}\boldsymbol{Z}_{3,2} + \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \bigl[ \hat{ \varTheta}_{d} - G_{a}s^{2}\boldsymbol{E}_{\boldsymbol{Z}_{5,6}} \boldsymbol{Z}_{5,6} - ( \boldsymbol{E}_{\boldsymbol{Z}_{1,2}} \boldsymbol{Z}_{1,2} - \boldsymbol{E}_{\boldsymbol{Z}_{3,2}} \boldsymbol{Z}_{3,2} ) \bigr] \\ =& \boldsymbol{U}_{2}\boldsymbol{Z}_{3,2} + \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \hat{ \varTheta}_{d} - \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} G_{a}s^{2}\boldsymbol{E}_{\boldsymbol{Z}_{5,6}} \boldsymbol{Z}_{5,6} - \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \boldsymbol{E}_{\boldsymbol{Z}_{1,2}}\boldsymbol{Z}_{1,2} \\ &{}+ \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \boldsymbol{E}_{\boldsymbol{Z}_{3,2}}\boldsymbol{Z}_{3,2} \\ =:&\boldsymbol{U}_{2}\boldsymbol{Z}_{3,2} + \boldsymbol{T}_{d - 2}\hat{\varTheta}_{d} + \boldsymbol{U}_{2c_{1}}\boldsymbol{Z}_{5,6} + \boldsymbol{U}_{2c_{2}}\boldsymbol{Z}_{1,2} + \boldsymbol{U}_{2c_{3}}\boldsymbol{Z}_{3,2} , \end{aligned}$$

(124)

where

$$\begin{aligned} \begin{aligned} & \boldsymbol{T}_{d - 2} = \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta}, \qquad \boldsymbol{U}_{2c_{1}} = - \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} G_{a}s^{2}\boldsymbol{E}_{\boldsymbol{Z}_{5,6}}, \\ &\boldsymbol{U}_{2c_{2}} = - \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \boldsymbol{E}_{\boldsymbol{Z}_{1,2}},\qquad \boldsymbol{U}_{2c_{3}} = \boldsymbol{E}_{2c}G_{\mathit{act}}G_{\theta} \boldsymbol{E}_{\boldsymbol{Z}_{3,2}}. \end{aligned} \end{aligned}$$

(125)

Combining similar terms in Eq. (124) results in

$$\begin{aligned} \boldsymbol{Z}_{1,2} =& ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} ( \boldsymbol{U}_{2} + \boldsymbol{U}_{2c_{3}} )\boldsymbol{Z}_{3,2} + ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} \boldsymbol{U}_{2c_{1}}\boldsymbol{Z}_{5,6} + ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} \boldsymbol{T}_{d - 2}\hat{\varTheta}_{d} \\ =:&\boldsymbol{U}_{2}^{c_{1}}\boldsymbol{Z}_{3,2} + \boldsymbol{U}_{2}^{c_{2}}\boldsymbol{Z}_{5,6} + ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} \boldsymbol{T}_{d - 2}\hat{\varTheta}_{d} , \end{aligned}$$

(126)

where

$$ \boldsymbol{U}_{2}^{c_{1}} = ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} ( \boldsymbol{U}_{2} + \boldsymbol{U}_{2c_{3}} ),\qquad \boldsymbol{U}_{2}^{c_{2}} = ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1}\boldsymbol{U}_{2c_{1}}. $$

(127)

Hereby combining Eq. (126) and Fig. 14(b), the overall transfer equation can be obtained:

$$\begin{aligned} \boldsymbol{Z}_{1,0} =& \boldsymbol{U}_{1} \boldsymbol{Z}_{2,1} = \boldsymbol{U}_{1} \boldsymbol{U}_{2}^{c_{1}}\boldsymbol{Z}_{3,2} + \boldsymbol{U}_{1}\boldsymbol{U}_{2}^{c_{2}} \boldsymbol{Z}_{5,6} + \boldsymbol{U}_{1} ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} \boldsymbol{T}_{d - 2}\hat{\varTheta}_{d} \\ =& \boldsymbol{U}_{1}\boldsymbol{U}_{2}^{c_{1}} \boldsymbol{U}_{3}\boldsymbol{U}_{4}\boldsymbol{U}_{5} \boldsymbol{U}_{6}\boldsymbol{U}_{7}\boldsymbol{Z}_{7,0} + \boldsymbol{U}_{1}\boldsymbol{U}_{2}^{c_{2}} \boldsymbol{U}_{6}\boldsymbol{U}_{7}\boldsymbol{Z}_{7,0} + \boldsymbol{U}_{1} ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1}\boldsymbol{T}_{d - 2}\hat{ \varTheta}_{d} \\ = &\boldsymbol{U}_{1} \bigl( \boldsymbol{U}_{2}^{c_{1}} \boldsymbol{U}_{3}\boldsymbol{U}_{4}\boldsymbol{U}_{5} + \boldsymbol{U}_{2}^{c_{2}} \bigr)\boldsymbol{U}_{6} \boldsymbol{U}_{7}\boldsymbol{Z}_{7,0} + \boldsymbol{U}_{1} ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1}\boldsymbol{T}_{d - 2}\hat{ \varTheta}_{d} \\ =:&\boldsymbol{T}_{7 - 1}\boldsymbol{Z}_{7,0} + \boldsymbol{T}_{d}\hat{\varTheta}_{d} , \end{aligned}$$

(128)

where

$$ \boldsymbol{T}_{7 - 1} = \boldsymbol{U}_{1} \bigl( \boldsymbol{U}_{2}^{c_{1}}\boldsymbol{U}_{3} \boldsymbol{U}_{4}\boldsymbol{U}_{5} + \boldsymbol{U}_{2}^{c_{2}} \bigr)\boldsymbol{U}_{6}\boldsymbol{U}_{7},\qquad \boldsymbol{T}_{d} = \boldsymbol{U}_{1} ( \boldsymbol{I}_{4} - \boldsymbol{U}_{2c_{2}} )^{ - 1} \boldsymbol{T}_{d - 2}. $$

(129)

Up to Eq. (128), the remaining procedure to acquire the transfer functions $\frac{\varTheta}{\hat{\varTheta}_{d}}$ and $\frac{\ddot{Y}_{5,6}}{\hat{\varTheta}_{d}}$ is the same as that in Eqs. (113) to (118a)–(118b), and thus is omitted.

The dynamics parameters used in [32] are listed in Table 2. Based on Eqs. (118a)–(118b), the transfer functions $\frac{\varTheta}{V}$, $\frac{\ddot{Y}_{5,6}}{V}$ for an open-loop system and the transfer functions $\frac{\varTheta}{\hat{\varTheta}_{d}}$, $\frac{\ddot{Y}_{5,6}}{\hat{\varTheta}_{d}}$ for a closed-loop system with both position control and vibration suppression are shown in Figs. 15–18, respectively.

Fig. 15

Bode plot of $\frac{\varTheta}{V}$ for an open-loop system

Table 2 Dynamics parameters for the SAMII

Comparing Figs. 15 and 17, the magnitude in Fig. 17 stays at 0 in the low frequency region. This means that the terminal link can track the angular position according to the input signal. Moreover, the magnitude in Fig. 18 is significantly reduced compared with that in Fig. 16. This illustrates that the vibration of the beam tip is well suppressed. The above simulation results can be validated according to the experimental data and another modeling method in [32] (see Figs. 8, 9, 14 and 15 in [32]). However, due to copyright concern, those figures could not be reproduced here. Interested readers can download that paper.

Fig. 16

Bode plot of $\frac{\ddot{Y}_{5,6}}{V}$ for an open-loop system

Fig. 17

Bode plot of $\frac{\varTheta}{\hat{\varTheta}_{d}}$ for a closed-loop system with both position control and vibration suppression

Fig. 18

Bode plot of $\frac{\ddot{Y}_{5,6}}{\hat{\varTheta}_{d}}$ for a closed-loop system with both position control and vibration suppression

It should be noted that although the example addressed here is in planar configuration, there are no inherited difficulties in studying its spatial configuration as in [36] by considering the direction cosine matrices corresponding to the equilibrium orientations of two adjacent links.

6 Conclusion

Based on MSTMM, this paper presents a novel approach to model the linear controlled multibody systems in the frequency domain. The proposed method is fit for general spatial linear multibody systems under linear control. It maintains the original merits of MSTMM and makes several breakthroughs in the following aspects:

• 1. There is no need to augment the state vector by adding “1” or control signal.

• 2. The transfer equations of the controlled (mechanical) element are derived, while the control force (or control input signal) is considered separately rather than merged into the transfer matrix of the element. Meanwhile, control only affects the form of controlled (mechanical) elements’ transfer equations, and does not influence the transfer equations of other mechanical elements.

• 3. Further, the transfer equation of the control subsystem is defined separately rather than integrated in the transfer equation of the controlled (mechanical) element. This makes the control subsystem share a parallel position with mechanical elements in the system modeling process, and ensures the encapsulation as well as modularity of transfer matrices of mechanical elements and the control subsystem, respectively. It also enables a straightforward representation of the control relations and processing in the dynamics system.

• 4. The topology figure of the dynamics model of controlled multibody systems is proposed by combining the topology figure with block diagrams. It intuitively depicts the process of measurement, the emerging of error signal, the resolving of the controller, and the production of the control force (or control input signal to the plant) by an actuator driven by the control signal.

• 5. The overall transfer equation of the controlled chain system and tree system are deduced. No matter how complicated the topology of a system is, the transfer matrix of the control subsystem has a general form. Moreover, the transfer matrix of a control subsystem is determined by itself and will not be influenced by other control subsystems in the dynamics system.

A numerical example is given to illustrate the application of the proposed method and to validate the proposed method compared with the reported literature. The proposed method greatly reduces the procedures to study the linear controlled multibody systems since it is stylized. It also lays a potential foundation to automatically deduce the overall transfer equation of linear controlled multibody systems with a computer.