Index reduction by minimal extension for the inverse dynamics simulation of cranes

Abstract

The present work deals with the inverse dynamics simulation of underactuated mechanical systems relying on servo constraints. The servo-constraint problem of discrete mechanical systems is governed by differential–algebraic equations (DAEs) with high index. We propose a new index reduction approach, which makes possible the stable numerical integration of the DAEs. The new method is developed in the framework of a specific crane formulation and facilitates a reduction from index five to index three and even to index one. Particular attention is placed on the special case in which the reduced index-1 formulation is purely algebraic. In this case the system at hand can be classified as differentially flat system. Both redundant coordinates and minimal coordinates can be employed within the newly developed approach. The success of the proposed method is demonstrated with two representative numerical examples.

1 Introduction

In this paper we present a new approach to the inverse dynamics simulation of discrete mechanical systems. The present approach is relying on the use of servo constraints for the partial specification of the motion of mechanical systems (see, e.g., [4, 14, 18]). In particular, we focus ourselves on the specification of trajectories of specific points of a multibody system such as the end effector of a robot.

The partial specification of the motion of a multibody system by means of servo constraints typically leads to a problem formulation in terms of differential–algebraic equations (DAEs). If minimal coordinates are used, then the differential part of the DAEs corresponds to the equations of motion, whereas the algebraic part is related to the servo constraints. The servo constraints enforce the desired motion along prescribed trajectories and thus specify the control outputs of the system. To determine the associated control inputs required to steer the system such that the prescribed trajectories are tracked, the DAEs need to be solved. By this a simulation approach to the feedforward control of multibody systems can be realized.

In the special case of fully actuated multibody systems, the simulation approach to the inverse dynamics problem yields index-3 DAEs that can be integrated in analogy to the DAEs corresponding to constrained mechanical systems (see, e.g., [21]). However, the situation changes considerably if underactuated mechanical systems are dealt with. In this type of systems the number of degrees of freedom exceeds the number of controls. Examples of underactuated systems are cranes and flexible multibody systems. The use of servo constraints in the context of underactuated multibody systems leads to a broad diversity of servo-constraint problems (see, in particular, the recent papers [5, 10, 20]). One indicator of problem diversity is the (differentiation) index of the underlying DAEs that typically ranges from three to five and even higher. Consequently, to facilitate a stable numerical integration, some kind of index reduction approach needs to be applied.

In the present work we newly propose to apply a specific index reduction technique called minimal extension (see Kunkel and Mehrmann [16]). So far index reduction by minimal extension has been successfully applied to circuit simulation [16, Sect. 4] and multibody systems [16, Sect. 5]. It was also applied to infinite dimensional systems arising in elastodynamics and flexible multibody systems [1]. To the best of our knowledge, the minimal extension procedure has not been applied previously to the type of underactuated servo-constraint problems considered herein.

To develop the new method in a concise way, we confine our presentation to underactuated mechanical systems belonging to a specific class of cranes. The crane formulation under consideration fits into the more general framework presented in [15]. The corresponding crane model can be often classified as differentially flat system in which the load coordinates play the role of flat outputs. The corresponding servo-constraint problem is governed by DAEs with index five. We shall show that the index reduction by minimal extension can be applied easily to reduce the index of the DAEs to three and even to one. An alternative index reduction approach is the projection method previously developed in [6, 9].

The present work is structured as follows. In Sect. 2 we start with an outline of the formulation of servo constraint problems. In Sect. 3 we first introduce index reduction by minimal extension in the context of constrained mechanical systems. Then we develop the index reduction approach for the servo-constraint problem in the framework of a specific crane model formulated in terms of redundant coordinates. After that we show in Sect. 4 that the advocated minimal extension approach can be also applied to crane models formulated in terms of minimal coordinates. The discretization of the resulting minimally extended DAEs is dealt with in Sect. 5. In this connection, both alternative formulations in terms of redundant and minimal coordinates are considered. The newly developed methodology is then applied to a planar overhead crane (Sect. 6) and a three-dimensional rotary crane (Sect. 7). Eventually, conclusions are drawn in Sect. 8.

2 Mechanical systems with servo constraints

Using minimal coordinates, the DAEs governing the inverse dynamics of discrete mechanical systems consist of the equations of motion and the servo constraints [4, 6]. In particular, the equations of motion have the form

$$\begin{aligned} \boldsymbol {\mathcal{M}} ( \boldsymbol {\mu} ) \ddot{ \boldsymbol {\mu} } = \boldsymbol {f} ( \boldsymbol {\mu } , \dot{ \boldsymbol {\mu} }) + \boldsymbol {\mathcal{B}} ^{T}( \boldsymbol {\mu} ) \boldsymbol {u} \end{aligned}$$

(1a)

with minimal coordinates $\boldsymbol {\mu} \in\mathbb{R}^{f}$, positive definite mass matrix $\boldsymbol {\mathcal{M}} \in\mathbb{R}^{f,f}$, generalized forces $\boldsymbol {f} \in\mathbb{R} ^{f}$, control inputs $\boldsymbol {u} \in\mathbb{R}^{a}$, and input transformation matrix $\boldsymbol {\mathcal{B}} \in\mathbb{R}^{a,f}$. Furthermore, $t\in\mathbb{I}$ denotes the time, and $\mathbb{I}=[t_{0},t_{f}]\subset\mathbb{R}$ is the time interval of interest. The equations of motion are subject to the servo constraints

$$\begin{aligned} \boldsymbol {s} ( \boldsymbol {\mu} ) = \boldsymbol {\gamma} , \end{aligned}$$

(1b)

where $\boldsymbol {\gamma} \colon\mathbb{I}\rightarrow\mathbb{R}^{a}$ is the desired output function. Note that the number $a$ of control inputs is assumed to be equal to the number of independent servo constraints. Correspondingly, the Jacobian of the servo constraints $\boldsymbol {\mathcal{S}} ( \boldsymbol {\mu} ): = D \boldsymbol {s} ( \boldsymbol {\mu} )$ is assumed to have full (row) rank. We note at this point that we understand system (1a)–(1b) in the so-called behavior context, that is, we regard the control inputs as variables [17, Ch. 3.6].

We focus our attention on underactuated mechanical systems in which the number of controls is lower than the number of degrees of freedom, that is, $a < f$.

A distinguishing feature of the DAEs (1a)–(1b) is that, in general, $\boldsymbol {\mathcal{B}} \neq \boldsymbol {\mathcal{S}}$. This is in sharp contrast to mechanical systems subject to holonomic constraints. The difference between holonomic and servo constraints is further reflected in the rank of the matrix $\boldsymbol {\mathcal{P}} := \boldsymbol {\mathcal{S}} \boldsymbol {\mathcal{M}} ^{-1} \boldsymbol {\mathcal{B}} ^{T}$ and in the index of the DAEs (1a)–(1b). For a precise definition of the differentiation index, which we denote simply by index, we refer to [11].

If the matrix $\boldsymbol {\mathcal{P}}$ has full rank (equal to $a$), then there exists an invertible matrix $\boldsymbol {\mathcal{H}} \in \mathbb {R}^{a,a}$ such that $\boldsymbol {\mathcal{B}} = \boldsymbol {\mathcal{H}} \boldsymbol {\mathcal{S}}$. This implies that there exist Lagrange multipliers $\boldsymbol {\lambda} \in \mathbb{R}^{a}$ such that $\boldsymbol {\mathcal{B}} ^{T} \boldsymbol {u} = \boldsymbol {\mathcal{S}} ^{T} \boldsymbol {\lambda}$. Accordingly, the DAEs (1a)–(1b) assume the well-known structure of the equations of motion pertaining to (holonomically) constrained mechanical systems written in terms of redundant coordinates. In this special case, the DAEs (1a)–(1b) are known to have index 3. Using the terminology introduced by Blajer [4], we speak of an orthogonal realization of the servo constraints.

In general, the matrix $\boldsymbol {\mathcal{P}}$ is rank deficient, and the realization of the servo constraints is either mixed orthogonal–tangential or purely tangential in the sense of Blajer [4]. Then the so-called controlled and constrained subspaces do not coincide. In particular, the rank of the matrix $\boldsymbol {\mathcal{P}}$ measures the number of directions of the constrained space which can be directly actuated by the control inputs [6]. For $\mbox{rank}( \boldsymbol {\mathcal{P}} ) < a$, the index of the DAEs (1a)–(1b) always exceeds 3.

We already mentioned that many examples of mechanical systems employing servo constraints lead to DAEs of index 5. Nevertheless, there are examples with arbitrarily high index, see Example 2 in [4]. In the present work we restrict ourselves to crane models that typically yield DAEs of index 5, see, for example [6, 8, 9]. Similarly, the motion of more involved crane-type manipulators such as the wire mechanism dealt with in [13] is governed by DAEs of index 5.

The simulation of index-5 problems is highly challenging. Even the popular Radau IIa scheme, a Runge–Kutta method with three stages, which is a method of order 5 for ODEs, does not converge for general index-5 problems. Thus, index reduction techniques are preferred to reduce the index of the DAEs to 3 or even lower.

To yield a reduction of the index from 5 to 3, Blajer and Kołodziejczyk [6] have proposed a specific projection technique that has been further refined in [9]. The projection approach requires the computation of time-dependent projection matrices in order to split the dynamics of the underactuated system into constrained and unconstrained parts.

In the present work we newly propose an alternative method to reduce the index of the DAEs under consideration. Our method relies on the index reduction by minimal extension originally developed by Kunkel and Mehrmann [16] for more general DAEs. Due to the semiexplicit structure of the DAEs (1a)–(1b), the technique of minimal extension turns out to be especially attractive for the purpose of index reduction.

3 Index reduction by minimal extension

In this section we provide a short introduction to the index reduction approach by minimal extension. Then we present its application to the servo-constraint problem. A common approach for the reduction of the index of general nonlinear DAEs

$$\boldsymbol {F} (t, \boldsymbol {y} , \dot{ \boldsymbol {y} }) = \boldsymbol {0} ,\quad \boldsymbol {y} (t_{0})= \boldsymbol {y} _{0}, $$

is given by the derivative array approach [17, Chap. 6.2]. In this equation, $\boldsymbol {y} _{0}\in\mathbb{R}^{n}$ are prescribed initial conditions, and $\boldsymbol {F} \colon\mathbb{I}\times\mathbb{R}^{n}\times\mathbb{R}^{n} \rightarrow\mathbb{R}^{n}$. Let the DAEs be of index $\mu$. Then we have to differentiate all equations $(\mu-1)$ times and compute suitable projections to find algebraic and differential equations which, together, form an equivalent system of index 1. We refer to [17] for further details. For large systems of high index, the derivative array may become very large and cause memory problems. In addition, we have to invest high computational effort to find the mentioned projection matrices.

The complexity of the index reduction method can be significantly reduced if additional information about the structure of the system is available. This is the case for the semiexplicit DAEs of interest for which the algebraic constraints are explicitly given. Hence, it is sufficient to add the derivatives of those equations. This then leads to a reduced derivative array. In fact, introducing so-called dummy variables [19], we do not even need any projection matrices. This procedure is then called minimal extension [16].

3.1 Minimal extension for mechanical systems

We apply the index reduction technique of minimal extension to the system of equations typically governing the motion of a multibody system; see also [16]. To this end, consider the DAEs

$$\begin{aligned} \boldsymbol {M} ( \boldsymbol {q} )\ddot{ \boldsymbol {q} } = \boldsymbol {f} ( \boldsymbol {q} , \dot{ \boldsymbol {q} }) - \boldsymbol {G} ^{T}( \boldsymbol {q} ) \boldsymbol {\lambda} ,\qquad \boldsymbol {g} ( \boldsymbol {q} ) = \boldsymbol {0} . \end{aligned}$$

The redundant coordinates $\boldsymbol {q} \in\mathbb{R}^{n}$ are subject to $m$ holonomic constraints with associated constraint functions $\boldsymbol {g} ( \boldsymbol {q} )\in \mathbb{R} ^{m}$, Lagrange multipliers $\boldsymbol {\lambda} \in\mathbb{R}^{m}$, and constraint Jacobian $\boldsymbol {G} ( \boldsymbol {q} ) = D \boldsymbol {g} ( \boldsymbol {q} ) \in\mathbb{R}^{m,n}$, which is assumed to have full rank. Moreover, $\boldsymbol {M} ( \boldsymbol {q} )\in\mathbb{R}^{n,n}$ is a symmetric mass matrix, and $\boldsymbol {f} \in\mathbb{R}^{n}$ contains the conjugate forces acting on the system, except for the forces of constraint.

It is well known that the present DAEs have index 3 [17, Ex. 4.22]. Since $\boldsymbol {G} ( \boldsymbol {q} )$ has full rank, there exists an orthogonal matrix $\boldsymbol {Q} \in\mathbb{R}^{n,n}$ such that $\boldsymbol {G} ( \boldsymbol {q} ) \boldsymbol {Q}$ has the block structure

$$\boldsymbol {G} ( \boldsymbol {q} ) \boldsymbol {Q} = \begin{bmatrix} \boldsymbol {G} _{1} & \boldsymbol {G} _{2} \end{bmatrix} $$

with an invertible matrix $\boldsymbol {G} _{2} \in\mathbb{R}^{m,m}$. The matrix $\boldsymbol {Q}$ then allows us to partition the position variables $\boldsymbol {q}$ into $\boldsymbol {q} _{1}\in\mathbb{R}^{n-m}$ and $\boldsymbol {q} _{2}\in \mathbb{R}^{m}$ by

$$\begin{bmatrix} \boldsymbol {q} _{1} \\ \boldsymbol {q} _{2} \end{bmatrix} := \boldsymbol {Q} ^{T} \boldsymbol {q} . $$

For the reduced derivative array, we add to the original system the two derivatives of the constraints, that is,

$$\boldsymbol {G} ( \boldsymbol {q} ) \dot{ \boldsymbol {q} } = \boldsymbol {0} \quad\text{and}\quad \dot{ \boldsymbol {G} }( \boldsymbol {q} ) \dot{ \boldsymbol {q} } + \boldsymbol {G} ( \boldsymbol {q} ) \ddot{ \boldsymbol {q} } = \boldsymbol {0} . $$

To avoid the expensive search for projectors, we introduce two dummy variables $\widehat{ \boldsymbol {q} }_{2} := \dot{ \boldsymbol {q} }_{2}$ and $\widetilde { \boldsymbol {q} }_{2} := \ddot{ \boldsymbol {q} }_{2}$. With the variables $\boldsymbol {q} _{1}$, $\boldsymbol {q} _{2}$, $\widehat{ \boldsymbol {q} }_{2}$, $\widetilde{ \boldsymbol {q} }_{2}$, and $\boldsymbol {\lambda}$, the extended system is then square. Replacing every occurrence of $\dot{ \boldsymbol {q} }_{2}$ and $\ddot{ \boldsymbol {q} }_{2}$ by the corresponding dummy variables, we obtain the overall system

$$\begin{aligned} \boldsymbol {M} ( \boldsymbol {q} ) \boldsymbol {Q} \begin{bmatrix} \ddot{ \boldsymbol {q} }_{1}\\ \widetilde{ \boldsymbol {q} }_{2} \end{bmatrix} &= \boldsymbol {f} ( \boldsymbol {q} _{1}, \boldsymbol {q} _{2}, \dot{ \boldsymbol {q} }_{1}, \widehat{ \boldsymbol {q} }_{2}) - \boldsymbol {G} ^{T}( \boldsymbol {q} ) \boldsymbol {\lambda} , \\ \boldsymbol {0} &= \boldsymbol {g} ( \boldsymbol {q} _{1}, \boldsymbol {q} _{2}), \\ \boldsymbol {0} &= \boldsymbol {G} ( \boldsymbol {q} ) \boldsymbol {Q} \begin{bmatrix} \dot{ \boldsymbol {q} }_{1}\\ \widehat{ \boldsymbol {q} }_{2} \end{bmatrix} , \\ \boldsymbol {0} &= \dot{ \boldsymbol {G} }( \boldsymbol {q} ) \boldsymbol {Q} \begin{bmatrix} \dot{ \boldsymbol {q} }_{1}\\ \widehat{ \boldsymbol {q} }_{2} \end{bmatrix} + \boldsymbol {G} ( \boldsymbol {q} ) \boldsymbol {Q} \begin{bmatrix} \ddot{ \boldsymbol {q} }_{1}\\ \widetilde{ \boldsymbol {q} }_{2} \end{bmatrix} . \end{aligned}$$

Note that, to prevent clumsy notation, we write $\boldsymbol {G} ( \boldsymbol {q} )$ instead of $\boldsymbol {G} ( \boldsymbol {q} _{1}, \boldsymbol {q} _{2})$ and similarly $\boldsymbol {M} ( \boldsymbol {q} )$ instead of $\boldsymbol {M} ( \boldsymbol {q} _{1}, \boldsymbol {q} _{2})$.

The proof that the resulting DAEs have index 1 is given in [17, Th. 6.12]. Note that the size of the system has been increased by twice the number of constraints. Thus, for most applications, the system is still of moderate format.

Remark 1

In general the transformation matrix $\boldsymbol {Q}$ can be found by a Gaussian elimination. In many applications, however, it is possible to guess a permutation matrix $\boldsymbol {Q}$ that yields the needed regular block $\boldsymbol {G} _{2}$. In this case, it is possible to choose $\boldsymbol {Q}$ as the identity matrix if a suitable reordering of the variables is assumed and all variables keep their physical meaning.

3.2 Application to the inverse dynamics of cranes

The DAEs describing mechanical systems subject to servo constraints (cf. Sect. 2) or, more generally, systems subject to both servo and holonomic constraints, exhibit a semiexplicit structure and are thus very similar to the system dealt with in the previous section. Consequently, we can apply a similar procedure to achieve an index reduction for this kind of problems.

In the present work we focus ourselves on the minimal extension approach for cranes. In a first step we choose to use specific redundant coordinates for the description of the inverse dynamics problem. However, our method can also be applied to the corresponding crane formulation in terms of minimal coordinates. This will be shown subsequently in Sect. 4.

As has been demonstrated in previous works dealing with the description of crane models (see, e.g., Fliess et al. [12, Sect. 4.1] for a planar overhead crane, Blajer and Kołodziejczyk [9] for a three-dimensional rotary crane, and Heyden and Woernle [13] for a parallel wire-suspended mechanism), it is especially convenient to divide the crane system into two separate subsystems. The first subsystem belongs to the motor drives, whereas the second subsystem belongs to the load. Correspondingly we distinguish between crane (or actuated) coordinates $\boldsymbol {p} \in R^{n-a}$ and load coordinates $\boldsymbol {x} \in\mathbb{R}^{a}$. Using these coordinates, we can write the DAEs governing the controlled motion of cranes in the form

$$\begin{aligned} \begin{bmatrix} \boldsymbol {M} _{1}( \boldsymbol {p} ) & \quad \boldsymbol {0} \\ \boldsymbol {0} & \quad \boldsymbol {M} _{2} \end{bmatrix} \begin{bmatrix} \ddot{ \boldsymbol {p} }\\ \ddot{ \boldsymbol {x} } \end{bmatrix} &= \begin{bmatrix} \boldsymbol {f} _{1}( \boldsymbol {p} , \dot{ \boldsymbol {p} }) \\ \boldsymbol {f} _{2}( \boldsymbol {x} ,\dot{ \boldsymbol {x} }) \end{bmatrix} + \begin{bmatrix} \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) \\ \boldsymbol {0} \end{bmatrix} \boldsymbol {u} - \begin{bmatrix} \boldsymbol {G} _{1}^{T}( \boldsymbol {p} , \boldsymbol {x} )\\ \boldsymbol {G} _{2}^{T}( \boldsymbol {p} , \boldsymbol {x} ) \end{bmatrix} \boldsymbol {\lambda} , \end{aligned}$$

(2a)

$$\begin{aligned} \boldsymbol {0} &= \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {x} ), \end{aligned}$$

(2b)

$$\begin{aligned} \boldsymbol {x} &= \boldsymbol {\gamma} . \end{aligned}$$

(2c)

Here, the first row block in (2a) corresponds to the actuated subsystem, whereas the second row block in (2a) corresponds to the load. The redundant coordinates

$$ \boldsymbol {q} = \begin{bmatrix} \boldsymbol {p} \\ \boldsymbol {x} \end{bmatrix} $$

(3)

are subject to the holonomic constraints (2b) with associated constraint functions $\boldsymbol {g} \in \mathbb{R}^{m}$ and constraint Jacobian $\boldsymbol {G} = [ \boldsymbol {G} _{1}\ \boldsymbol {G} _{2}] \in\mathbb{R} ^{m,n}$. In this connection, $\boldsymbol {G} _{1} = \partial_{ \boldsymbol {p} } \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {x} )\in\mathbb{R}^{m,n-a}$ denotes the partial derivative w.r.t. the crane coordinates $\boldsymbol {p}$, and $\boldsymbol {G} _{2} = \partial_{ \boldsymbol {x} } \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {x} )\in\mathbb{R}^{m,a}$ denotes the partial derivative w.r.t. the load coordinates $\boldsymbol {x}$. The holonomic constraints link both subsystems at hand and lead to constraint forces with associated Lagrange multipliers $\boldsymbol {\lambda} \in\mathbb{R}^{m}$ in (2a).

The servo constraints (2c) specify the desired trajectory of the load via the prescribed function $\boldsymbol {\gamma} \colon\mathbb{I}\rightarrow\mathbb{R}^{a}$. The control inputs $\boldsymbol {u} \in\mathbb{R}^{a}$ regulate the control forces acting on the first subsystem. In this connection, $\boldsymbol {B} _{1}\in\mathbb {R}^{a,n-a}$ denotes the input transformation matrix. Besides the constraint and control forces, additional forces acting on the system are contained in the conjugate force vectors $\boldsymbol {f} _{1}\in\mathbb{R}^{n-a}$ and $\boldsymbol {f} _{2}\in\mathbb{R}^{a}$. Similarly, the mass matrix is split into the submatrices $\boldsymbol {M} _{1}\in \mathbb{R} ^{{n-a},{n-a}}$ and $\boldsymbol {M} _{2}\in\mathbb{R}^{a,a}$.

Next, we apply the index reduction technique outlined in Sect. 3.1 to system (2a)–(2c) in order to obtain an extended but equivalent system of index 3. Since the holonomic constraint (2b) only causes an index of 3, we just have to add the derivatives of the servo constraints (2c). The addition of these two derivatives and the introduction of two dummy variables $\widehat{ \boldsymbol {x} } := \dot{ \boldsymbol {x} }$ and $\widetilde{ \boldsymbol {x} } := \ddot{ \boldsymbol {x} }$ leads to the system

$$\begin{aligned} \begin{bmatrix} \boldsymbol {M} _{1}( \boldsymbol {p} ) & \boldsymbol {0} \\ \boldsymbol {0} & \boldsymbol {M} _{2} \end{bmatrix} \begin{bmatrix} \ddot{ \boldsymbol {p} }\\ \widetilde{ \boldsymbol {x} } \end{bmatrix} &= \begin{bmatrix} \boldsymbol {f} _{1}( \boldsymbol {p} , \dot{ \boldsymbol {p} }) \\ \boldsymbol {f} _{2}( \boldsymbol {x} ,\widehat { \boldsymbol {x} }) \end{bmatrix} + \begin{bmatrix} \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) \\ \boldsymbol {0} \end{bmatrix} \boldsymbol {u} - \begin{bmatrix} \boldsymbol {G} _{1}^{T}( \boldsymbol {p} , \boldsymbol {x} )\\ \boldsymbol {G} _{2}^{T}( \boldsymbol {p} , \boldsymbol {x} ) \end{bmatrix} \boldsymbol {\lambda} , \end{aligned}$$

(4a)

$$\begin{aligned} \boldsymbol {0} &= \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {x} ), \end{aligned}$$

(4b)

$$\begin{aligned} \boldsymbol {x} &= \boldsymbol {\gamma} , \end{aligned}$$

(4c)

$$\begin{aligned} \widehat{ \boldsymbol {x} } &= \dot{ \boldsymbol {\gamma} }, \end{aligned}$$

(4d)

$$\begin{aligned} \widetilde{ \boldsymbol {x} } &= \ddot{ \boldsymbol {\gamma} }. \end{aligned}$$

(4e)

As we will show in Proposition 1, under certain assumptions, this system has index 3.

3.2.1 Proof of index 3

In the following we state several assumptions that are typically satisfied for crane models. In particular, these assumptions hold for the examples investigated in Sects. 6 and 7. We emphasize that we do not analyze the most general case but restrict ourselves to a model that ensures that the underlying DAEs (2a)–(2c) have index 5. The assumptions serve the purpose to minimize technical issues in the subsequent analysis. Furthermore, the assumptions guarantee that the procedure of minimal extension can be applied twice in order to obtain an equivalent system of index 1, as shall be shown subsequently in Sect. 3.3.

Assumption 1

Consider system (2a)–(2c) with $m \le a \le{n-a}$. Let $\boldsymbol {M} _{1}\in\mathbb{R}^{{n-a},{n-a}}$ be positive definite, and $\boldsymbol {G} _{2} \in\mathbb{R}^{m,a}$ have full rank. This implies that there exists a matrix $\boldsymbol {P} _{2} \in\mathbb{R}^{a,a-m}$ whose columns span the null space of $\boldsymbol {G} _{2}$. Thus,

$$ \boldsymbol {G} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} ) \boldsymbol {P} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} )= \boldsymbol {0} . $$

(5)

Define $\overline{ \boldsymbol {z} }\in\mathbb{R}^{a-m}$ by

$$ \overline{ \boldsymbol {z} }(t, \boldsymbol {p} ) := \boldsymbol {P} _{2}^{T}( \boldsymbol {p} , \boldsymbol {\gamma } ) \bigl( \boldsymbol {f} _{2}( \boldsymbol {\gamma} ,\dot{ \boldsymbol {\gamma} }) - \boldsymbol {M} _{2} \ddot{ \boldsymbol {\gamma} } \bigr) $$

(6)

and introduce $\overline{ \boldsymbol {h} }\in\mathbb{R}^{a}$ by

$$ \overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) := \begin{bmatrix} \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {\gamma} ) \\ \overline{ \boldsymbol {z} }(t, \boldsymbol {p} ) \end{bmatrix} . $$

(7)

Let $\overline{ \boldsymbol {H} }\in\mathbb{R}^{a,{n-a}}$ given by

$$ \overline{ \boldsymbol {H} }(t, \boldsymbol {p} ) := \partial_{ \boldsymbol {p} }\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) $$

(8)

have full rank, and let $\overline{ \boldsymbol {P} }\in\mathbb{R}^{a,a}$ defined by

$$ \overline{ \boldsymbol {P} }(t, \boldsymbol {p} ) := \overline{ \boldsymbol {H} }(t, \boldsymbol {p} ) \boldsymbol {M} _{1}^{-1}( \boldsymbol {p} ) \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) $$

(9)

be invertible.

Proposition 1

Given Assumption  1, the DAEs (4a)–(4e) are of index 3.

Proof

The idea of the proof is to reduce system (4a)–(4e) to a system that has the structure of a constrained multibody system for which the index is known to be 3. As a first step, we eliminate the variables $\boldsymbol {x}$, $\widehat{ \boldsymbol {x} }$, and $\widetilde{ \boldsymbol {x} }$ since they are directly given by $\boldsymbol {\gamma}$ and its derivatives. Then, we use the second part of Eq. (4a), namely

$$ \boldsymbol {M} _{2} \ddot{ \boldsymbol {\gamma} } = \boldsymbol {f} _{2}( \boldsymbol {\gamma} ,\dot{ \boldsymbol {\gamma} })- \boldsymbol {G} _{2}^{T}( \boldsymbol {p} , \boldsymbol { \gamma} ) \boldsymbol {\lambda} , $$

(10)

to extract an equation for $\boldsymbol {\lambda}$. Since $\boldsymbol {G} _{2}\in\mathbb{R}^{m,a}$ is assumed to have full rank, the last equation yields

$$\boldsymbol {\lambda} = \bigl( \boldsymbol {G} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} ) \boldsymbol {G} _{2}^{T}( \boldsymbol {p} , \boldsymbol {\gamma} ) \bigr)^{-1} \boldsymbol {G} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} ) \bigl( \boldsymbol {f} _{2}( \boldsymbol {\gamma} , \dot{ \boldsymbol {\gamma} }) - \boldsymbol {M} _{2} \ddot{ \boldsymbol {\gamma} } \bigr) =: \overline{ \boldsymbol {\lambda} }(t, \boldsymbol {p} ). $$

In addition to that, premultiplying (10) by $\boldsymbol {P} _{2}^{T}( \boldsymbol {p} , \boldsymbol {\gamma} )$ and taking into account (5) give

$$ \overline{ \boldsymbol {z} }(t, \boldsymbol {p} ) = \boldsymbol {0} , $$

(11)

where $\overline{ \boldsymbol {z} }(t, \boldsymbol {p} )$ has been defined in (6). Accordingly, the $a$ equations in (10) yield $m$ equations for the determination of $\overline{ \boldsymbol {\lambda} }(t, \boldsymbol {p} )$ along with $a-m$ equations $\overline { \boldsymbol {z} }(t, \boldsymbol {p} )= \boldsymbol {0}$, which can be viewed as additional algebraic constraints. To summarize, we eventually obtain the system

$$\begin{aligned} \boldsymbol {M} _{1}( \boldsymbol {p} ) \ddot{ \boldsymbol {p} } &= \overline{ \boldsymbol {f} }_{1}(t, \boldsymbol {p} ,\dot{ \boldsymbol {p} }) + \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) \boldsymbol {u} , \end{aligned}$$

(12a)

$$\begin{aligned} \boldsymbol {0} &= \overline{ \boldsymbol {h} }(t, \boldsymbol {p} ), \end{aligned}$$

(12b)

where

$$\overline{ \boldsymbol {f} }_{1}(t, \boldsymbol {p} ,\dot{ \boldsymbol {p} }):= \boldsymbol {f} _{1}( \boldsymbol {p} ,\dot { \boldsymbol {p} })- \boldsymbol {G} _{1}^{T}( \boldsymbol {p} , \boldsymbol {\gamma} ) \overline{ \boldsymbol {\lambda } }(t, \boldsymbol {p} ), $$

and $\overline{ \boldsymbol {h} }(t, \boldsymbol {p} )$ has been defined in (7). The DAEs (12a)–(12b) consist of $n-a$ differential equations (12a) and $m + (a-m) = a$ algebraic equations (12b) for the determination of $\boldsymbol {p} \in\mathbb{R}^{n-a}$ and $\boldsymbol {u} \in \mathbb{R}^{a}$. In particular, the DAEs (12a)–(12b) assume the semiexplicit structure known from multibody dynamics. More precisely, the DAEs (12a)–(12b) are Hessenberg index-3 (see, e.g., Ascher and Petzold [2, Sect. 9.1.1]). Provided that Assumption 1 holds, the DAEs (12a)–(12b) have index 3. To see this, we can argue along the lines of Sect. 2. In particular, the argument hinges on the full rank assumption for the matrix $\overline{ \boldsymbol {P} }$ defined in (9). □

Remark 2

Proposition 1 implies that the original DAEs (2a)–(2c) have index 5 at most. This follows from the fact that two differentiation steps were sufficient to obtain DAEs of index 3.

3.3 Reduction to index 1

Next, we show that the procedure of minimal extension can be applied a second time to eventually reach DAEs of index 1. However, due to the fact that the extended system (4a)–(4e) does not exhibit the desired Hessenberg form anymore, we cannot directly apply our index reduction method to the DAEs (4a)–(4e). First, we have to find the equations that have to be differentiated.

Here we benefit from the proof of Proposition 1, in which these equations were already identified. Accordingly, to apply index reduction by minimal extension a second time, we have to add the derivatives of the constraints (12b). In this way, the original system is extended by $2a$ algebraic constraints. Correspondingly, $2a$ additional dummy variables have to be introduced to reach a square system. For this purpose, we have available the first and second time derivative of the crane coordinates $\boldsymbol {p} \in\mathbb{R}^{n-a}$. That is, we have $2(n-a)$ variables at our disposal. Note that this complies with the relation $a \le{n-a}$ in Assumption 1. Although the second index reduction can be performed for the general case $a \le{n-a}$, we focus in what follows on the special case $a = {n-a}$.

3.3.1 The special case of purely algebraic equations

In the sequel we shall focus on the special case $a = {n-a}$, which applies to the numerical examples dealt with in Sects. 6 and 7. In this case the introduction of dummy derivatives implies that all differential variables in (12a)–(12b) are converted to algebraic ones. Thus, after the second index reduction, no differential variables are present anymore, and the resulting system of equations is purely algebraic. This indicates that the specific systems under consideration are differentially flat.

Provided that $a = {n-a}$, we introduce $\widehat{ \boldsymbol {p} }:=\dot{ \boldsymbol {p} }$ and $\widetilde{ \boldsymbol {p} }:=\ddot{ \boldsymbol {p} }$ as additional dummy variables. We eventually arrive at the system

$$\begin{aligned} \boldsymbol {M} _{1}( \boldsymbol {p} ) \widetilde{ \boldsymbol {p} } &= \overline{ \boldsymbol {f} }_{1}(t, \boldsymbol {p} ,\widehat{ \boldsymbol {p} }) + \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) \boldsymbol {u} , \end{aligned}$$

(13a)

$$\begin{aligned} \boldsymbol {0} &= \overline{ \boldsymbol {h} }(t, \boldsymbol {p} ), \end{aligned}$$

(13b)

$$\begin{aligned} \boldsymbol {0} &= \overline{ \boldsymbol {H} }(t, \boldsymbol {p} )\widehat{ \boldsymbol {p} } + \partial _{t} \overline { \boldsymbol {h} }(t, \boldsymbol {p} ), \end{aligned}$$

(13c)

$$\begin{aligned} \boldsymbol {0} &= \overline{ \boldsymbol {H} }(t, \boldsymbol {p} )\widetilde{ \boldsymbol {p} } + \boldsymbol {\eta} (t, \boldsymbol {p} , \widehat{ \boldsymbol {p} }), \end{aligned}$$

(13d)

where the $i$th component of the vector-valued function $\boldsymbol {\eta } (t, \boldsymbol {p} ,\widehat{ \boldsymbol {p} })$ is given by

$$ \eta_{i}(t, \boldsymbol {p} ,\widehat{ \boldsymbol {p} }) = \widehat{ \boldsymbol {p} }^{T} \partial^{2}_{ \boldsymbol {p} \boldsymbol {p} }\overline{h}_{i}(t, \boldsymbol {p} ) \widehat{ \boldsymbol {p} } + 2\partial^{2}_{t \boldsymbol {p} }\overline{h}_{i}(t, \boldsymbol {p} )\widehat{ \boldsymbol {p} } + \partial^{2}_{tt} \overline{h}_{i}(t, \boldsymbol {p} ) $$

(14)

for $i=1,\ldots,a$. Since system (13a)–(13d) is purely algebraic, it is easy to see that the DAEs have index 1. In particular, system (13a)–(13d) constitutes $4a$ algebraic equations for the determination of the $4a$ variables $\boldsymbol {p}$, $\widehat{ \boldsymbol {p} }$, $\widetilde{ \boldsymbol {p} }$ and $\boldsymbol {u}$.

Remark 3

The assumptions made in Assumption 1 guarantee the unique solvability of the algebraic system (13a)–(13d).

Remark 4

Alternatively, the above extension procedure can also be applied directly to system (4a)–(4e). In this case the new constraints (13c) and (13d) have to be appended to the DAEs (4a)–(4e). In addition to that, the dummy variables $\widehat{ \boldsymbol {p} }:=\dot{ \boldsymbol {p} }$ and $\widetilde{ \boldsymbol {p} }:=\ddot { \boldsymbol {p} }$ have to be introduced. Again, we arrive at a purely algebraic system of equations that is equivalent to system (13a)–(13d).

Remark 5

A careful inspection of the present index-1 formulation shows that all unknowns (redundant coordinates, Lagrange multipliers, and control inputs) can be expressed in terms of the output functions $\boldsymbol {\gamma} (t)$ along with the derivatives thereof up to fourth order. This corresponds to the fact that the crane models under consideration can be classified as differentially flat systems.

Remark 6

As mentioned before, the second index reduction can be also performed for ${n-a}>a$. In this case the introduction of dummy derivatives still leaves differential variables in the resulting index-1 DAEs. This is indicative for systems with internal dynamics (or zero dynamics). In this case additional issues may arise such as the stability of the internal dynamics.

4 Minimal coordinates

In this section we show that the minimal extension procedure can also be applied to crane formulations in terms of minimal coordinates. We start with the minimally extended index-3 formulation (4a)–(4e) and express the redundant coordinates (3) in terms of minimal coordinates $\boldsymbol {\mu} \in\mathbb {R}^{f}$, where $f=n-m$ denotes the number of degrees of freedom. Thus,

$$ \boldsymbol {q} = \boldsymbol {\varphi} ( \boldsymbol {\mu} ) \quad\mbox{or}\quad \begin{bmatrix} \boldsymbol {p} \\ \boldsymbol {x} \end{bmatrix} = \begin{bmatrix} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} ) \\ \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} ) \end{bmatrix} . $$

(15)

Note that by definition the coordinate mapping (15) satisfies identically the holonomic constraints (4b), that is, $\boldsymbol {g} \circ \boldsymbol {\varphi} ( \boldsymbol {\mu} )= \boldsymbol {0}$ for all $\boldsymbol {\mu} \in\mathbb{R}^{f}$. We refer to Sects. 6.3 and 7.3, where the coordinate mapping (15) is detailed in the context of specific examples.

Using the redundant coordinates (3), it is natural to select the derivatives of the load coordinates $\boldsymbol {x} \in\mathbb {R}^{a}$ as dummy variables (cf. Sect. 3.2). Similarly, differentiating the minimal coordinates twice with respect to time, we get the corresponding velocities $\dot{ \boldsymbol {\mu} }\in \mathbb{R}^{f}$ and accelerations $\ddot{ \boldsymbol {\mu} }\in\mathbb{R}^{f}$, from which we need to select appropriate dummy variables. To this end, we split the minimal coordinates into $\boldsymbol {\mu} _{1}\in\mathbb{R}^{f-a}$ and $\boldsymbol {\mu} _{2}\in\mathbb{R}^{a}$ such that

$$ D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2})\in\mathbb{R}^{a,a} \quad \mbox{is nonsingular.} $$

(16)

With a slight abuse of notation, we use $\boldsymbol {\varphi} ( \boldsymbol {\mu } _{1}, \boldsymbol {\mu} _{2})$ to write the mapping (15) after the coordinate partition has been performed. Furthermore, in (16) and in the sequel, $D_{\alpha} \boldsymbol {\varphi} ( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2})$ with $\alpha =1$ or $\alpha=2$ denotes the partial derivative with respect to the first or second argument, respectively. Now we choose the dummy variables

$$\begin{aligned} \widehat{ \boldsymbol {\mu} }_{2} &= \dot{ \boldsymbol {\mu} }_{2}, \end{aligned}$$

(17a)

$$\begin{aligned} \widetilde{ \boldsymbol {\mu} }_{2} &= \ddot{ \boldsymbol {\mu} }_{2}. \end{aligned}$$

(17b)

Differentiating the mapping (15) with respect to time, we obtain

$$\begin{aligned} \dot{ \boldsymbol {p} }&= D_{1} \boldsymbol {\varphi} _{1}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2})\dot { \boldsymbol {\mu} }_{1} + D_{2} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\widehat { \boldsymbol {\mu} }_{2}, \end{aligned}$$

(18a)

$$\begin{aligned} \ddot{ \boldsymbol {p} }&= D_{1} \boldsymbol {\varphi} _{1}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2})\ddot { \boldsymbol {\mu} }_{1} + D_{2} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\widetilde{ \boldsymbol {\mu} }_{2} + \boldsymbol {g} _{1}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2},\dot{ \boldsymbol {\mu} }_{1}, \widehat{ \boldsymbol {\mu} }_{2}) \end{aligned}$$

(18b)

and

$$\begin{aligned} \widehat{ \boldsymbol {x} }&= D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2})\dot { \boldsymbol {\mu} }_{1} + D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\widehat{ \boldsymbol {\mu} }_{2}, \end{aligned}$$

(19a)

$$\begin{aligned} \widetilde{ \boldsymbol {x} }&= D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu } _{2})\ddot{ \boldsymbol {\mu} }_{1} + D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\widetilde{ \boldsymbol {\mu } }_{2} + \boldsymbol {g} _{2}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2},\dot{ \boldsymbol {\mu} }_{1},\widehat { \boldsymbol {\mu} }_{2}), \end{aligned}$$

(19b)

where

$$ \boldsymbol {g} _{\alpha}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2},\dot{ \boldsymbol {\mu} }_{1},\widehat { \boldsymbol { \mu} }_{2}) = \frac{\text{d}}{\text{d}t} \bigl(D_{1} \boldsymbol { \varphi} _{\alpha}( \boldsymbol {\mu } _{1}, \boldsymbol {\mu} _{2}) \bigr) \dot{ \boldsymbol {\mu} }_{1} + \frac{\text{d}}{\text{d}t} \bigl(D_{2} \boldsymbol { \varphi} _{\alpha}( \boldsymbol {\mu } _{1}, \boldsymbol {\mu} _{2}) \bigr) \widehat{ \boldsymbol {\mu} }_{2}. $$

(20)

These relationships can now be inserted into the minimally extended index-3 DAEs (4a)–(4e). In addition to that, in order to eliminate the Lagrange multipliers $\boldsymbol {\lambda}$ from (4a), we multiply (4a) from the left by $D \boldsymbol {\varphi} ( \boldsymbol {\mu } )^{T}$. A straightforward calculation yields the minimally extended index-3 formulation in terms of minimal coordinates given by

$$\begin{aligned} \boldsymbol {\mathcal{M}} _{11}( \boldsymbol {\mu} ) \ddot{ \boldsymbol {\mu} }_{1} & = \boldsymbol {h} _{1}( \boldsymbol {\mu} ,\dot { \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol { \mu} }_{2}) - \boldsymbol {\mathcal{M}} _{12}( \boldsymbol {\mu} )\widetilde { \boldsymbol { \mu} }_{2} - \boldsymbol {\mathcal{B}} _{1}^{T}( \boldsymbol {\mu} ) \boldsymbol {u} , \end{aligned}$$

(21a)

$$\begin{aligned} \boldsymbol {\mathcal{M}} _{21}( \boldsymbol {\mu} ) \ddot{ \boldsymbol {\mu} }_{1} & = \boldsymbol {h} _{2}( \boldsymbol {\mu} ,\dot { \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol { \mu} }_{2}) - \boldsymbol {\mathcal{M}} _{22}( \boldsymbol {\mu} )\widetilde { \boldsymbol { \mu} }_{2} - \boldsymbol {\mathcal{B}} _{2}^{T}( \boldsymbol {\mu} ) \boldsymbol {u} , \end{aligned}$$

(21b)

$$\begin{aligned} D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\ddot{ \boldsymbol {\mu} }_{1} &= \ddot{ \boldsymbol {\gamma} }- \boldsymbol {g} _{2}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol { \mu} }_{2}) - D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2})\widetilde{ \boldsymbol {\mu } }_{2}, \end{aligned}$$

(21c)

$$\begin{aligned} { \boldsymbol {0} }&= D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2})\dot{ \boldsymbol {\mu } }_{1} + D_{2} \boldsymbol { \varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2})\widehat{ \boldsymbol {\mu } }_{2} - \dot{ \boldsymbol {\gamma} }, \end{aligned}$$

(21d)

$$\begin{aligned} { \boldsymbol {0} }&= \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} ) - { \boldsymbol {\gamma} } \end{aligned}$$

(21e)

Here,

$$\begin{aligned} \boldsymbol {\mathcal{M}} _{\alpha\beta}( \boldsymbol {\mu} ) &= \sum\limits _{\gamma=1}^{2} D_{\alpha} \boldsymbol {\varphi} _{\gamma}^{T}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2}) \boldsymbol {M} _{\gamma}D_{\beta } \boldsymbol {\varphi} _{\gamma}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}), \end{aligned}$$

(22a)

$$\begin{aligned} \boldsymbol {h} _{\alpha}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol {\mu } }_{2}) &= \sum\limits _{\gamma=1}^{2} D_{\alpha} \boldsymbol {\varphi} _{\gamma}^{T}( \boldsymbol { \mu} _{1}, \boldsymbol {\mu} _{2}) ( \boldsymbol {f} _{\gamma}- \boldsymbol {M} _{\gamma} \boldsymbol {g} _{\gamma}), \end{aligned}$$

(22b)

$$\begin{aligned} \boldsymbol {\mathcal{B}} _{\alpha}^{T}( \boldsymbol {\mu} ) &= D_{\alpha} \boldsymbol { \varphi } _{1}^{T}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2}) \boldsymbol {B} ^{T}_{1}. \end{aligned}$$

(22c)

Note that, to simplify the notation, $( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2})$ has often been replaced by $\boldsymbol {\mu}$ as an argument of the functions considered. Similarly, the arguments of functions pertaining to the underlying formulation in terms of redundant coordinates have been suppressed.

System (21a)–(21e) constitutes a set of $f+3a$ index-3 DAEs for the determination of the differential variables ${ \boldsymbol {\mu} }_{1}\in \mathbb{R}^{f-a}$ and the algebraic variables $\boldsymbol {u}$, ${ \boldsymbol {\mu} }_{2}$, $\widehat{ \boldsymbol {\mu} }_{2}$, $\widetilde{ \boldsymbol {\mu} }_{2}\in\mathbb{R}^{a}$.

4.1 Commutative process

We finally show that minimal coordinates can also be employed from the outset, prior to the index reduction approach. Indeed, we may also start from the formulation in terms of minimal coordinates given by system (1a)–(1b).

• 1. In a first step the coordinate mapping (15) is employed to convert the index-5 formulation in terms of redundant coordinates (2a)–(2c) to the corresponding index-5 formulation in terms of minimal coordinates (1a)–(1b). This conversion is a standard procedure relying on the projection matrix $D \boldsymbol {\varphi} ( \boldsymbol {\mu } )$. Thus, we get the index-5 DAEs

  $$\begin{aligned} \boldsymbol {\mathcal{M}} ( \boldsymbol {\mu} ) \ddot{ \boldsymbol {\mu} } & = \boldsymbol {h} ( \boldsymbol {\mu } ,\dot{ \boldsymbol {\mu} }) - \boldsymbol {\mathcal{B}} ^{T}( \boldsymbol {\mu} ) \boldsymbol {u} , \end{aligned}$$

  (23a)
  $$\begin{aligned} \boldsymbol {0} & = \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} ) - { \boldsymbol {\gamma} }, \end{aligned}$$

  (23b)

  where the reduced mass matrix $\boldsymbol {\mathcal{M}} ( \boldsymbol {\mu} )=D \boldsymbol {\varphi} ^{T}( \boldsymbol {\mu} ) \boldsymbol {M} D \boldsymbol {\varphi} ( \boldsymbol {\mu} )$ assumes the partitioned form

  $$ \boldsymbol {\mathcal{M}} ( \boldsymbol {\mu} ) = \begin{bmatrix} \boldsymbol {\mathcal{M}} _{11}( \boldsymbol {\mu} ) & \quad \boldsymbol {\mathcal{M}} _{12}( \boldsymbol {\mu} ) \\ \boldsymbol {\mathcal{M}} _{21}( \boldsymbol {\mu} ) & \quad \boldsymbol {\mathcal{M}} _{22}( \boldsymbol {\mu} ) \end{bmatrix} . $$

  (24)

  Here, the submatrices are given by (22a). Similarly, $\boldsymbol {h}$ and $\boldsymbol {\mathcal {B}}$ in (23a) can be assembled from (22b) and (22c), respectively. Note that comparing the servo constraints (23b) with (1b) shows that $\boldsymbol {\varphi} _{2}( \boldsymbol {\mu} )= \boldsymbol {s} ( \boldsymbol {\mu} )$.

• 2. Now index reduction by minimal extension can be applied to system (23a)–(23b). To this end, partition the minimal coordinates subject to condition (16), differentiate the servo constraints (23b) twice with respect to time, and introduce the dummy variables (17a)–(17b). It is easy to see that this procedure yields again the index-3 DAEs (21a)–(21e).

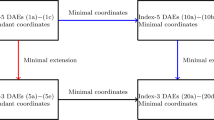
Obviously, the two steps to arrive at the minimally extended set of index-3 DAEs in terms of minimal coordinates (21a)–(21e) do commute. That is, the final result is independent of the order of the steps (i) minimal extension and (ii) introduction of minimal coordinates. This is summarized in the commutative diagram in Fig. 1.

Fig. 1

Commutative diagram for index reduction and the introduction of minimal coordinates

Remark 7

An alternative way of reducing the index from 5 to 3 is the projection method originally proposed by Blajer and Kołodziejczyk [6]. This approach requires the design of a suitable projection matrix and eventually yields $f+a$ index-3 DAEs. Whereas in the present approach the servo constraints are enforced on position, velocity, and acceleration level (see (21e), (21d), and (21c)), the projection method enforces the servo constraints only on position and acceleration level. Correspondingly, the present approach is characterized by $f+3a$ index-3 DAEs.

5 Discretization

Having reduced the index of the equations of motion to three, we need to discuss the temporal discretization for the numerical simulation. For general DAEs of index 3, we have to take care of the stability of the used numerical integration method. However, the semiexplicit form allows us to apply the Euler backward scheme. Here we profit from the simple structure of the system obtained by the minimal extension procedure.

5.1 Index-3 formulation in terms of redundant coordinates

The minimally extended index-3 formulation in terms of redundant coordinates (4a)–(4e) can be recast in the form

$$\begin{aligned} \boldsymbol {M} _{1}( \boldsymbol {p} )\ddot{ \boldsymbol {p} } &= \boldsymbol {f} _{1}( \boldsymbol {p} , \dot{ \boldsymbol {p} }) + \boldsymbol {B} _{1}^{T}( \boldsymbol {p} ) \boldsymbol {u} - \boldsymbol {G} _{1}^{T}( \boldsymbol {p} , \boldsymbol {\gamma} ) \boldsymbol {\lambda} , \end{aligned}$$

(25a)

$$\begin{aligned} \boldsymbol {0} &= \boldsymbol {M} _{2}\ddot{ \boldsymbol {\gamma} } - \boldsymbol {f} _{2}( \boldsymbol { \gamma } ,\dot{ \boldsymbol {\gamma} }) + \boldsymbol {G} _{2}^{T}( \boldsymbol {p} , \boldsymbol { \gamma} ) \boldsymbol {\lambda} , \end{aligned}$$

(25b)

$$\begin{aligned} \boldsymbol {0} &= \boldsymbol {g} ( \boldsymbol {p} , \boldsymbol {\gamma} ). \end{aligned}$$

(25c)

The DAEs (25a)–(25c) provide $n-a$ differential equations (25a) along with $a+m$ algebraic equations (25b) and (25c) for the determination of $\boldsymbol {p} \in \mathbb{R} ^{n-a}$, $\boldsymbol {u} \in\mathbb{R}^{a}$, and $\boldsymbol {\lambda} \in\mathbb{R}^{m}$. In particular, the DAEs (25a)–(25c) are in semiexplicit form, so that we can expect the simple Euler backward discretization to work well (see Ascher and Petzold [2, Sect. 10.1.1]). Accordingly, we consider the scheme

$$\begin{aligned} & \boldsymbol {p} _{n+1}- \boldsymbol {p} _{n} = \Delta t \boldsymbol {v} _{n+1}, \end{aligned}$$

(26a)

$$\begin{aligned} & \boldsymbol {M} _{1}( \boldsymbol {p} _{n+1}) ( \boldsymbol {v} _{n+1}- \boldsymbol {v} _{n} ) \\ &\quad = \Delta t \bigl( \boldsymbol {f} _{1}( \boldsymbol {p} _{n+1}, \boldsymbol {v} _{n+1}) + \boldsymbol {B} _{1}^{T}( \boldsymbol {p} _{n+1}) \boldsymbol {u} _{n+1} - \boldsymbol {G} _{1}^{T} \bigl( \boldsymbol {p} _{n+1}, \boldsymbol {\gamma} (t_{n+1})\bigr) \boldsymbol {\lambda } _{n+1} \bigr), \end{aligned}$$

(26b)

$$\begin{aligned} & \boldsymbol {0} = \boldsymbol {M} _{2}\ddot{ \boldsymbol {\gamma} }(t_{n+1}) - \boldsymbol {f} _{2}\bigl( \boldsymbol {\gamma} (t_{n+1}),\dot{ \boldsymbol { \gamma} }(t_{n+1})\bigr) + \boldsymbol {G} _{2}^{T}\bigl( \boldsymbol {p} _{n+1}, \boldsymbol {\gamma} (t_{n+1})\bigr) \boldsymbol {\lambda} _{n+1}, \end{aligned}$$

(26c)

$$\begin{aligned} & \boldsymbol {0} = \boldsymbol {g} \bigl( \boldsymbol {p} _{n+1}, \boldsymbol {\gamma} (t_{n+1}) \bigr). \end{aligned}$$

(26d)

In a typical step of size $\Delta t = t_{n+1}-t_{n}$ we seek approximations $(\cdot)_{n+1}$ to $(\cdot)(t_{n+1})$ given the corresponding quantities $(\cdot)_{n}$ as the result of the previous step. For the initial step, we require consistent initial values $\boldsymbol {p} _{0}$ and $\boldsymbol {v} _{0}$ that have to satisfy $\boldsymbol {g} ( \boldsymbol {p} _{0}, \boldsymbol {\gamma} (t_{0}))= \boldsymbol {0}$ along with

$$\boldsymbol {G} _{1}\bigl( \boldsymbol {p} _{0}, \boldsymbol {\gamma} (t_{0}) \bigr) \boldsymbol {v} _{0} + \boldsymbol {G} _{2}\bigl( \boldsymbol {p} _{0}, \boldsymbol {\gamma} (t_{0})\bigr)\dot{ \boldsymbol {\gamma} }(t_{0})= \boldsymbol {0} . $$

The scheme (26a)–(26d) provides $2n+m-a$ algebraic equations for the determination of $\boldsymbol {p} _{n+1}$, $\boldsymbol {v} _{n+1}\in\mathbb{R}^{n-a}$, $\boldsymbol {u} _{n+1}\in\mathbb{R}^{a}$, and $\boldsymbol {\lambda} _{n+1}\in\mathbb{R}^{m}$.

5.2 Index-3 formulation in terms of minimal coordinates

For the minimally extended index-3 formulation in terms of minimal coordinates (21a)–(21e), we apply an Euler backward discretization as well. The corresponding scheme is given by

$$\begin{aligned} &{ \boldsymbol {\mu} }_{1_{n+1}}-{ \boldsymbol {\mu} }_{1_{n}} = \Delta t \boldsymbol {\nu } _{1_{n+1}}, \end{aligned}$$

(27a)

$$\begin{aligned} & \boldsymbol {\mathcal{M}} _{11}( \boldsymbol {\mu} _{n+1}) ( \boldsymbol {\nu} _{1_{n+1}}- \boldsymbol {\nu} _{1_{n}} ) \\ &\quad = \Delta t \bigl( \boldsymbol {h} _{1}( \boldsymbol {\mu} _{n+1}, \boldsymbol {\nu} _{1_{n+1}},\widehat{ \boldsymbol {\mu} }_{2_{n+1}}) - \boldsymbol {\mathcal{M}} _{12}( \boldsymbol { \mu} _{n+1})\widetilde{ \boldsymbol {\mu } }_{2_{n+1}} - \boldsymbol { \mathcal{B}} _{1}^{T}( \boldsymbol {\mu} _{n+1}) \boldsymbol {u} _{n+1} \bigr), \end{aligned}$$

(27b)

$$\begin{aligned} & \boldsymbol {\mathcal{M}} _{21}( \boldsymbol {\mu} _{n+1}) ( \boldsymbol {\nu} _{1_{n+1}}- \boldsymbol {\nu} _{1_{n}} ) \\ &\quad = \Delta t \bigl( \boldsymbol {h} _{2}( \boldsymbol {\mu} _{n+1}, \boldsymbol {\nu} _{1_{n+1}},\widehat{ \boldsymbol {\mu} }_{2_{n+1}}) - \boldsymbol {\mathcal{M}} _{22}( \boldsymbol { \mu} _{n+1})\widetilde{ \boldsymbol {\mu} }_{2_{n+1}} - \boldsymbol { \mathcal{B}} _{2}^{T}( \boldsymbol {\mu} _{n+1}) \boldsymbol {u} _{n+1} \bigr), \end{aligned}$$

(27c)

$$\begin{aligned} &D_{1} \boldsymbol {\varphi} _{2}({ \boldsymbol {\mu} }_{1_{n+1}},{ \boldsymbol {\mu} }_{2_{n+1}}) ( \boldsymbol {\nu} _{1_{n+1}}- \boldsymbol {\nu} _{1_{n}} ) \\ &\quad = \Delta t \bigl(\ddot{ \boldsymbol {\gamma} }(t_{n+1})- \boldsymbol {g} _{2}( \boldsymbol { \mu} _{n+1}, \boldsymbol {\nu} _{1_{n+1}},\widehat { \boldsymbol {\mu} }_{2_{n+1}}) - D_{2} \boldsymbol {\varphi} _{2}({ \boldsymbol {\mu } }_{1_{n+1}},{ \boldsymbol { \mu} }_{2_{n+1}})\widetilde{ \boldsymbol {\mu } }_{2_{n+1}} \bigr), \end{aligned}$$

(27d)

$$\begin{aligned} &{ \boldsymbol {0} } = D_{1} \boldsymbol {\varphi} _{2}({ \boldsymbol {\mu} }_{1_{n+1}},{ \boldsymbol {\mu } }_{2_{n+1}}) \boldsymbol {\nu} _{1_{n+1}} + D_{2} \boldsymbol { \varphi} _{2}({ \boldsymbol {\mu } }_{1_{n+1}},{ \boldsymbol {\mu} }_{2_{n+1}}) \widehat{ \boldsymbol {\mu} }_{2_{n+1}} - \dot{ \boldsymbol {\gamma} }(t_{n+1}), \end{aligned}$$

(27e)

$$\begin{aligned} &{ \boldsymbol {0} } = \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{n+1}) - { \boldsymbol {\gamma} }(t_{n+1}). \end{aligned}$$

(27f)

The scheme (27a)–(27f) provides $2(f+a)$ algebraic equations for the determination of ${ \boldsymbol {\mu} }_{1_{n+1}}$, $\boldsymbol {\nu } _{1_{n+1}}\in\mathbb{R}^{f-a}$ and ${ \boldsymbol {\mu} }_{2_{n+1}}$, $\widehat{ \boldsymbol {\mu} }_{2_{n+1}}$, $\widetilde{ \boldsymbol {\mu} }_{2_{n+1}}$, $\boldsymbol {u} _{n+1}\in\mathbb{R}^{a}$.

6 Planar overhead crane

As a first example, we consider a planar overhead crane that allows traveling and hoisting motions (see Fig. 2). This servo-constraint problem was originally formulated in terms of minimal coordinates in [6] and was recast in redundant coordinates in [3, 8].

Fig. 2

Planar model of the overhead crane

The description of the overhead crane is based on $n=4$ redundant coordinates, $m=1$ holonomic constraint, and $a=2$ controls. In particular, the crane coordinates $\boldsymbol {p} \in\mathbb{R}^{2}$ and the load coordinates $\boldsymbol {x} \in\mathbb{R}^{2}$ are given by

$$\boldsymbol {p} = \begin{bmatrix} s \\ l \end{bmatrix} , \qquad \boldsymbol {x} = \begin{bmatrix} x \\ z \end{bmatrix} . $$

Here, $s$ measures the horizontal position of the trolley, $l$ is the cable length, and $(x,z)$ denote the coordinates of the load. The redundant coordinates have to satisfy the holonomic constraint

$$g( \boldsymbol {p} , \boldsymbol {x} ) = \frac{1}{2} \bigl( (x-s)^{2} + z^{2} - l^{2} \bigr) = 0. $$

The holonomic constraint gives rise to the associated constraint Jacobian, which can be decomposed into

$$\begin{aligned} \boldsymbol {G} _{1}( \boldsymbol {p} , \boldsymbol {x} ) &= \begin{bmatrix} -(x-s) &\quad -l \end{bmatrix} , \\ \boldsymbol {G} _{2}( \boldsymbol {p} , \boldsymbol {x} ) &= \begin{bmatrix} x-s & \quad z \end{bmatrix} . \end{aligned}$$

In addition to that, the underlying index-5 DAEs (2a)–(2c) employ the mass matrices

$$\boldsymbol {M} _{1} = \begin{bmatrix} m_{t} &\quad 0 \\ 0 & \quad \frac{J}{r^{2}} \end{bmatrix} , \qquad \boldsymbol {M} _{2} = \begin{bmatrix} m & \quad 0 \\ 0 & \quad m \end{bmatrix} , $$

where $m_{t}$ is the mass of the trolley, $J$ is the moment of inertia of the winch of radius $r$, and $m$ is the mass of the load. Further, the quantities needed in (2a)–(2c) are given by

$$\boldsymbol {f} _{1} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} , \qquad \boldsymbol {f} _{2} = \begin{bmatrix} 0 \\ -mg \end{bmatrix} , \qquad \boldsymbol {B} _{1} = \begin{bmatrix} 1 & \quad 0 \\ 0 & \quad \frac{1}{r} \end{bmatrix} . $$

The servo constraints (2c) are used to prescribe the trajectory of the load. Accordingly,

$$\boldsymbol {\gamma} = \begin{bmatrix} x_{d} \\ z_{d} \end{bmatrix} , $$

where $x_{d}$ and $z_{d}$ are prescribed functions of time. The corresponding control inputs assume the form

$$\boldsymbol {u} = \begin{bmatrix} F_{t} \\ M_{w} \end{bmatrix} , $$

where $F_{t}$ is the force acting on the trolley, and $M_{w}$ is the torque acting on the winch.

6.1 Verification of Assumption 1

To verify Assumption 1, we first choose

$$\boldsymbol {P} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} ) = \begin{bmatrix} -z_{d} \\ x_{d}-s \end{bmatrix} $$

such that condition (5) is satisfied. Now (6) yields

$$\overline{z}(t, \boldsymbol {p} ) = m \bigl( z_{d}\ddot{x}_{d} - (x_{d}-s) (g+\ddot{z}_{d}) \bigr). $$

Furthermore, the constraint function (7) reads

$$\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} \frac{1}{2} ( (x_{d}-s)^{2} + z_{d}^{2} - l^{2} ) \\ m ( z_{d}\ddot{x}_{d} - (x_{d}-s)(g+\ddot{z}_{d}) ) \end{bmatrix} , $$

so that (8) yields

$$\overline{ \boldsymbol {H} }(t, \boldsymbol {p} ) = \begin{bmatrix} \boldsymbol {G} _{1}( \boldsymbol {p} , \boldsymbol {\gamma} ) \\ \partial_{ \boldsymbol {p} }\overline{ z}(t, \boldsymbol {p} ) \end{bmatrix} = \begin{bmatrix} -(x_{d}-s) & \quad -l \\ m(g+\ddot{z}_{d}) & \quad 0 \end{bmatrix} . $$

Eventually, (9) gives

$$\overline{ \boldsymbol {P} }(t, \boldsymbol {p} ) = \begin{bmatrix} -\frac{x_{d}-s}{m_{t}} & \quad -\frac{lr}{J} \\ \frac{m}{m_{t}}(g+\ddot{z}_{d}) & \quad 0 \end{bmatrix} . $$

Note that in practical applications we have $l > 0$ and $g+\ddot{z}_{d} > 0$. The last inequality holds due to the fact that the cable (which in the present model is assumed to be inextensible and massless) connecting the load with the winch can only sustain tensile (and no compressive) forces. This can be easily verified by applying Newton’s second law of motion. Thus, $\overline{ \boldsymbol {H} }(t, \boldsymbol {p} )$ has full rank, and $\overline{ \boldsymbol {P} }(t, \boldsymbol {p} )$ is invertible. Consequently, Assumption 1 is satisfied, and Proposition 1 holds.

We further remark that the minimally extended index-3 DAEs (12a)–(12b) can now be set up for the overhead crane. It only remains to calculate

$$\overline{ \boldsymbol {f} }_{1}(t, \boldsymbol {p} ) = \frac{m}{l^{2}} \bigl( (x_{d}-s)\ddot {x}_{d} + z_{d}(g+ \ddot{z}_{d}) \bigr) \begin{bmatrix} -(x_{d}-s) \\ -l \end{bmatrix} $$

to complete the description of the DAEs (12a)–(12b).

6.2 Index-1 formulation (13a)–(13d)

As explained in Sect. 3.3, the index-1 formulation (13a)–(13d) yields a purely algebraic system of equations that facilitates an analytical solution of the inverse dynamics problem under consideration. The additional quantities needed in (13c) and (13d) read

$$\partial_{t}\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} (x_{d}-s)\dot{x}_{d} + z_{d}\dot{z}_{d} \\ m ( \dot{z}_{d}\ddot{x}_{d}-\dot{x}_{d}(g+\ddot{z}_{d})+z_{d} x^{(3)}_{d}-(x_{d}-s)z^{(3)}_{d} ) \end{bmatrix} $$

and

$$\begin{aligned} &\partial^{2}_{ \boldsymbol {p} \boldsymbol {p} }\overline{h}_{1}(t, \boldsymbol {p} ) = \begin{bmatrix} 1 & \quad 0 \\ 0 & \quad -1 \end{bmatrix} , \qquad \partial^{2}_{ \boldsymbol {p} \boldsymbol {p} } \overline{h}_{2}(t, \boldsymbol {p} ) = \begin{bmatrix} 0 & \quad 0 \\ 0 & \quad 0 \end{bmatrix} , \\ &\partial^{2}_{t \boldsymbol {p} }\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} -\dot{x}_{d} & \quad 0 \\ m z^{(3)}_{d} & \quad 0 \end{bmatrix} , \\ &\partial^{2}_{tt}\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} \dot{x}_{d}^{2}+\dot{z}_{d}^{2}+(x_{d}-s)\ddot{x}_{d} + z_{d}\ddot{z}_{d} \\ m ( -\ddot{x}_{d} g+2\dot{z}_{d} x^{(3)}_{d}-2\dot{x}_{d} z^{(3)}_{d}+z_{d} x^{(4)}_{d}-(x_{d}-s)z^{(4)}_{d} ) \end{bmatrix} . \end{aligned}$$

In the present case it is possible to get a closed-form analytical solution of (13a)–(13d), which serves as a reference solution in the numerical example presented further.

6.3 Minimal coordinates

We next aim at the minimally extended index-3 system (21a)–(21e) for the overhead crane in terms of minimal coordinates. Since the planar overhead crane has $f=n-m=3$ degrees of freedom, we choose

$$\boldsymbol {\mu} = \begin{bmatrix} s & \quad l &\quad \varphi \end{bmatrix} ^{T} $$

as minimal coordinates. These coordinates have been also used in the original description of the present servo-constraint problem in [6]. The coordinate mappings in (15) assume the form

$$\boldsymbol {\varphi} _{1}( \boldsymbol {\mu} ) = \begin{bmatrix} s \\ l \end{bmatrix} \quad \mbox{and}\quad \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} ) = \begin{bmatrix} s+l\sin\varphi\\ -l\cos\varphi \end{bmatrix} . $$

For the minimal extension procedure, we split the minimal coordinates into

$$\boldsymbol {\mu} _{1} = \begin{bmatrix} s \end{bmatrix} \quad\mbox{and}\quad \boldsymbol {\mu} _{2} = \begin{bmatrix} l &\quad \varphi \end{bmatrix} ^{T} $$

such that the Jacobian

$$D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2}) = \begin{bmatrix} \sin\varphi & \quad l\cos\varphi \\ -\cos\varphi& \quad l\sin\varphi \end{bmatrix} $$

is guaranteed to be nonsingular. Thus, condition (16) is met. We further get

$$D_{1} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2}) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} , \qquad D_{2} \boldsymbol { \varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}) = \begin{bmatrix} 0 & \quad 0 \\ 1 & \quad 0 \end{bmatrix} , \qquad D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} . $$

Now, (20) gives rise to

$$\boldsymbol {g} _{1} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \quad\mbox{and}\quad \boldsymbol {g} _{2} = \begin{bmatrix} 2\hat{\varphi}\hat{l}\cos\varphi-l\hat{\varphi }^{2}\sin \varphi\\ 2\hat{\varphi}\hat{l}\sin\varphi+l\hat{\varphi}^{2}\cos\varphi \end{bmatrix} . $$

Note that the minimal extension procedure implies the equalities $\hat {l}=\dot{l}$ and $\hat{\varphi}=\dot{\varphi}$. Furthermore, (22a)–(22c) yields

$$\begin{aligned} & \boldsymbol {\mathcal{M}} _{11}( \boldsymbol {\mu} ) = \begin{bmatrix} m_{t}+m \end{bmatrix} , \qquad \boldsymbol {\mathcal{M}} _{12}( \boldsymbol {\mu} ) = \begin{bmatrix} m\sin\varphi & \quad ml\cos\varphi \end{bmatrix} , \\ & \boldsymbol {\mathcal{M}} _{21}( \boldsymbol {\mu} ) = \boldsymbol {\mathcal{M}} _{12}^{T}( \boldsymbol {\mu} ), \qquad \boldsymbol {\mathcal{M}} _{22}( \boldsymbol {\mu} ) = \begin{bmatrix} \frac{J}{r^{2}}+m & \quad 0 \\ 0 & \quad ml^{2} \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} \boldsymbol {h} _{1}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol { \mu} }_{2}) &= \begin{bmatrix} \ ml\hat{\varphi}^{2}\sin\varphi-2m\hat{\varphi }\hat {l}\cos\varphi\ \end{bmatrix} , \\ \boldsymbol {h} _{2}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol { \mu} }_{2}) &= \begin{bmatrix} ml\hat{\varphi}^{2}+mg\cos\varphi\\ -ml(g\sin\varphi +2\hat {\varphi}\hat{l}) \end{bmatrix} , \\ \boldsymbol {\mathcal{B}} _{1}^{T}( \boldsymbol {\mu} ) &= \begin{bmatrix} 1 & \quad 0 \end{bmatrix} , \\ \boldsymbol {\mathcal{B}} _{2}^{T}( \boldsymbol {\mu} ) &= \begin{bmatrix} 0 & \quad \frac{1}{r} \\ 0 & \quad 0 \end{bmatrix} . \end{aligned}$$

This completes the index-3 DAEs (21a)–(21e) for the overhead crane in terms of minimal coordinates.

6.4 Numerical example

The data for the present numerical example have been taken from [6]. Accordingly, the prescribed trajectory of load $m$ is defined by

$$ \boldsymbol {\gamma} (t) = \boldsymbol {\gamma} _{0} + ( \boldsymbol {\gamma} _{f} - \boldsymbol { \gamma } _{0}) s(\tau) $$

(28)

with

$$ \boldsymbol {\gamma} _{0} = \begin{bmatrix} x_{d}(t_{0}) \\ z_{d}(t_{0}) \end{bmatrix} = \begin{bmatrix} 0 \\ -4 \end{bmatrix} \quad\mbox{at } t_{0} = 0 $$

and

$$ \boldsymbol {\gamma} _{f} = \begin{bmatrix} x_{d}(t_{f}) \\ z_{d}(t_{f}) \end{bmatrix} = \begin{bmatrix} 5 \\ -1 \end{bmatrix} \quad\mbox{at } t_{f} = 3. $$

The interpolating polynomial $s(\tau)$ takes the form

$$ s(\tau) = 70\tau^{9} - 315 \tau^{8} + 540 \tau^{7} -420 \tau^{6} + 126\tau^{5} \quad\mbox{with } \tau= \frac{t}{t_{f}-t_{0}}. $$

(29)

Accordingly, the motion of load $m$ is subjected to a rest-to-rest maneuver on a straight-line trajectory. Starting at rest, the initial configuration of the system is given by

$$ \boldsymbol {q} _{0} = [s_{0} \quad l_{0} \quad x_{0} \quad z_{0}]^{T} = [0 \quad4 \quad0 \quad {-}4]^{T}. $$

(30)

The remaining parameters are given by $m_{t} = 10$, $m = 100$, $J = 0.1$, $g = 9.81$, and $r = 0.1$. The simulation results for different time step sizes are depicted in Figs. 3 and 4. In each diagram, the numerical solution (NUM) is compared to the analytical reference solution (REF). It can be observed that the numerical solution converges to the analytical reference solution when the time step size is reduced. We do not distinguish between the use of redundant and minimal coordinates since both formulations yield very similar results. This also applies for our implementation of the projection method proposed in [6]. The motion of the overhead crane is illustrated in Fig. 5 with some snapshots at consecutive points in time.

Fig. 3

Planar overhead crane: Comparison between the numerical results (NUM) obtained with $\Delta t = 0.1$ and the analytical reference solution (REF)

Fig. 4

Planar overhead crane: Comparison between the numerical results (NUM) obtained with $\Delta t = 0.01$ and the analytical reference solution (REF)

Fig. 5

Planar overhead crane: Snapshots at specific points in time

7 Three-dimensional rotary crane

In the second example we deal with the three-dimensional rotary crane depicted in Fig. 6. This servo-constraint problem has originally been dealt with in [9]. It can be viewed as a 3d extension of the planer crane treated in the previous section. The 3d crane makes use of $n=6$ redundant coordinates that are subjected to $m=1$ holonomic constraint. Moreover, $a=3$ servo constraints are used to prescribe the trajectory of the load. The crane coordinates $\boldsymbol {p} \in \mathbb{R}^{3}$ and the load coordinates $\boldsymbol {x} \in\mathbb{R}^{3}$ are given by

$$\boldsymbol {p} = \begin{bmatrix} \varphi\\ s \\ l \end{bmatrix} , \qquad \boldsymbol {x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} . $$

The position of the load (mass $m$) is specified by the Cartesian coordinates $(x,y,z)$ relative to an inertial reference frame. In addition to the location $s$ of the trolley and the length $l$ of the hoisting rope, the angle $\varphi$ measures the rotation of the bridge (or girder) about the $z$-axis relative to the $x$-axis. Accordingly, the motion of the suspension point is described by polar coordinates $(s,\varphi)$ relative to the origin of the reference frame. The redundant coordinates have to satisfy the holonomic constraint

$$g( \boldsymbol {p} , \boldsymbol {x} ) = \frac{1}{2} \bigl( (x-s \cos\varphi)^{2} + (y - s \sin \varphi)^{2} + z^{2} - l^{2} \bigr) = 0. $$

The associated constraint Jacobian assumes the partitioned form

$$\begin{aligned} \boldsymbol {G} _{1}( \boldsymbol {p} , \boldsymbol {x} ) &= \begin{bmatrix} (x \sin\varphi- y \cos\varphi)s & \quad (s - x \cos\varphi- y \sin\varphi) & \quad -l \end{bmatrix} , \\ \boldsymbol {G} _{2}( \boldsymbol {p} , \boldsymbol {x} ) &= \begin{bmatrix} (x-s \cos\varphi) & \quad (y - s \sin\varphi) & \quad z \ \end{bmatrix} . \end{aligned}$$

In the underlying index-5 DAEs (2a)–(2c), the mass matrices are given by

$$\boldsymbol {M} _{1} = \begin{bmatrix} J_{b} + m_{t} s^{2} & \quad 0 & \quad 0 \\ 0 & \quad m_{t} & \quad 0 \\ 0 & \quad 0 & \quad J_{w}/r_{w}^{2} \end{bmatrix} , \qquad \boldsymbol {M} _{2} = \begin{bmatrix} m & \quad 0 & \quad 0 \\ 0 & \quad m & \quad 0 \\ 0 & \quad 0 & \quad m \end{bmatrix} , $$

where $J_{b}$ is the moment of inertia of the bridge relative to the $z$-axis, $J_{w}$ is the moment of inertia of the winch (of radius $r_{w}$), and $m_{t}$ is the mass of the trolley. Further, the quantities needed in (2a)–(2c) are given by

$$\boldsymbol {f} _{1} = \begin{bmatrix} 2 m_{t} s \dot{s} \dot{\varphi} \\ -m_{t} s \dot{\varphi}^{2} \\ 0 \end{bmatrix} , \qquad \boldsymbol {f} _{2} = \begin{bmatrix} 0 \\ 0 \\ -mg \end{bmatrix} , \qquad \boldsymbol {B} _{1} = \begin{bmatrix} 1 & \quad 0 & \quad 0 \\ 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad \frac{1}{r_{w}} \end{bmatrix} . $$

The servo constraints (2c) are used to prescribe the trajectory of the load. Accordingly,

$$\boldsymbol {\gamma} = \begin{bmatrix} x_{d} \\ y_{d} \\ z_{d} \end{bmatrix} , $$

where $x_{d}$, $y_{d}$, and $z_{d}$ are prescribed functions of time. The control inputs assume the form

$$\boldsymbol {u} = \begin{bmatrix} M_{b} \\ F_{t} \\ M_{w} \end{bmatrix} . $$

Here, $M_{b}$ is the torque acting about the $z$-axis on the bridge, $F_{t}$ is the force acting along the girder on the trolley, and $M_{w}$ is the torque acting on the winch.

Fig. 6

Model of the three-dimensional rotary crane

7.1 Verification of Assumption 1

To verify Assumption 1, we first choose

$$\boldsymbol {P} _{2}( \boldsymbol {p} , \boldsymbol {\gamma} ) = \begin{bmatrix} -z_{d} & \quad 0 \\ 0 & \quad -z_{d} \\ x_{d}-s \cos\varphi & \quad y_{d}-s \sin\varphi \end{bmatrix} $$

such that condition (5) is satisfied. Now (6) yields

$$\overline{ \boldsymbol {z} }(t, \boldsymbol {p} ) = \begin{bmatrix} m (z_{d} \ddot{x}_{d} - (x_{d}-s \cos\varphi )(g+\ddot {z}_{d}) ) \\ m ( z_{d}\ddot{y}_{d} - (y_{d}-s \sin\varphi)(g+\ddot{z}_{d}) ) \end{bmatrix} . $$

Furthermore, the constraint function (7) reads

$$\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} \frac{1}{2} ( (x_{d}-s \cos\varphi)^{2} + (y_{d} - s \sin\varphi)^{2} + z_{d}^{2} - l^{2} ) \\ m (z_{d} \ddot{x}_{d} - (x_{d}-s \cos\varphi)(g+\ddot{z}_{d}) ) \\ m ( z_{d}\ddot{y}_{d} - (y_{d}-s \sin\varphi)(g+\ddot{z}_{d}) ) \end{bmatrix} , $$

so that (8) yields

$$\overline{ \boldsymbol {H} }(t, \boldsymbol {p} ) = \begin{bmatrix} \boldsymbol {G} _{1}( \boldsymbol {p} , \boldsymbol {\gamma} ) \\ \partial_{ \boldsymbol {p} }\overline{ z}(t, \boldsymbol {p} ) \end{bmatrix} = \begin{bmatrix} (x_{d} \sin\varphi- y_{d} \cos\varphi)s & \quad (s - x_{d}\cos\varphi- y_{d} \sin\varphi) & \quad -l \\ -m s (g+\ddot{z}_{d})\sin\varphi & \quad m (g+\ddot{z}_{d}) \cos\varphi & \quad 0 \\ m s (g+\ddot{z}_{d}) \cos\varphi & \quad m (g + \ddot{z}_{d}) \sin\varphi & \quad 0 \end{bmatrix} . $$

Eventually, (9) gives

$$\overline{ \boldsymbol {P} }(t, \boldsymbol {p} ) = \begin{bmatrix} \frac{(x_{d} \sin\varphi-y_{d} \cos\varphi)s}{J_{b}+m_{t} s^{2}} & \quad \frac{s-x_{d} \cos\varphi- y_{d} \sin\varphi}{m_{t}} & \quad -\frac{l r_{w}}{J_{w}} \\ -\frac{ m s (g+\ddot{z}_{d})\sin\varphi}{J_{b}+m_{t} s^{2}} & \quad \frac{m(g+\ddot{z}_{d}) \cos\varphi}{m_{t}} & \quad 0 \\ \frac{m s (g+\ddot{z}_{d}) \cos\varphi}{J_{b}+m_{t} s^{2}} & \quad \frac{m(g+\ddot{z}_{d}) \sin\varphi}{m_{t}} & \quad 0 \end{bmatrix} . $$

As in the case of the planar overhead crane, the hoisting rope can only sustain tensile forces such that $g+\ddot{z}_{d} > 0$. Moreover, in practical applications, $l > 0$. This implies that $\overline{ \boldsymbol {H} }(t, \boldsymbol {p} )$ has full rank and $\overline{ \boldsymbol {P} }(t, \boldsymbol {p} )$ is invertible. Consequently, Assumption 1 is satisfied, and Proposition 1 holds.

We further remark that the minimally extended index-3 DAEs (12b) can now be set up for the rotary crane. To complete the description of the DAEs (12a)–(12b), it only remains to calculate

$$\begin{aligned} \overline{ \boldsymbol {f} }_{1}(t, \boldsymbol {p} ) =& \begin{bmatrix} 2 m_{t} s \dot{s} \dot{\varphi}\\ -m_{t} s \dot{\varphi}^{2} \\ 0 \end{bmatrix} + \frac{m}{l^{2}} \bigl( (x_{d}-s \cos\varphi)\ddot{x}_{d} + (y_{d}-s \sin \varphi) \ddot{y}_{d} +z_{d}(g+ \ddot{z}_{d}) \bigr) \\ &{}\times\begin{bmatrix} (x_{d} \sin\varphi-y \cos\varphi)s \\ s-x \cos\varphi - y \sin\varphi\\ -l \end{bmatrix}. \end{aligned}$$

7.2 Index-1 formulation (13a)–(13d)

As explained in Sect. 3.3, the index-1 formulation (13a)–(13d) yields a purely algebraic system of equations, which facilitates an analytical solution of the inverse dynamics problem under consideration. The additional quantities needed in (13c) and (13d) read

$$\partial_{t}\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) = \begin{bmatrix} (x_{d}-s \cos\varphi)\dot{x}_{d} + (y_{d}-s \sin\varphi) \dot{y}_{d} +z_{d}\dot{z}_{d} \\ m ( z_{d} x_{d}^{(3)}+\dot{z}_{d} \ddot{x}_{d} - (x_{d}-s \cos\varphi) z_{d}^{(3)}-\dot{x}_{d} (g+ \ddot{z}_{d}) ) \\ m ( \dot{z}_{d}\ddot{y}_{d}+z_{d} y_{d}^{(3)}-(y_{d}-s \sin\varphi) z_{d}^{(3)} -\dot{y}_{d}(g+\ddot{z}_{d}) ) \end{bmatrix} $$

and

$$\begin{aligned} \partial^{2}_{ \boldsymbol {p} \boldsymbol {p} }\overline{h}_{1}(t, \boldsymbol {p} ) &= \begin{bmatrix} (x_{d} \cos\varphi+y_{d} \sin\varphi)s & \quad x_{d} \sin\varphi- y_{d}\cos\varphi & \quad 0 \\ x_{d} \sin\varphi- y_{d} \cos\varphi & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad -1 \end{bmatrix} , \\ \partial^{2}_{ \boldsymbol {p} \boldsymbol {p} }\overline{h}_{2}(t, \boldsymbol {p} ) &= \begin{bmatrix} -ms(g + \ddot{z}_{d}) \cos\varphi & \quad -m(g + \ddot{z}_{d}) \sin\varphi & \quad 0 \\ -m(g + \ddot{z}_{d})\sin\varphi & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \end{bmatrix} \\ \partial^{2}_{ \boldsymbol {p} \boldsymbol {p} }\overline{h}_{3}(t, \boldsymbol {p} ) &= \begin{bmatrix} -ms(g+\ddot{z}_{d}) \sin\varphi & \quad m(g + \ddot{z}_{d}) \cos\varphi & \quad 0 \\ m(g+\ddot{z}_{d}) \cos\varphi & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \end{bmatrix} , \\ \partial^{2}_{t \boldsymbol {p} }\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) &= \begin{bmatrix} s (\dot{x}_{d} \sin\varphi-\dot{y}_{d} \cos\varphi) & \quad -(\dot{x}_{d}\cos\varphi+\dot{y}_{d} \sin\varphi) & \quad 0 \\ -m s z_{d}^{(3)} \sin\varphi & \quad m z_{d}^{(3)} \cos\varphi & \quad 0 \\ ms z_{d}^{(3)} \cos\varphi & \quad m z_{d}^{(3)} \sin\varphi & \quad 0 \end{bmatrix} , \\ \partial^{2}_{tt}\overline{ \boldsymbol {h} }(t, \boldsymbol {p} ) &= \begin{bmatrix} (x_{d}-s \cos\varphi) \ddot{x}_{d} + \dot{x}_{d}^{2} + (y_{d}-s \sin\varphi)\ddot{y}_{d} + \dot{y}_{d}^{2} + \dot{z}_{d}^{2} + z_{d} \ddot{z}_{d} \\ m( x_{d}^{(4)}z_{d} +2 \dot{z}_{d} x_{d}^{(3)}+ \ddot{x}_{d} \ddot{z}_{d} - \ddot{x}_{d}(g + \ddot{z}_{d})-(x_{d}-s\cos\varphi)z_{d}^{(4)} - 2\dot{x}_{d} z_{d}^{(3)} ) \\ m ( y_{d}^{(4)}z_{d} +2 \dot{z}_{d} y_{d}^{(3)}+ \ddot{y}_{d} \ddot{z}_{d} - \ddot{y}_{d}(g + \ddot{z}_{d})-(y_{d}-s\sin\varphi)z_{d}^{(4)} - 2\dot{y}_{d} z_{d}^{(3)} ) \end{bmatrix} . \end{aligned}$$

As in the case of the planar overhead crane, it is possible to get a closed-form analytical solution of (13a)–(13d), which serves as a reference solution in the numerical example presented below.

7.3 Minimal coordinates

We next aim at the minimally extended index-3 system (21a)–(21e) for the rotary crane in terms of minimal coordinates. To this end, we express the load position relative to the suspension point by means of the cable length $l$ and three angles $(\varphi ,\theta _{1},\theta_{2})$; cf. Fig. 6. That is,

$$\begin{bmatrix} x_{d}-s\cos\varphi\\ y_{d}-s\sin\varphi\\ z_{d} \end{bmatrix} = -l \boldsymbol {t} (\varphi,\theta_{1}, \theta_{2}). $$

Here, $\boldsymbol {t} (\varphi,\theta_{1},\theta_{2}) = \boldsymbol {R} (\varphi,\theta _{1},\theta _{2}) \boldsymbol {e} _{3}$ is a unit vector that points from the load to the suspension point and follows from the canonical base vector $\boldsymbol {e} _{3} = [0 \ 0 \ 1]^{T}$ by applying successive elementary rotations with angles $(\theta_{2},\theta_{1},\varphi)$ about fixed axes $(- \boldsymbol {e} _{2},- \boldsymbol {e} _{1}, \boldsymbol {e} _{3})$. This procedure leads to the associated rotation matrix $\boldsymbol {R} (\varphi,\theta_{1},\theta_{2})$ and eventually yields

$$\boldsymbol {t} (\varphi,\theta_{1},\theta_{2}) = \begin{bmatrix} \ - (\sin\theta_{2}\cos\varphi+ \cos\theta_{2}\sin\theta_{1}\sin \varphi ) \ \\ \cos\theta_{2}\sin\theta_{1}\cos\varphi- \sin\theta_{2}\sin\varphi\\ \cos\theta_{2}\cos\theta_{1} \end{bmatrix} . $$

Then the coordinate mappings in (15) can be written in the form

$$\boldsymbol {\varphi} _{1}( \boldsymbol {\mu} ) = \begin{bmatrix} \varphi\\ s \\ l \end{bmatrix} \quad \mbox{and}\quad \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} ) = \begin{bmatrix} \ (s+l\sin\theta_{2}) \cos\varphi+ l \cos\theta_{2} \sin\theta_{1} \sin \varphi\ \\ (s+l\sin\theta_{2}) \sin\varphi- l \cos\theta_{2} \sin\theta_{1} \cos \varphi\\ -l \cos\theta_{2} \cos\theta_{1} \end{bmatrix} $$

such that $f=n-m=5$ minimal coordinates

$$ \boldsymbol {\mu} = \begin{bmatrix} \varphi & \quad s & \quad l & \quad \theta_{1} & \quad \theta_{2} \end{bmatrix} ^{T} $$

(31)

are used. The same set of coordinates has been also employed in [7]. For the minimal extension procedure, we split the minimal coordinates into

$$\boldsymbol {\mu} _{1} = \begin{bmatrix} \varphi & \quad s \end{bmatrix} ^{T} \quad \mbox{and}\quad \boldsymbol {\mu} _{2} = \begin{bmatrix} l & \quad \theta_{1} & \quad \theta_{2} \end{bmatrix} ^{T}. $$

We obtain

$$\begin{aligned} &D_{2} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}) \\ &\quad = \begin{bmatrix} \sin\theta_{2} \cos\varphi+ \cos\theta_{2} \sin\theta_{1} \sin \varphi\ & \ l\cos\theta_{2} \cos\theta_{1} \sin\varphi\ & \ l \cos\theta_{2} \cos\varphi- l \sin\theta_{2} \sin\theta_{1} \sin\varphi \\ \sin\theta_{2} \sin\varphi- \cos\theta_{2} \sin\theta_{1} \cos \varphi\ & \ -l \cos\theta_{2} \cos\theta_{1} \cos\varphi\ & \ l \cos\theta_{2}\sin\varphi+ l \sin\theta_{2} \sin\theta_{1} \cos\varphi \\ -\cos\theta_{2} \cos\theta_{1} \ & \ l \cos\theta_{2} \sin\theta_{1} \ & \ l \sin\theta_{2} \cos\theta_{1} \end{bmatrix} . \end{aligned}$$

This matrix is nonsingular for realistic parameter values ($l>0$ and $|\theta_{2}|<\pi/2$). Accordingly, condition (16) is satisfied. We further get

$$\begin{aligned} &D_{1} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}) = \begin{bmatrix} 1 & \quad 0 \\ 0 & \quad 1 \\ 0 & \quad 0 \end{bmatrix} , \qquad D_{2} \boldsymbol {\varphi} _{1}( \boldsymbol {\mu} _{1}, \boldsymbol {\mu} _{2}) = \begin{bmatrix} 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \\ 1 & \quad 0 & \quad 0 \end{bmatrix} , \\ &D_{1} \boldsymbol {\varphi} _{2}( \boldsymbol {\mu} _{1}, \boldsymbol { \mu} _{2}) = \begin{bmatrix} -(s+l\sin\theta_{2}) \sin\varphi+ l \cos\theta_{2} \sin\theta_{1}\cos\varphi & \quad \cos\varphi \\ (s + l \sin\theta_{2}) \cos\varphi+ l \cos\theta_{2} \sin\theta_{1}\sin\varphi & \quad \sin\varphi \\ 0 & \quad 0 \end{bmatrix} . \end{aligned}$$

Now, (20) gives rise to $\boldsymbol {g} _{1} = \boldsymbol {0}$. Furthermore, $\boldsymbol {g} _{2}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol {\mu} }_{2})$ and $\boldsymbol {h} _{\alpha}( \boldsymbol {\mu} ,\dot{ \boldsymbol {\mu} }_{1},\widehat{ \boldsymbol {\mu} }_{2})$ can be calculated straightforwardly from (20) and (22b), respectively. In this connection we remark that the minimal extension procedure implies the equalities $\hat {l}=\dot{l}$, $\hat{\theta}_{1}=\dot{\theta}_{1}$, and $\hat{\theta }_{2}=\dot {\theta}_{2}$. Eventually, (22a)–(22c) yields

$$\begin{aligned} \boldsymbol {\mathcal{M}} _{11}( \boldsymbol {\mu} ) &= \begin{bmatrix} J_{b}+m_{t}s^{2}+m ( (s+l\sin\theta_{2})^{2}+(l\cos\theta_{2} \sin\theta_{1})^{2} ) & \quad ml\cos\theta_{2}\sin\theta_{1} \\ ml\cos\theta_{2}\sin\theta_{1} & \quad m+m_{t} \ \end{bmatrix} , \\ \boldsymbol {\mathcal{M}} _{12}( \boldsymbol {\mu} ) &= \begin{bmatrix} -ms\cos\theta_{2}\sin\theta_{1} & \quad -ml(s+l\sin\theta_{2})\cos\theta_{2}\cos\theta_{1} & \quad ml\sin\theta_{1}(l+s\sin\theta_{2}) \\ m \sin\theta_{2} & \quad 0 & \quad ml \cos\theta_{2} \end{bmatrix} , \\ \boldsymbol {\mathcal{M}} _{21}( \boldsymbol {\mu} ) &= \boldsymbol {\mathcal{M}} _{12}^{T}( \boldsymbol {\mu} ), \\ \boldsymbol {\mathcal{M}} _{22}( \boldsymbol {\mu} ) &= \begin{bmatrix} m+\frac{J_{w}}{r_{w}^{2}} & \quad 0 & \quad 0 \\ 0 & \quad ml^{2} \cos^{2}{\theta_{2}} & \quad 0 \\ 0 & \quad 0 & \quad ml^{2} \end{bmatrix} \end{aligned}$$

and

$$\boldsymbol {\mathcal{B}} _{1}^{T}( \boldsymbol {\mu} ) = \begin{bmatrix} 1 & \quad 0 & \quad 0 \\ 0 & \quad 1 & \quad 0 \end{bmatrix} , \qquad \boldsymbol {\mathcal{B}} _{2}^{T}( \boldsymbol {\mu} ) = \begin{bmatrix} 0 & \quad 0 & \quad \frac{1}{r_{w}} \\ 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \\ \end{bmatrix} . $$

7.4 Numerical example

In the numerical example we make use of the data provided in [7]. In particular, the inertia parameters are given by $m = 100$, $m_{t} = 10$, $J_{w} = 0.1$, $r_{w} = 0.1$, and $J_{b} = 480$. The servo constraints are used to prescribe a rest-to-rest maneuver of the load specified by $\boldsymbol {\gamma} (t) = \boldsymbol {\gamma} _{0} + ( \boldsymbol {\gamma} _{f} - \boldsymbol {\gamma } _{0}) s(t)$ with $\boldsymbol {\gamma} _{0} = [5 \ 0 \ {-}5]$ at $t_{0} =0$ and $\boldsymbol {\gamma} _{f} = [ -2 \ 2 \ {-}2 ]$ at $t_{f} = 20$. The function $s(t)$ is composed of three phases,

$$s(t) = \textstyle\begin{cases} s_{I}(t) & \mbox{for } 0 \le t < 5, \\ s_{\mathit{II}}(t) & \mbox{for } 5 \le t < 15, \\ s_{\mathit{III}}(t) & \mbox{for } 15 \le t \le 20 \end{cases} $$

with

$$\begin{aligned} s_{I}(t) &= \frac{1}{\tau-\tau_{0}} \biggl(-\frac{5t^{8}}{2{\tau _{0}}^{7}}+ \frac {10t^{7}}{{\tau_{0}}^{6}} - \frac{14t^{6}}{2{\tau_{0}}^{5}} +\frac{7t^{5}}{2{\tau _{0}}^{4}} \biggr), \\ s_{\mathit{II}}(t) &= \frac{1}{\tau-\tau_{0}} \biggl(t - \frac{\tau _{0}}{2} \biggr), \\ s_{\mathit{III}}(t) &= 1+ \frac{1}{\tau-\tau_{0}} \biggl(-\frac{5(\tau -t)^{8}}{2{\tau _{0}}^{7}}+ \frac{10(\tau-t)^{7}}{{\tau_{0}}^{6}} - \frac{14(\tau -t)^{6}}{2{\tau _{0}}^{5}} +\frac{7(\tau-t)^{5}}{2{\tau_{0}}^{4}} \biggr). \end{aligned}$$

Using the minimal coordinates (31), the initial configuration of the rotary crane at $t_{0}=0$ is defined by $\boldsymbol {\mu} _{0} = [ 0 \ 5 \ 5 \ 0 \ 0 ] ^{T}$. The motion of the crane is starting at rest such that $\dot{ \boldsymbol {\mu } }_{0}= \boldsymbol {0}$.

The simulation results for different time step sizes are depicted in Figs. 7 and 8. In each diagram, the numerical solution (NUM) is compared to the analytical reference solution (REF). It can be observed that the numerical solution converges to the analytical reference solution when the time step size is reduced. Both alternative formulations in terms of redundant and minimal coordinates yield practically the same results. Similar observations can be made for our implementation of the projection method due to [9]. The motion of the rotary crane is illustrated in Fig. 9 with some snapshots at consecutive points in time.

Fig. 7

Rotary crane: Comparison between the numerical results (NUM) obtained with $\Delta t = 1$ and the analytical reference solution (REF)

Fig. 8

Rotary crane: Comparison between the numerical results (NUM) obtained with $\Delta t = 0.1$ and the analytical reference solution (REF)

Fig. 9

Rotary crane: Snapshots at specific points in time

8 Conclusions

We showed that index reduction by minimal extension can be applied successfully to the index-5 DAEs governing the servo-constraint problem of cranes. It was demonstrated that the present approach is applicable to alternative problem formulations relying on either redundant or minimal coordinates. The use of redundant coordinates proved to be especially beneficial to the newly proposed index reduction procedure. They lead to a striking simplicity of the minimally extended index-3 formulation. On the other hand, minimal coordinates can be also applied. They may either be used from the outset or introduced after the minimal extension procedure has been applied. The connection between the alternative descriptions is well illustrated with the commutative diagram in Fig. 1.

The minimally extended index-3 DAEs formulated in terms of either redundant or minimal coordinates were directly discretized by means of the Euler backward scheme. The newly developed time-stepping schemes can be viewed as an alternative to the schemes previously proposed by Blajer and Kołodziejczyk [6, 9]. Their schemes rely on a direct discretization of the index-3 DAEs that emanate from a specific projection method applied to the underlying index-5 system. In contrast to the projection method, the minimal extension approach advocated in the present work does not require the introduction of projection matrices. The numerical investigations documented in Sects. 6 and 7 indicate that the present method is clearly competitive.

We further demonstrated that a second application of the minimal extension approach makes possible the ultimate reduction to index one. In this connection we focused on inverse dynamics problems whose index-1 DAEs assume the form of purely algebraic equations. As was shown in Sect. 3.3.1, this situation arises for the specific case $n-a = a$. The purely algebraic system of equations can be used to determine the complete solution to the inverse dynamics problem in terms of the control outputs and time derivatives thereof up to and including fourth order. This result confirms the well-known fact that cranes often belong to the class of differentially flat systems (see [15] and the references therein).

Although the detailed investigations of the index reduction method presented herein are confined to mechanical models belonging to a specific class of cranes, the proposed methodology can be also applied to the broad diversity of underactuated mechanical systems. For example, in some applications the underlying DAEs of the servo-constraint problem may have index greater than five; in others the system might be nonflat and exhibit internal dynamics (see the recent papers [5, 10, 20] for investigations in this direction).