1 Introduction

There are a variety of important and diverse applications for generalized thermoelasticity in recent years, which have caught the attention of many researchers. The fabrication of microchips, as well as many mechanical structures, require elastic thin plates. Size-based continuum mechanics theories are becoming increasingly important with the development of micro- and nanotechnology. There is no doubt that every profession needs to be modified at some point. Therefore, significant and advantageous characteristics and processes can always be improved, as well as mechanical and production processes. A large number of existing models of physical procedures have been changed using fractional calculus over the past several decades, and its applications are employed in many fields including physics, continuum mechanics, and biology. Conversely, when it comes to fractional differential operators, they are not local. Therefore, the current and previous states of the system are used to revise its state.

The Kirchhoff–Love model (Love 1888) of plate deformation and stress in two dimensions is used to investigate how moments and forces influence thin plates. Kirchhoff’s theory is based on Euler–Bernoulli beams and has the following kinematic considerations: (i) during deformation, the thickness of the plate (\(h\)) remains constant and is small in comparison to its lateral dimensions; (ii) the central plane of the plate does not exhibit any inplane deformation and remains normal after bending or deforming; (iii) the midsurface displacement’s component amounts are negligible in comparison to the plate thickness; (iv) normal stress, shear deformation, and strain in the transverse direction can be disregarded. Modern alternatives to fractional-order derivatives are MDDs. Temporal remodeling can be better achieved with MDDs than with FODs. There is a greater demonstration of the memory effect in this case. To explain the memory effect in thermoelasticity, a better MDD model of thermoelasticity was introduced. “MDD is defined in an integral form of a common derivative with a kernel function on a slip-in interval”. Recently, to define the memory dependence, Yu et al. (2014) improved Lord–Shulman (LS) theory by introducing MDD into the rate of heat flux in generalized thermoelasticity theory as \(\left ( 1+\chi D_{\chi} \right ) q_{i} =- K_{ij} T_{,i}\), (\(0<\chi \leq 1 \)) .

The higher-order Taylor’s series expansion of Fourier’s law that incorporates MDD and kernel functions is presented by Abouelregal et al. (2021a). Abouelregal et al. (2021b) used MD derivatives to develop a new generalized mathematical thermoelastic model consisting of various phase delays and a high-order heat-transfer law. A memory-dependent heat-conduction model with dual phase lags was derived using the modified fractional derivative of Caputo and the higher-order MDD by Abouelregal (2022). Ezzat et al. (2014, 2015, 2016, 2017) discussed the MDD-LS model of generalized thermoelasticity and this was used to solve a few one-dimensional problems. Utilizing the MDD with two temperatures with the modified GN heat-conduction equation, Kaur and Singh (2023) analyzed the fluctuations in a transversely isotropic thick circular plate subjected to ring loading. With the aid of a transversely isotropic, homogeneous plate containing ring loads and two hyperbolic temperatures, Kaur and Singh (2021a) explored fluctuations in fractional-order strain. Kaur and Singh (2021b) investigated the thermoelastic damping in a Kirchhoff–Love plate. Kaur et al. (2020) investigated forced flexural vibrations in a transversely isotropic thermoelastic thin rectangular plate (TRP) using a Kirchhoff–Love plate.

A general model based on Hamilton’s principle was developed by El Kadiri et al. (2002) to describe nonlinear free vibrations of rectangular, homogeneous and composite plates and fully clamped beams at large displacement amplitudes. A nonlinear mechanics theory for shells and plates was developed by Amabili (2008). The vibrations of rectangular plates generated by harmonically excited vibrations of large amplitudes were studied by Amabili (2006). Hamilton’s principle and spectral analysis were used by Beidouri et al. (2006) for the geometric analysis of nonlinear vibrations in thin structures. In a recent study, Majid et al. (2021) examined the impacts of force transverse vibrations on accurately shaped rectangular plates supported by clamped, simply clamped, and simple clamps subjected to significant amplitudes. Other researchers also developed various theories of thermoelasticity, such as Kaur et al. (2020, 2021, 2020), Alzahrani et al. (2020), Trivedi et al. (2022), Sur and Kanoria (2018), Lata et al. (2020), Gupta et al. (2022), Marin et al. (2013), and Kaur and Singh (2021, 2022).

The present investigation focuses on a higher-order memory-dependent derivative (MDD) effect on forced flexural vibrations due to time-harmonic concentrated loads in a TRP. With the DFFT technique, expressions for lateral deflection, thermoelastic damping, temperature distribution, frequency shift, and thermal moment, have been found in the transformed domain for simply supported (SS) TRP. We have demonstrated the effectiveness of the higher-order MDD kernel function on the resultant quantities.

2 Basic equations

2.1 Constitutive equations

A linear elastic solid has the following motion equation according to Kirchhoff (1888):

$$ t_{ij,j} + f_{i} = \rho \ddot{u}_{i}, $$
(1)
$$\begin{aligned} & t_{ij} = c_{ijkl} e_{kl} - \beta _{ij} T, \end{aligned}$$
(2)
$$\begin{aligned} & e_{ij} = \frac{1}{2} \left ( u_{i,j} + u_{j,i} \right ),\quad i,j=1,2,3, \end{aligned}$$
(3)
$$\begin{aligned} & \beta _{ij} =c_{ijkl} \alpha _{kl}, \end{aligned}$$
(4)

where \(c_{ijkl} ( c_{ijkl} = c_{klij} = c_{jikl} = c_{ijlk} )\) are elastic parameters, \(\beta _{ij} = \beta _{i} \delta _{ij}\), \(K_{ij} = K_{i} \delta _{ij}\), \(K_{ij}^{*} = K_{i}^{*} \delta _{ij} \), \(i\) is not summed,

2.2 Heat-conduction equation

Using Green and Naghdi (1992) and Bachher (2019), the constitutive equation for ATM with GN-III theory with higher-order memory-dependent derivatives is:

$$ K_{ij}^{*} T_{,ij} + K_{ij} \dot{T}_{,ij} = \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} D_{\chi}^{r} \right ) \left ( \beta _{ij} T_{0} \ddot{e}_{ij} + \rho C_{E} \ddot{T} \right ), $$
(5)

where the rth-order MDD for a differentiable function \(f(t)\) with delay \(\chi > 0\) for a fixed time \(t\) presented by Wang and Li (2011) is:

$$ D_{\chi}^{r} f \left ( t \right ) = \frac{1}{\chi} \int _{t-\chi}^{t} K \left ( t-\xi \right ) f^{r} \left ( \xi \right ) d\xi . $$
(6)

The \(K(t-\xi )\) and \(\chi \) is determined from the material properties. From Ezzat et al. (2014, 2015, 2016) the following kernel function \(K(t - \xi )\) is used

$$ K \left ( t-\xi \right ) =1- \frac{2\beta}{\chi} \left ( t-\xi \right ) + \frac{\alpha ^{2}}{\chi ^{2}} \left ( t-\xi \right )^{2} = \left \{ \textstyle\begin{array}{l} 1\\ 1+ {\left ( \xi -t \right )} / {\chi} \\ \xi -t+1\\ \left [ 1+ {\left ( \xi -t \right )} / {\chi} \right ]^{2} \end{array}\displaystyle \right . \textstyle\begin{array}{c} \alpha =0,\beta =0,\\ \alpha =0,\beta =1/2,\\ \alpha =0,\beta =\chi /2,\\ \alpha =1,\beta =1, \end{array} $$
(7)

where \(\alpha \) and \(\beta \) are constants. Additionally, the comma indicates the derivative w. r. t. the space variable and the dot superimposed on it signifies the time derivative.

3 Method and formulation of the problem

3.1 Formulation

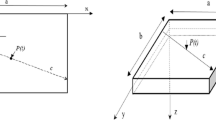
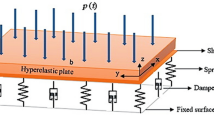
Consider a homogeneous, transversely isotropic thermoelastic thin rectangular plate TRP (Fig. 1) with Cartesian axes \((x,y,z)\) having length \(a\) (\(0\leq x\leq a\)), width \(b\) (\(- \frac{b}{2} \leq y\leq \frac{b}{2} \)) and thickness \(h\) (\(- \frac{h}{2} \leq z\leq \frac{h}{2} \)). A right-handed set is formed by placing the midsurface of the TRP in the \(x\)–\(y\) plane and the \(z\)-axis toward the thickness direction. The origin is chosen to be at one corner of the center surface of the plate in the chosen coordinate system, as shown in Fig. 1.

Fig. 1
figure 1

Schematic design of the TRP

Full size image

The Kirchhoff–Love plate theory is consistent with the deformation of the TRP. Rao (2007) provides the displacement components for a minor deflection of a straightforward bending problem using the fundamental classical theory of a thin plate.

$$ u_{1} \left ( x,y,z,t \right ) = -z \frac{\partial w}{\partial x}, u_{2} \left ( x,y,z,t \right ) = -z \frac{\partial w}{\partial y}, u_{3} \left ( x,y,z,t \right ) = w \left ( x,y,t \right ). $$
(8)

The TRP’s normal and shear strain components are

$$\begin{aligned} & e_{xx} = -z \frac{\partial ^{2} w}{\partial x^{2}}, \end{aligned}$$
(9)
$$\begin{aligned} & e_{yy} =-z \frac{\partial ^{2} w}{\partial y^{2}}, \end{aligned}$$
(10)
$$\begin{aligned} & e_{xy} =-2z \frac{\partial ^{2} w}{\partial x\partial y}, \end{aligned}$$
(11)
$$\begin{aligned} & e_{zz} = e_{yz} = e_{xz} =0. \end{aligned}$$
(12)

According to Eringen theory, with the use of equation (8), the constitutive equation derived from equation (2) becomes

$$\begin{aligned} & t_{xx} = c_{11} \left ( -z \frac{\partial ^{2} w}{\partial x^{2}} \right ) + c_{12} \left ( -z \frac{\partial ^{2} w}{\partial y^{2}} \right ) - \beta _{1} T, \end{aligned}$$
(13)
$$\begin{aligned} & t_{yy} = c_{12} \left ( -z \frac{\partial ^{2} w}{\partial x^{2}} \right ) + c_{11} \left ( -z \frac{\partial ^{2} w}{\partial y^{2}} \right ) - \beta _{1} T, \end{aligned}$$
(14)
$$\begin{aligned} & t_{xy} = \left ( c_{11} - c_{12} \right ) \frac{1}{2} \left ( -2z \frac{\partial ^{2} w}{\partial x\partial y} \right ), \end{aligned}$$
(15)
$$\begin{aligned} & t_{yz} = t_{xz} =0, \end{aligned}$$
(16)

where \(\beta _{1} =\ (c_{11} + c_{13} ) \alpha _{1} + C_{13} \alpha _{3} \).

As per Rao (2007), the \(M_{xx}\), \(M_{yy}\), and \(M_{xy}\) are given by

$$\begin{aligned} & M_{xx} \left ( x,y,t \right ) = \int _{\frac{-h}{2}}^{\frac{h}{2}} t_{xx} zdz, \end{aligned}$$
(17)
$$\begin{aligned} & M_{yy} \left ( x,y,t \right ) = \int _{\frac{-h}{2}}^{\frac{h}{2}} t_{yy} zdz, \end{aligned}$$
(18)
$$\begin{aligned} & M_{xy} \left ( x,y,t \right ) = \int _{\frac{-h}{2}}^{\frac{h}{2}} t_{xy} zdz. \end{aligned}$$
(19)

After multiplication of (13)–(15) by \(z\), integration w.r.t \(z\), and with the help of equations (17)–(19) yields

$$\begin{aligned} & M_{xx} = - c_{11} \left ( I \frac{\partial ^{2} w}{\partial x^{2}} \right ) - c_{12} \left ( I \frac{\partial ^{2} w}{\partial y^{2}} \right ) - M_{T}, \end{aligned}$$
(20)
$$\begin{aligned} & M_{yy} = - c_{12} \left ( I \frac{\partial ^{2} w}{\partial x^{2}} \right ) - c_{11} \left ( I \frac{\partial ^{2} w}{\partial y^{2}} \right ) - M_{T}, \end{aligned}$$
(21)
$$\begin{aligned} & M_{xy} = \left ( c_{11} - c_{12} \right ) \left ( -I \frac{\partial ^{2} w}{\partial x\partial y} \right ), \end{aligned}$$
(22)

where

$$\begin{aligned} & M_{T} \left ( x,y,t \right ) = \beta _{1} \int _{\frac{-h}{2}}^{\frac{h}{2}} Tzdz, \end{aligned}$$
(23)
$$\begin{aligned} &I= \frac{h^{3}}{12}. \end{aligned}$$
(24)

According to Rao (2007), Ventsel and Krauthammer (2002), the transverse equation of motion with forced vibrations of the TRP is written as

$$ \frac{\partial ^{2} M_{xx}}{\partial x^{2}} +2 \frac{\partial ^{2} M_{xy}}{\partial x\partial y} + \frac{\partial ^{2} M_{yy}}{\partial y^{2}} +q \left ( x,y,t \right ) = \rho h \frac{\partial ^{2} w}{\partial t^{2}}. $$
(25)

It is assumed that inside the plate at a point \(\left ( \varepsilon ,\mu \right )\), a time-harmonic concentrated load is applied such that

$$ q \left ( x,y,t \right ) =P \delta _{\varepsilon} \left ( x \right ) \delta _{\mu} \left ( y \right ) e^{i\omega t}, $$

where \(P\) is a constant.

Equation (25) with the help of (20)–(24) becomes

$$ \begin{aligned}[b] &c_{11} I \left ( \frac{\partial ^{4} w}{\partial x^{4}} + \frac{\partial ^{4} w}{\partial y^{4}} +2 \frac{\partial ^{4} w}{\partial x^{2} \partial y^{2}} \right ) + \left ( \frac{\partial ^{2} M_{T}}{\partial x^{2}} + \frac{\partial ^{2} M_{T}}{\partial y^{2}} \right ) +\rho h \frac{\partial ^{2}}{\partial t^{2}} \left ( w \right ) \\ &\quad =-P \delta _{\varepsilon} \left ( x \right ) \delta _{\mu} \left ( y \right ) e^{i\omega t}. \end{aligned} $$
(26)

Therefore, using (8), equation (5) becomes

$$ \begin{aligned}[b] &\left ( K_{1}^{*} + K_{1} \frac{\partial}{\partial t} \right ) \left ( \frac{\partial ^{2} T}{\partial x^{2}} + \frac{\partial ^{2} T}{\partial y^{2}} \right ) + \left ( K_{3}^{*} + K_{3} \frac{\partial}{\partial t} \right ) \frac{\partial ^{2} T}{\partial z^{2}} \\ &\quad = \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} D_{\chi}^{r} \right ) \left ( \beta _{1} T_{0} \frac{\partial ^{2}}{\partial t^{2}} \left ( -2z \left ( \frac{\partial ^{2} w}{\partial x^{2}} + \frac{\partial ^{2} w}{\partial y^{2}} \right ) \right ) +\rho C_{E} \ddot{T} \right ). \end{aligned} $$
(27)

The following dimensionless quantities (DQ) are presented in order to simplify the solution:

$$ \begin{aligned} x ' &= \frac{x}{L}, t_{xx} ' = \frac{t_{xx}}{c_{11}}, y ' = \frac{y}{L}, t ' = \frac{c_{1} t}{L}, z ' = \frac{z}{L}, w ' = \frac{w}{L},\\ M_{T} ' &= \frac{M_{T}}{T_{0} Ah}, T ' = \frac{T}{T_{0}}, c_{11} = \rho c_{1}^{2}. \end{aligned} $$
(28)

Using DQ as in equation (28) in equations (26) and (27), and then suppressing primes yields

$$\begin{aligned} & \left [ \nabla ^{4} + \delta _{1} \frac{\partial ^{2}}{\partial t^{2}} \right ] w + \delta _{2} \nabla ^{2} M_{T} =-P \delta _{\varepsilon} \left ( x \right ) \delta _{\mu} \left ( y \right ) e^{i\omega t}, \end{aligned}$$
(29)
$$\begin{aligned} & \left ( K_{1}^{*} + K_{1} \frac{c_{1}}{L} \frac{\partial}{\partial t} \right ) \nabla ^{2} T+ \left ( K_{3}^{*} + K_{3} \frac{c_{1}}{L} \frac{\partial}{\partial t} \right ) \frac{\partial ^{2} T}{\partial z^{2}} \\ &\quad = \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} D_{\chi}^{r} \right ) \left ( \delta _{3} \frac{\partial ^{2}}{\partial t^{2}} \left ( -2z \nabla ^{2} w \right ) + \delta _{4} \ddot{T} \right ), \end{aligned}$$
(30)

where

$$ \delta _{1} = \frac{12 L^{2}}{h^{2}} ,\delta _{2} = \frac{T_{0} L}{h c_{11}}, \delta _{3} = c_{1}^{2} \beta _{1}^{2},\delta _{4} =\rho C_{E} c_{1}^{2}. $$

To find the solution to the problem, we can express the time-harmonic behavior as follows:

$$ \left [ w \left ( x,y,t \right ),T \left ( x,y,z,t \right ) \right ] = \left [ \overline{w} \left ( x,y \right ), \overline{T} \left ( x,y,z \right ) \right ] e^{i\omega t}. $$
(31)

As a result,

$$ M_{T} \left ( x,y,t \right ) = e^{i\omega t} \beta _{1} \int _{\frac{-h}{2}}^{\frac{h}{2}} \overline{T} \left ( x,y,z \right ) zdz = \overline{M}_{T} \left ( x,y,t \right ) e^{i\omega t}. $$
(32)

Using equation (31) in (29) and (30) we have

$$\begin{aligned} & \left [ \nabla ^{4} - \delta _{1} \omega ^{2} \right ] \overline{w} + \delta _{2} \nabla ^{2} \overline{M}_{T} =-P \delta _{\varepsilon} \left ( x \right ) \delta _{\mu} \left ( y \right ), \end{aligned}$$
(33)
$$\begin{aligned} & \left [ \left ( K_{1}^{*} + K_{1} \frac{c_{1}}{L} i\omega \right ) \nabla ^{2} + \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} G^{r} \right ) \delta _{4} \omega ^{2} \right ] \overline{T} + \left ( K_{3}^{*} + K_{3} \frac{c_{1}}{L} i\omega \right ) \frac{\partial ^{2} \overline{T}}{\partial z^{2}} \\ &\quad {}-2z \delta _{3} \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} G^{r} \right ) \omega ^{2} \nabla ^{2} \overline{w} = 0, \end{aligned}$$
(34)

where \(\mathrm{G}^{r} = \left ( i\omega \right )^{r-1} \left [ \left ( 1- \mathrm{e}^{-\mathrm{i}\omega \chi} \right ) \left ( 1- \frac{2\beta}{\chi \mathrm{i}\omega} - \frac{2\alpha ^{2}}{\chi ^{2} \omega ^{2}} \right ) - \left ( \alpha ^{2} -2\beta + \frac{2 \alpha ^{2}}{\chi \mathrm{i}\omega} \right ) \mathrm{e}^{-\mathrm{i}\omega \chi} \right ]\).

3.2 Thermal field in the thickness direction

It can be assumed that the TRP’s thermal gradient along the x and y directions is very small as compared to its thickness,

$$ \left ( \frac{\partial ^{2}}{\partial x^{2}} + \frac{\partial ^{2}}{\partial y^{2}} \right ) \overline{T} \ll \frac{\partial ^{2} \overline{T}}{\partial z^{2}}. $$
(35)

As a result,

$$ \frac{\partial ^{2} \overline{T}}{\partial z^{2}} + p^{2} \overline{T} = \delta _{5} \mathrm{z}\nabla ^{2} \overline{w}, $$
(36)

where

$$p=\omega \sqrt{\frac{\left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} G^{r} \right ) \rho C_{E} c_{1}^{2}}{\left ( K_{3}^{*} + K_{3} \frac{c_{1}}{L} i\omega \right )}},\ \delta _{5} = \ \frac{2 \delta _{3} \left ( 1+ \sum _{r=1}^{N} \frac{\chi ^{r}}{r!} G^{r} \right ) \ \omega ^{2}}{\left ( K_{3}^{*} + K_{3} \frac{c_{1}}{L} i\omega \right )} . $$

In our scenario, it is assumed that no heat flows between the upper and lower surfaces of the TRP

$$ \frac{\partial \overline{T}}{\partial z} =0\ at\ z=\pm \frac{h}{2}. $$
(37)

As a result, the temperature distribution is given by

$$ \overline{T} = \frac{2 \beta _{1}^{2}}{\rho C_{E}} \left ( z- \frac{\sin pz}{p \cos \frac{ph}{2}} \right ) \nabla ^{2} \overline{w}. $$
(38)

Using (38) in (23) yields

$$ \overline{M}_{T} = \frac{\beta _{1}^{3} h^{3}}{6\rho C_{E}} \left ( 1+f \left ( p \right ) \right ) \nabla ^{2} \overline{w}, $$
(39)

where

$$ f \left ( p \right ) = \frac{24}{p^{3} h^{3}} \left ( \frac{ph}{2} - \tan \frac{ph}{2} \right ). $$

Now, applying equation (39) to equation (33) yields

$$\begin{aligned} & \nabla ^{4} \overline{w} - \eta ^{4} \overline{w} = \epsilon _{2}, \end{aligned}$$
(40)
$$\begin{aligned} & \text{where}\ \eta ^{4} = \frac{ \delta _{1} \omega ^{2}}{\left ( 1+ \epsilon _{1} \left ( 1+f \left ( p \right ) \right ) \right )}, \epsilon _{1} = \delta _{2} \frac{\beta _{1} h^{3}}{12\rho C_{E}}, \epsilon _{2} = \frac{-P \delta _{\varepsilon} \left ( x \right ) \delta _{\mu} \left ( y \right )}{\left ( 1+ \epsilon _{1} \left ( 1+f \left ( p \right ) \right ) \right )}. \end{aligned}$$
(41)

3.3 Initial conditions

The initial conditions for an undeformed and homogeneous plate, at a uniform temperature \(T_{0}\) and without rotation are considered as follows:

$$ \left . w \left ( x,y,t \right ) \right \vert _{t=0} = \left . \frac{\partial w \left ( x,y,t \right )}{\partial t} \right \vert _{t=0} =0, \left . \mathrm{T} \left ( x,y,t \right ) \right \vert _{t=0} = \left . \frac{\partial \mathrm{T} \left ( x,y,z,t \right )}{\partial t} \right \vert _{t=0} =0. $$
(42)

3.4 Mechanical boundary conditions

It is considered that the TRP ends are simply supported. Therefore, for simply supported edges \(x = 0,a\), \(y=0, b\), the bending moment and deflection must be zero

$$\begin{aligned} & \left . w \left ( x,y,t \right ) \right \vert _{x=0,a} = \left . M_{xx} \right \vert _{x=0,a} =0, \left . w \left ( x,y,t \right ) \right \vert _{y=0,b} = \left . M_{yy} \right \vert _{y=0,b} =0, \\ &\left . M_{T} (x,y,t) \right \vert _{x=0,a,y=0,b} =0, \end{aligned}$$
(43)
$$\begin{aligned} & \left . M_{xx} \right \vert _{x=0,a} = \left [ - c_{11} \left ( I \frac{\partial ^{2} w}{\partial x^{2}} \right ) - c_{12} \left ( I \frac{\partial ^{2} w}{\partial y^{2}} \right ) - M_{T} \right ]_{x=0,a} =0. \end{aligned}$$
(44)

Subsequently \(w \left ( x,y,t \right ) =0 \) along the edge \(x\ =0,\ a\), all the derivatives of \(w\ \mathrm{w}.\mathrm{r}.\mathrm{t}. \ y\) are also zero. Therefore,

$$ \left . \frac{\partial w \left ( x,y,t \right )}{\partial y} \right \vert _{x=0,a} =0, \left . \frac{\partial ^{2} w \left ( x,y,t \right )}{\partial y^{2}} \right \vert _{x=0,a} =0. $$
(45)

If we use (45) in \(\left . M_{xx} \right \vert _{x=0,a} =0\) it yields

$$ \left . \frac{\partial ^{2} w}{\partial x^{2}} \right \vert _{x=0,a} =0. $$
(46)

Likewise, \(\left . M_{yy} \right \vert _{y=0,b} =0\) infers

$$ \left . \frac{\partial ^{2} w}{\partial y^{2}} \right \vert _{y=0,b} =0. $$
(47)

3.5 Solution of vibration

As per Debnath and Bhatta (2007) “the double finite Fourier sine transform (DFFST) of a function F on a domain over a rectangular region \(0\leq x\leq a\), \(0\leq y\leq b\) as a function of \(f_{s} \):

$$ D F_{is} \left ( f \left ( x,y \right ) \right ) = f_{s} \left ( m,n \right ) = \int _{0}^{a} \int _{0}^{b} F \left ( x,y \right ) sin \left ( \frac{m\pi x}{a} \right ) sin \left ( \frac{n\pi y}{b} \right ) dydx. $$
(48)

The inverse double Fourier sine transform of a function \(f_{s}\) will be:

$$ D F_{is}^{-1} \left ( f_{s} \left ( m,n \right ) \right ) = f \left ( x,y \right ) = \left ( \frac{4}{ab} \right ) \sum _{m=1}^{\infty} \sum _{n=1}^{\infty} f_{s} \left ( m,n \right ) sin \left ( \frac{m\pi x}{a} \right ) sin \left ( \frac{n\pi y}{b} \right ). $$
(49)

Theorem 1: If a function F vanishes on the boundary of the rectangular region \(0\leq x\leq a\), \(0\leq y\leq b\) then:

$$ D F_{is} \left ( \frac{\partial ^{2} F \left ( x,y \right )}{\partial x^{2}} + \frac{\partial ^{2} F \left ( x,y \right )}{\partial y^{2}} \right ) = - \pi ^{2} \left ( \frac{m^{2}}{a^{2}} + \frac{n^{2}}{b^{2}} \right ) f_{s} \left ( m,n \right ). $$
(50)

With the help of Pasquel (2019) and Al-Khaled (2018) equation (46) can be solved using a DFFST in the \(x\) and \(y\) directions defined by equations (52) and (53) as

$$ \overline{w} \left ( x,y \right ) = \left ( \frac{4}{ab} \right ) \sum _{m=1}^{\infty} \sum _{n=1}^{\infty} \overline{w}_{s} \left ( m,n \right ) \sin \left ( \frac{m\pi}{a} x \right ) \sin \left ( \frac{n\pi}{b} y \right ), $$
(51)

where \(m\) is the wavenumber along \(x\) and \(n\) along \(y\) directions.

Equation (42) with the help of equation (55) yields the value of \(\overline{w}_{s} \left ( m,n \right )\) as

$$ \overline{w}_{s} \left ( m,n \right ) = \frac{-P \sin \left ( \frac{m\pi \varepsilon}{a} \right ) \sin \left ( \frac{n\pi \mu}{b} \right )}{\delta _{6}}, $$
(52)

where \(\delta _{6} = \left ( 1+ \epsilon _{1} \left ( 1+f \left ( p \right ) \right ) \right ) \left \{ \left ( \frac{m^{2} \pi ^{2}}{a^{2}} + \frac{n^{2} \pi ^{2}}{b^{2}} \right )^{2} - \eta ^{4} \right \} \).

As a result, the expression for the TRP’s lateral deflection, temperature distribution, and the thermal moment is given by

$$\begin{aligned} & w \left ( x,y,t \right ) = \left ( \frac{4}{ab} \right ) \sum _{m=1,n=1}^{\infty} \overline{w}_{s} \left ( m,n \right ) \sin \left ( \frac{m\pi}{a} x \right ) \sin \left ( \frac{n\pi}{b} y \right ) e^{i \omega _{mn} t}, \end{aligned}$$
(53)
$$\begin{aligned} & \begin{aligned}[b] T \left ( x,y,z,t \right ) &=- \frac{\beta _{1}^{2}}{\rho C_{E}} \left ( \frac{8}{ab} \right ) \left ( z- \frac{\sin pz}{p \cos \frac{ph}{2}} \right ) \sum _{m=1,n=1}^{\infty} \left ( \frac{m^{2} \pi ^{2}}{a^{2}} + \frac{n^{2} \pi ^{2}}{b^{2}} \right )\\ &\quad {}\times \overline{w}_{s} \left ( m,n \right ) \sin \left ( \frac{m\pi}{a} x \right ) \sin \left ( \frac{n\pi}{b} y \right ) e^{i \omega _{mn} t}, \end{aligned} \end{aligned}$$
(54)
$$\begin{aligned} & \begin{aligned}[b] M_{T} \left ( x,y,t \right ) &= \frac{\beta _{1}^{3} h^{3}}{3\rho C_{E}} \left ( \frac{2}{ab} \right ) \left ( 1+f \left ( \omega \right ) \right ) \sum _{m=1,n=1}^{\infty} \left ( \frac{m^{2} \pi ^{2}}{a^{2}} + \frac{n^{2} \pi ^{2}}{b^{2}} \right )\\ &\quad {}\times \overline{w}_{s} \left ( m,n \right ) \sin \left ( \frac{m\pi}{a} x \right ) \sin \left ( \frac{n\pi}{b} y \right ) e^{i \omega _{mn} t}. \end{aligned} \end{aligned}$$
(55)

3.6 Resonance conditions

Equation (41) provides the harmonic vibration frequency \(\omega _{mn}\) of a Kirchhoff TRP as

$$ \omega _{mn} = \omega _{0} \left [ 1+ \frac{\epsilon _{1}}{2} \left ( 1+f \left ( p_{0} \right ) \right ) \right ], $$
(56)
$$ \begin{aligned} \text{where }&\epsilon _{1} \ll 1, \omega _{0} = \frac{h}{2 \sqrt{3} L} \left ( \frac{m^{2} \pi ^{2}}{a^{2}} + \frac{n^{2} \pi ^{2}}{b^{2}} \right ), p_{0} = \omega _{0} \sqrt{\frac{\left ( 1+ G^{r} \right ) \rho C_{E} c_{1}^{2}}{\left ( K_{3}^{*} + K_{3} \frac{c_{1}}{L} i \omega _{0} \right )}},\\ &n,m=1,2,3,4,\dots . \end{aligned} $$
(57)

The expression of thermoelastic damping is written as

$$ Q^{-1} =2 \left \vert \frac{\omega _{mn}^{I}}{\omega _{mn}^{R}} \right \vert , $$
(58)

where \(\omega _{mn}^{R}\) and \(\omega _{mn}^{I}\) are the real and imaginary parts of frequency \(\omega _{mn}\). The frequency shift because of thermal variations is written as:

$$ \omega _{S} = \left \vert \frac{\omega _{mn}^{R} - \omega _{0}}{\omega _{0}} \right \vert . $$
(59)

4 Numerical results and discussion

To show our theoretical results and the effect of MDD, physical data of copper material is taken from Dhaliwal and Singh (1980) for numerical calculation

$$ \mathrm{c}_{11} =3.07\times 10^{11}\ \mathrm{N}\, \mathrm{m}^{-2},\qquad \mathrm{c}_{12} =1.650\times 10^{11}\ \mathrm{N}\, \mathrm{m}^{-2}, $$
$$ \mathrm{c}_{13} =1.027\times 10^{10}\ \mathrm{N}\, \mathrm{m}^{-2},\qquad \mathrm{c}_{33} =3.581\times 10^{11}\ \mathrm{N}\, \mathrm{m}^{-2}, $$
$$ \mathrm{c}_{44} =1.510\times 10^{11}\ \mathrm{N}\, \mathrm{m}^{-2},\qquad \mathrm{C}_{\mathrm{E}} =4.27\times 10^{2}\ \mathrm{j}\, \mathrm{k} \mathrm{g}^{-1}\, \mathrm{K}^{-1}, $$
$$ \beta _{1} =7.04\times 10^{6}\ \mathrm{N}\, \mathrm{m}^{-2}\, \mathrm{K}^{-1},\qquad \beta _{3} =6.90\times 10^{6}\ \mathrm{N}\, \mathrm{m}^{-2}\, \mathrm{K}^{-1}, $$
$$ \mathrm{K}_{1} =0.690\times 10^{2}\ \mathrm{W}\, \mathrm{m}^{-1} \,\mathrm{K}^{-1},\qquad \mathrm{K}_{3} =0.690\times 10^{2}\ \mathrm{W}\, \mathrm{m}^{-1}\, \mathrm{K}^{-1}, $$
$$ \mathrm{K}_{1}^{*} =0.02\times 10^{2}\ \mathrm{N}\, \mathrm{s}^{-2}\, \mathrm{K}^{-1},\qquad \mathrm{K}_{3}^{*} =0.04\times 10^{2}\ \mathrm{N}\, \mathrm{s}^{-2} \, \mathrm{deg}^{-1}, $$
$$ \frac{\mathrm{L}}{\mathrm{h}} =10, \frac{\mathrm{b}}{\mathrm{h}} =0.5,\qquad \rho =8.836\times 10^{3}\ \mathrm{k} \mathrm{g}\, \mathrm{m}^{-3}. $$

Figures 2(a and b) demonstrate the deviation in the dimensionless lateral deflection \(w\) w.r.t length and breadth of the thin plate with different mode numbers (\(n=1\), \(m=1\)) and mode numbers (\(n=2\), \(m=2\)) and the MDD kernel function value \(\left [ 1+ \frac{\left ( \xi -t \right )}{\chi} \right ]^{2}\) when \(\alpha =1\), \(\beta =1\), respectively. It is observed in Fig. 2(a) that at the boundary of the plate the deflection in the lateral direction is zero and we have the maximum deflection at the center of the plate. Moreover, as the value of the mode number increases, as shown in Fig. 2(b), there is a corresponding change in the lateral deflection. At the boundary of the plate the deflection is zero, hence, it satisfies the boundary condition.

Fig. 2
figure 2

(a and b). Deviation of Dimensionless Lateral Deflection \(w \) with MDD

Full size image

Figures 3(a and b) show the deviation of dimensionless thermal moment \(M_{T}\) w.r.t length and breadth of the thin plate with different mode numbers (\(n=1\), \(m=1\)) and mode numbers (\(n=2\), \(m=2\)) and the MDD kernel function value \(\left [ 1+ \frac{\left ( \xi -t \right )}{\chi} \right ]^{2}\) when \(\alpha =1\), \(\beta =1\), respectively. It is observed in Fig. 3(a) that at the boundary of the plate the thermal moment is zero and we have the maximum variation at the center of the plate. The variation in the thermal moment shows the opposite behavior from the lateral deflection. Moreover, as the value of the mode number increases, as shown in Fig. 3(b), there is a corresponding change in the thermal moment. At the boundary of the plate the thermal moment is zero, hence, it satisfies the boundary condition.

Fig. 3
figure 3

(a and b). Deviation of Dimensionless Thermal Moment \(M_{T}\) with the length of the thin plate

Full size image

Figures 4(a and b) display the deviation of the dimensionless temperature distribution w.r.t length and breadth of the thin plate with different mode numbers (\(n=1\), \(m=1\)) and mode numbers (\(n=2\), \(m=2\)), and the MDD kernel function value \(\left [ 1+ \frac{\left ( \xi -t \right )}{\chi} \right ]^{2}\) when \(\alpha =1\), \(\beta =1\), respectively. It is observed in Fig. 4(a) that at the boundary of the plate the temperature distribution is zero and we have the maximum variation at the center of the plate. The variation in the temperature distribution shows the opposite behavior from the lateral deflection. Moreover, as the value of the mode number increases, as shown in Fig. 3(b), there is a corresponding change in the temperature distribution. At the boundary of the plate the temperature distribution is zero, hence, it satisfies the boundary condition.

Fig. 4
figure 4

(a and b). Deviation of Dimensionless Temperature Distribution with MDD

Full size image

Figure 5 displays the variation in dimensionless thermoelastic damping with the change in the values of \(\alpha \ \text{and} \ \beta \) the parameters of the kernel function of the MDD with mode numbers (\(n=2\), \(m=2\)). The curves clearly illustrate that the kernel function influences the thermoelastic damping. Without the MDD, the thermoelastic damping is sharply decreased, whereas, it is different in the case with the higher-order parameter of the MDD. As the value of the higher-order parameter of the MDD increases, there is shift in the peak of the thermoelastic damping.

Fig. 5
figure 5

Variation of dimensionless thermoelastic damping

Full size image

Figure 6 displays the variation in the dimensionless frequency shift with the change in the values of \(\alpha \ \text{and} \ \beta \) the parameters of the kernel function of the MDD with mode numbers (\(n=2\), \(m=2\)). The curves clearly illustrate that the kernel function influences the frequency shift. Without the MDD, the thermoelastic damping is sharply decreased, whereas it is different in the case with the higher-order parameter of the MDD. As the value of the higher-order parameter of the MDD increases, there is a shift in the graphs of the frequency shift.

Fig. 6
figure 6

Variation of dimensionless Frequency Shift

Full size image

5 Conclusions

The purpose of this study was to discuss higher-order memory-dependent derivatives with a delay-time parameter. Based on Taylor-series expansions to Fourier’s law for higher-order MDD, a thermomechanical model is proposed for predicting the thermomechanical response of a rectangular transversely isotropic thermoelastic plate under a concentrated time-harmonic load. This model can be used to obtain different cases for many thermoelasticity models with and without memory dependence. The study and discussion were conducted on solutions based on a higher-order MDD kernel function. Based on the results obtained, the following conclusions can be drawn:

  • A thin plate closed-form mathematical model is developed with Kirchhoff–Love plate theory and MDD. This study not only considered the size effect but also studied the memory, mechanical, and thermal-field effects.

  • It has been observed that with the usage of higher-order MDD in the heat-conduction equation, the frequency shift and thermoelastic damping is predicted to be low, contrary to the heat-conduction equation without MDD. This infers that the memory-dependent derivatives can reduce damping and frequency shifts and improve MEMS/NEMS quality.

  • The MDD theory is used to study and illustrate lateral deflections, thermal moments, and temperature distributions, and it is seen that the MDDs have a major effect on all the parameters of the thin plate.