1 Introduction

In recent years, polymeric materials and advanced composite materials have been widely used in engineering applications. A linear elastic analysis may give inaccurate results for such materials. Due to the viscoelastic properties of composite materials, demand for utilizing the viscoelastic theory has gained considerable attention. Time-dependent viscoelastic materials express both elastic and viscose properties. In viscoelastic materials, the state of strain depends on the present stress and the stress history (Christensen 1982). Zhang and Cheng (1998) presented a nonlinear mathematical model of simply supported viscoelastic thin plates based on the Karman’s hypotheses of large deflection and the Boltzmann’s law of viscoelastic material in the case of constant Poisson ratio. Kennedy (1998) developed the finite element method for the nonlinear viscoelastic analysis of composite plates and shells. The creep model was represented as an exponential series plus a steady flow terms. Hammerand and Kapania (2000) analyzed the linear viscoelastic composite plates and shells using the finite element method. To evaluate the hereditary integrals, a direct integration scheme was employed. One disadvantage of heredity integral equations is that a large number of time steps are needed. Oliveira and Creus (2000) presented the finite element method for modeling the failure behavior of composite plates and shells in the presence of large displacements and creep. Zenkour (2004) studied the quasi static buckling analysis of fiber reinforced viscoelastic composite rectangular plate with simply supported edges using a unified shear deformable theory and the effective moduli method. Salehi and Safi-Djahanshahi (2010) presented the geometrically nonlinear analysis of viscoelastic rectangular plates subjected to in-plane compression based on the Boltzmann superposition principle and third order shear deformation theory. The static response of inhomogeneous fiber-reinforced viscoelastic sandwich plate was studied by Allam et al. (2010) using the first order shear deformation theory. They utilized the method of effective moduli and Illyushin’s approximation to solve the equations governing the bending response of viscoelastic sandwich plate with simply supported boundary conditions. Jafari et al. (2011, 2014) employed the finite strip method for the stability analysis of composite viscoelastic thick rectangular plates with variable thickness based on the higher order shear deformation theory and the effective moduli method. The linear viscoelastic response of a rectangular plate based on first-order and third-order shear deformation theories was investigated by Nguyen et al. (2012). They determined the compliance and relaxation modulus of viscoelastic behavior by Prony series. Amoushahi and Azhari (2013, 2014) analyzed the thin and moderately thick viscoelastic rectangular plates with different end conditions by expressing the relaxation modulus in terms of Prony series using the finite strip method.

Since the exact solution of plate problems is available only for special simple cases, approximate methods have been introduced to solve different problems of plates. Recently, since the approximation functions of meshfree methods can be built without dividing the plate domain, these methods have grown in popularity to solve the problems of partial differential equations. The static analysis of moderately thick plate using hp cloud method has been studied by Garcia et al. (2000) based on Mindlin’s theory. Due to the lack of Kronecker-delta properties of approximation functions, Lagrange multipliers have been used to impose essential boundary conditions. In the present paper, the hp cloud method is employed for discretization. In this method, a set of arbitrary nodes with no connectivity among them are laid in the domain of the plate. Similar to most meshfree methods, in the hp cloud method the approximation functions lack the Kronecker-delta property and Lagrange multipliers are used to impose the Dirichlet boundary conditions. In the present research, the approximation functions have the Kronecker-delta property and the essential boundary conditions can be enforced directly. So, the hp cloud method used in this study is named “simple hp cloud method.”

A viscoelastic problem can be considered in the time or Laplace domain. To avoid direct time integration, when the accurate Laplace inverse is available, the use of Laplace domain approach is justified due to the much simpler formulation and the improvement of computational efficiency. Therefore, in the present research, time history of critical buckling load of the moderately thick viscoelastic Mindlin’s plates with various shapes is studied by the effective moduli method based on the Laplace–Carson transformation. The organization of this paper is as follows: In Sect. 2, the hp cloud method is introduced briefly and the extraction of equations is described based on the Mindlin theory and the method of effective moduli. In Sect. 3, the numerical results are presented. The time history of critical buckling loads of viscoelastic plates with rectangular, skew, trapezoidal, right-angled triangular, circular, and hexagonal shapes, as well as arbitrarily shaped viscoelastic plates, is considered. Section 4 presents the conclusions.

2 Governing equations

2.1 Simple hp cloud method

In this study, the approximation functions are built by the simple hp cloud method. Suppose that \(\mathbf{Q}_{N}\) is an arbitrary selected set of scattered nodes \(\mathbf{x}_{\alpha }\),

$$ \mathbf{Q}_{N} = \{ \mathbf{x}_{1}, \mathbf{x}_{2}, \dots , \mathbf{x}_{N} \} , \quad \mathbf{x}_{\alpha } \in \varOmega . $$
(1)

Each node \(\mathbf{x}_{\alpha }\) is associated with cloud \(\omega_{\alpha }\), which is centered at \(\mathbf{x}_{\alpha }\) and has radius \(h_{\alpha }\). Defining the function \(r_{\alpha }\) as

$$ r_{\alpha } = \frac{\Vert \mathbf{x} - \mathbf{x}_{\alpha } \Vert }{h _{\alpha }}, $$
(2)

the weight functions \(W_{\alpha }\) in the form of a quartic B-spline can be written as

$$ W_{\alpha } ( \mathbf{x} ) = \left\{ \textstyle\begin{array}{l@{\quad}l} 1-6 r_{\alpha }^{2} +8 r_{\alpha }^{3} -3 r_{\alpha }^{4}, & 0\leq r_{\alpha } \leq 1, \\ 0, & r_{\alpha } >1. \end{array}\displaystyle \right. $$
(3)

To obtain the shape functions of the hp cloud method, two kinds of functions must be determined, namely, partition of unity functions, \(\psi_{\alpha } ( \mathbf{x} ) \), and enrichment functions, \(L_{\alpha i} ( \mathbf{x} )\). Then we have

$$ u^{\mathrm{hp}} ( \mathbf{x} ) = \sum_{\alpha =1}^{N} \sum_{i =1} ^{m_{\alpha }} u_{\alpha i} \bigl( \psi_{\alpha } ( \mathbf{x} ) L_{\alpha i} ( \mathbf{x} )\bigr) $$
(4)

where \(N\) is the number of selected nodes and \(m_{\alpha }\) is the number of terms of enrichment function for node \(\mathbf{x}_{\alpha }\).

In this work, Shepard functions are used to build a partition of unity with low computational cost. Shepard functions are simpler forms of moving least square interpolations (Duarte and Oden 1996a, 1996b; Oden et al. 1998):

$$ \psi_{\alpha } ( \mathbf{x} ) = \mathbf{P} ( \mathbf{x} ) \mathbf{A}^{-1} ( \mathbf{x} ) \mathbf{B}_{\alpha } ( \mathbf{x} ) . $$
(5)

Avoiding the non-economical process of calculating the inverse matrix at every node, by setting \(\mathbf{P} ( \mathbf{x} ) =\{1 \}\), one obtains

$$ \mathrm{A} ( \mathbf{x} ) = \sum_{\beta } W_{\beta } ( \mathbf{x} ) , \qquad \mathrm{B}_{\alpha } ( \mathbf{x} ) = W _{\alpha } ( \mathbf{x} ). $$
(6)

So Shepard functions are calculated as follows:

$$ \psi_{\alpha } ( \mathbf{x} )= \frac{W_{\alpha } ( \mathbf{x} )}{ \sum_{\beta } W_{\beta } ( \mathbf{x} )}. $$
(7)

Enrichment functions are constructed at a very low cost by selecting complete polynomials. Each node may have a different order of polynomial.

So the approximation functions can be written in the matrix form as follows:

$$ \mathbf{N}^{\alpha } = \psi_{\alpha } \mathbf{L}_{\alpha }. $$
(8)

For an arbitrary node \(\mathbf{x}_{\alpha }\), the cloud shape functions of the simple hp cloud method have the property of Kronecker-delta, i.e., \(\mathbf{N}^{\alpha } ( \mathbf{x}_{\beta } )= \delta_{\alpha \beta }\), if the two conditions below hold:

1. Effective radius, \(h_{\alpha }\), is shorter than the distance between the node \(\mathbf{x}_{\alpha }\) and the distributed neighboring nodes on plate mid-surfaces. So Eq. (9) is obtained as

$$ \begin{aligned}[c] & W_{\beta } ( \mathbf{x} = \mathbf{x}_{\gamma } ) =0 \quad \mbox{if }\beta \neq \gamma , \\ & W_{\beta } ( \mathbf{x} = \mathbf{x}_{\gamma } ) =1 \quad \mbox{if } \beta = \gamma , \\ & \sum_{\beta } W _{\beta } ( \mathbf{x} = \mathbf{x}_{\gamma } ) = W_{ \beta } ( \mathbf{x} = \mathbf{x}_{\gamma } ) =1. \end{aligned} $$
(9)

Substituting Eq. (9) into Eq. (7), Eq. (10) is obtained, i.e.,

$$ \begin{aligned}[c] & \psi_{\alpha } ( \mathbf{x} = \mathbf{x}_{\gamma } ) =0 \quad \mbox{if } \alpha \neq \gamma , \\ & \psi_{\alpha } ( \mathbf{x} = \mathbf{x}_{\gamma } ) =1 \quad \mbox{if }\alpha = \gamma . \end{aligned} $$
(10)

Plugging Eqs. (9)–(10) into Eq. (4), Eq. (11) is obtained as

$$ u^{\mathrm{hp}} ( \mathbf{x} = \mathbf{x}_{\boldsymbol{\gamma }} )= \sum _{\alpha =1}^{N} \sum_{i =1}^{m_{\alpha }} u_{\gamma i} \bigl( \psi_{\gamma } ( \mathbf{x} = \mathbf{x}_{\gamma } ) L_{ \gamma i} ( \mathbf{x} = \mathbf{x}_{\gamma } )\bigr)= \sum _{i =1}^{m_{ \alpha }} u_{\gamma i} L_{\gamma i} ( \mathbf{x} = \mathbf{x}_{\gamma } ). $$
(11)

2. The values of the terms of the enrichment functions at \(\mathbf{x} _{\alpha }\) are 1 only for one term, and 0 for the other terms. For imposing condition 2, it is enough to define a complete polynomial (of order 2 for moderately thick plates) in the following form:

$$ \mathbf{L}_{\gamma } ( \mathbf{x} ) = \bigl[ 1 \ x - x_{\gamma } \ y -y_{\gamma } \ ( x - x_{\gamma } ) ^{2} \ ( x - x_{\gamma } ) ( y - y_{\gamma } ) \ ( y - y_{\gamma } ) ^{2} \bigr] . $$
(12)

Plugging Eq. (12) into Eq. (11), Eq. (13) is obtained. Hence the essential boundary conditions of the simple hp cloud method are imposed directly without any additional work. We have

$$ u^{\mathrm{hp}} ( \mathbf{x} = \mathbf{x}_{\gamma } ) = \sum _{i =1} ^{m_{\alpha }} u_{\gamma i} L_{\gamma i} ( \mathbf{x} = \mathbf{x}_{\gamma } ) = u_{\gamma 1}. $$
(13)

Figure 1 shows the distribution of considered nodes on the domain of various shapes of plate to apply the simple hp cloud method.

Fig. 1
figure 1

Distribution of nodes on the domain of plates of various shapes

Full size image

2.2 Mindlin theory

According to the Uflyand–Mindlin’s plate theory (Uflyand 1984), the plate displacement field may be written as

$$ \mathbf{u} ( x, y, z ) = \left \{ \textstyle\begin{array}{c} u ( x, y, z ) \\ v ( x, y, z ) \\ w ( x, y,z ) \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} - z \theta_{x} \\ - z \theta_{y} \\ w ( x, y ) \end{array}\displaystyle \right \} $$
(14)

where \(\theta_{x}\) and \(\theta_{y}\) are the rotations with respect to \(y\)- and \(x\)-axes, respectively, and \(w ( x, y )\) is a transversal displacement of a reference plate.

2.3 Strain–displacement relations

The strain vector of plate can be stated as

$$ \boldsymbol{\varepsilon } = \boldsymbol{\varepsilon }_{L} + \boldsymbol{\varepsilon }_{\mathrm{NL}} $$
(15)

where \(\boldsymbol{\varepsilon }_{L}\) is the linear part and \(\boldsymbol{\varepsilon }_{\mathrm{NL}}\) is the nonlinear part of the strain vector. The linear part of the strain vector in Eq. (15) is given by

$$ \boldsymbol{\varepsilon }_{L} = \langle \varepsilon_{x}\ \varepsilon_{y}\ \gamma_{xy}\ \gamma_{xz}\ \gamma_{yz} \rangle ^{T} = \bigl\langle - z \theta_{x, x}\ {-}z \theta_{y, y}\ {-}z ( \theta_{x, y} + \theta_{y, x} )\ w_{,x} - \theta_{x}\ w_{, y}- \theta_{y} \bigr\rangle ^{T}, $$
(16)

and the nonlinear part is

$$ \boldsymbol{\varepsilon }_{\mathrm{NL}} = \biggl\langle \frac{1}{2} \biggl( \frac{ \partial w}{\partial x} \biggr)^{2} \ \frac{1}{2} \biggl( \frac{\partial w}{\partial y} \biggr)^{2} \ \frac{\partial w}{\partial x} \frac{\partial w}{\partial y} \ 0 \ 0 \biggr\rangle ^{T}. $$
(17)

The bending curvature \(\boldsymbol{\kappa }\), shear curvature \(\boldsymbol{\varGamma }\), and linear part of strain \(\boldsymbol{\varepsilon }_{L}\) are defined as follows:

$$\begin{aligned} \boldsymbol{\kappa } =& \bigl\langle - \theta_{x, x}\ {-}\theta_{y, y}\ {-}( \theta_{x, y} + \theta_{y, x} ) \bigr\rangle ^{T}, \end{aligned}$$
(18)
$$\begin{aligned} \boldsymbol{\varGamma } =& \langle w_{, x} - \theta_{x}\ w_{, y} - \theta_{y} \rangle ^{T}, \end{aligned}$$
(19)

and

$$ \boldsymbol{\varepsilon }_{L} = \left \{ \textstyle\begin{array}{l} - z \boldsymbol{\kappa } \\ \boldsymbol{\varGamma } \end{array}\displaystyle \right \} . $$
(20)

2.4 Viscoelastic material properties

For a viscoelastic material, the relaxation function \(\omega ( t ) \) can be defined by Prony series as follows:

$$ \omega ( t ) = c_{1} + c_{2} e^{- \tau }, \qquad \tau =\frac{t}{t_{s}} $$
(21)

where \(c_{1}\) and \(c_{2}\) are constants, \(\tau \) is a dimensionless parameter, \(t_{s}\) is the relaxation time, and \(t\) is time.

The bulk \(K ( t ) \) and shear \(G ( t ) \) moduli can be expressed by the relaxation function in the time domain as

$$ K ( t ) = K, \qquad G ( t ) = \frac{3}{2} K\omega ( t ) . $$
(22)

On the other hand, Eqs. (23) always hold

$$ K ( t ) = \frac{E(t)}{3(1-2 \nu ( t ) )}, \qquad G ( t ) = \frac{E ( t ) }{2(1+\nu ( t ) )}. $$
(23)

So the viscoelastic modulus \(E(t)\) and Poisson ratio \(\nu ( t ) \) in the time domain can be stated as

$$ E(t) = \frac{9 K\omega ( t ) }{2+ \omega ( t ) }, \qquad \nu ( t ) = \frac{1- \omega ( t ) }{2+ \omega ( t ) } . $$
(24)

2.5 Constitutive equations

The constitutive equation for a linear viscoelastic material in the Laplace–Carson domain (see Appendix) is expressed as follows (Levesque et al. 2007):

$$ \overline{\sigma }_{ij} = \overline{C}_{ijkl} \overline{ \varepsilon } _{kl} $$
(25)

where \(\overline{\sigma }_{ij}\) and \(\overline{\varepsilon }_{kl}\) are the Laplace–Carson of time-dependent stress and strain, respectively, and \(\overline{C}_{ijkl}\) is the effective modulus in the Laplace–Carson domain.

Neglecting the plate normal stress, the constitutive relations for the isotropic viscoelastic material in the Laplace–Carson domain can be written as

$$ \left \{ \textstyle\begin{array}{c} \overline{\boldsymbol{\sigma }}_{b} \\ \overline{\boldsymbol{\sigma }}_{s} \end{array}\displaystyle \right \} = \left [ \textstyle\begin{array}{c@{\quad }c} \overline{\mathbf{C}}_{b} & \mathbf{0} \\ \mathbf{0} & \overline{\mathbf{C}}_{s} \end{array}\displaystyle \right ] \overline{\boldsymbol{\varepsilon }}_{L} $$
(26)

where \(\overline{\boldsymbol{\sigma }}_{b}\) and \(\overline{ \boldsymbol{\sigma }}_{s}\) are the bending and shear stresses in the Laplace–Carson domain, respectively. We have

$$\begin{aligned} \overline{\boldsymbol{\sigma }}_{b} = \left \{ \textstyle\begin{array}{c} \overline{\sigma }_{x} \\ \overline{\sigma }_{y} \\ \overline{\tau }_{xy} \end{array}\displaystyle \right \} , \qquad \overline{\boldsymbol{\sigma }}_{s} = \left \{ \textstyle\begin{array}{c} \overline{\tau }_{xz} \\ \overline{\tau }_{yz} \end{array}\displaystyle \right \} , \qquad \overline{\mathbf{C}}_{b} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \overline{c}_{11} & \overline{c}_{12} & 0 \\ \overline{c}_{12} & \overline{c}_{22} & 0 \\ 0 & 0 & \overline{c}_{44} \end{array}\displaystyle \right ] , \qquad \overline{ \mathbf{C}}_{s} = \left [ \textstyle\begin{array}{c@{\quad }c} \overline{c}_{55} & 0 \\ 0 & \overline{c}_{66} \end{array}\displaystyle \right ]. \end{aligned}$$
(27)

The components of effective modulus tensors can be written as (see Appendix)

$$ \overline{c}_{11} = \overline{c}_{22} = \frac{3 K \overline{\omega } ( 2+ \overline{\omega } ) }{ ( 1+2 \overline{\omega } ) }, \qquad \overline{c}_{12} = \frac{3 K \overline{\omega } ( 1- \overline{ \omega } ) }{ ( 2+ \overline{\omega } ) }, \qquad \overline{c} _{44} =\overline{c}_{55} = \overline{c}_{66}= \frac{3 K \overline{ \omega }}{2} $$
(28)

where \(\overline{\omega }\) is a dimensionless relaxation function in the Laplace–Carson domain.

The plate stress resultants can be expressed as follows:

$$\begin{aligned} \overline{\mathbf{M}} =& \langle \overline{M}_{x}\ \overline{M}\ _{y} \overline{M}_{xy} \rangle ^{T} = \int_{- \frac{h}{2}}^{ \frac{h}{2}} \overline{\boldsymbol{\sigma }}_{b} z\,dz = \overline{ \mathbf{D}}_{b} \overline{ \boldsymbol{\kappa }}, \end{aligned}$$
(29)
$$\begin{aligned} \overline{ \mathbf{Q}} =& \langle \overline{Q}_{x}\ \overline{Q}_{y} \rangle ^{T} = \int_{- \frac{h}{2}}^{\frac{h}{2}} \overline{ \boldsymbol{\sigma }}_{s}\, dz = \alpha \overline{\mathbf{D}}_{s} \overline{ \boldsymbol{\varGamma }} \end{aligned}$$
(30)

where \(\overline{\mathbf{D}}_{b} = \frac{h^{3}}{12} \overline{ \mathbf{C}}_{b}\), \(h\) is the plate thickness, \(\overline{\mathbf{D}} _{s} = \overline{\mathbf{C}}_{s} h\), and \(\alpha \) is a shear correction factor.

2.6 Approximation of the displacement

Assume the displacement field can be formulated as the product of two functions, one being a function of geometrical parameters and the other a known exponential function of time:

$$ \mathbf{u} ( x,y,t ) = \left \{ \textstyle\begin{array}{c} w ( x,y,t ) \\ \theta_{x} ( x,y,t ) \\ \theta_{y} ( x,y,t ) \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} w ( x,y ) \\ \theta_{x} ( x,y ) \\ \theta_{y} ( x,y ) \end{array}\displaystyle \right \} f(t). $$
(31)

Then the Laplace–Carson transform of \(\mathbf{u} ( x,y,t ) \) can be written as

$$ \overline{\mathbf{u}} ( x,y,s ) = \mathbf{u} ( x,y ) \overline{f}. $$
(32)

The function \(f ( t ) \) can be chosen as

$$ f ( t ) =1- e^{-\tau }, \quad \tau = \frac{t}{t_{s}}. $$
(33)

2.7 Simple hp cloud discretization

According to the simple hp cloud method, the following equations are defined:

$$\begin{aligned} \mathbf{U} =& \left [ \textstyle\begin{array}{c@{\ }c@{\ }c@{\ }c} \mathbf{U}_{1} & \mathbf{U}_{2} & \ldots & \mathbf{U}_{N} \end{array}\displaystyle \right ] ^{T}, \end{aligned}$$
(34)
$$\begin{aligned} \boldsymbol{\theta } =& \langle \theta_{x} \theta _{y} \rangle ^{T} = \mathbf{N}_{\theta } \mathbf{U}, \qquad w = \mathbf{N}_{w} \mathbf{U} \end{aligned}$$
(35)

where \(\mathbf{N}_{\theta }\) and \(\mathbf{N}_{w}\) are the cloud shape functions, and \(N\) is the number of arbitrary points in the mid-surface. Other parameters can be written as:

$$ \mathbf{U}_{i} = \langle w_{i}\ \theta_{x_{i}}\ \theta_{y_{i}} \rangle ^{T}, \qquad \mathbf{N}_{\theta }^{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 0 & \mathbf{N}^{i} & 0 \\ 0 & 0 & \mathbf{N}^{i} \end{array}\displaystyle \right ] , \qquad \mathbf{N}_{w}^{i} = \left [ \textstyle\begin{array}{c@{\ }c@{\ }c} \mathbf{N}^{i} & 0 & 0 \end{array}\displaystyle \right ] . $$
(36)

Thus, the strains \(\boldsymbol{\kappa }\) and \(\boldsymbol{\varGamma }\) can be discretized in the following form:

$$ \boldsymbol{\kappa } = \mathbf{B}_{b} \mathbf{U}, \qquad \boldsymbol{\varGamma } = \mathbf{B}_{s} \mathbf{U} $$
(37)

where

$$ \mathbf{B}_{b}^{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 0 & - \mathbf{N}_{, x}^{i} & 0 \\ 0 & 0 & - \mathbf{N}_{, y}^{i} \\ 0 & - \mathbf{N}_{, y}^{i} & - \mathbf{N}_{, x}^{i} \end{array}\displaystyle \right ] , \qquad \mathbf{B}_{s}^{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{N}_{, x}^{i} & - \mathbf{N}^{i} & 0 \\ \mathbf{N}_{, y}^{i} & 0 & - \mathbf{N}^{i} \end{array}\displaystyle \right ] . $$
(38)

Using virtual work principle and integrating over the thickness, Eq. (39) is obtained in the Laplace–Carson domain as

$$ \delta \mathbf{U}^{T} \biggl( \int_{A} \mathbf{B}_{b}^{T} \overline{ \mathbf{D}}_{b} \overline{f} \mathbf{B}_{b} \,dA + \int_{A} \mathbf{B} _{s}^{T} \overline{ \mathbf{D}}_{s} \overline{f} \mathbf{B}_{s} \,dA - \int_{A} \mathbf{B}_{G}^{T} \overline{ \mathbf{N}^{m}} \mathbf{B}_{G} \,dA \biggr) \mathbf{U} =0 $$
(39)

in which

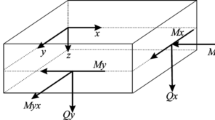
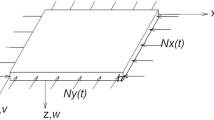
$$ \mathbf{B}_{G}^{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{N}_{, x}^{i} & 0 & 0 \\ \mathbf{N}_{, y}^{i} & 0 & 0 \end{array}\displaystyle \right ] , \qquad \mathbf{N}^{m} = \left [ \textstyle\begin{array}{c@{\quad }c} N_{x} & N_{xy} \\ N_{xy} & N_{y} \end{array}\displaystyle \right ] . $$
(40)

\(\mathbf{N}^{m}\) is the matrix of inplane forces \(N_{x}\), \(N_{y}\) and \(N_{xy}\) (as illustrated in Fig. 2).

Fig. 2
figure 2

Rectangular plate under compressive and shear loads

Full size image

So we obtain

$$ ( \overline{\mathbf{K}} - \overline{\mathbf{K}}_{G} ) \mathbf{U} = \boldsymbol{0} $$
(41)

where

$$ \overline{\mathbf{K}} = \int_{A} \mathbf{B}_{b}^{T} \overline{ \mathbf{D}}_{b} \overline{f} \mathbf{B}_{b} \,dA + \int_{A} \mathbf{B} _{s}^{T} \overline{ \mathbf{D}}_{s} \overline{f} \mathbf{B}_{s} \,dA, \qquad \overline{\mathbf{K}}_{G} = \int_{A} \mathbf{B}_{G}^{T} \overline{ \mathbf{N} ^{m}} \mathbf{B}_{G} \,dA. $$
(42)

\(\overline{\mathbf{K}}\) and \(\overline{\mathbf{K}}_{G}\) are the stiffness and geometry matrices in the Laplace–Carson domain.

2.8 Illyushin approximation method

Each component of stiffness matrix in the Laplace–Carson domain, \(K_{pl}(\overline{\omega })\), can be approximated using Illyushin approximation as follows (Zenkour 2004):

$$ K_{pl} ( \overline{\omega } )\cong \sum_{j =1}^{4} f_{j} \phi_{j} ( \overline{\omega } ) $$
(43)

in which \(\phi_{j} ( \overline{\omega } )\) are some known kernels in the Laplace–Carson domain and may be chosen in the following form:

$$ \phi_{1} =1, \qquad \phi_{2} = \overline{\omega },\qquad \phi_{3} = \frac{1}{\overline{ \omega }},\qquad \phi_{4} = \frac{1}{1+0.5 \overline{\omega }}. $$
(44)

The coefficients \(f_{i}\) are determined by solving the algebraic equations

$$ \sum_{j =1}^{4} f_{i} \varphi_{ij} = \gamma_{i} $$
(45)

where

$$ \varphi_{ij} = \int_{0}^{1} \phi_{i} \phi_{j} \,d \overline{\omega }, \qquad \gamma_{i} = \int_{0}^{1} \phi_{i} K_{pl} ( \overline{\omega } ) \,d \overline{ \omega }. $$
(46)

Using Eq. (43), Eq. (41) is approximated by equation (47) as follows:

$$ ( \tilde{\mathbf{K}} - \tilde{\mathbf{K}}_{\mathbf{G}} )\mathbf{U}= \mathbf{0} $$
(47)

where \(\tilde{\mathbf{K}}\) and \(\tilde{\mathbf{K}}_{\mathbf{G}}\) are the approximated stiffness and geometry matrices, respectively.

2.9 Returning to the time domain

Each component of the stiffness matrix in the time domain, \(K_{pl}(t)\), is determined using the inverse Laplace–Carson transformation in the following form (Zenkour 2004):

$$ K_{pl} ( t )\cong \sum_{j =1}^{4} f_{j} \theta_{j} ( t ) $$
(48)

where \(\theta_{j} ( t )\) is the inverse Laplace–Carson transformation of \(\phi_{j} ( \overline{\omega } )\), namely,

$$ \begin{aligned}[b] & \theta_{1} =1, \qquad \theta_{2} = c_{1} + c_{2} e^{- \tau }, \qquad \theta_{3} = \frac{1}{c _{1}} \biggl( 1- \frac{c_{2}}{ ( c_{1} + c_{2} ) } e^{-\beta \tau } \biggr) , \\ & \theta_{4} =\frac{1}{1+0.5 c_{1}} \biggl(1- \frac{0.5 c_{2}}{1+0.5 ( c_{1} + c_{2} ) } e^{- \alpha \tau } \biggr), \end{aligned} $$
(49)

in which

$$ \alpha = \frac{1+0.5 c_{1}}{1+0.5( c_{1} + c_{2} )}, \qquad \beta = \frac{- c _{1}}{( c_{1} + c_{2} )}, \qquad \tau = \frac{t}{t_{s}}. $$
(50)

2.10 Stability analysis

Applying the inverse Laplace–Carson transform, Eq. (51) in the time domain is obtained as

$$ \vert \mathbf{K} - \mathbf{K}_{G} \vert =0. $$
(51)

The critical load, \(N(t)\), is calculated by solving the eigenvalue problem and finding the minimum eigenvalue of Eq. (51).

3 Numerical results

3.1 General setup

In the computations, regular distributions of 25, 15, and 21 nodes are used for quadrilateral, hexagonal, triangular, and circular plates (Fig. 1), respectively. A \(2\times 2\) Gauss integration is used to evaluate the integral numerically. For calculating the enrichment functions, a complete polynomial of order 2 is used for all nodes. The material properties are supposed to be as follows: \(K=3\times 10^{7}\ \frac{\mbox{N}}{\mbox{m}^{2}}\), \(c_{1} =0.1\), \(c_{2} =0.9\). In the numerical results, the local buckling coefficient becomes dimensionless as follows:

$$ k ( t )= b^{2} N ( t ) / \pi^{2} D $$
(52)

where \(D\) is the flexural rigidity of the elastic plate, i.e.,

$$ D = \frac{E h^{3}}{12 ( 1- \nu^{2} ) }. $$
(53)

In Eq. (53), the elastic Poison ratio and the elastic modulus are assumed to be 0.3 and \(0.3\times 10^{7}\ \frac{\mbox{N}}{\mbox{m}^{2}}\), respectively. The ratio of thickness over the length of the plate, \(h/a\), is assumed to be 0.1 unless otherwise stated. The shear correction factor is assumed to be \(5/6\).

In this section, a variety of plates subjected to compressive load (Fig. 3) are considered to show the efficiency and suitability of the proposed method.

Fig. 3
figure 3

(a) Square, (b) Skew, (c) Trapezoidal, (d) Right-angled triangular, (e) Hexagonal, and (f) Circular plate under compression

Full size image

3.2 Verification

To evaluate the accuracy of the assumptions in Sect. 2.6, a viscoelastic square plate subjected to uniaxial compression is considered. The local buckling coefficient of the viscoelastic square plate is calculated (see Fig. 4 for its time history) by the ABAQUS software, and the problem is also solved by the presented method.

Fig. 4
figure 4

Local buckling coefficient of a viscoelastic square plate with simply supported edges under uniaxial compression versus the time parameter (\(h/a=0.1\), \(b/a=1\))

Full size image

(It is noted that for analyzing the problem with ABAQUS software, for different values of compressive load, the central displacement–time curves are drawn, and the time in which the central deformation pattern of viscoelastic plate changes is investigated.)

In addition, Figs. 5 and 6 compare the buckling coefficients of a simply supported moderately thick time-dependent viscoelastic square plate obtained by the present method and the results calculated by other available methods under uniaxial and biaxial compressive loads, respectively. It is noted that Zenkour (2004), Jafari et al. (2011), and Jafari et al. (2014) have assumed that the displacement field is independent of time (\(\mathbf{u}=\mathbf{u} ( x,y, )\), \(f ( t ) =1\)). This assumption yields that the results are exact at time zero and at infinity, and for other times the results have some error. Using this assumption, Eq. (39) can be written as

$$ \delta \mathbf{U}^{T} \biggl( \int_{A} \mathbf{B}_{b}^{T} \overline{ \mathbf{D}}_{b} \mathbf{B}_{b} \,dA + \int_{A} \mathbf{B}_{s}^{T} \overline{ \mathbf{D}}_{s} \mathbf{B}_{s} \,dA - \int_{A} \mathbf{B}_{G}^{T} \overline{ \mathbf{N}^{m}} \mathbf{B}_{G} \,dA \biggr) \mathbf{U} = 0. $$
(54)

So we obtain

$$ \biggl( \int_{A} \mathbf{B}_{b}^{T} \overline{ \mathbf{D}}_{b} \mathbf{B}_{b} \,dA + \int_{A} \mathbf{B}_{s}^{T} \overline{ \mathbf{D}} _{s} \mathbf{B}_{s} \,dA - \int_{A} \mathbf{B}_{G}^{T} \overline{ \mathbf{N}^{m}} \mathbf{B}_{G} \,dA \biggr) \mathbf{U} = \boldsymbol{0} . $$
(55)

Defining

$$ \overline{\mathbf{K}} = \int_{A} \mathbf{B}_{b}^{T} \overline{ \mathbf{D}}_{b} \mathbf{B}_{b} \,dA + \int_{A} \mathbf{B}_{s}^{T} \overline{ \mathbf{D}}_{s} \mathbf{B}_{s} \,dA, \qquad \overline{\mathbf{K}}_{G} = \int _{A} \mathbf{B}_{G}^{T} \overline{ \mathbf{N}^{m}} \mathbf{B}_{G} \,dA, $$
(56)

Eq. (57) is obtained as

$$ ( \overline{\mathbf{K}} - \overline{\mathbf{K}}_{G} ) \mathbf{U} = \boldsymbol{0}. $$
(57)
Fig. 5
figure 5

Time-dependent buckling coefficient of a viscoelastic square plate with simply supported edges under uniaxial compression

Full size image
Fig. 6
figure 6

Time-dependent buckling coefficient of a viscoelastic square plate with simply supported edges under biaxial compression

Full size image

Also, in order to evaluate the accuracy of the presented results, the buckling coefficients of viscoelastic plate at the first time (\(\tau =0\)) can be compared with the results obtained for elastic materials. Table 1 shows the buckling coefficients of a simply supported moderately thick viscoelastic plate with various shapes at the first time under uniaxial and biaxial compression.

Table 1 Buckling coefficients of a viscoelastic plate at the first time (\(\tau =0\)) with simply supported edges under uniaxial and biaxial compression
Full size table

3.3 Rectangular plates

Figure 7 displays the time history of the buckling coefficient of a clamped moderately thick viscoelastic square plate under uniaxial and biaxial compression.

Fig. 7
figure 7

Buckling coefficient of a viscoelastic rectangular plate with clamped edges under uniaxial and biaxial compression versus the time parameter

Full size image

Figure 8 shows the time history of a simply supported moderately thick viscoelastic square plate (Fig. 3(a)) under shear load.

Fig. 8
figure 8

Buckling coefficient of a viscoelastic square plate with simply supported edges under shear load versus the time parameter

Full size image

The results indicate that the critical load of viscoelastic plates decreases with respect to time, as the thickness-to-length ratio increases.

3.4 Skew plates

Figure 9 shows the time history of the buckling coefficient of a moderately thick viscoelastic skew plate (Fig. 3(b)) under uniaxial compression with clamped edges.

Fig. 9
figure 9

Buckling coefficient of a viscoelastic skew plate with clamped edges under uniaxial compression versus the time parameter

Full size image

The buckling coefficient of skew plates increases with respect to time as the angle increases. Also, the critical load of viscoelastic plate increases with respect to time as the rigidity in the edges increases.

3.5 Trapezoidal plates

Figure 10 shows the time history of the buckling coefficient of a moderately thick viscoelastic trapezoidal plate (Fig. 3(c)) under uniaxial compression with simply supported edges.

Fig. 10
figure 10

Buckling coefficient of a viscoelastic trapezoidal plate with simply supported edges under uniaxial compression versus the time parameter

Full size image

The results show that when \(c=0\), the buckling coefficient converges to the results of the rectangular plate.

3.6 Right-angled triangular plates

The effect of time on the buckling coefficient of a simply supported moderately thick viscoelastic right-angled triangular plate (Fig. 3(d)) under biaxial compression is shown in Fig. 11.

Fig. 11
figure 11

Buckling coefficient of a viscoelastic right-angled triangular plate with simply supported edges under biaxial compression versus the time parameter

Full size image

3.7 Hexagonal plates

Figure 12 displays the time history of the buckling coefficient of a simply supported moderately thick viscoelastic hexagonal plate (Fig. 3(e)) under biaxial compression.

Fig. 12
figure 12

Buckling coefficient of a viscoelastic hexagonal plate with simply supported edges under biaxial compression versus the time parameter

Full size image

3.8 Circular plates

Figure 13 shows the time history of buckling coefficient of a moderately thick viscoelastic circular plate (Fig. 3(f)) under biaxial compression with simply supported edges.

Fig. 13
figure 13

Buckling coefficient of a viscoelastic circular plate with simply supported edges under biaxial compression versus the time parameter

Full size image

3.9 Plates with arbitrary shapes

The effect of time on the buckling coefficients of moderately thick viscoelastic arbitrarily shaped plates (Fig. 14) subjected to uniaxial compression with simply supported edges is displayed in Figs. 15 and 16.

Fig. 14
figure 14

Arbitrarily shaped plates under uniaxial compression

Full size image
Fig. 15
figure 15

Buckling coefficient of an arbitrarily shaped viscoelastic plate with simply supported edges under uniaxial compression versus the time parameter

Full size image
Fig. 16
figure 16

Buckling coefficient of an arbitrarily shaped viscoelastic plate with simply supported edges under uniaxial compression versus the time parameter (\(h/r=0.1\))

Full size image

4 Conclusions

A simple hp cloud method was developed for the stability analysis of moderately thick time-dependent viscoelastic plates with various and different boundary conditions shapes using the Laplace–Carson transformation. Plates were subjected to uniaxial and biaxial compression and shear load. The bulk modulus was assumed to be constant. The mechanical properties of viscoelastic materials were considered by the effective moduli method in the Laplace–Carson domain. The displacement field was assumed to be the product of two functions, one being a function of geometrical parameters and the other a known exponential function of time. The problem was solved by approximating the stiffness matrix by some known kernels in the Laplace–Carson domain and returned to the time domain by the inverse Laplace–Carson transformation. The solution was obtained by solving an eigenvalue problem.

For constructing the shape functions based on the simple hp cloud method, Shepard function was utilized for a partition of unity and a complete polynomial of order 2 was used as an enrichment function. The cloud shape functions have Kronecker-delta properties, so the essential boundary conditions can be directly enforced.

The effect of time on the critical load of viscoelastic plates was studied. Also the effect of different parameters such as boundary conditions, aspect ratio, and plate thickness on the time history of buckling coefficients of viscoelastic plates with various shapes (rectangular, skew, trapezoidal, right-angled triangular, hexagonal, circular, and arbitrary shape) was evaluated. The results were compared to other available references, and the proposed method showed good agreement. The results showed that the critical load of viscoelastic plates decreases in time.