Vibration behavior of a viscoelastic composite microbeam under simultaneous electrostatic and piezoelectric actuation

Abstract

In this paper, the static and dynamic response of a clamped–clamped viscoelastic nanocomposite microbeam under combined electrostatic and piezoelectric actuations is analyzed. The equations of motion of the system are derived using the Euler–Bernoulli beam theory, Kelvin–Voigt model and Hamilton principle. The nonlinear model for the system is studied by considering stretching of the mid-plane, a DC electrostatic force, an AC harmonic force and a DC piezoelectric actuation. The static deflection and natural frequency of the system is extracted, and the influence of system parameters on the primary resonance behavior of the system is studied. It is shown that, based on various electrostatic and piezoelectric excitations, hardening or softening behavior is expected. So, one can tune these voltages such that this highly nonlinear system behaves linearly close to resonance frequency. Also it is shown that damping characteristics of the system with viscoelastic material not only depends on the damping coefficient of the system, but also on its other parameters.

1 Introduction

Batch fabrication, small size, low price, energy consumption, and high durability have caused the MEMS devices to be widely used in the past two decades in many scientific research fields such as biotechnological, aerospace, automotive, medical, signal processing, robotic and manufacturing (Younis 2011; Senturia 2001). Among many elements which are used as the basis of microstructures, microbeams have received great attention due to their widespread applications (Ghayesh et al. 2013a, 2013b). The nature of these structures introduces an evident coupling between electrical and mechanical behavior of the system which is not ignorable. Due to the importance and wide application of microbeam-based microstructures, many analytical/numerical analyses from various viewpoints, considering various configurations of the microbeam with different load types, were performed, and applicable results were extracted. For example, the static deflection and instability of the nonlinear micro/nano cantilever beam with tip mass was studied by Mojahedi et al. (2010). Using a homotopy perturbation method, they investigated the effects of van der Waals and Casimir forces on the static deflection and pull-in instability of the system. In another study, Ghayesh et al. (2013a, 2013b) employed the modified couple stress theory to investigate the nonlinear size-dependent resonant behavior of an electrically actuated clamped–clamped microbeam. They investigated the static and dynamic behavior of the system by means of the pseudo-arc length continuation technique.

Other researchers considered other aspects of this basic structure such as nonlinear resonant behavior (Kim et al. 2012) and nonlinear dynamics (Kacem et al. 2011) of the microbeam resonator.

One of the inherent phenomena which appear in these devices is the pull-in phenomenon. In many applications such as resonators, it is necessary to work in the region far from the pull-in instability. Piezoelectric materials are one of the best candidates to control the behavior of the microdevices. In recent years, the applications of the smart materials such as piezoelectric materials have received serious attention. The piezoelectric materials are light, they can be easily attached on the structure, are able to provide rapid response through electromechanical coupling, and have high ability in reducing vibrations (Rezazadeh et al. 2009). So, the response analysis of the microsystems with the presence of the piezoelectric material is of great interest.

A microbeam under piezoelectric actuation was studied by Rezazadeh et al. (2009). They applied a voltage on the piezoelectric layers which were bonded on the surfaces of the microbeam and calculated the critical piezoelectric force for avoiding of the instability in the microcantilever beam and clamped–clamped microbeam. They validated the results by known buckling capacity of the Beck column.

The nonlinear response of an inhomogenous piezoelectrically actuated microcantilever beam was derived by Mahmoodi and Jalili (2007) using the multiple scale method. They considered inextensibility conditions for the microbeam.

The nonlinear response of a microcantilever beam under electrostatic and piezoelectric actuation was investigated by Chen et al. (2013). They considered the Euler–Bernoulli hypothesis and used a developed periodicity-ratio (PR) approach to analyze the behavior of the system. They considered the effects the of moment, shear, damping and axial forces in equations.

In another work, a micro-switch as a microcantilever beam was investigated under combination of electrostatic and piezoelectric actuation by Raeisifard et al. (2014). They considered nonlinearities due to inertia, curvature, electrostatic forces, and piezoelectric actuator.

Also, many other researches were performed by considering the influence of the piezoelectric patch (Ghazavi et al. 2010; Hosseinzadeh and Ahamadian 2010; Rezazadeh et al. 2006; Zamanian and Khadem 2010).

In fact, the force required for a given deformation corresponds to the stiffness of the structure, and the natural frequency of vibration is a measure of the response time. Commonly, increasing the stiffness reduced to decreasing the response time and vice versa. On the other hand, vibration with high frequency (low response time) and large amplitude (low stiffness) is one of the most favorable characteristics for MEMS applications (Senturia 2001). Among many materials, composite materials have good and favorable characteristics and, among them, CNT reinforced nanocomposite materials are the best with properties rivaling those of other materials (Ashrafi et al. 2006), which is the consequence of small size and exceptional mechanical properties (Qian et al. 2002).

The static and dynamic responses of a viscoelastic microplate under combined electrostatic and piezoelectric actuations were studied by Fu and Zhang (2009). They considered the standard solid model and von Karman’s plate theory for studying voltage control behavior.

In another paper, Fu et al. (2009) investigated nonlinear dynamic stability for an electrically actuated clamped–guided viscoelastic microbeam. Considering the standard linear solid model, the Euler–Bernoulli hypothesis and the Galerkin method, they investigated the effect of the environmental and inner damping, geometric nonlinear creep quantity and the symmetric electrostatic load on the principal region of instability.

The deflection, natural frequency and damping quality factor of a viscoelastic microplate under an electrostatic actuation were investigated by Jalali and Khadem (2010). They assumed a CNT-reinforced nanocomposite microplate, with electrostatic actuation applied on it and obtained static pull-in instability of the microplate.

Also, the response of a resonant viscoelestic clamped–clamped microbeam under electric actuation was studied by Zamanian et al. (2010). Considering mid-plane stretching, they solved a nonlinear dynamic equation using multiple scale and Galerkin methods.

Nonlinear free vibrations of viscoelastic microcantilevers with a piezoelectric actuator layer were investigated by Shooshtari et al. (2012). In this study, the microcantilever complies with the Euler–Bernoulli beam theory and Kelvin–Voigt model. Then, the Galerkin approximation is utilized for separation of time and displacement variables, and finally, using the method of multiple scales, the analytical relations for nonlinear natural frequency and amplitude of the vibration are derived.

The viscoelastic materials have almost high damping characteristics which make these materials an inappropriate choice for some applications.

In this paper, a geometrically nonlinear microbeam is considered taking into account the simultaneous viscous, electrostatic and piezoelectric effects, and the influence of the viscoelastic damping on the nonlinear forced response of the system as well as other parameters is studied. For this purpose, the system is considered as a clamped–clamped CNT reinforced microbeam under combination of electrostatic and piezoelectric actuations. In this study, the nonlinear Euler–Bernoulli beam theory and Kelvin–Voigt viscoelastic model are implemented, and the effect of mid-plane stretching is considered. The material properties of the viscoelastic material are derived by using the Eshelby–Mori–Tanaka method (Chen and Cheng 1996). The equations of motion are extracted using Hamilton’s energy principle and then these equations are solved by using the directly applied multiple scale perturbation method and Galerkin procedure. Finally, the influence of the damping on the nonlinear response of the system is investigated.

2 Mathematical modeling

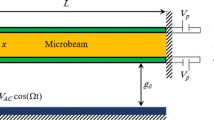
As shown in Fig. 1, in this paper a clamped–clamped uniform microbeam with constant geometrical and material properties is considered, in which L is the length, and w _c is the width of the microbeam. The microbeam is simultaneously under a combination of electrostatic and piezoelectric actuation. Electrostatic actuation is defined by $v_{\mathrm{dc}} + v_{\mathrm{ac}}\cos (\hat{\varOmega} t)$, where v _dc is the DC polarization voltage, v _ac is the amplitude of the applied AC voltage, and $\hat{\varOmega}$ is the actuation frequency. Also, piezoelectric actuation is expressed as v _P , a DC voltage, that is applied to upper and lower sides of the piezoelectric layer. Compared with the length of the microbeam, it is assumed that the air gap is very small.

Fig. 1

Schematic of an electrostatically actuated microbeam with piezoelectric layer

Also, it is assumed that the microbeam follows the Euler–Bernoulli beam theory in which rotary inertia and shear deformation are traditionally neglected. Hamilton’s principle is used to derive the governing equation of motion of the system. So, the kinetic energy of the system can be calculated as

$$ K = \frac{1}{2}\int_{0}^{L} M(s) \bigl( \dot{V}^{2} + \dot{W}^{2} \bigr) \,ds $$

(1)

where s is the position along the length of the microbeam and M(s) is mass per unit length of the microbeam which can be obtained as

$$ M(s) = w_{c}\rho_{1}t_{1} + (H_{l_{1}} - H_{l_{2}})w_{c}\rho_{2}t_{2} $$

(2)

where ρ ₁ and ρ ₂ are the specific densities of the microbeam and piezoelectric layer, respectively, w _c is the width of microbeam and the piezoelectric layer, and t ₁ and t ₂ are the thicknesses of the microbeam and the piezoelectric layer, respectively. In order to add the mass of the piezoelectric layer to the microbeam, a Heaviside function is used that is represented by $H_{l_{i}}$ and expressed as follows:

$$ H_{l_{i}} = \mathit{Heaviside}\ \mathit{function}\ (s - l_{i}) = \left \{ \begin{array}{l@{\quad }l} 1, & s > l_{i}, \\ 0, & s < l_{i}. \end{array} \right . $$

(3)

As the piezoelectric layer is attached just to the part of the microbeam length, the neutral axis changes for each section of the microbeam. For s<l ₁ and s>l ₂ where the piezoelectric layer does not exist, the neutral axis is the same as the geometric center of the microbeam’s cross-section. But for l ₁<s<l ₂, where the piezoelectric layer exists, the neutral axis is a distance P from the center of the microbeam. According to Timoshenko (1940), by introducing $n = \frac{E_{1}}{E_{2}}$, where E ₁ and E ₂ are the Young’s moduli of the microbeam and the piezoelectric layer, respectively, and, by considering Fig. 2, one can obtain

$$ P\sum_{i} A_{i} = \sum _{i} Y_{i}A_{i},\quad i = 1,2 $$

(4)

where A _i and Y _i are the cross-section and neutral axis of each layer, respectively. So, P is defined as

$$\begin{aligned} \begin{array} {l} P(t_{1}nw_{c} + t_{2}w_{c}) = \biggl(\frac{t_{1}}{2} \biggr)t_{1}nw_{c} + \biggl(\frac{t_{2}}{2} + t_{1} \biggr)t_{2}w_{c} \quad \Longrightarrow \\ P = \frac{(\frac{t_{1}}{2})t_{1}n + (\frac{t_{2}}{2} + t_{1})t_{2}}{t_{1}n + t_{2}}. \end{array} \end{aligned}$$

(5)

And so

$$ P = \frac{E_{2}t_{2}(t_{1} + t_{2})}{2(E_{1}t_{1} + E_{2}t_{2})}. $$

(6)

Because of the viscoelastic characteristics of the microbeam, a classical linear viscoelastic model, i.e., Kelvin–Voigt model is implemented:

$$ \sigma_{1} = E_{1}\varepsilon_{s} + \hat{C} \dot{\varepsilon}_{s} $$

(7)

where σ ₁ is the axial stress of the microbeam, ε _s is the strain, and $\hat{C}$ is the viscoelastic damping coefficient. Also, the stress–strain relationship for one directional piezoelectric material can be written as (Preumont 1997)

$$ \sigma_{2} = E_{2}\varepsilon_{s} - E_{2}d_{31}\frac{v_{P}}{t_{2}} $$

(8)

where σ ₂ is the axial stress of the piezoelectric layer and d ₃₁ is the piezoelectric strain constant that usually is negative.

Fig. 2

(a) Original cross-section of microbeam and piezoelectric, (b) equivalent cross-section of part (a)

Based on the nonlinear Euler–Bernoulli beam theory, the strain of the microbeam can be written in the form of (Nayfeh and Pai 2004)

$$ \varepsilon_{s} = e - kP $$

(9)

where e is the axial strain and k is the curvature bending of the microbeam in the sz plane. In order to facilitate the use of numerical or analytical methods, the Taylor series expansion is used (Nayfeh and Pai 2004):

$$\begin{aligned} \begin{array} {rcl} e &=& \sqrt{ \bigl(1+ V' \bigr)^{2} + W^{\prime 2}} - 1 = V' + \frac{1}{2}W^{\prime 2} - \frac{1}{2}V'W^{\prime 2} + \cdots \,, \\ k &=& \theta' = \biggl(W' - V'W' + V^{\prime 2}W' - \frac{1}{3}W^{\prime 3} \biggr)' \end{array} \end{aligned}$$

(10)

in which V and W are the mid-plane displacement of the microbeam in the x and y direction, respectively (Fig. 3).

Fig. 3

A segment on the microbeam before and after deformation in fixed and local coordinate systems

Also the total potential energy of the system may be obtained as

$$ U = \int_{0}^{v} \int_{0}^{\varepsilon} \sigma_{1} \,d\varepsilon \,dv_{1} + \int _{0}^{v} \int_{0}^{\varepsilon} \sigma_{2} \,d\varepsilon \,dv_{2} $$

(11)

where v ₁ and v ₂ are the length of microbeam and piezoelectric layers, respectively. Expanding Eq. (11) reduces to

$$\begin{aligned} V =& (1 - H_{l_{1}})\int_{0}^{L} \int _{ - \frac{t_{1}}{2}}^{\frac{t_{1}}{2}} \int_{0}^{\varepsilon} \sigma_{1}w_{c}\,d\varepsilon \,dz\,ds + (H_{l_{1}} - H_{l_{2}})\int_{0}^{L} \int _{ - \frac{t_{1}}{2} - P}^{\frac{t_{1}}{2} - P} \int_{0}^{\varepsilon} \sigma_{1}w_{c}\,d\varepsilon \,dz\,ds \\ &{}+ (H_{l_{1}} - H_{l_{2}})\int _{0}^{L} \int_{ - \frac{t_{1}}{2} - P}^{\frac{t_{1}}{2} - P + t_{2}} \int_{0}^{\varepsilon} \sigma_{2}w_{c} \,d\varepsilon \,dz\,ds + H_{l_{2}}\int_{0}^{L} \int_{ - \frac{t_{1}}{2}}^{\frac{t_{1}}{2}} \int_{0}^{\varepsilon} \sigma_{1}w_{c}\,d\varepsilon \,dz\,ds. \end{aligned}$$

(12)

Substituting Eqs. (7), (8) and (9) into Eq. (12) and considering Eq. (6), the potential energy of the system may be expressed as

$$\begin{aligned} V =& \frac{1}{2}\int_{0}^{L} B_{1}(s)e^{2}\,ds - \int_{0}^{L} B_{2}(s)v_{P}e\,ds + \frac{1}{2}\int _{0}^{L} B_{3}(s) k^{2}\,ds - \int_{0}^{L} B_{4}(s) v_{P}k \,ds \\ &{}+ \int_{0}^{L} B_{5}(s) e\dot{e} \,ds + \int_{0}^{L} B_{6}(s) k\dot{k} \,ds. \end{aligned}$$

(13)

Furthermore, the external force of the system which is due to the electrostatic actuation can be written as

$$ F = \int_{0}^{L} Qw\,ds $$

(14)

where Q is the electrostatic force expressed as follows:

$$ Q = - \frac{1}{2}\varepsilon_{0}w_{c} \frac{(v{}_\mathrm{dc} + v_\mathrm{ac}\cos (\hat{\varOmega} t))^{2}}{(h + W)^{2}} $$

(15)

where ε ₀ is dielectric constant of the medium and h is the capacitor gap. Also, in this equation the fringing field effect of the electric field is neglected. According to Hamilton’s principle, we have

$$ \int_{t_{1}}^{t_{2}} (\delta K - \delta U + \delta F) = 0. $$

(16)

Substituting Eqs. (1), (13) and (15) into Eq. (16), the equations of motion, neglecting terms over the third order nonlinearities, are obtained as

$$\begin{aligned} &M(s)\ddot{V} - \bigl(B_{1}(s)V' \bigr)' - \bigl(B_{5}(s)\dot{V}' \bigr)' \\ &\quad {}= \biggl(B_{1}(s) \biggl[\frac{1}{2}W^{\prime 2} - V'W^{\prime 2} \biggr] \biggr)' - \biggl(B_{2}(s)v_{P} \biggl[1 - \frac{1}{2}W^{\prime 2} + V'W^{\prime 2} \biggr] \biggr)' \\ &\qquad {} + \bigl(W' \bigl(B_{3}(s) \bigl[W' - V'W' \bigr]' \bigr)' - 2V'W' \bigl(B_{3}(s)W'' \bigr)' \bigr)' \\ &\qquad {} + \bigl(B'_{4}(s)v_{P} \bigl[W' + 2V^{\prime 2}W' - 2V'W' - W^{\prime 3} - V^{\prime 3}W' \bigr] \bigr)' \\ &\qquad {}+ \bigl(B_{5}(s) \bigl[W' \dot{W}' - \dot{V}'W^{\prime 2} - V'W' \dot{W}' \bigr] \bigr)' + \bigl(W' \bigl(B_{6}(s) \bigl[\dot{W}' - \dot{V}'W' - \dot{V}'\dot{W}' \bigr]' \bigr)' \\ &\qquad {}- 2V'W' \bigl(B_{6}(s) \dot{W}'' \bigr)' \bigr)' \end{aligned}$$

(17)

and

$$\begin{aligned} &\bigl(B_{3}(s)W''\bigr)'' + M(s)\ddot{W} + \bigl(B_{6}(s)\dot{W}'' \bigr)'' \\ &\quad {}= \biggl(B_{1}(s)\biggl[V'W' + \frac{1}{2}W^{\prime 3} - W'V^{\prime 2} \biggr]\biggr)' \\ &\qquad {}+ B_{5}(s) \bigl(W^{\prime 2} \dot{W}' + \dot{V}'W' - \dot{V}'W'V'\bigr) + \biggl( \bigl(B_{3}(s) \bigl(W'V'\bigr)' \bigr)'\bigl(1 - V'\bigr) \\ &{}\qquad {}+ \bigl(W^{\prime 2} + V' - V^{\prime 2}\bigr) \bigl(B_{3}(s)W'' \bigr)' - \biggl(B_{3}(s)\biggl[V^{\prime 2}W' - \frac{1}{3}W^{\prime 3}\biggr]' \biggr)'\biggr)' \\ &\qquad {}- \bigl(B_{2}(s)v_{P}\bigl(W' - W'V'\bigr)\bigr)' - \bigl( \bigl(B'_{4}(s)v_{P}\bigl(1 - V' - W^{\prime 2} - 3V'W^{\prime 2} \bigr)\bigr)' \\ &\qquad {}+ \bigl(B_{6}(s)\bigl[V'\dot{W} + \dot{V}'W'\bigr]'\bigr)' \bigl(1 - V'\bigr) + \bigl(B_{3}(s)\dot{W}'' \bigr)'\bigl[V' - V^{\prime 2} + W^{\prime 2}\bigr] \\ &\qquad {}- \bigl(B_{3}(s)\bigl[V^{\prime 2} \dot{W}' + 2V'\dot{V}'W' - W^{\prime 2}\dot{W}'\bigr]' \bigr)'\bigr)' - \frac{1}{2}\varepsilon_{0}w_{c} \frac{(v{}_\mathrm{dc} + v_\mathrm{ac}\cos (\hat{\varOmega} t))^{2}}{(h + W)^{2}} \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{array} {l} B_{1}(s) = (1 - H_{l_{1}})E_{1}A_{1} + (H_{l_{1}} - H_{l_{2}}) (E_{1}A_{1} + E_{2}A_{2}) + H_{l_{2}}E_{1}A_{1}, \\ B_{2}(s) = (H_{l_{1}} - H_{l_{2}})\frac{E_{2}A_{2}d_{31}}{t_{2}}, \\ B_{3}(s) = (1 - H_{l_{1}})E_{1}I_{1} + (H_{l_{1}} - H_{l_{2}}) (E_{1}I_{3} + E_{2}I_{2}) + H_{l_{2}}E_{1}I_{1}, \\ B_{4}(s) = (H_{l_{1}} - H_{l_{2}})\frac{E_{2}A_{3}d_{31}}{t_{2}}, \\ B_{5}(s) = (1 - H_{l_{1}})\bar{C}I_{1} + (H_{l_{1}} - H_{l_{2}})\bar{C}I_{3} + H_{l_{2}}E_{1} \bar{C}I_{1}, \\ B_{6}(s) = \bar{C}A_{1}, \\ A_{1} = w_{c}t_{1},\qquad A_{2} = w_{c}t_{2},\qquad A_{3} = \frac{w_{c}}{2} \bigl(t_{1}t_{2} + t_{2}^{2} - 2t_{2}P\bigr), \\ I_{1} = \frac{w_{c}}{12}t_{1}^{3},\qquad I_{3} = \frac{w_{c}}{12}t_{1}^{3} + t_{1}w_{c}P^{2}, \\ I_{2} = w_{c} \biggl( \biggl(\frac{1}{3}t_{2}^{3} \biggr) + \biggl(\frac{1}{2}t_{1}t_{2}^{2} \biggr) + \biggl(\frac{1}{4}t_{2}t_{1}^{2} \biggr) + t_{2}P^{2} - \bigl(t_{2}^{2} + t_{1}t_{2}\bigr)P \biggr). \end{array} \end{aligned}$$

(19)

For a slender beam, the longitudinal inertia in Eq. (17) may be negligible (Zamanian and Khadem 2008). Also based on the SI system of units, by considering the order of magnitude of the microbeam and piezoelectric thickness and the order of magnitude of the piezoelectric constant, according to Zamanian and Khadem (2008), B ₃(s) and B ₄(s) can be ignored when compared to B ₁(s) and B ₂(s). Also damping is negligible compared to stiffness in the longitudinal direction. To facilitate the extraction of the equation of motion, terms above the third order nonlinearities are ignored. By applying the above mentioned simplifications in (17), one can obtain

$$ \biggl(V'B_{1}(s) + \frac{1}{2}W^{\prime 2}B_{1}(s) \biggr)' - B'_{3}(s)v_{P} = 0. $$

(20)

Integrating Eq. (20) yields the following equation:

$$ V' = - \frac{1}{2}W^{\prime 2} + \frac{B_{3}(s)}{B_{1}(s)}v_{P} + \frac{B_{c}(t)}{B_{1}(s)}. $$

(21)

Equation (21) shows that the axial deformation is of the same order as of the quadratic transversal deformation, which means O(V)=O(W ²).

Also B _c (t) is the constant of integration that can be determined using the longitudinal boundary conditions:

$$ v(0) = 0, \qquad V(L)= \hat{f}. $$

(22)

So B _c (t) becomes

$$\begin{aligned} B_{c}(t) = \frac{\hat{f} + \frac{1}{2}\int_{0}^{L} W^{\prime 2}\,dx - \frac{E_{2}d_{31}A_{2}}{t_{2}(E_{1}A_{1} + E_{2}A_{2})}v_{P}(l_{2} - l_{1})}{\frac{l_{1}}{E_{1}A_{1}} + \frac{l_{2} - l_{1}}{E_{1}A_{1} + E_{2}A_{2}} + \frac{L - l_{1}}{E_{1}A_{1}}}. \end{aligned}$$

(23)

Substituting V′ from Eq. (21) into (18) by considering the mentioned simplifications, recalling that O(V)=O(W ²), and keeping the terms up to cubic nonlinearities, the equation of transverse vibration of the microbeam is obtained as

$$\begin{aligned} &\bigl(B_{3}(s)W''\bigr)'' + \bigl(B_{6}(s)\dot{W}'' \bigr)'' + M(s)\ddot{W} \\ &\qquad {} - B_{5}(s) \biggl(\frac{W'\int_{0}^{L} W'\dot{W}'ds\,}{ B_{1}(s)(\frac{l_{1}}{E_{1}A_{1}} + \frac{l_{2} - l_{1}}{E_{1}A_{1} + E_{2}A_{2}} + \frac{L - l_{1}}{E_{1}A_{1}})}\biggr) \\ &\qquad {} + \biggl(\frac{\hat{f} + \frac{1}{2}\int_{0}^{L} W^{\prime 2}\,dx - \frac{E_{2}d_{31}A_{2}}{t_{2}(E_{1}A_{1} + E_{2}A_{2})}v_{P}(l_{2} - l_{1})}{\frac{l_{1}}{E_{1}A_{1}} + \frac{l_{2} - l_{1}}{E_{1}A_{1} + E_{2}A_{2}} + \frac{L - l_{1}}{E_{1}A_{1}}}W'\biggr) \\ &\quad {} = \frac{1}{2}\varepsilon_{0}w_{c} \frac{(v{}_\mathrm{dc} + v_\mathrm{ac}\cos (\hat{\varOmega} t))^{2}}{(h + W)^{2}}. \end{aligned}$$

(24)

It is easier to study and analyze the dimensionless form of this equation. So the nonlinear equation of motion can be rewritten in the dimensionless form as

$$\begin{aligned} \begin{array} {l} \frac{\partial^{2}(H_{n1}(x)\frac{d^{2}w}{dx^{2}})}{\partial x^{2}} + M_{n}(x)\frac{d^{2}w}{dx^{2}} + C\frac{\partial^{3}}{\partial x^{2}\partial \tau} \biggl(H_{n2}(x) \frac{d^{2}w}{dx^{2}}\biggr) \\ \qquad {}- \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)\frac{d^{2}w}{dx^{2}} - 2\beta C\varGamma \biggl(\frac{\partial w}{\partial \tau},w\biggr)\frac{\partial}{\partial x}\biggl(H_{n3}(x) \frac{\partial w}{\partial x}\biggr) \\ \quad {}= \frac{\eta (v_\mathrm{dc} + v_\mathrm{ac}\cos (\hat{\varOmega} \tau ))^{2}}{(1 - w)^{2}} - \gamma_{P2}v_{P}\biggl( \frac{d^{2}H_{l_{1} / L}}{dx^{2}} - \frac{d^{2}H_{l_{2} / L}}{dx^{2}}\biggr), \\ w\vert_{x = 0} = 0,\qquad \frac{\partial w}{\partial x} \bigg\vert _{x = 0} = 0, \qquad w \vert_{x = 1} = 0,\qquad \frac{\partial w}{\partial x} \bigg\vert _{x = 1} =0. \end{array} \end{aligned}$$

(25)

Equation (25) is a dimensionless integral-partial-differential equation with linear and nonlinear terms. The dimensionless variables appearing in Eq. (25) are:

$$\begin{aligned} w = - \frac{W}{h},\qquad x = \frac{s}{L},\qquad \tau = \frac{t}{T},\qquad T =\sqrt{\frac{\rho_{1}t_{1}w_{c}L^{4}}{E_{1}I_{1}}}. \end{aligned}$$

(26)

The parameters in the above equation are defined as follows:

$$\begin{aligned} \begin{array} {l} \varGamma (a,b) = \int _{0}^{L} \frac{\partial a}{\partial x} \frac{\partial b}{\partial x}\,dx, \\ M_{n}(x) = 1 + \frac{\rho_{2}t{}_{2}}{\rho_{1}t{}_{1}}(H_{l_{1} / L} - H_{l_{2} / L}), \\ H_{n1}(x) = (1 - H_{l_{1} / L}) + \biggl(\frac{\bar{I}_{1}}{I_{1}} + \frac{E_{2}I_{2}}{E_{1}I_{1}}\biggr) (H_{l_{1} / L} - H_{l_{2} / L}) + H_{l_{2} / L}, \\ H_{n2}(x) = (1 - H_{l_{1} / L}) + \frac{\bar{I}_{1}}{I_{1}}(H_{l_{1} / L} - H_{l_{2} / L}) + H_{l_{2} / L}, \\ H_{n3}(x) = (1 - H_{l_{1} / L}) + \frac{E_{1}A_{1}}{E_{1}A_{1} + E_{2}A_{2}}(H_{l_{1} / L} - H_{l_{2} / L}) + H_{l_{2} / L}, \\ \alpha = \alpha_{1}\biggl(\frac{1 + \frac{E_{2}t_{2}}{E_{1}t_{1}}}{(1 + \frac{E_{2}t_{2}}{E_{1}t_{1}})(1 - \frac{l_{2} - l_{1}}{L}) + \frac{l_{2} - l_{1}}{L}}\biggr),\qquad \alpha_{1} = \frac{\hat{f}A_{1}L}{I_{1}},\qquad \varOmega = \hat{\varOmega} T, \\ \beta = \beta_{1}\biggl(\frac{1 + \frac{E_{2}t_{2}}{E_{1}t_{1}}}{(1 + \frac{E_{2}t_{2}}{E_{1}t_{1}})(1 - \frac{l_{2} - l_{1}}{L}) + \frac{l_{2} - l_{1}}{L}}\biggr),\qquad \beta_{1} = 6\biggl(\frac{h}{t_{1}}\biggr)^{2}, \\ \eta = \frac{6\varepsilon_{0}L^{4}}{E_{1}t_{1}^{3}h^{3}},\qquad C =\frac{\hat{C}E_{1}}{T}, \\ \gamma_{P1} = \gamma_{1}\biggl(\frac{6(\frac{l_{2} - l_{1}}{L})\frac{E_{2}}{E_{1}}}{(1 + \frac{E_{2}t_{2}}{E_{1}t_{1}})(1 - \frac{l_{2} - l_{1}}{L}) + \frac{l_{2} - l_{1}}{L}}\biggr), \qquad \gamma_{1} = \frac{2L^{2}d_{31}v_{P}}{t_{1}^{3}}, \\ \gamma_{P2} = \gamma_{2}\biggl(\frac{E_{2}t_{2}}{E_{1}t_{1}} + \frac{E_{2}}{E_{1}} - \frac{(\frac{E_{2}}{E_{1}})^{2}\frac{t_{2}}{t_{1}}(1 + \frac{t_{2}}{t_{1}})}{1 + \frac{E_{2}t_{2}}{E_{1}t_{1}}}\biggr),\qquad \gamma_{2} =3 \gamma_{1}\sqrt{\frac{6}{\alpha_{1}}}; \end{array} \end{aligned}$$

(27)

α, β, η, C, γ _P1, and γ _P2 are dimensionless parameters, which represent the axial load, mid-plane stretching, the electrostatic force, damping, piezoelectric axial force, and piezoelectric bending moment, respectively.

3 Governing equation of the static response

In order to extract the equation of the static response of the microbeam, terms with time derivatives, including inertia, damping, and variable forcing, have been assumed to be zero in Eq. (25). So, one obtains

$$\begin{aligned} \begin{array} {l} \frac{\partial^{2}(H_{n1}(x)\frac{d^{2}w_{s}}{dx^{2}})}{\partial x^{2}} - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)\frac{d^{2}w_{s}}{dx^{2}} \\ \quad {}= \frac{\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{2}} + \gamma_{P2}v_{P}\biggl( \frac{d^{2}H_{l_{1} / L}}{dx^{2}} - \frac{d^{2}H_{l_{2} / L}}{dx^{2}}\biggr), \\ w_{s}\vert_{ x = 0} = 0,\qquad \frac{\partial w_{s}}{\partial x} \bigg\vert _{x = 0} = 0,\qquad w_{s}\vert_{x = 1} = 0,\qquad \frac{\partial w_{s}}{\partial x} \bigg\vert _{ x = 1} = 0. \end{array} \end{aligned}$$

(28)

4 Governing equation of the dynamic response

For electrostatic actuation, first, the microbeam is deflected due to a DC voltage v _dc which is defined by w _s (x) and then, the dynamic forced response of the system appears about this static equilibrium position which is defined by u(x,t). So the total deflection of the microbeam consists of two parts as follows:

$$ w(x,t) = w_{s}(x) + u(x,\tau ). $$

(29)

Using Eq. (29) in Eq. (25), eliminating the static deflection terms represented by (28), and expanding the electrical term about the static position, the dynamic equation of motion of the microbeam is obtained:

$$\begin{aligned} \begin{array} {l} \frac{\partial^{2}(H_{n1}(x)\frac{\partial^{2}u}{\partial x^{2}})}{\partial x^{2}} + M_{n}(x)\frac{\partial^{2}u}{\partial \tau^{2}} \\ \quad {}= \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)\frac{\partial^{2}u}{\partial x^{2}} \\ \qquad {}+ 2\beta \varGamma (w_{s},u)\frac{d^{2}w_{s}}{dx^{2}} + \beta \varGamma (u,u)\frac{d^{2}w_{s}}{dx^{2}} + 2\beta \varGamma (w_{s},u) \frac{\partial^{2}u}{\partial x^{2}} + \beta \varGamma (u,u)\frac{\partial^{2}u}{\partial x^{2}} \\ \qquad {}+ \frac{2\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{3}}u + \frac{3\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{4}}u^{2} + \frac{4\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{5}}u^{3}, \\ u\vert_{ x = 0} = 0,\qquad \frac{\partial u}{\partial x} \bigg\vert _{x = 0} = 0, \qquad u\vert_{x = 1} = 0,\qquad \frac{\partial u}{\partial x} \bigg\vert _{x = 1} = 0. \end{array} \end{aligned}$$

(30)

4.1 Linear eigenvalue problem

Eliminating nonlinear, damping and forcing terms from Eq. (30) and taking u=φ(x)e ^iωτ, the equation of the linear eigenvalue problem will be:

$$ \begin{array} {l} \frac{d^{2}}{dx^{2}} \biggl(H_{1n}(x)\frac{d^{2}\varphi}{dx^{2}}\biggr) - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P} \bigr)\frac{d^{2}\varphi}{ dx^{2}} - 2\beta \varGamma (w_{s},\varphi ) \frac{d^{2}w_{s}}{dx^{2}} \\ \quad {}- \biggl(\frac{2\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{3}}\biggr)\varphi = 0, \\ \varphi \vert_{x = 0} = 0,\qquad \frac{\partial \varphi}{\partial x} \bigg\vert _{x = 0} = 0, \qquad \varphi \vert_{x = 1} = 0,\qquad \frac{\partial \varphi}{\partial x} \bigg\vert _{x = 1} = 0 \end{array} $$

(31)

where φ(x) is the linear mode shape and ω is the natural frequency of the microbeam about its static deflection.

5 Static response of the system

In order to solve Eq. (28), the Galerkin method is implemented. So, w _s can be approximated as

$$ w_{s} = \sum_{i = 1}^{n} R_{s[i]}\varphi_{s[i]} $$

(32)

where R _s[i] are unknown constants that would be obtained by applying the Galerkin method and φ _s[i] is the ith undamped mode shape of a simple microbeam which is defined by:

$$\begin{aligned} \begin{array} {l} \frac{d^{4}\varphi_{s[i]}}{dx^{4}} - ( \alpha - \gamma_{P1}v_{P}) \frac{d^{2}\varphi_{s[i]}}{dx^{2}} - ( \varOmega_{[i]})^{2}\varphi_{s[i]} = 0,\quad i = 1,2,3, \ldots, \\ \frac{d\varphi_{s[i]}}{dx} \bigg\vert _{x = 0} = 0,\qquad \varphi_{s[i]} \vert_{x = 0} = 0,\qquad \frac{d\varphi_{s[i]}}{dx} \bigg\vert _{x = 1} = 0,\qquad \varphi_{s[i]}\vert_{x = 1}= 0. \end{array} \end{aligned}$$

(33)

One can easily observe that Eq. (33) is the eigenvalue problem of a simple microbeam under axial loading (α−γ _P1 v _P ), φ _s[i] is the ith mode shape, and Ω _[i] is the ith natural frequency of the system. This equation is a linear differential equation with constant coefficients. The characteristic equation for Eq. (33) can be obtained as

$$ g^{4} - (\alpha - \gamma_{P1}v_{P})g^{2} - (\varOmega_{[i]})^{2} = 0. $$

(34)

This equation has two complex conjugate roots:

$$\begin{aligned} \begin{array}{l} g_{1} = \frac{1}{4}\sqrt{(\alpha - \gamma_{P1}v_{P}) + \sqrt{(\alpha - \gamma_{P1}v_{P})^{2} + 4(\varOmega_{[i]})^{2}}}, \\ g_{2} = \frac{1}{4}\sqrt{ - (\alpha - \gamma_{P1}v_{P}) + \sqrt{(\alpha - \gamma_{P1}v_{P})^{2} + 4(\varOmega_{[i]})^{2}}} i \end{array} \end{aligned}$$

(35)

where g ₁, g ₂ are the positive roots. The solution of Eq. (34) is expressed as:

$$ \varphi_{s[i]} = C_{1}\cosh (g_{1}x) + C_{2}\sinh (g_{1}x) + C_{3}\sin (g_{r}x) + C_{4}\cos (g_{r}x) $$

(36)

where C ₁, C ₂, C ₃ and C ₄ are the coefficients that are obtained using boundary conditions. Also g _r is the real part of g ₂.

Using Eq. (36) in (31), multiplying the resulting equation by φ _s[m] and integrating the outcome from x=0 to x=1, a system of algebraic equations with variables R _s[i] is obtained. Then, the coefficients R _s[i] are calculated using numerical methods.

6 Natural frequencies of the system

In order to obtain the natural frequency of vibration for the deflected microbeam about its static position, the Galerkin method is used. So, it is assumed that

$$ \varphi = \sum_{i = 1}^{M} R_{d[i]} \varphi_{d[i]} $$

(37)

where φ _d[i] is a comparison function that satisfies all boundary conditions. Considering some simplifications, the following equation with spring coefficient $2\eta v_{\mathrm{dc}}^{2}$ and axial load (βΓ(w _s ,w _s )+α−γ _P1 v _P ) is used for obtaining comparison functions:

$$\begin{aligned} \begin{array} {l} \frac{d^{4}\varphi_{d[i]}}{dx^{4}} - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P} \bigr)\frac{d^{2}\varphi_{d[i]}}{dx^{2}} - \bigl(2 \eta v_\mathrm{dc}^{2} + \varOmega^{2}_{1[i]} \bigr) \varphi_{d[i]} = 0, \\ \varphi_{d[i]}\vert_{x = 0} = 0,\qquad \frac{d\varphi_{d[i]}}{dx} \bigg\vert _{x = 0} = 0,\qquad \varphi_{d[i]}\vert_{x = 1} = 0,\qquad \frac{d\varphi_{d[i]}}{dx}\bigg\vert _{x = 1} = 0. \end{array} \end{aligned}$$

(38)

The characteristic equation of Eq. (38) can be considered as

$$\begin{aligned} R^{4} - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P} \bigr)R^{2} - \bigl(2\eta v_\mathrm{dc}^{2} + \varOmega^{2}_{1[i]} \bigr) = 0. \end{aligned}$$

(39)

Equation (39) has four roots in which R ₁ and R ₂ are the positive roots:

$$\begin{aligned} \begin{array}{l} R_{1} = \frac{1}{4}\sqrt{\bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr) + \sqrt{ \begin{array}{l} \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)^{2}\\ \quad {}+ 4\bigl(\varOmega^{2}_{1[i]} + 2\eta v_\mathrm{dc}^{2}\bigr) \end{array}}}, \\ R_{2} = \frac{1}{4}\sqrt{ - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P} \bigr) + \sqrt{\begin{array}{l} \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)^{2}\\ \quad {}+ 4\bigl(\varOmega^{2}_{1[i]} + 2\eta v_\mathrm{dc}^{2}\bigr) \end{array}}} i. \end{array} \end{aligned}$$

(40)

So, the solution of Eq. (38) is expressed as

$$ \varphi_{d[i]} = X_{1}\cosh (R_{1}x) + X_{2}\sinh (R_{1}x) + X_{3}\sin (R_{r}x) + X_{4}\cos (R_{r}x) $$

(41)

where X ₁,X ₂,X ₃ and X ₄ are the coefficients that are obtained by applying the boundary conditions. Also R _r is the real part of R ₂. Now, by using Eq. (41) in Eq. (37), multiplying the outcome by φ _d[m] and integrating the result over the microbeam length from 0 to 1, R _d[i] is obtained:

$$\begin{aligned} &\int_{0}^{L} \sum_{i = 1}^{M} R_{d[i]}(1 - w_{s})^{3}\frac{d^{2}}{dx^{2}} \biggl(H_{n1}(x)\frac{d^{2}\varphi_{1[i]}}{dx^{2}}\biggr) \varphi_{d[m]}\,dx \\ &\quad {}- \int_{0}^{L} \sum _{i = 1}^{M} R_{d[i]} (1 - w_{s})^{3} \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr)\frac{d^{2}\varphi_{1[i]}}{dx^{2}}\varphi_{d[m]}\,dx \\ &\quad {}- 2\beta \int_{0}^{L} \sum _{i = 1}^{M} R_{d[i]} \varGamma ( \varphi_{1[i]},w_{s})\varphi_{d[m]}\frac{d^{2}w_{s}}{dx^{2}}(1 - w_{s})^{3}\,dx \\ &\quad {}- \omega^{2}\int_{0}^{L} \sum _{i = 1}^{M} R_{d[i]} M(x) (1 - w_{s})^{3}\varphi_{1[i]}\varphi_{d[m]}\,dx - 2\eta v_\mathrm{dc}^{2}\int_{0}^{L} \sum _{i =1}^{M} R_{d[i]} \varphi_{1[i]}\varphi_{d[m]}\,dx = 0. \end{aligned}$$

(42)

By equating the determinant of the coefficients matrix to zero, the linear natural frequencies of the system can be obtained.

7 Primary resonance

In this section, the dynamic response of the system to the primary resonance excitation is investigated using the multiple scale method. First, a bookkeeping parameter ε is introduced to show the weakness of the nonlinear terms and fast and slow time scales T ₀=τ, T ₁=ετ and T ₂=ε ² τ. Hence, the temporal operators can be expanded as:

$$\begin{aligned} \begin{array} {l} \frac{\partial}{\partial t} = D_{0} + \varepsilon D_{1} + \varepsilon^{2}D_{2} + O\bigl(\varepsilon^{3}\bigr), \\ \frac{\partial^{2}}{\partial t^{2}} = D_{0}^{2} + 2\varepsilon D_{0}D_{1} + \varepsilon^{2}D_{1}^{2} + 2\varepsilon^{2}D_{0}D_{2} + O\bigl( \varepsilon^{3}\bigr). \end{array} \end{aligned}$$

(43)

Also, u(x,τ) can be written as a third expansion in the form of

$$ u(x,\tau ) = \varepsilon u_{1}(x,T_{0},T_{1},T_{2}) + \varepsilon^{2}u_{2}(x,T_{0},T_{1},T_{2}) + \varepsilon^{3}u_{3}(x,T_{0},T_{1},T_{2}). $$

(44)

In order to balance the effect of nonlinearity, damping and forcing terms, C and v _Ac are replaced with ε ² C and ε ³ v _Ac, respectively. Equating the coefficients of the same powers of ε leads to the following set of linear partial differential equations:

(Order ε ¹):

$$\begin{aligned} L(u_{1}) =& M_{n}(x)\frac{\partial^{2}u_{1}}{\partial T_{0}^{2}} + \frac{\partial^{2}}{\partial x^{2}} \biggl(H_{n1}(x)\frac{\partial^{2}u_{1}}{\partial x^{2}}\biggr) - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P}\bigr) \frac{\partial^{2}u_{1}}{\partial x^{2}} \\ &{} - 2\beta \varGamma (w_{s},u_{1}) \frac{d^{2}w_{s}}{dx^{2}} - \frac{2\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{3}}u_{1} = 0; \end{aligned}$$

(45)

(Order ε ²):

$$\begin{aligned} L(u_{2}) = \beta \varGamma (u_{1},u_{1}) \frac{d^{2}w_{s}}{dx^{2}} + 2\beta \varGamma (w_{s},u_{1}) \frac{d^{2}u_{1}}{dx^{2}} + \frac{3\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{4}}u_{1}^{2} - 2M{}_{n}(x)\frac{\partial^{2}u_{1}}{\partial T_{0}\partial T_{1}}; \end{aligned}$$

(46)

(Order ε ³):

$$\begin{aligned} L(u_{3}) =& - 2M_{n}(x)\frac{\partial^{2}u_{2}}{\partial T_{0}\partial T_{1}}\partial T - M_{n}(x) \biggl(\frac{\partial^{2}u_{1}}{\partial T_{1}^{2}} + 2\frac{\partial^{2}u_{1}}{\partial T_{0}\partial T_{2}}\biggr) \\ &{} - C\frac{\partial^{3}}{\partial x^{2}\partial T_{0}}\biggl(H_{n2}(x)\frac{\partial^{2}u_{1}}{\partial x^{2}}\biggr) + 2 \beta C\varGamma \biggl(\frac{\partial u_{1}}{\partial T_{0}},w_{s}\biggr)\frac{\partial}{\partial x} \biggl(H_{n3}(x)\frac{dw_{s}}{dx}\biggr) \\ &{}+ 2\beta \varGamma (u_{1},u_{2})\frac{d^{2}w_{s}}{dx^{2}} + 2 \beta \varGamma (w_{s},u_{2})\frac{\partial^{2}u_{1}}{\partial x^{2}} + 2\beta \varGamma (w_{s},u_{1})\frac{\partial^{2}u_{2}}{\partial x^{2}} \\ &{} + \beta \varGamma (u_{1},u_{1})\frac{\partial^{2}u_{1}}{\partial x^{2}} + \frac{6\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{4}}u_{1}u_{2} + \frac{4\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{5}}u_{1}^{3} \\ &{}+ \frac{2\eta v_\mathrm{dc}v_\mathrm{ac}\cos (\varOmega T_{0})}{(1 - w_{s})^{4}}. \end{aligned}$$

(47)

The solution of Eq. (45) is

$$\begin{aligned} u_{1}(T_{0},T_{1},T_{2}) = A(T_{1},T_{2})e^{i\omega T_{0}}\phi (x) + \bar{A}(T_{1},T_{2})e^{ - i\omega T_{0}}\phi (x) \end{aligned}$$

(48)

where A and $\bar{A}$ are the complex amplitudes and their conjugates, respectively, that will be determined by applying the solvability condition at third order. The eigenfunction ϕ(x) describes normalized mode shapes so that $\int_{0}^{1} \phi^{2}(x) \,dx = 1$.

By substituting Eq. (48) into Eq. (46),

$$\begin{aligned} L(u_{2}) =& \bigl(A^{2}e^{2i\omega T_{0}} + 2A\bar{A} + \bar{A}^{2}e^{ - 2i\omega T_{0}}\bigr)h(x) - 2M_{n}(x)\omega i \biggl(\frac{\partial A(T_{1},T_{2})}{\partial T_{1}}e^{i\omega T_{0}} \\ &{}-\frac{\partial \bar{A}(T_{1},T_{2})}{\partial T_{1}}e^{ - i\omega T_{0}}\biggr) \end{aligned}$$

(49)

where

$$\begin{aligned} h(x) = \beta \varGamma (\phi,\phi )\frac{d^{2}w_{s}}{dx^{2}} + 2\beta \varGamma (w_{s},\phi )\frac{d^{2}\phi}{dx^{2}} + \frac{3\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{4}} \phi^{2}. \end{aligned}$$

(50)

The particular solution of Eq. (49) may be expressed as

$$ u_{2}(T_{0},T_{2}) = \psi_{1}(x)A^{2}e^{2i\omega T_{0}} + 2\psi_{2}(x)A\bar{A} + \psi_{1}(x)\bar{A}^{2}e^{ - 2i\omega T_{0}} $$

(51)

where ψ ₁(x) and ψ ₂(x) are the solutions of the boundary value problem,

$$\begin{aligned} \begin{array} {l} \frac{d^{2}}{dx^{2}} \biggl(H_{n1}(x)\frac{d^{2}\psi_{i}}{dx^{2}}\biggr) - 4\omega^{2} \delta_{1i}M_{n}(x)\psi_{1} - \bigl(\beta \varGamma (w_{s},w_{s}) + \alpha - \gamma_{P1}v_{P} \bigr)\frac{d^{2}\psi_{i}(x)}{dx^{2}} \\ \quad {}- 2\beta \varGamma (w_{s},\psi_{i})\frac{d^{2}w_{s}}{dx^{2}} - \frac{2\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{3}}\psi_{i} = h(x), \\ \psi_{i}\vert_{x = 0} = 0,\qquad \frac{\partial \psi_{i}}{\partial x} \bigg\vert _{x = 0} = 0,\qquad \psi_{i}\vert_{x = 1} = 0,\qquad \frac{\partial \psi_{i}}{\partial x}\bigg\vert _{x = 1} = 0. \end{array} \end{aligned}$$

(52)

In Eq. (52), δ _1i is the Kronecker delta. Implementing Galerkin method and using the linear symmetric mode shapes of the deflected microbeam about its static position as comparison functions, the solution of Eq. (52) can be obtained.

Substituting Eqs. (48) and (51) into Eq. (47), replacing Ω by ω+ε ² σ, where σ is a detuning parameter to express the nearness of the excitation frequency to the natural frequency, yields

$$\begin{aligned} L(u_{3}) =& \biggl[ - 2\omega i\frac{dA}{dT_{2}}M_{n}(x) \phi (x) - i\omega AC\chi^{\upsilon} + \chi (x)A^{2}\bar{A} + \bar{F}(x)e^{i\sigma T_{2}}\biggr]e^{i\omega T_{0}} + \mathit{c.c.} \\ &{}+ \mathit{N.S.T.} \end{aligned}$$

(53)

where $\mathit{c.c}$. indicates complex conjugate of the preceding terms and $\mathit{N.S.T}$. means the other terms that do not produce secular terms. Also

$$\begin{aligned} \begin{array}{rcl} \chi^{\upsilon} &=& C\frac{d^{2}}{dx^{2}} \biggl(H_{n2}(x) \frac{d^{2}\phi}{ dx^{2}} \biggr) - 2\beta C\varGamma (\phi,w_{s}) \frac{d}{dx} \biggl(H_{n3}(x)\frac{dw_{s}}{dx} \biggr), \\ \bar{F}(x) &=& \frac{\eta v_\mathrm{dc}v_\mathrm{ac}}{(1 - w_{s})^{2}}. \end{array} \end{aligned}$$

(54)

The function χ(x) is defined as

$$ \chi (x) = \chi_{q}^{g} + \chi_{c}^{g} + \chi_{q}^{e} + \chi_{c}^{e} $$

(55)

where $\chi_{q}^{g}$ and $\chi_{c}^{g}$ are the quadratic and cubic geometric nonlinear terms and $\chi_{q}^{e}$ and $\chi_{c}^{e}$ are the quadratic and cubic electric nonlinear terms, respectively, which are defined as:

$$\begin{aligned} \begin{array} {l} \chi_{q}^{g} = \bigl(2\alpha_{1}\varGamma (\psi_{1},\phi ) + 4 \alpha_{1}\varGamma (\psi_{2},\phi )\bigr)\frac{d^{2}w_{s}}{dx^{2}} + \biggl(2\alpha_{1}\frac{d^{2}\psi_{1}}{dx^{2}} + 4\alpha_{1} \frac{d^{2}\psi_{2}}{dx^{2}}\biggr)\varGamma (w_{s},\phi ) \\ \phantom{\chi_{q}^{g} =}+\bigl(2\alpha_{1}\varGamma (\psi_{1},w_{s}) + 4\alpha_{1}\varGamma (\psi_{2},w_{s})\bigr) \frac{d^{2}\phi}{dx^{2}}, \\ \chi_{q}^{e} = \frac{6\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{4}}(2\phi \psi_{2} + \phi \psi_{1}), \\ \chi_{c}^{g} = 3\beta \varGamma (\phi,\phi ) \frac{d^{2}\phi}{ dx^{2}}, \\ \chi_{c}^{e} = \frac{12\eta v_\mathrm{dc}^{2}}{(1 - w_{s})^{5}}\phi^{3}. \end{array} \end{aligned}$$

(56)

The left-hand side of Eq. (53) is self-adjoint. So, the inhomogeneous equation (53) has a solution if the right-hand side of this equation is orthogonal to every solution of the corresponding homogeneous self-adjoint equation, that is, $\phi (x)e^{i\omega T_{0}}$. So, the solvability condition would be obtained by multiplying the right-hand side of inhomogenous equation (53) to $\phi (x)e^{i\omega T_{0}}$ and then, integrating the outcome from x=0 to x=1 as

$$ 2i\omega \biggl(\bar{M}\frac{dA}{dT_{2}} + \frac{\mu A}{2} \biggr) + 8SA^{2}\bar{A} - Fe^{i\sigma T_{2}} = 0 $$

(57)

where

$$\begin{aligned} \begin{array} {l} S = S_{q}^{g} + S_{c}^{g} + S_{q}^{e} + S_{c}^{e}, \\ S_{q}^{g} = - \frac{1}{8}\int_{0}^{L} \chi_{q}^{g}\phi \,dx, \\ S_{c}^{g} = - \frac{1}{8}\int_{0}^{L} \chi_{c}^{g}\phi \,dx, \\ S_{q}^{e} = - \frac{1}{8}\int_{0}^{L} \chi_{q}^{e}\phi \,dx, \\ S_{c}^{e} = - \frac{1}{8}\int_{0}^{L} \chi_{c}^{e}\phi \,dx, \\ \mu = C\int_{0}^{L} \chi^{\upsilon} \phi \,dx, \\ \bar{M} = \int_{0}^{L} M_{n}(x) \phi^{2}\,dx, \\ F = \int_{0}^{L} \bar{F} \phi \,dx = \int _{0}^{L} \frac{\eta v_\mathrm{dc}v_\mathrm{ac}}{(1 - w_{s})^{2}} \phi \,dx. \end{array} \end{aligned}$$

(58)

Expressing A in polar form gives

$$ A = \frac{1}{2}ae^{i\vartheta} $$

(59)

where a and ϑ are amplitude and phase angle of the response, respectively. Considering $\vartheta = \sigma T_{2} - \hat{\theta}$ and substituting Eq. (59) into (57), and splitting into real and imaginary parts, the following equations are obtained:

$$\begin{aligned} \begin{array}{l} \bar{M} \frac{da}{dT_{2}} = - \frac{\mu}{2}a + \frac{F}{\omega} \sin \hat{\theta}, \\ \bar{M}\frac{d\hat{\theta}}{dT_{2}} = \sigma \bar{M} - \frac{Sa^{2}}{\omega} + \frac{F}{a\omega} \cos \hat{\theta}. \end{array} \end{aligned}$$

(60)

The point where $\frac{da}{dT_{2}} = 0$ and $\frac{d\hat{\theta}}{dT_{2}} = 0$ corresponds to a singular point of the system and shows its steady-state motion. So, in the steady-state condition this equilibrium criterion can be written as

$$\begin{aligned} a_{0}^{2} \biggl( \biggl(\frac{\mu}{2} \biggr)^{2} + \biggl(\sigma \bar{M} - \frac{Sa_{0}^{2}}{\omega} \biggr)^{2} \biggr) = \frac{F^{2}}{\omega^{2}}. \end{aligned}$$

(61)

Equation (61) shows that the amplitude a ₀ is maximum when term $(\sigma \bar{M} - \frac{Sa_{0}^{2}}{\omega} )^{2}$ is equal to zero, and so

$$ \sigma = \frac{Sa_{0}^{2}}{\omega \bar{M}}. $$

(62)

As a result, the maximum a ₀ will be

$$ a_{0} = \frac{2F}{\omega \mu}. $$

(63)

Finally, the nonlinear resonance frequency is obtained as

$$ \varOmega = \omega + \frac{4SF^{2}}{\bar{M}\omega^{3}\mu^{2}}. $$

(64)

At last, solving Eq. (61) for σ yields

$$ \sigma = \pm \frac{1}{a_{0}}\sqrt{ \biggl( \frac{F^{2}}{\omega^{2}} - \mu^{2}a_{0}^{2} \biggr)} + \frac{Sa_{0}^{2}}{\omega}. $$

(65)

8 Results and discussion

Numerical values which are used in the analysis are listed in Table 1. Also dimensionless values, in accordance to Table 1, are shown in Table 2. It is necessary to note that in this paper a (10, 10) SWNT was selected as a reinforcement and polymethyl methacrylate (PMMA) was used as a matrix material because of its good variable-climate-resisting property. The elastic modulus of CNT/PMMA nanocomposite was estimated by the Eshelby–Mori–Tanaka method (Chen and Cheng 1996).

Table 1 Geometrical and material properties of the microbeam and piezoelectric layer

Table 2 Values of parameters

For 28 % volume fraction of aligned (10, 10) SWNT fibers, and the aspect ratio of fibers greater than 1000, the elastic modulus of SWNT/PMMA nanocomposite is obtained as 166 GPa.

Neglecting the viscoelastic effects of the structure, the results of this work are compared with those of Zamanian and Khadem (2008, 2010) for the static deflection and frequency response, respectively, and good agreement between the results is obtained. They are shown in Figs. 5 and 16.

Figure 4 shows the variation of the static deflection of the microbeam with respect to polarization voltage. It is shown that, considering the boundary condition of the system, the maximum static response occurred in the center of the microbeam and it increased as v _dc increased.

Fig. 4

Variations of static deflection with respect to x for l ₂−l ₁=L

Figure 5 shows the variation of the static deflection with electrostatic voltage, for this work and that of Zamanian and Khadem (2008), and represents a good agreement. In this comparison, it is considered that the piezoelectric layer covered 0.8 length of the microbeam and that the viscoelastic effect of the microbeam is eliminated.

Fig. 5

Comparison of the effect of $\eta v_{\mathrm{dc}}^{2}$ on the central static deflection for this work and that of Zamanian and Khadem (2008)

Figure 6 shows the variation of the static response with different lengths of the piezoelectric patch. It is necessary to note that in the corresponding equation, the effects of the nonlinear geometrical, electrostatic and piezoelectric terms have been considered. It is observed that for a constant piezoelectric length, the static deflection is increased as the electrostatic voltage is increased. By increasing the length of the piezoelectric layer from 0 to 0.5L, for a constant value of $\eta v_{\mathrm{dc}}^{2}$, the static deflection is increased and, from 0.5L to L, it is decreased. Because of the piezoelectric layer effects in Eq. (28), static behavior of the microbeam changes for different length of the piezoelectric layer.

Fig. 6

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the central static deflection microbeam for different piezoelectric layer length

Considering Eq. (27), by increasing the length of the piezoelectric layer, γ _P1 v _P increases. Also Eq. (28) illustrates that the term γ _P2 v _P for l ₂−l ₁=L and l ₂−l ₁=0 goes to zero. So, decreasing the piezoelectric length causes the system stiffness to decrease and the microbeam deflection to increase. As a result, for the electrostatic voltage far from pull-in voltage, by decreasing the length of the piezoelectric layer from L to 0.5L, the static deflection is increased. Also it is shown that the pull-in voltage for different length of the piezoelectric layer is varied, but, this phenomenon occurs for the deflection about w _s ≈0.4. Also, it is shown that for the microbeam without a piezoelectric layer, due to lower stiffness of the system, the microbeam response became unstable for lower electrostatic voltage and so, pull-in occurred sooner.

Figure 7 shows the maximum static deflection of the microbeam for different values of γ ₁. Increasing the piezoelectric voltage causes the static deflection to increase and the pull-in voltage to decrease. Also, it is shown that the static deflection has a nonzero value for $\eta v_{\mathrm{dc}}^{2} = 0$, and is increased as the absolute value of γ ₁ is increased.

Fig. 7

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the central static deflection microbeam for different γ ₁

In Fig. 8, the maximum static deflection of the microbeam for different values of β ₁ is investigated. It is shown that by increasing β ₁ the static deflection of the microbeam is decreased. As β ₁ increased, the stiffness of the system also increased due to increasing the mid-plane stretching and so, the static deflection is decreased. Also it is observed that a lower β ₁ leads to the sooner pull-in instability.

Fig. 8

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the central static deflection microbeam for different β ₁

Figure 9 shows the effect of γ ₁ on the static deflection of the microbeam for l ₂−l ₁=0.5L. It is shown that by increasing the absolute value of γ ₁, which means the increase of piezoelectric voltage for a microbeam with piezoelectric layer l ₂−l ₁=0.5L, the static deflection is continuously increased. This happened due to terms with coefficients of γ _P1 v _P and γ _P2 v _P in the static equation (28).

Fig. 9

Effect of γ ₁ on the central static deflection microbeam with piezoelectric layer length equal to l ₂−l ₁=0.5L

Figure 10 shows the effect of β ₁ on the static deflection of the microbeam for l ₂−l ₁=0.8L. Considering Eq. (27), it is demonstrated that the maximum deflection occurs for the minimum stretching of the neutral axis. It is shown that by increasing β ₁ the static deflection of the system is suddenly decreased and after that, increasing β ₁ has only a small effect on the static deflection.

Fig. 10

Effect of β ₁ on the central static deflection microbeam with piezoelectric layer length equal to l ₂−l ₁=0.8L

Figure 11 shows the variations of natural frequency of the system with respect to $\eta v_{\mathrm{dc}}^{2}$ for different lengths of the piezoelectric layer. It is shown that by increasing the length of the piezoelectric layer from 0 to 0.8L, the natural frequency is decreased, and for 0.8L to L is increased.

Fig. 11

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the natural frequency of microbeam for different piezoelectric layer length

Figures 12 and 13 show the variations of the natural frequency of the system relative to $\eta v_{\mathrm{dc}}^{2}$. It is shown that, for a constant $\eta v_{\mathrm{dc}}^{2}$ far from the pull-in voltage, as the absolute value of γ ₁ is increased, the natural frequency of the system is decreased, but, as the absolute value of β ₁ is increased, the natural frequency of the system is increased.

Fig. 12

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the natural frequency of microbeam for different γ ₁

Fig. 13

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the natural frequency of microbeam for different β ₁

The effects of γ ₁ and β ₁ on the natural frequency of the system are shown in Figs. 14 and 15, respectively. It is shown that by increasing γ ₁ or β ₁ the natural frequency of the system is increased.

Fig. 14

Effect of γ ₁ on the natural frequency of microbeam with piezoelectric layer length equal to l ₂−l ₁=0.5L

Fig. 15

Effect of β ₁ on the natural frequency of microbeam with piezoelectric layer length equal to l ₂−l ₁=0.8L

Figure 16 shows the frequency response of the elastic system with a complete piezoelectric layer for $\eta v_{\mathrm{dc}}^{2} = 20$ which is compared to Zamanian and Khadem (2010), and a good and favorable agreement is obtained.

Fig. 16

Comparison between frequency response of this work with Zamanian and Khadem (2010) in $\eta v_{\mathrm{dc}}^{2} = 20$ with piezoelectric layer L

Figure 17 shows the variations of the vibration amplitude with respect to the detuning parameter σ. According to Eq. (61), the frequency response of the system depends on the various system parameters. All these parameters are positive except for S which can be positive or negative. S contains the nonlinear stiffness terms that include geometry, piezoelectric and electrostatic nonlinearities. For S>0, according to Eq. (64), the nonlinear resonance frequency becomes greater than the linear one, i.e., $\frac{\varOmega}{\omega} > 1$. This causes the hardening behavior of the system. In the same manner, for S<0 the nonlinear resonance frequency is lower than the linear one and the softening behavior appears. As shown in Fig. 17, by increasing the electrostatic voltage, the system represents a more softening behavior. For constant piezoelectric parameters, increasing the electrostatic voltage reduces to decreasing S to negative values, and so, the softening behavior appears. Also, as $\eta v_{\mathrm{dc}}^{2}$ is increased, the vibration amplitude is increased, which is due to the increasing value of F in Eq. (58).

Fig. 17

Frequency response of microbeam for different actuation electrostatic voltage

Figure 18 depicts the variation of the vibration amplitude relative to the detuning parameter σ. It is shown that increasing the absolute value γ ₁ makes the system softer and, by tuning the value of γ ₁, one can expect a linear response from a nonlinear system. Also, as shown in this figure, the amplitude of a nonlinear vibration is increased as the absolute value of γ ₁ is increased. By increasing γ ₁, the static deflection of the microbeam is increased and, according to Eqs. (28), (58) and (63), w _s , F and also a ₀ are subsequently increased.

Fig. 18

Frequency response of microbeam for different γ ₁

Figure 19 shows the effect of β ₁ on the dynamic response of the microbeam. It is shown that increasing the value of β ₁ leads to increasing the hardening behavior of the system. Increasing the value of β ₁ causes the static deflection to decrease and the natural frequency of the system to increase, and so, according to Eq. (63), leads to a decreasing amplitude of the vibration.

Fig. 19

Frequency response of microbeam for different β ₁

Figure 20 shows the frequency response of the microbeam for different AC voltages. As shown in this figure, by increasing the AC voltage, according to Eqs. (58) and (63), the nonlinear vibration amplitude is increased, and the nonlinear resonance occurs at a higher excitation frequency. Also one can observe that the hardening state of the system remains unchanged due to the variation of v _ac.

Fig. 20

Frequency response of microbeam for different AC voltage

The effect of the electrostatic voltage on the damping of the system is shown in Fig. 21. As shown in this figure, the damping characteristic of the system is increased as the electrostatic voltage is increased, especially near the pull-in voltage. So, one can say that for a viscoelastic microbeam, the damping of the system not only depends on the viscoelastic damping coefficient C, but also on other parameters of the system, for example, electrostatic voltage.

Fig. 21

Effect of $\eta v_{\mathrm{dc}}^{2}$ on the damping of system for C=0.001

Figures 22 and 23 show the variation of the damping characteristics of the system to β ₁ and γ ₁, and one can easily observe that β ₁ has no evident effect on the damping of the system. But, the damping characteristic is increased as γ ₁ is increased.

Fig. 22

Effect of β ₁ on the damping of system for C=0.001

Fig. 23

Effect of γ ₁ on the damping for C=0.001

9 Conclusion

In this paper, the nonlinear dynamic response of a nanocomposite microbeam is studied under electric and piezoelectric actuations. The microbeam has been assumed as a clamped–clamped Euler–Bernoulli microbeam and having a symmetric piezoelectric patch deposited on it. The Galerkin method and a perturbation method are applied to solve the nonlinear equation of motion.

According to the obtained result, for a specific length of the piezoelectric, the hardening behavior occurs for lower values of the DC voltage in electrostatic actuation and, by increasing the value of this DC voltage, a softening behavior is detected. Also, for a piezoelectric actuation by increasing piezoelectric voltage values, a softening behavior is observed. At the same time, an increase of the mid-plane stretching causes a hardening of the system. Also it is shown that damping characteristics of the system depends on both damping coefficient C and on other parameters of the system.