1 Introduction

Optical encryption techniques have been extensively utilized in the field of image cryptography because of their high-speed, parallel processing and information hiding in different dimensions, i.e., multiple degrees of freedom [1]. The double random phase encoding (DRPE) in the Fourier transform (FT) domain, proposed by Refregier and Javidi in 1995 [2], is the most innovative optical image encryption technique. DRPE was combined with various optical transform domains [3,4,5,6,7,8], such as fresnel transform (FrT) [3, 4], fractional Fourier transform (FrFT) [5], gyrator transform (GT) [6, 7], and so on [8,9,10], to expand the key space and enhance the security. However, the conventional DRPE cryptosystems need the holographic technique to record complex ciphertext consisting of both the amplitude and phase information, which requires high stability of the optical architecture. Additionally, due to the linear structure, they are vulnerable to some types of attack algorithms [11,12,13], such as known-plaintext attack (KPA) [11], chosen-plaintext attack (CPA) [12], and chosen-ciphertext attack (CCA) [13]. To break down the linearity, a nonlinear asymmetric cryptosystem based on phase truncated Fourier transform (PTFT) was proposed by Qin and Peng [14] to further enhance security. But in addition to the silhouette problem [15], PTFT is also vulnerable to a special attack developed based on the amplitude-phase retrieval algorithm (APRA) [16]. Futhermore, Lang et al. [17] introduced undercover amplitude modulation that generated additional key streams and then proposed a security-enhanced scheme by utilizing chaos in the double random phase-amplitude encoding (DRPAE). The DRPAE can resist the traditional KPA and is much more secure than the conventional DRPE. However, the DRPAE is still vulnerable to a hybrid two-step attack (HTSA) [18].

The optical image encryption schemes based on phase retrieval algorithms [19,20,21,22,23,24,25,26,27,28,29,30] have been widely developed due to the nonlinearity of cryptosystems and their easy optical implementation for decryption. Wang et al. [20] proposed a phase retrieval algorithm that encodes the plaintext to the phase-only mask at the Fourier plane in a 4-f structure. Li et al. [21] modified the method by encrypting the plaintext as the phase-only mask at the input plane. Chang et al. [22] further proposed retrieving multiple phase-only masks for higher security and greater recovered quality. Situ et al. [23] proposed the most representative encryption method that separately retrieves two phase-only masks at the input and FrT planes without using any lens to make the implementation easier. The phase retrieval algorithms have also been applied in other optical transform domains to obtain higher security [24, 25]. However, these conventional schemes are mainly limited to two-dimensional (2D) space, and there is a simple and explicit relationship between the plaintext and ciphertext, which makes it easy to be exploited by illegal attackers. Additionally, the security of the cryptosystems is constrained due to the small key space and low sensitivity of secret keys.

Chen et al. [26] extended the conventional phase retrieval algorithm to three-dimensional (3D) space, which considers the 2D plaintex as a series of particles distributed in 3D space, then encrypts the series of particles into the phase-only mask. The 3D phase retrieval algorithms [26, 27] overcome the limitations inherent in conventional 2D phase retrieval algorithms and confuse the relationship between the plaintext and ciphertext, which could achieve larger key space and higher security. However, these schemes divide the 2D plaintext into multiple parts distributed in 3D space and then code them in succession, the quality of the decrypted images is affected due to the serious crosstalk of the decryption process. Thus, these schemes are only suitable for encoding images with a low decrypted quality. In 2021, Shan et al. [28] proposed a cascaded 3D phase retrieval algorithm in which the 2D plaintext was converted into a series of sparse images to form 3D distributed patterns under the constraints of binary amplitude masks (BAMs), and then encoded into two phase-only masks to serve as the ciphertext.

Recently, Shan et al. [29] proposed another 3D single-phase encoding algorithm (3D-SPEA) by generating a sparse volumetric ciphertext. Although the security of the cryptosystems was effectively improved by using complementary and orthogonal BAMs to enlarge the key space and confuse the relationship between the plaintext and the ciphertext, which makes CPA no longer valid for the cryptosystem. However, since 3D-SPEA only encrypts the 2D plaintext into a sparse volumetric ciphertext distributed in 3D space, the convergence speed of the iterative process is slow, and the key sensitivity is low. The 3D-SPEA is vulnerable to being attacked when BAMs are obtained by illegal attackers. Additionally, BAMs have to be stored and transmitted as secret keys during the decryption process, which adds an additional workload for the cryptosystem. Based on the description of these above algorithms [26,27,28,29], it is clear that although there have been considerable researches on 3D phase retrieval algorithms, their security and performances still need further improvement.

In optical image encryption techniques, the image is encrypted using random phase masks (RPMs), and all RPMs have to be sent to the receiver side to decrypt the original image. Thus, the security of these methods becomes vulnerable due to the key distribution. In recent years, optical encryption methods utilizing chaos theory have been extensively proposed. Singh et al. [31] proposed a new DRPE method using fractional Fourier transform and chaos theory for image encryption, in which random phase masks are generated using iterative chaos maps. This method makes it unnecessary to transmit the whole random phase masks during decryption, but only needs to transmit the keys of the chaotic map, which greatly reduces the cost of the cryptosystem. Wang et al. [32] proposed a security-enhanced image encryption method based on Fresnel diffraction with chaotic phase, which combines ordinary FrT with a special phase generated by a chaotic system to substantially improve the sensitivity of keys. Obviously, these methods improve the encryption method by utilizing chaos theory and make the performance of the encryption scheme better.

In this paper, to enhance the performance and security of 3D phase retrieval algorithms, we propose a 3D double-phase encoding algorithm (3D-DPEA) in the GT domain, in which a plaintext is encrypted into two sparse volumetric ciphertexts under the constraints of chaos-generated BAMs. Then, the two volumetric ciphertexts are multiplexed into corresponding 2D ciphertexts for the convenience of storage and transmission. First, due to the synergistic adjustment of the two sparse volumetric ciphertexts during the iterative process, the convergence speed of the iteration would be significantly increased, and the quality of the recovered decrypted image can also be improved. Additionally, the sensitivity of secret keys could be significantly improved by some orders of magnitude because the BAMs are generated by the logistic-tent (LT) chaotic map, which is closely related to the rotation angles of GT and the LT chaotic map has several advantages such as nonlinear, pseudorandom behavior, and high sensitivity of initial conditions. As a result, the proposed encryption scheme not only eliminates the explicit/linear relationship between the plaintext and the ciphertext, rendering CPA attack invalid for the cryptosystem, but also significantly enhances security. For decryption, once a coherent beam crosses two sparse volumetric ciphertexts sequentially, the corresponding decrypted image can be obtained by recording an intensity pattern. Moreover, BAMs will not impose an additional burden on the storage and transmission of secret keys.

The remaining sections of this paper are organized as follows. Section 2 presents the background knowledge of the gyrator transform, the logistic-tent chaotic map and 3D single-phase encoding algorithm, respectively. In Sect. 3, the processes of the proposed 3D-DPEA encryption and decryption are introduced in detail. In Sect. 4, numerical simulation results and security analysis are presented. Finally, conclusions are stated in Sect. 5.

2 Basic theory

2.1 Gyrator transform

The optical gyrator transform (GT), first proposed by Simon and validated by using a six-lens optical system in 2007 [33, 34], belongs to the class of linear canonical transform (LCT) that produces the twisted rotation in position-spatial frequency planes of phase space. The GT is widely used for optical and digital image processing [35]. The mathematical definition of GT for a two-dimensional function \(f\left(x,y\right)\in {\mathcal{L}}^{2}\left({\mathbb{R}}\right)\) can be expressed as

$$G\left(u,v\right)={\mathcal{G}}^{\alpha }\left[f\left(x,y\right)\right]\left(u,v\right)=\iint f\left(x,y\right){\mathcal{K}}_{\alpha }\left(x,y;u,v\right)dxdy$$
(1)

and the GT kernel is given by

$${\mathcal{K}}_{\alpha }\left(x,y;u,v\right)=\frac{1}{\left|\text{sin}\;\alpha \right|}\text{exp}\left[i2\pi \frac{\left(xy+uv\right)\text{cos}\;\alpha -xv-yu}{\text{sin}\;\alpha }\right]$$
(2)

where f(x,y) and G(u,v) represent the input and output functions of GT, respectively, and the parameter α is the rotation angle of GT. When \(\alpha =\pi /2\), the GT corresponds to a FT with rotation of the coordinates at \(\pi /2\). When \(\alpha =3\pi /2\), it corresponds to the inverse FT with rotation of the coordinates at \(\pi /2\). The GT obeys index additivity and periodicity, which means that GT satisfies the properties expressed in Eq. (3) and (4).

$${\mathcal{G}}^{\alpha }\left\{{\mathcal{G}}^{\beta }\left[f\left(x,y\right)\right]\right\}={\mathcal{G}}^{\alpha +\beta }\left[f\left(x,y\right)\right]$$
(3)
$${\mathcal{G}}^{\alpha }\left[f\left(x,y\right)\right]={\mathcal{G}}^{\alpha +2\pi }\left[f\left(x,y\right)\right]$$
(4)

The inverse transform of \({\mathcal{G}}^{\alpha }\) is expressed as \({\mathcal{G}}^{-\alpha }\) or \({\mathcal{G}}^{2\pi -\alpha }\).

The optical gyrator transform is utilized to complete the proposed image encryption scheme, in which the rotation angle \(\alpha\) serves as the secret key.

2.2 The logistic-tent chaotic map

The chaotic maps are frequently used in encryption techniques for secure transmission due to their features such as nonlinear complex dynamical structure, pseudorandom behavior, and high sensitivity of initial value and parameters [36]. As we all know, the most classic one-dimension (1D) chaotic maps are the logistic chaotic map and the tent chaotic map. However, the 1D chaotic maps have some drawbacks [37] as follows:

  1. a)

    The chaotic behaviors are limited and discontinuous;

  2. b)

    The vulnerability of low-computation-cost analysis using iteration and correlation functions;

  3. c)

    The output sequence is not relatively uniformly distributed.

The logistic-tent(LT) chaotic map, which combines two existing 1D chaotic maps (the logistic chaotic map and the tent chaotic map), was proposed by Khan et al. [38] to solve the above shortcomings and improve the performance of a 1D chaotic system. The Eq. (5) is the defining equation of the LT chaotic map.

$${x}_{n+1}=\left\{\begin{array}{c}\left[r{x}_{n}\left(1-{x}_{n}\right)+\frac{\left(4-r\right)}{2}{x}_{n}\right]mod1,{x}_{n}<0.5\\ \left[r{x}_{n}\left(1-{x}_{n}\right)+\frac{\left(4-r\right)}{2}\left(1-{x}_{n}\right)\right]mod1,{x}_{n}\ge 0.5\end{array}\right.$$
(5)

where parameter \(r\in (\text{0,4}]\), and the mod operation ensures that the sequence generated by the LT chaotic map is within (0, 1).

Figure 1 displays the bifurcation diagram of the LT chaotic map. All space of the LT chaotic map’s bifurcation characteristics is fully occupied. Compared with the simple 1D chaotic map, the LT chaotic map has larger chaotic ranges and superior chaotic properties, and its sequence is similar to a uniform-distribution within (0, 1).

Fig. 1
figure 1

The bifurcation diagram of the LT chaotic map

Full size image

2.3 3D single-phase encoding algorithm

The 3D single-phase encoding algorithm (3D-SPEA) [29] is the prototype of our proposed 3D-DPEA scheme, which encrypts the plaintext into a sparse volumetric ciphertext. As shown in Fig. 2, the pixels of the sparse volumetric ciphertext are distributed into a volumetric field consisting of M planes under the constraints of randomly generated BAMs. Then, the volumetric ciphertext is multiplexed into a 2D ciphertext for storage and transmission. During the decryption process, the pixels of 2D ciphertext are distributed in 3D space under the constraints of corresponding BAMs to form the sparse volumetric ciphertext, and then display the sparse volumetric ciphertext in a cascaded arrangement by spatial light modulators (SLMs). Once a correct plane-wave beam crosses the sparse volumetric ciphertext sequentially, the decrypted image will be detected and received by a CCD camera.

Fig. 2
figure 2

Optical schematic of the 3D-SPEA

Full size image

By using complementary and orthogonal BAMs as constraints, the 3D-SPEA encrypts the plaintext image into sparse volumetric ciphertexts (SCs) distributed in 3D space. This effectively expands the key space and confuses the relationship between the plaintext and the ciphertext, significantly enhancing resistance to CPA attack and greatly improving the security of the cryptosystem.

However, 3D-SPEA still has several shortcomings that need to be solved. First, the convergence speed of the encryption iteration process in 3D-SPEA is relatively slow. This is due to the algorithm completely encrypting the original image into a sparse volumetric ciphertext distributed in 3D space. Second, according to the analysis of traditional phase retrieval algorithms [17,18,19,20,21], the key sensitivity of 3D-SPEA remains poor. If an unauthorized attacker acquires the BAMs during the key transmission process, they could determine the pixel distribution of the sparse volumetric ciphertext in 3D space through brute-force attacks such as exhaustive search, thereby compromising the security of the cryptographic system. Hence, it is necessary to enhance the security of the cryptographic system. Finally, during decryption, the whole randomly generated BAMs based on 3D-SPEA must be stored and transmitted as keys, which adds an additional burden to the cryptographic system.

Therefore, this paper focuses on resolving the aforementioned issues to improve 3D-SPEA. Firstly, we replace the randomly generated BAMs with chaos-generated BAMs produced using LT chaotic sequences closely related to the keys. This approach improves the sensitivity of secret keys and makes the storage and transmission of BAMs no longer a burden. Secondly, expanding the key space and adopting other transform domains to improve 3D-SPEA, we aim to enhance the performance and security of phase retrieval algorithm. Specifically, by encoding the original image into two or more sparse volumetric ciphertexts, the key space can be further expanded. Additionally, due to the joint adjustment of these sparse volumetric ciphertexts during the iteration process, the convergence speed could be significantly improved, and the decryption image will be recovered with higher quality. However, the iterative calculations for encryption and the optical implementation for decryption will become more complex. Therefore, it is crucial to evaluate the trade-off between the complexity and performance of the cryptosystem.

3 The proposed 3D-DPEA optical image encryption scheme

To overcome these weaknesses of the 3D-SPEA, we propose the modified 3D double-phase encoding algorithm (3D-DPEA) based on the gyrator transform (GT) domain, cascaded sparse volumetric ciphertexts through phase encoding under the constraints of chaos-generated binary amplitude masks (BAMs). The detailed architecture of the proposed 3D-DPEA scheme is presented as follows:

3.1 Chaos-generated binary amplitude masks

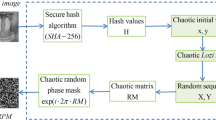
Inspired by the security analysis of these methods [31, 32] using chaos theory for image encryption, we propose a method to generate binary amplitude masks (BAMs) through the logistic-tent (LT) chaotic map and then apply it to the encryption scheme in order to improve the sensitivity of secret keys and facilitate the storage and transmission of BAMs no longer a burden on the cryptosystem. The detailed construction process of chaos-generated BAMs is as follows:

  • (1) We will use the LT chaotic map to generate BAMs, and the initial value x0, function parameter r, and truncated position T of the LT chaotic map will serve as the keys. Additionally, we will provide a specific function in encryption process to illustrate the relationship between the aforementioned keys of the LT chaotic map and the keys of the 3D-DPEA.

  • (2) Suppose the original image is with the size of W × H, we will generate the LT chaotic sequence \(\left[{x}_{1},{x}_{2},\cdots {x}_{T+W*H}\right]\) based on the given function and the keys of the 3D-DPEA discarding the previous T values in the sequence to increase randomness and disturbance. Then reshape the sequence \(\left[{x}_{T+1,}{x}_{T+2,}\cdots {x}_{T+W*H}\right]\) that discarded previous T values into a 2D matrix \(X\left(x,y\right)\) by regular permutation, as shown in Eq. (6).

    $$X\left(x,y\right)=\left[\begin{array}{cccc}{x}_{T+1}& {x}_{T+2}& \cdots & {x}_{T+H}\\ {x}_{T+H+1}& {x}_{T+H+2}& \cdots & {x}_{T+2H}\\ \vdots & \vdots & \ddots & \vdots \\ {x}_{T+\left(W-1\right)*H+1}& {x}_{T+\left(W-1\right)*H+2}& \cdots & {x}_{T+W*H}\end{array}\right]$$
    (6)

  • (3) the chaos-generated BAMs according to Eq. (7) will be generated based on the pixel values of the aforementioned 2D matrix \(X\left(x,y\right)\) and the number of planes of sparse volumetric ciphertext N in the 3D-DPEA

    $${B}_{n}\left({x}_{n},{y}_{n}\right)=\left\{\begin{array}{c}1,X\left(x,y\right)\in \left(\frac{n-1}{N},\frac{n}{N}\right)\\ 0,X\left(x,y\right)\notin \left(\frac{n-1}{N},\frac{n}{N}\right)\end{array}\right.\begin{array}{cc}& \end{array}n=\text{1,2},\cdots \cdots ,N$$
    (7)

Since the output sequence generated by the LT chaotic map is approximately uniformly distributed within (0, 1), these chaos-generated BAMs are complementary and orthogonal, their superposition forms a white matrix. Therefore, the chaos-generated BAMs can serve as a constraint to iteratively encode the plaintext image into sparse volumetric ciphertext in 3D space.

Thus, the keys of the 3D-DPEA can directly influence the pixel distribution of the BAMs, further affecting the distribution of the sparse volumetric ciphertext generated by iterative encoding in 3D space, significantly enhancing the sensitivity of the keys. Additionally, it means that we can directly reconstruct BAMs using the keys of the 3D-DPEA without storing and transmitting the whole BAMs, which significantly reduces the workload of the cryptosystem.

3.2 The 3D double-phase encoding algorithm for optical encryption and decryption

By introducing the gyrator transform, the cascaded structure and chaos-generated BAMs, the modified 3D-DPEA is proposed. Figure 3 shows the electro-optical setup of the proposed 3D-DPEA. Under the constraints of chaos-generated BAMs, the 3D-DPEA generates cascaded two sparse volumetric ciphertexts by encoding the plaintext, and the two sparse volumetric ciphertexts consist of M and N planes, respectively. Then, the two sparse volumetric ciphertexts are multiplexed into the corresponding 2D ciphertexts for storage and transmission. When the correct coherent beams sequentially pass through the cascaded sparse volumetric ciphertexts displayed by the SLMs, the decrypted image will be detected and received by the CCD camera at the output plane.

Fig. 3
figure 3

Electro-optical setup of the proposed 3D-DPEA

Full size image

The 3D-DPEA extends the key space by encoding the original image into two cascaded sparse volumetric ciphertexts and increases key sensitivity by generating BAMs using chaotic sequences closely related with the rotation angle keys to further improve the security of the cryptosystem while maintaining resistance to CPA attacks. Additionally, it eliminates the burden of storing and transmitting the whole BAMs as keys by utilizing chaos theory. Moreover, due to the synergistic adjustment of the two sparse volumetric ciphertexts during the iterative process, the convergence speed of the iteration will be significantly increased, and the quality of the recovered decrypted image will also be improved.

3.2.1 Encryption process

The encryption flowchart of the proposed scheme is shown in Fig. 4. Assuming the encryption of original image P, the encryption process is as follows:

  • (1) Generate BAMs using the LT chaotic sequence closely related to the keys of 3D-DPEA. Since the 3D-DPEA iteratively encodes the original image into two cascaded sparse volumetric ciphertexts, it is necessary to generate two sets of orthogonal and complementary BAMs using the LT chaotic map. To achieve this, we first define the mapping relationship between the keys of the LT chaotic map \(\left\{{x}_{0},{r}_{1},{T}_{1}\right\},\left\{{y}_{0},{r}_{2},{T}_{2}\right\}\) and the keys of 3D-DPEA \({\alpha }_{n}\left(n=\text{1,2},\dots ,M+N\right)\). For example, it can be defined as Eq. (8).

    $$\left\{\begin{array}{c}\begin{array}{c}{t}_{1}=\frac{\sum\limits_{n=1}^{M}{\alpha }_{n}}{3}\\ {x}_{0}=\frac{{t}_{1}}{{t}_{1}+0.05}\end{array}\\ \begin{array}{c}{r}_{1}=\frac{{t}_{1}}{2{t}_{1}+0.05}\\ {T}_{1}=1000{t}_{1}\end{array}\end{array}\right.\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}\left\{\begin{array}{c}\begin{array}{c}{t}_{2}=\frac{\sum\limits_{n=M+1}^{M+N}{\alpha }_{n}}{4}\\ {y}_{0}=\frac{{t}_{2}}{{t}_{2}+0.06}\end{array}\\ \begin{array}{c}{r}_{2}=\frac{{t}_{2}}{2{t}_{2}+0.06}\\ {T}_{2}=1000{t}_{2}\end{array}\end{array}\right.$$
    (8)

    where t is an intermediate parameter. Then, based on the given function and the rotation angle of 3D-DPEA, we can calculate the parameters of the LT chaotic map \(\left\{{x}_{0},{r}_{1},{T}_{1}\right\},\left\{{y}_{0},{r}_{2},{T}_{2}\right\}\) and use them as keys to generate two sets of independent chaotic sequences. Subsequently, following the procedure outlined in Sect. 3.1, these two sets of independent sequences will be used to generate two sets of BAMs \({B}_{n}\left(n=\text{1,2},\cdots ,M+N\right)\), serving as constraints in the 3D-DPEA encryption and decryption processes.

  • (2) C10 and C20 are respectively assigned as the initial values of ciphertexts C1 and C2 and the values are randomly distributed in \([\text{0,2}\pi ]\). Additionally, C1i−1 and C2i−1 are the values retrieved in the ith iteration. Then, using the two sets of BAMs generated in step (1), we extract the corresponding sparse volumetric ciphertexts \({SC}_{n}(n=1,2,\dots ,M+N)\) from the ciphertexts C1 and C2, which can be expressed as Eq. (9).

    $$S{C}_{n}{}^{i}=\left\{\begin{array}{c}{C}_{1}{}^{i-1}\times {B}_{n}+\left(1-{B}_{n}\right),n=\text{1,2},\cdots ,M\\ {C}_{2}{}^{i-1}\times {B}_{n}+\left(1-{B}_{n}\right),n=M+1,M+2,\cdots ,M+N\end{array}\right.$$
    (9)

    where \({SC}_{n}^{i-1}\) represents the sparse ciphertexts retrieved in the ith iteration, consisting of M + N planes. Ciphertext C1 distributes its pixels in a sparse volumetric ciphertext in a 3D space composed of M planes, while the sparse volumetric ciphertext corresponding to ciphertext C2 consists of N planes.

  • (3) After a coherent beam propagates from the first plane of sparse volumetric ciphertexts. The first sparse ciphertext \(S{C}_{1}\left({x}_{1},{y}_{1}\right)\) is transformed by the GT with the rotation angle \({\alpha }_{1}\). The complex function \({f}_{1}\left({x}_{1},{y}_{1}\right)\) just after the first plane can be described by

    $${f}_{1}\left({x}_{1},{y}_{1}\right)={\mathcal{G}}^{{\alpha }_{1}}\left[S{C}_{1}{}^{i-1}\left({x}_{1},{y}_{1}\right)\right]$$
    (10)

    where \({\mathcal{G}}^{\alpha }\left[\cdot \right]\) represents GT, with the superscript α denoting the rotation angle key of the GT. with rotation angle \(\alpha\). And the superscript \(\left(i-1\right)\) of \(S{C}_{1}\left({x}_{1},{y}_{1}\right)\) denotes that it is the value retrieved during the (i-1)th iteration process.

    As a coherent beam continues to propagate and cross the other planes of sparse volumetric ciphertexts sequentially. \({f}_{n}\left({x}_{n},{y}_{n}\right)\) is digitally multiplied with the function \(S{C}_{n}\left({x}_{n},{y}_{n}\right)\), which result is transformed by the GT with the rotation angle \({\alpha }_{n}\). The complex function \({f}_{n}\left({x}_{n},{y}_{n}\right)\) after the nth plane can be given by

    $${f}_{n}\left({x}_{n},{y}_{n}\right)={\mathcal{G}}^{{\alpha }_{n}}\left[{f}_{n-1}\left({x}_{n-1},{y}_{n-1}\right)S{C}_{n}{}^{i-1}\left({x}_{n},{y}_{n}\right)\right]$$
    (11)

    where \(n=2,\dots ,M,M+1,M+2,\dots ,M+N\), and \(\left({x}_{n},{y}_{n}\right)\) denotes the coordinate of the nth plane. Therefore, the final complex function \({f}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)\) at the output plane can be depicted as

    $${f}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)={\mathcal{G}}^{{\alpha }_{M+N}}\left[{f}_{M+N}{}_{-1}\left({x}_{M+N-1},{y}_{M+N-1}\right)S{C}_{M+N}{}^{i-1}\left({x}_{M+N},{y}_{M+N}\right)\right]$$
    (12)

  • (4) The original image \(P\left(u,v\right)\) is employed as the amplitude constraint to update \({f}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)\) as

    $$f^{\prime}\left(u,v\right)=P\left(u,v\right)\frac{{f}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)}{\left|{f}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)\right|}$$
    (13)

    where \(\left|\cdot \right|\) represents the modulus computation of the argument and \(\left(u,v\right)\) denotes the coordinate of the output plane.

  • (5) Then, propagate \(f^{\prime}\left(u,v\right)\) back to the \(M+N\) planes of sparse volumetric ciphertexts sequentially. The modified function \(f^{\prime}\left(u,v\right)\) at the output plane is transformed by the inverse GT with the rotation angle \({\alpha }_{M+N}\), which can be mathematically expressed as

    $${g}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)={\mathcal{G}}^{-{\alpha }_{M+N}}\left[f^{\prime}\left(u,v\right)\right]$$
    (14)

    The (M + N)th plane of the ciphertext \(S{C}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)\) can be updated as

    $$S{C}_{M+N}{}^{i}\left({x}_{M+N},{y}_{M+N}\right)=\text{exp}\left\{i\times \text{arg}\left\{\frac{{g}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)}{{f}_{M+N-1}\left({x}_{M+N-1},{y}_{M+N-1}\right)}\right\}\right\}\times {B}_{M+N}+\left(1-{B}_{M+N}\right)$$
    (15)

    where the arg function is used to extract the phase of the input data and the superscript i of \(S{C}_{M+N}\left({x}_{M+N},{y}_{M+N}\right)\) denotes values retrieved in ith iteration.

    Then the beam goes on back propagating and crossing the planes sequentially. The complex function \({g}_{n}\left({x}_{n},{y}_{n}\right)\) is transformed by the inverse GT with the rotation angle \({\alpha }_{n}\), which can be depicted as

    $${g}_{n}\left({x}_{n},{y}_{n}\right)={\mathcal{G}}^{-{\alpha }_{n}}\left[\frac{{g}_{n+1}\left({x}_{n+1},{y}_{n+1}\right)}{S{C}_{n+1}\left({x}_{n+1},{y}_{n+1}\right)}\right]$$
    (16)

    The nth plane of the ciphertext \(S{C}_{\text{n}}\left({x}_{n},{y}_{n}\right)\) can be updated as

    $$S{C}_{n}{}^{i}\left({x}_{n},{y}_{n}\right)=\text{exp}\left\{i\times \text{arg}\left\{\frac{{g}_{n}\left({x}_{n},{y}_{n}\right)}{{f}_{n-1}\left({x}_{n-1},{y}_{n-1}\right)}\right\}\right\}\times {B}_{n}+\left(1-{B}_{n}\right)$$
    (17)

    The first plane of the ciphertext \(S{C}_{1}\left({x}_{1},{y}_{1}\right)\) can be updated as

    $$S{C}_{1}{}^{i}\left({x}_{1},{y}_{1}\right)=\text{exp}\left\{i\times \text{arg}\left\{{g}_{1}\left({x}_{1},{y}_{1}\right)\right\}\right\}\times {B}_{1}+\left(1-{B}_{1}\right)$$
    (18)

  • (6) Finally, the updated ciphertexts \({C}_{1}\) and \({C}_{2}\) are respectively synthesized by two sparse volumetric ciphertexts under the constraints of corresponding BAMs, which can be represented as Eq. (19) and (20).

    $${C}_{1}{}^{i}=\sum_{n=1}^{M}\left(S{C}_{n}{}^{i}\times {B}_{n}\right)$$
    (19)
    $${C}_{2}{}^{i}=\sum_{n=M+1}^{M+N}\left(S{C}_{n}{}^{i}\times {B}_{n}\right)$$
    (20)
Fig. 4
figure 4

The encryption flowchart of of the proposed scheme

Full size image

The procedure of Eqs. (9)-(20) are the ith iteration of the encryption process. The iteration should execute until the CC value between the original image and the decrypted image reaches the preset threshold or the number of iterations reaches the preset upper limit K. As a result, the final ciphertexts \({C}_{1}\) and \({C}_{2}\) are retrieved after the iteration process is completed, while the rotation angle \({\alpha }_{n}\left(n=\text{1,2},\dots ,M+N\right)\) are regarded as the security keys.

3.2.2 Decryption process

Compared with the encryption process, the decryption process does not require any complex iterative procedure. We first generate the BAMs \({B}_{n}\left(n=\text{1,2},\cdots ,M+N\right)\) based on the rotation angle key of the 3D-DPEA and the preset function according to Eq. (8), and then we extract the corresponding sparse volumetric ciphertexts \(S{C}_{n}\left(n=\text{1,2},\dots ,M+N\right)\) from the final ciphertexts \({C}_{1}\) and \({C}_{2}\) under the constraints of BAMs according to Eq. (21).

$$S{C}_{n}=\left\{\begin{array}{c}{C}_{1}\times {B}_{n}+\left(1-{B}_{n}\right),n=\text{1,2},\cdots ,M\\ {C}_{2}\times {B}_{n}+\left(1-{B}_{n}\right),n=M+1,M+2,\cdots ,M+N\end{array}\right.$$
(21)

Then, the sparse volumetric ciphertexts \(S{C}_{n}\left(n=\text{1,2},\dots ,M+N\right)\) consisting of M + N planes are displayed in a cascaded arrangement by SLMs, which are fixed at the corresponding preset places. Once a coherent beam crosses the sparse volumetric ciphertexts sequentially, the corresponding decrypted image \({P}^{\prime}\left(u,v\right)\) will be detected and received at the output plane by a CCD camera, which can be depicted mathematically as

$${P}^{\prime}\left(u,v\right)=\left|{\mathcal{G}}^{{\alpha }_{M+N}}\left\{\cdots \left\{{\mathcal{G}}^{{\alpha }_{2}}\left[{\mathcal{G}}^{{\alpha }_{1}}\left(S{C}_{1}\right)\times S{C}_{2}\right]\right\}\right\}\cdots \times S{C}_{M+N}\right|$$
(22)

Thus, the decryption process of 3D-DPEA can be realized either through optical devices or digital method. By contrast, the encryption process must be conducted only digitally.

The correlation coefficient (CC) between the decrypted image \({P}^{\prime}\) and the original image P is utilized to evaluate the security of the proposed scheme objectively, which can be calculated by

$$CC=\frac{\sum \sum \left[P-E\left(P\right)\right]\left[{P}^{\prime}-E\left({P}^{\prime}\right)\right]}{\sqrt{\left\{\sum \sum {\left[P-E\left(P\right)\right]}^{2}\right\}\left\{\sum \sum {\left[{P}^{\prime}-E\left({P}^{\prime}\right)\right]}^{2}\right\}}}$$
(23)

where \(E\left(\cdot \right)\) is an operator that calculates the mean value of the input. The range of CC is from 0 to 1, reflecting the similarity between the original and decrypted images. The higher the CC value, the higher the quality of decryption can be achieved. The CC value of 1 indicates that the decrypted image exactly matches the original image.

4 Numerical simulations and security analysis

4.1 Simulation results of the proposed scheme

To verify the feasibility and security of the proposed 3D-DPEA scheme, numerical simulations are performed on a computer with Intel(R) Core(TM) i7-8550U CPU @1.80 GHz and with the MATLAB 2014. The grayscale image with a resolution of 512 × 512 pixels (Lena), as shown in Fig. 6(a), was selected from the CVG-UGR database [39] as the original image for the experiments. The first ciphertext \({C}_{1}\) distributes its pixels in a volume field consisting of 3 planes, and the volume field of the second ciphertext \({C}_{2}\) consists of 4 planes. In other words, the values of M and N are selected as \(M=3,N=4\). The rotation angles of the corresponding GT are set as follows:\({\alpha }_{1}=0.2,{\alpha }_{2}=0.4,{\alpha }_{3}=0.6,{\alpha }_{4}=0.2,{\alpha }_{5}=0.4,{\alpha }_{6}=0.6,{\alpha }_{7}=0.8\).

Figure 5 depicts the 7 chaos-generated BAMs using Eq. (8) with rotation angles of the GT, where (a)-(c) are used as amplitude constraints for the first ciphertext and (d)-(g) are used for the second. Note that two groups of BAMs are complementary and orthogonal, respectively. After applying the proposed scheme, a plaintext is encrypted into two sparse volumetric ciphertexts by using chaos-generated BAMs shown in Fig. 5(a)-(g) as constraints. Then, the two sparse volumetric ciphertexts are multiplexed into the corresponding 2D ciphertexts \({C}_{1}\) and \({C}_{2}\), as shown in Fig. 6(b) and (c), respectively. Figure 6(d) depicts the decrypted image \({P}^{1}\) with all correct keys, where the CC value between the original image and the decrypted image is 1. It can be seen that the proposed scheme is feasible and effective.

Fig. 5
figure 5

(a)-(c) 3 BAMs used as amplitude constraints for the first ciphertext; (d)-(g) 4 BAMs used as amplitude constraints of the second ciphertext

Full size image
Fig. 6
figure 6

(a) Original image; (b) first ciphertext image; (c) second ciphertext image; (d) decrypted image

Full size image

To evaluate the statistical properties of the proposed scheme, the image histograms of the original image and the ciphertext images are analyzed as shown in Fig. 7. As can be observed, the regularities of the plaintext image are not preserved and the histograms of two ciphertext images are fairly uniformly distributed. As a result, potential attackers will be unable to exploit the statistical properties to glean any useful information.

Fig. 7
figure 7

Histogram analysis of (a) original image; (b) first ciphertext image; (c) second ciphertext image

Full size image

Next, the decryption results using different incorrect BAMs are also present to verify the significance of BAMs, as shown in Fig. 8. The first ciphertext and second ciphertext are displayed directly by SLMs instead of the corresponding sparse volumetric ciphertext extracted by BAMs, respectively. The decrypted images are recorded when a coherent beam directly crosses the multiplexed ciphertext, as shown in Fig. 8(a) and (b). Obviously, the decrypted results without BAMs are incorrect, proving the necessity of BAMs for decryption. Additionally, the accuracy of BAMs is crucial for decryption. If BAMs are randomly generated rather than on the basis of the correct key and pre-designed functional relationship, the decrypted images are shown in Fig. 8(c) and (d). This demonstrates that if the proposed scheme wants to obtain the correct decryption image, BAMs must be generated according to the correct key and the pre-designed function relationship. In other words, the generation of BAMs plays a critical role in the decryption of the proposed scheme.

Fig. 8
figure 8

Decrypted images by using (a) the first ciphertext directly; (b) the second ciphertext directly; (c) randomly generated BAMs as amplitude constraints for the first ciphertext; (d) randomly generated BAMs as amplitude constraints for the second ciphertext

Full size image

4.2 Performance analysis compared with 3D-SPEA

4.2.1 Convergence speed analysis

In order to better demonstrate the effectiveness and security of the proposed scheme, we apply the 3D-SPEA [25] to the GT domain and compare it with the proposed 3D-DPEA scheme. In the 3D-SPEA, the pixels of the sparse volumetric ciphertext are distributed into a volumetric field consisting of M planes under the constraints of randomly generated BAMs, and the rotation angles are set as follows:\({\beta }_{1}=0.2,{\beta }_{2}=0.4,{\beta }_{3}=0.6,{\beta }_{4}=0.8\). The relationships between the CC value and the iteration number of the 3D-SPEA and the proposed scheme are calculated, as shown in Fig. 9. The proposed scheme demonstrates fast convergence and a high CC value can be achieved by only a few iterations, even up to 1. It can therefore be concluded that the proposed scheme facilitates higher convergence speed and better decrypted image quality.

Fig. 9
figure 9

The CC values versus the iteration number of the 3D-SPEA and the proposed scheme

Full size image

Furthermore, we also analyze the time cost of the encryption process by 3D-SPEA and the proposed scheme as shown in Table 1. If the termination condition for the iteration is set to a preset CC threshold of 0.999, it can be observed that the proposed scheme is much faster than the 3D-SPEA. This is because, although the computational complexity and time consumption of each iteration in the proposed scheme increases, the proposed scheme converges much faster and only requires about 10 iterations to reach the preset CC threshold, whereas the 3D-SPEA requires around 80 iterations. The significant reduction in the number of iterations greatly shortens the total encryption time for the proposed scheme, significantly improving real-time performance compared to the 3D-SPEA.

Table 1 The time consumed by the encryption process of the 3D-SPEA and the proposed 3D-DPEA scheme
Full size table

4.2.2 Key sensitivity analysis

To analyze the sensitivitiy of the rotation angle, the decryption processes are performed by varying one decrypted rotation angle and fixing the others. Figure 10(a) and (b) show the relationship between the CC and deviation from the correct rotation angle value in two encryption algorithms. We deviate the decrypted rotation angles in succession when all but one rotation angle is correct in the 3D-SPEA. The CC as the functions of rotation angle derivation values \(\Delta {\beta }_{n}\left(n=\text{1,2},\text{3,4}\right)\) in the range from \(-{10}^{-2}\) to \({10}^{-2}\) is shown in Fig. 10(a). Analogously, we successively shift the decrypted rotation angles from the corresponding rotation angle utilized in the proposed scheme when other rotation angles are correct. Figure 10(b) shows the CC as a function of the rotation angle deviation values \(\Delta {\alpha }_{n}\left(n=\text{1,2},\cdots ,7\right)\) ranging from \(-{10}^{-13}\) to \({10}^{-13}\). It can be seen that the CC value in the 3D-SPEA increases gradually when the rotation angle deviation is less than \({10}^{-2}\), and the CC value approximates 1 when the rotation angle deviation is less than \({10}^{-3}\). However, the CC value in the proposed scheme rapidly approximates to 0 when the deviation of the rotation angles is about \({10}^{-14}\), which indicates that the sensitivities of rotation angles in the proposed scheme are some orders of magnitude higher than those of the 3D-SPEA.

Fig. 10
figure 10

The CC for rotation angle deviation value of (a) the 3D-SPEA; (b) the proposed scheme

Full size image

Furthermore, several decrypted results are depicted in Fig. 11 and Fig. 12 to illustrate the secret key sensitivity and security enhancement of the proposed scheme more intuitively. The deviations of \({10}^{-3}\) are successively added to the correct rotation angles \({\beta }_{n}\left(n=\text{1,2},\text{3,4}\right)\) for decryption in the 3D-SPEA and the decrypted image are shown in Fig. 11(a)-(b), respectively. The decrypted images in the proposed scheme using incorrect key with the rotation angles deviation \(\Delta {\alpha }_{n}\left(n=\text{1,2},\cdots ,7\right)\) of \({10}^{-14}\) are shown in Fig. 12(a)-(g), respectively. Obviously, it demonstrates the proposed scheme can achieve far higher sensitivity to secret keys and security.

Fig. 11
figure 11

(a)-(d) Decrypted image of the 3D-SPEA using wrong key with the rotation angle deviation \(\Delta {\beta }_{n}\left(n=\text{1,2},\text{3,4}\right)\) of \({10}^{-3}\), respectively

Full size image
Fig. 12
figure 12

(a)-(g) Decrypted image of the proposed scheme using wrong key with the rotation angle deviation \(\Delta {\alpha }_{n}\left(n=\text{1,2},\cdots ,7\right)\) of \({10}^{-14}\), respectively

Full size image

4.3 Security analysis

4.3.1 Ciphertext leak attack analysis

The proposed scheme encrypts the plaintext into two sparse volumetric ciphertexts, and then two 2D ciphertexts are synthesized from the corresponding sparse volumetric ciphertexts for storage and transmission. Thus, it is necessary to assess the security of the proposed scheme when one of the two ciphertexts is obtained by intruders. Figure 13 shows the decrypted images generated using one correct ciphertext only, with all correct rotation angles. It is observed that no information about the original image can be extracted from the decrypted images when only one ciphertext is obtained by intruders. In other words, the decryption cannot be performed unless both two ciphertexts are authorized. We can assign two ciphertexts to two different authorities to achieve the maximum security.

Fig. 13
figure 13

Decrypted images using only one ciphertext of (a) the first ciphertext; (b) the second ciphertext

Full size image

4.3.2 Occlusion attack analysis

During transmission of the ciphertext, there is a great possibility that the ciphertext can be polluted by some noise and the information may be partially lost. Thus, the robustness against noise attack and occlusion attack of the proposed scheme is also tested.

We first destroy the pixels of the ciphertext to some extent to analyze the ability to resist occlusion attack. The corresponding decrypted images when two ciphertext images are occluded by 6.25%, 12.5%, and 25%, respectively, are shown in Fig. 14(d)-(f) and (j)-(l), respectively. The fact that the primary information of the original image can still be recognized with the increase of the occlusion region indicates that the proposed scheme can resist occlusion attack.

Fig. 14
figure 14

First ciphertext occluded by (a) 6.25%, (b) 12.5%, (c) 25%; (d)-(f) decrypted image from (a)-(c), respectively; (g)-(i) second ciphertext occluded by (g) 6.25%, (h) 12.5%, (i) 25%; (j)-(l) decrypted image from (g)-(i), respectively

Full size image

4.3.3 Noise attack analysis

To assess the robustness against the noise attack, the image with a certain intensity of Gaussian noise can be described as follow

$${C}_{i}{}^{\prime}={C}_{i}\left[1+bG\right],i=\text{1,2}$$
(24)

where \({C}_{i}\) is the original image, \({C}_{i}{}^{\prime}\) is the polluted image, and G is the Gaussian noise with zero-mean and one standard deviation, and the coefficient b is the noise strength. Figure 15(a)-(e) show the decrypted images by using contaminated fisrt ciphertext when the noise strength varies from 0.2 to 1.0, respectively. Figure 15(f)-(j) show the decrypted images by using the contaminated second ciphertext when the noise strength varies from 0.2 to 1.0, respectively. It can be seen that the majority of information in the original image is still easily recognized from the decrypted results with the naked eyes, even if the noise strength reaches the maximum value. Consequently, the results shown in Fig. 14 and Fig. 15 demonstrate that the proposed scheme exhibits sufficient robustness against noise attack and occlusion attack.

Fig. 15
figure 15

Decrypted images from contaminated first ciphertext by Gaussian noises with different noise strengths b: (a) 0.2, (b) 0.4, (c) 0.6, (d) 0.8, (e) 1.0, respectively; decrypted images from contaminated second ciphertext by Gaussian noises with different noise strengths b: (f) 0.2, (g) 0.4, (h) 0.6, (i) 0.8, (j) 1.0, respectively

Full size image

4.3.4 Differential attack analysis

The differential attack is a chosen plaintext attack, and the anti-differential attack performance depends on the sensitivity to plaintext. The number of pixels change rate (NPCR) and the unified average changing intensity (UACI) were used to assess their sensitivity. The calculation formulas are Eq. (25) and (26).

$$NPCR=\frac{{\sum }_{x,y}D\left(x,y\right)}{W\times H}\times 100\%$$
(25)
$$UACI=\frac{\sum \left[{c}_{1}\left(x,y\right)-{c}_{2}\left(x,y\right)\right]}{W\times H}\times 100\%$$
(26)

where W and H are the width and height of two ciphertext images (\({c}_{1}\) and \({c}_{2}\)) respectively, and \(D\left(x,y\right)\) is defined as

$$D\left(x,y\right)=\left\{\begin{array}{c}1,{c}_{1}\left(x,y\right)\ne {c}_{2}\left(x,y\right)\\ 0,{c}_{1}\left(x,y\right)={c}_{2}\left(x,y\right)\end{array}\right.$$
(27)

The ideal values of NPCR and UACI are NPCR = 99.6094%, UACI = 33.4635%. When the calculation results of NPCR and UACI are closer to the ideal values, it indicates that the proposed scheme is more resistant to differential attack.

To evaluate the resistance of the proposed scheme to the differential attack, we calculate the NPCR and UACI of ciphertext images with a one-bit difference between the original images. Table 2 shows the mean NPCR and UACI of three test images. All results are close to the ideal values. Therefore, we can infer that the proposed scheme is sensitive to plaintext and can well resist CPA and KPA from the results.

Table 2 The mean NPCR and UACI of ciphertext images with one-bit difference between the plain images
Full size table

4.4 Limitations Analysis

The 3D-DPEA scheme confuses the relationship between plaintext and ciphertext, rendering CPA ineffective and significantly increasing the sensitivity of the key. This makes it unrealistic for unauthorized users to find the pixel distribution of the sparse volumetric ciphertext in 3D space through brute force attacks, and greatly enhance the security of the cryptosystem. However, performing decryption through an optical system is still a challenging task in practical applications. Because optical decryption systems require extremely precise alignment, any slight dislocation of mask can result in decryption failure or degraded image quality. Therefore, optical systems need a stable laboratory environment to ensure the precise alignment of optical components and the stable operation of the system, which significantly increases costs and complexity in practical applications.

5 Conclusions

In this paper, we present a novel 3D double-phase encoding algorithm (3D-DPEA) in the GT domain, in which a plaintext is encrypted into two sparse volumetric ciphertexts in 3D space, to achieve faster and higher-quality decryption. And then a modified optical image encryption scheme is proposed by utilizing chaos-generated BAMs in the 3D-DPEA. The proposed scheme not only substantially enhances security by enlarging the key space and improving the sensitivity of the secret keys, but also makes BAMs no longer a burden of key storage and transmission. Meanwhile, the proposed scheme maintains resistance to CPA and KPA. Numerical simulation results have demonstrated the good robustness of the proposed scheme to resist attack in different aspects, such as differential attack, occlusion attack, and noise attack. In summary, compared with the previous 3D phase retrieval algorithms, the 3D-DPEA can offer higher performance and security and the proposed scheme has good application prospects in the field of information security.

However, the proposed encryption scheme has certain limitations in practical applications, such as the requirement for precise alignment of the optical decryption system and a stable laboratory environment. Therefore, our future research will focus on designing structured phase masks and their application in phase retrieval algorithms to address the issue of axial alignment in optical implementations. This will help resolve technical challenges and promote the practical application of optical decryption systems.